Material Transport under a Wave Train in Interaction with Constant Wind: A Eulerian RANS Approach Combined with a Lagrangian Particle Dispersion Model
Abstract
:1. Introduction
2. Governing Equations and Problem Setup
2.1. Eulerian RANS Framework
2.2. Lagrangian Particle Dispersion Framework
2.3. Flow Configuration
2.3.1. Wave Formulation
2.3.2. Wind–Wave Interaction Simulation
2.3.3. Particle Tracking
3. Results
3.1. Numerical Simulation Validation
3.1.1. Non-Breaking Wave Simulation
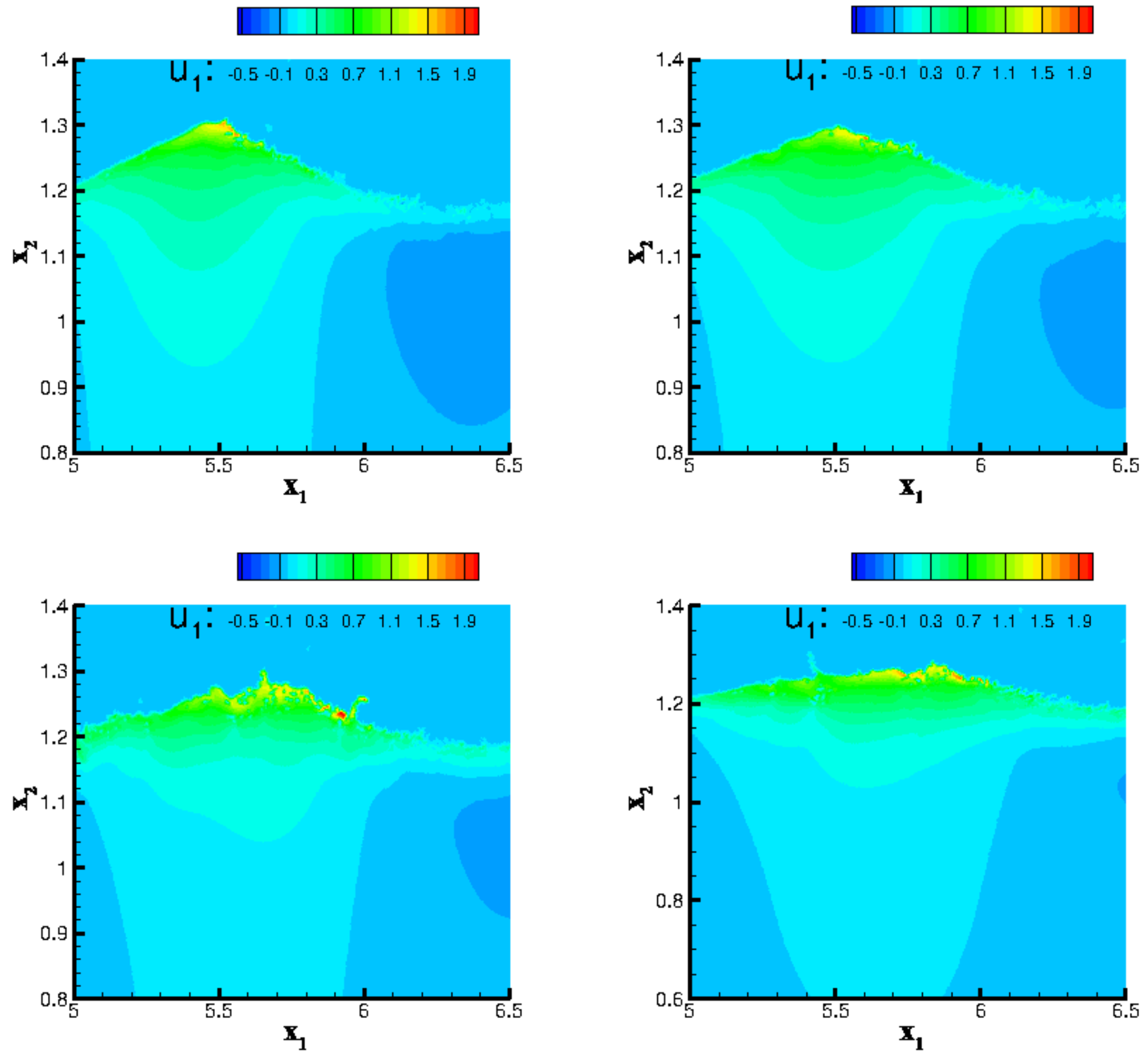
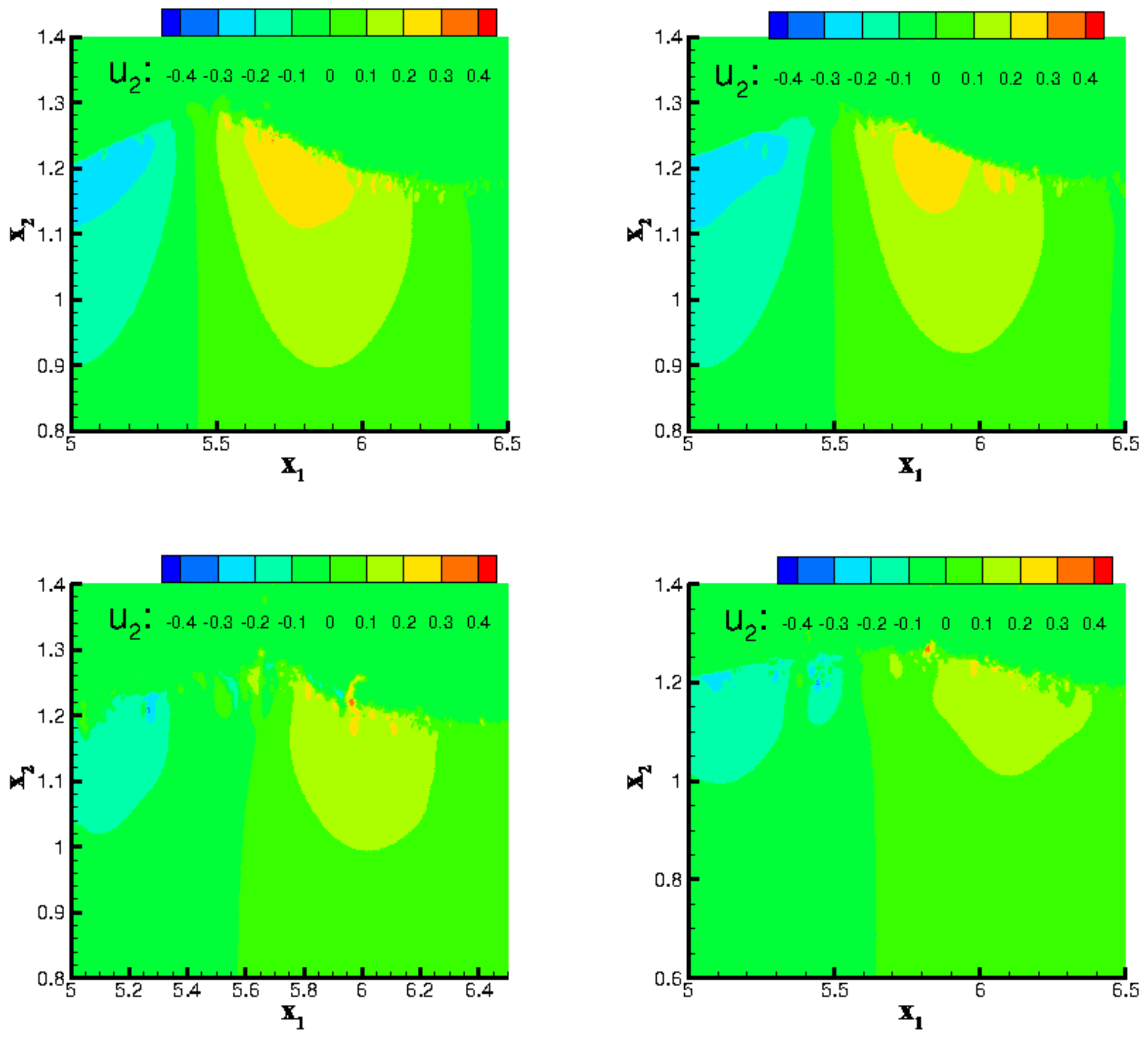
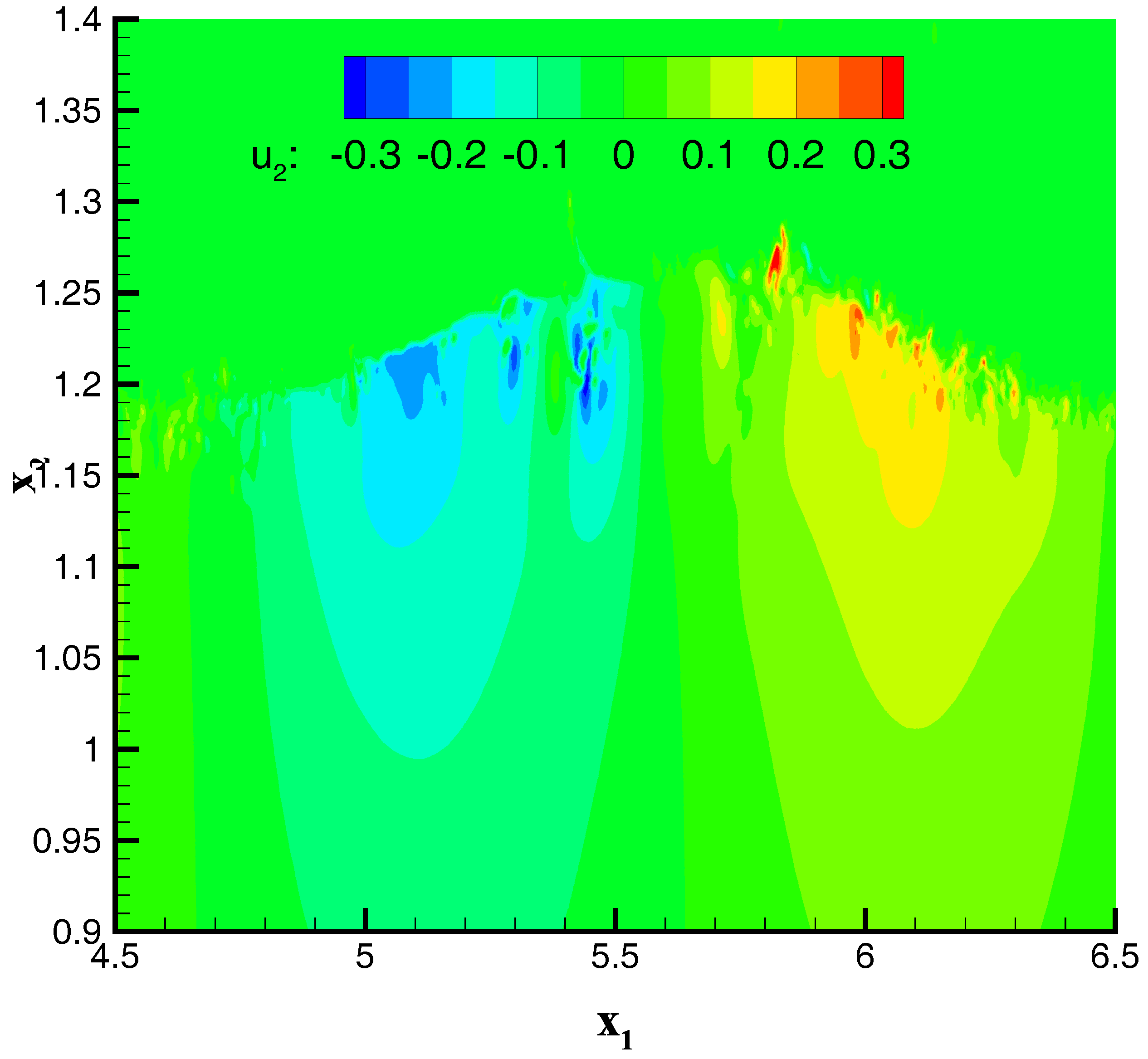
3.1.2. Wind–Wave Simulation
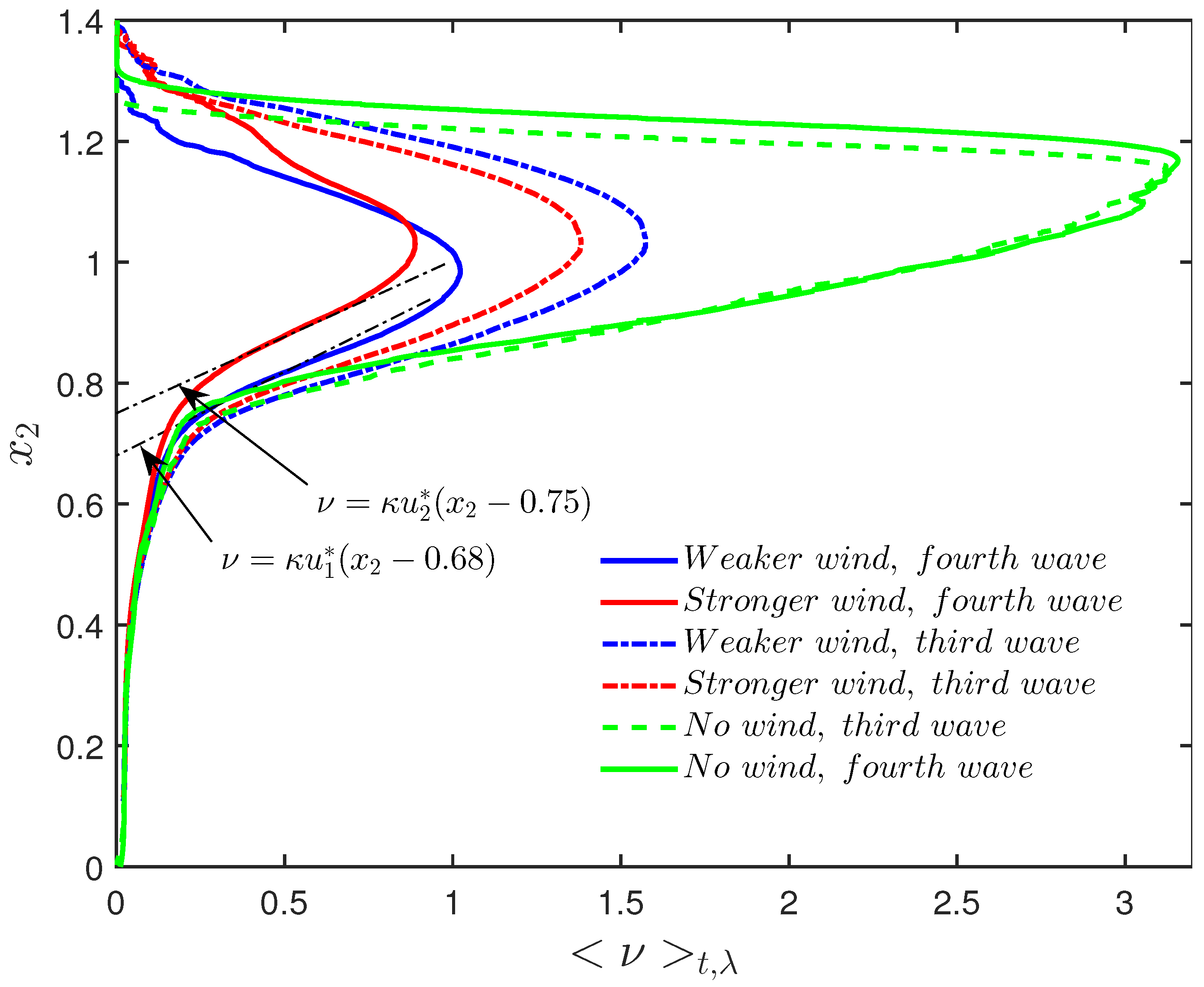
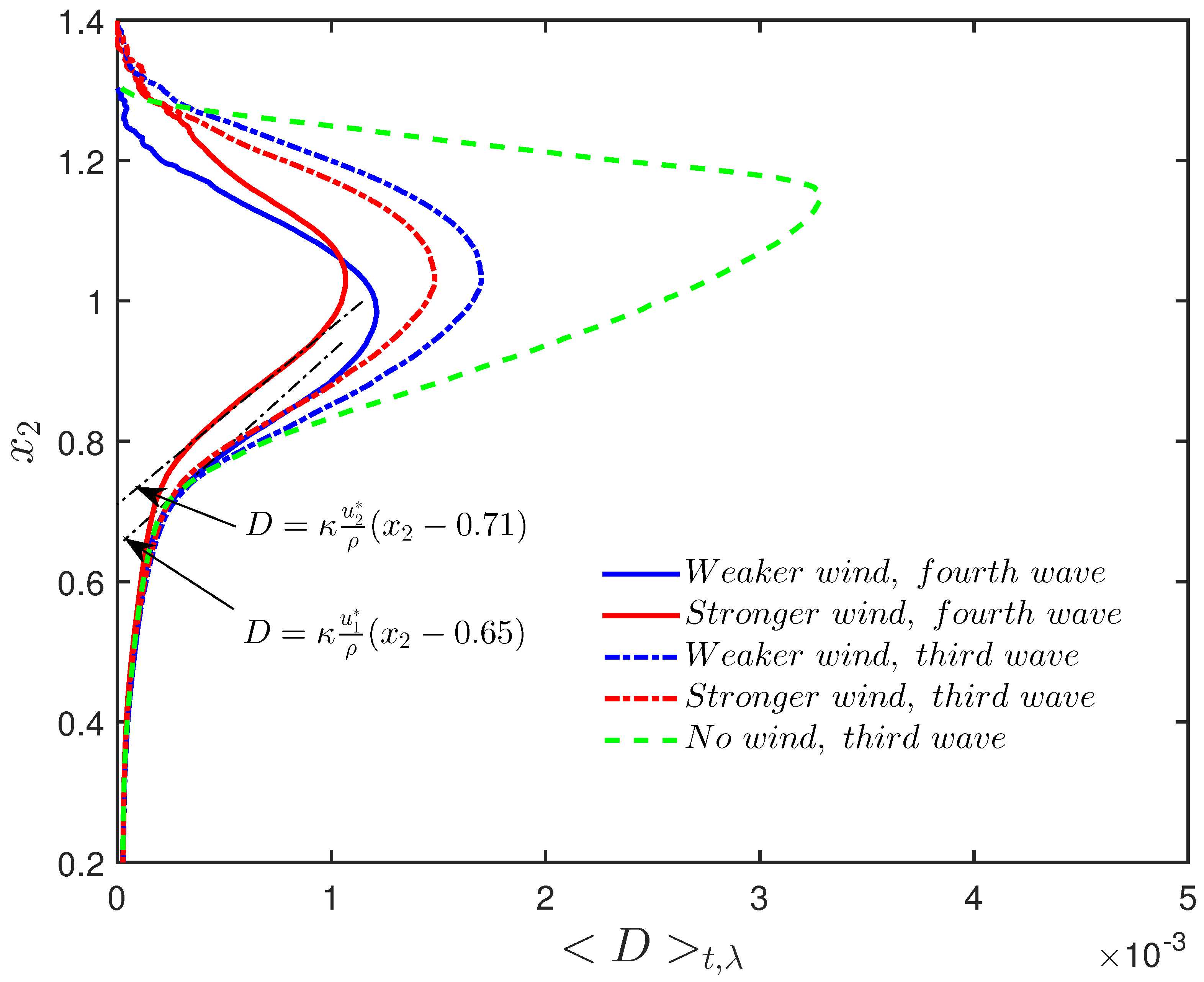
3.2. Drift Current Formation
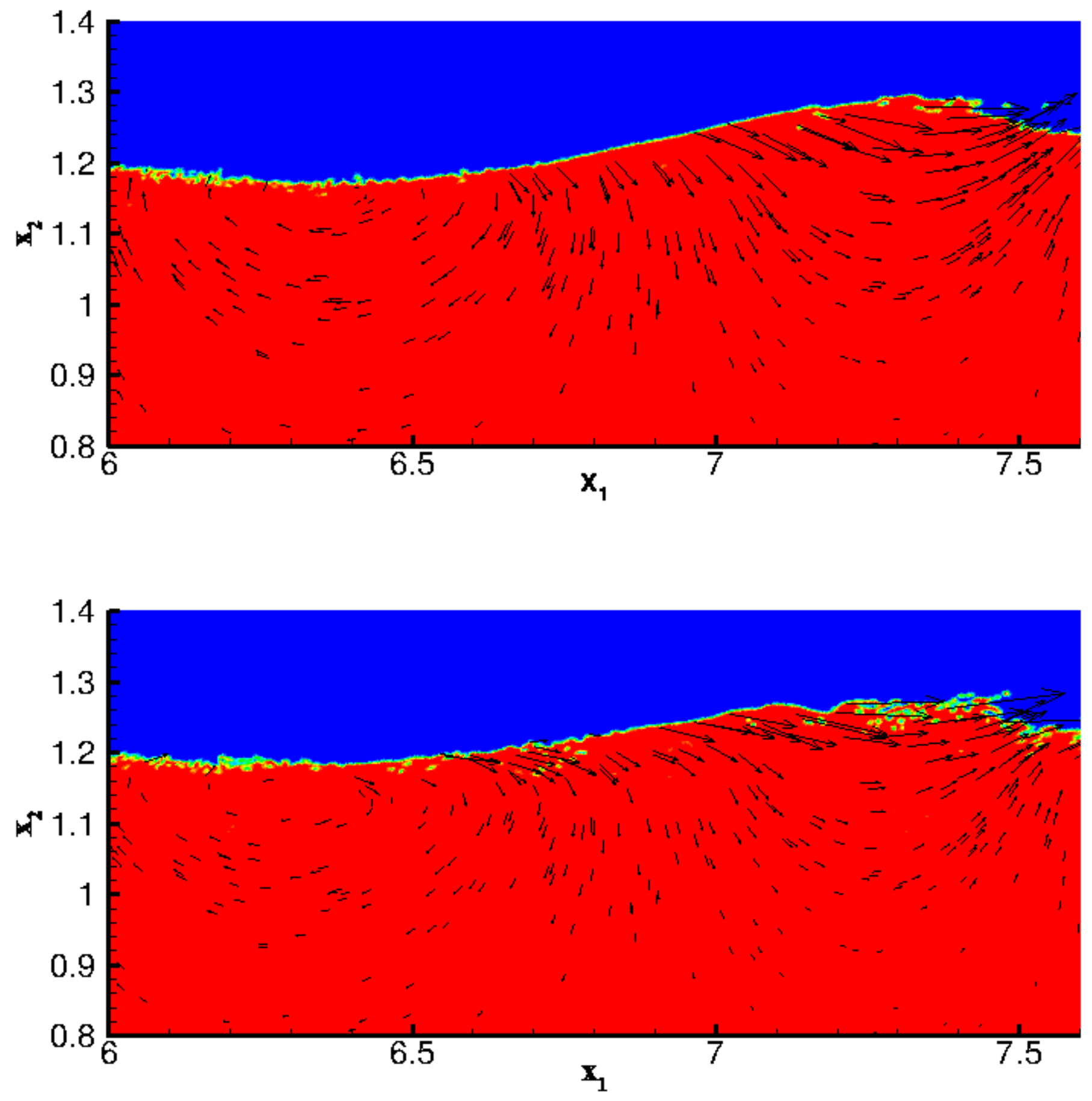
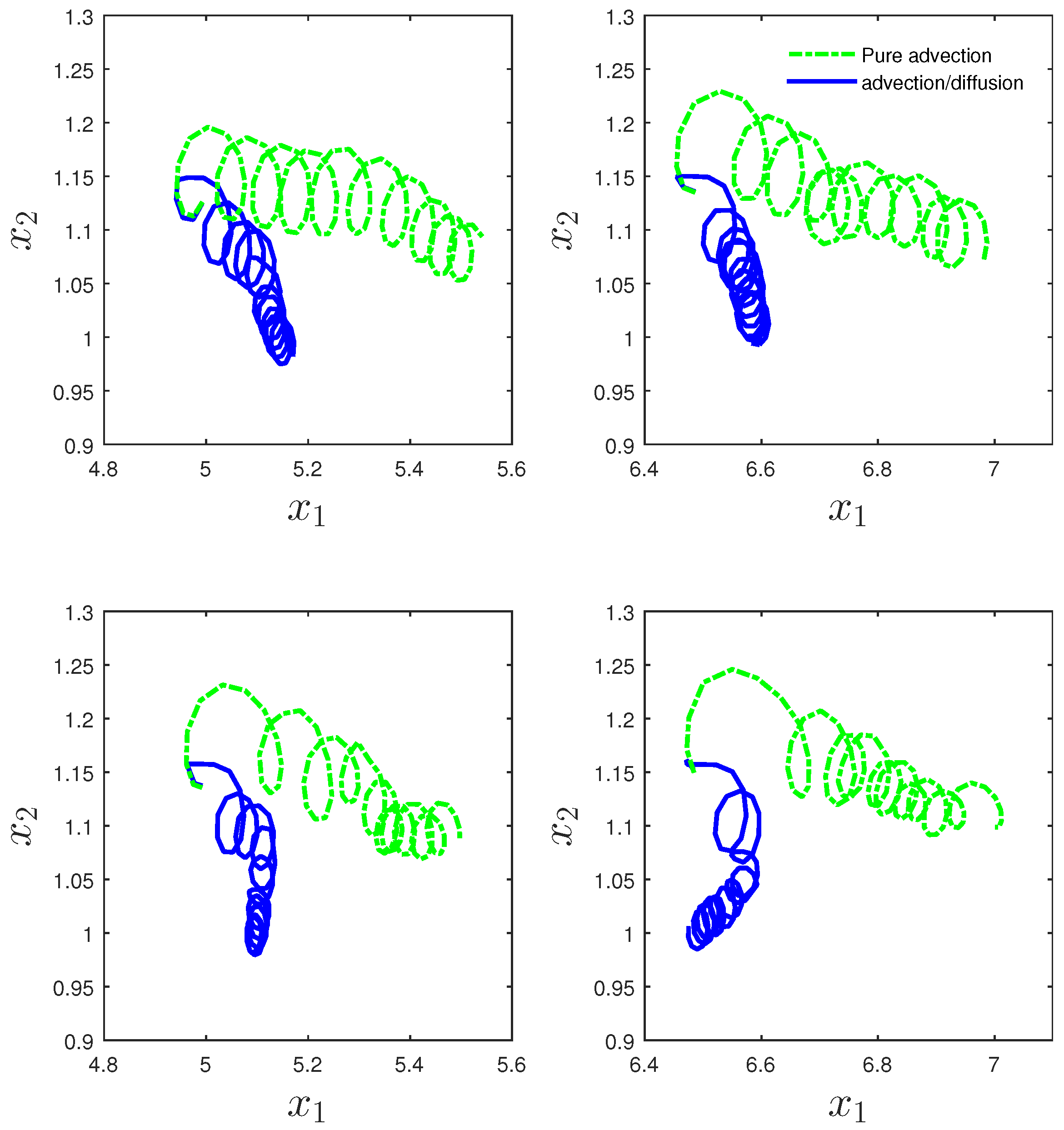
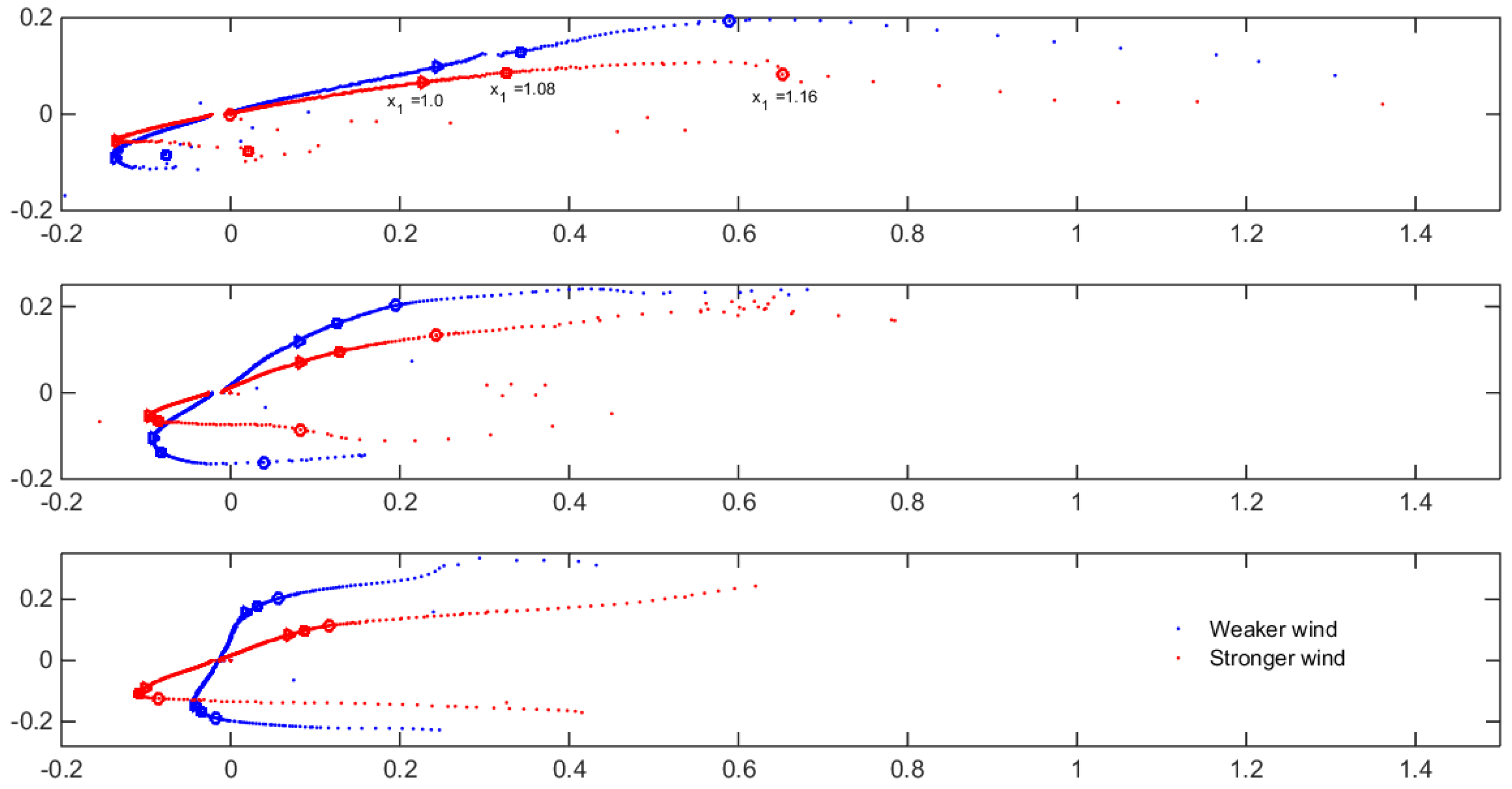
3.3. Particle Tracking and Vertical Mixing
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Melville, W.K.; Veron, F.; White, C.J. The velocity field under breaking waves: coherent structures and turbulence. J. Fluid Mech. 2002, 454, 203–233. [Google Scholar] [CrossRef]
- Peirson, W.L.; Banner, M.L. Aqueous surface layer flows induced by microscale breaking wind waves. J. Fluid Mech. 2003, 479, 1–38. [Google Scholar] [CrossRef]
- Pizzo, N.E.; Melville, W.K. Vortex generation by deep-water breaking waves. J. Fluid Mech. 2013, 734, 198–218. [Google Scholar] [CrossRef] [Green Version]
- Grare, L.; Peirson, W.L.; Branger, H.; Walker, J.W.; Giovanangeli, J.P.; Makin, V. Growth and dissipation of wind-forced, deep-water waves. J. Fluid Mech. 2013, 722, 5–50. [Google Scholar] [CrossRef] [Green Version]
- Sajjadi, S.G.; Thomas, N.H.; Hunt, J.C.R. Wind-over-Wave Couplings: Perspectives and Prospects; Institute of Mathematics and Its Applications: Southend-on-Sea, UK, 1999. [Google Scholar]
- Ekman, V.W. On the influence of the earth’s rotation on ocean currents. Arkiv för Matematik Astronomi Och Fysik 1950, 2, 1–53. [Google Scholar]
- Thomas, J.S. A theory of steady wind-driven currents in shallow water with variable eddy viscosity. J. Phys. Oceanogr. 1975, 5, 136–142. [Google Scholar] [CrossRef]
- Madsen, O.S. A realisitic model of the wind-induced ekman boundary layer. J. Phys. Oceanogr. 1977, 7, 248–255. [Google Scholar] [CrossRef]
- Thorpe, S.A. On the determination of kv in the near-surface ocean from acoustic measurements of bubbles. J. Phys. Oceanogr. 1984, 14, 855–863. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S. Mass transport in water waves. Phil. Trans. R. Soc. Lond. A 1953, 245, 535–581. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S. Mass transport in the boundary layer at a free oscillating surface. J. Fluid Mech. 1960, 8, 293–306. [Google Scholar] [CrossRef]
- Sullivan, P.P.; McWilliams, J.C. Dynamics of winds and currents coupled to surface waves. Annu. Rev. Fluid Mech. 2010, 42, 19–42. [Google Scholar] [CrossRef]
- Thais, L.; Magnaudet, J. Turbulent structure beneath surface gravity waves sheared by the wind. J. Fluid Mech. 1996, 328, 313–344. [Google Scholar] [CrossRef]
- Peirson, W.L.; Garcia, A.W. On the wind-induced growth of slow water waves of finite steepness. J. Fluid Mech. 2008, 608, 243–274. [Google Scholar] [CrossRef]
- Deike, L.; Pizzo, N.; Melville, W.K. Lagrangian transport by breaking surface waves. J. Fluid Mech. 2017, 829, 364–391. [Google Scholar] [CrossRef]
- Fuster, D.; Agbaglah, G.; Josserand, C.; Popinet, S.; Zaleski, S. Numerical simulation of droplets, bubbles and waves: State of the art. Fluid Dyn. Res. 2009, 41, 065001. [Google Scholar] [CrossRef]
- Pizzo, N.E.; Deike, L.; Melville, W.K. Current generation by deep-water breaking waves. J. Fluid Mech. 2016, 803, 275–291. [Google Scholar] [CrossRef]
- Sullivan, P.P.; Edson, J.B.; Hristov, T.; McWilliams, J.C. Large eddy simulations and observations of atmospheric marine boundary layers above non-equilibrium surface waves. J. Atmos. Sci. 2008, 65. [Google Scholar] [CrossRef]
- Sullivan, P.P.; McWilliams, J.C.; Moeng, C.H. Simulation of turbulent flow over idealized water waves. J. Fluid Mech. 2000, 404, 47–85. [Google Scholar] [CrossRef]
- Kihara, N.; Hanazaki, H.; Mizuya, T.; Ueda, H. Relationship between airflow at the critical height and momentum transfer to the traveling waves. Phys. Fluids 2007, 19. [Google Scholar] [CrossRef]
- Shen, L.; Zhang, X.; Yue, D.K.P.; Triantafyllou, M.S. Turbulent flow over a flexible wall undergoing a streamwise travelling wave motion. J. Fluid Mech. 2003, 484, 197–221. [Google Scholar] [CrossRef]
- Hafsi, A.; Tejada-Martínez, A.E.; Veron, F. Dns of scalar transfer across an air–water interface during inception and growth of langmuir circulation. Comput. Fluids 2017, 158, 49–56. [Google Scholar] [CrossRef]
- Berloff, P.S.; McWilliams, J.C. Material transport in oceanic gyres. part i: Phenomenology. J. Phys. Oceanogr. 2002, 32, 764–796. [Google Scholar] [CrossRef]
- Berloff, P.S.; McWilliams, J.C. Material transport in oceanic gyres. part II: Hierarchy of stochastic models. J. Phys. Oceanogr. 2002, 32, 797–830. [Google Scholar] [CrossRef]
- Wilson, J.D.; Sawford, B.L. Review of lagrangian stochastic models for trajectories in the turbulent atmosphere. Bound.-Lay. Meteorol. 1996, 78, 191–210. [Google Scholar] [CrossRef]
- Korotenko, K.A.; Mamedovc, R.M.; Kontarb, A.E.; Korotenkob, L.A. Particle tracking method in the approach for prediction of oil slick transport in the sea: modelling oil pollution resulting from river input. J. Mar. Syst. 2004, 48, 159–170. [Google Scholar] [CrossRef]
- Golshan, R.; Boufadel, M.C.; Rodriguez, V.A.; Geng, X.; Gao, F.; King, T.; Robinson, B.; Tejada-Martínez, A.E. Oil droplet transport under non-breaking waves: An eulerian rans approach combined with a lagrangian particle dispersion model. J. Mar. Sci. Eng. 2018, 6, 7. [Google Scholar] [CrossRef]
- Visser, W.A. Using random walk models to simulate the vertical distribution of particles in a turbulent water column. Mar. Ecol. Prog. Ser. 1997, 158, 275–281. [Google Scholar] [CrossRef] [Green Version]
- Dimou, K. 3-D Hybrid Eulerian-LagRangian/Particle Tracking Model For Simulating Mass Transport in Coastal Water Bodies. Ph.D. Thesis, Massachusetts Institute of Technology, Department of Civil and Environmental Engineering, Hong Kong, China, 1992. [Google Scholar]
- Ermak, D.L.; Nasstrom, J.S. A lagrangian stochastic diffusion method for inhomogeneous turbulence. Atmos. Environ. 2000, 34, 1059–1068. [Google Scholar] [CrossRef]
- Gouesbet, G.; Berlemont, A. Eulerian and lagrangian approaches for predicting the behaviour of discrete particles in turbulent flows. Prog. Energy Combust. Sci. 1999, 25, 133–159. [Google Scholar] [CrossRef]
- Hunter, J.R.; Craig, P.D.; Phillips, H.E. On the use of random walk models with spatially variable diffusivity. J. Comput. Phys. 1993, 106, 366–376. [Google Scholar]
- Chen, Y.S.; Kim, S.W. Computations of Turbulent Flows Using an Extended k − ϵ Turbulence Closure Model; Report NASA CR-179204; NASA-Marshall Space Flight Center: Huntsville, AL, USA, 1987.
- Yakhot, V.; Orszag, S.A.; Thangam, S.; Gatski, T.B.; Speziale, C.G. Development of turbulence models for shear flows by a double expansion technique. Phys. Fluids A 1992, 4, 1510–1520. [Google Scholar] [CrossRef] [Green Version]
- ANSYS. ANSYS 15.0.0, Theory Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2013. [Google Scholar]
- Taylor, G. Diffusion by continuous movement. Proc. Lond. Math. Soc. 1921, 20, 196–212. [Google Scholar] [CrossRef]
- Tejada-Martínez, A.E.; Akkerman, I.; Bazilevs, Y. Large-eddy simulation of shallow water langmuir turbulence using isogeometric analysis and the residual-based variational multiscale method. J. Appl. Mech. 2012, 79, 010909. [Google Scholar] [CrossRef]
- Gardiner, C.W. Handbook of Stochastic Methods: For Physics, Chemistry, and the Natural Sciences (Springer Series in Synergetics); Springer: New York, NY, USA, 1990. [Google Scholar]
- Lai, A.C.K.; Nazaroff, W.W. Modeling indoor particle deposition from turbulent flow onto smooth surfaces. J. Aerosol Sci. 2000, 31, 463–476. [Google Scholar] [CrossRef]
- Wilcox, D.C. Reassessment of the scale determining equation for advanced turbulence models. AIAA 1988, 26, 1299–1310. [Google Scholar] [CrossRef]
- Laccarino, G.; Ooi, A.; Durbin, P.A.; Behnia, M. Reynolds averaged simulation of unsteady separated flow. Int. J. Heat Fluid Flow 2003, 24, 147–156. [Google Scholar] [CrossRef]
- Dean, R.G.; Dalrymple, R.A. Water Wave Mechanics for Engineers and Scientists; World Scientific: Singapore, 1991. [Google Scholar]
- Jenkins, A.D. Wind and wave induced currents in a roatating sea with depth-varying eddy viscosity. J. Phys. Oceanogr. 1986, 14, 938–951. [Google Scholar]
- Jenkins, A.D. Do strong winds blow waves flat? Proc. Ocean Wave Meas. Anal. 2001, 494–500. [Google Scholar] [CrossRef]
- Golshan, R. Residual-Based Variational Multiscale LES with Wall-Modeling for Oceanic Boundary Layers in Shallow Water. Ph.D. Thesis, University of South Florida, Department of Civil and Environmental Engineering, Tampa, FL, USA, 2014. [Google Scholar]
- Golshan, R.; Tejada-Martínez, A.E.; Juha, M.J.; Bazilevs, Y. LES and RANS simulation of wind and wave forced oceanic turbulent boundary layers using the residual-based variational multiscale method with near-wall modeling. Comput. Fluids 2017, 142, 96–108. [Google Scholar] [CrossRef]
- Sinha, N. Towards RANS Parameterization of Vertical Mixing by Langmuir Turbulence in Shallow Coastal Shelves Doctoral Dissertation. Ph.D. Thesis, University of South Florida, Department of Civil and Environmental Engineering, Tampa, FL, USA, 2013. [Google Scholar]
- Sinha, N.; Tejada-Martínez, A.E.; Akan, C.; Grosch, C.E. Toward a k-profile parameterization of langmuir turbulence in shallow coastal shelves. J. Phys. Oceanogr. 2015, 45. [Google Scholar] [CrossRef]
- Ghodke, C.; Apte, S. Dns study of particle-bed-turbulence interactions in an oscillatory wall-bounded flow. J. Fluid Mech. 2016, 792, 232–251. [Google Scholar] [CrossRef]
- Ghodke, C.; Apte, S. The effects of roughness on second-order turbulence statistics in oscillatory flows. Comput. Fluids 2018, 162, 160–170. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sinha, N.; Golshan, R. Material Transport under a Wave Train in Interaction with Constant Wind: A Eulerian RANS Approach Combined with a Lagrangian Particle Dispersion Model. Fluids 2018, 3, 40. https://doi.org/10.3390/fluids3020040
Sinha N, Golshan R. Material Transport under a Wave Train in Interaction with Constant Wind: A Eulerian RANS Approach Combined with a Lagrangian Particle Dispersion Model. Fluids. 2018; 3(2):40. https://doi.org/10.3390/fluids3020040
Chicago/Turabian StyleSinha, Nityanand, and Roozbeh Golshan. 2018. "Material Transport under a Wave Train in Interaction with Constant Wind: A Eulerian RANS Approach Combined with a Lagrangian Particle Dispersion Model" Fluids 3, no. 2: 40. https://doi.org/10.3390/fluids3020040



