Development and Analyses of Artificial Intelligence (AI)-Based Models for the Flow Boiling Heat Transfer Coefficient of R600a in a Mini-Channel
Abstract
:1. Introduction
2. Basic Idea of Support Vector Machines (SVMs)
3. An Overview of ANNs
4. An Overview of the Existing Correlations
4.1. Magdalena Piasecka Correlation
4.2. Dutkowski Correlation
4.3. Li and Wu Correlation
5. Results and Discussion
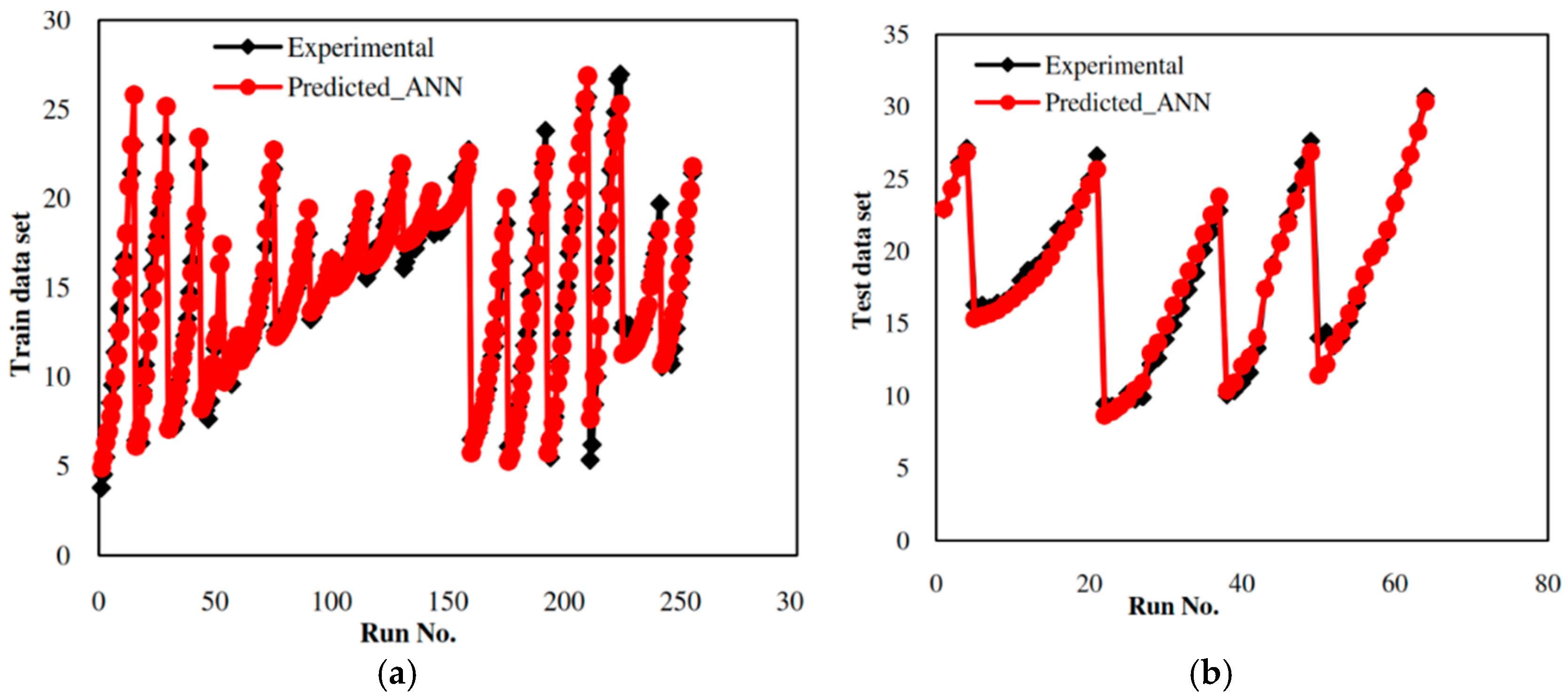
5.1. Development of the ANN-Based Model
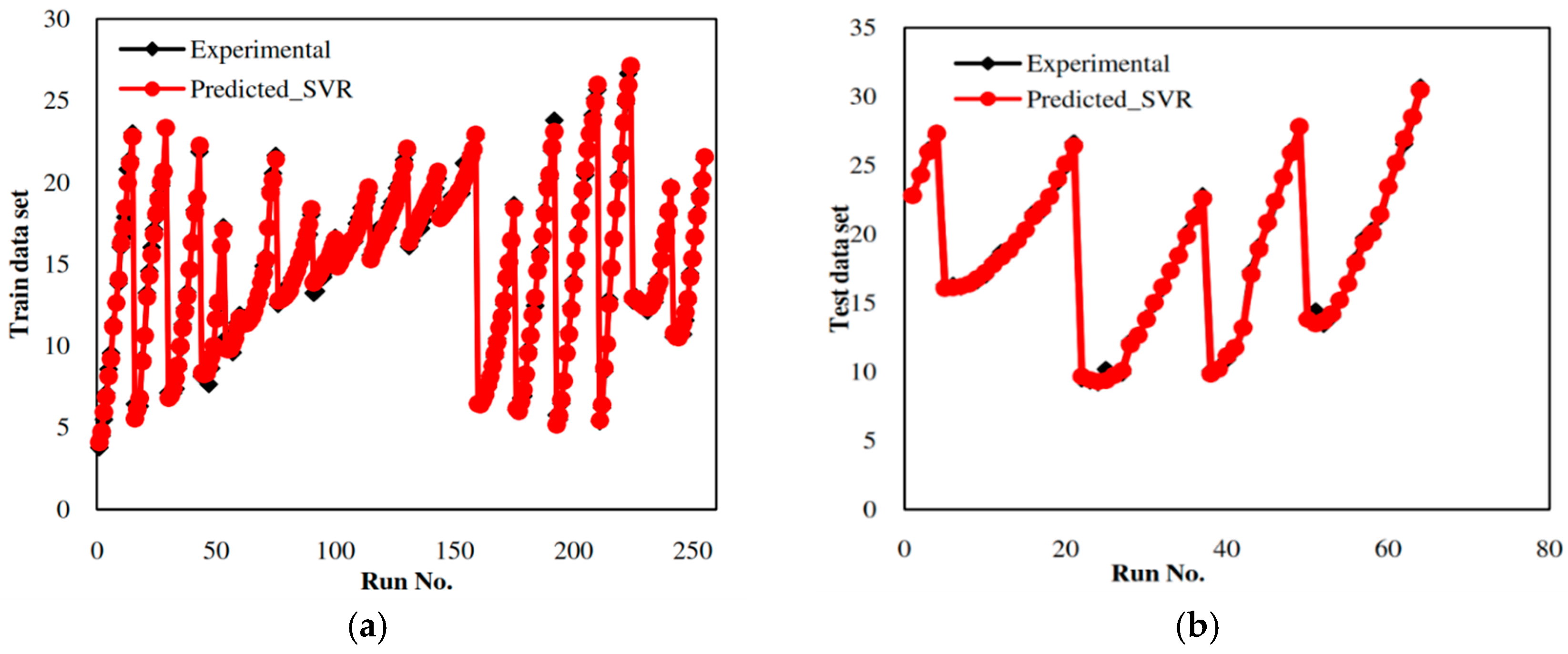
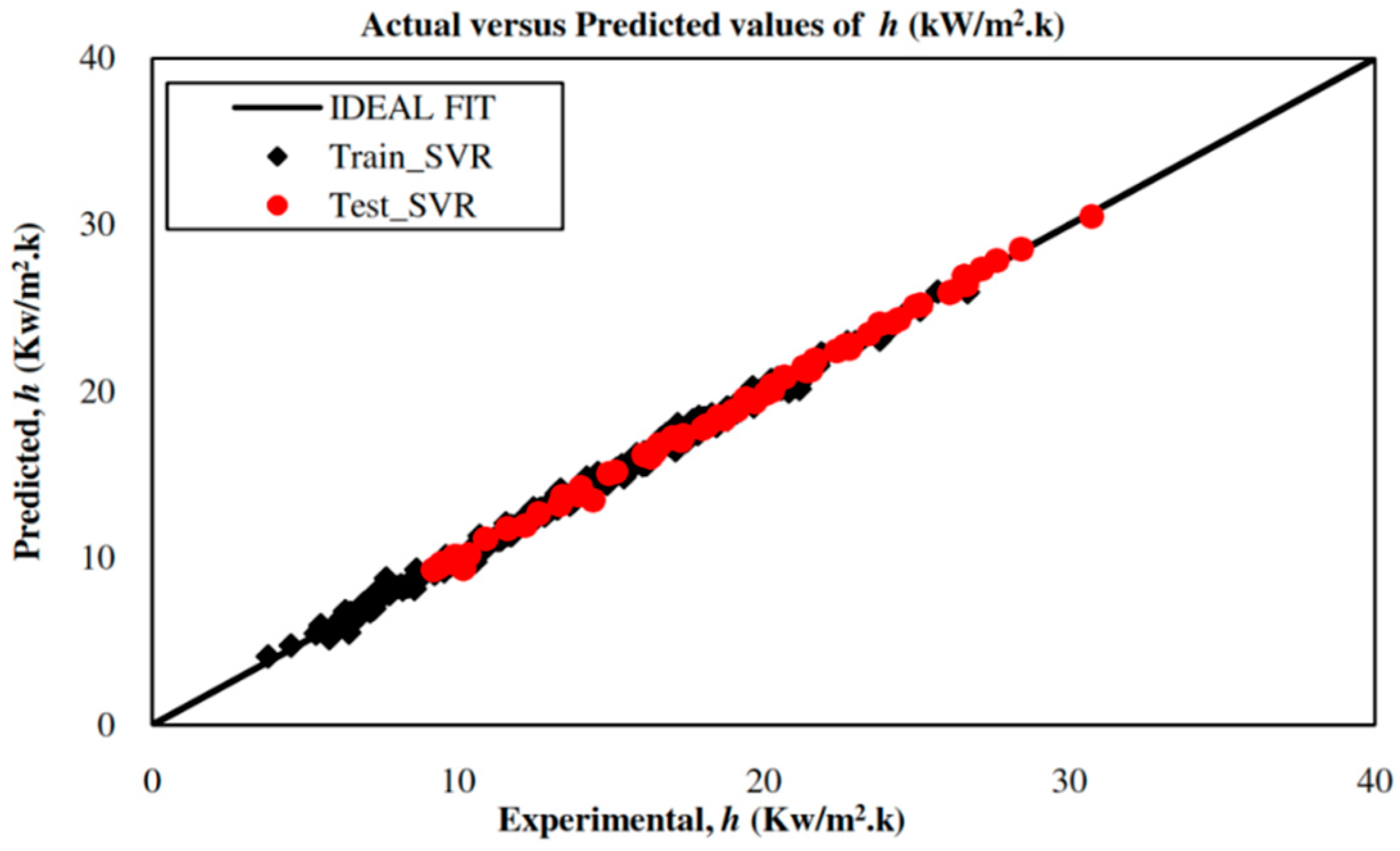
5.2. Development of an SVR-Based Model
5.3. Comparative Study
5.4. Parametric Study
5.4.1. Effect of Heat Flux and Vapor Quality on the Heat Transfer Coefficient of R600a
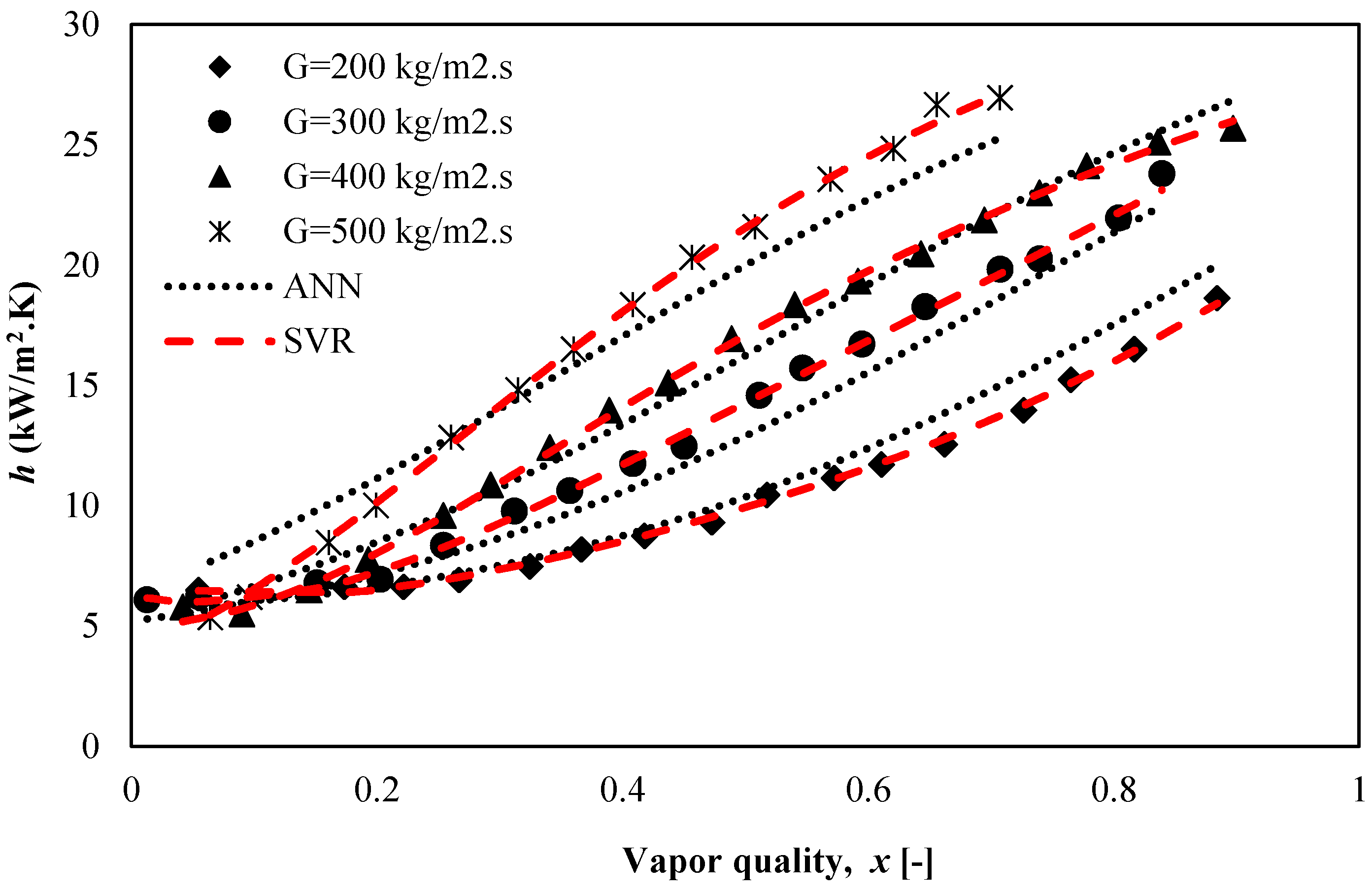
5.4.2. Effect of Mass Flux on the Heat Transfer Coefficient, h of R600a
5.4.3. Effect of Saturation Temperature on the Heat Transfer Coefficient of R600a
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| C | cost function |
| dh | hydraulic diameter, m |
| f (m) | regression function |
| G | mass flux, kg/m2·s |
| hlv | latent heat of vaporization, J/kg |
| K(mi mj) | kernel function |
| L | Lagrangian multiplier (dual form) |
| mi | input vector |
| ni | output vector |
| qw | heat flux density, W/m2 |
| Q2ext | leave-one-out cross validation for test dataset |
| Q2Loo | leave-one-out cross validation for training dataset |
| w | weight vector |
| x | vapor quality |
| z | bias term |
| Greek Symbols | |
| Γ | surface development parameter |
| ε | loss function |
| γ | regularization parameter |
| α and α* | Lagrangian multiplier |
| ϕ(mi) | high dimensional feature function for input space m |
| K | thermal conductivity, W/m·K |
| μ | dynamic viscosity, kg/m·s |
| ρ | density, kg/m3 |
| σ | surface tension, N/m |
References
- Kandlikar, S.G. Fundamental issues related to flow boiling in minichannels and microchannels. Exp. Therm. Fluid Sci. 2002, 26, 389–407. [Google Scholar] [CrossRef] [Green Version]
- Rao, M.; Khandekar, S. Simultaneously Developing Flows Under Conjugated Conditions in a Mini-Channel Array: Liquid Crystal Thermography and Computational. Heat Transf. Eng. 2009, 30, 751–761. [Google Scholar] [CrossRef]
- Copetti, J.B.; Macagnan, M.H.; Zinani, F. Experimental study on R-600a boiling in 2.6 mm tube. Int. J. Refrig. 2013, 36, 325–334. [Google Scholar] [CrossRef]
- Choi, K.I.; Oh, J.T.; Saito, K.; Jeong, J.S. Comparison of heat transfer coefficient during evaporation of natural refrigerants and R-1234yf in horizontal small tube. Int. J. Refrig. 2014, 41, 210–218. [Google Scholar] [CrossRef]
- de Oliveira, J.D.; Copett, J.B.; Passos, J.C. An experimental investigation on flow boiling heat transfer of R-600a in a horizontal small tube. Int. J. Refrig. 2016, 72, 97–110. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Zaidi, S. Development of support vector regression (SVR)-based model for prediction of circulation rate in a vertical tube thermosiphon reboiler. Chem. Eng. Sci. 2012, 69, 514–521. [Google Scholar] [CrossRef]
- Parveen, N.; Zaidi, S.; Danish, M. Support Vector Regression Prediction and Analysis of the Copper (II) Biosorption Efficiency. Indian Chem. Eng. 2017, 59, 295–311. [Google Scholar] [CrossRef]
- Akande, K.O.; Owolabi, T.O.; Olatunji, S.O.; Raheem, A.A.A. A hybrid particle swarm optimization and support vector regression model for modelling permeability prediction of hydrocarbon reservoir. J. Pet. Sci. Eng. 2017, 150, 43–53. [Google Scholar] [CrossRef]
- Santamaría-Bonfil, G.; Reyes-Ballesteros, A.; Gershenson, C. Wind speed forecasting for wind farms: A method based on support vector regression. Renew. Energy 2016, 85, 790–809. [Google Scholar] [CrossRef]
- Moazami, S.; Noori, R.; Amiri, B.J.; Yeganeh, B.; Partani, S.; Safavi, S. Reliable prediction of carbon monoxide using developed support vector machine. Atmos. Pollut. Res. 2016, 7, 412–418. [Google Scholar] [CrossRef]
- Zaidi, S. Novel application of Support Vector Machines to model the two phase-boiling heat transfer coefficient in a vertical tube thermosiphon reboiler. Chem. Eng. Res. Des. 2015, 98, 44–58. [Google Scholar] [CrossRef]
- Parveen, N.; Zaidi, S.; Danish, M. Support vector regression model for predicting the sorption capacity of lead (II). Perspect. Sci. 2016, 8, 629–631. [Google Scholar] [CrossRef]
- Parveen, N.; Zaidi, S.; Danish, M. Development of SVR-based model and comparative analysis with MLR and ANN models for predicting the sorption capacity of Cr(VI). Process Saf. Environ. Prot. 2017, 107, 428–437. [Google Scholar] [CrossRef]
- Yunos, Y.M.; Rosli, M.A.; Ghazali, N.M.; Pamitran, A.S. Performance of natural refrigerants in two phase flow. J. Teknol. Sci. Eng. 2016, 78, 77–83. [Google Scholar]
- Kim, M.; Lim, B.; Chu, E. The Performance Analysis of a Hydrocarbon Refrigerant R-600a in a Household Refrigerator/Freezer. KSME Int. J. 1998, 12, 753–760. [Google Scholar] [CrossRef]
- Vapnik, V.N. An overview of statistical learning theory. IEEE Trans. Neural Netw. 1999, 10, 988–999. [Google Scholar] [CrossRef] [PubMed]
- Gunn, S. Support Vector Machines for Classification and Regression; ISIS Technical Report; University of Southampton: Southampton, UK, 1997; pp. 1–42. [Google Scholar]
- Hearst, M.A.; Dumais, S.T.; Osman, E.; Platt, J.; Scholkopf, B. Support vector machines. IEEE Intell. Syst. 1998, 13, 18–28. [Google Scholar] [CrossRef]
- Vapnik, V.; Golowich, S.E.; Smola, A. Support Vector Method for Function Approximation, Regression Estimation, and Signal Processing. Adv. Neural Inf. Process. Syst. 1996, 9, 281–287. [Google Scholar]
- Sibi, P.; Jones, S.; Siddarth, P. Analysis of different activation functions using back propagation neural networks. J. Theor. Appl. Inf. Technol. 2013, 47, 1264–1268. [Google Scholar]
- Devabhaktuni, V.; Yagoub, M.; Fang, Y.; Xu, J.; Zhang, Q.-J. Neural networks for microwave modeling: Model development issues and nonlinear modeling techniques. Int. J. RF Microw. Comput. Eng. 2001, 11, 4–21. [Google Scholar] [CrossRef]
- Kung, C.; Yang, W.; Kung, C. A Study on Image Quality Assessment using Neural Networks and Structure Similarty. J. Comput. 2011, 6, 2221–2228. [Google Scholar] [CrossRef]
- Sempértegui-Tapia, D.F.; Ribatski, G. Flow boiling heat transfer of R134a and low GWP refrigerants in a horizontal micro-scale channel. Int. J. Heat Mass Transf. 2017, 108, 2417–2432. [Google Scholar] [CrossRef]
- Sherrod, P.H. DTREG: Predictive Modeling Software; DTREG: Brentwood, TN, USA, 2013. [Google Scholar]
- Peng, H.; Ling, X. Predicting thermal-hydraulic performances in compact heat exchangers by support vector regression. Int. J. Heat Mass Transf. 2015, 84, 203–213. [Google Scholar] [CrossRef]
- Piasecka, M. Correlation for flow boiling heat transfer in minichannels with various orientations. Int. J. Heat Mass Transf. 2015, 81, 114–121. [Google Scholar] [CrossRef]
- Dutkowski, K. Heat Transfer and Pressure Drop during Single-Phase and Two-Phase Flow in Minichannels (in Polish), Monograph; The Publishing House of Kozalin University of Technology: Kozalin, Poland, 2011. [Google Scholar]
- Li, W.; Wu, Z. A general correlation for evaporative heat transfer in micro/mini-channels. Int. J. Heat Mass Transf. 2010, 53, 1778–1787. [Google Scholar] [CrossRef]
- Bertsch, S.S.; Groll, E.A.; Garimella, S.V. Effects of heat flux, mass flux, vapor quality, and saturation temperature on flow boiling heat transfer in microchannels. Int. J. Multiph. Flow 2009, 35, 142–154. [Google Scholar] [CrossRef] [Green Version]
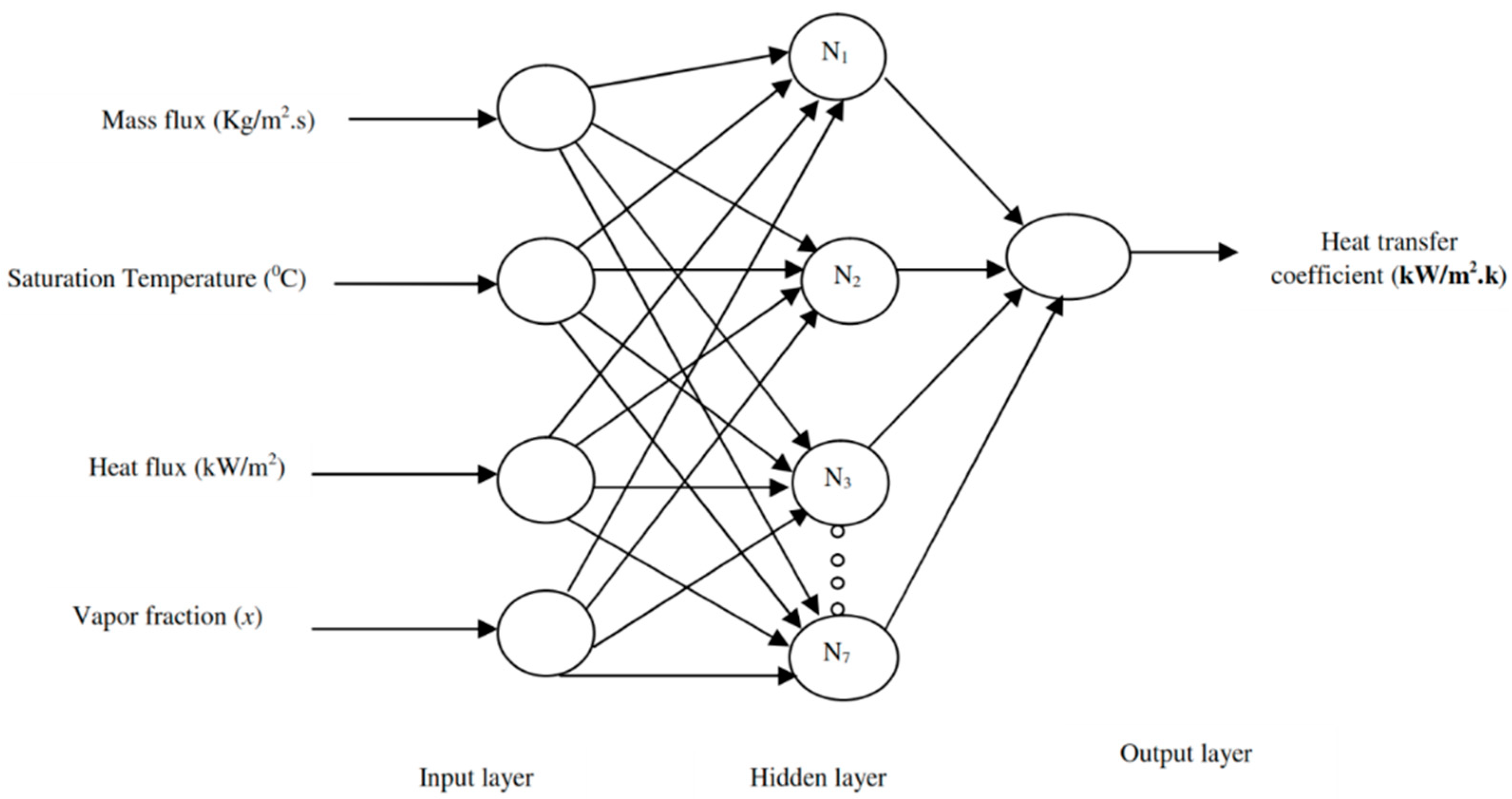




| Hidden Layer 1 Neurons | % Residual Variance |
|---|---|
| 2 | 8.27490 |
| 3 | 10.72571 |
| 4 | 4.03148 |
| 5 | 4.51386 |
| 6 | 8.74758 |
| 7 | 3.22918 (Optimal value) |
| 8 | 3.99854 |
| 9 | 4.41057 |
| 10 | 6.25276 |
| 11 | 5.57635 |
| 12 | 4.74811 |
| 13 | 6.90271 |
| 14 | 4.34555 |
| 15 | 4.46499 |
| Statistical Indices | Train Data | Test Data |
|---|---|---|
| AARE (%) | 4.12 | 5.14 |
| R | 0.9884 | 0.9842 |
| RMSE | 0.8142 | 0.8608 |
| SD | 4.7469 | 5.2438 |
| MRE | 0.0412 | 0.0514 |
| MAE (%) | 1.02 | 1.05 |
| Q2LOO (Train data), Q2ext (Test data) | 0.9832 | 0.9685 |
| Model | C | γ = 1/2σ2 | ε | Kernel Type | Loss Function | Number of Support Vectors | Number of Training Points |
|---|---|---|---|---|---|---|---|
| Heat transfer coefficient, h | 4907.6 | 1.3486 | 0.001 | RBF | ε-insensitive | 175 | 255 |
| Statistical Indices | Train Data | Test Data |
|---|---|---|
| AARE (%) | 2.05 | 1.15 |
| R | 0.9978 | 0.9991 |
| RMSE | 0.3241 | 0.2365 |
| SD | 5.4354 | 4.8343 |
| MRE | 0.02045 | 0.0115 |
| MAE (%) | 0.41 | 0.28 |
| Q2LOO (Train data), Q2ext (Test data) | 0.9955 | 0.9986 |
| Correlations | Model Evaluation Indices | |||||
|---|---|---|---|---|---|---|
| AARE (%) | R2 | RMSE | SD | MRE | MAE (%) | |
| SVR (Present study) | 1.15 | 0.9981 | 0.2365 | 4.8343 | 0.0115 | 0.28 |
| ANN (Present study) | 5.14 | 0.9685 | 0.8608 | 5.2438 | 0.0514 | 1.05 |
| Piasecka [24] | 62.52 | 0.1600 | 35.61 | 14.0801 | 6.252 | 33.2313 |
| Dutkowski [24,25] | 43.89 | 0.2624 | 15.32 | 12.2 | 4.3893 | 13.68 |
| Li and Wu [26] | 47.68 | 0.0095 | 16.19 | 17.78 | 4.76 | 18.35 |
| Absolute Deviation (AD) (%) | % of ANN Model Predicted Values | Cumulative Score | % of SVR Model Predicted Values | Cumulative Score |
|---|---|---|---|---|
| AD < 5 | 61.96 | 61.96 | 93.73 | 93.73 |
| 5 < AD < 10 | 23.53 | 85.49 | 5.09 | 98.82 |
| AD > 10 | 14.51 | 100 | 1.18 | 100 |
| Total | 100 | 100 |
| Absolute Deviation (AD) (%) | % of ANN Model Predicted Values | Cumulative Score | % of SVR Model Predicted Values | Cumulative Score |
|---|---|---|---|---|
| AD < 5 | 68.75 | 68.75 | 96.88 | 96.88 |
| 5 < AD < 10 | 28.12 | 96.87 | 3.12 | 100 |
| AD > 10 | 3.13 | 100 | 0.00 | |
| Total | 100 | 100 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parveen, N.; Zaidi, S.; Danish, M. Development and Analyses of Artificial Intelligence (AI)-Based Models for the Flow Boiling Heat Transfer Coefficient of R600a in a Mini-Channel. ChemEngineering 2018, 2, 27. https://doi.org/10.3390/chemengineering2020027
Parveen N, Zaidi S, Danish M. Development and Analyses of Artificial Intelligence (AI)-Based Models for the Flow Boiling Heat Transfer Coefficient of R600a in a Mini-Channel. ChemEngineering. 2018; 2(2):27. https://doi.org/10.3390/chemengineering2020027
Chicago/Turabian StyleParveen, Nusrat, Sadaf Zaidi, and Mohammad Danish. 2018. "Development and Analyses of Artificial Intelligence (AI)-Based Models for the Flow Boiling Heat Transfer Coefficient of R600a in a Mini-Channel" ChemEngineering 2, no. 2: 27. https://doi.org/10.3390/chemengineering2020027




