Measurement of Volumetric Mass Transfer Coefficient in Bubble Columns
Abstract
:1. Introduction
2. Materials and Methods
3. Theoretical Model Describing the Mass Transfer during DPM
4. Results
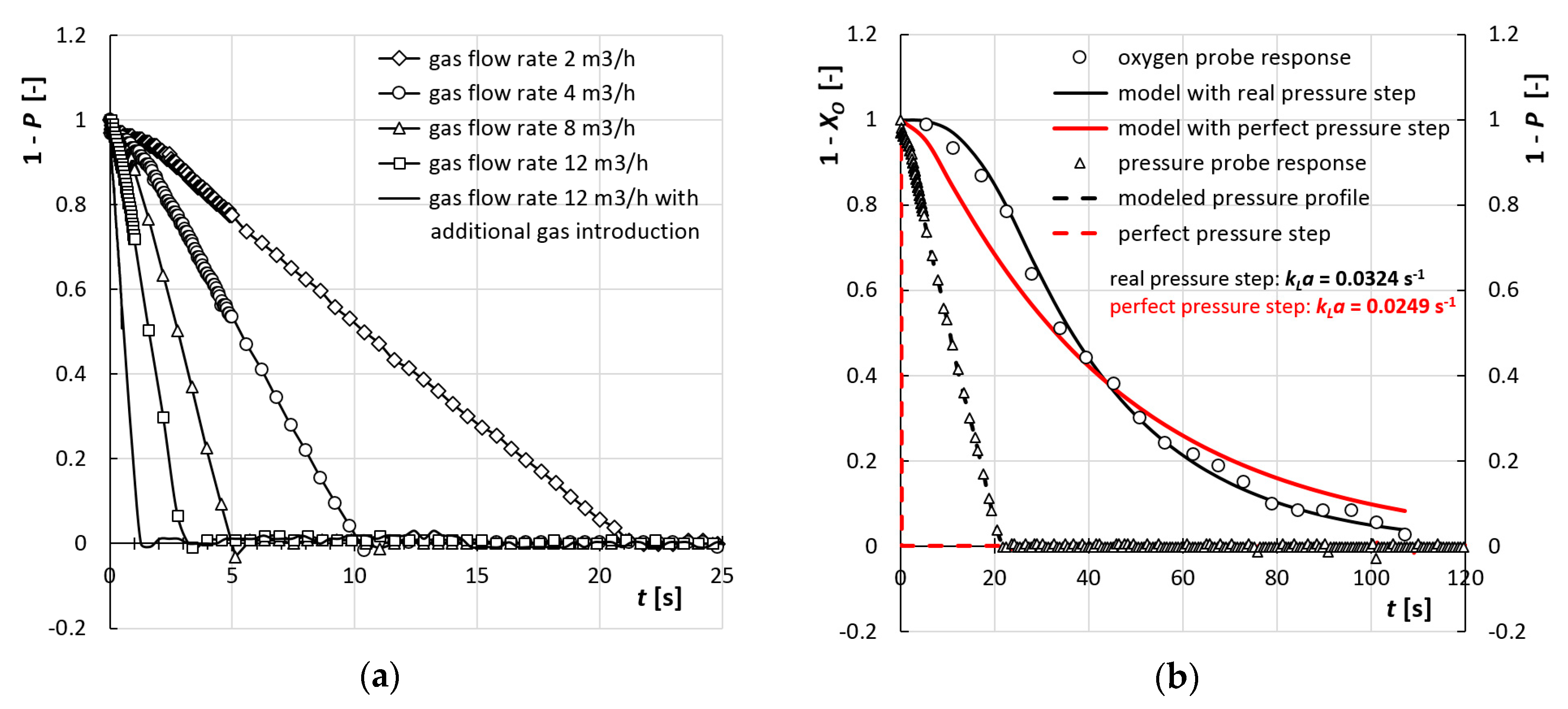
4.1. Description of Hydrodynamics
4.2. Mass Transfer—Comparision of Ideal and Non-Ideal Pressure Step
4.3. Mass Transfer—Comparison of Pure Oxygen and Air Absorption
5. Discussion
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Degaleesan, S.; Dudukovic, M.; Pan, Y. Experimental study of gas-induced liquid-flow structures in bubble columns. AIChE J. 2001, 47, 1913–1931. [Google Scholar] [CrossRef]
- Kantarci, N.; Borak, F.; Ulgen, K.O. Bubble column reactors. Process Biochem. 2005, 40, 2263–2283. [Google Scholar] [CrossRef]
- Kraakman, N.J.R.; Rocha-Rios, J.; van Loosdrecht, M.C.M. Review of mass transfer aspects for biological gas treatment. Appl. Microbiol. Biotechnol. 2011, 91, 873–886. [Google Scholar] [CrossRef] [PubMed]
- Shah, Y.T.; Kelkar, B.G.; Godbole, S.P.; Deckwer, W.D. Design parameters estimations for bubble column reactors. AIChE J. 1982, 28, 353–379. [Google Scholar] [CrossRef]
- Manjrekar, O.N.; Sun, Y.J.; He, L.; Tang, Y.J.; Dudukovic, M.P. Hydrodynamics and mass transfer coefficients in a bubble column photo-bioreactor. Chem. Eng. Sci. 2017, 168, 55–66. [Google Scholar] [CrossRef]
- Thobie, C.; Gadoin, E.; Blel, W.; Pruvost, J.; Gentric, C. Global characterization of hydrodynamics and gas-liquid mass transfer in a thin-gap bubble column intended for microalgae cultivation. Chem. Eng. Process. 2017, 122, 76–89. [Google Scholar] [CrossRef]
- Miron, A.S.; Camacho, F.G.; Gomez, A.C.; Grima, E.M.; Chisti, Y. Bubble-column and airlift photobioreactors for algal culture. AIChE J. 2000, 46, 1872–1887. [Google Scholar] [CrossRef]
- Garcia-Ochoa, F.; Gomez, E. Bioreactor scale-up and oxygen transfer rate in microbial processes: An overview. Biotechnol. Adv. 2009, 27, 153–176. [Google Scholar] [CrossRef] [PubMed]
- Akita, K.; Yoshida, F. Gas holdup and volumetric mass-transfer coefficient in bubble columns—Effects of liquid properties. Ind. Eng. Chem. Process Des. Dev. 1973, 12, 76–80. [Google Scholar] [CrossRef]
- Deckwer, W.D.; Burckhart, R.; Zoll, G. Mixing and mass-transfer in tall bubble columns. Chem. Eng. Sci. 1974, 29, 2177–2188. [Google Scholar] [CrossRef]
- Deckwer, W.D.; Nguyentien, K.; Kelkar, B.G.; Shah, Y.T. Applicability of axial-dispersion model to analyze mass-transfer measurements in bubble-columns. AIChE J. 1983, 29, 915–922. [Google Scholar] [CrossRef]
- Letzel, H.M.; Schouten, J.C.; Krishna, R.; van den Bleek, C.M. Gas holdup and mass transfer in bubble column reactors operated at elevated pressure. Chem. Eng. Sci. 1999, 54, 2237–2246. [Google Scholar] [CrossRef]
- Vasconcelos, J.M.T.; Rodrigues, J.M.L.; Orvalho, S.C.P.; Alves, S.S.; Mendes, R.L.; Reis, A. Effect of contaminants on mass transfer coefficients in bubble column and airlift contactors. Chem. Eng. Sci. 2003, 58, 1431–1440. [Google Scholar] [CrossRef]
- Lau, R.; Peng, W.; Velazquez-Vargas, L.G.; Yang, G.Q.; Fan, L.S. Gas-liquid mass transfer in high-pressure bubble columns. Ind. Eng. Chem. Res. 2004, 43, 1302–1311. [Google Scholar] [CrossRef]
- Vandu, C.O.; Krishna, R. Volumetric mass transfer coefficients in slurry bubble columns operating in the churn-turbulent flow regime. Chem. Eng. Process. 2004, 43, 987–995. [Google Scholar] [CrossRef]
- Vandu, C.O.; Krishna, R. Influence of scale on the volumetric mass transfer coefficients in bubble columns. Chem. Eng. Process. 2004, 43, 575–579. [Google Scholar] [CrossRef]
- Han, L.; Al-Dahhan, M.H. Gas-liquid mass transfer in a high pressure bubble column reactor with different sparger designs. Chem. Eng. Sci. 2007, 62, 131–139. [Google Scholar] [CrossRef]
- Gourich, B.; Vial, C.; El Azher, N.; Soulami, M.B.; Ziyad, M. Influence of hydrodynamics and probe response on oxygen mass transfer measurements in a high aspect ratio bubble column reactor: Effect of the coalescence behaviour of the liquid phase. Biochem. Eng. J. 2008, 39, 1–14. [Google Scholar] [CrossRef]
- Gogate, P.R.; Pandit, A.B. Survey of measurement techniques for gas-liquid mass transfer coefficient in bioreactors. Biochem. Eng. J. 1999, 4, 7–15. [Google Scholar] [CrossRef]
- Linek, V.; Sinkule, J. The influence of gas and liquid axial-dispersion on determination of kLa by dynamic method. Chem. Eng. Res. Des. 1991, 69, 308–312. [Google Scholar]
- Scargiali, F.; Russo, R.; Grisafi, F.; Brucato, A. Mass transfer and hydrodynamic characteristics of a high aspect ratio self-ingesting reactor for gas-liquid operations. Chem. Eng. Sci. 2007, 62, 1376–1387. [Google Scholar] [CrossRef]
- Linek, V.; Benes, P.; Sinkule, J.; Moucha, T. Non-ideal pressure step method for kLa measurement. Chem. Eng. Sci. 1993, 48, 1593–1599. [Google Scholar] [CrossRef]
- Linek, V.; Benes, P.; Vacek, V. Dynamic pressure method for kLa measurement in large-scale bioreactors. Biotechnol. Bioeng. 1989, 33, 1406–1412. [Google Scholar] [CrossRef] [PubMed]
- Fujasova, M.; Linek, V.; Moucha, T. Mass transfer correlations for multiple-impeller gas-liquid contactors. Analysis of the effect of axial dispersion in gas and liquid phases on “local” kLa values measured by the dynamic pressure method in individual stages of the vessel. Chem. Eng. Sci. 2007, 62, 1650–1669. [Google Scholar] [CrossRef]
- Scargiali, F.; Busciglio, A.; Grisafi, F.; Brucato, A. Simplified dynamic pressure method for kLa measurement in aerated bioreactors. Biochem. Eng. J. 2010, 49, 165–172. [Google Scholar] [CrossRef]
- Moucha, T.; Rejl, F.J.; Kordac, M.; Labik, L. Mass transfer characteristics of multiple-impeller fermenters for their design and scale-up. Biochem. Eng. J. 2012, 69, 17–27. [Google Scholar] [CrossRef]
- Garcia-Ochoa, F.; Gomez, E. Prediction of gas-liquid mass transfer coefficient in sparged stirred tank bioreactors. Biotechnol. Bioeng. 2005, 92, 761–772. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Ochoa, F.; Gomez, E.; Santos, V.E.; Merchuk, J.C. Oxygen uptake rate in microbial processes: An overview. Biochem. Eng. J. 2010, 49, 289–307. [Google Scholar] [CrossRef]
- Blazej, M.; Annus, J.; Markos, J. Comparison of gassing-out and pressure-step dynamic methods for kLa measurement in an airlift reactor with internal loop. Chem. Eng. Res. Des. 2004, 82, 1375–1382. [Google Scholar] [CrossRef]
- Blazej, M.; Jurascik, M.; Annus, J.; Markos, J. Measurement of mass transfer coefficient in an airlift reactor with internal loop using coalescent and non-coalescent liquid media. J. Chem. Technol. Biotechnol. 2004, 79, 1405–1411. [Google Scholar] [CrossRef]
- Jurascik, M.; Blazej, M.; Annus, J.; Markos, J. Experimental measurements of volumetric mass transfer coefficient by the dynamic pressure-step method in internal loop airlift reactors of different scale. Chem. Eng. J. 2006, 125, 81–87. [Google Scholar] [CrossRef]
- Zahradnik, J.; Fialova, M.; Ruzicka, M.; Drahos, J.; Kastanek, F.; Thomas, N.H. Duality of the gas-liquid flow regimes in bubble column reactors. Chem. Eng. Sci. 1997, 52, 3811–3826. [Google Scholar] [CrossRef]
- Ruzicka, M.C.; Zahradnik, J.; Drahos, J.; Thomas, N.H. Homogeneous-heterogeneous regime transition in bubble columns. Chem. Eng. Sci. 2001, 56, 4609–4626. [Google Scholar] [CrossRef]
- Linek, V.; Vacek, V.; Sinkule, J.; Benes, P. Measurement of Oxygen by Membrane-Covered Probes: Guidelines for Applications in Chemical and Biochemical Engineering; Ellis Horwood: Chichester, UK, 1988; Halsted Press: New York, NY, USA, 1988; ISBN 0745801994. [Google Scholar]
- Danckwerts, P.V. Gas-Liquid Reactions; McGraw-Hill Book Company: New York, NY, USA, 1970; ISBN 9780070152878. [Google Scholar]
- Besagni, G.; Inzoli, F.; Ziegenhein, T. Two-Phase Bubble Columns: A Comprehensive Review. ChemEngineering 2018, 2, 13. [Google Scholar] [CrossRef]
- Besagni, G.; Inzoli, F.; Ziegenhein, T.; Lucas, D. Computational Fluid-Dynamic modeling of the pseudo-homogeneous flow regime in large-scale bubble columns. Chem. Eng. Sci. 2017, 160, 144–160. [Google Scholar] [CrossRef]
- Sharaf, S.; Zednikova, M.; Ruzicka, M.C.; Azzopardi, B.J. Global and local hydrodynamics of bubble columns—Effect of gas distributor. Chem. Eng. J. 2016, 288, 489–504. [Google Scholar] [CrossRef]
- Wilkinson, P.M.; Spek, A.P.; Vandierendonck, L.L. Design parameters estimation for scale-up of high-pressure bubble-columns. AIChE J. 1992, 38, 544–554. [Google Scholar] [CrossRef]
- Besagni, G.; Di Pasquali, A.; Gallazzini, L.; Gottardi, E.; Colombo, L.P.M.; Inzoli, F. The effect of aspect ratio in counter-current gas-liquid bubble columns: Experimental results and gas holdup correlations. Int. J. Multiph. Flow 2017, 94, 53–78. [Google Scholar] [CrossRef]
- Sasaki, S.; Uchida, K.; Hayashi, K.; Tomiyama, A. Effects of column diameter and liquid height on gas holdup in air-water bubble columns. Exp. Therm. Fluid Sci. 2017, 82, 359–366. [Google Scholar] [CrossRef]
- American Society of Civil Engineers. Measurement of Oxygen Transfer in Clean Water (ASCE/EWRI 2-06); American Society of Civil Engineers: Reston, VA, USA, 2007; ISBN 9780784408483. [Google Scholar]





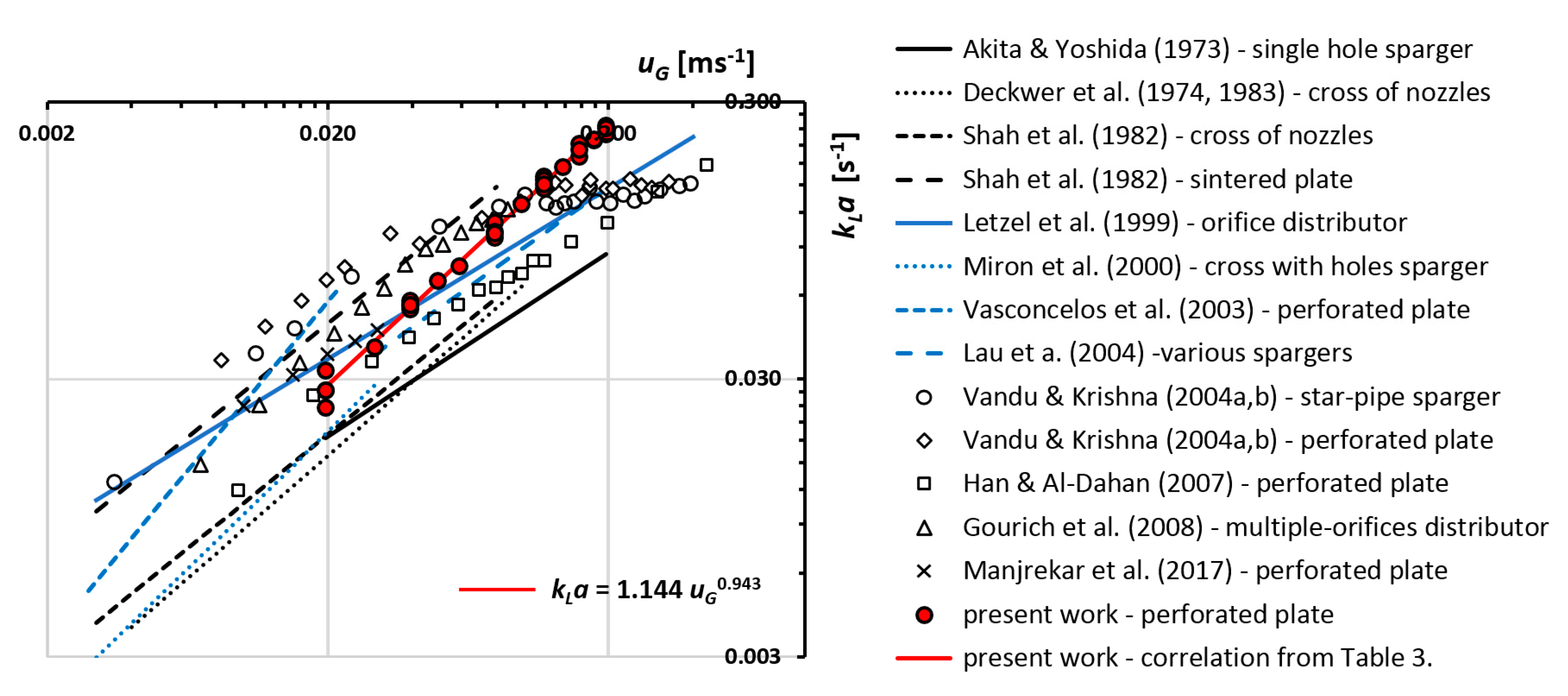

| Reference | kLa Correlation | Operating Conditions | Sparger | kLa Method |
|---|---|---|---|---|
| Akita & Yoshida 1973 [9] | D = 0.15–0.60m uG = 4–117 mm/s | single hole 5 mm | start-up method | |
| Deckwer et al., 1974, 1983 [10,11] | D = 0.15–0.2 m uG = 4–100 mm/s liquid circulation | cross of nozzles | standard dynamic | |
| Shah et al., 1982 [4] | D = 0.1–0.15 m uG = 2–80 mm/s | cross of nozzles | standard dynamic | |
| Shah et al., 1982 [4] | D = 0.2 m uG = 3–80 mm/s | sintered plate | standard dynamic | |
| Letzel et al., 1999 [12] | D = 0.15 m uG = 0–400 mm/s | orifice distributor | DPM | |
| Miron et al., 2000 [7] | D = 0.193 m uG = 2–30 mm/s liquid circulation | cross with holes | start-up method | |
| Vasconcelos et al., 2003 [13] | D = 0.193 m uG = 3–22 mm/s | perforated plate | standard dynamic | |
| Lau et al., 2004 [14] | D = 0.045-0.45 m uG = 3–68 mm/s liquid circulation | various spargers | start-up method | |
| Vandu & Krishna 2004 [15,16] | D = 0.1–0.38 m uG > 80 mm/s | perforated plate; sieve plate | start-up method | |
| Han & Al-Dahhan 2007 [17] | kLa data available | D = 0.162 m uG = 10–450 mm/s | perforated plate | oxygen-enriched method |
| Gourich et al., 2008 [18] | kLa data available | D = 0.1 m uG = 6–87 mm/s | multiple-orifices | standard dynamic |
| Manjrekar et al., 2017 [5] | kLa data available | D = 0.1 m uG = 10–30 mm/s | perforated plate | oxygen-enriched method |
| Physical-Chemical Property | Water |
|---|---|
| diffusivity of O2 [m2/s] | 2.143 × 10−9 |
| diffusivity of N2 [m2/s] | 1.903 × 10−9 |
| Henry’s constant of O2 [mol/(m3·atm)] | 1.257 |
| Henry’s constant of N2 [mol/(m3·atm)] | 0.6432 |
| conductivity [S/cm] | 0.002 × 10−3 |
| density [kg/m3] | 997 |
| viscosity [mPa·s] | 0.89 |
| surface tension [mN/m] | 71.0 |
| Correlation | Operating Conditions |
|---|---|
| D = 0.19m, uG = 20–200 mm/s | |
| 1 m clear liquid height perforated plate | |
| pure heterogeneous flow regime T = 25 °C, atmospheric pressure |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zedníková, M.; Orvalho, S.; Fialová, M.; Ruzicka, M.C. Measurement of Volumetric Mass Transfer Coefficient in Bubble Columns. ChemEngineering 2018, 2, 19. https://doi.org/10.3390/chemengineering2020019
Zedníková M, Orvalho S, Fialová M, Ruzicka MC. Measurement of Volumetric Mass Transfer Coefficient in Bubble Columns. ChemEngineering. 2018; 2(2):19. https://doi.org/10.3390/chemengineering2020019
Chicago/Turabian StyleZedníková, Mária, Sandra Orvalho, Marie Fialová, and Marek C. Ruzicka. 2018. "Measurement of Volumetric Mass Transfer Coefficient in Bubble Columns" ChemEngineering 2, no. 2: 19. https://doi.org/10.3390/chemengineering2020019





