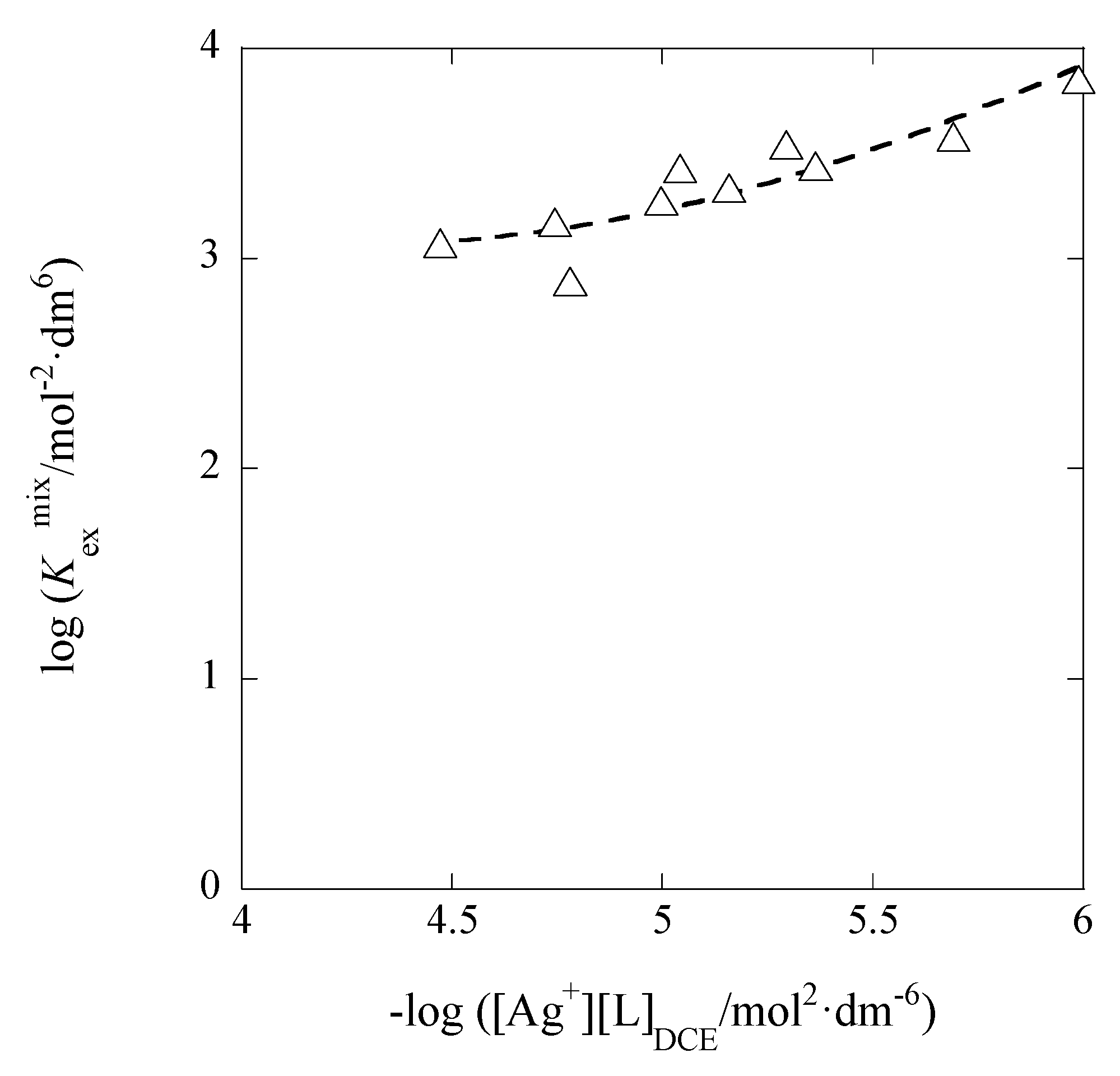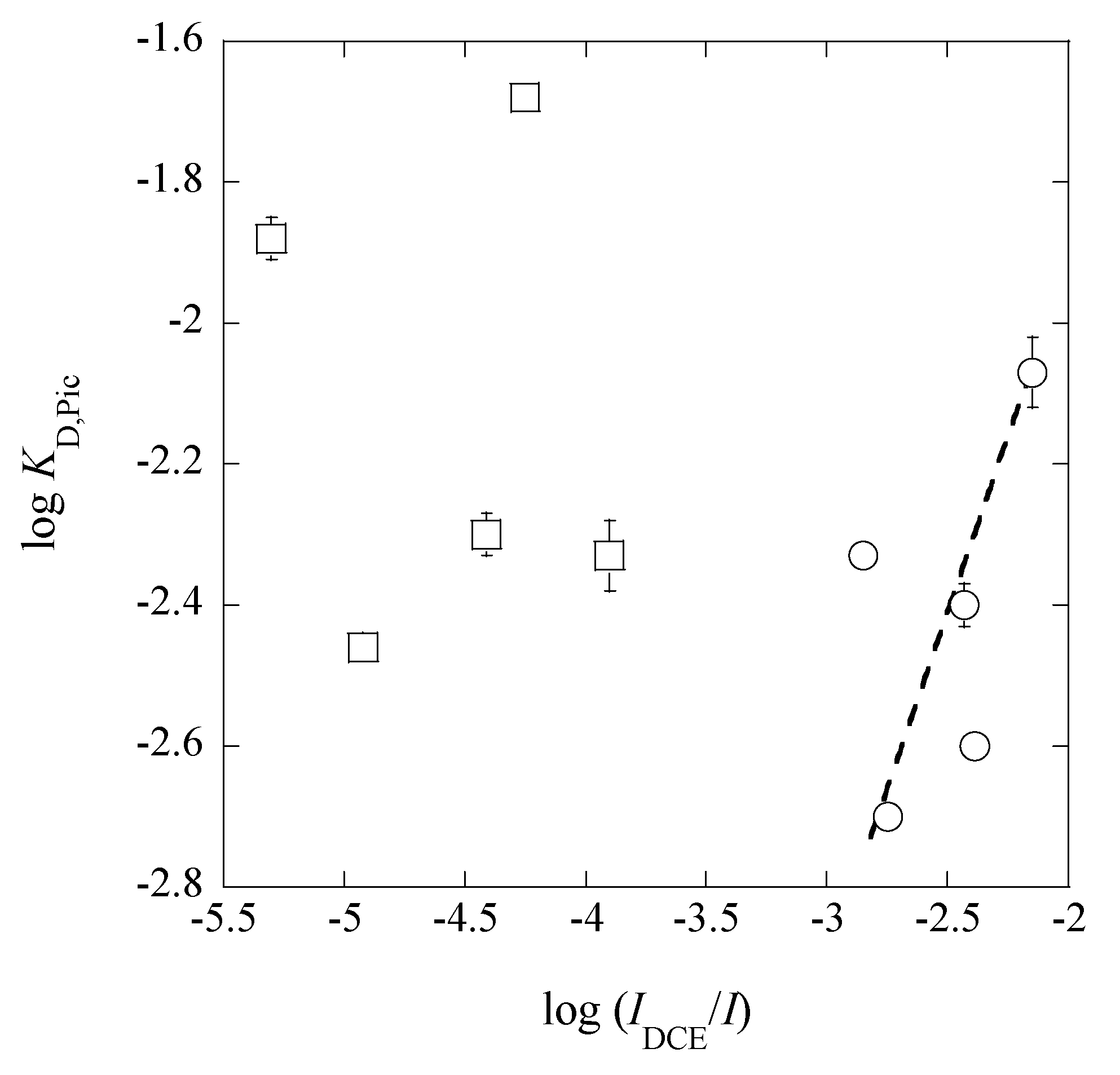1. Introduction
It is well known that crown compounds (L) extract alkali and alkaline-earth metal ions (M
z+,
z = 1, 2) from water (w) into various diluents [
1,
2,
3,
4]. In many extraction experiments, extraction constants for L have been determined so far [
1,
2,
3,
4,
5,
6,
7,
8]. For example, the two representative constants,
Kex and
Kex±, for the extraction of a univalent metal salt (M
IA) by L have been defined as [MLA]
org/
P [
2,
3] and [ML
+]
org[A
−]
org/
P [
1,
4] with
P = [M
+][L]
org[A
−], respectively. Generally, the
Kex value is effective for the evaluation of an extraction-ability and -selectivity of L against M
+ into low-polar diluents, while the
Kex± value is for those of L into high-polar ones. Here, the subscript ″org″ denotes an organic phase and A
− does a univalent pairing anion. For the latter
Kex±, its thermodynamic equilibrium constants have been reported [
4]. For the former
Kex, its thermodynamic treatment seems to be few. The authors were not able to find out the study with respect to a dependence of log
Kex on the ionic strength (
I) of the w phase.
Presences of equilibrium potential differences (Δ
φeq) between aqueous and diluent solutions have been recently reported for the extraction of some M
+ or M
2+ with L [
5,
6,
7]. This symbol Δ
φeq was defined as ∑{inner potential (
φ ) of ionic species in the w phase} − ∑{
φ of those in the org or diluent phase} [
8], according to the definition [
9,
10],
φw −
φorg, of an interfacial equilibrium potential-difference in the electrochemistry at liquid/liquid interfaces. In the above studies, an approximation method [
5,
6,
7,
8] for the Δ
φeq determination, namely the method with a use of a ″conditional″ distribution constant (
KD,A) of A
− into the org phase, has been described in comparison with its more-precise method with solving higher-degree equations [
6]. Here the ″conditional″ is due to the fact that the
KD,A values change depending on the Δ
φeq ones, even at fixed pressure and temperature. However, it is still not clarified whether the Δ
φeq values determined by the
KD,A values equal those coming from the distribution of M
+ into the org phases or not.
In the present paper, we determined the
Kex,
Kex±, and
KD,A values [
6,
8] at 298 K by the extraction experiments into 1,2-dichloroethane (DCE) with silver picrate (AgPic) and benzo-18-crown-6 ether (B18C6), in order to elucidate mainly the above two subjects for
I and Δ
φeq. The same experiments were performed under the condition of the presence of excess HNO
3 in the w phases. Then, an ion-pair formation constant (
K1,DCE/mol
−1·dm
3) for Ag(B18C6)
+Pic
− in the DCE phase, DCE saturated with water, and the Δ
φeq values were calculated from the relations,
K1,DCE =
Kex/
Kex± [
6,
8] and Δ
φeq = −(2.303
RT/
F){log
KD,A − log(
KD,A standardized at Δ
φeq = 0 V)} [
11], respectively. Here,
R,
T, and
F are usual meanings. On the basis of these data, the dependences of log
Kex and log
Kex± on the
I values and those of log
K1,DCE and log
Kex± on the
I values (
IDCE) of the DCE phases were examined. Moreover, a relation between the Δ
φeq values determined by the
KD,A ones and the conditional distribution constants (
KD,Ag) of Ag
+ into the DCE phases was discussed indirectly. For comparison, the
Kex± and
Kex values were experimentally determined at 298 K for the AgClO
4- and AgNO
3-B18C6 extraction into DCE. As basic data, the
KD,AgS value was determined in terms of a simple Ag
+Pic
− extraction experiment into DCE. The symbol
KD,AgS denotes the distribution constant of Ag
+ into the DCE phase standardized at Δ
φeq = 0 V, that is, the standard distribution one.
3. Discussion
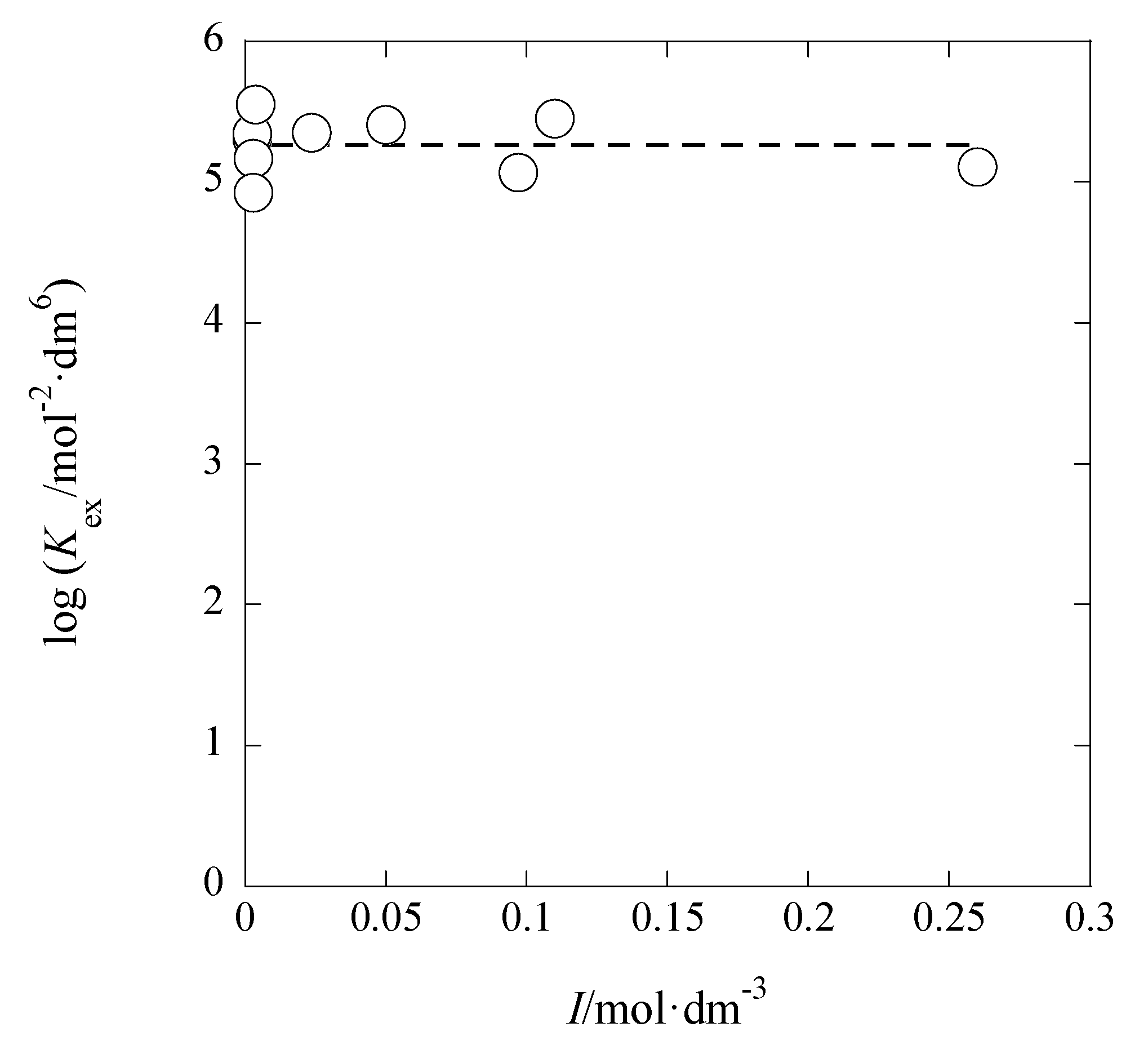
3.1. I Dependences of LogKex and LogKex±
The dependences of log
Kex and log
Kex± on
I are considered below. On the basis of their definitions, the
Kex value can be dependent on [M
+] and [A
−], while, in addition to these concentrations, the
Kex± value can be on [ML
+]
org and [A
−]
org. Therefore,
Kex is mainly a function of
I, while
Kex± is a function with the two parameters,
I and
Iorg; the relations [
14] of [M
+] =
aM/
y+(
I) and [A
−]
org =
aA,org/
y−,org(
Iorg) hold as examples (see below for the symbols
a and
y). The
I dependence of log
Kex± is of an approximate.
Figure 5 shows the log
Kex-versus-
I plot for the AgPic-B18C6 extraction system with DCE; in the plot, the average value of
I was employed as
I (
x-axis) of each system. Using the extended Debye-Hückel (DH) equation [
14], the extraction constant (
Kex0) at
I → 0 mol·dm
−3 is expressed as
where the symbols,
aj and
y, denote the activity of species
j (= M
+, A
−) and its activity coefficient with
I, respectively [
14]. Rearranging Equation (5), the following equation was obtained immediately:
The regression analysis of the plot in
Figure 5 based on this equation yielded the regression line with log(
Kex0/mol
−2·dm
6) = 5.28 ± 0.25 and
Bå = 44 ± 661 mol
−1/2·dm
3/2 Å at
r = 0.024 and
N (number of data) = 10, the fixed
A value (= 0.5114) in pure water, and 298 K. Considering the error of the experimental
Bå value, it is difficult to discuss the
Bå or
å value in this result. When the three parameters, log
Kex0,
A, and
Bå, had been used for the regression analysis, it gave the results of log
Kex0 > 0,
A < 0, and
Bå < 0. Consequently, we gave up such an analysis.
Similarly, the extraction constant (
Kex±0) at
I → 0 is expressed as
where the subscript “ML” means the complex ion ML
+. Rearranging this equation, we can immediately obtain
where
Kex±0′ denotes
Kex±0/(
yML,orgy−,org) (= [ML
+]
org[A
−]
org/
aM[L]
orgaA). Unfortunately, the analysis of the plot based on Equation (6a) did not yield the suitable result which satisfies the condition of
Bå > 0.
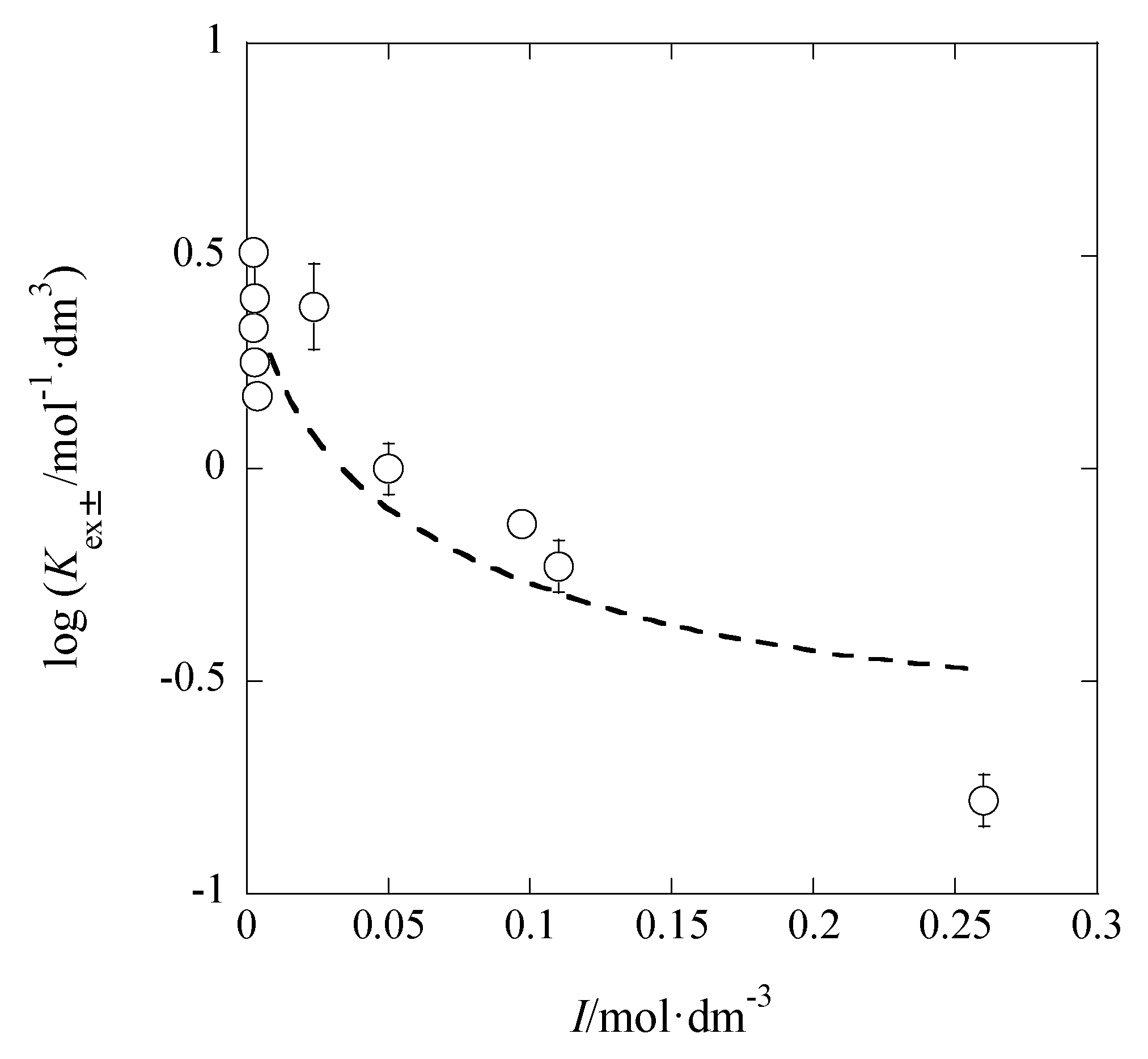
On the other hand, using the Davies equation without
Bå instead of the extended DH equation [
14], log
Kex±0′ = 0.60 ± 0.11 and
A = 2.05 ± 0.38 mol
−1/2·dm
3/2 were obtained (
Figure 6). The Davies equation is log
y = −
A/(1 +
) − 0.3
I} [
14], where
z shows a formal charge of ionic species with a sign (refer to the Introduction).
The analysis of the logKex-versus-I plot by the Davies equation yielded logKex0 = 5.29 ± 0.11 with A = 0.08 ± 0.40 mol−1/2·dm3/2. Within the calculation error of ±0.3, this logKex0 value was in accord with 5.3 determined by the DH equation (see above in this section).
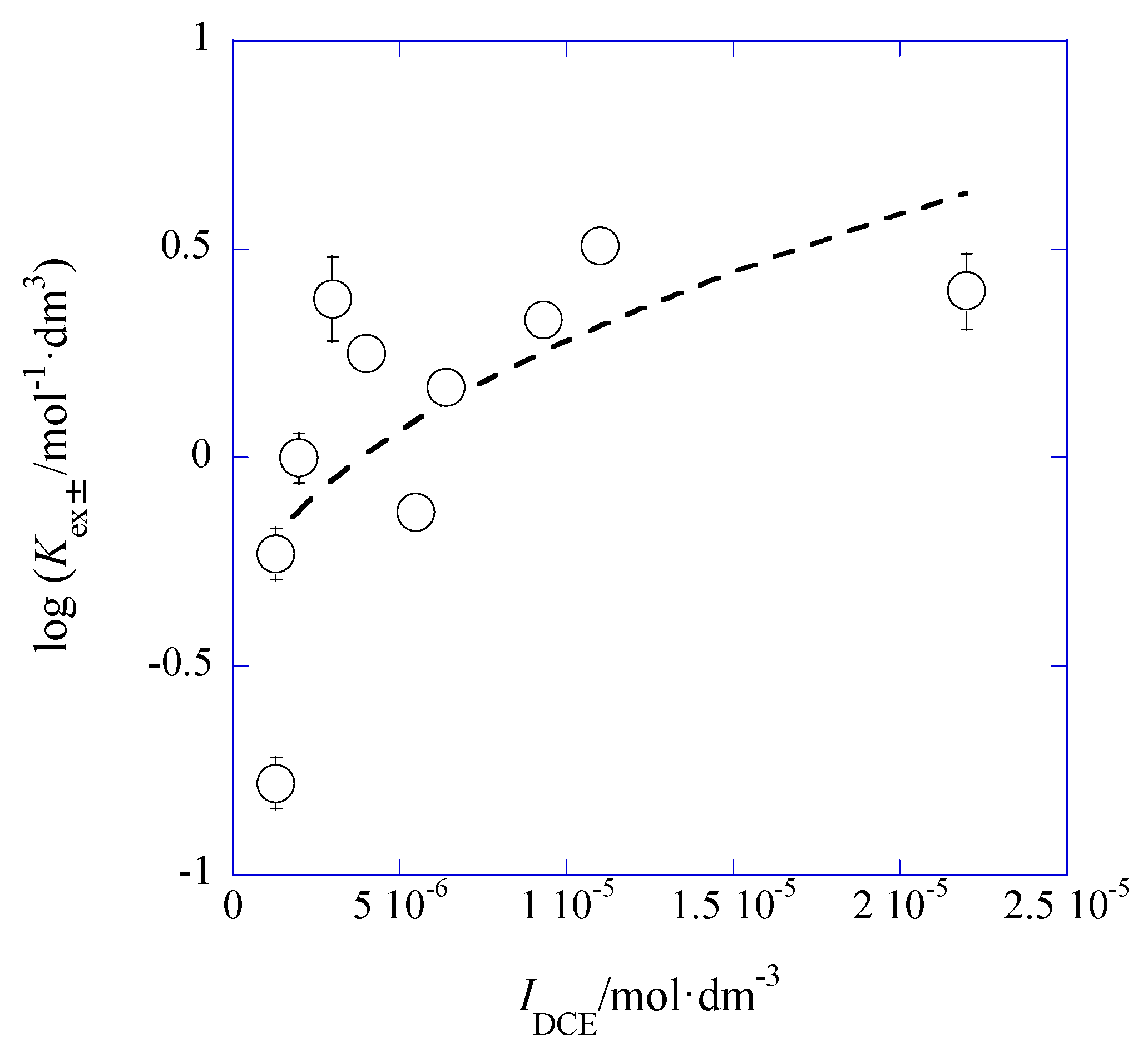
3.2. IDCE Dependence of LogKex±
Applying the DH limiting law [
14] for the system and rearranging Equation (6) at org = DCE, we can easily obtain
Hence, a plot of log
Kex± versus
IDCE yields log
Kex±0′′ and
ADCE values immediately. Here,
Kex±0′′ is defined as
aML,DCEaA,DCE/([M
+][L]
DCE[A
−]) (=
y+y−Kex±0).
Figure 7 shows its plot for the AgPic-18C6 extraction systems with DCE.
Also the average values of
IDCE were used for the plot (see
Section 3.1) and the
y+y− value in
Kex±0′′ was estimated on average (
N = 10) to be 0.76 ± 0.14. This product was calculated from the ion size parameters,
a(Ag
+) = 2.5 and
a(Pic
−) = 7 Å, in water [
15]. A plot analysis gave log
Kex±0′′ = −0.45 ± 0.24 and
ADCE = 116 ± 46 mol
−1/2·dm
3/2 at
r = 0.665. Accordingly, introducing
y+y− in log
Kex±0′′ = log
y+y− + log
Kex±0, the log
Kex±0 value became –0.36 ± 0.24. The experimental
ADCE value was much larger than its theoretical one (= 10.6 mol
−1/2·dm
3/2) for a pure DCE at 298 K. This difference between these
ADCE values may be due to simple errors caused by the narrow experimental
IDCE-range of (0.097–2.2) × 10
−5 mol·dm
−3 or to the condition where the diluent DCE was saturated with water.
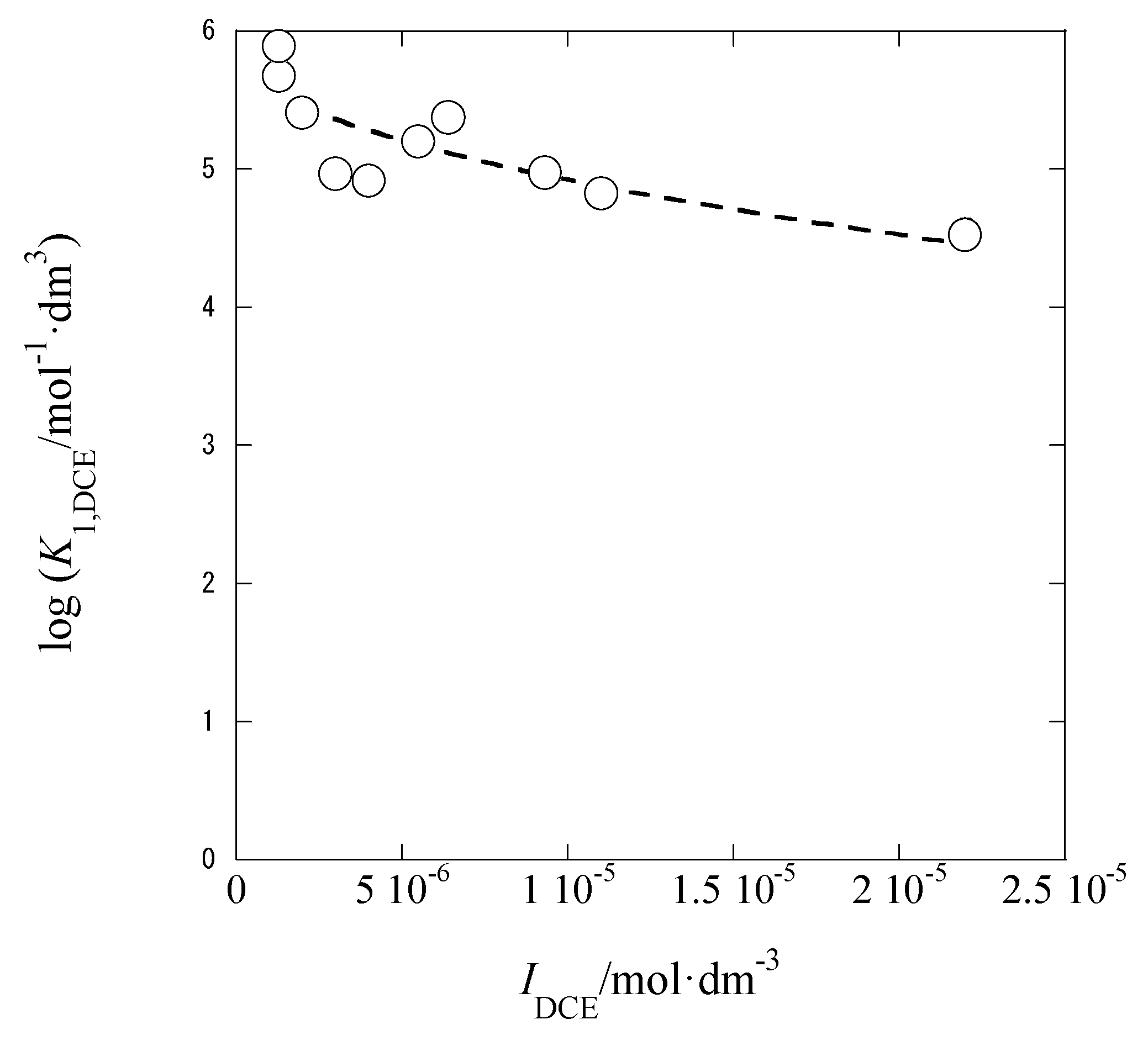
3.3. IDCE Dependences of LogK1,DCE
The thermodynamic ion-pair formation constant (
K1,org0) at
Iorg → 0 is described as
Rearranging this equation at org = DCE and ML
+ = AgB18C6
+ can give the following equation:
A plot of log
K1,DCE versus
IDCE is shown in
Figure 8. The plot analysis yielded the regression line with log
K1,DCE0 = 5.89 ± 0.19 and
ADCE = 152 ± 37 mol
−1/2·dm
3/2 at
r = 0.821 and
N = 10. This
ADCE value overlaps with the value (= 116) determined above (see
Section 3.2), within the calculation error (= 46) and much larger than the theoretical one too. The authors cannot clearly explain the larger experimental
ADCE values, as similar to
Section 3.2.
The logarithmic value, log
K1,DCEav, of simple average-
K1,DCE one was 5.36 ± 0.42 in the
IDCE range of (0.097-2.2) × 10
−5 mol·dm
−3 at
N = 10 and was smaller than the log
K1,DCE0 value (= 5.9 at
I → 0). Although the experimental
IDCE values were adequately small (
IDCE << 0.001), the magnitude of
K1,DCE decreased with an increase in
IDCE. Also, the log
K1,DCEav value was smaller than the log
KAgPic,DCE one (= 6.0, see
Section 2.1). From the log
Kex±0′ value (= 0.6) in
Section 3.1 and the log
Kex±0 one (= −0.36) in 3.2, we obtained log(
yAgB18C6,DCEy−,DCE) (= log
Kex±0 − log
Kex±0′) = −0.96 ± 0.27. Hence, the log
K1,DCE value was estimated to be 4.93 {= log
K1,DCE0 + log(
yAgB18C6,DCEy−,DCE) = 5.89−0.96}, being somewhat smaller than the log
K1,DCEav value (= 5.4). These facts indicate that the log
K1,DCEav value is not properly reflective of the log
K1,DCE one in Equation (7).
On the other hand, the log(KAgB18C6,DCE/mol−1·dm3) values were calculated from the relation logKML,org = logKex± − logKD,MS⋅KD,AS for a given IDCE. Here, we assumed that, considering the smaller IDCE values, the ratio, yMl,DCE/y+,DCE, of the activity coefficients in the thermodynamic complex-formation constant, KML,DCE0, equals unity. Accordingly, the approximation that an average value among the KAgB18C6,DCE ones equals the KAgB18C6,DCE0 value becomes valid. Consequently, as its logarithmic value, 7.77 ± 0.25 was obtained on average (N = 12) at 298 K.
3.4. A Trend between LogKD,Pic and Log(IDCE/I)
From a plot of log
KD,Pic versus log(
IDCE/
I), we obtained a theoretical line of log
KD,Pic = log(
IDCE/
I) − (0.09 ± 0.12) at
r = 0.398 (
Figure 9) under the condition of the fixed slope of unity, except for the points in the
I range of 0.024-0.26 mol·dm
−3. This trend suggests that the
KD,Pic values are basically proportional to the ratios of (
IDCE/
I), as reported before [
16]. The deviation of the five points in
Figure 9 can come from an effect of the higher
I values in (
IDCE/
I). An answer to this deviation is explained as follows.
For the case of only MA (or mixture of MX with small excess organic acid, HA) in w phase with L, we can propose the following equation for
I and
Iorg.
with the charge balance equation of [M
+] + [ML
+] = [A
−]. Similarly, the authors can obtain
in the org phase. The assumption that [AgB18C6
+]
DCE is much larger than [Ag
+]
DCE, namely [AgB18C6
+]
DCE ≈ [Pic
−]
DCE, was employed for the experiments. From Equations (8) and (8a), one can see easily the experimental relation that (
IDCE/
I) is basically proportional to
KD,Pic.
On the other hand, for the present case of mixture of MX with the small excess HA and excess HX (strong acid) in the w phase with L, the corresponding equations are
and
with the assumptions that [M
+] + [ML
+] + [H
+] ≈ [A
−] + [X
−] and [M
+]
org + [H
+]
org + [ML
+]
org + [HL
+]
org ≈ [A
−]
org (>> [X
−]
org), respectively. Therefore, Equations (9) and (9a) give the experimental relation of
and then its ratio becomes smaller than the
KD,Pic value in the case of [NO
3−] >> [Pic
−]. When [NO
3−] nearly equals [Pic
−] in Equation (9b), the log(
IDCE/
I) value deviates from the log
KD,Pic one by +0.3: that is, (
IDCE/
I) ≈
KD,Pic/2. However, such a deviation is comparable to experimental errors. Thus, Equation (9b) explains well the deviation of the five points from the regression line in
Figure 9. Obviously, the deviation becomes larger, when an excess of HX, such as HNO
3, was added in the w phase and X
− less distribute into the org phase than A
− does (for example, see the
KD,PicS &
KD,NO3S values in
Table 3).
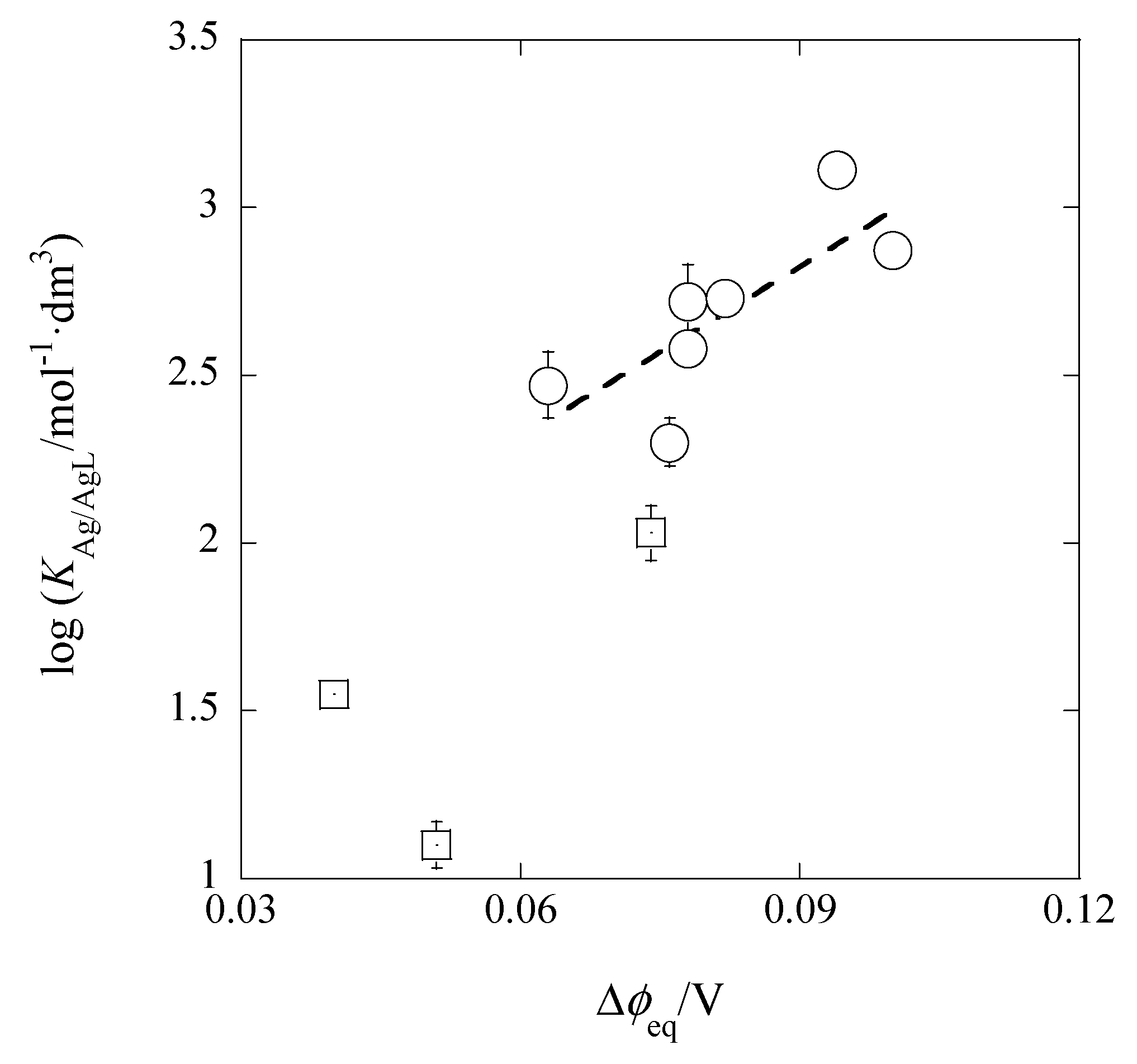
3.5. Δφeq Dependences of LogKM/ML and LogKex±
The log
KM/ML, defined as log([ML
+]
org/[M
+][L]
org) [
8], can be resolved as follows and calculated from log
Kex± − log
KD,A.
at 298 K with
Here, the term of log(
KD,MS⋅
KML,org) has to be a constant, because these two equilibrium constants are independent of Δ
φeq; log
KML,org = −(
F/2.303
RT) (standard formal potential of the ML
+ formation in the org phase) [
8]. The magnitude of the
KM/ML (or
KM/MLS) value shows an incorporation-ability into the org phase of L against M
+. Then, the plot of log
KM/ML versus Δ
φeq based on Equation (10) can yield a straight line with the slope of 17 V
−1 and the intercept of log
KD,MS⋅
KML,org.
Figure 10 shows its plot, of which the experimental regression line was log
KM/ML = (16.8 ± 6.1)Δ
φeq,Pic + (1.30 ± 0.50) at
r = 0.775 and
N = 7. Here, the three data (the squares in
Figure 10) were neglected from the calculation of the line, because their
I values were much larger than the values of the extraction systems without the presence of excess HNO
3 in the w phase (see
Table 1 and
Table 2). The Δ
φeq,Pic values show the Δ
φeq ones obtained from the experimental log
KD,Pic values. The predictable intercept value was calculated to be 1.30 (= log
KD,AgS + log
KAgB18C6,DCE = −6.47 + 7.77) ± 0.25, being in accord with the experimental value. Similarly, the slope value was in good agreement with its theoretical one (= 17). These facts indicate that the Δ
φeq,Pic values essentially correspond to the Δ
φeq ones in log
KD,Ag {see Equation (10a)}. In other words, the relation of log
KAg/AgB18C6 = (slope) × Δ
φeq,Pic + log
KD,AgS·
KAgB18C6,DCE is satisfied.
A plot of log
Kex± versus Δ
φeq for the A
− = Pic
−, ClO
4−, and NO
3− systems also gave a regression line with a slope of 19.3 ± 2.0 V
−1 and an intercept of −1.23 ± 0.18 at
r = 0.974 and
N = 7 in the narrow
I range (see
Table 1 for their basic data). This slope was very close to the theoretical value (= 17). As similar to the previous results [
11], these results indicate that the plot satisfies the relation of log
Kex± = 16.90Δ
φeq + log
KD,A + log
KD,AgS·
KAgB18C6,DCE (= 16.90Δ
φeq + log
KD,A + 1.30). The (log
KD,A + 1.3) term corresponds to the intercept [
11] within ±0.3 at least.
3.6. Evaluation of LogKex± Based on LogKD,AS
Using the log
KM/MLS and log
KD,AS values, we can immediately evaluate the log
Kex± value as follows. A thermodynamic cycle gives
by using Equations (10a) and (4). It is difficult to accurately determine the
KD,MS {or
KD,M(Δ
φeq): the function of Δ
φeq, see Equation (10a)} and
KML,org values. On the other hand, it is comparatively easy to determine the
KM/MLS value. So, if the log
KM/MLS {or log
KM/ML(Δ
φeq)} value is determined for given ML
+ and diluent, then the log
Kex± values can be calculated from Equation (11) with the log
KD,AS {or log
KD,A(Δ
φeq)} ones. In this study, we determined the log
KAg/AgLS value to be 1.30 from the data (see
Table 1) of the AgPic-B18C6 extraction systems with DCE. Calculated log
Kex± values for some A
− are listed in
Table 3, together with several experimental values.
The determination of the
Kex± values will be experimentally difficult for the Cl
− to I
− extraction systems, because of the precipitation [
18] of their silver salts. The same is true of the SCN
− extraction system, because of its low solubility product (= 1.0 × 10
−12 mol
2·dm
−6 [
18]) against Ag
+ in water. Also, AgN
3, which is a white insoluble crystal, is explosive [
19]. Therefore, the experimental
Kex± values were determined at 298 K for the ClO
4− and NO
3− extraction systems (see
Table 1). Considering the differences (0.03–0.26) between the log
KD,AS values at a fixed A
− in
Table 3 and the standard deviation (= 0.3) of the log
KAg/AgB18C6S value, these experimentally-obtained log
Kex± values are very close to the values evaluated here.
Similar results were obtained for the NaA-B18C6 extraction into DCE. Their log
Kex± values evaluated from log
KNa/NaB18C6S = 0.53, which were calculated here, were −2.8 for A
− = MnO
4− and −2.3 for ClO
4−. Their experimental log
Kex± values were −2.23 [
13] at
I = 0.0077 mol·dm
−3 for MnO
4− and −3.65 ± 0.07 at 0.074 for ClO
4− of which the value was re-calculated from the data reported before [
8]. These differences, ≤ ∣1.4∣, between the evaluated and experimental values were larger than those for the AgA-B18C6 extraction systems.
The above fact indicates that the log
Kex± values can be evaluated from a sum of the log
KAg/AgB18C6S and log
KD,AS (or log
KAg/AgB18C6 & log
KD,A) ones. Namely, the order, A
− = NO
3− < ClO
4− << Pic
−, in log
Kex± for a given extraction system at fixed AgB18C6
+ and DCE is fundamentally predicted from that of log
KD,AS (see
Table 3). Thus, for the systems where the extraction experiments are difficult, the present procedure becomes easy to evaluate the log
Kex± values. Also, the experimental intercepts (≈ log
Kex± [
13]) of the straight lines in
Figure 2 support this order: the intercepts were −4.05 for A
− = NO
3−, −0.92 for ClO
4−, and 2.20 for Pic
−.
4. Materials and Methods
4.1. Materials
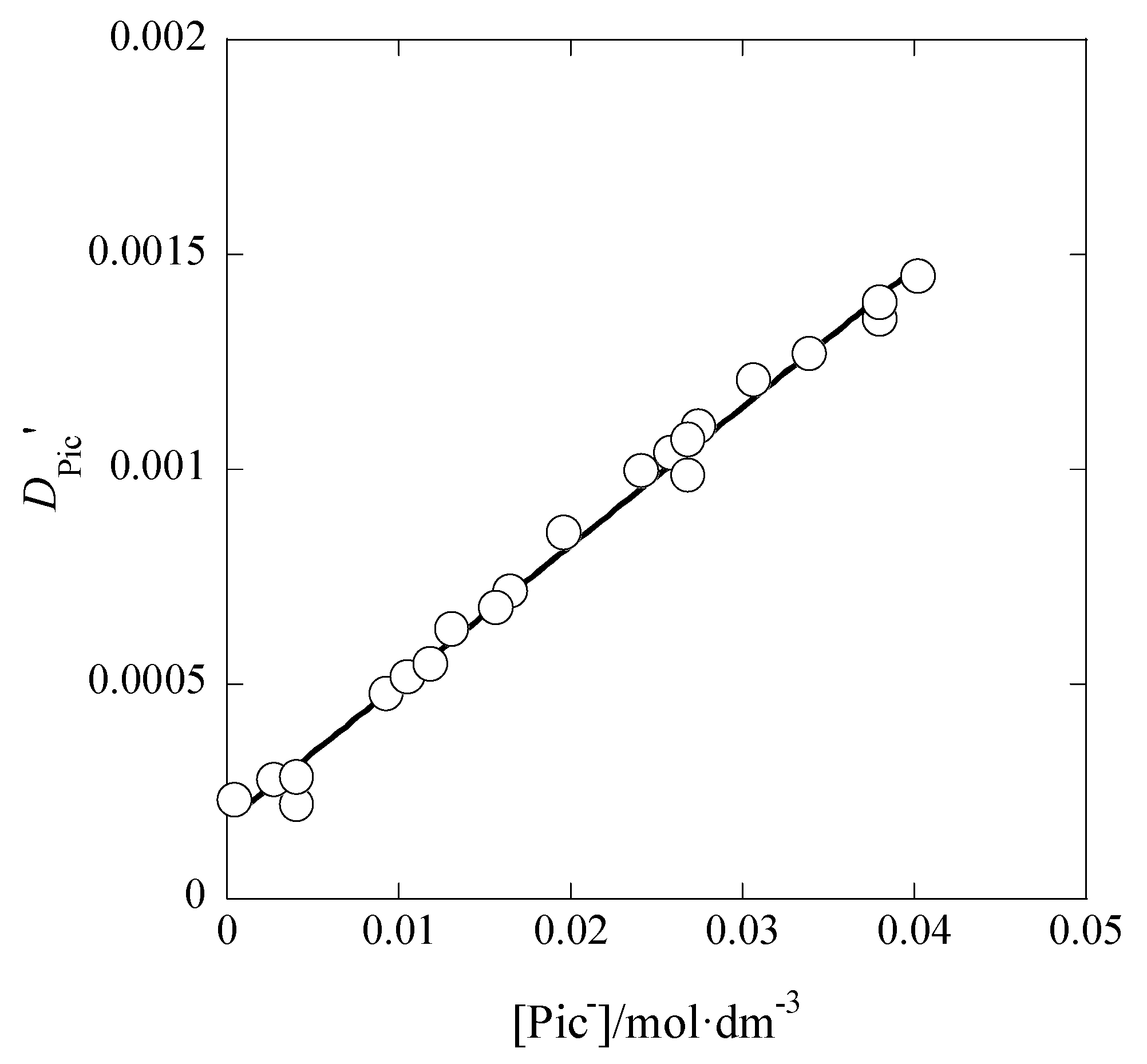
An aqueous solution of a commercial Ba(OH)2·8H2O (≥98%, Wako Pure Chemical Industries, Tokyo, Japan) and a solution with 2 equivalents of HPic·nH2O (≥99.5%, Wako Pure Chemical Industries, Tokyo, Japan) were mixed, that of Ag2SO4 (≥99.5%, Kanto Chemicals Co. Ltd., Tokyo, Japan) was added in the mixture, and immediately BaSO4 precipitated. After standing the mixture overnight, the thus-obtained yellow solution with the precipitate was filtered and then its filtrate was evaporated by a rotary evaporator (type RE1-N, Iwaki, Japan) in order to deposit a fine yellow crystal. The crystal obtained was filtered and dried in vacuo for 21 h. Found: 97.29% for Ag by the AAS measurements at 328.1 nm; 101% for Pic− by spectrophotometric measurements at 355.0 nm. An amount of water in the AgPic crystal was not detected by a Karl-Fischer titration. This crystal was employed only for the AgPic extraction experiments without B18C6.
Concentrations of the aqueous solution with AgNO
3 (≥99.8%, Kanto Chemicals Co. Ltd., Tokyo, Japan) and that with AgClO
4 (97%, Aldrich, Missouri, MO, USA) were determined by a precipitation titration with NaCl (99.98% ± 0.01%, Wako: standard reagent for volumetric analysis, Wako Pure Chemical Industries, Tokyo, Japan). A commercial DCE (guaranteed-pure reagent, Kanto Chemicals Co. Ltd., Tokyo, Japan) was treated with the same procedure as that described previously [
13,
16]. All other chemicals used in this study were of guaranteed-pure reagent grade.
4.2. Extraction Experiments
Procedures for both the AgPic extraction experiments and the AgA extraction ones with B18C6 into DCE were essentially the same as those [
8,
20] reported before. The latter experiments were performed by using mixtures of AgNO
3 with HPic in the w phases. The total concentration range of Ag(I) was 0.00041 to 0.043 mol·dm
−3 for the AgPic extraction and the ranges of AgNO
3, HPic, and B18C6 were (1.5 or 5.0) × 10
−4, (3.3 or 3.4) × 10
−3, and (0.4–7.5) × 10
−4 mol·dm
−3, respectively, for the Ag(I) extraction with B18C6. The extraction of AgB18C6
+ with NO
3− or Ag(B18C6)NO
3 was negligible, compared with that of AgB18C6
+ with Pic
− or Ag(B18C6)Pic (see
Figure 2 or the log
Kex± and log
Kex values in
Table 1). After the extraction operations, the w phases were in the pH ranges of 2.68–2.74 at the system of
I = 0.0025 mol·dm
−3 and 2.70–3.37 at that of 0.0031 (see
Table 1).
For the AgPic extraction by B18C6 into DCE in the presence of “excess HNO3“ in the w phases, the total concentrations of AgNO3 and HPic were fixed at 1.5 × 10−4 and 0.0033 or 0.0034 mol·dm−3, respectively. Under this condition, the total concentration, [HNO3]t, of HNO3 in the w phase was changed in the range of 0.025 to 0.25 mol·dm−3. After the extraction operations, the w phases were in the pH ranges of 1.64 and 1.65 at [HNO3]t = 0.025 mol·dm−3, 1.34–1.38 at 0.050, 1.06 at 0.10, and 0.62–0.68 at 0.25.
Used apparatus, such as the atomic absorption spectrophotometer, UV-V, centrifuge, mechanical shaker, and pH meter with the glass electrode, were the same as those [
8,
16] described previously.
5. Conclusions
The I or IDCE dependences of the logKex± and logKex values for the present extraction systems were clarified experimentally. Their experimental equations were logKex = 5.3 – 2×0.51) and logKex± = 0.6 − 2×2.0 = −0.5 + 2×116. However, the magnitudes of these changes in logKex± or logKex with I or IDCE were insignificant in practical separation. It was also suggested that the style of M(I) employed in the extraction experiments with L, either the simple salt MPic or the mixture of MX with HPic and excess HX, largely control whether the logKD,Pic values are dependent on the log(IDCE/I ) ones or not. The logKex±-versus-Δφeq plot for the Pic−, ClO4−, and NO3− systems yielded the good positive correlation. On the basis of the plot of logKAg/AgB18C6 versus Δφeq,Pic, it was indirectly proved that the Δφeq values obtained from the KD,Pic ones is common to those from the KD,Ag values. Moreover, the logKex± values were predicted from the sum of the logKD,AS and logKAg/AgB18C6S ones for given MB18C6+ and DCE at least. At the same time, the order in Kex± reflected that in KD,AS.