Ultrashort Laser Pulse Focusing by Amplitude and Phase Zone Plates
Abstract
:1. Introduction
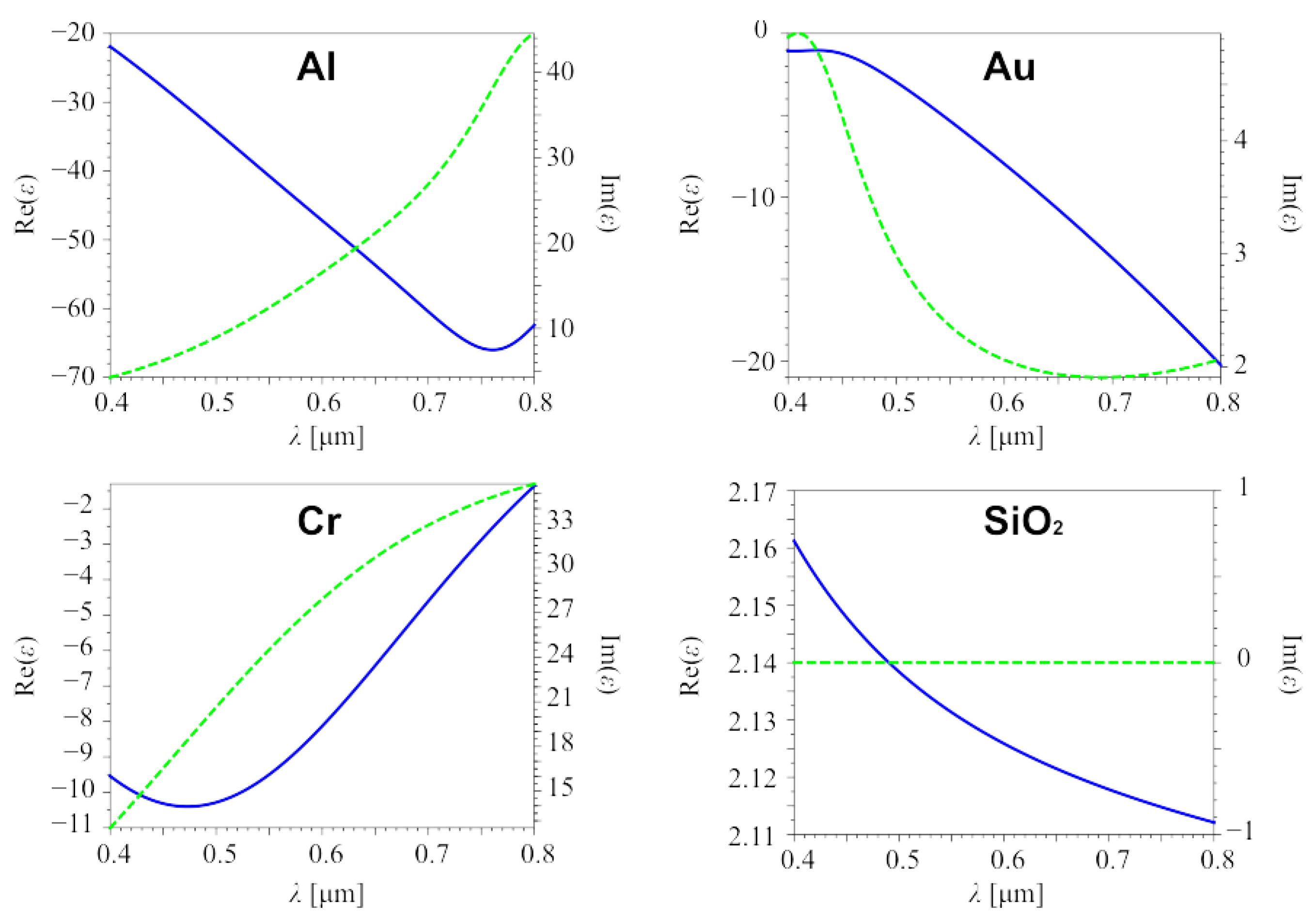
2. Materials and Methods
3. Results and Discussion
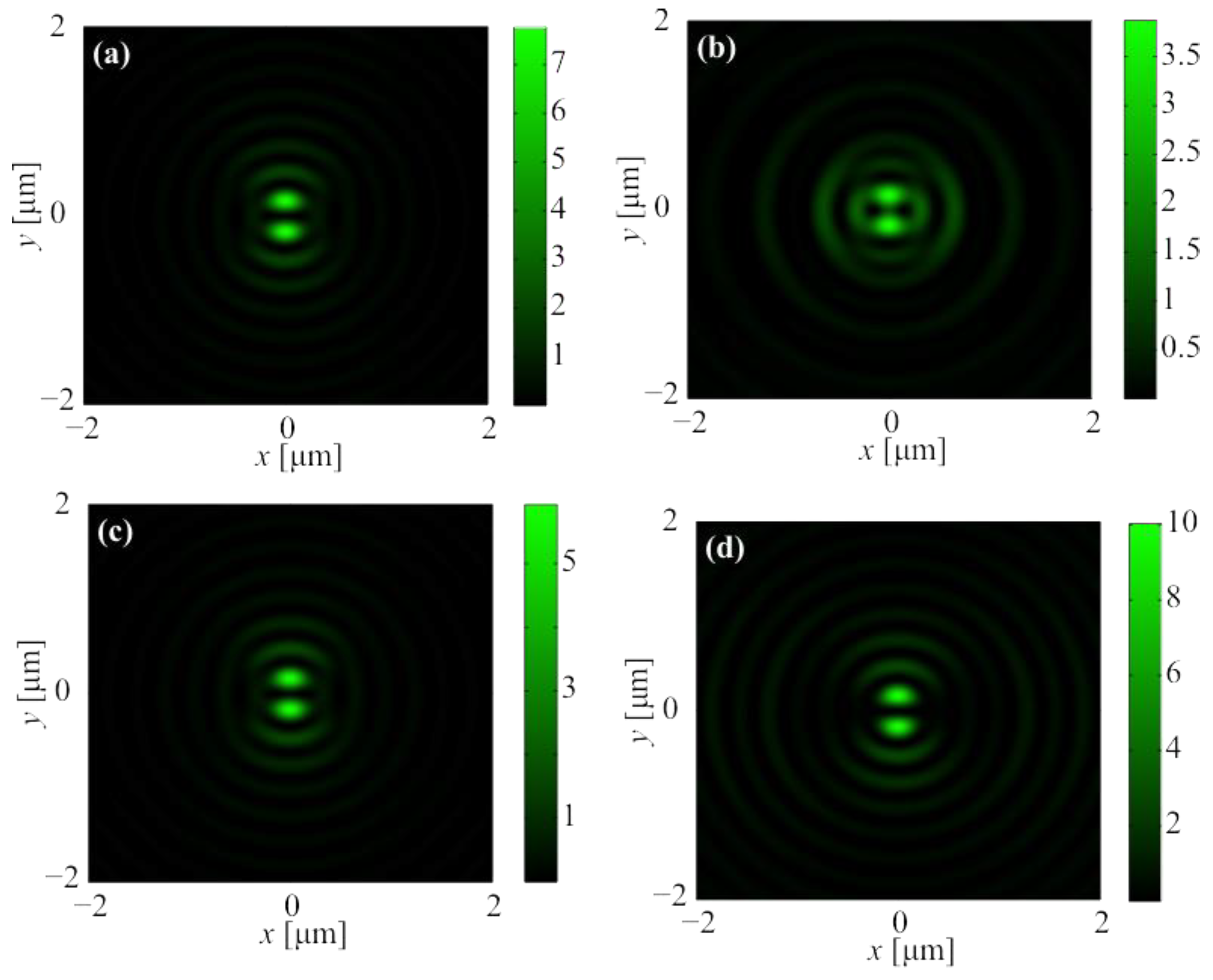
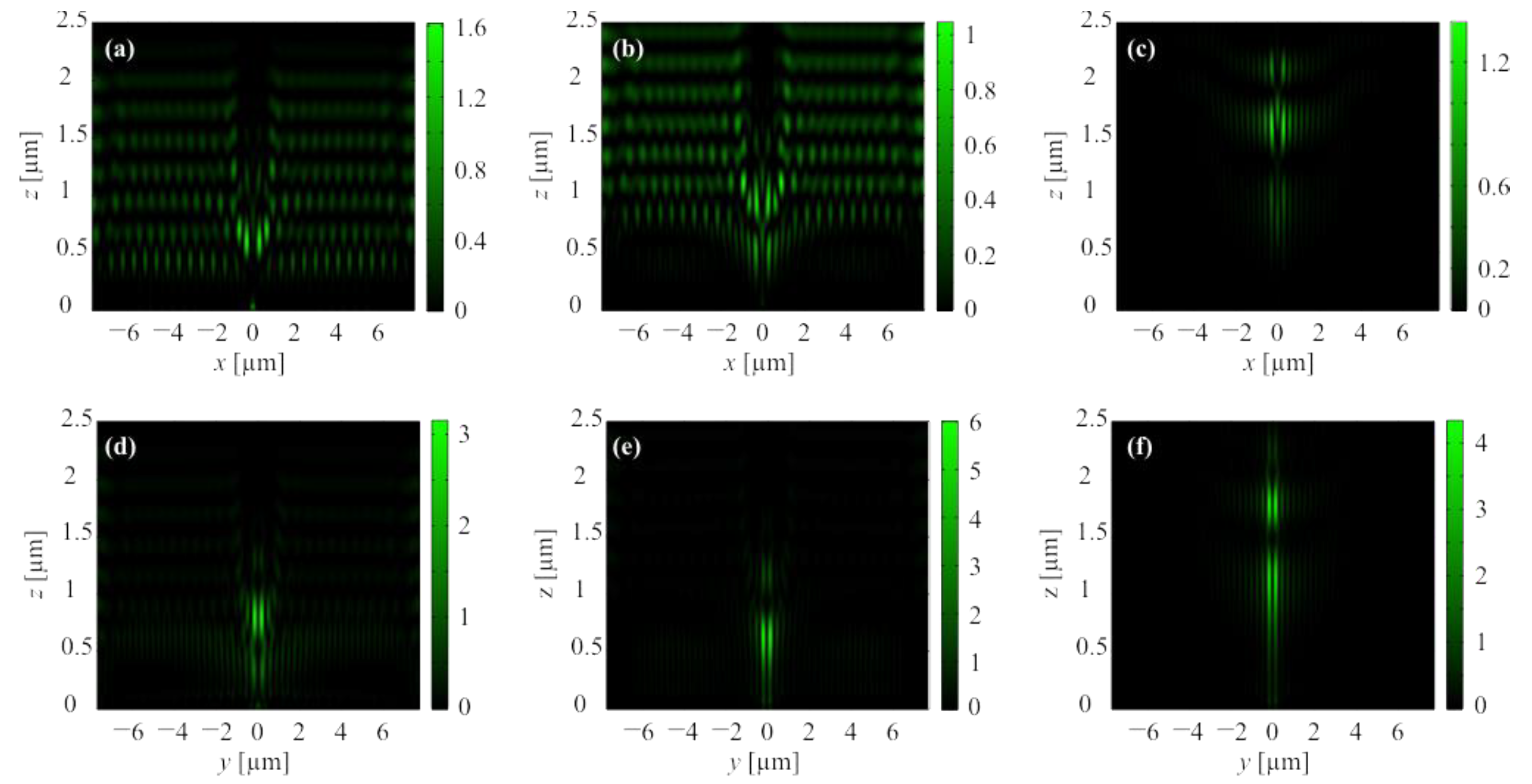
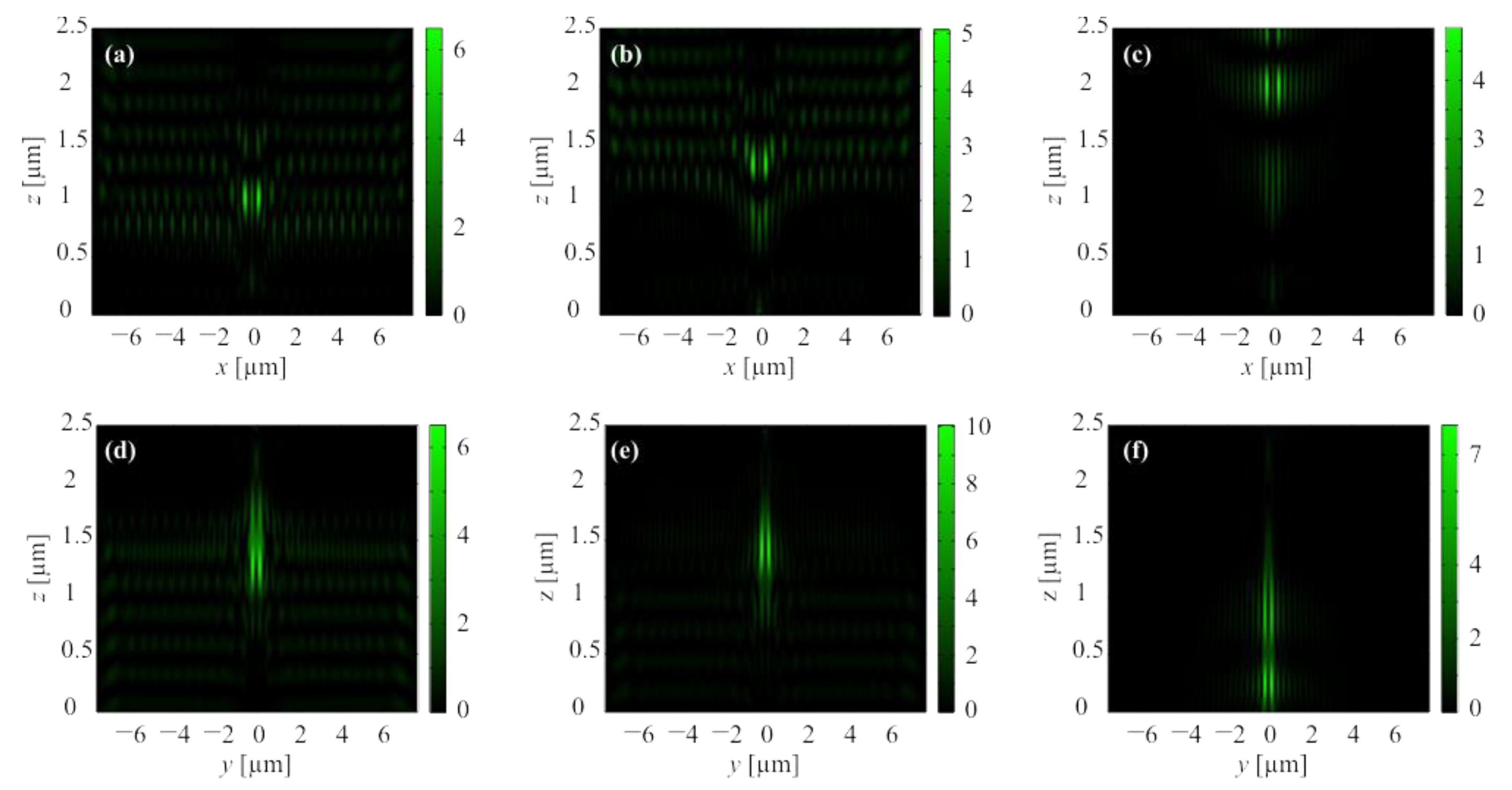
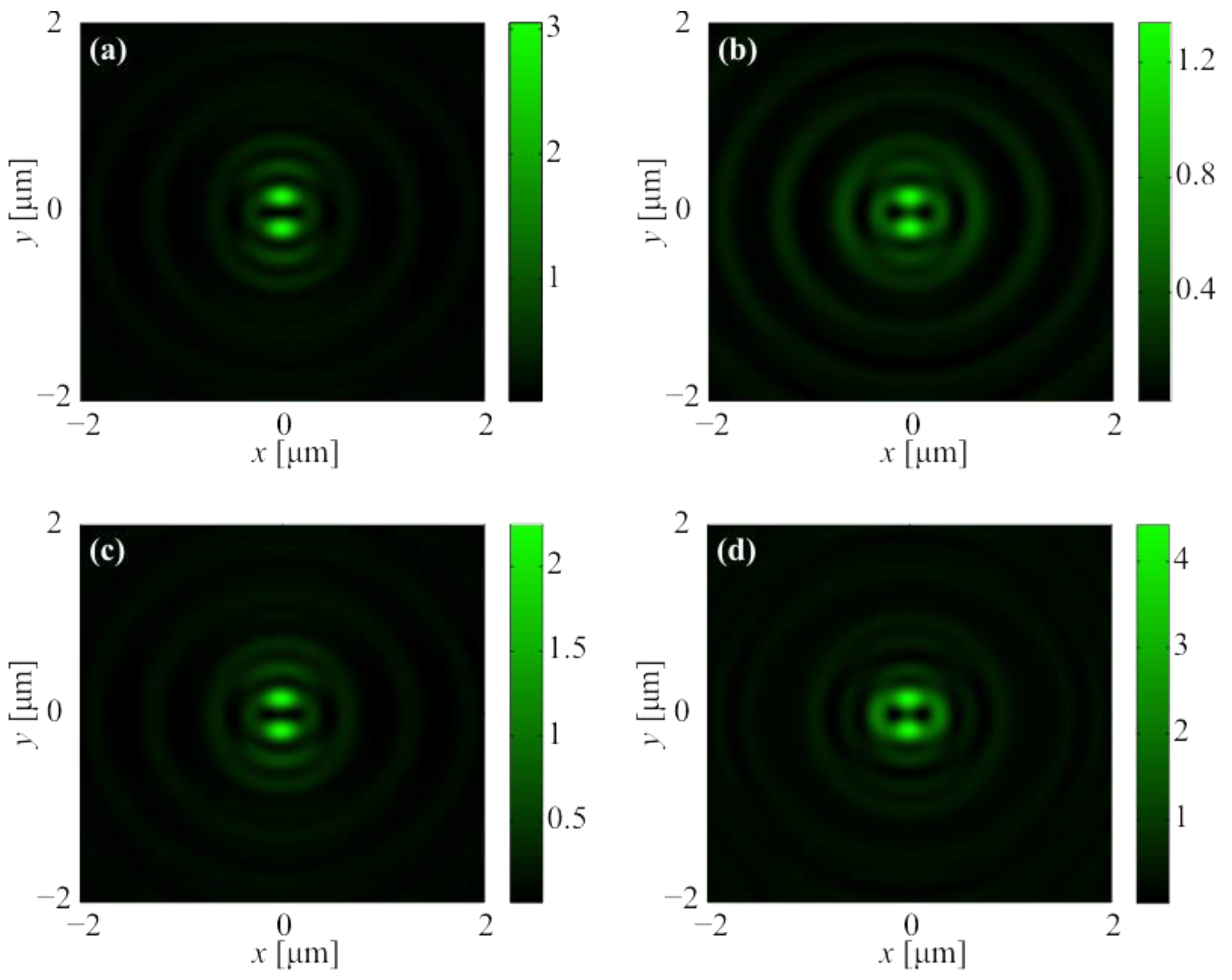
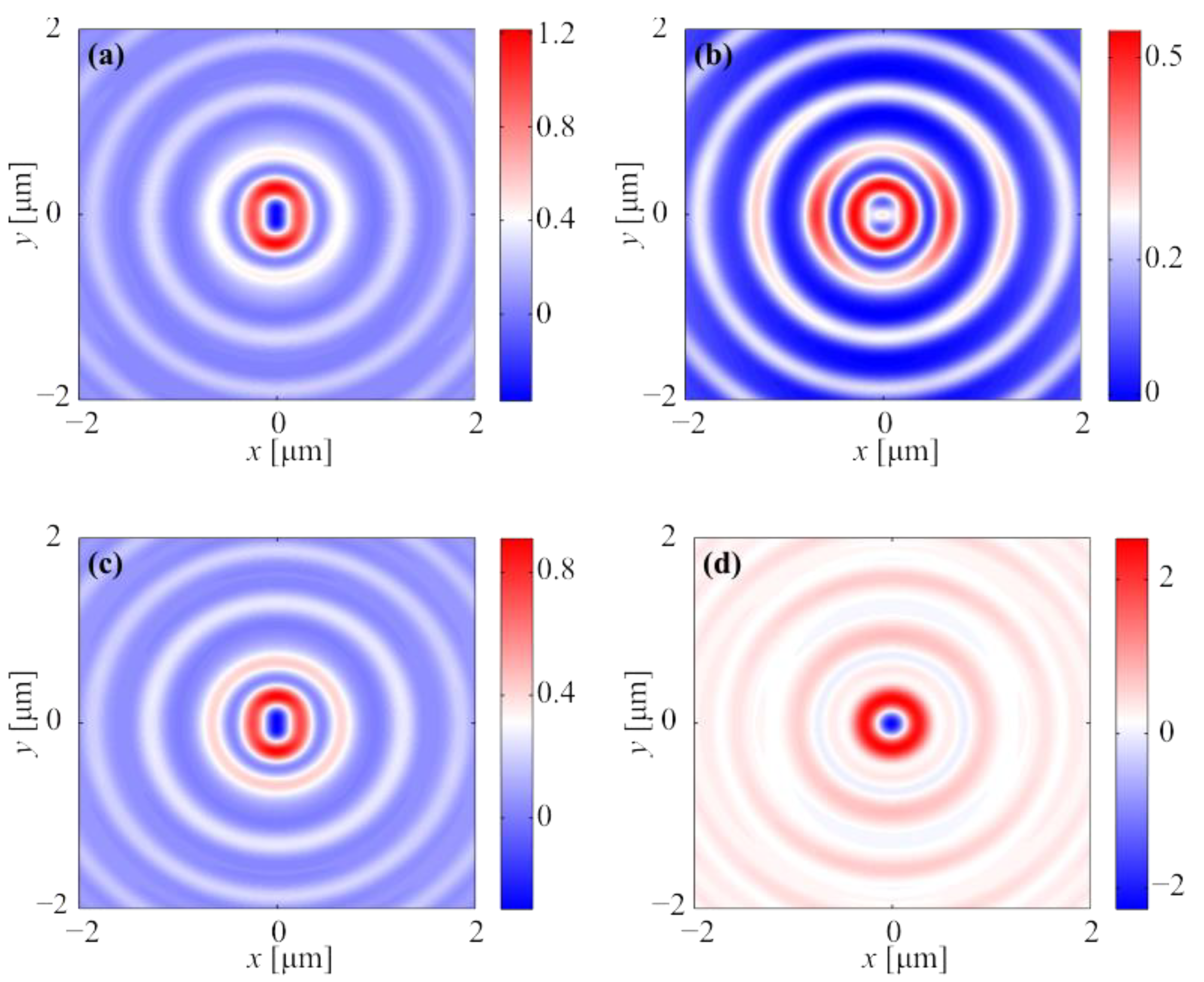
3.1. Instantaneous Distributions of Light Field in the Focus
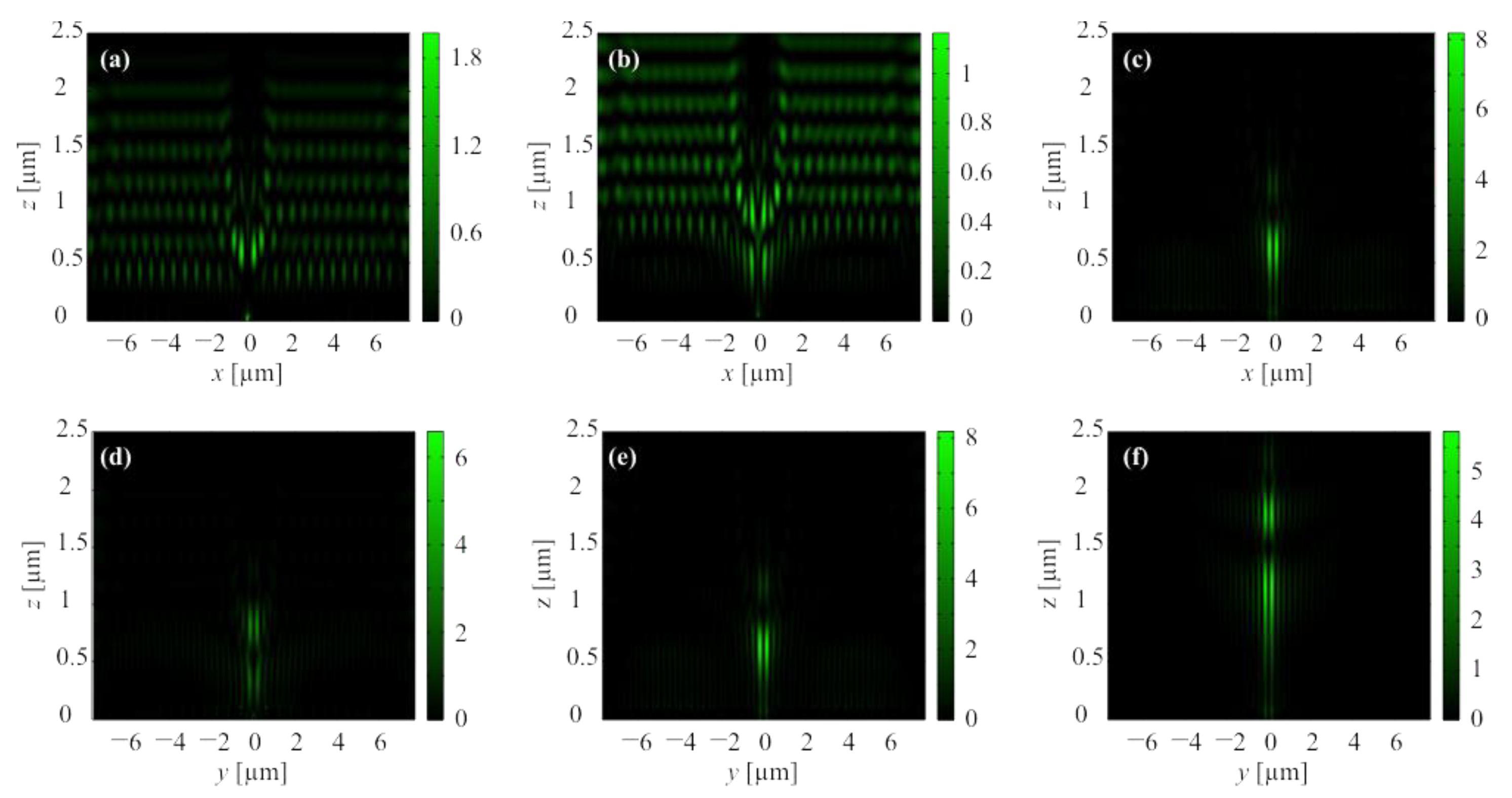
3.2. Averaged Distributions of Light Field in the Focus
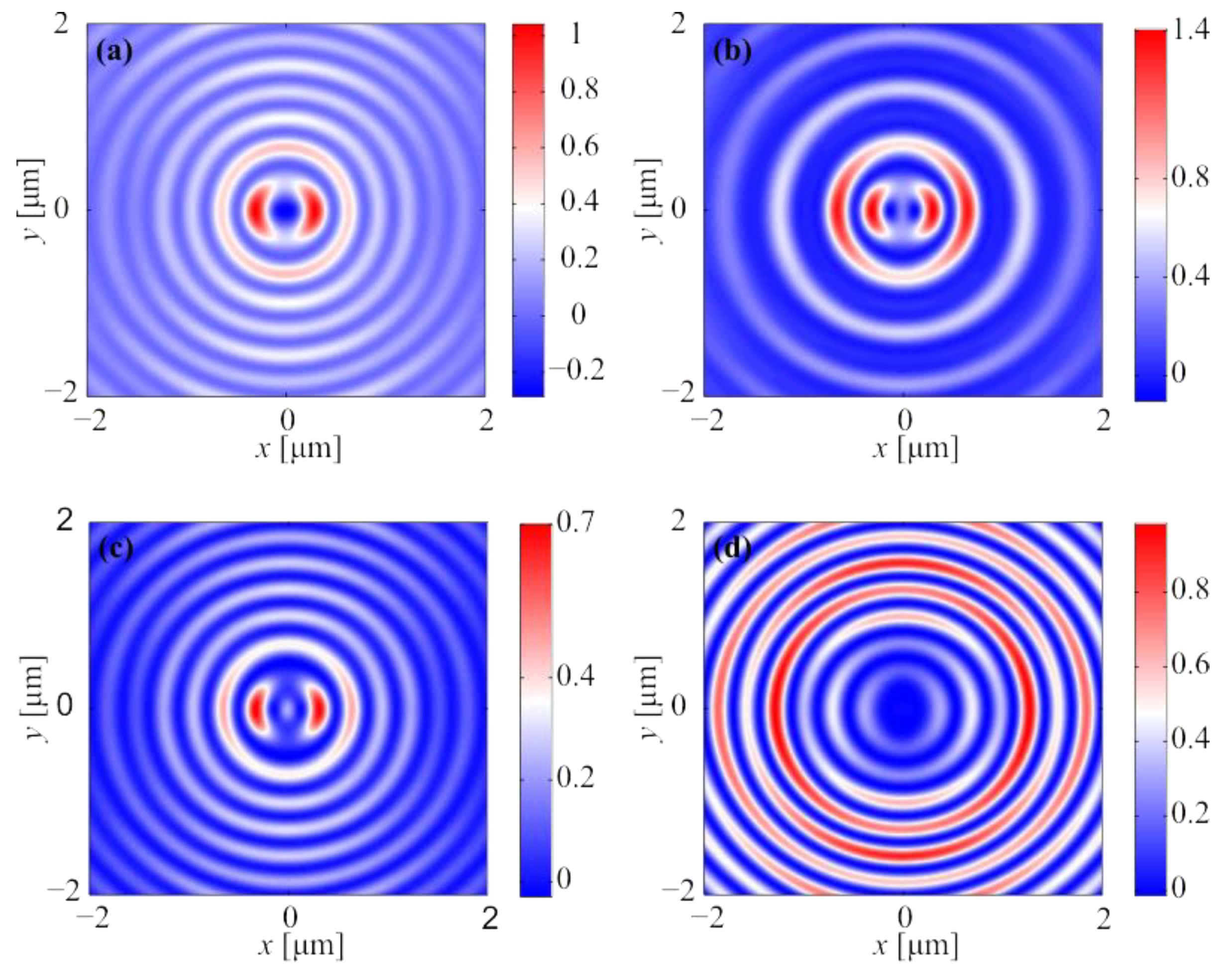
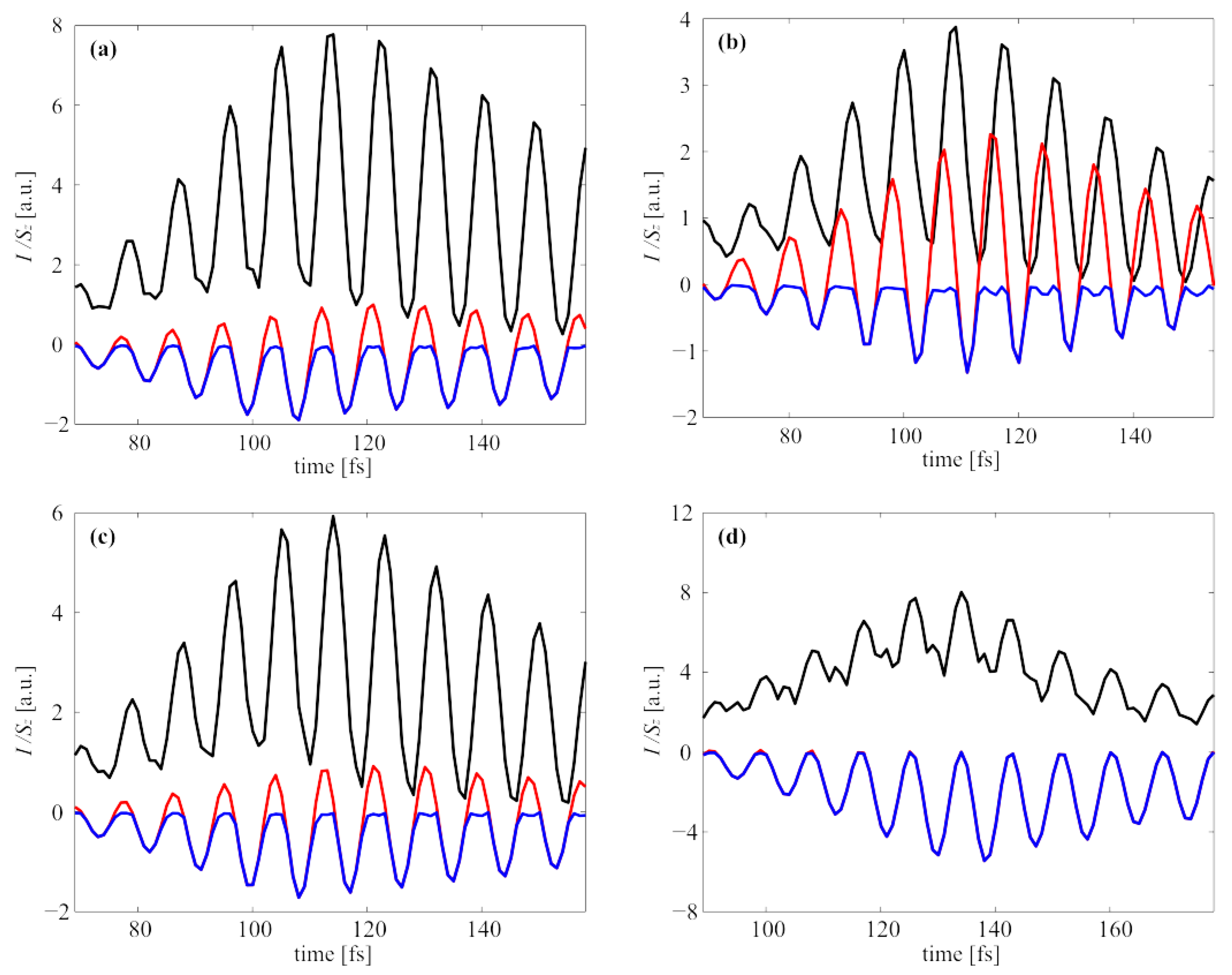
3.3. Dynamics of Intensity and Longitudinal Component of Poynting Vector in the Focus
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zuo, R.; Liu, W.; Cheng, H.; Chen, S.; Tian, J. Breaking the Diffraction Limit with Radially Polarized Light Based on Dielectric Metalenses. Adv. Opt. Mat. 2018, 6, 1800795. [Google Scholar] [CrossRef]
- Chang, K.-H.; Chen, Y.-C.; Chang, W.-H.; Lee, P.-T. Efficient modulation of subwavelength focusing via metaaperture-based plasmonic lens for multifunction applications. Sci. Rep. 2018, 8, 13648. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Stafeev, S.S.; Nalimov, A.G. Vortex energy flow in the tight focus of a non-vortex field with circular polarization. Comput. Opt. 2020, 44, 5–11. [Google Scholar] [CrossRef]
- Wang, S.; Wu, P.C.; Su, V.-C.; Lai, Y.-C.; Chen, M.-K.; Kuo, H.Y.; Chen, B.H.; Han Chen, Y.; Huang, T.-T.; Wang, J.-H.; et al. A broadband achromatic metalens in the visible. Nat. Nanotechnol. 2018, 13, 227–232. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Stafeev, S.S.; Nalimov, A.G.; Kotlyar, M.V.; O’Faolain, L.; Kozlova, E.S. Tight focusing of laser light using a chromium Fresnel zone plate. Opt. Express 2017, 25, 19662–19671. [Google Scholar] [CrossRef]
- Zhuang, J.; Zhang, L.; Deng, D. Tight-focusing properties of linearly polarized circular Airy Gaussian vortex beam. Opt. Lett. 2020, 45, 296–299. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Stafeev, S.S.; Kovalev, A.A. Sharp focusing of a light field with polarization and phase singularities of an arbitrary order. Comput. Opt. 2019, 43, 337–346. [Google Scholar] [CrossRef]
- Li, M.; Cai, Y.; Yan, S.; Liang, Y.; Zhang, P.; Yao, B. Orbit-induced localized spin angular momentum in strong focusing of optical vectorial vortex beams. Phys. Rev. A 2018, 97, 053842. [Google Scholar] [CrossRef]
- Volpe, A.; Gaudiuso, C.; Ancona, A. Sorting of Particles Using Inertial Focusing and Laminar Vortex Technology: A Review. Micromachines 2019, 10, 594. [Google Scholar] [CrossRef]
- Stafeev, S.S.; Kozlova, E.S.; Nalimov, A.G. Focusing a second-order cylindrical vector beam with a gradient index Mikaelian lens. Comput. Opt. 2020, 44, 29–33. [Google Scholar] [CrossRef]
- Lavanya, M.; Thiruarul, D.; Rajesh, K.B.; Mahadevan, G.; Velauthapillai, D.; Jaroszewicz, Z. Energy flux density for higher-order cylindrical vector vortex beam tightly focused through a dielectric interface. J. Opt. 2021, 50, 548–558. [Google Scholar] [CrossRef]
- Rahimian, M.G.; Jain, A.; Larocque, H.; Corkum, P.B.; Karimi, E.; Bhardwaj, V.R. Spatially controlled nano-structuring of silicon with femtosecond vortex pulses. Sci. Rep. 2020, 10, 12643. [Google Scholar] [CrossRef] [PubMed]
- Kohmura, Y.; Zhakhovsky, V.; Takei, D.; Suzuki, Y.; Takeuchi, A.; Inoue, I.; Inubushi, Y.; Inogamov, N.; Ishikawa, T.; Yabashi, M. Nano-structuring of multi-layer material by single x-ray vortex pulse with femtosecond duration. Appl. Phys. Lett. 2018, 112, 123103. [Google Scholar] [CrossRef]
- Bhuyan, M.K.; Velpula, P.K.; Colombier, J.P.; Olivier, T.; Faure, N.; Stoian, R. Single-shot high aspect ratio bulk nanostructuring of fused silica using chirp-controlled ultrafast laser Bessel beams. Appl. Phys. Lett. 2014, 104, 021107. [Google Scholar] [CrossRef]
- Podlipnov, V.V.; Ivliev, N.A.; Khonina, S.N.; Nesterenko, D.V.; Vasilev, V.S.; Achimova, E.A. Investigation of photoinduced formation of microstructures on the surface of carbaseole-containing azopolymer depending on the power density of incident beams. Comput. Opt. 2018, 42, 779–785. [Google Scholar] [CrossRef]
- Chattaraj, S.; Madhukar, A. Multifunctional all-dielectric nano-optical systems using collective multipole Mie resonances: Toward on-chip integrated nanophotonics. J. Opt. Soc. Am. B 2016, 33, 2414–2423. [Google Scholar] [CrossRef]
- Bunandar, D.; Lazovich, T.; Gould, M.; Braid, R.; Ramey, C.; Harris, N.C. Programmable Nanophotonics for Computation. In Proceedings of the 2018 IEEE 15th International Conference on Group IV Photonics (GFP), Cancun, Mexico, 29–31 August 2018. [Google Scholar] [CrossRef]
- Xian, M.; Xu, Y.; Ouyang, X.; Cao, Y.; Lan, S.; Li, X. Segmented cylindrical vector beams for massively-encoded optical data storage. Sci. Bull. 2020, 65, 2072–2079. [Google Scholar] [CrossRef]
- Singh, B.K.; Nagar, H.; Roichman, Y.; Arie, A. Particle manipulation beyond the diffraction limit using structured super-oscillating light beams. Light Sci. Appl. 2017, 6, 17050. [Google Scholar] [CrossRef]
- Rodrigues Ribeiro, R.S.; Dahal, P.; Guerreiro, A.; Jorge, P.A.S.; Viegas, J. Fabrication of Fresnel plates on optical fibres by FIB milling for optical trapping, manipulation and detection of single cells. Sci. Rep. 2017, 7, 4485. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Nalimov, A.G.; Kovalev, A.A.; Porfirev, A.P.; Stafeev, S.S. Transfer of spin angular momentum to a dielectric particle. Comput. Opt. 2020, 44, 333–342. [Google Scholar] [CrossRef]
- Mendis, B.G. A semi-classical theory of magnetic inelastic scattering in transmission electron energy loss spectroscopy. Ultramicroscopy 2021, 230, 113390. [Google Scholar] [CrossRef] [PubMed]
- Meng, Z.; Traverso, A.J.; Ballmann, C.W.; Troyanova-Wood, M.A.; Yakovlev, V.V. Seeing cells in a new light: A renaissance of Brillouin spectroscopy. Adv. Opt. Photon. 2016, 8, 300–327. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, T.; Yang, S.; Wang, T.; Wang, Y. Validation of vectorial theories for the focusing of high numerical aperture Fresnel zone plates. Opt. Commun. 2018, 429, 119–126. [Google Scholar] [CrossRef]
- Geints, Y.E.; Minin, O.V.; Panina, E.K.; Minin, I.V. Controlling near-field focusing of a mesoscale binary phase plate in an optical radiation field with circular polarization. Comput. Opt. 2021, 45, 512–519. [Google Scholar] [CrossRef]
- Huang, P.; Zhou, Z.; Ren, H. Fresnel zone plate fabricated using a polyvinyl chloride gel. Opt. Eng. 2018, 57, 117101. [Google Scholar] [CrossRef]
- Kim, J.; Kim, H.; Lee, G.-Y.; Kim, J.; Lee, B.; Jeong, Y. Numerical and Experimental Study on Multi-Focal Metallic Fresnel Zone Plates Designed by the Phase Selection Rule via Virtual Point Sources. Appl. Sci. 2018, 8, 449. [Google Scholar] [CrossRef]
- Kozlova, E.S.; Kotlyar, V.V. Simulation of tight focusing of laser light by gold zone plate. In Proceedings of the 20th International Conference on Transparent Optical Networks (ICTON), Bucharest, Romania, 1–5 July 2018. [Google Scholar] [CrossRef]
- Wang, H.; Deng, Y.; He, J.; Gao, P.; Yao, N.; Wang, C.; Luo, X. Subwavelength light focusing of plasmonic lens with dielectric filled nanoslits structures. J. Nanophotonics 2014, 8, 083079. [Google Scholar] [CrossRef]
- Zaitcev, V.D.; Stafeev, S.S.; Kotlyar, V.V. Diffraction of laser radiation by a binary zone plate with fractional order. Proc. SPIE 2021, 12295, 1229517. [Google Scholar] [CrossRef]
- Peng, R.; Li, X.; Zhao, Z.; Wang, C.; Hong, M.; Luo, X. Super-Resolution Long-Depth Focusing by Radially Polarized Light Irradiation Through Plasmonic Lens in Optical Meso-field. Plasmonics 2014, 9, 55–60. [Google Scholar] [CrossRef]
- Kozlova, E.S.; Kotlyar, V.V.; Stafeev, S.S.; Fomchenkov, S.A. Fresnel Zone Plate in Thin Aluminum Film. In Proceedings of the Photonics & Electromagnetics Research Symposium-Spring (PIERS-Spring), Rome, Italy, 17–20 June 2019; pp. 4333–4338. [Google Scholar] [CrossRef]
- Kozlova, E.; Stafeev, S.; Fomchenkov, S.; Podlipnov, V.; Savelyeva, A.; Kotlyar, V. Measuring of Transverse Energy Flows in a Focus of an Aluminum Lens. Photonics 2022, 9, 592. [Google Scholar] [CrossRef]
- Kozlov, S.A.; Samartsev, V.V. Fundamentals of Femtosecond Optics, 1st ed.; Woodhead Publishing: Sawston, UK, 2013. [Google Scholar]
- Kozlova, E.S.; Kotlyar, V.V. Temporary compression of femtosecond pulses in the focusof truncated microellipsoid. Comput. Opt. 2014, 38, 380–385. [Google Scholar] [CrossRef]
- Bruening, S.; Gillner, A.; Du, K. Multi beam microprocessing for printing and embossing applications with high power ultrashort pulsed lasers. Adv. Opt. Technol. 2021, 10, 25. [Google Scholar] [CrossRef]
- Yu, Y.; Bai, S.; Wang, S.; Hu, A. Ultrashort Pulsed Laser Manufacturing and Surface Processing of Microdevices. Engineering 2018, 4, 779–786. [Google Scholar] [CrossRef]
- Wang, X.; Yu, H.; Lia, P.; Zhang, Y.; Wen, Y.; Qiu, Y.; Liu, Z.; Li, Y.; Liu, L. Femtosecond laser-based processing methods and their applications in optical device manufacturing: A review. Opt. Laser Technol. 2021, 135, 106687. [Google Scholar] [CrossRef]
- Yulianto, N.; Kadja, G.T.M.; Bornemann, S.; Gahlawat, S.; Majid, N.; Triyana, K.; Abdi, F.F.; Wasisto, H.S.; Waag, A. Ultrashort Pulse Laser Lift-Off Processing of InGaN/GaN Light-Emitting Diode Chips. ACS Appl. Electron. Mater. 2021, 3, 778–788. [Google Scholar] [CrossRef]
- Latz, C.; Asshauer, T.; Rathjen, C.; Mirshahi, A. Femtosecond-Laser Assisted Surgery of the Eye: Overview and Impact of the Low-Energy Concept. Micromachines 2021, 12, 122. [Google Scholar] [CrossRef]
- Liebmann, M.; Treffer, A.; Bock, M.; Wallrabe, U.; Grunwald, R. Ultrashort Vortex Pulses with Controlled Spectral Gouy Rotation. Appl. Sci. 2020, 10, 4288. [Google Scholar] [CrossRef]
- Nie, J.; Liu, G.; Zhang, R. Propagation and spatiotemporal coupling characteristics of ultrashort Gaussian vortex pulse. Opt. Laser Technol. 2018, 101, 446–450. [Google Scholar] [CrossRef]
- Zhang, T.; Hu, H.; Chen, J.; Zhan, Q. Tunable mode-locked fiber laser to generate ultrashort cylindrical vector beams. Laser Phys. Lett. 2018, 18, 035102. [Google Scholar] [CrossRef]
- Chen, J.; Wan, C.; Chong, A.; Zhan, Q. Experimental demonstration of cylindrical vector spatiotemporal optical vortex. Nanophotonics 2021, 10, 427. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Zhu, Y. Probability distribution of the orbital angular momentum mode of the ultrashort Laguerre-Gaussian pulsed beam propagation in oceanic turbulence. Results Phys. 2018, 11, 698–705. [Google Scholar] [CrossRef]
- Zukersteina, M.; Hrabovsky, J.; Sladek, J.; Mirza, I.; Levy, Y.; Bulgakova, N.M. Formation of tubular structures and microneedles on silicon surface by doughnut-shaped ultrashort laser pulses. Appl. Surf. Sci. 2022, 592, 153228. [Google Scholar] [CrossRef]
- Syubaev, S.A.; Zhizhchenko, A.Y.; Pavlov, D.V.; Gurbatov, S.O.; Pustovalov, E.V.; Porfirev, A.P.; Khonina, S.N.; Kulinich, S.A.; Rayappan, J.B.B.; Kudryashov, S.I.; et al. Plasmonic Nanolenses Produced by Cylindrical Vector Beam Printing for Sensing Applications. Sci. Rep. 2019, 9, 19750. [Google Scholar] [CrossRef]
- Tsibidis, G.D.; Stratakis, E. Ripple formation on silver after irradiation with radially polarised ultrashort-pulsed lasers. J. Appl. Phys. 2017, 121, 163106. [Google Scholar] [CrossRef]
- Zhu, G.; Howe, J.; Durst, M.; Zipfel, W.; Xu, C. Simultaneous spatial and temporal focusing of femtosecond pulses. Opt. Express 2005, 13, 2153–2159. [Google Scholar] [CrossRef] [PubMed]
- Sergynin, S.K.; Khorin, P.A. Diffraction of pulsed linearly polarized Gaussian laser beams on a spiral phase plate. In Proceedings of the 2022 VIII International Conference on Information Technology and Nanotechnology (ITNT), Samara, Russia, 23–27 May 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Khonina, S.N.; Golub, I. Tighter focus for ultrashort pulse vector light beams: Change of the relative contribution of different field components to the focal spot upon pulse shortening. J. Opt. Soc. Am. A 2018, 35, 985–991. [Google Scholar] [CrossRef]
- Chen, J.; Yu, L.; Wan, C.; Zhan, Q. Spin–Orbit Coupling within Tightly Focused Circularly Polarized Spatiotemporal Vortex Wavepacket. ACS Photonics 2022, 9, 793–799. [Google Scholar] [CrossRef]
- Tang, Y.; Perrie, W.; Rico Sierra, D.; Li, Q.; Liu, D.; Edwardson, S.P.; Dearden, G. Laser–Material Interactions of High-Quality Ultrashort Pulsed Vector Vortex Beams. Micromachines 2021, 12, 376. [Google Scholar] [CrossRef]
- Couairon, A.; Sudrie, L.; Franco, M.; Prade, B.; Mysyrowicz, A. Surface physics, nanoscale physics, low-dimensional systems-Filamentation and damage in fused silica induced by tightly focused femtosecond laser pulses. Phys. Rev. B 2005, 71, 125435. [Google Scholar] [CrossRef]
- Vial, A.; Laroche, T.; Dridi, M.; Le Cunff, L. A new model of dispersion for metals leading to a more accurate modeling of plasmonic structures using the FDTD method. Appl. Phys. A 2011, 103, 849–853. [Google Scholar] [CrossRef]
- Rakic, A.D.; Djurisic, A.B.; Elazar, J.M.; Majewski, M.L. Optical properties of metallic films for vertical-cavity optoelectronic devices. Appl. Opt. 1998, 37, 5271–5283. [Google Scholar] [CrossRef] [PubMed]
- Kotlyar, V.V.; Nalimov, A.G.; Stafeev, S.S.; O’Faolain, L. Single metalens for generating polarization and phase singularities leading to a reverse flow of energy. J. Opt. 2019, 21, 055004. [Google Scholar] [CrossRef]
- Kozlova, E.S.; Stafeev, S.S.; Fomchenkov, S.A.; Podlipnov, V.V.; Kotlyar, V.V. Transverse intensity at the tight focus of a second-order cylindrical vector beam. Comput. Opt. 2021, 45, 165–171. [Google Scholar] [CrossRef]
- Golovashkin, D.L.; Kasanskiy, N.L. Solving diffractive optics problem using graphics processing units. Opt. Mem. Neural Netw. Inf. Opt. 2011, 20, 85–89. [Google Scholar] [CrossRef]
- Kazanskiy, N.L. Modeling diffractive optics elements and devices. Proc. SPIE 2018, 10774, 107740O. [Google Scholar] [CrossRef]
- Kazanskiy, N.L.; Skidanov, R.V. Technological line for creation and research of diffractive optical elements. Proc. SPIE 2019, 11146, 111460W. [Google Scholar] [CrossRef]





| m | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| rm, μm | 0.595 | 0.921 | 1.219 | 1.505 | 1.784 | 2.060 | 2.334 | 2.606 | 2.877 |
| m | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| rm, μm | 3.147 | 3.417 | 3.686 | 3.954 | 4.223 | 4.491 | 4.758 | 5.026 | 5.293 |
| m | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| rm, μm | 5.561 | 5.828 | 6.095 | 6.362 | 6.629 | 6.896 | 7.162 | 7.429 | 7.696 |
| j | Δεj | λj | ηj |
|---|---|---|---|
| 1 | 0.69616630 | 0.06840430 | 0 |
| 2 | 0.40794260 | 0.11624140 | 0 |
| 3 | 0.89747928 | 9.88961612 | 0 |
| ε∞ = 1 | |||
| j | Aj | ωj | δj |
|---|---|---|---|
| 1 | 1940.97224801 | 0.82045170 | 0.84324200 |
| 2 | 4.70650987 | 7.81961316 | 0.79006450 |
| 3 | 11.39553922 | 9.15664513 | 3.42108050 |
| 4 | 0.55813006 | 17.58906478 | 8.56409500 |
| ε∞ = 1 | |||
| ωp = 54.86566321 | |||
| νc = 0.11901600 | |||
| j | Aj | ωj | δj |
|---|---|---|---|
| 1 | 11.36293409 | 2.10177425 | 0.61027400 |
| 2 | 1.18363911 | 4.20354850 | 0.87362900 |
| 3 | 0.65677021 | 15.03654881 | 2.20306450 |
| 4 | 2.64548647 | 21.79767648 | 6.31500000 |
| 5 | 2.01482608 | 67.45935814 | 5.60642000 |
| ε∞ = 1 | |||
| ωp = 39.86873462 | |||
| νc = 0.13420950 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kozlova, E.; Kotlyar, V. Ultrashort Laser Pulse Focusing by Amplitude and Phase Zone Plates. Photonics 2022, 9, 662. https://doi.org/10.3390/photonics9090662
Kozlova E, Kotlyar V. Ultrashort Laser Pulse Focusing by Amplitude and Phase Zone Plates. Photonics. 2022; 9(9):662. https://doi.org/10.3390/photonics9090662
Chicago/Turabian StyleKozlova, Elena, and Victor Kotlyar. 2022. "Ultrashort Laser Pulse Focusing by Amplitude and Phase Zone Plates" Photonics 9, no. 9: 662. https://doi.org/10.3390/photonics9090662





