Controlled Excitation of Supermodes in a Multicore Fiber with a 5 × 5 Square Array of Strongly Coupled Cores
Abstract
:1. Introduction
2. Theoretical Background
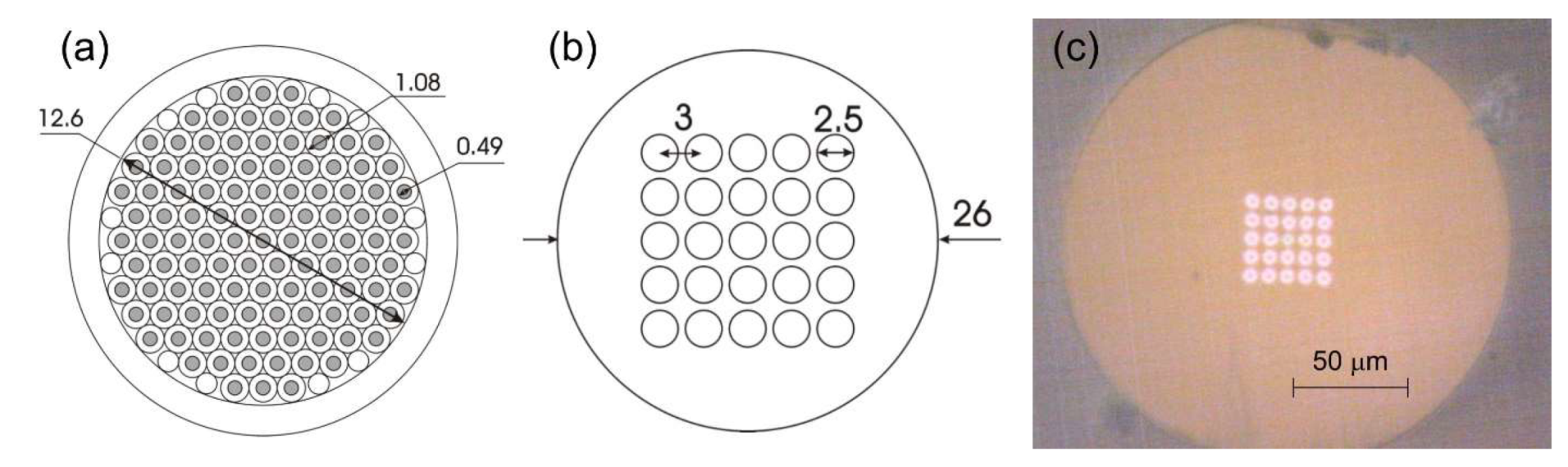
3. MCF Fabrication
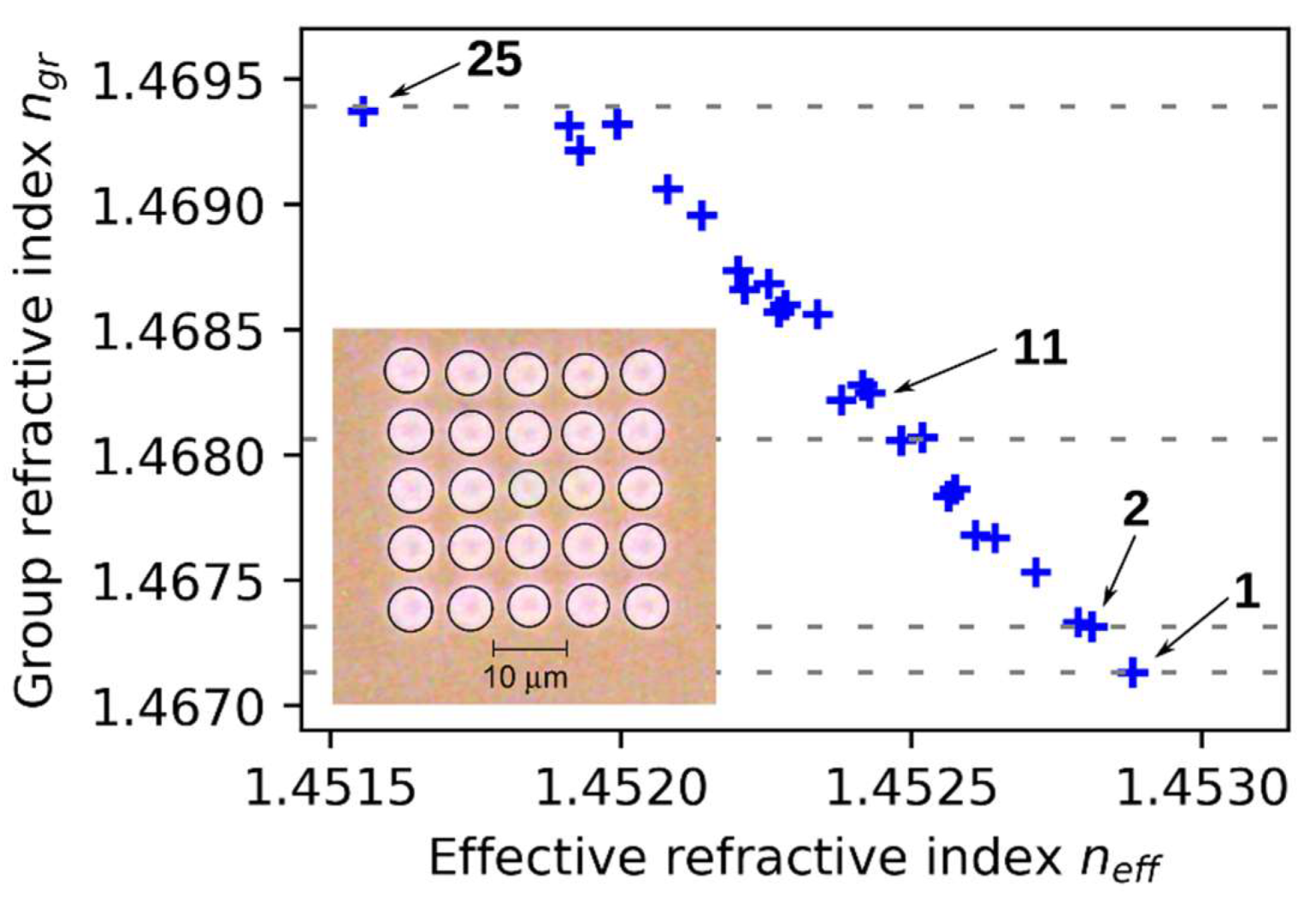
4. Supermodes in the Fabricated MCF
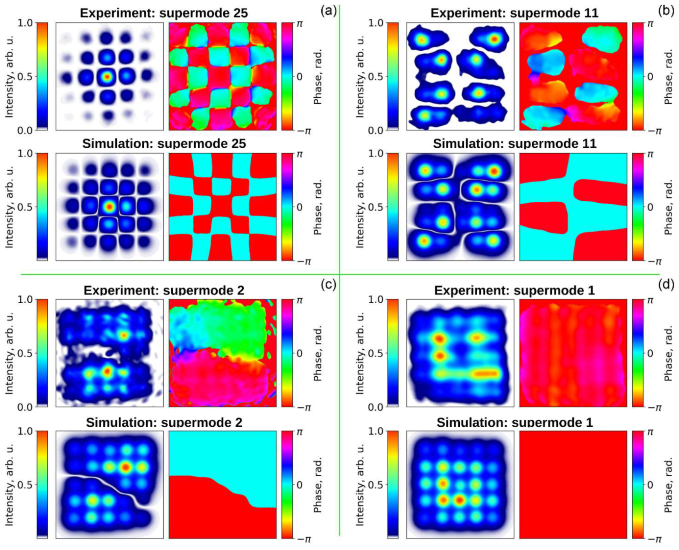
5. Experimental Study of Supermodes Propagation in MCF
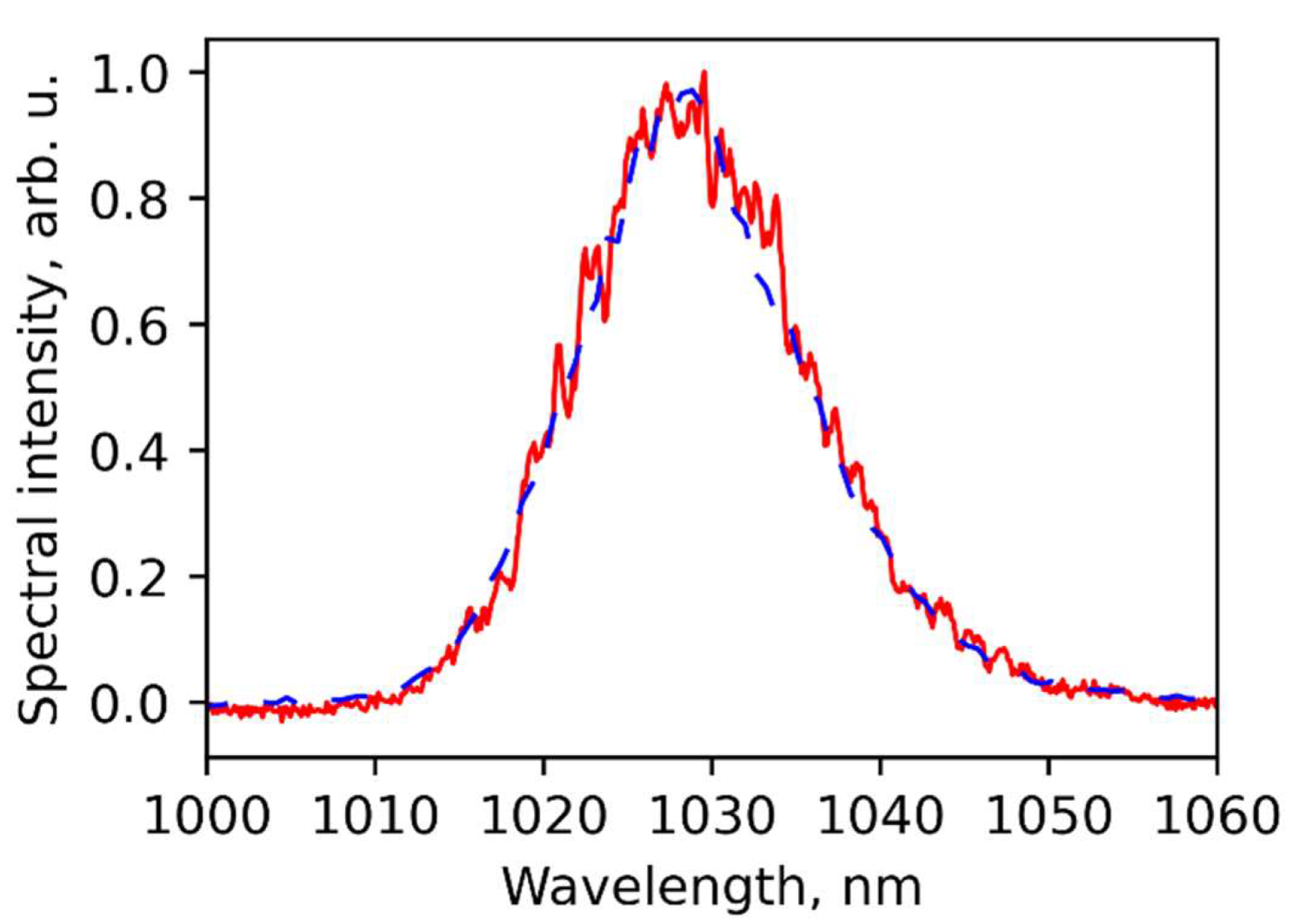
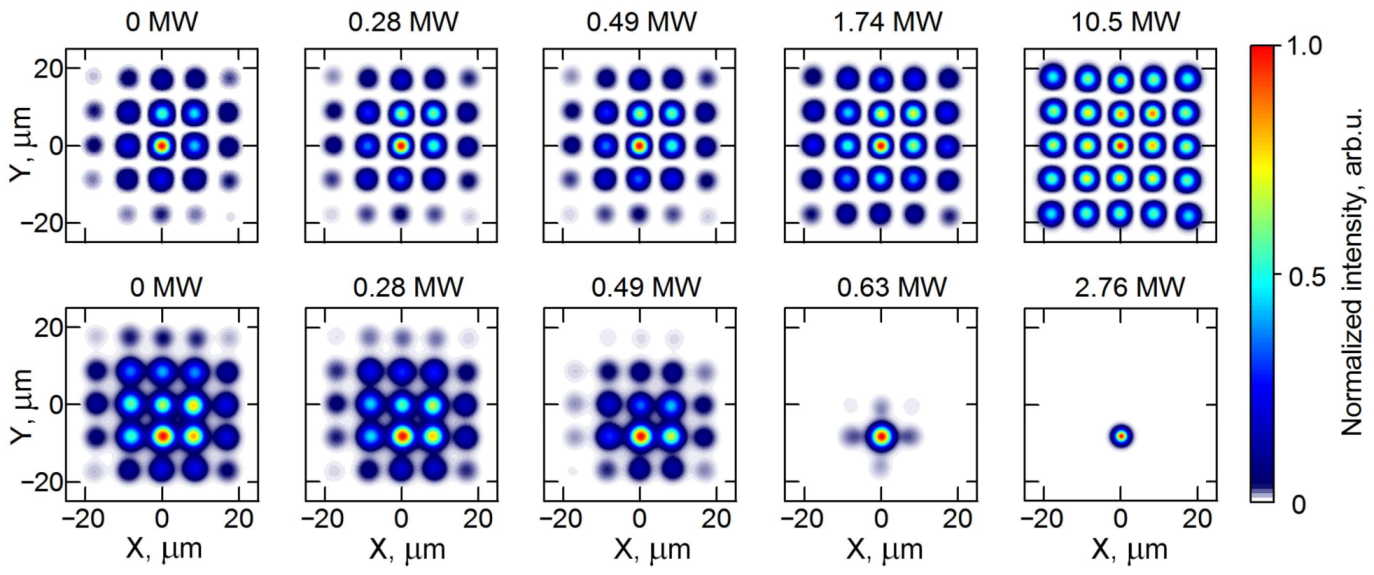
6. Numerical Modeling of Nonlinear Light Propagation
7. Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Richardson, D. New optical fibres for high-capacity optical communications. Phil. Trans. R. Soc. A 2016, 374, 20140441. [Google Scholar] [CrossRef] [Green Version]
- Berdague, S.; Facq, P. Mode division multiplexing in optical fibers. Appl. Opt. 1982, 21, 1950–1955. [Google Scholar] [CrossRef]
- Ryf, R.; Randel, S.; Gnauck, A.H.; Bolle, C.; Essiambre, R.; Winzer, P.J.; Peckham, D.W.; McCurdy, A.; Lingle, R. Space-division multiplexing over 10 km of three-mode fiber using coherent 6 × 6 MIMO processing. In Proceedings of the Optical Fiber Communication Conference/National Fiber Optic Engineers Conference, Los Angeles, CA, USA, 6–10 March 2011; p. PDPB10. [Google Scholar] [CrossRef]
- Ryf, R.; Fontaine, N.K.; Chen, H.; Guan, B.; Huang, B.; Esmaeelpour, M.; Gnauck, A.H.; Randel, S.; Yoo, S.; Koonen, A.; et al. Mode-multiplexed transmission over conventional graded-index multimode fibers. Opt. Express 2015, 23, 235–246. [Google Scholar] [CrossRef] [Green Version]
- Lavoute, L.; Roy, P.; Desfarges-Berthelemot, A.; Kermene, V.; Fevrier, S. Design of microstructured single-mode fiber combining large mode area and high rare earth ion concentration. Opt. Express 2006, 14, 2994–2999. [Google Scholar] [CrossRef]
- Wong, W.S.; Peng, X.; McLaughlin, J.M.; Dong, L. Breaking the limit of maximum effective area for robust single-mode propagation in optical fibers. Opt. Lett. 2005, 30, 2855–2857. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Cooper, L.J.; Sahu, J.K.; Clarkson, W.A. Efficient single-mode operation of a cladding-pumped ytterbium-doped helical-core fiber laser. Opt. Lett. 2006, 31, 226–228. [Google Scholar] [CrossRef]
- Liu, C.; Chang, G.; Litchinitser, N.; Guertin, D.; Jacobsen, N.; Tankala, K.; Galvanauskas, A. Chirally Coupled Core Fibers at 1550-nm and 1064-nm for Effectively Single-Mode Core Size Scaling. In Proceedings of the 2007 Conference on Lasers and Electro-Optics (CLEO), Baltimore, MD, USA, 6–11 May 2007; pp. 1–2. [Google Scholar] [CrossRef]
- Gaponov, D.A.; Fevrier, S.; Devautour, M.; Roy, P.; Likhachev, M.E.; Aleshkina, S.S.; Salganskii, M.Y.; Yashkov, M.V.; Guryanov, A.N. Management of the high-order mode content in large (40 μm) core photonic bandgap Bragg fiber laser. Opt. Lett. 2010, 35, 2233–2235. [Google Scholar] [CrossRef] [PubMed]
- Ramachandran, S.; Nicholson, J.W.; Ghalmi, S.; Yan, M.F.; Wisk, P.; Monberg, E.; Dimarcello, F.V. Light propagation with ultralarge modal areas in optical fibers. Opt. Lett. 2006, 31, 1797–1799. [Google Scholar] [CrossRef]
- Kaminow, I.; Li, T.; Willner, A.E. Optical Fiber Telecommunications Volume VIB: Systems and Networks, 6th ed.; Elsevier Science: Oxford, UK, 2013. [Google Scholar]
- Willner, A. Optical Fiber Telecommunications VII, 1st ed.; Academic Press: London, UK, 2020. [Google Scholar]
- Saitoh, K.; Matsuo, S. Multicore Fiber Technology. J. Lightware Technol. 2016, 34, 55–66. [Google Scholar] [CrossRef]
- Sano, A.; Takara, H.; Kobayashi, T.; Kawakami, H.; Kishikawa, H.; Nakagawa, T.; Miyamoto, Y.; Abe, Y.; Ono, H.; Shikama, K.; et al. 409-Tb/s + 409-Tb/s crosstalk suppressed bidirectional MCF transmission over 450 km using propagation-direction interleaving. Opt. Express 2013, 21, 16777–16783. [Google Scholar] [CrossRef] [Green Version]
- Dynes, J.F.; Kindness, S.J.; Tam, S.W.; Plews, A.; Sharpe, A.W.; Lucamarini, M.; Frohlich, B.; Yuan, Z.L.; Penty, R.V.; Shields, A.J. Quantum key distribution over multicore fiber. Opt. Express 2016, 24, 8081–8087. [Google Scholar] [CrossRef] [Green Version]
- Lin, R.; Udalcovs, A.; Ozolins, O.; Pang, X.; Gan, L.; Tang, M.; Fu, S.; Popov, S.; Silva, T.F.D.; Xavier, G.B.; et al. Telecommunication Compatibility Evaluation for Co-existing Quantum Key Distribution in Homogenous Multicore Fiber. IEEE Access 2020, 8, 78836–78846. [Google Scholar] [CrossRef]
- Ramirez, L.P.; Hanna, M.; Bouwmans, G.; Hamzaoui, H.E.; Bouazaoui, M.; Labat, D.; Delplace, K.; Pouysegur, J.; Guichard, F.; Rigaud, P.; et al. Coherent beam combining with an ultrafast multicore Yb-doped fiber amplifier. Opt. Express 2015, 23, 5406–5416. [Google Scholar] [CrossRef] [Green Version]
- Klenke, A.; Muller, M.; Stark, H.; Stutzki, F.; Hupel, C.; Schreiber, T.; Tunnermann, A.; Limpert, J. Coherently combined 16-channel multicore fiber laser system. Opt. Lett. 2018, 43, 1519–1522. [Google Scholar] [CrossRef]
- Lhermite, J.; Suran, E.; Kermene, V.; Louradour, F.; Desfarges-Berthelemot, A.; Barthelemy, A. Coherent combining of 49 laser beams from a multiple core optical fiber by a spatial light modulator. Opt. Express 2010, 18, 4783–4789. [Google Scholar] [CrossRef] [PubMed]
- Lin, D.; Carpenter, J.; Feng, Y.; Jain, S.; Jung, Y.; Feng, Y.; Zervas, M.N.; Richardson, D.J. Reconfigurable structured light generation in a multicore fibre amplifier. Nat. Commun. 2020, 11, 3986. [Google Scholar] [CrossRef]
- Xia, C.; Bai, N.; Ozdur, I.; Zhou, X.; Li, G. Supermodes for optical transmission. Opt. Express 2011, 19, 16653–16664. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Zang, J.; Raghuraman, S.; Chen, S.; Goel, C.; Xia, N.; Ishaaya, A.; Yoo, S. Large-Mode-Area Multicore Yb-Doped Fiber for an Efficient High Power 976 Nm Laser. Opt. Express 2021, 29, 21992. [Google Scholar] [CrossRef]
- Dostovalov, A.V.; Skvortsov, M.I.; Wolf, A.A.; Labuntsov, V.I.; Egorova, O.N.; Semjonov, S.L.; Babin, S.A. Seven-Core Fibre Raman Laser with Intercore Coupling. Quantum Electron. 2020, 50, 1088–1090. [Google Scholar] [CrossRef]
- Skvortsov, M.I.; Abdullina, S.R.; Wolf, A.A.; Dostovalov, A.V.; Vlasov, A.A.; Lobach, I.A.; Wabnitz, S.; Babin, S.A. Random Raman Fiber Laser Based on a Twin-Core Fiber with FBGs Inscribed by Femtosecond Radiation. Opt. Lett. 2019, 44, 295. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chekhovskoy, I.S.; Rubenchik, A.M.; Shtyrina, O.V.; Fedoruk, M.P.; Turitsyn, S.K. Nonlinear combining and compression in multicore fibers. Phys. Rev. A 2016, 94, 043848. [Google Scholar] [CrossRef] [Green Version]
- Rubenchik, A.M.; Chekhovskoy, I.S.; Fedoruk, M.P.; Shtyrina, O.V.; Turitsyn, S.K. Nonlinear pulse combining and pulse compression in multi-core fibers. Opt. Lett. 2015, 40, 721–724. [Google Scholar] [CrossRef] [PubMed]
- Minardi, S.; Eilenberger, F.; Kartashov, Y.V.; Szameit, A.; Ropke, U.; Kobelke, J.; Schuster, K.; Bartelt, H.; Nolte, S.; Torner, L.; et al. Three-Dimensional Light Bullets in Arrays of Waveguides. Phys. Rev. Lett. 2010, 105, 263901. [Google Scholar] [CrossRef]
- Aceves, A.B.; Shtyrina, O.V.; Rubenchik, A.M.; Fedoruk, M.P.; Turitsyn, S.K. Spatiotemporal optical bullets in two-dimensional fiber arrays and their stability. Phys. Rev. A 2015, 91, 033810. [Google Scholar] [CrossRef] [Green Version]
- Aceves, A.B.; Angelis, C.D.; Trillo, S.; Wabnitz, S. Storage and steering of self-trapped discrete solitons in nonlinear waveguide arrays. Opt. Lett. 1994, 19, 332–334. [Google Scholar] [CrossRef]
- Antikainen, A.; Agrawal, G.P. Supercontinuum Generation in Seven-Core Fibers. J. Opt. Soc. Am. B 2019, 36, 2927. [Google Scholar] [CrossRef]
- Aceves, A.B.; De Angelis, C.; Peschel, T.; Muschall, R.; Lederer, F.; Trillo, S.; Wabnitz, S. Discrete self-trapping, soliton interactions, and beam steering in nonlinear waveguide arrays. Phys. Rev. E 1996, 53, 1172–1189. [Google Scholar] [CrossRef]
- Andrianov, A.V.; Kalinin, N.A.; Koptev, M.Y.; Egorova, O.N.; Kim, A.V.; Litvak, A.G. High-energy femtosecond pulse shaping, compression, and contrast enhancement using multicore fiber. Opt. Lett. 2019, 44, 303–306. [Google Scholar] [CrossRef]
- Balakin, A.A.; Skobelev, S.A.; Anashkina, E.A.; Andrianov, A.V.; Litvak, A.G. Coherent propagation of laser beams in a small-sized system of weakly coupled optical light guides. Phys. Rev. A 2018, 98, 043857. [Google Scholar] [CrossRef]
- Balakin, A.A.; Skobelev, S.A.; Andrianov, A.V.; Anashkina, E.A.; Litvak, A.G. Coherent propagation and amplification of intense laser pulses in hexagonal multicore fibers. Opt. Lett. 2020, 45, 3224–3227. [Google Scholar] [CrossRef]
- Balakin, A.A.; Litvak, A.G.; Skobelev, S.A. Coherent propagation and amplification of intense wave beams in a deformed multicore fiber. Phys. Rev. A 2020, 102, 023527. [Google Scholar] [CrossRef]
- Balakin, A.A.; Skobelev, S.A.; Andrianov, A.V.; Anashkina, E.A.; Litvak, A.G. Coherent amplification of high-power laser radiation in multicore fibers from a rectangular array of cores. Opt. Lett. 2021, 46, 246–249. [Google Scholar] [CrossRef] [PubMed]
- Tunnermann, H.; Shirakawa, A. Self-focusing in multicore fibers. Opt. Express 2015, 23, 2436–2445. [Google Scholar] [CrossRef]
- Andrianov, A.V.; Kalinin, N.A.; Anashkina, E.A.; Egorova, O.N.; Lipatov, D.S.; Kim, A.V.; Semjonov, S.L.; Litvak, A.G. Selective Excitation and Amplification of Peak-Power-Scalable Out-of-Phase Supermode in Yb-Doped Multicore Fiber. J. Lightwave Technol. 2020, 38, 2464–2470. [Google Scholar] [CrossRef]
- Christodoulides, D.N.; Joseph, R.I. Discrete self-focusing in nonlinear arrays of coupled waveguides. Opt. Lett. 1988, 13, 794–796. [Google Scholar] [CrossRef]
- Andrianov, A.; Kalinin, N.; Anashkina, E.; Leuchs, G. Highly efficient coherent beam combining of tiled aperture arrays using out-of-phase pattern. Opt. Lett. 2020, 45, 4774–4777. [Google Scholar] [CrossRef]
- Gonda, T.; Imamura, K.; Sugizaki, R. Multicore fiber for bi-directional transmission. In Proceedings of the 2016 21st OptoElectronics and Communications Conference (OECC) Held Jointly with 2016 International Conference on Photonics in Switching (PS), Niigata, Japan, 3–7 July 2016; pp. 1–3. [Google Scholar]
- Kobayashi, T.; Nakamura, M.; Hamaoka, F.; Shibahara, K.; Mizuno, T.; Sano, A.; Kawakami, H.; Isoda, A.; Nagatani, M.; Yamazaki, H.; et al. 1-Pb/s (32 SDM/46 WDM/768 Gb/s) C-band Dense SDM Transmission over 205.6-km of Single-mode Heterogeneous Multi-core Fiber using 96-Gbaud PDM-16QAM Channels. In Proceedings of the Optical Fiber Communication Conference, Los Angeles, CA, USA, 19–23 March 2017. paper Th5B.1. [Google Scholar] [CrossRef] [Green Version]
- Jain, S.; Castro, C.; Jung, Y.; Hayes, J.; Sandoghchi, R.; Mizuno, T.; Sasaki, Y.; Amma, Y.; Miyamoto, Y.; Bohn, M.; et al. 32-core erbium/ytterbium-doped multicore fiber amplifier for next generation space-division multiplexed transmission system. Opt. Express 2017, 25, 32887–32896. [Google Scholar] [CrossRef]
- Chavez-Pirson, A.; Hwang, B.; Nguyen, D.; Luo, T.; Jiang, S. New approach to image amplification based on an optically pumped multi-core optical fiber. In Proceedings of the SPIE Optics + Photonics, Novel Optical Systems Design and Optimization IX, San Diego, CA, USA, 13–17 August 2006; pp. 67–74. [Google Scholar] [CrossRef]
- Xiong, H.; Gan, J.; Wu, Y. Kuznetsov-Ma Soliton Dynamics Based on the Mechanical Effect of Light. Phys. Rev. Lett. 2017, 119, 153901. [Google Scholar] [CrossRef]
- Xiong, H.; Wu, Y. Optomechanical Akhmediev Breathers. Laser Photonics Rev. 2018, 12, 1700305. [Google Scholar] [CrossRef]
- Andrianov, A.; Anashkina, E.; Muravyev, S.; Kim, A. All-fiber design of hybrid Er-doped laser/Yb-doped amplifier system for high-power ultrashort pulse generation. Opt. Lett. 2010, 35, 3805–3807. [Google Scholar] [CrossRef]
- Bobkov, K.; Andrianov, A.; Koptev, M.; Muravyev, S.; Levchenko, A.; Velmiskin, V.; Aleshkina, S.; Semjonov, S.; Lipatov, D.; Guryanov, A.; et al. Sub-MW peak power diffraction-limited chirped-pulse monolithic Yb-doped tapered fiber amplifier. Opt. Express 2017, 25, 26958–26972. [Google Scholar] [CrossRef]
- Egorova, O.N.; Astapovich, M.S.; Belkin, M.E.; Semenov, S.L. Fiber-Optic Delay Line Using Multicore Fiber. Bull. Lebedev Phys. Inst. 2017, 44, 5–7. [Google Scholar] [CrossRef]
- Andrianov, A.; Anashkina, E.; Kim, A.; Meyerov, I.; Lebedev, S.; Sergeev, A.; Mourou, G. Three-dimensional modeling of CPA to the multimillijoule level in tapered Yb-doped fibers for coherent combining systems. Opt. Express 2014, 22, 28256–28269. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalinin, N.A.; Anashkina, E.A.; Egorova, O.N.; Zhuravlev, S.G.; Semjonov, S.L.; Kim, A.V.; Litvak, A.G.; Andrianov, A.V. Controlled Excitation of Supermodes in a Multicore Fiber with a 5 × 5 Square Array of Strongly Coupled Cores. Photonics 2021, 8, 314. https://doi.org/10.3390/photonics8080314
Kalinin NA, Anashkina EA, Egorova ON, Zhuravlev SG, Semjonov SL, Kim AV, Litvak AG, Andrianov AV. Controlled Excitation of Supermodes in a Multicore Fiber with a 5 × 5 Square Array of Strongly Coupled Cores. Photonics. 2021; 8(8):314. https://doi.org/10.3390/photonics8080314
Chicago/Turabian StyleKalinin, Nikolay A., Elena A. Anashkina, Olga N. Egorova, Sergey G. Zhuravlev, Sergei L. Semjonov, Arkady V. Kim, Alexander G. Litvak, and Alexey V. Andrianov. 2021. "Controlled Excitation of Supermodes in a Multicore Fiber with a 5 × 5 Square Array of Strongly Coupled Cores" Photonics 8, no. 8: 314. https://doi.org/10.3390/photonics8080314




