Numerical Analysis of Nonlinear Dynamics Based on Spin-VCSELs with Optical Feedback
Abstract
:1. Introduction
2. The Theoretical Model
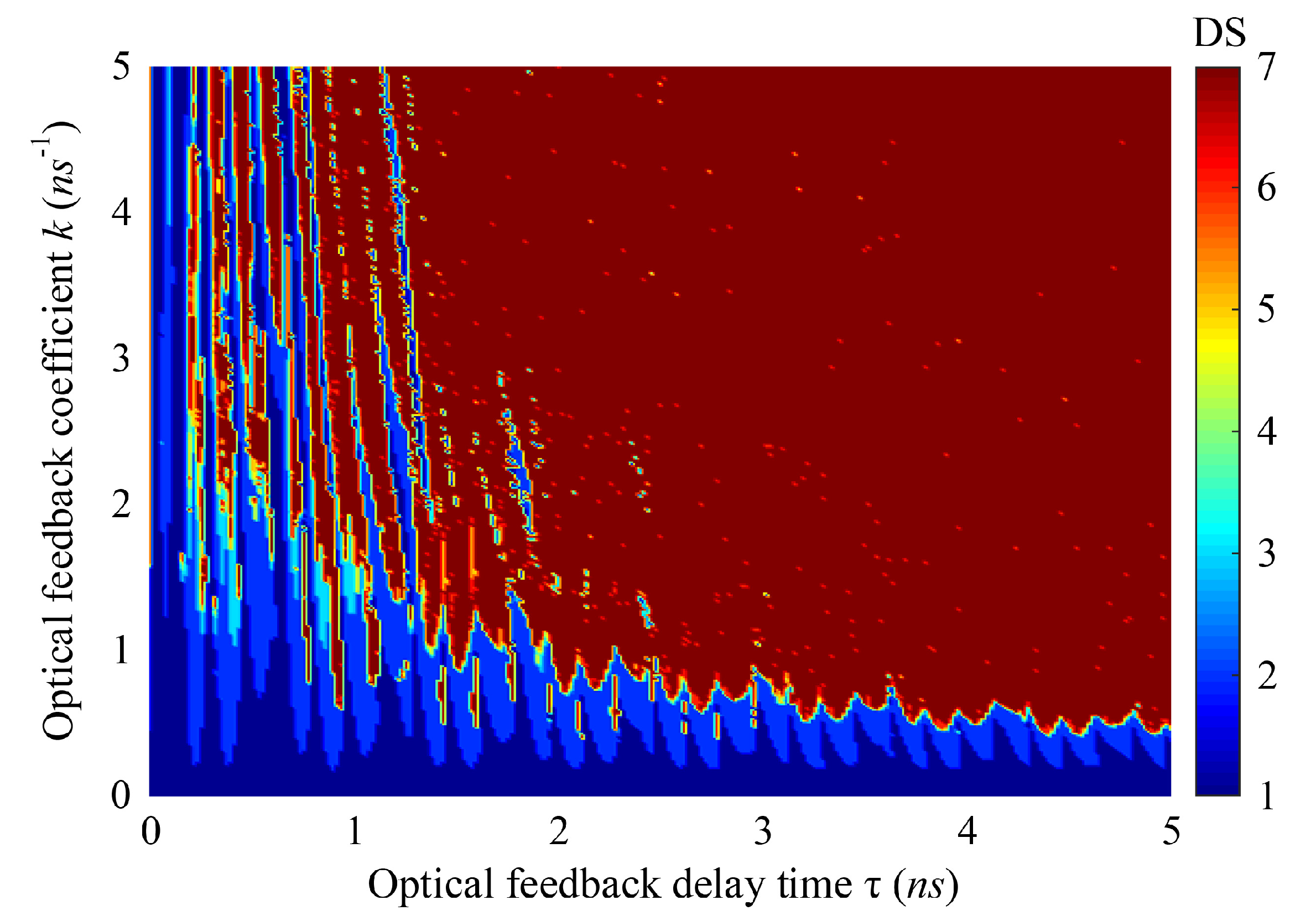
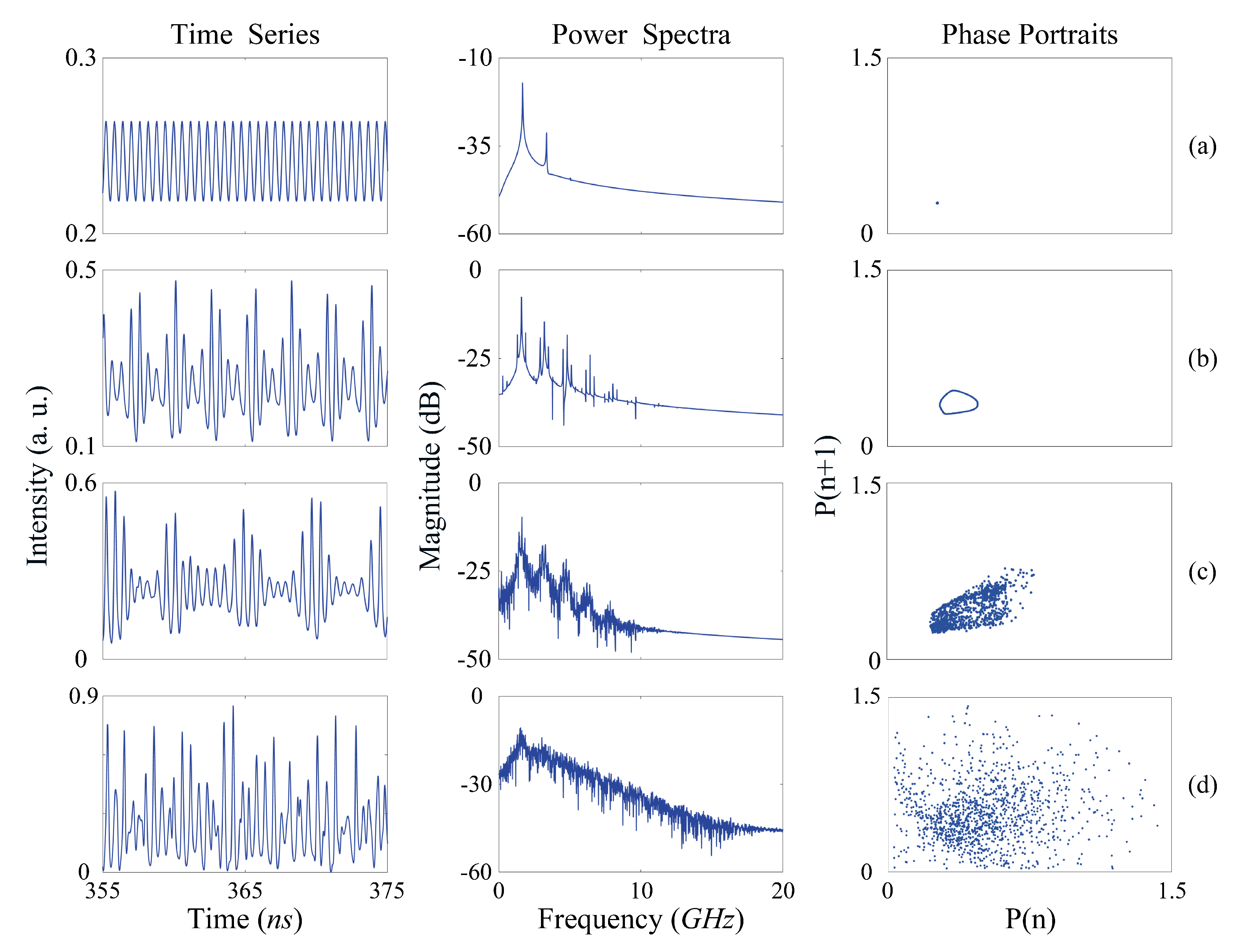
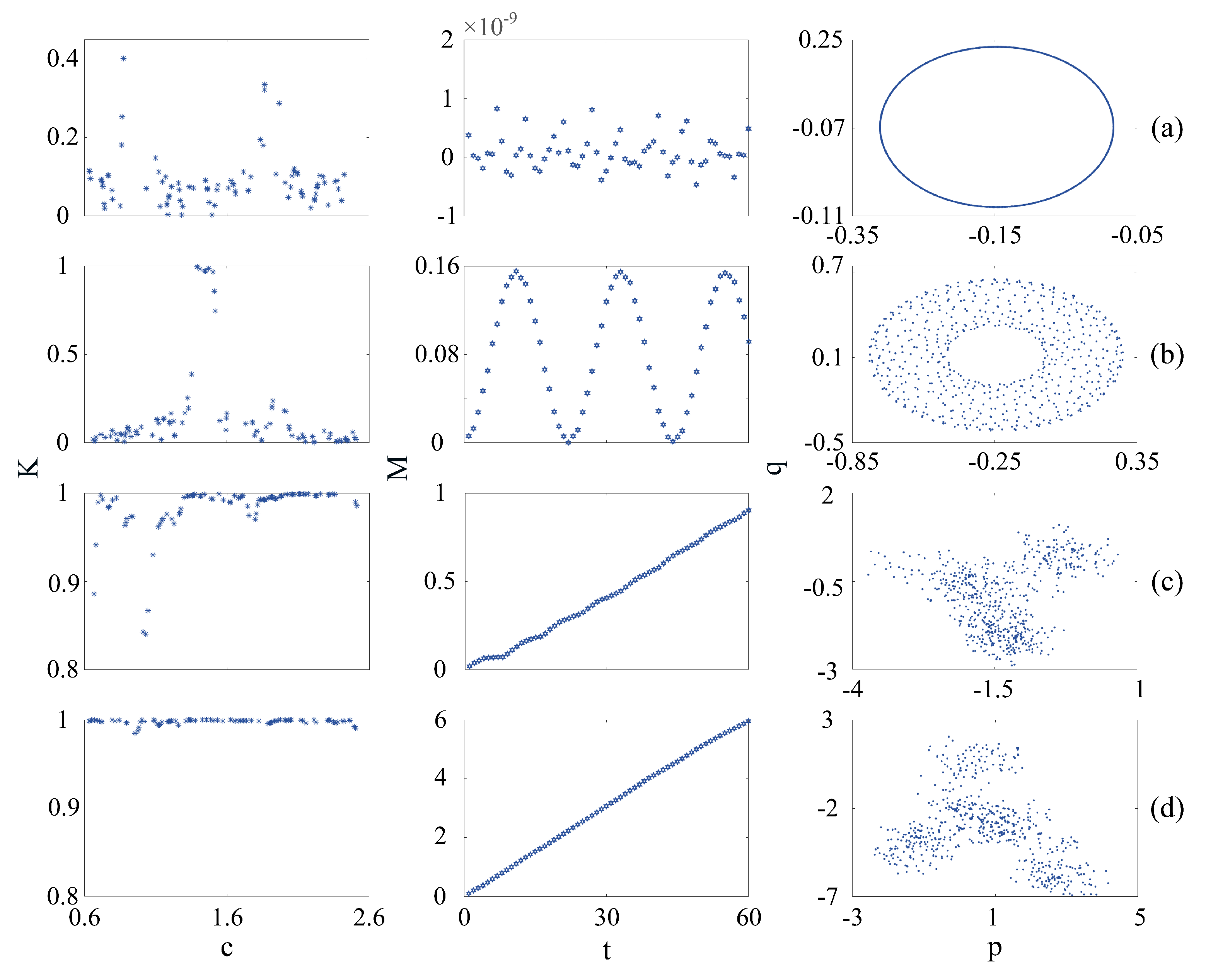
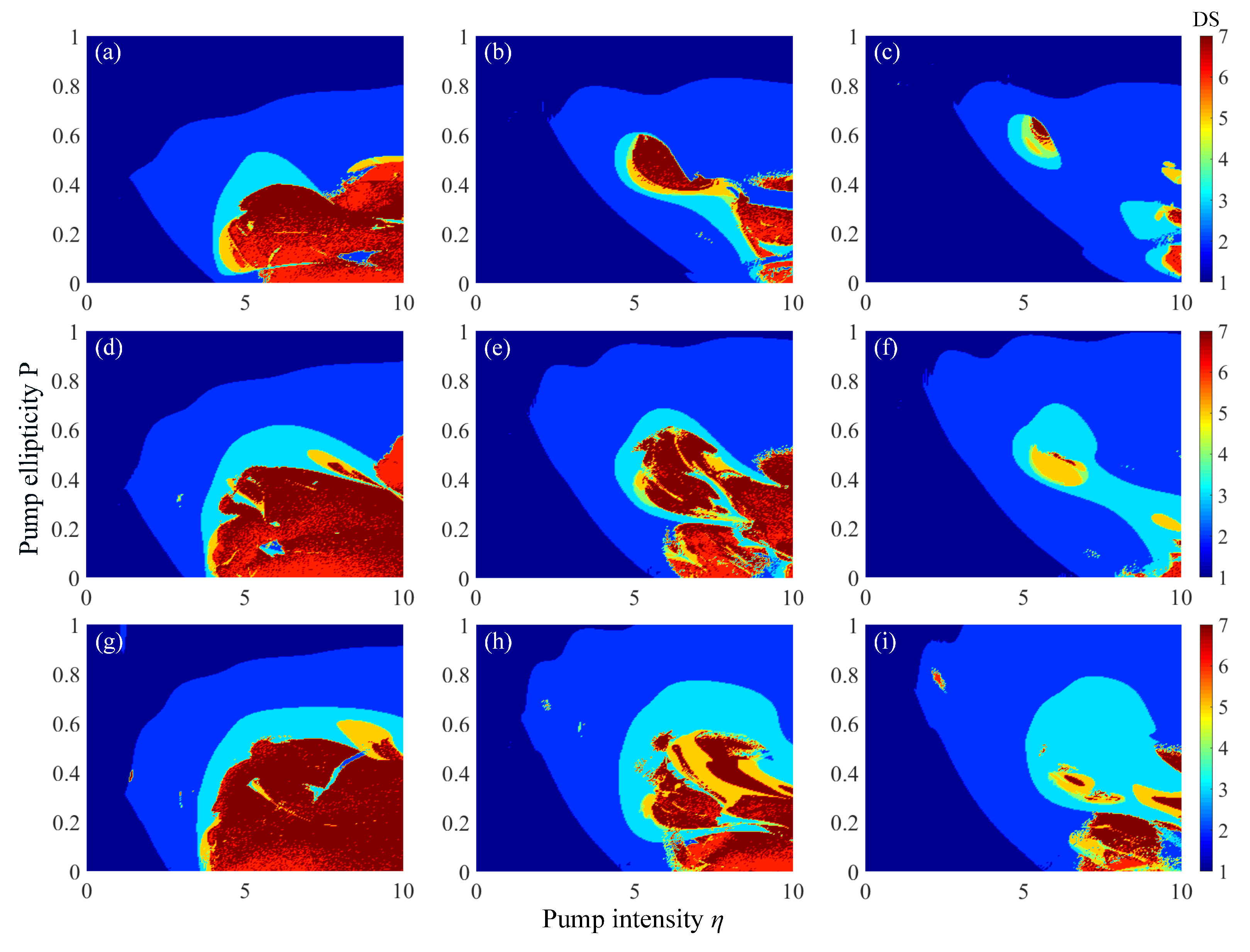
3. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- San Miguel, M.; Feng, Q.; Moloney, J.V. Light-polarization dynamics in surface-emitting semiconductor lasers. Phys. Rev. A 1995, 52, 1728–1739. [Google Scholar] [CrossRef] [PubMed]
- Gøthgen, C.; Oszwaldowski, R.; Petrou, A.; Zutic, I. Analytical model of spin-polarized semiconductor lasers. Appl. Phys. Lett. 2008, 93, 042513. [Google Scholar] [CrossRef] [Green Version]
- Koyama, F. Recent advances of VCSEL photonics. J. Lightwave Technol. 2006, 24, 4502–4513. [Google Scholar] [CrossRef]
- Gerhardt, N.C.; Hofmann, M.R. Spin-controlled vertical-cavity surface-emitting lasers. Adv. Opt. Technol. 2012, 2012, 268949. [Google Scholar] [CrossRef]
- Nguimdo, R.M.; Verschaffelt, G.; Danckaert, J.; Van der Sande, G. Loss of time-delay signature in chaotic semiconductor ring lasers. Opt. Lett. 2012, 37, 2541–2544. [Google Scholar] [CrossRef]
- Han, H.; Shore, K.A. Dynamical characteristics of nano-lasers subject to optical injection and phase conjugate feedback. IET Optoelectron. 2018, 12, 25–29. [Google Scholar] [CrossRef] [Green Version]
- Li, X.Z.; Li, S.S.; Chan, S.C. Correlated random bit generation using chaotic semiconductor laser under unidirectional optical injection. IEEE Photonics J. 2017, 9, 1505411. [Google Scholar] [CrossRef]
- Zhao, Z.; Cheng, M.; Luo, C.; Deng, L.; Zhang, M.; Fu, S.; Tang, M.; Shum, P.; Liu, D. Synchronized random bit sequences generation based on analog-digital hybrid electro-optic chaotic sources. J. Lightw. Technol. 2018, 36, 4995–5002. [Google Scholar] [CrossRef]
- Sugano, C.; Kanno, K.; Uchida, A. Reservoir computing using multiple lasers with feedback on a photonic integrated circuit. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 1500409. [Google Scholar] [CrossRef]
- Hou, Y.S.; Xia, G.Q.; Yang, W.Y.; Wang, D.; Jayaprasath, E.; Jiang, Z.F.; Hu, C.X.; Wu, Z.M. Prediction performance of reservoir computing system based on a semiconductor laser subject to double optical feedback and optical injection. Opt. Exp. 2018, 26, 10211–10219. [Google Scholar] [CrossRef]
- Argyris, A.; Syvridis, D.; Larger, L.; Annovazzi-Lodi, V.; Colet, P.; Fischer, I.; García-Ojalvo, J.; Mirasso, C.R.; Pesquera, L.; Shore, K.A. Chaos-based communications at high bit rates using commercial fibre-optic links. Nature 2005, 438, 343–346. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.Y.; Li, J.C.; He, C.; Zhang, Z.D.; Song, T.T.; Xu, C.J.; Wang, G.J. Long-distance multi-channel bidirectional chaos communication based on synchronized VCSELs subject to chaotic signal injection. Opt. Commun. 2016, 377, 1–9. [Google Scholar] [CrossRef]
- Cui, S.; Zhang, J. Chaotic secure communication based on single feedback phase modulation and channel transmission. IEEE Photonics J. 2019, 11, 7905208. [Google Scholar] [CrossRef]
- Li, N.Q.; Susantu, H.; Cemlyn, B.; Henning, I.D.; Adams, M.J. Secure communication systems based on chaos in optically pumped spin-VCSELs. Opt. Lett. 2017, 42, 3494–3497. [Google Scholar] [CrossRef]
- Lin, F.Y.; Liu, J.M. Chaotic lidar. IEEE J. Sel. Top. Quantum Electron. 2004, 10, 991–997. [Google Scholar] [CrossRef]
- Wang, L.; Guo, Y.; Li, P.; Zhao, T.; Wang, Y.; Wang, A. White-chaos radar with enhanced range resolution and anti-jamming capability. IEEE Photon. Technol. Lett. 2017, 29, 1723–1726. [Google Scholar] [CrossRef]
- Zhou, P.; Li, N.Q.; Pan, S.L. Photonic microwave harmonic down-converter based on stabilized period-one nonlinear dynamics of semiconductor lasers. Opt. Lett. 2019, 44, 4869–4872. [Google Scholar] [CrossRef]
- Xia, L.; Huang, D.; Xu, J.; Liu, D. Simultaneous and precise fault locating in WDM-PON by the generation of optical wideband chaos. Opt. Lett. 2013, 38, 3762–3764. [Google Scholar] [CrossRef]
- Rontani, D.; Choi, D.; Chang, C.Y.; Locquet, A.; Citrin, D.S. Compressive sensing with optical chaos. Sci. Rep. 2016, 6, 35206. [Google Scholar] [CrossRef] [Green Version]
- Adams, M.J.; Alexandropoulos, D. Parametric analysis of spin-polarized VCSELs. IEEE J. Quantum Electron. 2009, 45, 744–749. [Google Scholar] [CrossRef]
- Torre, M.S.; Susanto, H.; Li, N.Q.; Schires, K.; Salvide, M.F.; Henning, I.D.; Adams, M.J.; Hurtado, A. High frequency continuous birefringence-induced oscillations in spin-polarized vertical-cavity surface-emitting lasers. Opt. Lett. 2017, 42, 1628–1631. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oestreich, M.; Hubner, J.; Hagele, D.; Bender, M.; Gerhardt, N.; Hofmann, M.; Ruhle, W.W.; Kalt, H.; Hartmann, T.; Klar, P.; et al. Spintronics: Spin electronics and optoelectronics in semiconductors. Adv. Solid State Phys. 2001, 41, 173–186. [Google Scholar]
- Lindemann, M.; Xu, G.; Pusch, T.; Michalzik, R.; Hofmann, M.R.; Žutić, I.; Gerhardt, N.C. Ultrafast spin-lasers. Nature 2019, 568, 212–215. [Google Scholar] [CrossRef]
- Gerhardt, N.C.; Li, M.Y.; Jähme, H.; Höpfner, H.; Ackemann, T.; Hofmann, M.R. Ultrafast spin-induced polarization oscillations with tunable lifetime in vertical-cavity surface-emitting lasers. Appl. Phys. Lett. 2011, 99, 151107. [Google Scholar] [CrossRef]
- Yokota, N.; Nisaka, K.; Yasaka, H.; Ikeda, K. Spin polarization modulation for high-speed vertical-cavity surface-emitting lasers. Appl. Phys. Lett. 2018, 113, 171102. [Google Scholar] [CrossRef]
- Lindemann, M.; Xu, G.; Pusch, T.; Michalzik, R.; Hofmann, M.R.; Žutić, I.; Gerhardt, N.C. Ultrafast Spin-Lasers for Optical Data Communication. In Proceedings of the 2019 Conference on Lasers and Electro-Optics Europe & European Quantum Electronics Conference, Munich, Germany, 23–27 January 2019; p. 19148647. [Google Scholar]
- Hövel, S.; Gerhardt, N.C.; Brenner, C.; Hofmann, M.R.; Lo, F.-Y.; Reuter, D.; Wieck, A.D.; Schuster, E.; Keune, W. Spin-controlled LEDs and VCSELs. Phys. Stat. Sol. (A) 2007, 204, 500–507. [Google Scholar] [CrossRef]
- Holub, M.; Shin, J.; Saha, D.; Bhattacharya, P. Electrical spin injection and threshold reduction in a semiconductor laser. Phys. Rev. Lett. 2007, 98, 146603. [Google Scholar] [CrossRef] [PubMed]
- Fujino, H.; Koh, S.; Iba, S.; Fujimoto, T.; Kawaguchi, H. Circularly polarized lasing in a (110)-oriented quantum well vertical-cavity surface-emitting laser under optical spin injection. Appl. Phys. Lett. 2009, 94, 131108. [Google Scholar] [CrossRef]
- Gahl, A.; Balle, S.; San Miguel, M. Polarization dynamics of optically pumped VCSELs. IEEE J. Quantum Electron. 1999, 35, 342–351. [Google Scholar] [CrossRef]
- Susanto, H.; Schires, K.; Adams, M.J.; Henning, I.D. Spin-flip model of spin-polarized vertical-cavity surface-emitting lasers: Asymptotic analysis, numerics, and experiments. Phys. Rev. A 2015, 92, 063838. [Google Scholar] [CrossRef] [Green Version]
- Alharthi, S.S.; Al Seyab, R.K.; Henning, I.D.; Adams, M.J. Simulated dynamics of optically pumped dilute nitride 1300 nm spin vertical-cavity surface-emitting lasers. IET Optoelectron. 2014, 8, 117–121. [Google Scholar] [CrossRef] [Green Version]
- Al Seyab, R.K.; Alexandropoulos, D.; Henning, I.D.; Adams, M.J. Instabilities in spin-polarized vertical-cavity surface-emitting lasers. IEEE Photonics J. 2011, 3, 799–809. [Google Scholar] [CrossRef]
- Li, N.Q.; Susanto, H.; Cemlyn, B.R.; Henning, I.D.; Adams, M.J. Stability and bifurcation analysis of spin-polarized vertical-cavity surface-emitting lasers. Phys. Rev. A 2017, 96, 013840. [Google Scholar] [CrossRef] [Green Version]
- Li, N.Q.; Alexandropoulos, D.; Susanto, H.; Henning, I.D.; Adams, M.J. Stability analysis of quantum-dot spin-VCSELs. Electronics 2016, 5, 83. [Google Scholar] [CrossRef] [Green Version]
- Alexandropoulos, D.; Al-Seyab, R.; Henning, I.D.; Adams, M.J. Instabilities in quantum-dot spin-VCSELs. Opt. Lett. 2012, 37, 1700–1702. [Google Scholar] [CrossRef]
- Li, N.Q.; Susanto, H.; Cemlyn, B.R.; Henning, I.D.; Adams, M.J. Mapping bifurcation structure and parameter dependence in quantum dot spin-VCSELs. Opt. Exp. 2018, 26, 14636–14649. [Google Scholar] [CrossRef]
- Masoller, C.; Torre, M.S. Influence of optical feedback on the polarization switching of vertical-cavity surface-emitting lasers. IEEE J. Quantum Electron. 2005, 41, 483–489. [Google Scholar] [CrossRef]
- Panajotov, K.; Sciamanna, M.; Arteaga, M.A.; Thienpont, H. Optical feedback in vertical-cavity surface-emitting lasers. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 1700312. [Google Scholar] [CrossRef]
- Globisch, B.; Otto, C.; Schöll, E.; Lüdge, K. Influence of carrier lifetimes on the dynamical behavior of quantum-dot lasers subject to optical feedback. Phys. Rev. E 2012, 86, 046201. [Google Scholar] [CrossRef]
- Xia, G.Q.; Chan, S.C.; Liu, J.M. Multistability in a semiconductor laser with optoelectronic feedback. Opt. Express 2007, 15, 572–576. [Google Scholar] [CrossRef]
- Lin, F.Y.; Liu, J.M. Nonlinear dynamics of a semiconductor laser with delayed negative optoelectronic feedback. IEEE J. Quantum Electron. 2003, 39, 562–568. [Google Scholar] [CrossRef]
- Xie, Y.Y.; Lin, X.D.; Deng, T.; Wu, Z.M.; Fan, L.; Zhong, Z.Q.; Xia, G.Q. Experimental observation of current-induced bistability in a semiconductor laser with positive optoelectronic feedback. IEEE Photonics Technol. Lett. 2012, 24, 1434–1436. [Google Scholar] [CrossRef]
- Xie, Y.Y.; Che, H.J.; Zhao, W.L.; Huang, Y.X.; Xu, W.H.; Li, X.; Kan, Q.; Li, J.C. Dynamics of 1550-nm VCSELs with positive optoelectronic feedback: Theory and experiments. IEEE Photonics J. 2014, 6, 1502508. [Google Scholar] [CrossRef]
- Li, Q.L.; Lu, S.S.; Bao, Q.; Chen, D.W.; Hu, M.; Zeng, R.; Yang, G.W.; Li, S.Q. Simultaneous trilateral communication based on three mutually coupled chaotic semiconductor lasers with optical feedback. Appl. Opt. 2018, 57, 251–257. [Google Scholar] [CrossRef]
- Jiang, N.; Pan, W.; Yan, L.S.; Luo, B.; Zou, X.H.; Xiang, S.Y.; Yang, L.; Zheng, D. Multiaccess optical chaos communication using mutually coupled semiconductor lasers subjected to identical external injections. IEEE Photonics Technol. Lett. 2010, 22, 676–678. [Google Scholar] [CrossRef]
- Yokota, N.; Komukai, K.; Yoshida, M.; Yasaka, H. Numerical investigation of mutually injection-locked semiconductor lasers for direct IQ-signal generation. IEEE Photonics J. 2019, 11, 6602611. [Google Scholar] [CrossRef]
- Torre, M.S.; Masoller, C.; Shore, K.A. Numerical study of optical injection dynamics of vertical-cavity surface-emitting lasers. IEEE J. Quantum Electron. 2004, 40, 25–30. [Google Scholar] [CrossRef]
- Jiang, Z.F.; Wu, Z.M.; Jayaprasath, E.; Yang, W.Y.; Hu, C.X.; Xia, G.Q. Nonlinear dynamics of exclusive excited-state emission quantum dot Lasers under optical injection. Photonics 2019, 6, 58. [Google Scholar] [CrossRef] [Green Version]
- Mu, P.H.; Pan, W.; Li, N.Q. Analysis and characterization of chaos generated by free-running and optically injected VCSELs. Opt. Express 2018, 26, 15642–15655. [Google Scholar] [CrossRef]
- Correa-Mena, A.G.; Lee, M.W.; Zaldívar-Huerta, I.E.; Hong, Y.; Boudrioua, A. Investigation of the dynamical behavior of a high-power laser diode subject to stimulated brillouin scattering optical feedback. IEEE J. Quantum Electron. 2020, 56, 2000406. [Google Scholar] [CrossRef]
- Hohl, A.; Gavrielides, A. Bifurcation cascade in a semiconductor laser subject to optical feedback. Phys. Rev. Lett. 1999, 82, 1148–1151. [Google Scholar] [CrossRef]
- Haegeman, B.; Engelborghs, K.; Roose, D. Stability and rupture of bifurcation bridges in semiconductor lasers subject to optical feedback. Phys. Rev. E 2002, 66, 046216. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gottwald, G.A.; Melbourne, I. A new test for chaos in deterministic systems. In Proceedings of the Royal Society A: Mathematical Physical and Engineering Sciences, London, UK, 8 February 2004; pp. 603–611. [Google Scholar]
- Hu, J.; Tung, W.W.; Gao, J.B.; Cao, Y.H. Reliability of the 0–1 test for chaos. Phys. Rev. E 2005, 72, 056207. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Erzgräber, H.; Wieczorek, S.; Krauskopf, B. Dynamics of two semiconductor lasers coupled by a passive resonator. Phys. Rev. E 2010, 81, 056201. [Google Scholar] [CrossRef] [Green Version]
- Zachilas, L.; Psarianos, I.N. Examining the chaotic behavior in dynamical systems by means of the 0–1 test. J. Appl. Math. 2012, 2012, 681296. [Google Scholar] [CrossRef]
- Leon, F. Design and evaluation of a multiagent interaction protocol generating behaviours with different levels of complexity. Neurocomputing 2014, 146, 173–186. [Google Scholar] [CrossRef]
- Gottwald, G.A.; Melbourne, I. The 0–1 test for chaos: A review. In Chaos Detection and Predictability; Springer: Berlin, Germany, 2016; pp. 221–247. [Google Scholar]
- Krese, B.; Govekar, E. Nonlinear analysis of laser droplet generation by means of 0–1 test for chaos. Nonlinear Dyn. 2012, 67, 2101–2109. [Google Scholar] [CrossRef]
- Gottwald, G.A.; Melbourne, I. Implementation of the 0–1 test for chaos. SIAM J. Appl. Dyn. Syst. 2009, 8, 129–145. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, T.; Xie, Y.; Ye, Y.; Liu, B.; Chai, J.; Jiang, X.; Zheng, Y. Numerical Analysis of Nonlinear Dynamics Based on Spin-VCSELs with Optical Feedback. Photonics 2021, 8, 10. https://doi.org/10.3390/photonics8010010
Song T, Xie Y, Ye Y, Liu B, Chai J, Jiang X, Zheng Y. Numerical Analysis of Nonlinear Dynamics Based on Spin-VCSELs with Optical Feedback. Photonics. 2021; 8(1):10. https://doi.org/10.3390/photonics8010010
Chicago/Turabian StyleSong, Tingting, Yiyuan Xie, Yichen Ye, Bocheng Liu, Junxiong Chai, Xiao Jiang, and Yanli Zheng. 2021. "Numerical Analysis of Nonlinear Dynamics Based on Spin-VCSELs with Optical Feedback" Photonics 8, no. 1: 10. https://doi.org/10.3390/photonics8010010



