Mode Heterogeneous Multimode Power Splitter Based on Cascaded Mode-Dependent Splitters and Converters
Abstract
:1. Introduction
2. Design and Simulation
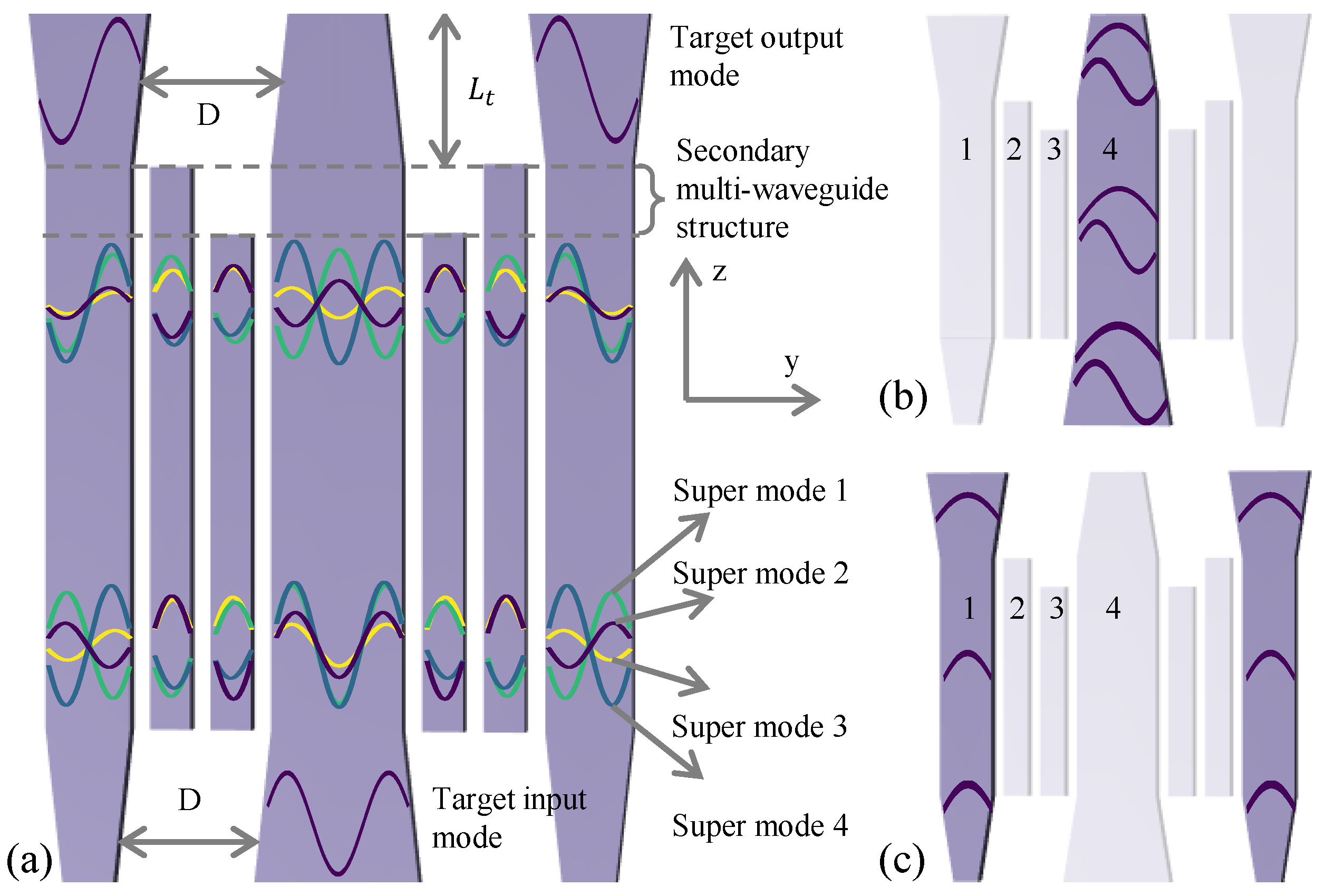
2.1. Principle
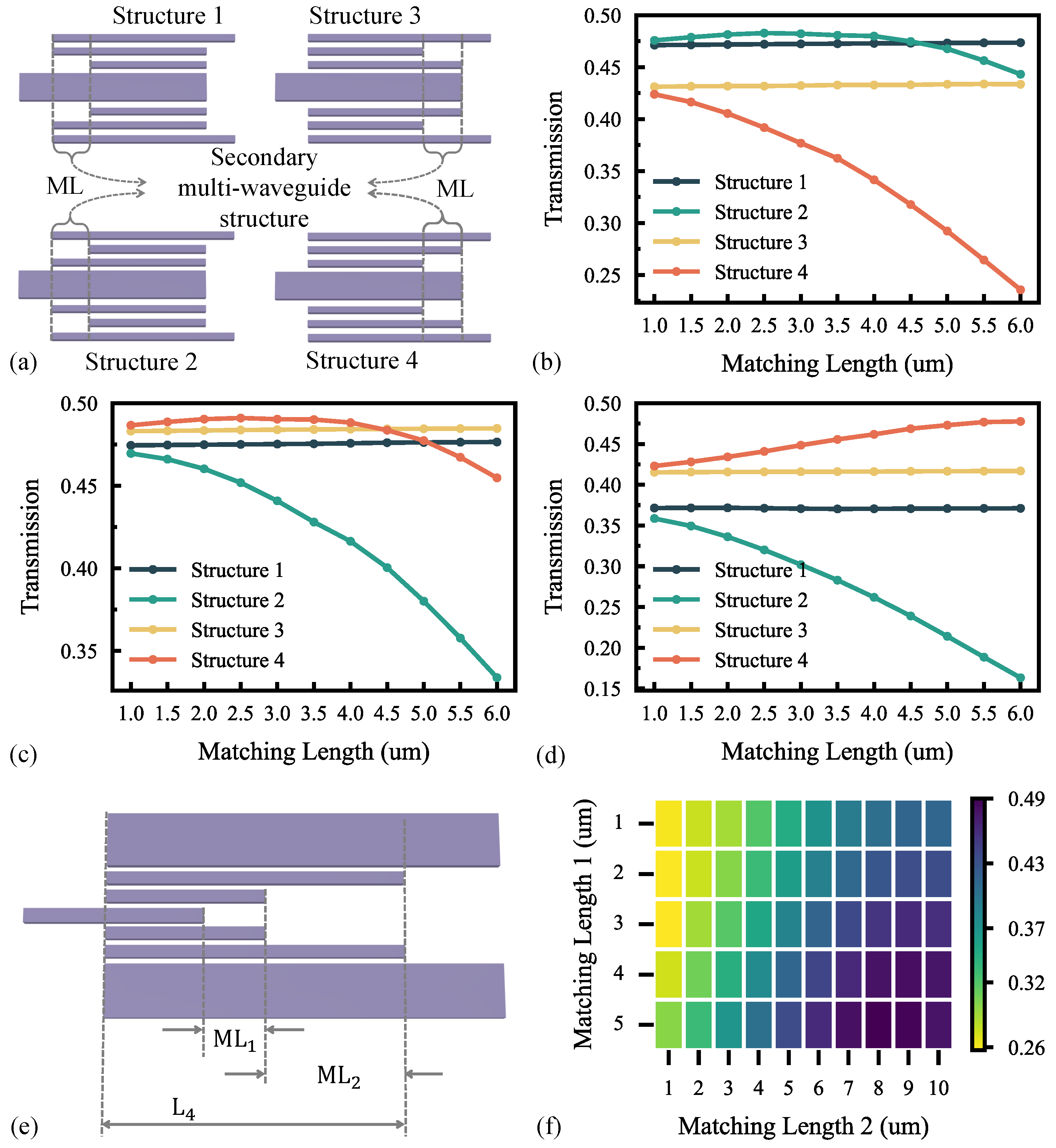
2.2. Optimization
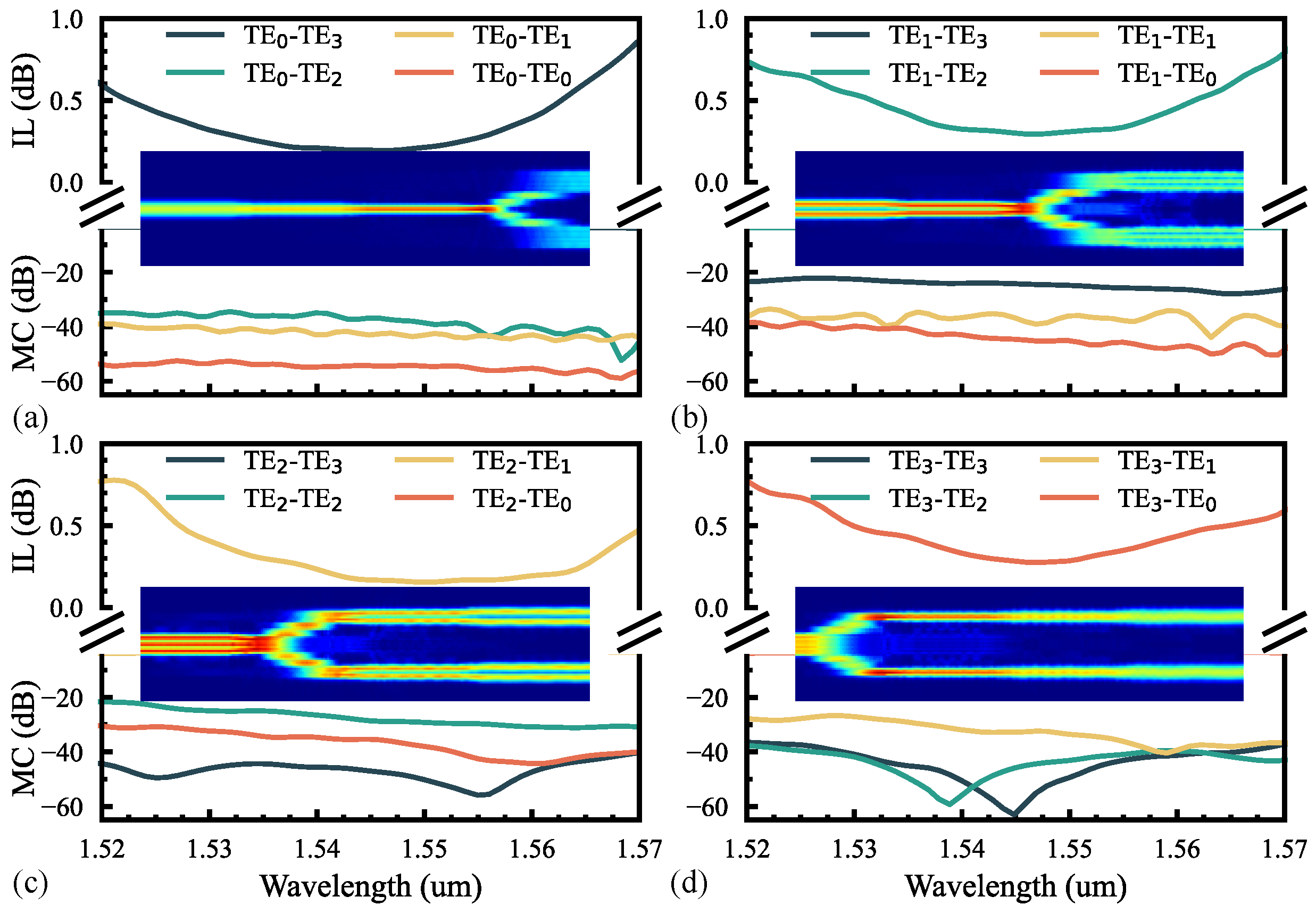
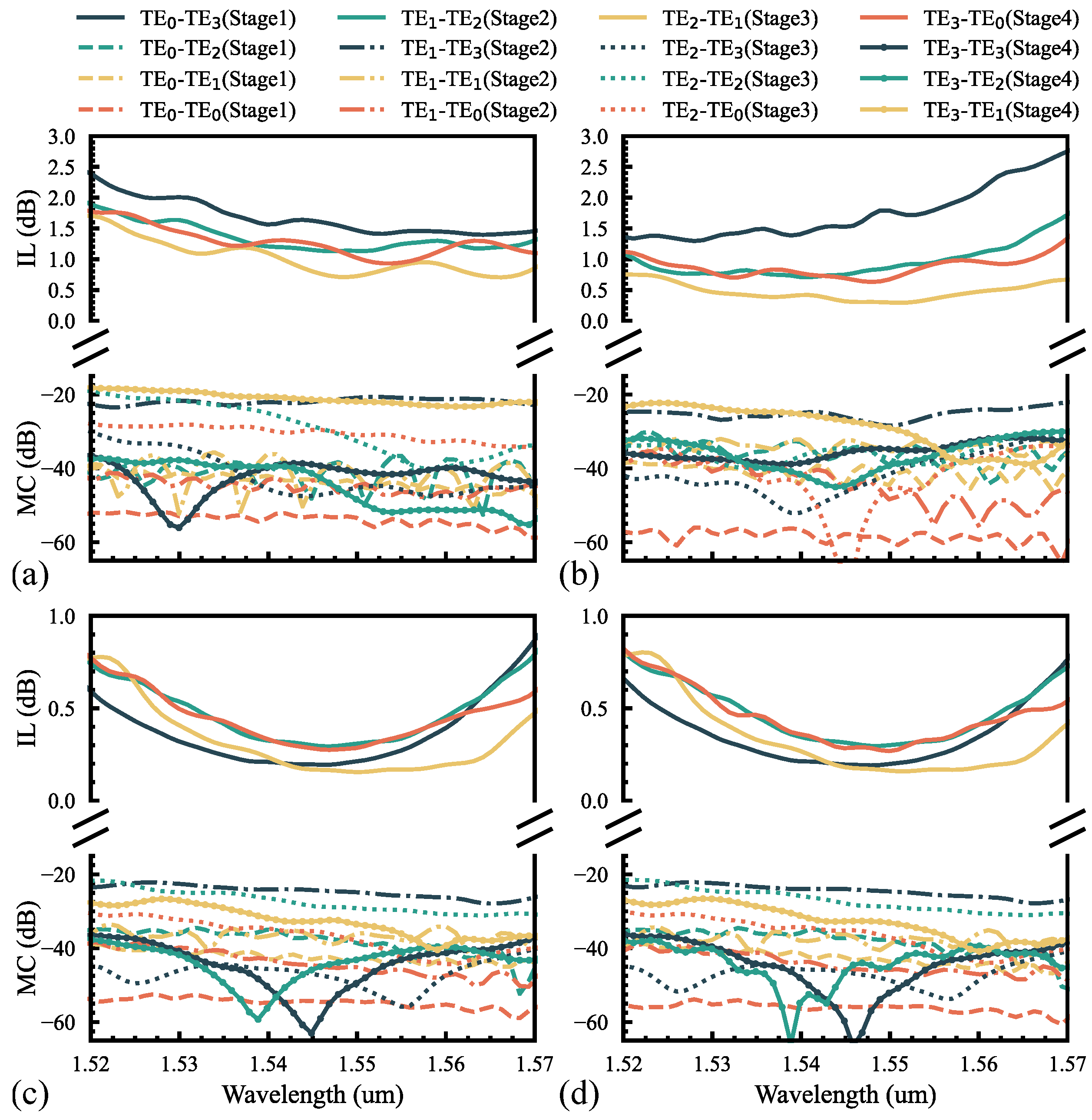
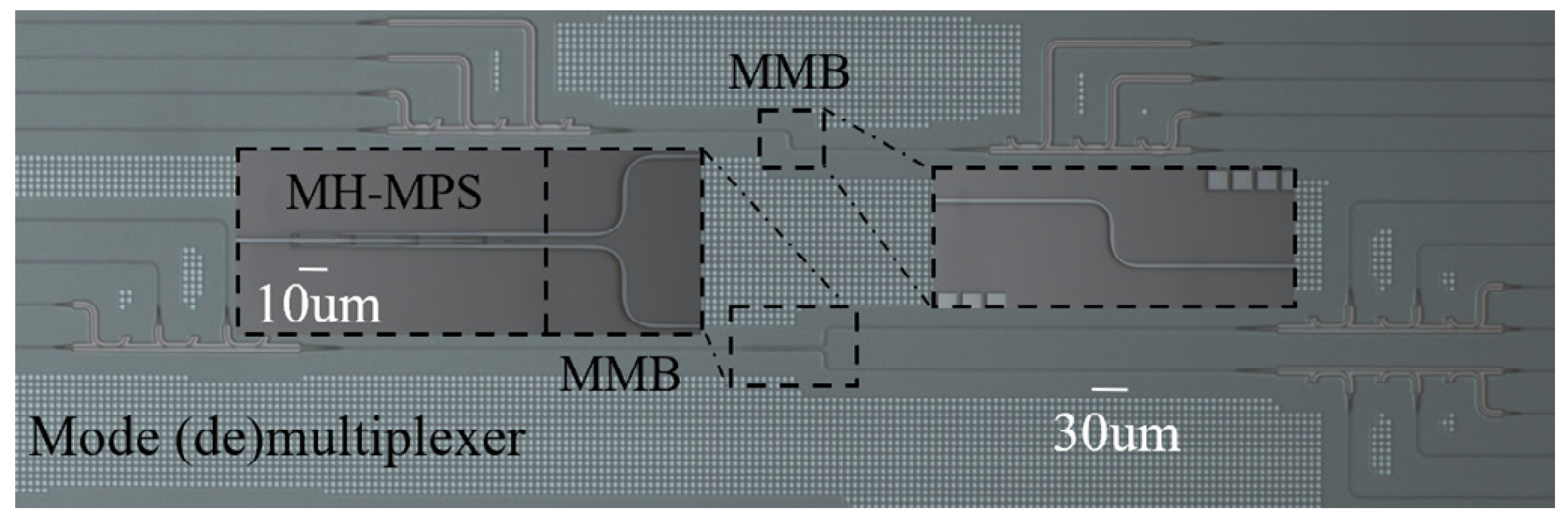
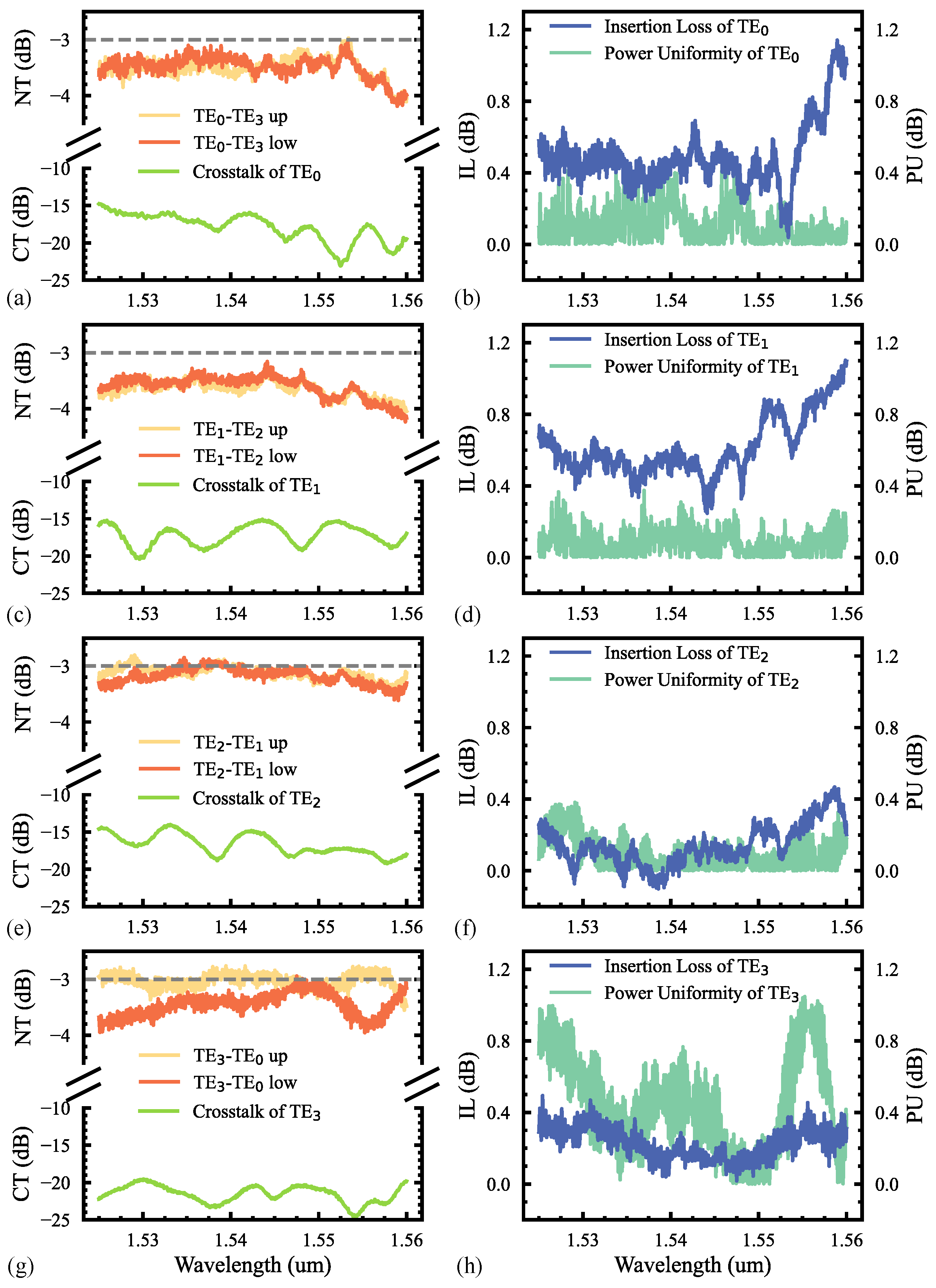
3. Fabrication and Characterization
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Atabaki, A.H.; Moazeni, S.; Pavanello, F.; Gevorgyan, H.; Notaros, J.; Alloatti, L.; Wade, M.T.; Sun, C.; Kruger, S.A.; Meng, H.; et al. Integrating Photonics with Silicon Nanoelectronics for the next Generation of Systems on a Chip. Nature 2018, 556, 349–354. [Google Scholar] [CrossRef] [PubMed]
- Rahim, A.; Spuesens, T.; Baets, R.; Bogaerts, W. Open-Access Silicon Photonics: Current Status and Emerging Initiatives. Proc. IEEE 2018, 106, 2313–2330. [Google Scholar] [CrossRef]
- Chen, X.; Milosevic, M.M.; Stanković, S.; Reynolds, S.; Bucio, T.D.; Li, K.; Thomson, D.J.; Gardes, F.; Reed, G.T. The Emergence of Silicon Photonics as a Flexible Technology Platform. Proc. IEEE 2018, 106, 2101–2116. [Google Scholar] [CrossRef]
- Dai, D.; Bowers, J.E. Silicon-Based on-Chip Multiplexing Technologies and Devices for Peta-Bit Optical Interconnects. Nanophotonics 2014, 3, 283–311. [Google Scholar] [CrossRef]
- Li, C.; Liu, D.; Dai, D. Multimode Silicon Photonics. Nanophotonics 2019, 8, 227–247. [Google Scholar] [CrossRef]
- Luo, L.W.; Ophir, N.; Chen, C.P.; Gabrielli, L.H.; Poitras, C.B.; Bergmen, K.; Lipson, M. WDM-Compatible Mode-Division Multiplexing on a Silicon Chip. Nat. Commun. 2014, 5, 3069. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; He, S.; Dai, D. On-Chip Silicon 8-Channel Hybrid (de)Multiplexer Enabling Simultaneous Mode- and Polarization-Division-Multiplexing. Laser Photonics Rev. 2014, 8, L18–L22. [Google Scholar] [CrossRef]
- Luo, Y.; Yu, Y.; Ye, M.; Sun, C.; Zhang, X. Integrated Dual-Mode 3 dB Power Coupler Based on Tapered Directional Coupler. Sci. Rep. 2016, 6, 23516. [Google Scholar] [CrossRef] [PubMed]
- Han, L.; Kuo, B.P.P.; Alic, N.; Radic, S. Ultra-Broadband Multimode 3dB Optical Power Splitter Using an Adiabatic Coupler and a Y-Branch. Opt. Express 2018, 26, 14800–14809. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Lu, L.; Zhang, P.; Chang, W.; Liu, D.; Zhang, M. Integrated Dual-Mode 3-dB Power Splitter Based on Multimode Interference Coupler. IEEE Photonics Technol. Lett. 2020, 32, 883–886. [Google Scholar] [CrossRef]
- Shiran, H.; Zhang, G.; Liboiron-Ladouceur, O. Dual-Mode Broadband Compact 2 × 2 Optical Power Splitter Using Sub-Wavelength Metamaterial Structures. Opt. Express 2021, 29, 23864–23876. [Google Scholar] [CrossRef] [PubMed]
- Chang, W.; Ren, X.; Ao, Y.; Lu, L.; Cheng, M.; Deng, L.; Liu, D.; Zhang, M. Inverse Design and Demonstration of an Ultracompact Broadband Dual-Mode 3 dB Power Splitter. Opt. Express 2018, 26, 24135–24144. [Google Scholar] [CrossRef] [PubMed]
- Xie, H.; Liu, Y.; Wang, Y.; Wang, Y.; Yao, Y.; Song, Q.; Du, J.; He, Z.; Xu, K. An Ultra-Compact 3-dB Power Splitter for Three Modes Based on Pixelated Meta-Structure. IEEE Photonics Technol. Lett. 2020, 32, 341–344. [Google Scholar] [CrossRef]
- Xu, H.; Dai, D.; Shi, Y. Ultra-Broadband on-Chip Multimode Power Splitter with an Arbitrary Splitting Ratio. OSA Contin. 2020, 3, 1212–1221. [Google Scholar] [CrossRef]
- Sun, C.; Ding, Y.; Li, Z.; Qi, W.; Yu, Y.; Zhang, X. Key Multimode Silicon Photonic Devices Inspired by Geometrical Optics. ACS Photonics 2020, 7, 2037–2045. [Google Scholar] [CrossRef]
- Xu, H.; Shi, Y. Ultra-Broadband Dual-Mode 3 dB Power Splitter Based on a Y-Junction Assisted with Mode Converters. Opt. Lett. 2016, 41, 5047–5050. [Google Scholar] [CrossRef]
- Chen, W.; Lin, J.; Li, H.; Wang, P.; Dai, S.; Liu, Y.; Yao, R.; Li, J.; Fu, Q.; Dai, T.; et al. Broadband Multimode 3 dB Optical Power Splitter Using Tapered Couplers. Opt. Express 2022, 30, 46236–46247. [Google Scholar] [CrossRef] [PubMed]
- Cooper, M.L.; Mookherjea, S. Numerically-Assisted Coupled-Mode Theory for Silicon Waveguide Couplers and Arrayed Waveguides. Opt. Express 2009, 17, 1583–1599. [Google Scholar] [CrossRef] [PubMed]

| Stage | (μm) | (μm) | L (μm) | ML (μm) |
|---|---|---|---|---|
| 1 | 0.36 | 1.56 | 15.57 | 2 |
| 2 | 0.76 | 1.16 | 16.57 | 2 |
| 3 | 1.16 | 0.76 | 17.88 | 6 |
| 4 | 1.56 | 0.36 | 19.33 | 4; 9 |
| Input Mode | 1.525–1.56 μm | 1.55 μm | ||||
|---|---|---|---|---|---|---|
| IL (dB) | CT (dB) | PU (dB) | IL (dB) | CT (dB) | PU (dB) | |
| <1.14 | <−14.8 | <0.46 | 0.47 | −18.79 | 0.026 | |
| <1.1 | <−15.08 | <0.38 | 0.63 | −16.7 | 0.032 | |
| <0.47 | <−14 | <0.38 | 0.26 | −17.64 | 0.074 | |
| <0.49 | <−19.53 | <1.05 | 0.16 | −19.53 | 0.168 | |
| Structure | Modes | Length (μm) | BW (nm) | IL (dB) | CT (dB) | PU (dB) |
|---|---|---|---|---|---|---|
| MMI [10] | 96.9 | 1530–1590 | <0.76 | <−20.50 | <0.9 | |
| SWG MMI [11] | 48.84 | 1500–1600 | <0.65 | <−17.00 | - | |
| Inverse design [12] | 2.88 | 1520–1580 | <1.50 | <−20.00 | - | |
| Inverse design [13] | 4.5 | 1530–1570 | <1.50 | <−15.00 | <0.35 | |
| Y-junction assisted with mode converters [16] | 120 | 1530–1610 | < 2.65 | <−13.30 | - | |
| Splitter using tapered couplers (PSO) [17] | 120 | 1520–1600 | <1.50 | <−14.12 | <0.88 | |
| This work | 87 | 1525–1560 | <1.14 | <−14.00 | <1.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Chen, H.; Fu, X.; Yang, L. Mode Heterogeneous Multimode Power Splitter Based on Cascaded Mode-Dependent Splitters and Converters. Photonics 2024, 11, 457. https://doi.org/10.3390/photonics11050457
Xu X, Chen H, Fu X, Yang L. Mode Heterogeneous Multimode Power Splitter Based on Cascaded Mode-Dependent Splitters and Converters. Photonics. 2024; 11(5):457. https://doi.org/10.3390/photonics11050457
Chicago/Turabian StyleXu, Xin, Hongliang Chen, Xin Fu, and Lin Yang. 2024. "Mode Heterogeneous Multimode Power Splitter Based on Cascaded Mode-Dependent Splitters and Converters" Photonics 11, no. 5: 457. https://doi.org/10.3390/photonics11050457





