High-Sensitivity Quantum-Enhanced Interferometers
Abstract
:1. Introduction
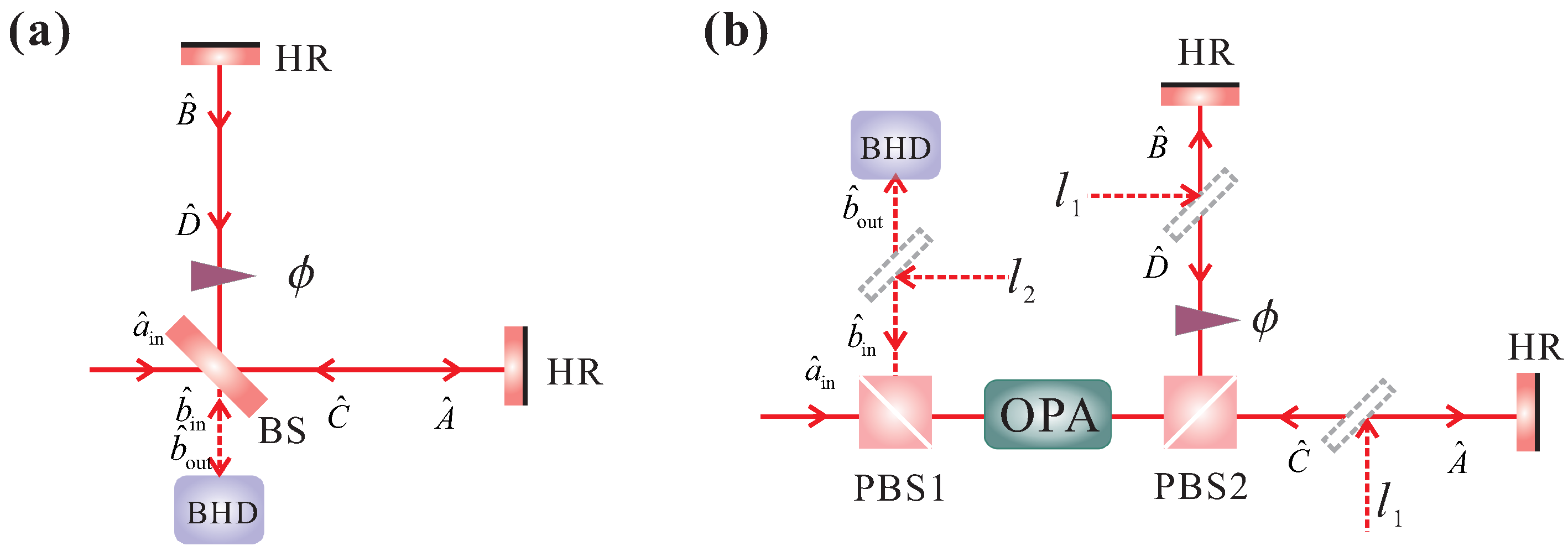
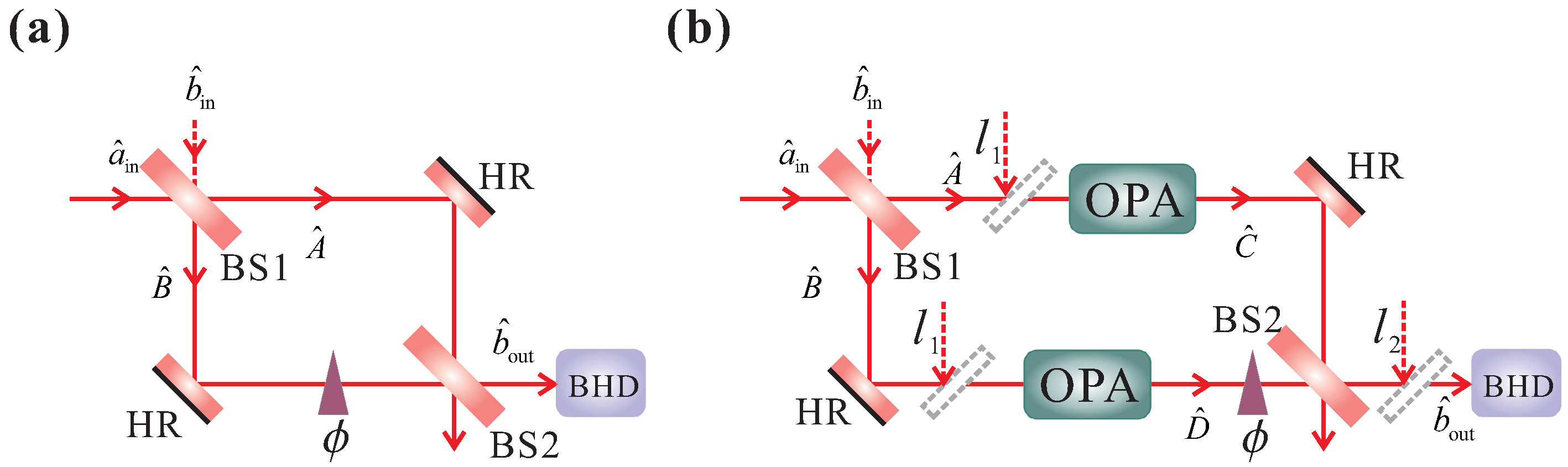
2. Quantum Interferometers
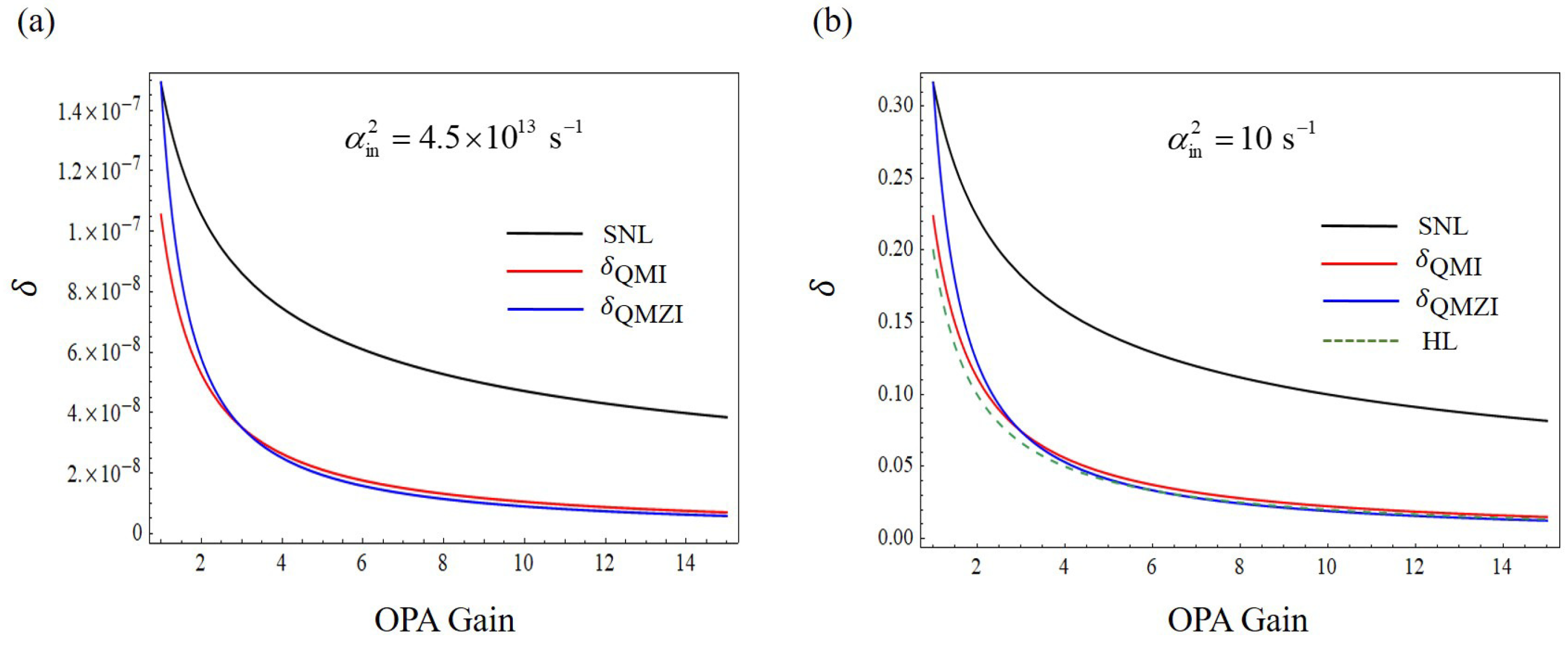
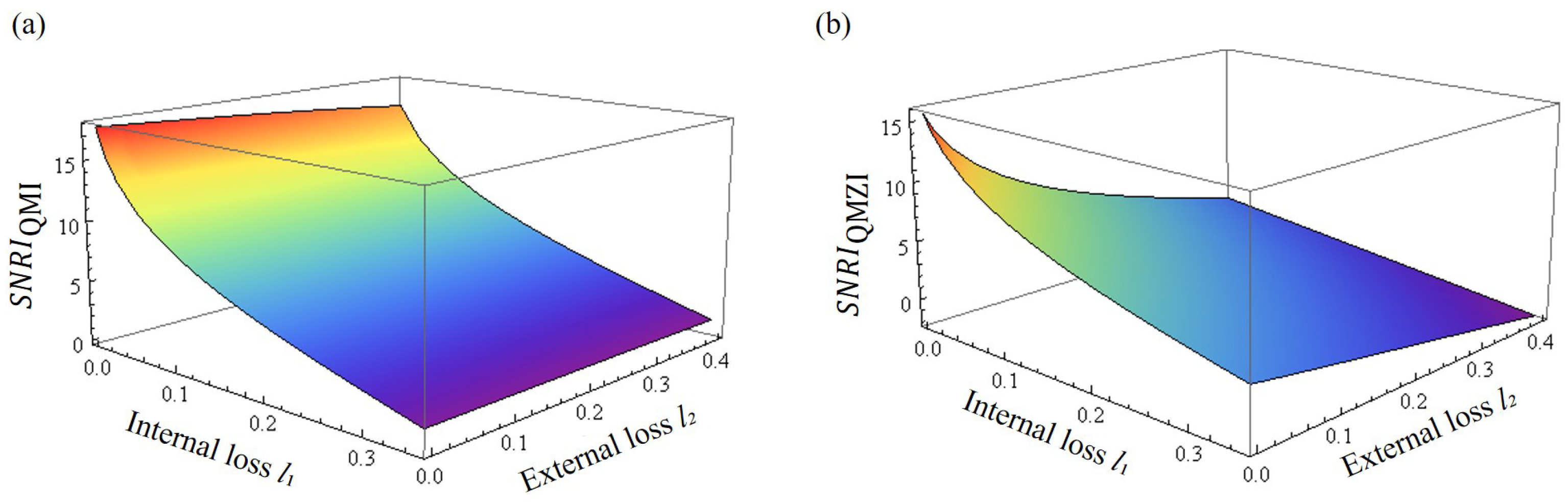
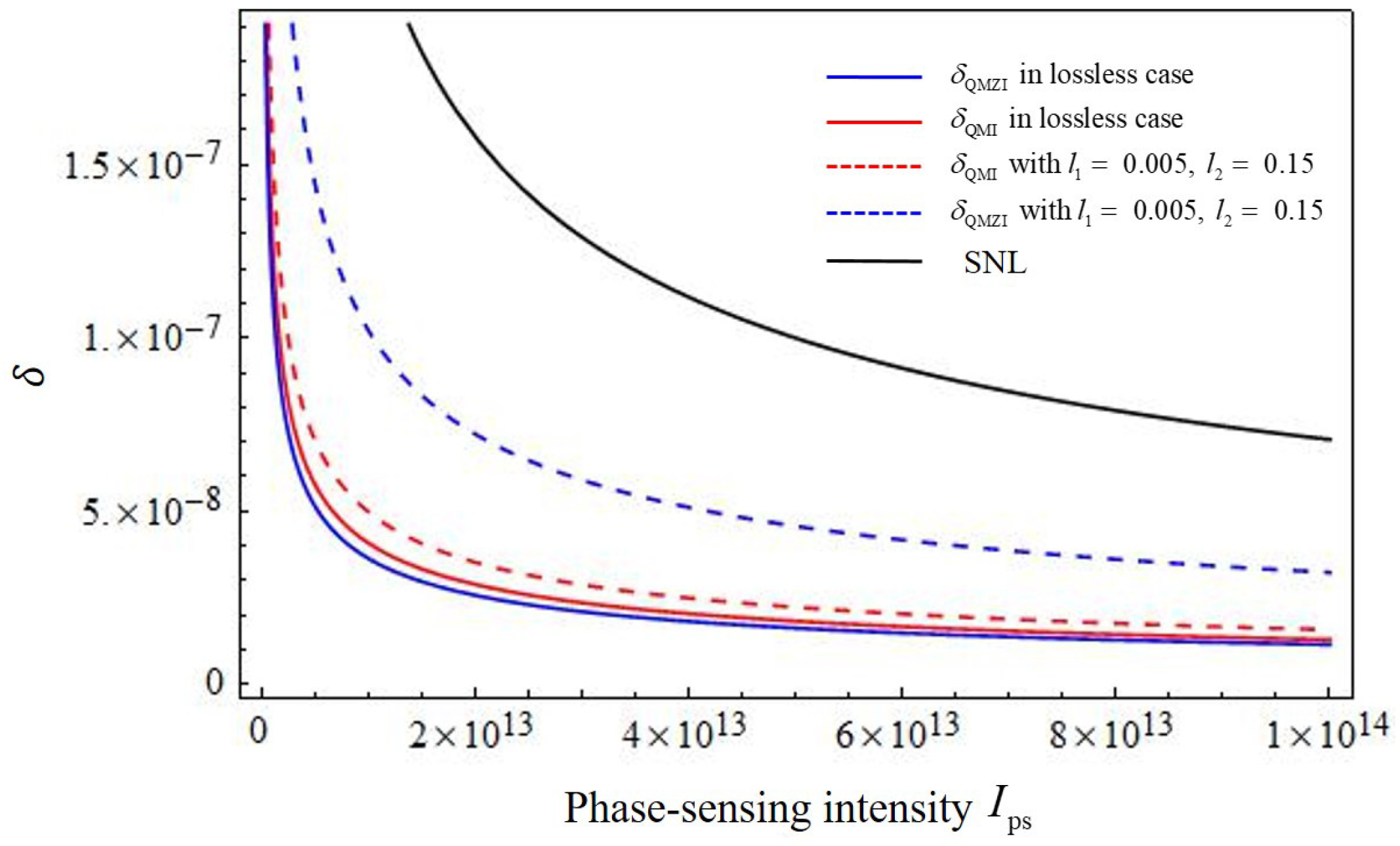
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Taylor, M.A.; Janousek, J.; Daria, V.; Knittel, J.; Hage, B.; Bachor, H.-A.; Bowen, W.P. Sub diffraction-Limited Quantum Imaging within a Living Cell. Phys. Rev. X 2014, 4, 011017. [Google Scholar]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Advances in quantum metrology. Nat. Photonics 2011, 5, 222–229. [Google Scholar] [CrossRef] [Green Version]
- Tse, M.; Yu, H.; Kijbunchoo, N.; Fernandez-Galiana, A.; Dupej, P.; Barsotti, L.; Blair, C.D.; Brown, D.D.; Dwyer, S.E.; Effler, A.; et al. Quantum-Enhanced Advanced LIGO Detectors in the Era of Gravitational-Wave Astronomy. Phys. Rev. Lett. 2019, 123, 231107. [Google Scholar] [CrossRef] [Green Version]
- Acernese, F.; Agathos, M.; Aiello, L.; Allocca, A.; Amato, A.; Ansoldi, S.; Antier, S.; Arene, M.; Arnaud, N.; Ascenzi, S.; et al. Increasing the Astrophysical Reach of the Advanced Virgo Detector via the Application of Squeezed Vacuum States of Light. Phys. Rev. Lett. 2019, 123, 231108. [Google Scholar] [CrossRef] [Green Version]
- Kimble, H.J.; Levin, Y.; Matsko, A.B.; Thorne, K.S.; Vyatchanin, S.P. Conversion of conventional gravitational-wave interferometers into quantum nondemolition interferometers by modifying their input and/or output optics. Phys. Rev. D 2001, 65, 022002. [Google Scholar] [CrossRef] [Green Version]
- Peters, A.; Chung, K.Y.; Chu, S. High-precision gravity measurements using atom interferometry. Metrologia 2001, 38, 25. [Google Scholar] [CrossRef]
- Rosi, G.; Sorrentino, F.; Cacciapuoti, L.; Prevedelli, M.; Tino, G. Precision measurement of the Newtonian gravitational constant using cold atoms. Nature 2014, 510, 518–521. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gault, W.; Shepherd, G. WAMDII—A wide angle Michelson Doppler imaging interferometer for spacelab. Adv. Space Res. 1982, 2, 111–114. [Google Scholar] [CrossRef] [Green Version]
- Boixo, S.; Davis, M.J.; Shaji, A. Quantum Metrology: Dynamics versus Entanglement. Phys. Rev. Lett. 2008, 101, 040403. [Google Scholar] [CrossRef] [Green Version]
- Holland, M.J.; Burnett, K. Interferometric detection of optical phase shifts at the Heisenberg limit. Phys. Rev. Lett. 1993, 71, 1355. [Google Scholar] [CrossRef]
- Xiao, M.; Wu, L.A.; Kimble, H.J. Precision Measurement beyond the Shot-Noise Limit. Phys. Rev. Lett. 1987, 59, 278. [Google Scholar] [CrossRef] [Green Version]
- Grangier, P.; Slusher, R.E.; Yurke, B.; LaPorta, A. Squeezed-Light-Enhanced Polarization Interferometer. Phys. Rev. Lett. 1987, 59, 19. [Google Scholar] [CrossRef]
- Degen, C.L.; Reinhard, F.; Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 2017, 89, 035002. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Miao, H.; Pang, B.H.; Evans, M.; Zhao, C.; Harms, J.; Schnabel, R.; Chen, Y. Proposal for gravitational-wave detection beyond the standard quantum limit through EPR entanglement. Nat. Photonics 2017, 13, 776–780. [Google Scholar] [CrossRef]
- Ou, Z.Y. Enhancement of the phase-measurement sensitivity beyond the standard quantum limit by a nonlinear interferometer. Phys. Rev. A 2012, 85, 023815. [Google Scholar] [CrossRef]
- Caves, C.M. Quantum mechanical noise in an interferometer. Phys. Rev. D 1981, 23, 1693. [Google Scholar] [CrossRef]
- Huang, Z.X.; Motes, K.R.; Anisimov, P.M.; Dowling, J.P.; Berry, D.W. Adaptive phase estimation with two-mode squeezed vacuum and parity measurement. Phys. Rev. A 2017, 95, 053837. [Google Scholar] [CrossRef] [Green Version]
- Liu, F.; Zhou, Y.Y.; Yu, J.; Guo, J.L.; Wu, Y.; Xiao, S.X.; Wei, D.; Zhang, Y.; Jia, X.J.; Xiao, M. Squeezingenhanced fiber Mach-Zehnder interferometer for lowfrequency phase measurement. Appl. Phys. Lett. 2017, 110, 021106. [Google Scholar] [CrossRef] [Green Version]
- Higgins, B.L.; Berry, D.W.; Bartlett, S.D.; Wiseman, H.M.; Pryde, G.J. Entanglement-free Heisenberg-limited phase estimation. Nature 2007, 450, 393–396. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xiang, G.Y.; Higgins, B.L.; Berry, D.W.; Wiseman, H.M.; Pryde, G.J. Entanglement-enhanced measurement of a completely unknown optical phase. Nat. Photonics 2010, 5, 43–47. [Google Scholar] [CrossRef] [Green Version]
- Yonezawa, H.; Nakane, D.; Wheatley, T.A.; Iwasawa, K.; Takeda, S.; Arao, H.; Ohki, K.; Tsumura, K.; Berry, D.W.; Ralph, T.C.; et al. Quantum-enhanced optical phase tracking. Science 2012, 337, 1514–1517. [Google Scholar] [CrossRef] [Green Version]
- Yu, J.; Qin, Y.; Qin, J.L.; Wang, H.; Yan, Z.H.; Jia, X.J.; Peng, K.C. Quantum Enhanced Optical Phase Estimation With a Squeezed Thermal State. Phys. Rev. Appl. 2020, 13, 024037. [Google Scholar] [CrossRef] [Green Version]
- Guo, X.S.; Breum, C.R.; Borregaard, J.; Izumi, S.; Larsen, M.V.; Gehring, T.; Christandl, M.; Neergaard-Nielsen, J.S.; Andersen, U.L. Distributed quantum sensing in a continuous variable entangled network. Nat. Phys. 2020, 16, 281–284. [Google Scholar] [CrossRef] [Green Version]
- Dinani, H.T.; Berry, D.W. Adaptive estimation of a time-varying phase with a power-law spectrum via continuous squeezed states. Phys. Rev. A 2017, 95, 063821. [Google Scholar] [CrossRef] [Green Version]
- Nagata, T.; Okamoto, R.; O’Brien, J.L.; Sasaki, K.; Takeuchi, S. Beating the Standard Quantum Limit with Four-Entangled Photons. Science 2007, 316, 726–729. [Google Scholar] [CrossRef] [Green Version]
- Huo, M.R.; Qin, J.L.; Cheng, J.L.; Yan, Z.H.; Qin, Z.Z.; Su, X.L.; Jia, X.J.; Xie, C.D.; Peng, K.C. Deterministic quantum teleportation through fiber channels. Sci. Adv. 2018, 4, eaas9401. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.Y.; Yu, J.; Yan, Z.H.; Jia, X.J.; Zhang, J.; Xie, C.D.; Peng, K.C. Quantum Secret Sharing among Four Players Using Multipartite Bound Entanglement of an Optical Field. Phys. Rev. Lett. 2018, 121, 150502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yan, Z.H.; Qin, J.; Qin, Z.Z.; Su, X.L.; Jia, X.J.; Xie, C.D.; Peng, K.C. Generation of non-classical states of light and their application in deterministic quantum teleportation. Fundam. Res. 2021, 1, 43–49. [Google Scholar] [CrossRef]
- Ma, L.X.; Lei, X.; Yan, J.L.; Li, R.Y.; Chai, T.; Yan, Z.H.; Jia, X.J.; Xie, C.D.; Peng, K.C. High-performance cavity-enhanced quantum memory with warm atomic cell. Nat. Commun. 2022, 13, 2368. [Google Scholar] [CrossRef] [PubMed]
- Nichols, R.; Bromley, T.R.; Correa, L.A.; Adesso, G. Practical quantum metrology in noisy environments. Phys. Rev. A 2016, 94, 042101. [Google Scholar] [CrossRef] [Green Version]
- Yurke, B.; McCall, S.L.; Klauder, J.R. SU(2) and SU(1,1) interferometers. Phys. Rev. A 1986, 33, 4033. [Google Scholar] [CrossRef] [PubMed]
- Hudelist, F.; Kong, J.; Liu, C.; Jing, J.; Ou, Z.Y.; Zhang, W. Quantum metrology with parametric amplifier-based photon correlation interferometers. Nat. Commun. 2014, 5, 3049. [Google Scholar] [CrossRef] [Green Version]
- Zheng, K.M.; Mi, M.H.; Wang, B.; Xu, L.Y.; Hu, L.; Liu, S.S.; Lou, Y.B.; Jing, J.T.; Zhang, L.J. Quantum-enhanced stochastic phase estimation with SU(1,1) interferometer. Photonics Res. 2020, 8, 1653–1661. [Google Scholar] [CrossRef]
- Li, J.M.; Liu, Y.H.; Cui, L.; Huo, N.; Assad, S.M.; Li, X.Y.; Ou, Z.Y. Joint measurement of multiple noncommuting parameters. Phys. Rev. A 2018, 97, 052127. [Google Scholar] [CrossRef] [Green Version]
- Zuo, X.J.; Yan, Z.H.; Feng, Y.N.; Ma, J.X.; Jia, X.J.; Xie, C.D.; Peng, K.C. Quantum interferometer combining squeezing and parametric amplification. Phys. Rev. Lett. 2020, 124, 173602. [Google Scholar] [CrossRef]
- Pooser, R.C.; Savino, N.; Batson, E.; Beckey, J.L.; Garcia, J.; Lawrie, B.J. Truncated nonlinear interferometry for quantum-enhanced atomic force microscopy. Phys. Rev. Lett. 2020, 124, 230504. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Liang, X.; Zhu, B.; Yan, Y.; Yuan, C.; Zhang, W.; Chen, L.Q. Protection of Noise Squeezing in a Quantum Interferometer with Optimal Resource Allocation. Phys. Rev. Lett. 2023, 130, 073601. [Google Scholar] [CrossRef] [PubMed]
- Heinze, J.; Danzmann, K.; Willke, B.; Vahlbruch, H. 10 dB Quantum-Enhanced Michelson Interferometer with Balanced Homodyne Detection. Phys. Rev. Lett. 2022, 129, 031101. [Google Scholar] [CrossRef]
- Zander, J.; Rembe, C.; Schnabel, R. 10 dB interferometer enhancement by squeezing of photon shot noise with sub-femtometer resolution and eye-safe optical power. Quantum Sci. Technol. 2023, 8, 01LT01. [Google Scholar] [CrossRef]
- Kalinin, N.; Dirmeier, T.; Sorokin, A.A.; Anashkina, E.A.; Sáchez-Soto, L.L. Quantum-enhanced interferometer using Kerr squeezing. Nanophotonics 2023, 00323. [Google Scholar] [CrossRef]
- Zuo, X.; Sun, Y.; Yan, Z.; Jia, X. High sensitivity quantum Michelson interferometer. Acta Phys. Sin. 2018, 67, 134202. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Wu, Y.; Nie, L.; Zuo, X. High-Sensitivity Quantum-Enhanced Interferometers. Photonics 2023, 10, 749. https://doi.org/10.3390/photonics10070749
Yu J, Wu Y, Nie L, Zuo X. High-Sensitivity Quantum-Enhanced Interferometers. Photonics. 2023; 10(7):749. https://doi.org/10.3390/photonics10070749
Chicago/Turabian StyleYu, Juan, Yinhua Wu, Liang Nie, and Xiaojie Zuo. 2023. "High-Sensitivity Quantum-Enhanced Interferometers" Photonics 10, no. 7: 749. https://doi.org/10.3390/photonics10070749
APA StyleYu, J., Wu, Y., Nie, L., & Zuo, X. (2023). High-Sensitivity Quantum-Enhanced Interferometers. Photonics, 10(7), 749. https://doi.org/10.3390/photonics10070749




