Numerical Simulation of a Light Field Structure in an Integrating Sphere via the Monte Carlo Method
Abstract
:1. Introduction
2. Materials and Methods
2.1. Integrated Cavity Absorption Meter
2.2. Numerical Simulation, Icammc Program
3. Results
3.1. Mirror Integrated Sphere
3.2. Fluorilon Sphere. Applicability of Various Phase Functions
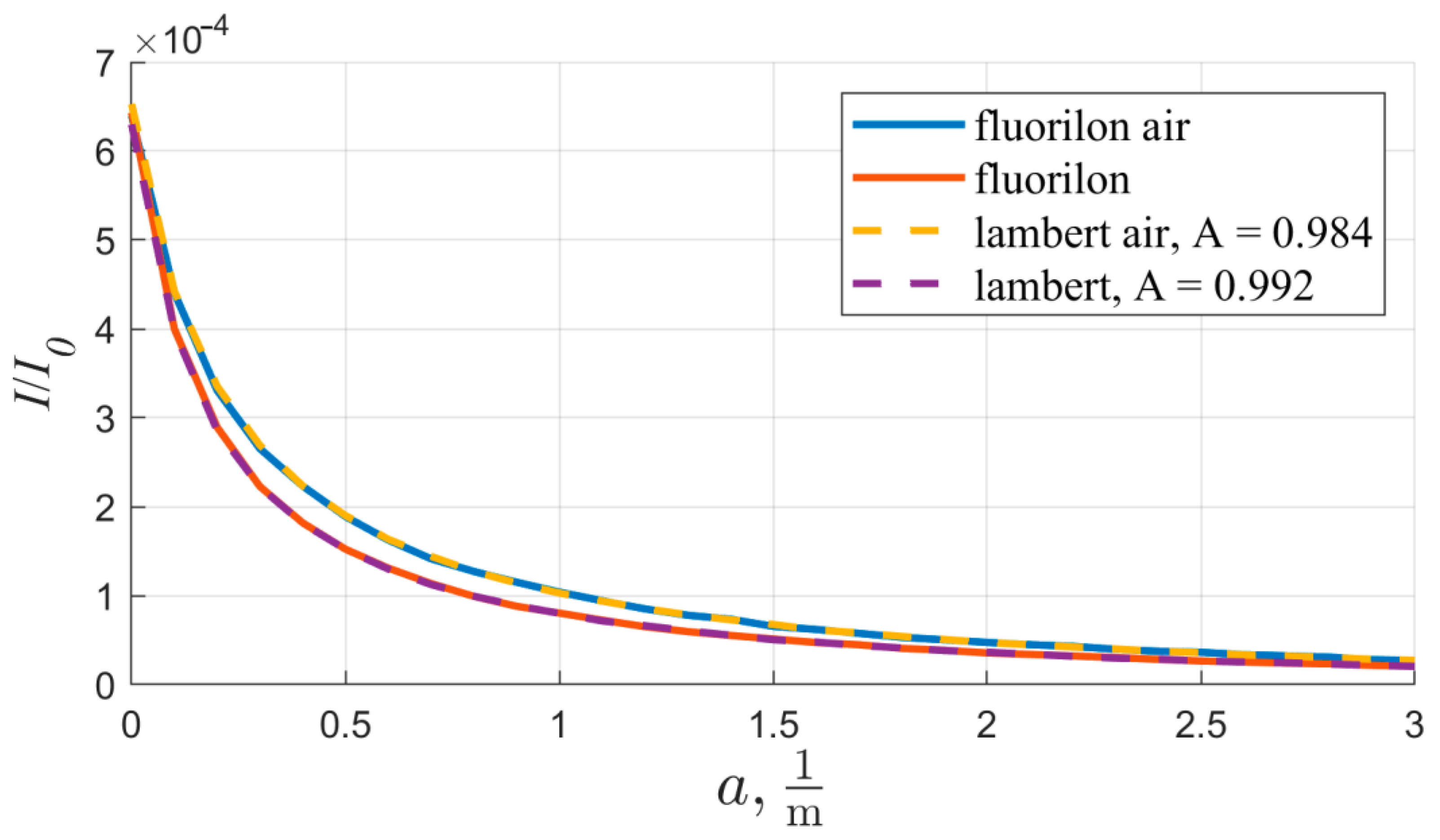
3.3. Applicability of the Lambert Approximation
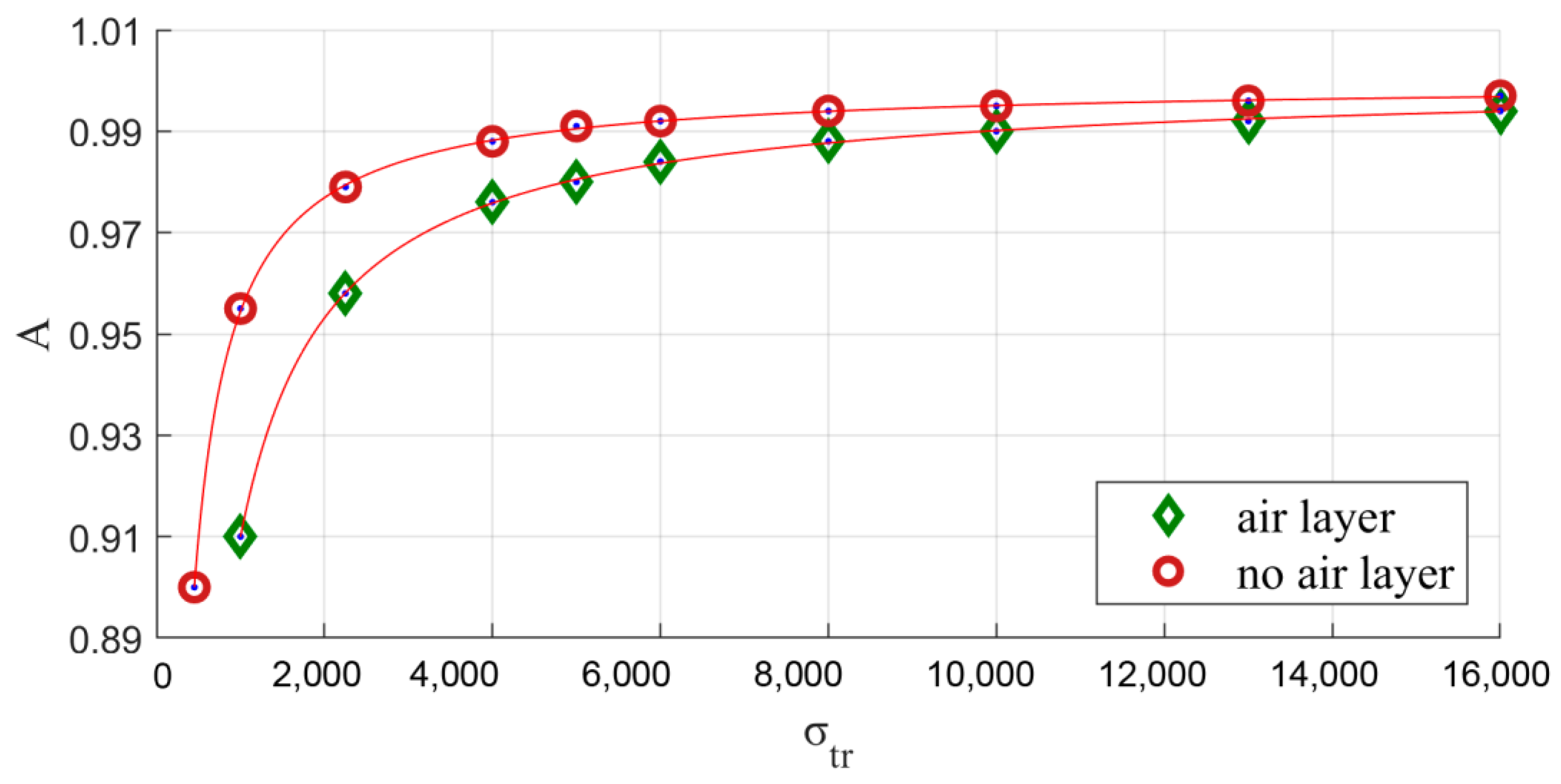
3.4. Air Layer between Quartz and Fluorilon
3.5. Diffusion Approximation
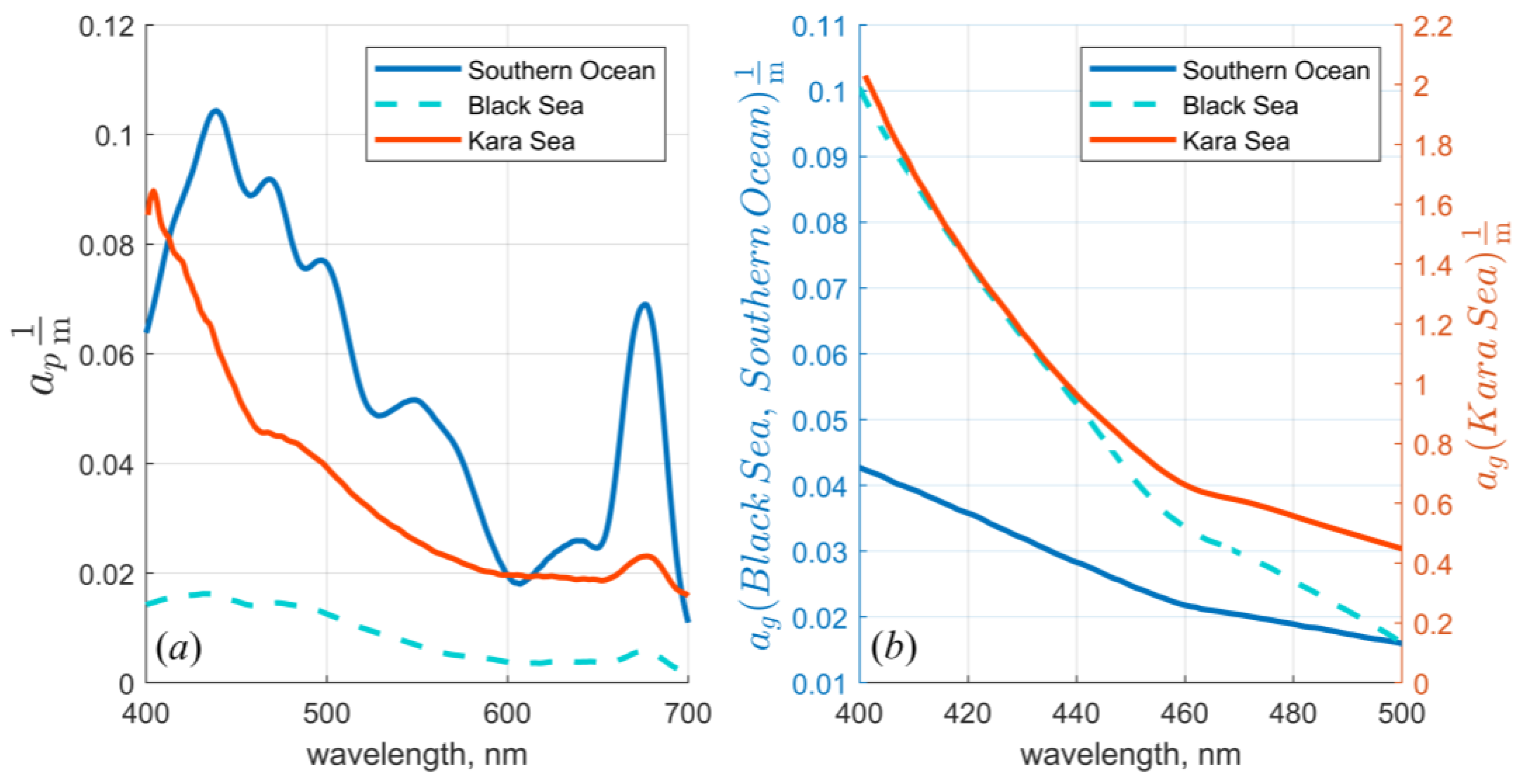
3.6. Oceanological Results Example
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shifrin, K.S. Physical Optics of Ocean Water; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Glukhovets, D.I.; Sheberstov, S.V.; Kopelevich, O.V.; Zaytseva, A.F.; Pogosyan, S.I. Measuring the sea water absorption factor using integrating sphere. Light Eng. 2018, 26, 120–126. [Google Scholar] [CrossRef]
- Mobley, C. The Oceanic Optics Book. 2022. Available online: https://ioccg.org/wp-content/uploads/2022/01/mobley-oceanicopticsbook.pdf (accessed on 24 January 2022).
- Duarte, C.M.; Lenton, T.M.; Wadhams, P.; Wassmann, P. Abrupt climate change in the Arctic. Nat. Clim. Chang. 2012, 2, 60–62. [Google Scholar] [CrossRef]
- Gulev, S.K.; Thorne, P.W.; Ahn, J.; Dentener, F.J.; Domingues, C.M.; Gerland, S.; Gong, D.; Kaufman, D.S.; Nnamchi, H.C.; Vose, R.S.; et al. Changing state of the climate system. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Natural Environment Research Council: Swindon, UK; New York, NY, USA; Cambridge University Press: Cambridge, UK, 2021; pp. 287–422. [Google Scholar]
- Perovich, D.K.; Jones, K.F.; Light, B.; Eicken, H.; Markus, T.; Stroeve, J.; Lindsay, R. Solar partitioning in a changing Arctic sea-ice cover. Ann. Glaciol. 2011, 52, 192–196. [Google Scholar] [CrossRef]
- Stroeve, J.C.; Markus, T.; Boisvert, L.; Miller, J.; Barrett, A. Changes in Arctic melt season and implications for sea ice loss. Geophys. Res. Lett. 2014, 41, 1216–1225. [Google Scholar] [CrossRef]
- Kirk, J.T.O. Light and Photosynthesis in Aquatic Ecosystems; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Kopelevich, O.V.; Sheberstov, S.V.; Burenkov, V.I.; Vazyulya, S.V.; Likhacheva, M.V. Assessment of underwater irradiance and absorption of solar radiation at water column from satellite data. In Proceedings of the Current Research on Remote Sensing, Laser Probing, and Imagery in Natural Waters SPIE, Moscow, Russian, 13 April 2007; Volume 6615, pp. 56–66. [Google Scholar] [CrossRef]
- Suslin, V.V.; Korolev, S.N.; Kucheryaviy, A.A.; Churilova, T.Y.; Krivenko, O.V. Photosynthetically available radiation on surface of the Black Sea based on ocean color data. In Proceedings of the Proc. SPIE 9680, 21st International Symposium Atmospheric and Ocean Optics: Atmospheric Physics SPIE, 96800T (19 November 2015), Tomsk, Russia, 22–26 June 2015; Volume 9680, pp. 159–164. [Google Scholar] [CrossRef]
- Kopelevich, O.V.; Vazyulya, S.V.; Grigoriev, A.V.; Khrapko, A.N.; Sheberstov, S.V.; Sahling, I.V. Penetration of visible solar radiation in waters of the Barents Sea depending on cloudiness and coccolithophore blooms. Oceanology 2017, 57, 402–409. [Google Scholar] [CrossRef]
- Fox, J.; Kramer, S.J.; Graff, J.R.; Behrenfeld, M.J.; Boss, E.; Tilstone, G.; Halsey, K.H. An absorption-based approach to improved estimates of phytoplankton biomass and net primary production. Limnol. Oceanogr. Lett. 2022, 7, 419–426. [Google Scholar] [CrossRef]
- Ciotti, A.M.; Lewis, M.R.; Cullen, J.J. Assessment of the relationships between dominant cell size in natural phytoplankton communities and the spectral shape of the absorption coefficient. Limnol. Oceanogr. 2002, 47, 404–417. [Google Scholar] [CrossRef]
- Pogosyan, S.I.; Zaitseva, A.F. Review of existing optical methods for determining in situ pigment phytoplankton composition. Water Chem. Ecol. 2015, 11, 35–43. (In Russian) [Google Scholar]
- Churilova, T.; Suslin, V.; Krivenko, O.; Efimova, T.; Moiseeva, N.; Mukhanov, V.; Smirnova, L. Light absorption by phytoplankton in the upper mixed layer of the Black Sea: Seasonality and parametrization. Front. Mar. Sci. 2017, 4, 90. [Google Scholar] [CrossRef]
- Ahn, Y.H.; Shanmugam, P. Detecting the red tide algal blooms from satellite ocean color observations in optically complex Northeast-Asia Coastal waters. Remote Sens. Environ. 2006, 103, 419–437. [Google Scholar] [CrossRef]
- Kopelevich, O.; Burenkov, V.; Sheberstov, S.; Vazyulya, S.; Kravchishina, M.; Pautova, L.; Silkin, V.; Artemiev, V.; Grigoriev, A. Satellite monitoring of coccolithophore blooms in the Black Sea from ocean color data. Remote Sens. Environ. 2014, 146, 113–123. [Google Scholar] [CrossRef]
- Richetta, P.J. Theory of Absorption and Scattering within Integrating Spheres. JOSA 1965, 55, 21–26. [Google Scholar] [CrossRef]
- Fry, E.S.; Kattawar, G.W.; Pope, R.M. Integrating cavity absorption meter. Appl. Opt. 1992, 31, 2055–2065. [Google Scholar] [CrossRef] [PubMed]
- Jávorfi, T.; Erostyák, J.; Gál, J.; Buzády, A.; Menczel, L.; Garab, G.; Naqvi, K.R. Quantitative spectrophotometry using integrating cavities. J. Photochem. Photobiol. B Biol. 2006, 82, 127–131. [Google Scholar] [CrossRef]
- Pogosyan, S.I.; Durgaryan, A.M.; Konyukhov, I.V.; Chivkunova, O.B.; Merzlyak, M.N. Absorption spectroscopy of microalgae, cyanobacteria, and dissolved organic matter: Measurements in an integrating sphere cavity. Oceanology 2009, 49, 866–871. [Google Scholar] [CrossRef]
- Available online: https://aviantechnologies.com/product/fluorilon-99wtm (accessed on 22 January 2022).
- Kirk, J.T.O. Modeling the performance of an integrating-cavity absorption meter: Theory and calculations for a spherical cavity. Appl. Opt. 1995, 34, 4397–4408. [Google Scholar] [CrossRef]
- Prokhorov, A.V.; Sapritsky, V.I.; Mekhontsev, S.N. Modeling of integrating spheres for photometric and radiometric applications. Opt. Radiat. Meas. III SPIE 1996, 2815, 118–125. [Google Scholar] [CrossRef]
- Rehman, A.; Ahmad, I.; Qureshi, S.A. Biomedical applications of integrating sphere: A review. Photodiagnosis Photodyn. Ther. 2020, 31, 101712. [Google Scholar] [CrossRef]
- Hu, D.; Sun, T.; Yao, L.; Yang, Z.; Wang, A.; Ying, Y. Monte Carlo: A flexible and accurate technique for modeling light transport in food and agricultural products. Trends Food Sci. Technol. 2020, 102, 280–290. [Google Scholar] [CrossRef]
- Glukhovets, D.I.; Kopelevich, O.V.; Sahling, I.V.; Artemiev, V.A.; Pautova, L.A.; Lange, E.K.; Kravchishina, M.D. Biooptical characteristics of the surface layer of the Baltic, Norwegian, and Barents seas in summer 2014–2016 from shipboard and satellite data. Oceanology 2017, 57, 410–418. [Google Scholar] [CrossRef]
- Glukhovets, D.; Kopelevich, O.; Yushmanova, A.; Vazyulya, S.; Sheberstov, S.; Karalli, P.; Sahling, I. Evaluation of the CDOM Absorption Coefficient in the Arctic Seas Based on Sentinel-3 OLCI Data. Remote Sens. 2020, 12, 3210. [Google Scholar] [CrossRef]
- Glukhovets, D.I.; Salyuk, P.A.; Artemiev, V.A.; Shtraikhert, E.A.; Zakharkov, S.P. Variability of bio-optical characteristics of surface water layer during transatlantic transect in 2019–2020. Oceanology 2021, 61, 872–880. [Google Scholar] [CrossRef]
- Glukhovets, D.; Sheberstov, S.; Vazyulya, S.; Yushmanova, A.; Salyuk, P.; Sahling, I.; Aglova, E. Influence of the Accuracy of Chlorophyll-Retrieval Algorithms on the Estimation of Solar Radiation Absorbed in the Barents Sea. Remote Sens. 2022, 14, 4995. [Google Scholar] [CrossRef]
- Yushmanova, A.V.; Glukhovets, D.I.; Khlebopashev, P.V.; Polukhin, A.A.; Seliverstova, A.M.; Zuev, O.A. Results of hydroptical and hydrochemical investigations of the surface layer of water obtained at the transition from the Baltic to the White Sea in June 2021. In Proceedings of the 28th International Symposium on Atmospheric and Ocean Optics: Atmospheric Physics SPIE, Tomsk, Russia, 4–8 July 2022; Volume 12341, pp. 964–968. [Google Scholar] [CrossRef]
- Yushmanova, A.V.; Vazyulya, S.V. Validation of satellite algorithms for calculating the absorption coefficient of colored dissolved organic matter in the Barents Sea. Sovremennye problemy distantsionnogo zondirovaniya Zemli iz kosmosa. 2022, 19, 147–158. [Google Scholar] [CrossRef]
- Sheberstov, S.V.; Glukhovets, D.I.; Kopelevich, O.V.; Zaitseva, A.F.; Pogosyan, S.I. Accounting of parameters of an integrating sphere in measuring the seawater absorption coefficient by ICAM method. Curr. Probl. Opt. Nat. Waters 2017, 198–204. (In Russian) [Google Scholar]
- Petzold, T.J. Volume Scattering Functions for Selected Ocean Waters; Scripps Institution of Oceanography La Jolla Ca Visibility Lab: UC San Diego, CA, USA, 1972; Available online: https://apps.dtic.mil/dtic/tr/fulltext/u2/753474.pdf (accessed on 15 April 2020).
- Kopelevich, O.V. Low-parametric model of seawater optical properties. In Ocean Optics; Monin, A.S., Ed.; I: Physical Ocean Optics: Moscow, Russia, 1983; pp. 150–248. (In Russian) [Google Scholar]
- Henyey, L.G.; Greenstein, J.L. Diffuse radiation in the galaxy. Astrophys. J. 1941, 93, 70–83. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics, 2nd ed.; Pergamon Press: Oxford, UK; London, UK, 1965; Volume 49, p. 485. [Google Scholar]
- Levin, I.M.; Kopelevich, O.V. Correlations between the inherent hydrooptical characteristics in the spectral range close to 550 nm. Oceanology 2007, 47, 344–349. [Google Scholar] [CrossRef]
- Ishimaru, A. Wave Propagation and Scattering in Randomly Inhomogeneous Media; I:World: Dayton, OH, USA, 1981. [Google Scholar]
- Morozov, E.G.; Spiridonov, V.A.; Molodtsova, T.N.; Frey, D.I.; Demidova, T.A.; Flint, M.V. Investigations of the ecosystem in the Atlantic sector of Antarctica (cruise 79 of the R/V Akademik Mstislav Keldysh). Oceanology 2020, 60, 721–723. [Google Scholar] [CrossRef]
- Gladyshev, S.V.; Simonova, O.A. Expeditions on ships of IO RAS 2022: Main tasks, participants, preliminary results. J. Oceanol. Res. 2022, 50, 151–202. [Google Scholar] [CrossRef]
- Pope, R.M.; Fry, E.S. Absorption spectrum (380–700 nm) of pure water. II. Integrating cavity measurements. Appl. Opt. 1997, 36, 8710–8723. [Google Scholar] [CrossRef]
- Burenkov, V.I.; Goldin, Y.A.; Kravchishina, M.D. The distribution of the suspended matter concentration in the Kara Sea in September 2007 based on ship and satellite data. Oceanology 2010, 50, 798. [Google Scholar] [CrossRef]
- Kravchishina, M.D.; Lein, A.Y.; Sukhanova, I.N.; Artem’Ev, V.A.; Novigatsky, A.N. Genesis and spatial distribution of suspended particulate matter concentrations in the Kara Sea during maximum reduction of the Arctic ice sheet. Oceanology 2015, 55, 623–643. [Google Scholar] [CrossRef]
- Vazyulya, S.V.; Kopelevich, O.V.; Sheberstov, S.V.; Artemiev, V.A. Satellite estimation of the coefficients of CDOM absorption and diffuse attenuation in the White and Kara seas. Curr. Probl. Remote Sens. Earth Space 2014, 11, 31–41. (In Russian) [Google Scholar]
- Churilova, T.; Moiseeva, N.; Skorokhod, E.; Efimova, T.; Buchelnikov, A.; Artemiev, V.; Salyuk, P. Parameterization of Light Absorption of Phytoplankton, Non-algal Particles and Coloured Dissolved Organic Matter in the Atlantic Region of the Southern Ocean (Austral Summer of 2020). Remote Sens. 2023, 15, 634. [Google Scholar] [CrossRef]
- Salyuk, P.A.; Glukhovets, D.I.; Moiseeva, N.A.; Artemiev, V.A.; Mayor, A.Y.; Khrapko, A.N. Phycoerythrin influence on the optical characteristics of seawater in the Atlantic sector of the Southern Ocean. In Proceedings of the 26th International Symposium on Atmospheric and Ocean Optics, Atmospheric Physics SPIE, Moscow, Russian, 6–10 July 2020; Volume 11560, pp. 1125–1130. [Google Scholar] [CrossRef]
- Six, C.; Thomas, J.C.; Garczarek, L.; Ostrowski, M.; Dufresne, A.; Blot, N.; Partensky, F. Diversity and evolution of phycobilisomes in marine Synechococcusspp.: A comparative genomics study. Genome Biol. 2007, 8, R259. [Google Scholar] [CrossRef] [PubMed]
- Vazyulya, S.; Deryagin, D.; Glukhovets, D.; Silkin, V.; Pautova, L. Regional Algorithm for Estimating High Coccolithophore Concentration in the Northeastern Part of the Black Sea. Remote Sens. 2023, 15, 2219. [Google Scholar] [CrossRef]
- Kopelevich, O.V.; Sheberstov, S.V.; Burenkov, V.I.; Vazyulya, S.V.; Pautova, L.A.; Silkin, V.A. New data about coccolithophore blooms in the Black Sea from satellite data; Current Problems in Optics of Natural Waters: Saint Petersburg, Russia, 2013; pp. 19–23. [Google Scholar]
- Yushmanova, A.; Kopelevich, O.; Vazyulya, S.; Sahling, I. Inter-annual variability of the seawater light absorption in surface layer of the northeastern Black Sea in connection with hydrometeorological factors. J. Mar. Sci. Eng. 2019, 7, 326. [Google Scholar] [CrossRef]
- Zatsepin, A.G.; Zavialov, P.O.; Kremenetskiy, V.V.; Poyarkov, S.G.; Soloviev, D.M. The upper desalinated layer in the Kara Sea. Oceanology 2010, 50, 657–667. [Google Scholar] [CrossRef]
- Zavialov, P.O.; Izhitskiy, A.S.; Osadchiev, A.A.; Pelevin, V.V.; Grabovskiy, A.B. The structure of thermohaline and bio-optical fields in the surface layer of the Kara Sea in September 2011. Oceanology 2015, 55, 461–471. [Google Scholar] [CrossRef]
- Osadchiev, A.A.; Frey, D.I.; Shchuka, S.A.; Tilinina, N.D.; Morozov, E.G.; Zavialov, P.O. Structure of the freshened surface layer in the Kara Sea during ice-free periods. J. Geophys. Res. Oceans 2021, 126, e2020JC016486. [Google Scholar] [CrossRef]
- Glukhovets, D.I.; Goldin, Y.A. Surface desalinated layer distribution in the Kara Sea determined by shipboard and satellite data. Oceanologia 2020, 62, 364–373. [Google Scholar] [CrossRef]
- Coble, P.G. Marine optical biogeochemistry: The chemistry of ocean color. Chem. Rev. 2007, 107, 402–418. [Google Scholar] [CrossRef] [PubMed]
- Szeto, M.; Werdell, P.J.; Moore, T.S.; Campbell, J.W. Are the world’s oceans optically different? J. Geophys. Res. Ocean. 2011, 116, C7. [Google Scholar] [CrossRef]
- Stramski, D.; Boss, E.; Bogucki, D.; Voss, K.J. The role of seawater constituents in light backscattering in the ocean. Prog. Oceanogr. 2004, 61, 27–56. [Google Scholar] [CrossRef]
- Bricaud, A.; Morel, A.; Babin, M.; Allali, K.; Claustre, H. Variations of light absorption by suspended particles with chlorophyll a concentration in oceanic (case 1) waters: Analysis and implications for bio-optical models. J. Geophys. Res. Ocean 1998, 103, 31033–31044. [Google Scholar] [CrossRef]
- Sullivan, J.M.; Twardowski, M.S.; Donaghay, P.L.; Freeman, S.A. Use of optical scattering to discriminate particle types in coastal waters. Appl. Opt. 2005, 44, 1667–1680. [Google Scholar] [CrossRef] [PubMed]
- Tian, P.; Chen, H.; Wang, P.; Liu, X.; Chen, X.; Zhou, G.; Zhang, S.; Lu, J.; Qiu, P.; Cui, X.; et al. Absorption and scattering effects of Maalox, chlorophyll, and sea salt on a micro-LED-based underwater wireless optical communication. Chin. Opt. Lett. 2019, 17, 100010. [Google Scholar] [CrossRef]
- Yaroslavsky, A.N.; Yaroslavsky, I.V.; Goldbach, T.; Schwarzmaier, H.J. Influence of the scattering phase function approximation on the optical properties of blood determined from the integrating sphere measurements. J. Biomed. Opt. 1999, 4, 47–53. [Google Scholar] [CrossRef]
- Hanssen, L.M. Effects of non-Lambertian surfaces on integrating sphere measurements. Appl. Opt. 1996, 35, 3597–3606. [Google Scholar] [CrossRef]
- Leathers, R.A.; Downes, T.V.; Davis, C.O. Analysis of a point-source integrating-cavity absorption meter. Appl. Opt. 2000, 39, 6118–6127. [Google Scholar] [CrossRef]
- Lerebourg, C.J.; Pilgrim, D.A.; Ludbrook, G.D.; Neal, R. Development of a point source integrating cavity absorption meter. J. Opt. A Pure Appl. Opt. 2002, 4, S56. [Google Scholar] [CrossRef]
- Röttgers, R.; Schönfeld, W.; Kipp, P.R.; Doerffer, R. Practical test of a point-source integrating cavity absorption meter: The performance of different collector assemblies. Appl. Opt. 2005, 44, 5549–5560. [Google Scholar] [CrossRef] [PubMed]
- Röttgers, R.; Doxaran, D.; Dupouy, C. Quantitative filter technique measurements of spectral light absorption by aquatic particles using a portable integrating cavity absorption meter (QFT-ICAM). Opt. Express 2016, 24, A1–A20. [Google Scholar] [CrossRef]
- Wollschläger, J.; Röttgers, R.; Petersen, W.; Zielinski, O. Stick or dye: Evaluating a solid standard calibration approach for point-source integrating cavity absorption meters (PSICAM). Front. Mar. Sci. 2019, 5, 534. [Google Scholar] [CrossRef]
- Kopelevich, O.V.; Sahling, I.V.; Vazyulya, S.V.; Glukhovets, D.I.; Sheberstov, S.V.; Burenkov, V.I.; Karalli, P.G.; Yushmanova, A.V. Bio-Optical Characteristics of the Seas, Surrounding the Western Part of Russia, from Data of the Satellite Ocean Color Scanners of 1998–2017; VASh FORMAT, OOO: Moscow, Russia, 2018; Available online: https://optics.ocean.ru/ (accessed on 22 November 2018). (In Russian)
- Zaitseva, A.F.; Konyukhov, I.V.; Kazimirko, Y.V.; Pogosyan, S.I. Optical characteristics and distribution of chromophoric dissolved organic matter in Onega Bay (White Sea) during the summer season (findings from an expedition from June 22 to 26, 2015). Oceanology 2018, 58, 233–239. [Google Scholar] [CrossRef]
- Demidov, A.B.; Sheberstov, S.V.; Gagarin, V.I.; Khlebopashev, P.V. Seasonal variation of the satellite-derived phytoplankton primary production in the Kara Sea. Oceanology 2017, 57, 91–104. [Google Scholar] [CrossRef]
- Bukanova, T.; Kopelevich, O.; Vazyulya, S.; Bubnova, E.; Sahling, I. Suspended matter distribution in the south-eastern Baltic Sea from satellite and in situ data. Int. J. Remote Sens. 2018, 39, 9317–9338. [Google Scholar] [CrossRef]
- Lisitzyn, A.P.; Kravchishina, M.D.; Kopelevich, O.V.; Burenkov, V.I.; Shevchenko, V.P.; Vazyulya, S.V.; Klyuvitkin, N.N.; Novigatskii, A.N.; Politova, N.V.; Sheberstov, S.V.; et al. Spatial and temporal variability in suspended particulate matter concentration within the active layer of the White Sea. In Doklady Earth Sciences; Springer Nat. BV: Berlin/Heidelberg, Germany, 2013; Volume 453, p. 1228. [Google Scholar] [CrossRef]
- Konyukhov, I.V.; Kotikova, A.F.; Belevich, T.A.; Ilyash, L.V.; Kravchishina, M.D.; Pogosyan, S.I. Functional Activity of Phytoplankton and Optical Properties of Suspended Particulate Matter in Onega Bay of the White Sea. Oceanology 2021, 61, 233–243. [Google Scholar] [CrossRef]

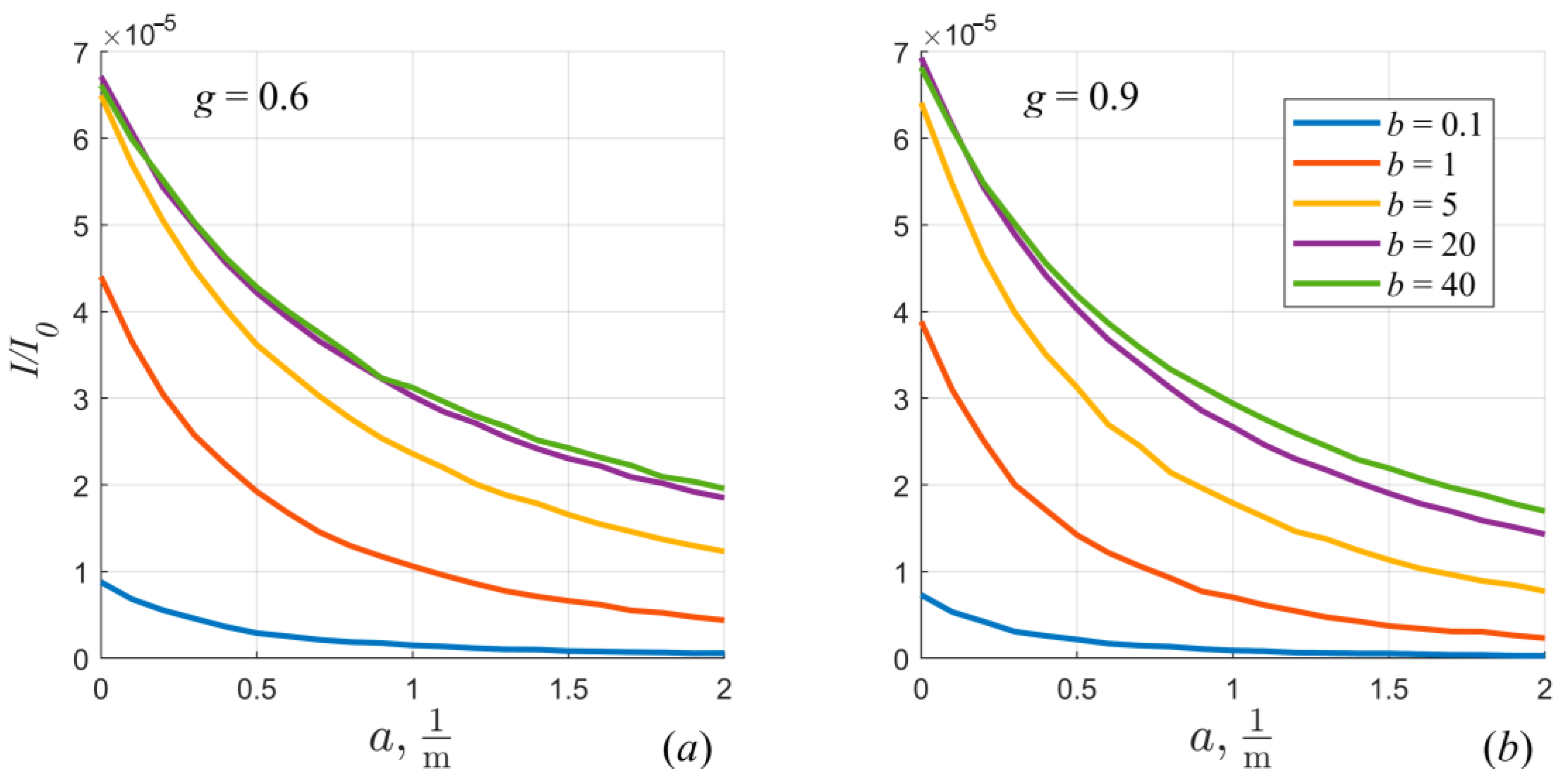
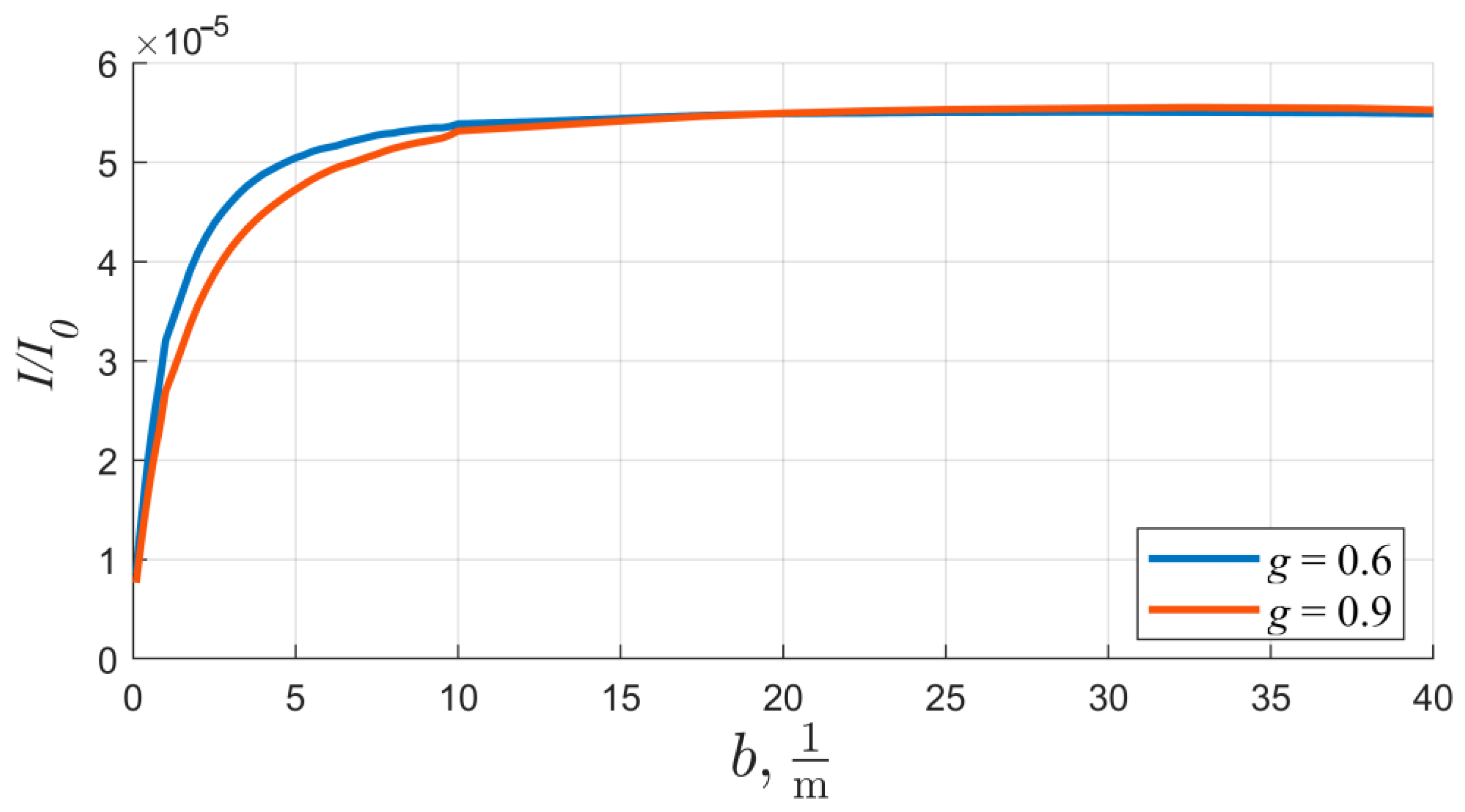
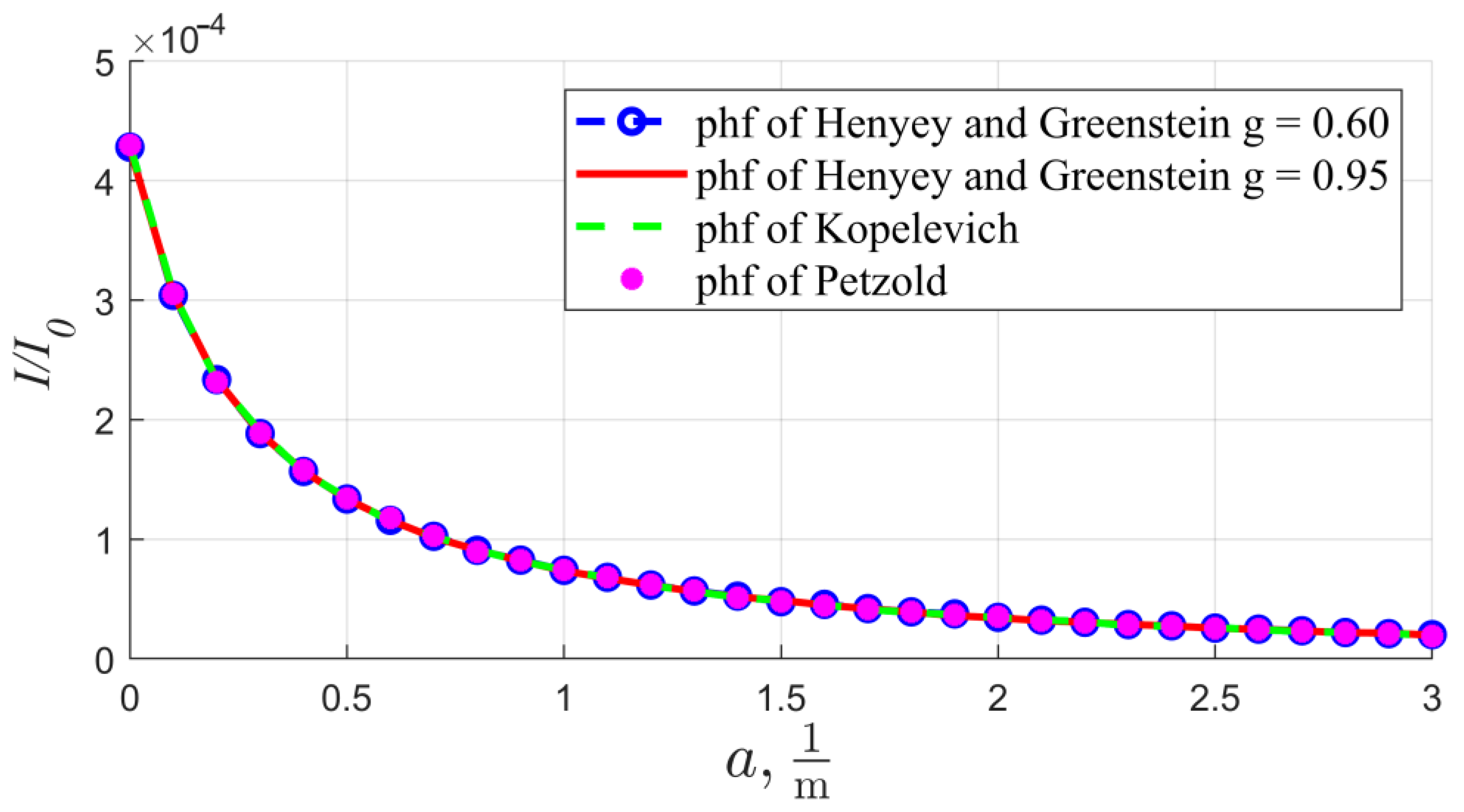
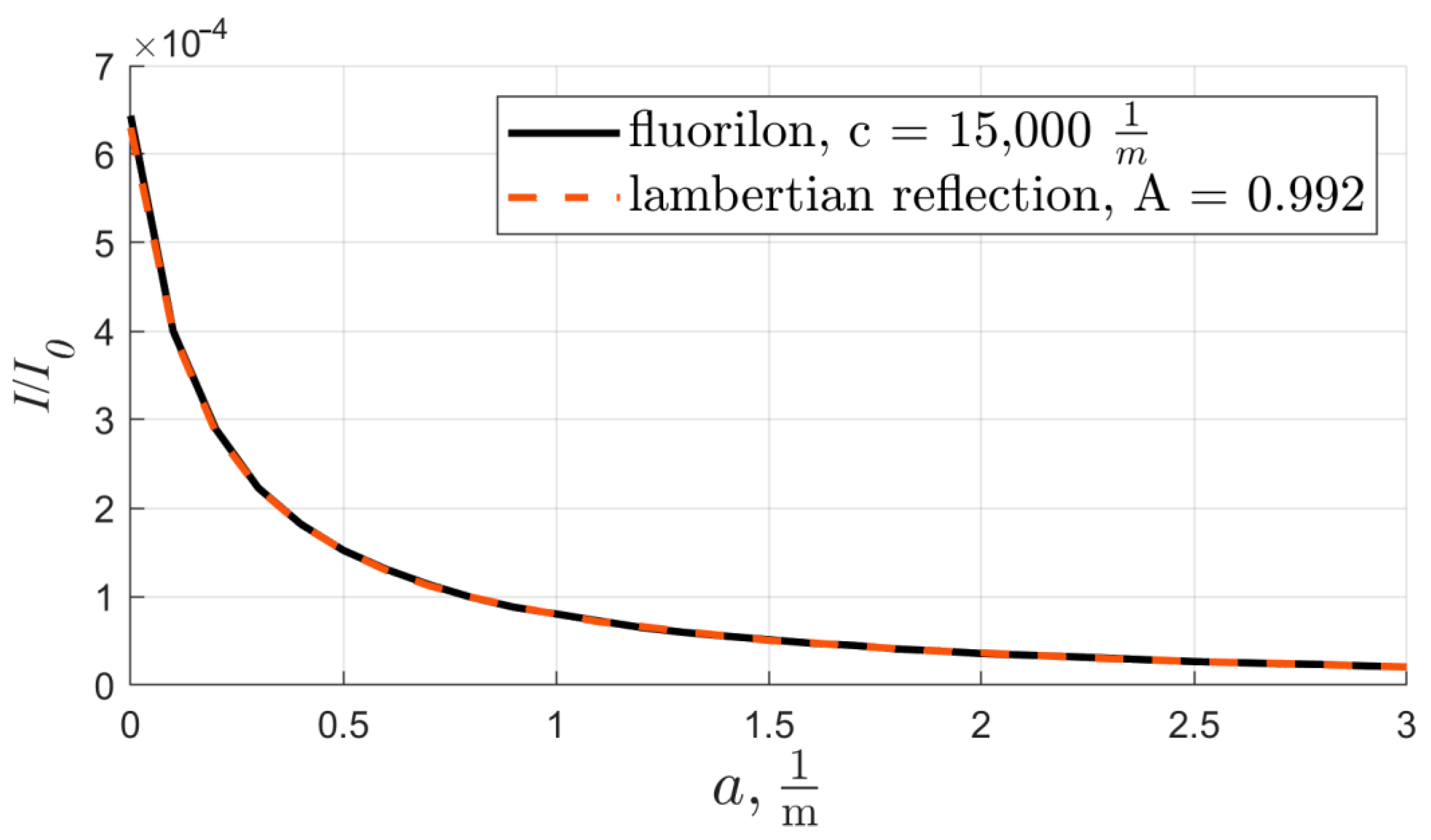

| b, m−1 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.7 | 1 | 5 | 10 | 15 | 20 | 30 | 40 |
| Re, % | 10.8 | 15.6 | 17 | 16.4 | 16.1 | 17.3 | 16 | 6.4 | 1.5 | 0.7 | 0.4 | 0.8 | 0.7 |
| k1 | k2 | R2 | RMSE | |
|---|---|---|---|---|
| air layer | 56.9 | 0.93 | 0.99 | 3.27 × 10−4 |
| no air layer | 41.8 | 0.99 | 0.99 | 3.18 × 10−4 |
| −1 | c, m−1 | A | ε, % | Aair | εair, % | |
|---|---|---|---|---|---|---|
| 450 | 1125 | 60 | 0.900 | 1.3 | 0.820 | 4.9 |
| 450 | 3000 | 85 | 0.900 | 1.9 | 0.820 | 5.0 |
| 1000 | 2500 | 60 | 0.955 | 2.1 | 0.910 | 1.8 |
| 2250 | 5625 | 60 | 0.979 | 1.2 | 0.958 | 1.4 |
| 2250 | 15,000 | 85 | 0.979 | 1.8 | 0.958 | 1.8 |
| 4000 | 10,000 | 60 | 0.988 | 1.5 | 0.976 | 1.6 |
| 5000 | 12,500 | 60 | 0.991 | 1.8 | 0.980 | 1.8 |
| 6000 | 15,000 | 60 | 0.992 | 1.0 | 0.984 | 1.0 |
| 6000 | 40,000 | 85 | 0.992 | 1.2 | 0.984 | 1.3 |
| 8000 | 20,000 | 60 | 0.994 | 1.5 | 0.988 | 1.4 |
| 10,000 | 25,000 | 60 | 0.995 | 1.3 | 0.990 | 1.4 |
| 13,000 | 32,500 | 60 | 0.996 | 2.0 | 0.992 | 2.2 |
| 16,000 | 40,000 | 60 | 0.997 | 1.2 | 0.994 | 1.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yushmanova, A.; Sheberstov, S.; Glukhovets, D.; Pogosyan, S. Numerical Simulation of a Light Field Structure in an Integrating Sphere via the Monte Carlo Method. Photonics 2023, 10, 593. https://doi.org/10.3390/photonics10050593
Yushmanova A, Sheberstov S, Glukhovets D, Pogosyan S. Numerical Simulation of a Light Field Structure in an Integrating Sphere via the Monte Carlo Method. Photonics. 2023; 10(5):593. https://doi.org/10.3390/photonics10050593
Chicago/Turabian StyleYushmanova, Anna, Sergey Sheberstov, Dmitry Glukhovets, and Sergey Pogosyan. 2023. "Numerical Simulation of a Light Field Structure in an Integrating Sphere via the Monte Carlo Method" Photonics 10, no. 5: 593. https://doi.org/10.3390/photonics10050593







