Variant of Constants in Subgradient Optimization Method over Planar 3-Index Assignment Problems
Abstract
:1. Introduction
- (i)
- at every fixed time slot, every machine works in parallel;
- (ii)
- each machine does a different task on a different time slot; and
- (iii)
- after the last time slot, all machines have completed all tasks.
2. Subgradient Optimization Methods and Modifications
- (i)
- and ;
- (ii)
- and is bounded for .
- (i)
- set for iterations where is a measure of the size of the problem; and
- (ii)
- successively halve both the values of and the number of iterations until is sufficiently small.
3. Subgradient Optimization Method for the Planar 3-Index Assignment Problem
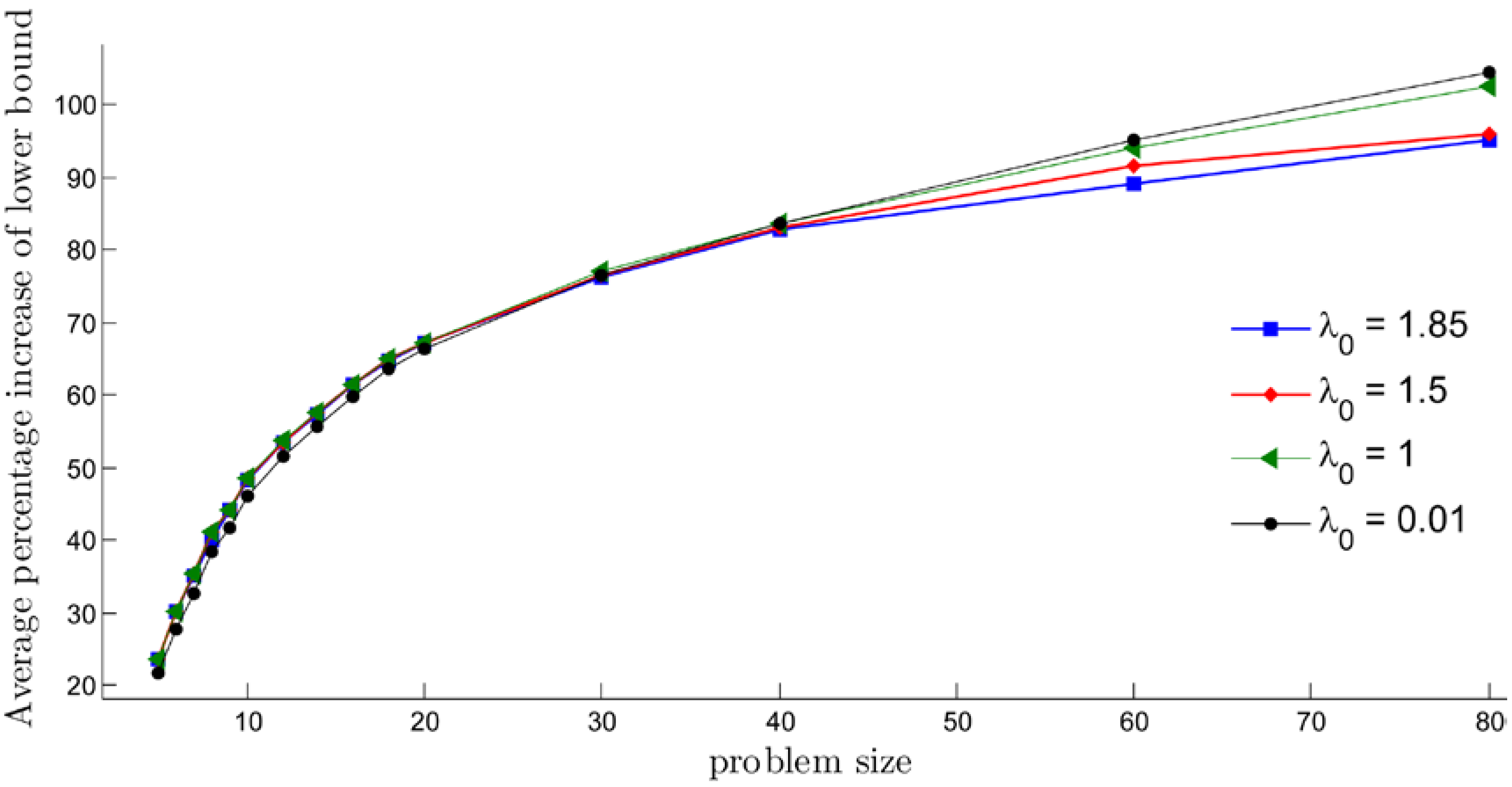
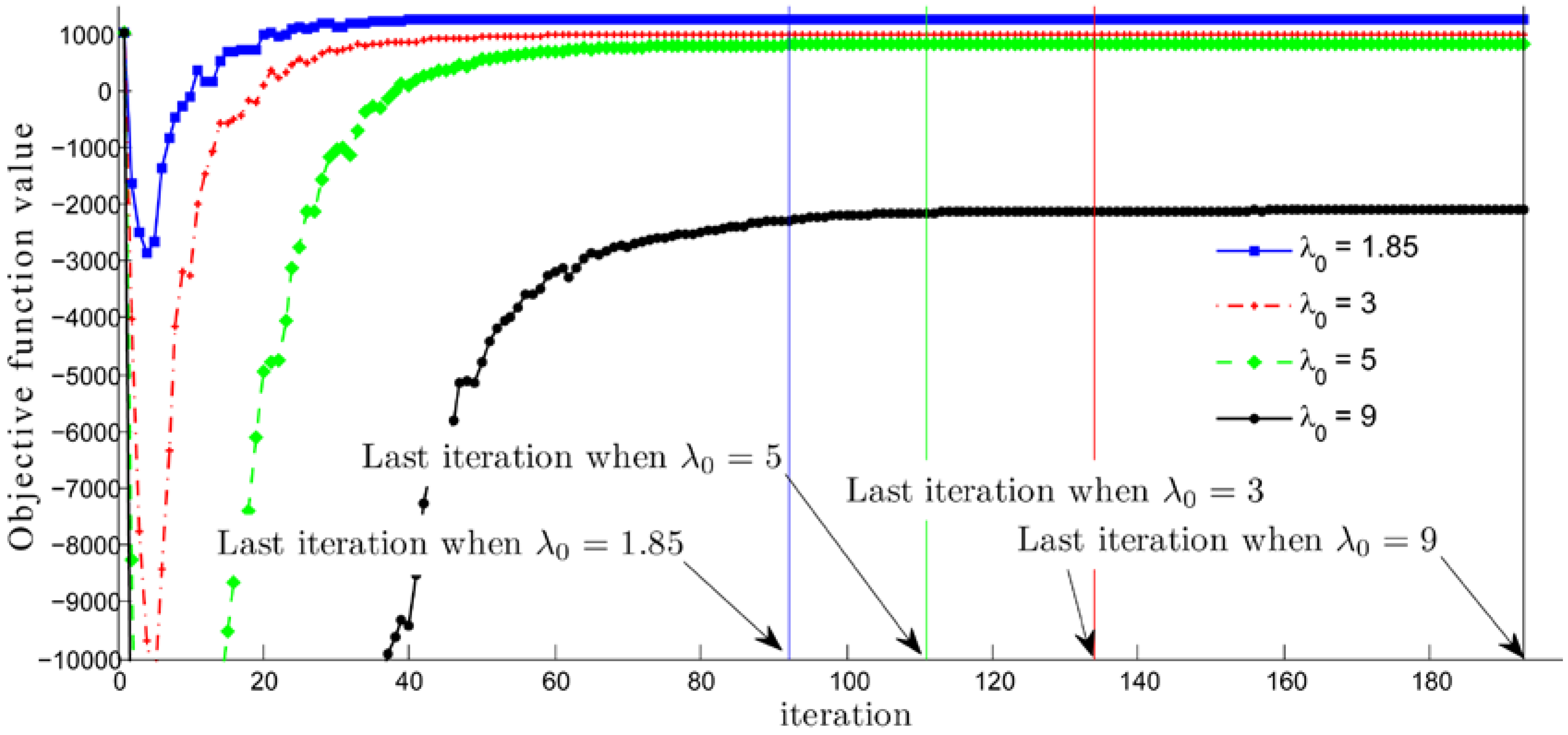
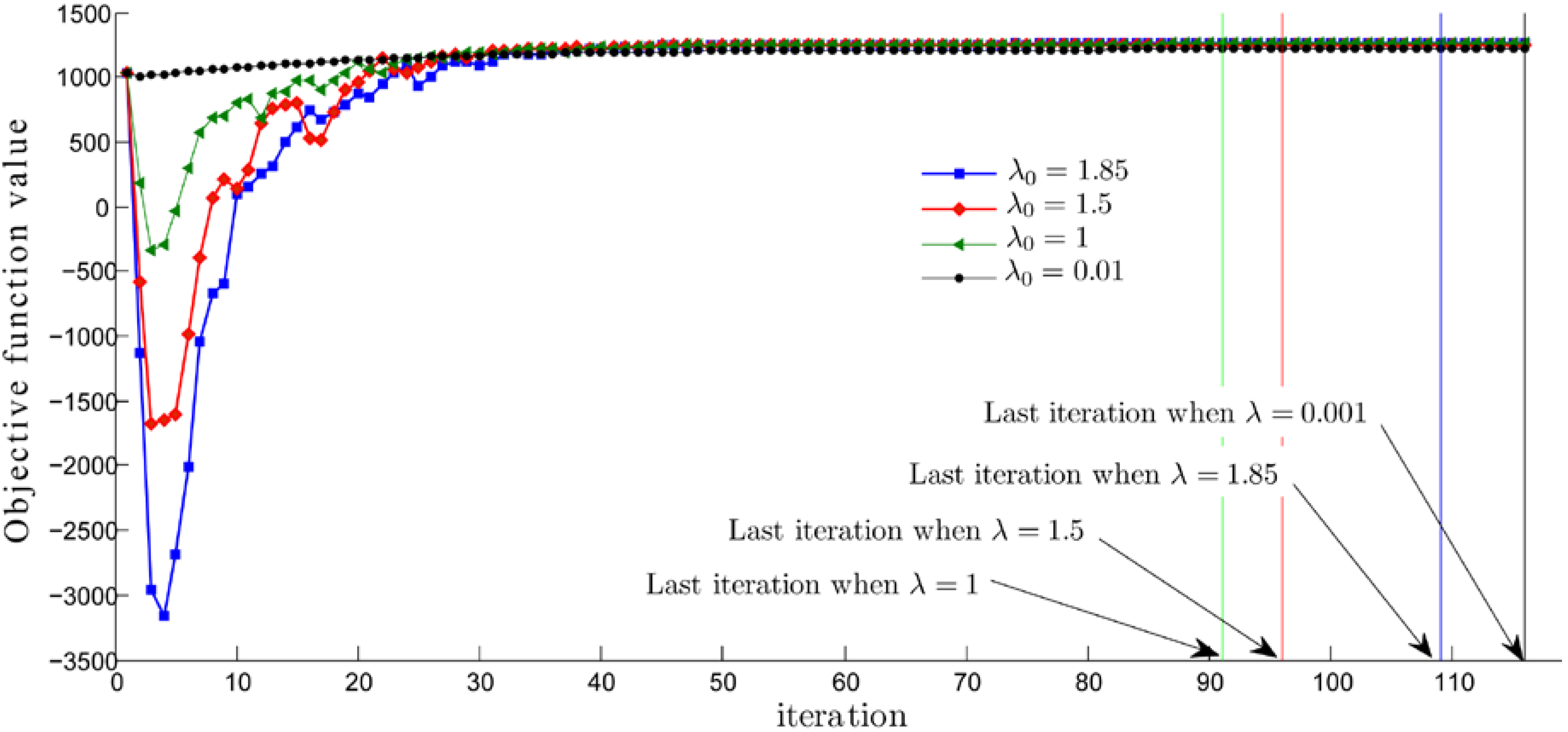
4. Computational Results and Conclusions
Conflicts of Interest
References
- Frieze, A.M. Complexity of a 3-dimensional assignment problem. Eur. J. Op. Res. 1983, 13, 161–164. [Google Scholar] [CrossRef]
- Kumar, S.; Russell, A.; Sundaram, R. Approximating Latin square extensions. Algorithmica 1999, 24, 128–138. [Google Scholar] [CrossRef]
- Gomes, C.; Regis, R.; Shmoys, D. An improved approximation algorithm for the partial Latin square extension problem. Oper. Res. Lett. 2004, 32, 479–484. [Google Scholar] [CrossRef]
- Katz-Rogozhnikov, D.; Sviridenko, M. Planar Three-Index Assignment Problem via Dependent Contention Resolution; IBM Research Report; Thomas, J., Ed.; Watson Research Center: Yorktown Height, New York, NY, USA, 2010. [Google Scholar]
- Magos, D.; Miliotis, P. An algorithm for the planar three-index assignment problem. Eur. J. Op. Res. 1994, 77, 141–153. [Google Scholar] [CrossRef]
- Shor, N. Minimization methods for non-differentiable functions. In Springer Series in Computational Mathematics; Springer-Verlag: Berlin; Heidelberg, Germany, 1985. [Google Scholar]
- Sherali, H.D.; Choi, G. Recovery of primal solutions when using subgradient methods to solve Lagrangian duals of linear programs. Oper. Res. Lett. 1996, 19, 105–113. [Google Scholar] [CrossRef]
- Fumero, F. A modified subgradient algorithm for Lagrangean relaxation. Comput. Op. Res. 2001, 28, 33–52. [Google Scholar] [CrossRef]
- Goffin, J.L. On convergence rate of subgradient optimization methods. Math. Program. 1977, 13, 329–347. [Google Scholar] [CrossRef]
- Held, M.; Wolfe, P.; Crowder, H.P. Validation of subgradient optimization. Math. Program. 1974, 6, 62–88. [Google Scholar] [CrossRef]
- Bazaraa, M.S.; Sherali, H.D. On the choice of step size in subgradient optimization. Eur. J. Op. Res. 1981, 7, 380–388. [Google Scholar] [CrossRef]
- Fischer, M.L. The Lagrangean relaxation method for solving integer programming problems. Manag. Sci. 1981, 72, 1–18. [Google Scholar] [CrossRef]
- Camerini, P.; Fratta, L.; Maffioli, F. On improving relaxation methods by modified gradient techniques. Math. Program. Study 1975, 3, 26–34. [Google Scholar]
- Kim, S.; Koh, S.; Ahn, H. Two-direction subgradient method for non-differentiable optimization problems. Oper. Res. Lett. 1987, 6, 43–46. [Google Scholar] [CrossRef]
- Kim, S.; Koh, S. On Polyak’s improved subgradient method. J. Optim. Theory Appl. 1988, 57, 355–360. [Google Scholar] [CrossRef]
- Norkin, V.N. Method of nondifferentiable function minimization with average of generalized gradients. Kibernetika 1980, 6, 86–89. [Google Scholar]
- Kim, S.; Ahn, H. Convergence of a generalized subgradient method for non-differentiable convex optimization. Math. Program. 1991, 50, 75–80. [Google Scholar] [CrossRef]
- Burkard, R.E.; Froehlich, K. Some remark on 3-dimensinal assignment problems. Methods Op. Res. 1980, 36, 31–36. [Google Scholar]
- Burkard, E. Admissible transformations and assignment problems. Vietnam J. Math. 2007, 35, 373–386. [Google Scholar]

| The Procedures | Magos and Miliotis’s Procedure [5] | Modified Procedure |
|---|---|---|
| The stopping criteria | iterations are allowed from the start of the procedure and subsequently iterations are gained after an improvement of at least 25% on the lower bound. | If there is 0.1% difference between the function values on the current and previous iterations, then the procedure stops. |
| The condition for decreasing the step length constant | iterations with the initial -value additional iterations for every 1% improvement are allowed. If no improvement is made within the iterations allowed, set and continue the procedure with that -value for at least iterations. | Set if no improvement on any iteration where no improvement occurs. |
| Step length formula in the iteration |
| 1.15 | 1.35 | 1.65 | 1.85 | |
| 0.60 | 0.70 | 0.80 | 0.90 | |
| 0.50 | 0.60 | 0.70 | 0.80 | |
| 0.35 | 0.55 | 0.65 | 0.75 |
| Problem | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| size | 0.001 | 0.01 | 0.05 | 0.075 | 0.1 | 0.3 | 0.5 | 0.75 | 1 |
| 5 | 19.383 | 21.886 | 23.360 | 23.517 | 23.388 | 23.664 | 23.629 | 23.677 | 23.688 |
| 6 | 24.604 | 27.864 | 29.917 | 30.169 | 30.292 | 30.348 | 30.342 | 30.249 | 30.347 |
| 7 | 29.387 | 32.801 | 35.053 | 35.311 | 35.422 | 35.513 | 35.490 | 35.505 | 35.521 |
| 8 | 34.668 | 38.362 | 40.744 | 40.958 | 41.054 | 41.104 | 41.115 | 41.091 | 41.086 |
| 9 | 37.907 | 41.616 | 43.939 | 44.171 | 44.253 | 44.263 | 44.309 | 44.313 | 44.288 |
| 10 | 42.018 | 46.064 | 48.332 | 48.497 | 48.585 | 48.653 | 48.642 | 48.639 | 48.588 |
| 12 | 47.469 | 51.489 | 53.501 | 53.517 | 53.668 | 53.686 | 53.679 | 53.682 | 53.665 |
| 14 | 51.941 | 55.728 | 57.421 | 57.646 | 57.676 | 57.667 | 57.668 | 57.673 | 57.632 |
| 16 | 56.453 | 59.814 | 61.398 | 61.394 | 61.476 | 61.472 | 61.472 | 61.480 | 61.398 |
| 18 | 60.624 | 63.762 | 65.060 | 65.104 | 65.101 | 65.104 | 65.118 | 65.089 | 65.087 |
| 20 | 63.162 | 66.230 | 67.383 | 67.366 | 67.414 | 67.420 | 67.408 | 67.371 | 67.265 |
| 30 | 74.366 | 76.614 | 77.174 | 77.197 | 77.177 | 77.175 | 77.166 | 77.031 | 76.950 |
| 40 | 81.060 | 83.725 | 84.042 | 84.051 | 84.043 | 84.028 | 83.899 | 83.818 | 83.573 |
| 60 | 93.747 | 95.043 | 95.160 | 95.180 | 95.169 | 95.133 | 94.999 | 94.516 | 93.945 |
| 80 | 104.453 | 104.469 | 104.510 | 104.525 | 104.491 | 104.428 | 104.174 | 103.484 | 102.454 |
| Problem | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| size | 0.001 | 0.01 | 0.05 | 0.075 | 0.1 | 0.3 | 0.5 | 0.75 | 1 | 1.25 | 1.5 | 1.85 |
| 5 | 349.7 | 62.2 | 45.2 | 40.2 | 42.0 | 54.8 | 48.2 | 49.8 | 60.7 | 54.4 | 55.8 | 88.6 |
| 6 | 366.4 | 80.0 | 59.4 | 60.7 | 60.6 | 63.1 | 64.3 | 68.7 | 76.5 | 75.6 | 73.2 | 97.2 |
| 7 | 386.0 | 91.8 | 69.8 | 68.9 | 68.8 | 75.0 | 76.0 | 79.2 | 90.4 | 87.3 | 83.5 | 105.6 |
| 8 | 380.8 | 101.1 | 76.1 | 75.6 | 76.1 | 83.2 | 87.4 | 89.2 | 99.9 | 96.5 | 94.2 | 111.0 |
| 9 | 360.2 | 108.4 | 78.3 | 80.4 | 80.6 | 84.3 | 90.0 | 95.4 | 103.2 | 99.2 | 96.0 | 108.0 |
| 10 | 383.5 | 110.3 | 80.9 | 80.0 | 82.0 | 90.0 | 93.6 | 97.7 | 107.4 | 104.2 | 100.6 | 110.5 |
| 12 | 371.0 | 120.0 | 85.4 | 86.5 | 89.5 | 97.2 | 98.1 | 107.2 | 116.7 | 113.2 | 109.2 | 108.4 |
| 14 | 378.5 | 127.3 | 90.2 | 93.9 | 97.2 | 99.8 | 106.1 | 115.5 | 121.3 | 120.6 | 115.6 | 111.4 |
| 16 | 381.5 | 132.2 | 93.3 | 96.5 | 98.5 | 104.3 | 113.2 | 117.8 | 130.0 | 122.5 | 120.8 | 111.3 |
| 18 | 364.3 | 136.0 | 101.9 | 100.5 | 101.0 | 108.9 | 115.7 | 121.4 | 133.5 | 131.7 | 125.8 | 116.8 |
| 20 | 356.3 | 141.1 | 100.9 | 102.0 | 103.7 | 113.5 | 121.3 | 125.4 | 138.1 | 132.3 | 126.2 | 112.1 |
| 30 | 322.2 | 162.5 | 111.8 | 116.5 | 115.9 | 125.7 | 129.7 | 140.5 | 152.9 | 150.1 | 146.7 | 114.4 |
| 40 | 296.6 | 172.8 | 121.4 | 124.6 | 125.2 | 139.0 | 144.3 | 150.7 | 168.9 | 163.4 | 156.7 | 119.2 |
| 60 | 264.7 | 204.4 | 137.2 | 141.5 | 139.2 | 152.7 | 162.2 | 172.6 | 192.6 | 189.0 | 184.4 | 131.1 |
| 80 | 247.8 | 242.3 | 154.0 | 152.2 | 152.9 | 170.6 | 182.8 | 189.3 | 249.0 | 218.0 | 200.2 | 148.1 |
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maneechai, S. Variant of Constants in Subgradient Optimization Method over Planar 3-Index Assignment Problems. Math. Comput. Appl. 2016, 21, 4. https://doi.org/10.3390/mca21010004
Maneechai S. Variant of Constants in Subgradient Optimization Method over Planar 3-Index Assignment Problems. Mathematical and Computational Applications. 2016; 21(1):4. https://doi.org/10.3390/mca21010004
Chicago/Turabian StyleManeechai, Sutitar. 2016. "Variant of Constants in Subgradient Optimization Method over Planar 3-Index Assignment Problems" Mathematical and Computational Applications 21, no. 1: 4. https://doi.org/10.3390/mca21010004





