Performance Tests on a Novel Un-Finned Thermosyphon Heat Exchanger Requiring a Single Charge
Abstract
:1. Introduction
| Type of Heat Pipe Used in Heat Exchanger | Pipe | Wick | Number of Pipes | Fin | Working Fluid/Filling Ratio | Effectiveness | Ref. |
|---|---|---|---|---|---|---|---|
| Conventional heat pipe | Material: copper do: 15 mm Lt: 600 mm Le: 300 mm | 100 mesh Stainless Steel | 8 | None | methanol | 0.16 | [3] |
| Material: copper do: 12.7 mm Le: 200 mm La: 10 mm Lc: 200 mm | 100 mesh brass | 25 | Type: plate fin Material: aluminum | R11, R123 | 0.26 | [4] | |
| do: 20 mm Wt: 2 mm Le: 310 mm La: 20 mm Lc: 310 mm | 100 mesh brass | 10 | Type: plate fin Material: aluminum | R410A, R134a, R22, and R407C | 25–70% (R410A, R134a, R22) 15–50% (R407C) | [5] | |
| Material: copper do: 44 mm Le: 600 mm Lc: 600 mm | Axial grooves | 4, 8 | Type: plate fin Material: aluminum | R134a | 0.47–0.53 | [6] | |
| Two-phase closed thermosyphon | Material: copper do: 15.88 mm Wt: 1.22 mm Le: 300 mm La: 150 mm Lc: 300 mm | None | 24 | Type: plate fin Material: copper (evaporator) aluminum (condenser) | Water/60% of the evaporator section | 0.18–0.63 | [7] |
| Material: steel do: 26.27 mm Wt: 7.65 mm Le: 300 mm La: 150 mm Lc: 300 mm | 10 | Type: circular spiral fin Material: steel Diameter: 52.7 mm | |||||
| Material: copper do: 15.88 mm Wt: 1.22 mm Le: 300 mm La: 150 mm Lc: 300 mm | 24 | None | |||||
| Material: copper di: 15 mm Lt: 660 mm Le: 300 mm Lc: 300 mm | None | 24 | Total: 32 fins/100 mm | R22 /60% of the evaporator section | - | [8] | |
| Material: copper do: 0.127 m Lt: 0.45 m | None | 7 | Type: plate fin Material: copper | methanol | 0.22–0.64 | [9] | |
| 3 | Type: cylindrical spine fins Material: copper Total: 300 fins | ||||||
| Material: copper di: 18 mm Lt: 365 m | 6 | Type: louvred fin Type: louvred fin Total: 96 louvres | |||||
| Material: copper do: 9.55 mm di: 7.55 mm Evaporator and condenser face dimension: 200 × 200 mm2 | None | 6 | Type: Wavy plate Material: Aluminum | R-134a/60% | 0.15–0.55 | [10] | |
| Material: steel do: 20 mm Le: 150 mm La: 5 mm Lc: 150 mm | None | 50 | Type: plate fin Material: steel | Water/ FR: 35% of the evaporator section | 0.28 | [11] | |
| Material: copper di: 2 mm Wt: 2 mm Le: 190 mm Lc: 190 m Lt: 600 mm | None | 1 | - | Water, R134a/50% of the evaporator section | 0.38–0.54 | [12] | |
| Material: copper do: 15 mm Le: 0.6 m La: 0.1 m Lc: 0.6 m | None | 90 | Type: plate fin Material: aluminum | water/60% of the evaporator section | 37–65% | [13] | |
| do: 15.9 mm di: 14.9 mm Lt: 900 mm Le: 300 mm Lc: 300 mm | None | 9 | Type: Wavy plate Material: Aluminum | Water/50% of the evaporator section | 0.07–0.26 | [14] | |
| Plate heat pipe Material: aluminum Le: 140 mm La: 60 mm Lc: 140 mm | None | 19 | Numerous fins were included between the heat pipe units. | δ-Al2O3-R141b | 0.15–0.6 | [15] | |
| Material: copper do: 20 mm Lt: 300 mm Le: 160 mm La: 15 mm Lc: 125 mm | None | 16 | Type: plate fin Material: Copper 180 × 180 mm | R134a, R410A /60% of the evaporator section | 35.7–57.7% | [16] | |
| Material: steel do: 32 mm Le: 480 mm La: 40 mm Lc: 480 mm | - | 31 | None | Water/30% | 0.09–0.19 | [17] | |
| Pulsating heat pipe | Material: copper di: 2 mm Wt: 2 mm Le: 190 mm La: 8 mm Lc: 190 m Lt: 358 mm | None | 1 | - | R134a/50% of the evaporator section | 0.29–0.76 | [18] |
| Material: copper do: 2 mm di: 1.8 mm Lt: 150 mm | None | 1 | - | ethanol | 0.14–0.42 | [19] | |
| Material: copper do: 3 mm di: 2 mm Lt: 92 mm | |||||||
| Material: copper di: 2.5 mm Wt: 2 mm Le: 360 mm La: 500 mm/750 mm/1000 mm Lc: 360 mm | None | 14 | - | Acetone, Ethanol, Water/ 25, 50,75% | - | [20] |
2. Equipment and Methods
2.1. Experimental Equipment
2.2. Theoretical Model
2.3. Calculation Procedure
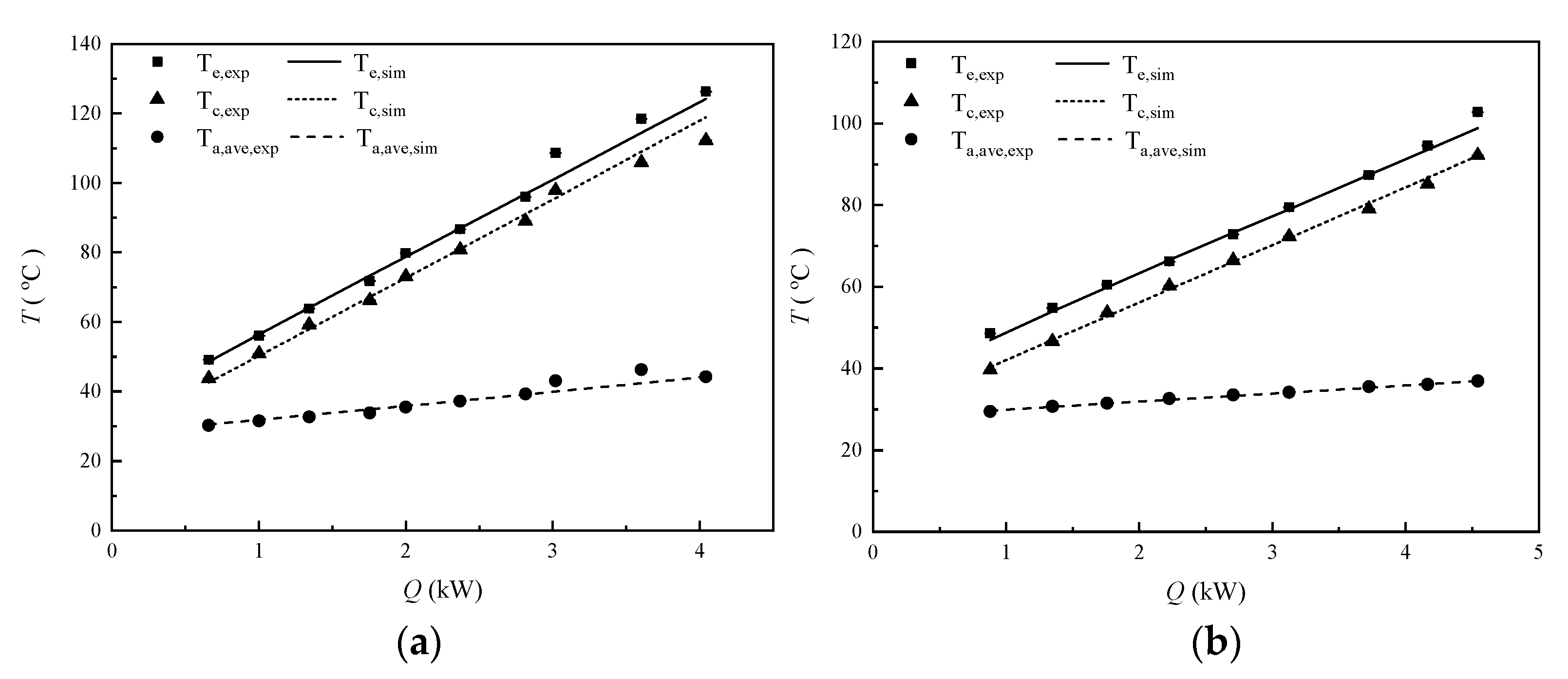
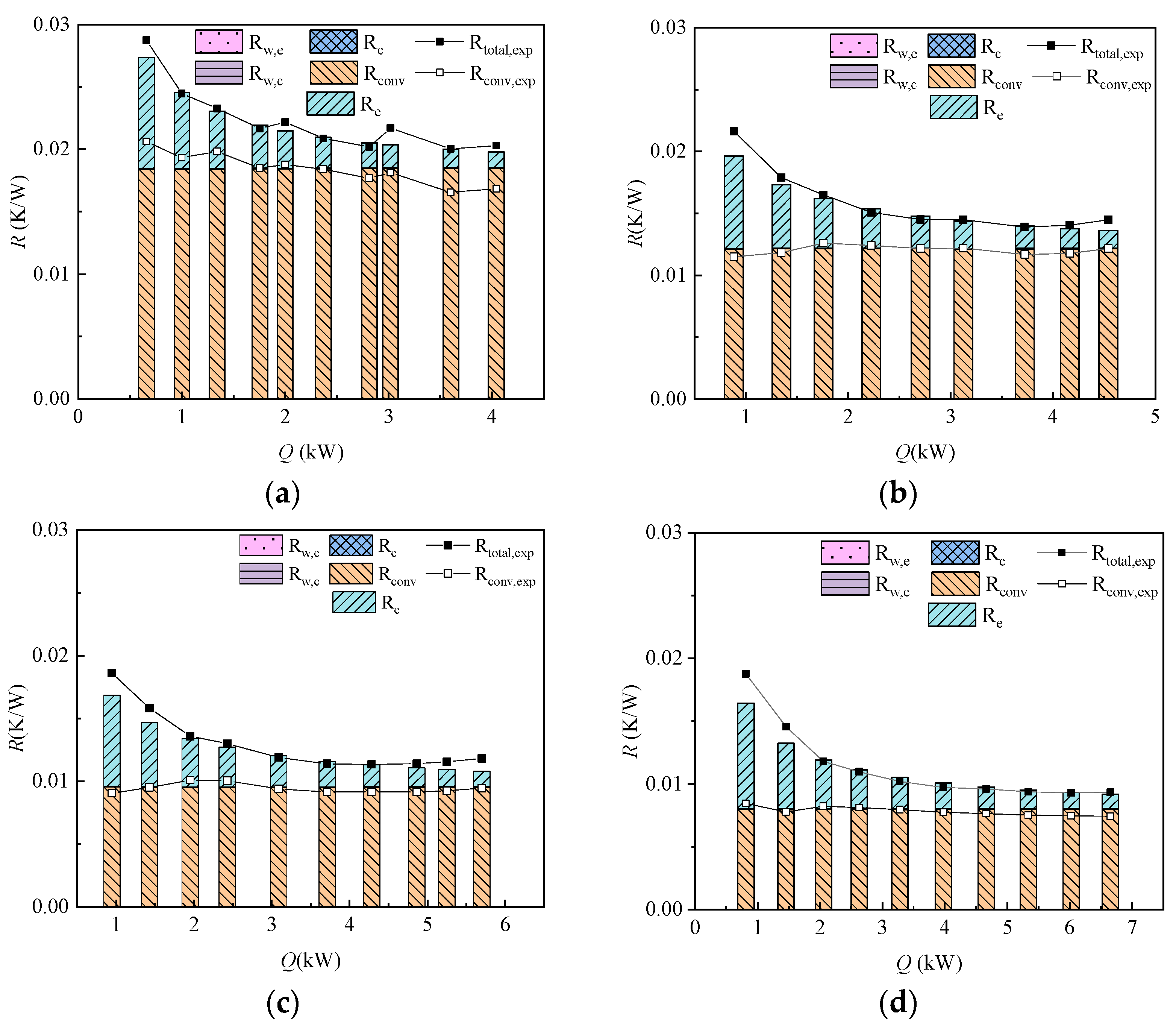
3. Results and Discussion
4. Conclusions
- The novel thermosyphon HPHX with a continuous closed tube for which only a single charge was required operated as 9×17 individual single-tube thermosyphons. The maximum cooling rate reached 6.65 kW under a heating pool temperature of 150 °C and a cooling air flow rate of 1600 CMH.
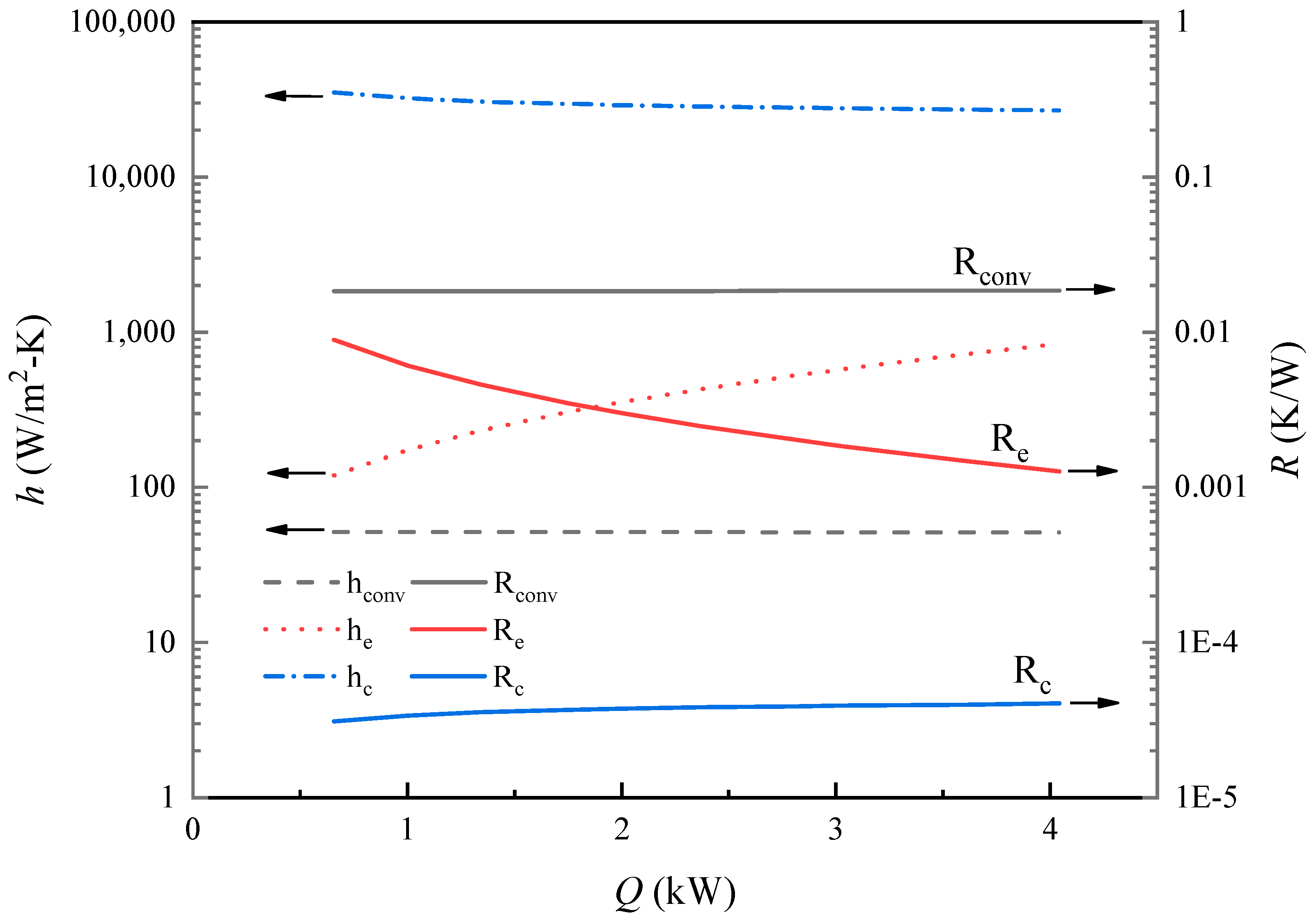
- The total resistance Rtot decreased with the heat transfer rate Q because the evaporator resistances Re decreased significantly with increasing Q due to enhanced boiling.
- As the cooling air flow rate increased from 400 to 1600 CMH, the total resistances considerably decreased, mainly due to the decrease of the convection resistance. The HPHX attained a maximum effective thermal conductivity of 10,096 W/mK under 1600 CMH.
- The convection resistance dominated especially at high heat transfer rates. Its proportion decreased with increasing cooling air flow rate as the convection resistance decreased.
- The theoretical model for single-tube thermosyphons correctly predicted the total resistance of the HPHX with error of less than ±10%.
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
Nomenclature
| A | heat transfer area (m2) |
| C | thermal capacity (W/K) |
| C* | ratio of heat capacity |
| d | diameter (mm) |
| F | cooling air flow rate (CMH) |
| g | gravitational acceleration (m/s2) |
| h | heat transfer coefficient (W/m2-K) |
| hfg | latent heat (kJ/kg) |
| k | thermal conductivity (W/m-K) |
| L | length (m) |
| n | row number of the heat pipe matrix |
| P | pressure (N/m2) |
| Pr | Prandtl number |
| Q | heat transfer rate (W) |
| Q″ | heat flux (W/m2) |
| R | resistance (°C/W) |
| Re | Reynolds number |
| ST | transverse pitch of the tubes (mm) |
| SL | longitudinal pitch of the tubes (mm) |
| T | temperature (°C) |
| Th | nominal heating pool temperature (°C) |
| U | overall heat transfer coefficient (W/m2-K) |
| Wt | wall thickness (mm) |
| Non-dimensional numbers | |
| NTU | number of heat transfer units of either side |
| Re | Reynolds number |
| Pr | Prandtl number |
| Greek symbols | |
| ε | effectiveness |
| μ | dynamic viscosity (Pa-s) |
| ρ | density (kg/m3) |
| σ | surface tension of the fluid (N/m) |
| ω | measurement uncertainty |
| Subscripts | |
| a | adiabatic section |
| avg | average |
| b | bubble |
| c | condenser |
| ca | cooling air |
| conv | convection |
| cr | critical |
| e | evaporator |
| f | cooling fluid |
| hp | heat pipe |
| i | inner |
| l | liquid |
| o | outer |
| tot | total |
| v | vapor |
| w | wall |
References
- Srimuang, W.; Amatachaya, P. A review of the applications of heat pipe heat exchangers for heat recovery. Renew. Sustain. Energy Rev. 2012, 16, 4303–4315. [Google Scholar] [CrossRef]
- Shabgard, H.; Allen, M.J.; Sharifi, N.; Benn, S.P.; Faghri, A.; Bergman, T.L. Heat pipe heat exchangers and heat sinks: Opportunities, challenges, applications, analysis, and state of the art. Int. J. Heat Mass Transf. 2015, 89, 138–158. [Google Scholar] [CrossRef]
- Noie-Baghban, S.H.; Majideian, G.R. Waste heat recovery using heat pipe heat exchanger (HPHE) for surgery rooms in hospitals. Appl. Therm. Eng. 2000, 20, 1271–1282. [Google Scholar] [CrossRef]
- Abd El-Baky, M.A.; Mohamed, M.M. Heat pipe heat exchanger for heat recovery in air conditioning. Appl. Therm. Eng. 2007, 27, 795–801. [Google Scholar] [CrossRef]
- Hassan, M.A.M. Investigation of performance of heat pipe as heat exchanger using alternative refrigerants. J. Energy Eng. 2013, 139, 18–24. [Google Scholar] [CrossRef]
- Shen, S.; Cai, W.; Wang, X.; Wu, Q.; Yon, H. Investigation of liquid desiccant regenerator with heat recovery heat pipe system. Energy Build. 2017, 146, 353–363. [Google Scholar] [CrossRef]
- Lukitobudi, A.R.; Akbarzadeh, A.; Johnson, P.W.; Hendy, P. Design, construction and testing of a thermosyphon heat exchanger for medium temperature heat recovery in bakeries. Heat Recover. Syst. CHP 1995, 15, 481–491. [Google Scholar] [CrossRef]
- Wu, X.P.; Johnson, P.; Akbarzadeh, A. Application of heat pipe heat exchangers to humidity control in air-conditioning systems. Appl. Therm. Eng. 1997, 17, 561–568. [Google Scholar] [CrossRef]
- Riffat, S.B.; Gan, G. Determination of effectiveness of heat-pipe heat recovery for naturally-ventilated buildings. Appl. Therm. Eng. 1998, 18, 121–130. [Google Scholar] [CrossRef]
- Yau, Y.H.; Tucker, A.S. The performance study of a wet six-row heat-pipe heat exchanger operating in tropical buildings. Int. J. Energy Res. 2003, 27, 187–202. [Google Scholar] [CrossRef]
- Yang, F.; Yuan, X.; Lin, G. Waste heat recovery using heat pipe heat exchanger for heating automobile using exhaust gas. Appl. Therm. Eng. 2003, 23, 367–372. [Google Scholar] [CrossRef]
- Noie, S.H. Investigation of thermal performance of an air-to-air thermosyphon heat exchanger using ε-NTU method. Appl. Therm. Eng. 2006, 26, 559–567. [Google Scholar] [CrossRef]
- Jouhara, H.; Merchant, H. Experimental investigation of a thermosyphon based heat exchanger used in energy efficient air handling units. Energy 2012, 39, 82–89. [Google Scholar] [CrossRef]
- Gedik, E.; Yilmaz, M.; Kurt, H. Experimental investigation on the thermal performance of heat recovery system with gravity assisted heat pipe charged with R134a and R410A. Appl. Therm. Eng. 2016, 99, 334–342. [Google Scholar] [CrossRef]
- Ma, H.; Yin, L.; Shen, X.; Lu, W.; Sun, Y.; Zhang, Y.; Deng, N. Experimental study on heat pipe assisted heat exchanger used for industrial waste heat recovery. Appl. Energy 2016, 169, 177–186. [Google Scholar] [CrossRef]
- Ramos, J.; Chong, A.; Jouhara, H. Experimental and numerical investigation of a cross flow air-to-water heat pipe-based heat exchanger used in waste heat recovery. Int. J. Heat Mass Transf. 2016, 102, 1267–1281. [Google Scholar] [CrossRef]
- Rittidech, S.; Dangeton, W.; Soponronnarit, S. Closed-ended oscillating heat-pipe (CEOHP) air-preheater for energy thrift in a dryer. Appl. Energy 2005, 81, 198–208. [Google Scholar] [CrossRef]
- Meena, P.; Rittidech, S.; Poomsa-ad, N. Closed-loop oscillating heat-pipe with check valves (CLOHP/CVs) air-preheater for reducing relative humidity in drying systems. Appl. Energy 2007, 84, 363–373. [Google Scholar] [CrossRef]
- Khandekar, S. Pulsating heat pipe based heat exchangers. In Proceedings of the 21st International Symposium on Transport Phenomena, Kaohsiung City, Taiwan, 2–5 November 2010. [Google Scholar]
- Czajkowski, C.; Nowak, A.I.; Błasiak, P.; Ochman, A.; Pietrowicz, S. Experimental study on a large scale pulsating heat pipe operating at high heat loads, different adiabatic lengths and various filling ratios of acetone, ethanol, and water. Appl. Therm. Eng. 2020, 165, 114534. [Google Scholar] [CrossRef]
- Kays, W.M.; London, A.L. Compact Heat Exchangers; McGraw Hills: San Francisco, CA, USA, 1984; ISBN 007112679-1. [Google Scholar]
- Incropera, F.P.; Lavine, A.S.; Bergman, T.L.; DeWitt, D.P. Principles of Heat and Mass Transfer; John Wiley & Sons: New York, NY, USA; Singapore Pte. Ltd.: Singapore, 2013; ISBN 047064615-1. [Google Scholar]
- Gross, U. Reflux condensation heat transfer inside a closed thermosyphon. Int. J. Heat Mass Transf. 1992, 35, 279–294. [Google Scholar] [CrossRef]
- Jafari, D.; Franco, A.; Filippeschi, S.; DiMarco, P. Two-phase closed thermosyphons: A review of studies and solar applications. Renew. Sustain. Energy Rev. 2016, 53, 575–593. [Google Scholar] [CrossRef]
- Jafari, D.; DiMarco, P.; Filippeschi, S.; Franco, A. An experimental investigation on the evaporation and condensation heat transfer of two-phase closed thermosyphons. Exp. Therm. Fluid Sci. 2017, 88, 111–123. [Google Scholar] [CrossRef]
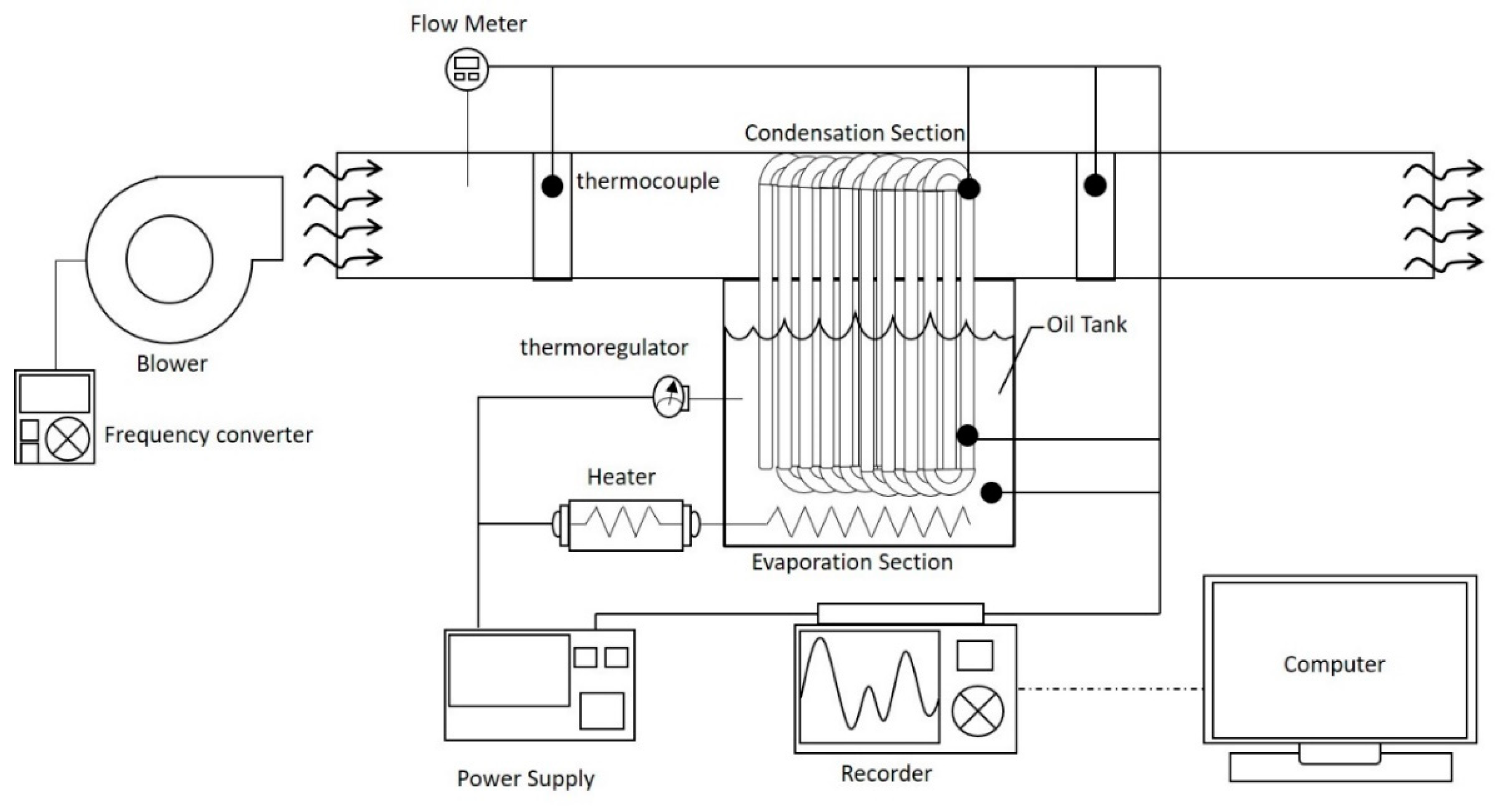

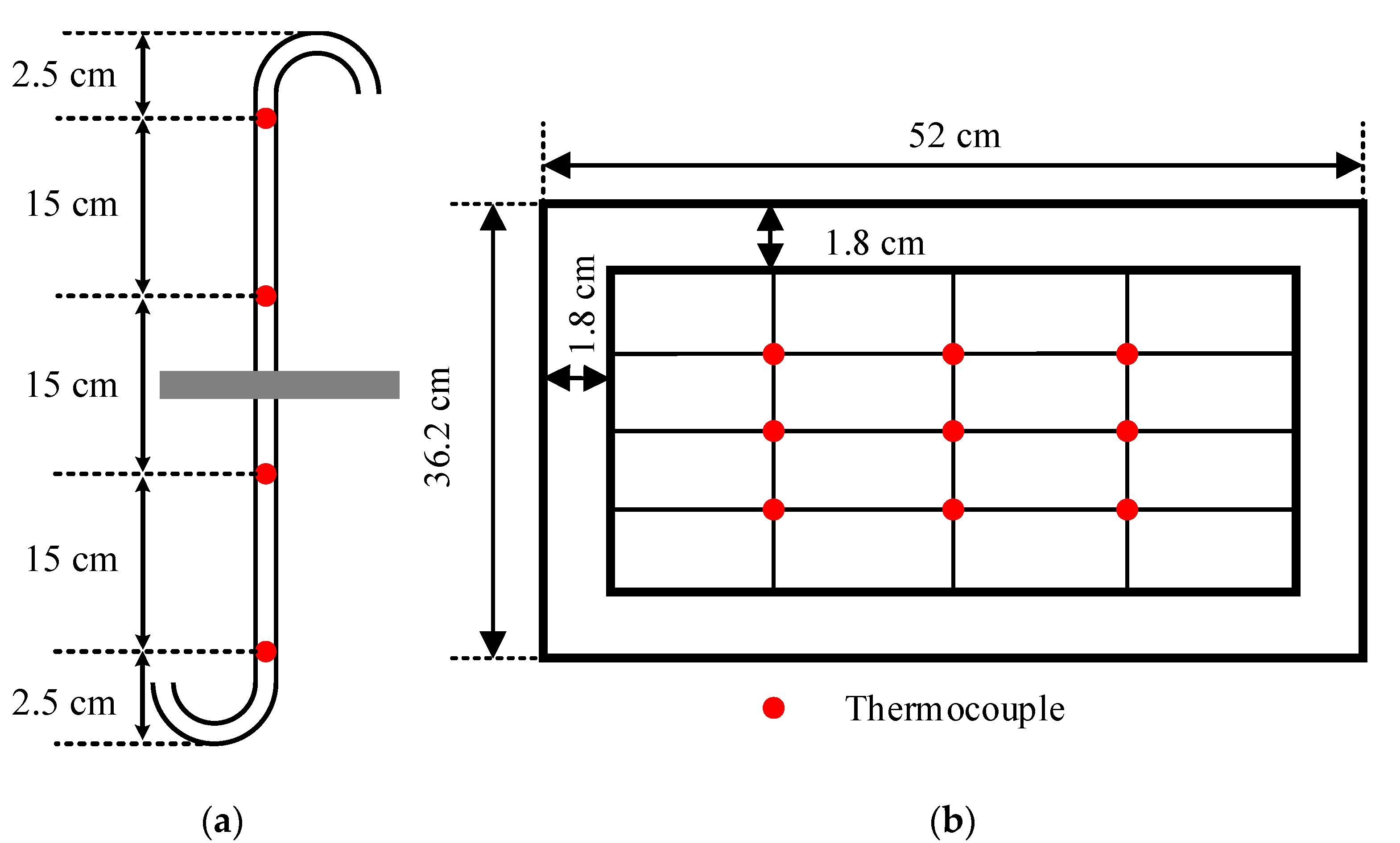



| Working Fluid/ Filling Ratio | Nominal Cooling Air Flow Rate (CMH) | Nominal Heating Pool Temperature Th (°C) |
|---|---|---|
| Water/40% | 400 | 60–160 |
| 800 | ||
| 1200 | 60–150 | |
| 1600 |
| evaporator length, Le | 235 mm |
| condenser length, Lc | 235 mm |
| tube OD | 9.5 mm |
| tube ID | 8.3 mm |
| longitudinal pitch of the tube bank, SL | 22.0 mm |
| transverse pitch of the tube bank, ST | 25.4 mm |
| row number of the tube bank, n | 9 |
| total tube number | 153 |
| cross-sectional area of the cooling air duct | 0.11 m2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, K.-S.; Wu, Y.-L.; Chu, Y.-P.; Wu, Y.-L.; Wong, S.-C. Performance Tests on a Novel Un-Finned Thermosyphon Heat Exchanger Requiring a Single Charge. Processes 2021, 9, 995. https://doi.org/10.3390/pr9060995
Yang K-S, Wu Y-L, Chu Y-P, Wu Y-L, Wong S-C. Performance Tests on a Novel Un-Finned Thermosyphon Heat Exchanger Requiring a Single Charge. Processes. 2021; 9(6):995. https://doi.org/10.3390/pr9060995
Chicago/Turabian StyleYang, Kai-Shing, Yan-Lin Wu, Yi-Pin Chu, Yu-Lieh Wu, and Shwin-Chung Wong. 2021. "Performance Tests on a Novel Un-Finned Thermosyphon Heat Exchanger Requiring a Single Charge" Processes 9, no. 6: 995. https://doi.org/10.3390/pr9060995




