Mechanism of the Breakage of Spherical Gypsum Particles under 3-Point Contact Conditions
Abstract
:1. Introduction
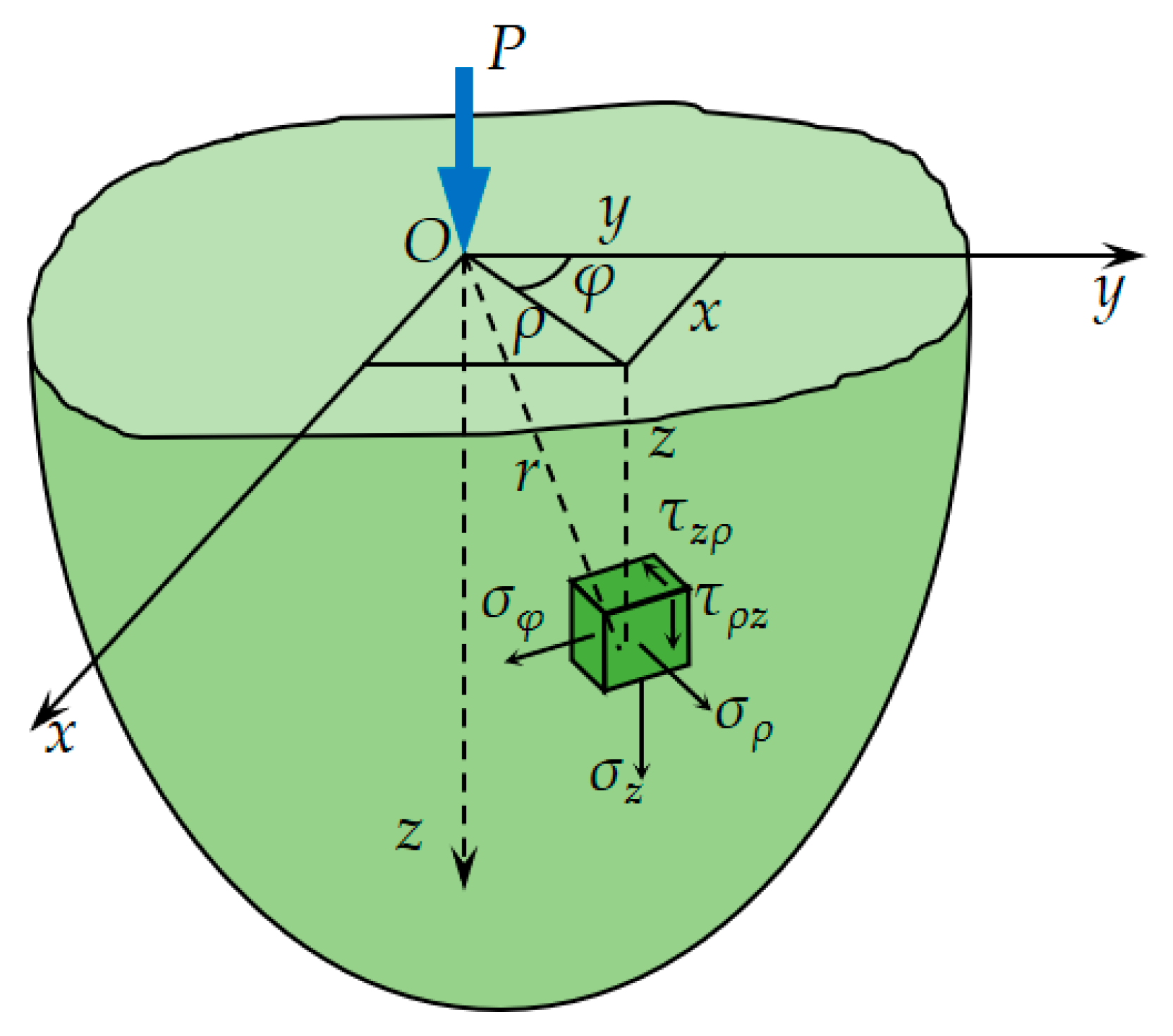
2. Theoretical Analysis
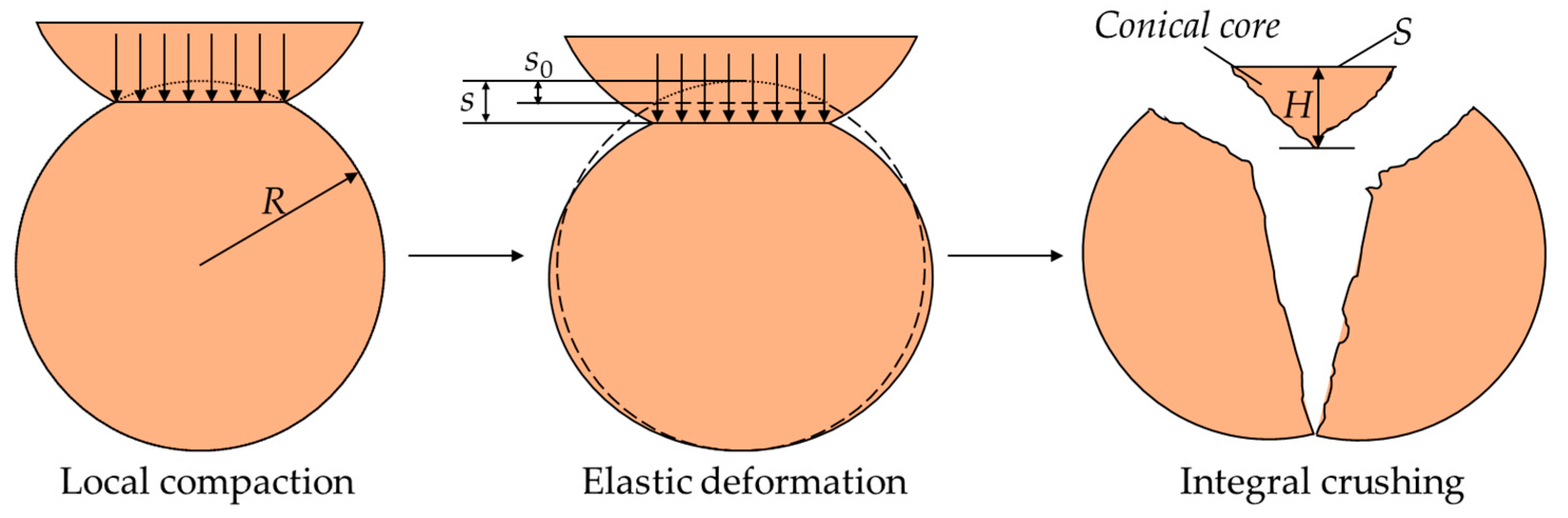
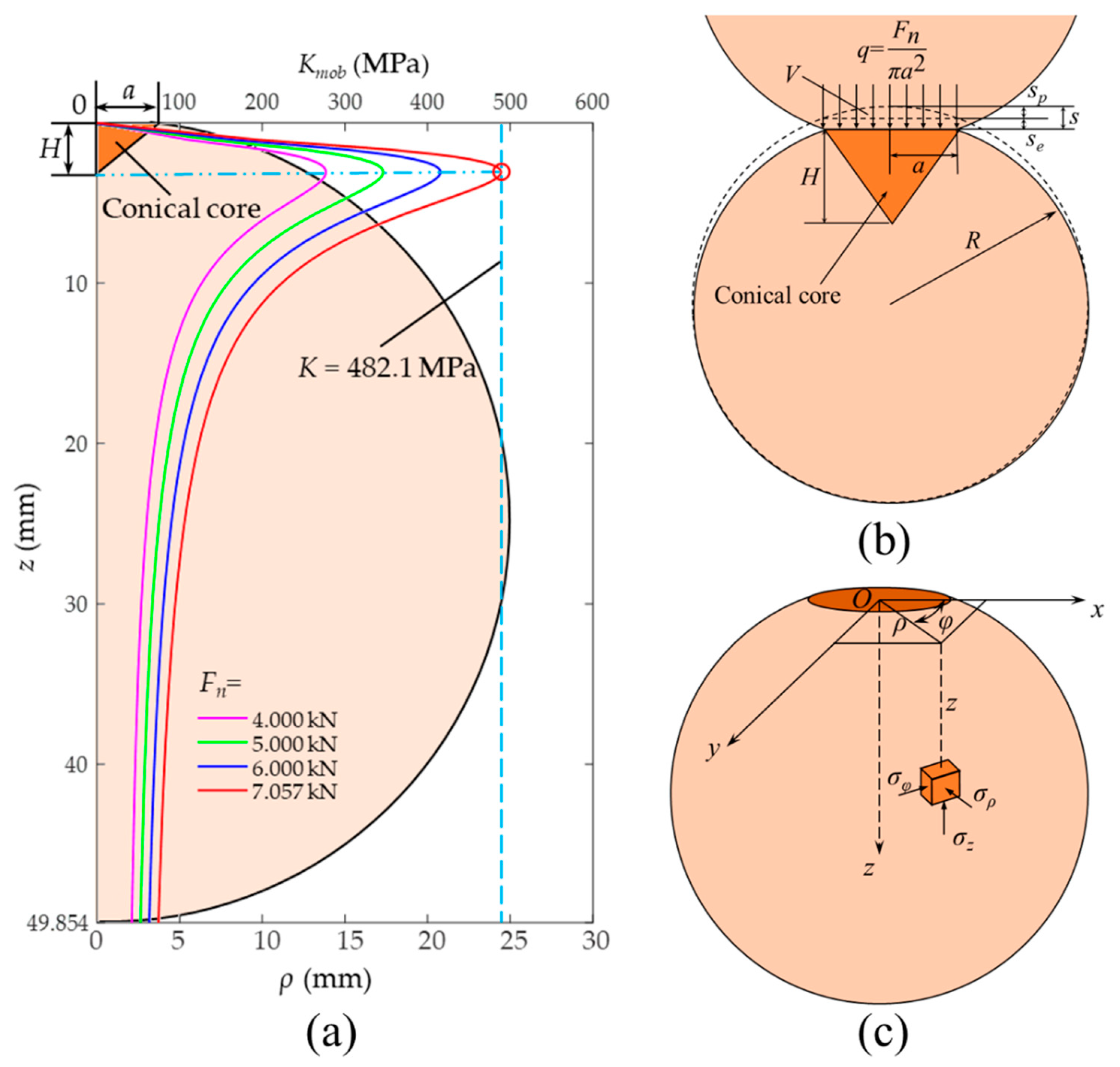
2.1. Model for Ball–Ball Normal Contact
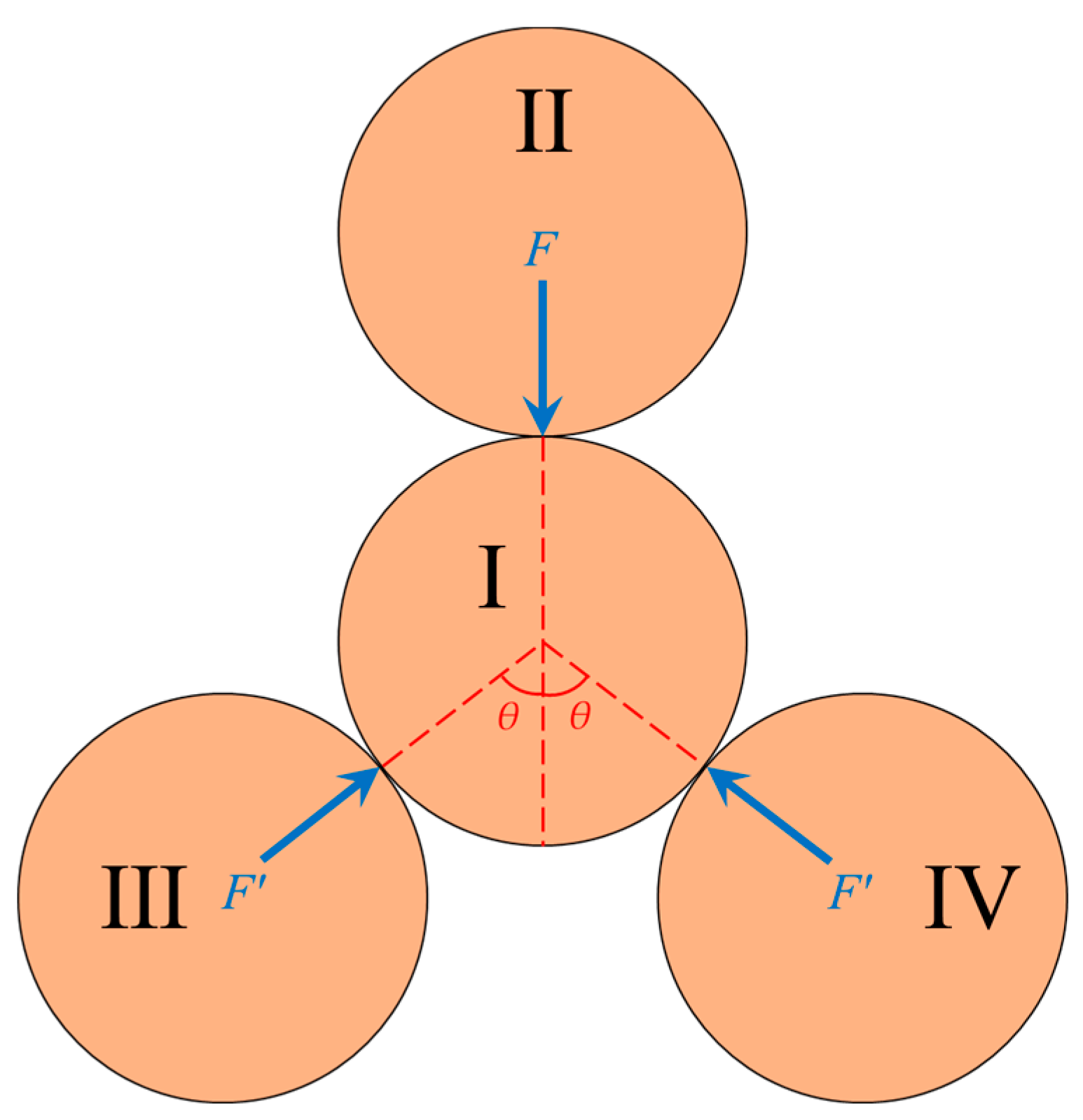
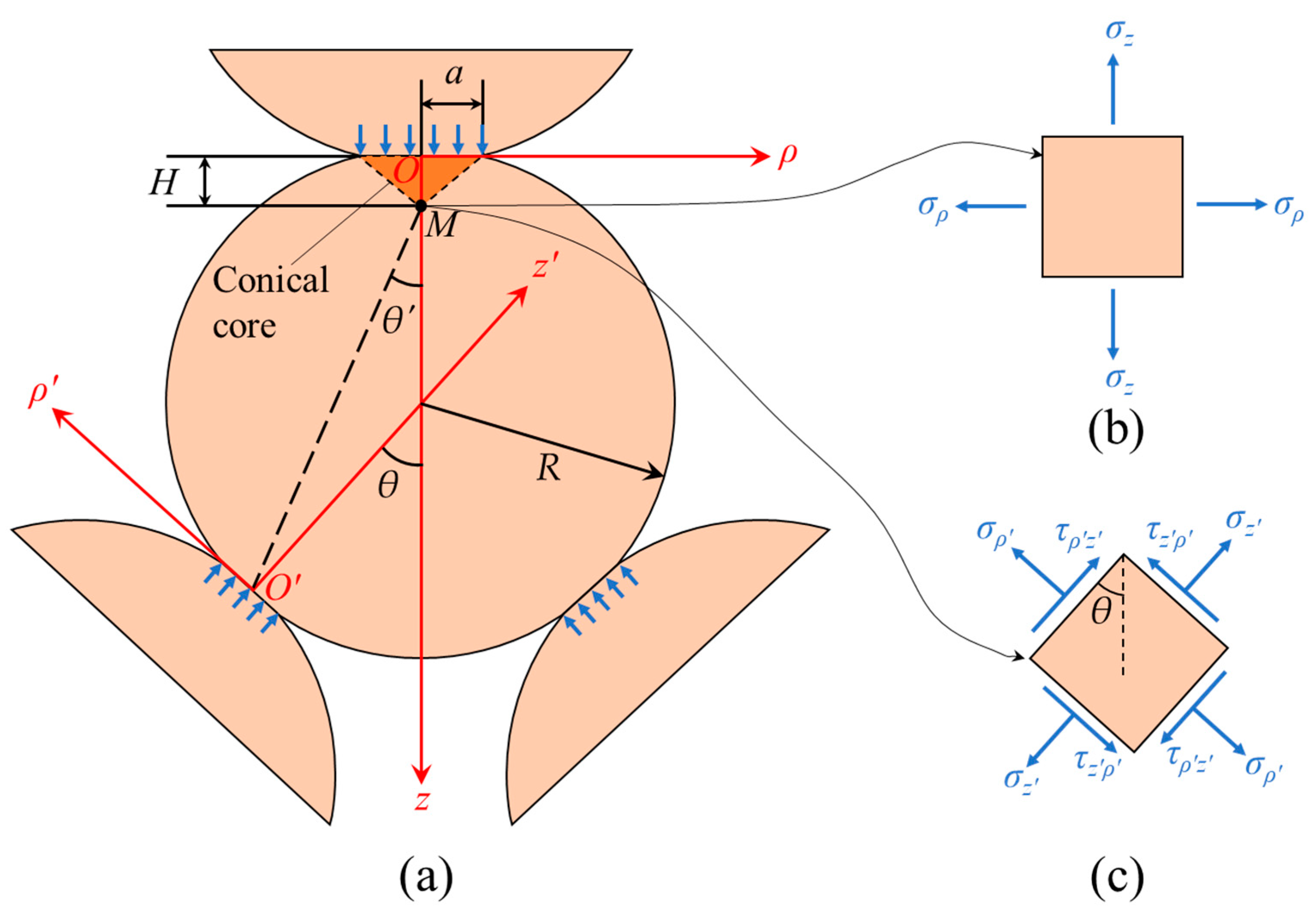
2.2. Solutions under Three-Point Contact Conditions
3. Particle Contact Test under Three-Point Contact Conditions
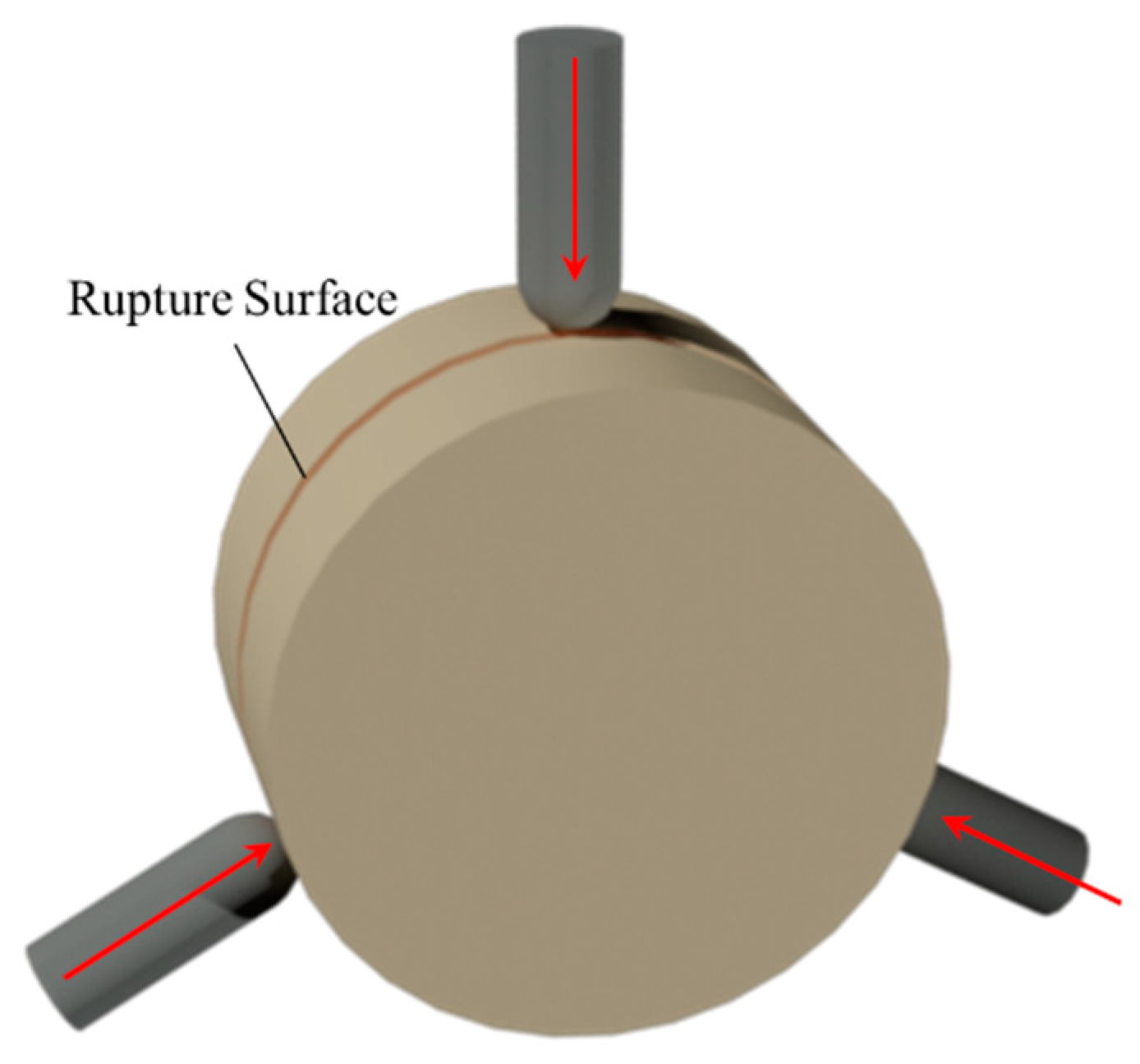
3.1. Materials and Methods
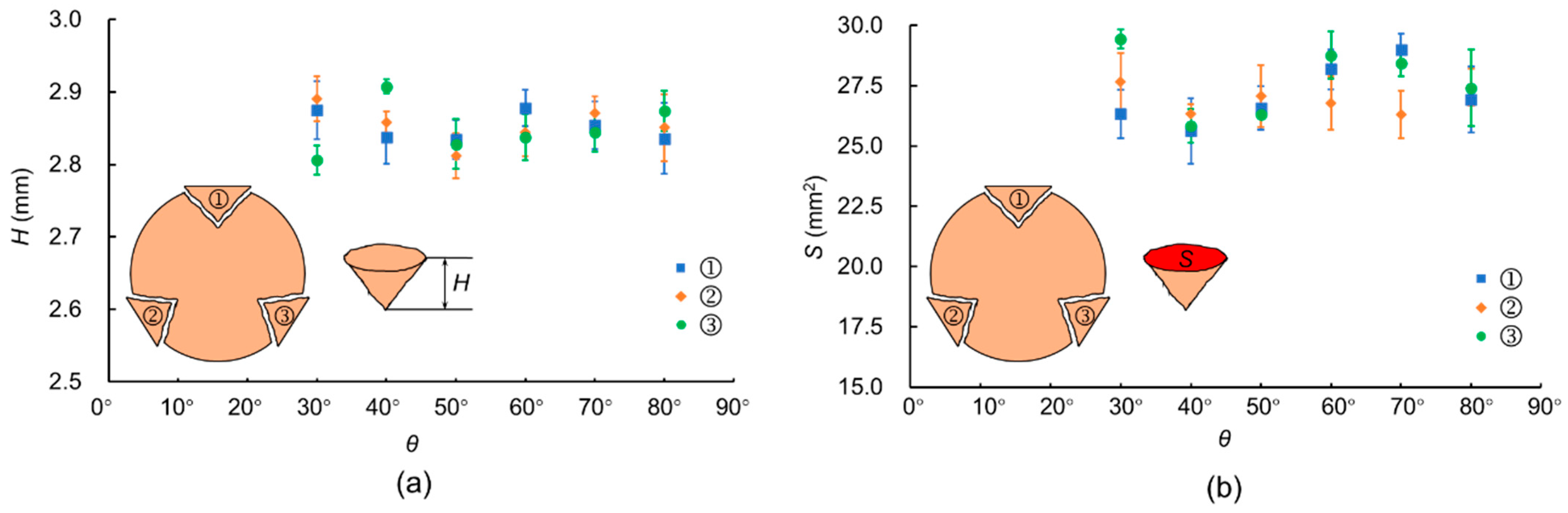
3.2. Results
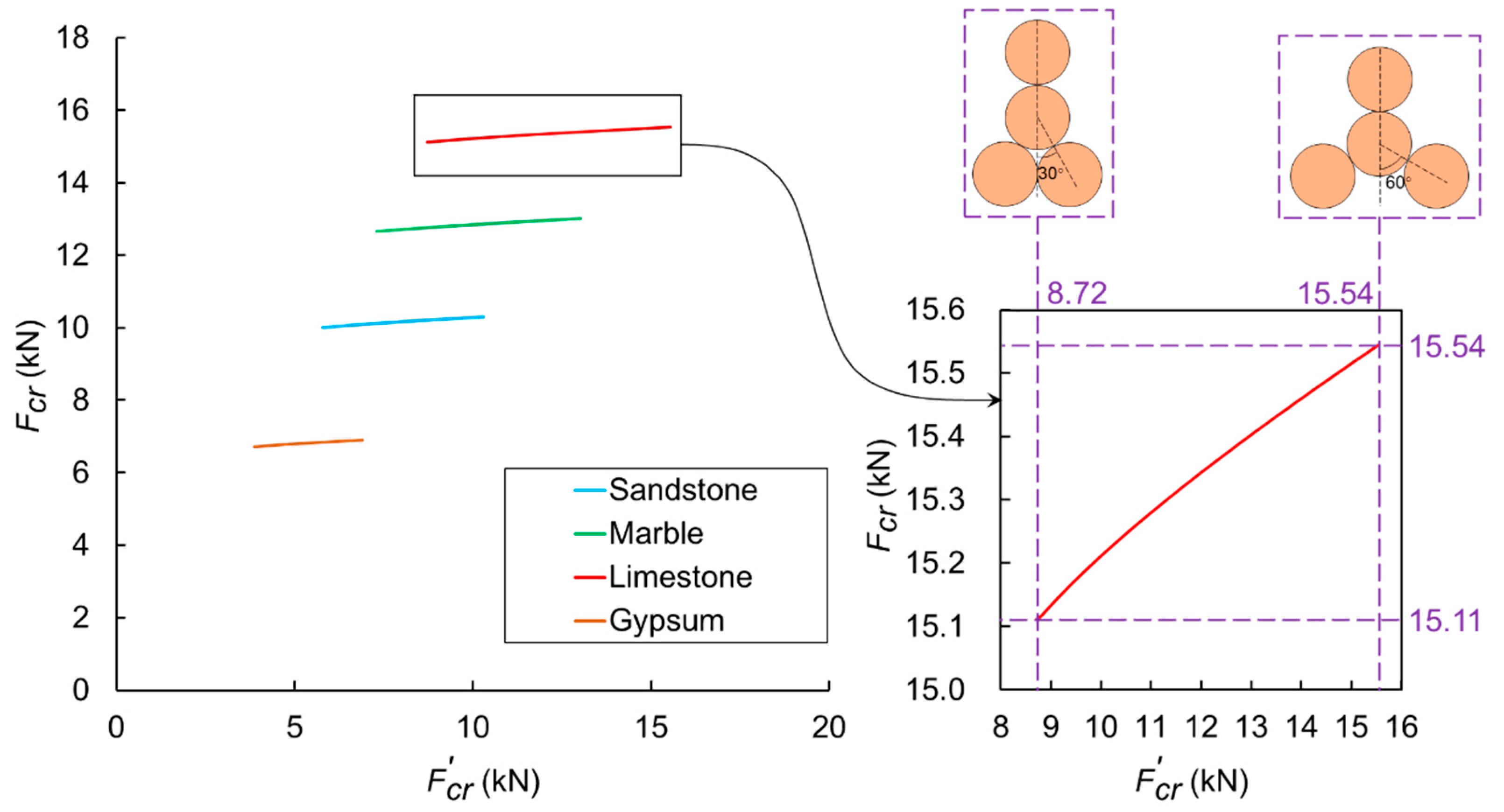
4. Discussion
5. Conclusions
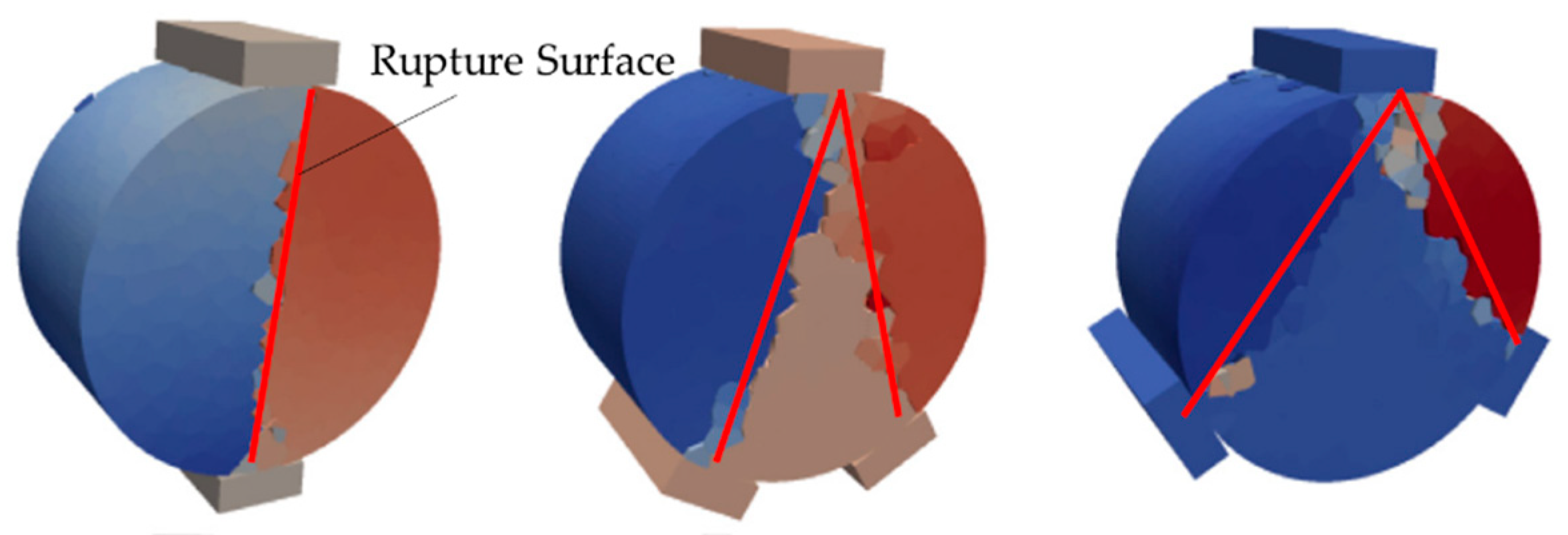
- Under three-point contact conditions, the fracture surface is a plane passing through the three contact points, which is different from the breakage form in the ball–ball normal contact test.
- Under multi-point contact conditions, the form of contact has a significant effect on the fracture morphology of particles.
- Under multi-point contact conditions, a conical core is formed under each contact point, and the size of the conical core depends on the magnitude of the normal force on the contact point at the moment of particle breakage.
- Multi-point contact effectively increases the difficulty of particle breakage. The stronger the constraint of the surrounding particles, the more difficult it is for the particle to break.
- The arrangement of particles in a coarse-grained soil structure affects the number and location of contact points between particles and their surrounding particles, thus affecting the difficulty of particle breakage and the breakage form. Therefore, the arrangement of particles affects the overall strength of the structure.
6. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, C.; Hou, R.; Zhou, J. Particle Contact Characteristics of Coarse-Grained Soils under Normal Contact. Eur. J. Environ. Civ. Eng. 2018, 22, s114–s129. [Google Scholar] [CrossRef]
- Dayakar, P.; Raju, K.V.B.; Sankaran, S. Improvement of Coarse Grained Soil by Permeation Grouting Using Cement Based HPMC Grout. Int. J. Emerg. Technol. Adv. Eng. 2014, 4, 17–22. [Google Scholar]
- Nakata, T.; Miura, S. Change in void structure due to particle breakage of volcanic coarse grained soil and its evaluation. Doboku Gakkai Ronbunshuu 2007, 63, 224–236. [Google Scholar] [CrossRef]
- Nguyen, B.T.; Ishikawa, T.; Murakami, T. Effects evaluation of grass age on hydraulic properties of coarse-grained soil. Transp. Geotechnics 2020, 25, 100401. [Google Scholar] [CrossRef]
- Indrawan, I.G.B.; Rahardjo, H.; Leong, E.C. Effects of coarse-grained materials on properties of residual soil. Eng. Geol. 2006, 82, 154–164. [Google Scholar] [CrossRef]
- Åström, J.A.; Herrmann, H.J. Fragmentation of Grains in a Two-Dimensional Packing. Eur. Phys. J. B 1998, 5, 551–554. [Google Scholar] [CrossRef]
- Ben-Nun, O.; Einav, I. The Role of Self-Organization during Confined Comminution of Granular Materials. Philos. Trans. A Math. Phys. Eng. Sci. 2010, 368, 231–247. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cavarretta, I.; Coop, M.; O’Sullivan, C. The Influence of Particle Characteristics on the Behaviour of Coarse Grained Soils. Geotechnique 2010, 60, 413–423. [Google Scholar] [CrossRef] [Green Version]
- Coop, M.R.; Sorensen, K.K.; Freitas, T.B.; Georgoutsos, G. Particle Breakage during Shearing of a Carbonate Sand. Geotechnique 2004, 54, 157–163. [Google Scholar] [CrossRef]
- Delenne, J.Y.; Youssoufi, M.S.E.; Cherblanc, F.; Bénet, J.C. Mechanical Behaviour and Failure of Cohesive Granular Materials. Int. J. Numer. Anal. Met. 2004, 28, 1577–1594. [Google Scholar] [CrossRef]
- Subero, J.; Ghadiri, M. Breakage Patterns of Agglomerates. Powder Technol. 2001, 120, 232–243. [Google Scholar] [CrossRef]
- Qiu, Z.; Cao, T.; Li, Y.; Wang, J.; Chen, Y. Rheological Behavior and Modeling of a Crushed Sandstone-Mudstone Particle Mixture. Processes 2018, 6, 192. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Huang, Y.; Qiao, M.; Chen, Z.; Song, T.; Kong, G.; Gao, H.; Guo, L. Effects of Water Soaked Height on the Deformation and Crushing Characteristics of Loose Gangue Backfill Material in Solid Backfill Coal Mining. Processes 2018, 6, 64. [Google Scholar] [CrossRef] [Green Version]
- Fu, P.C.; Dafalias, Y.F. Fabric Evolution within Shear Bands of Granular Materials and Its Relation to Critical State Theory. Int. J. Numer. Anal. Met. 2011, 35, 1918–1948. [Google Scholar] [CrossRef]
- Kim, D.; Ha, S. Effects of Particle Size on the Shear Behavior of Coarse Grained Soils Reinforced with Geogrid. Materials 2014, 7, 963–979. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Y. Test Granular Materials Failure Using Bi-Directional Simple Shear Apparatus: A Review. Appl. Sci. 2018, 8, 1140. [Google Scholar] [CrossRef] [Green Version]
- Lin, P.S.; Chang, C.W.; Chang, W.J. Characterization of Liquefaction Resistance in Gravelly Soil: Large Hammer Penetration Test and Shear Wave Velocity Approach. Soil Dyn. Earthq. Eng. 2004, 24, 675–687. [Google Scholar] [CrossRef]
- Tejchman, J.; Górski, J.; Einav, I. Effect of Grain Crushing on Shear Localization in Granular Bodies during Plane Strain Compression. Int. J. Numer. Anal. Met. 2012, 36, 1909–1931. [Google Scholar] [CrossRef]
- Wang, J.; Yan, H. On the Role of Particle Breakage in the Shear Failure Behavior of Granular Soils by Dem. Int. J. Numer. Anal. Met. 2013, 37, 832–854. [Google Scholar] [CrossRef]
- Anhdan, L.Q.; Tatsuoka, F.; Koseki, J. Viscous Effects on the Stress-Strain Behavior of Gravelly Soil in Drained Triaxial Compression. Geotech. Test. J. 2006, 29, 660–661. [Google Scholar] [CrossRef]
- Kongsukprasert, L.; Tatsuoka, F. Ageing and Viscous Effects on the Deformation and Strength Characteristics of Cement-Mixed Gravelly Soil in Triaxial Compression. Soils Found. 2005, 45, 55–74. [Google Scholar] [CrossRef] [Green Version]
- Lee, K.L.; Farhoomand, I. Compressibility and Crushing of Granular Soil in Anisotropic Triaxial Compression. Can. Geotech. J. 1967, 4, 68–86. [Google Scholar] [CrossRef]
- Maqbool, S.; Koseki, J. Large-Scale Triaxial Tests to Study Effects of Compaction Energy and Large Cyclic Loading History on Shear Behavior of Gravel. Soils Found. 2010, 50, 633–644. [Google Scholar] [CrossRef] [Green Version]
- McDowell, G.R.; Li, H. Discrete Element Modelling of Scaled Railway Ballast under Triaxial Conditions. Granul. Matter 2016, 18, 66. [Google Scholar] [CrossRef] [Green Version]
- Hardin, B.O. Crushing of Soil Particles. J. Geotech. Eng. 1985, 111, 1177–1192. [Google Scholar] [CrossRef]
- Nakata, Y.; Kato, Y.; Hyodo, M.; Hyde, A.F.; Murata, H. One-Dimensional Compression Behaviour of Uniformly Graded Sand Related to Single Particle Crushing Strength. Soils Found. 2001, 41, 39–51. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Zhao, C.; Zhang, Y.W.; Ouyang, G.B.; Yu, S.C.; Zhou, J. Particle Breakage Characteristics of Coarse-Grained Soil under Point-Point Contact. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Beijing, China, 2020. [Google Scholar] [CrossRef]
- Zhou, J. Experimental Study on Contact of Gypsum Particles. Chin. J. Tongji Univ. 2016, 44, 67–72. [Google Scholar] [CrossRef]
- Zhou, J.; Niu, Y.R.; Zhou, Y.H.; Zhang, J.; Zhao, C. The Ball-Surface Normal Contact Experiment Research and Numerical Simulation of Coarse Grained Soil. In Proceedings of the GeoShanghai 2018 International Conference: Fundamentals of Soil Behaviours; Springer: Singapore, 2018. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, Y.W.; Zhou, Y.; Zhang, J. Experimental Study on Particle Breakage of Coarse-Grained Soil Considering Normal Contact Force. Chin. J. Geotech. Eng. 2018, 40, 7–14. [Google Scholar] [CrossRef]
- Wang, Z.H.; Wang, P.J.; Jing, X.K.; Zhou, J.; Xiao, Z.C. A Study on Inter-Particle Contact Behaviors and Micro Contact Models of Coarse-Grained Soil. Chin. J. Rock Mech. Eng. 2018, 37, 1980–1992. [Google Scholar] [CrossRef]
- Yu, S.C.; Jia, M.; Zhou, J.; Zhao, C.; Li, L. Micro-Mechanism of Spherical Gypsum Particle Breakage under Ball–Plane Contact Condition. Appl. Sci. 2019, 9, 4795. [Google Scholar] [CrossRef] [Green Version]
- Niu, Y.R.; Zhou, J.; Zhao, C.; Li, L. Experimental Study on Multi-Point Contact Crushing of Spherical Sandstone Particles. Chin. J. Hohai University Nat. Sci. (under review).
- Niu, Y.R.; Zhao, C.; Li, L.; Zhou, J.; Zhang, Y.W.; Yu, S.C. Micromechanism of the Breakage of Two Spherical Gypsum Particles under Ball–Ball Normal Contact Conditions. (Manuscript in prepared).
- Niu, Y.R.; Li, L.; Zhang, Y.W.; Yu, S.C.; Zhou, J. Micromechanism of the Breakage of Two Spherical Gypsum Particles under Normal–Tangential Contact Conditions. Appl. Sci. 2021, 11, 4039. [Google Scholar] [CrossRef]
- Zhou, J.; Ouyang, G.B.; Luo, C.; Wang, Z. Experimental Research on Tangential Contact Characteristics of Marble Spherical Particles. Chin. J. Undergr. Sp. Eng. 2017, 13, 71–78, 116. [Google Scholar]
- Mindlin, R.D.; Deresiewicz, H. Elastic spheres in contact under varying oblique forces. J. Appl. Mech. 1953, 20, 327–344. [Google Scholar] [CrossRef]
- Hiramatsu, Y.; Oka, Y. Determination of the Tensile Strength of Rock by a Compression Test of an Irregular Test Piece. Int. J. Rock Mech. Min. 1966, 3, 89–90. [Google Scholar] [CrossRef]
- Chau, K.T.; Wei, X.X.; Wong, R.H.C.; Yu, T.X. Fragmentation of Brittle Spheres under Static and Dynamic Compressions: Experiments and Analyses. Mech. Mater. 2000, 32, 543–554. [Google Scholar] [CrossRef]
- Riccardo, A.; Aurélien, N.; Yannick, D.; Patrick, R. Effect of contact location on the crushing strength of aggregates. J. Mech. Phys. Solids 2019, 122, 406–417. [Google Scholar] [CrossRef] [Green Version]
- Christensen, R.M. Yield Functions/Failure Criteria for Isotropic Materials. Proc. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 1997, 453, 1473–1491. [Google Scholar] [CrossRef]
- Christensen, R.M. Yield Functions, Damage States, and Intrinsic Strength. Math. Mech. Solids 2000, 5, 285–300. [Google Scholar] [CrossRef]
- Russell, A.R.; Muir, W.D. Point Load Tests and Strength Measurements for Brittle Spheres. Int. J. Rock Mech. Min. 2009, 46, 272–280. [Google Scholar] [CrossRef]
- Wu, J. Elastic Mechanics; Higher Education Press: Beijing, China, 2001. [Google Scholar]
- Zhou, Y.H. Fracture Characteristics of Coarse Spherical Particles under Normal Contact Condition. Ph.D. Thesis, Tongji University, Shanghai, China, 2016. [Google Scholar]



| Unconfined Compressive Strength | Young’s Modulus | Poisson Ratio | Tensile Strength | Crushing Modulus |
|---|---|---|---|---|
| 54.6 MPa | 5.4 GPa | 0.26 | 2.9 MPa | 11.5 GPa |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, Y.; Li, L.; Zhang, Y.; Yu, S. Mechanism of the Breakage of Spherical Gypsum Particles under 3-Point Contact Conditions. Processes 2021, 9, 1029. https://doi.org/10.3390/pr9061029
Niu Y, Li L, Zhang Y, Yu S. Mechanism of the Breakage of Spherical Gypsum Particles under 3-Point Contact Conditions. Processes. 2021; 9(6):1029. https://doi.org/10.3390/pr9061029
Chicago/Turabian StyleNiu, Yiran, Lin Li, Yanwei Zhang, and Shicai Yu. 2021. "Mechanism of the Breakage of Spherical Gypsum Particles under 3-Point Contact Conditions" Processes 9, no. 6: 1029. https://doi.org/10.3390/pr9061029





