Carbon Dioxide Capture in Homogeneous and Heterogeneous Surfaces of Porous Silica Glass
Abstract
:1. Introduction
2. Experimental Methods
2.1. Preparation of Porous Silica Glass
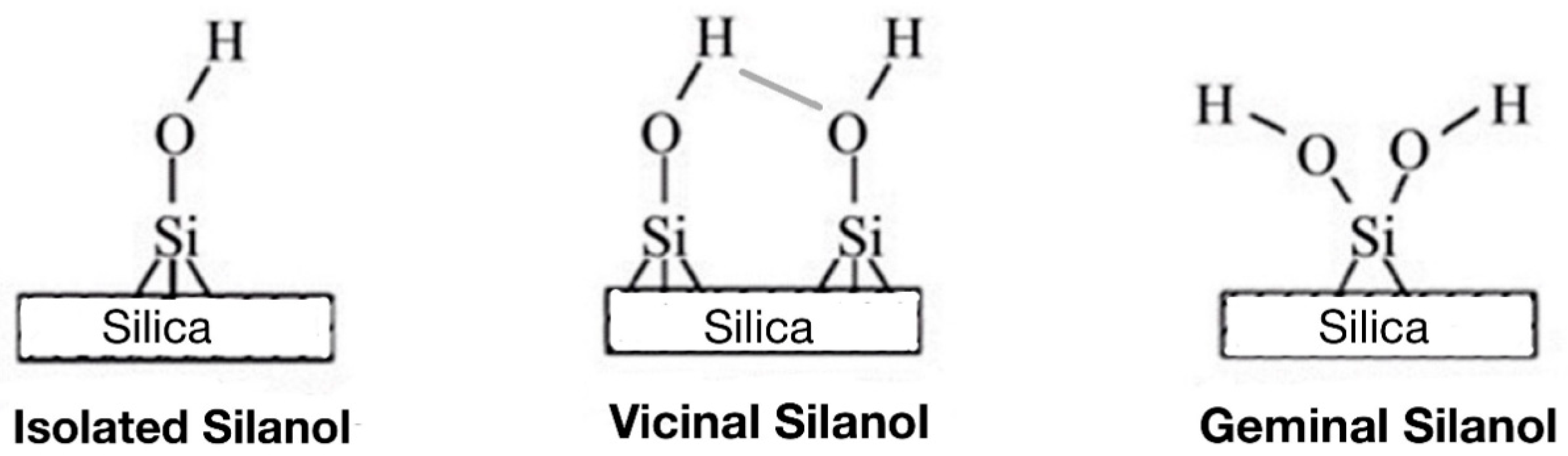
2.2. Determination of Surface Silanol Group Contents
2.3. Experimental Isotherms for N2 and CO2 Adsorption
3. Computational Methodology
3.1. Fluid Model
3.2. Porous Silica Glass Model
3.3. Model of Surface Functional Groups
3.4. Defective Surfaces
3.5. Grand Canonical Monte Carlo Ensemble
4. Results and Discussion
4.1. Experimental Results
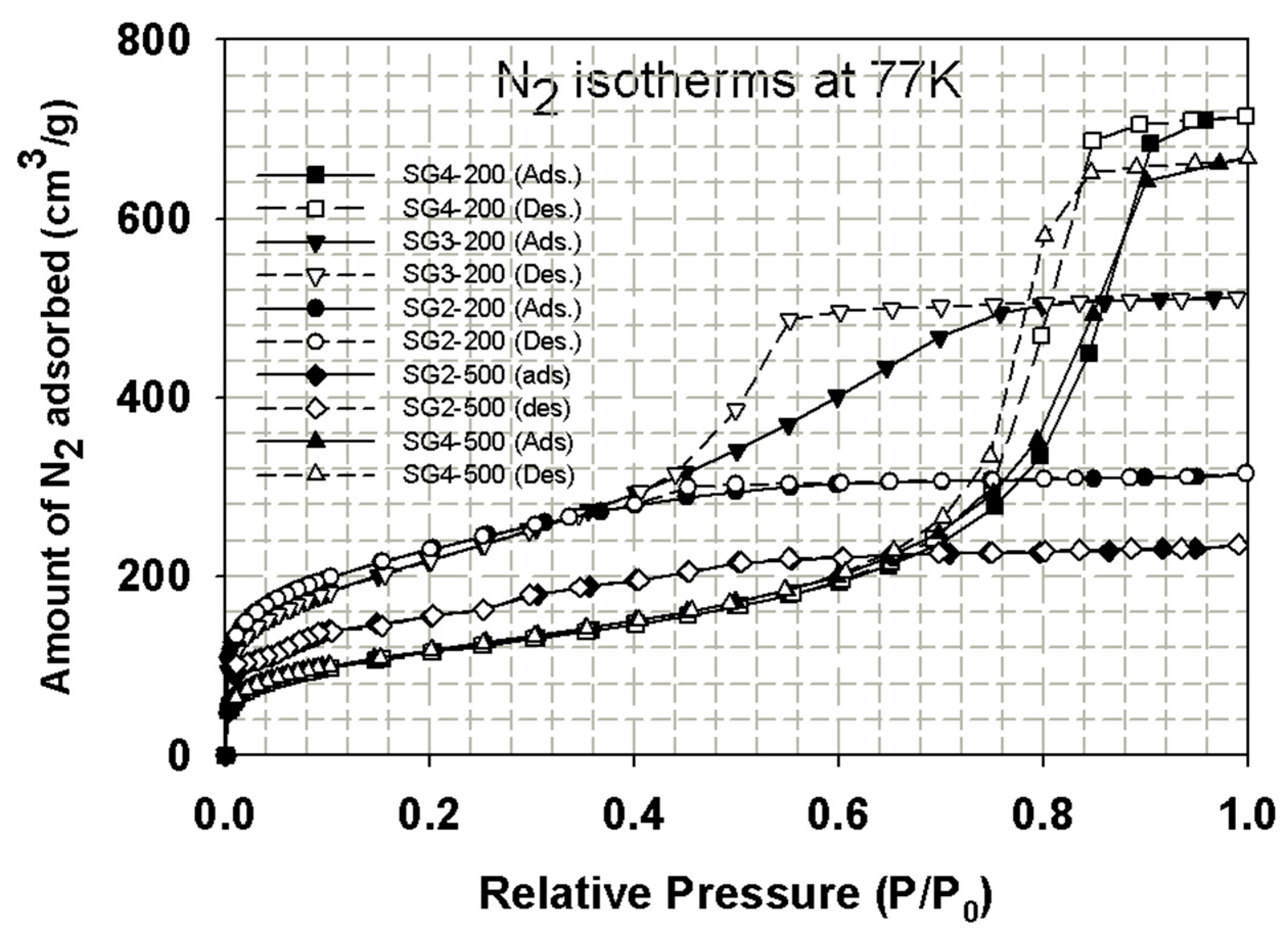
4.1.1. Porous Properties and Silanol Group Contents of Porous Silica Glass
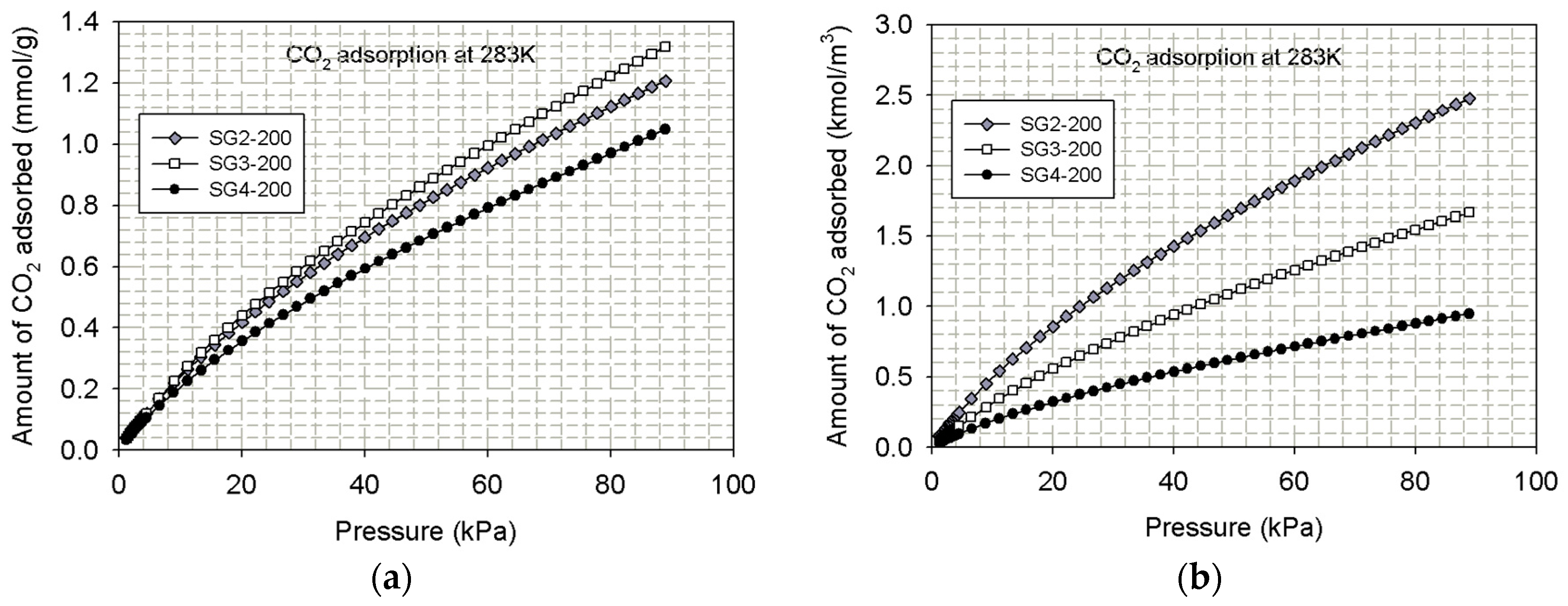
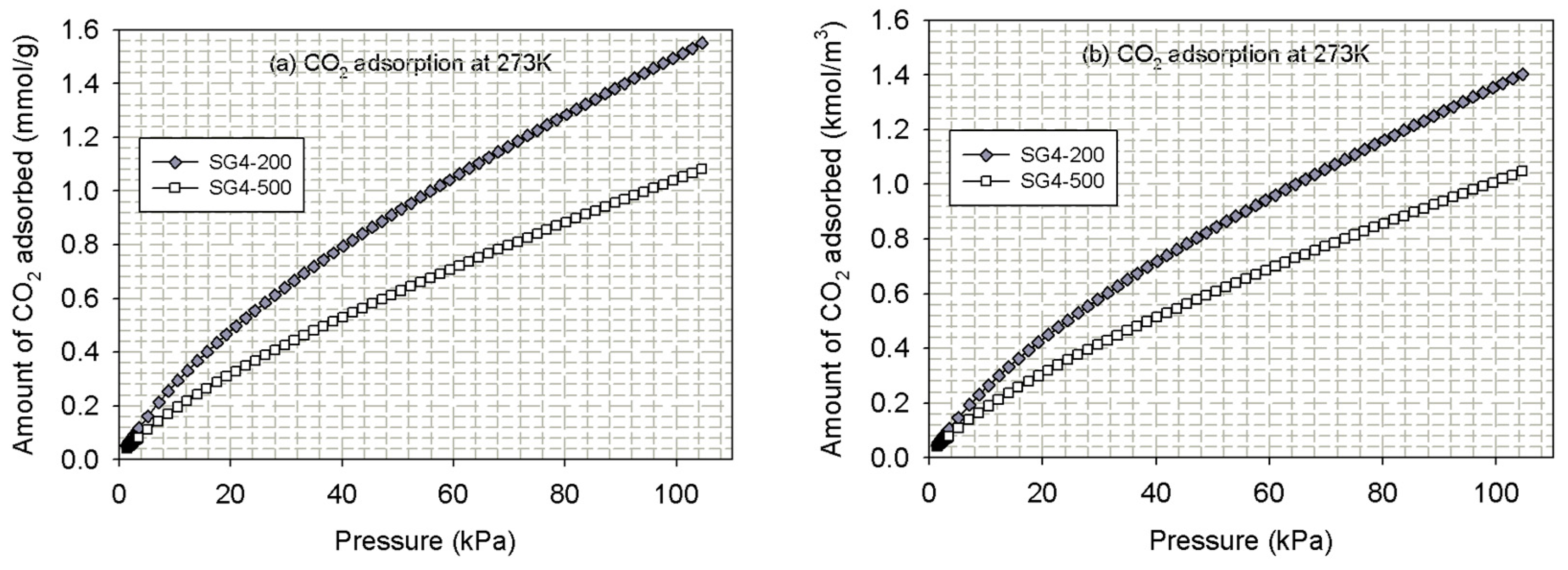
4.1.2. Experimental Isotherms for CO2 Adsorption
4.2. GCMC Simulation Results
4.2.1. Adsorption Isotherms for Various Pore Widths
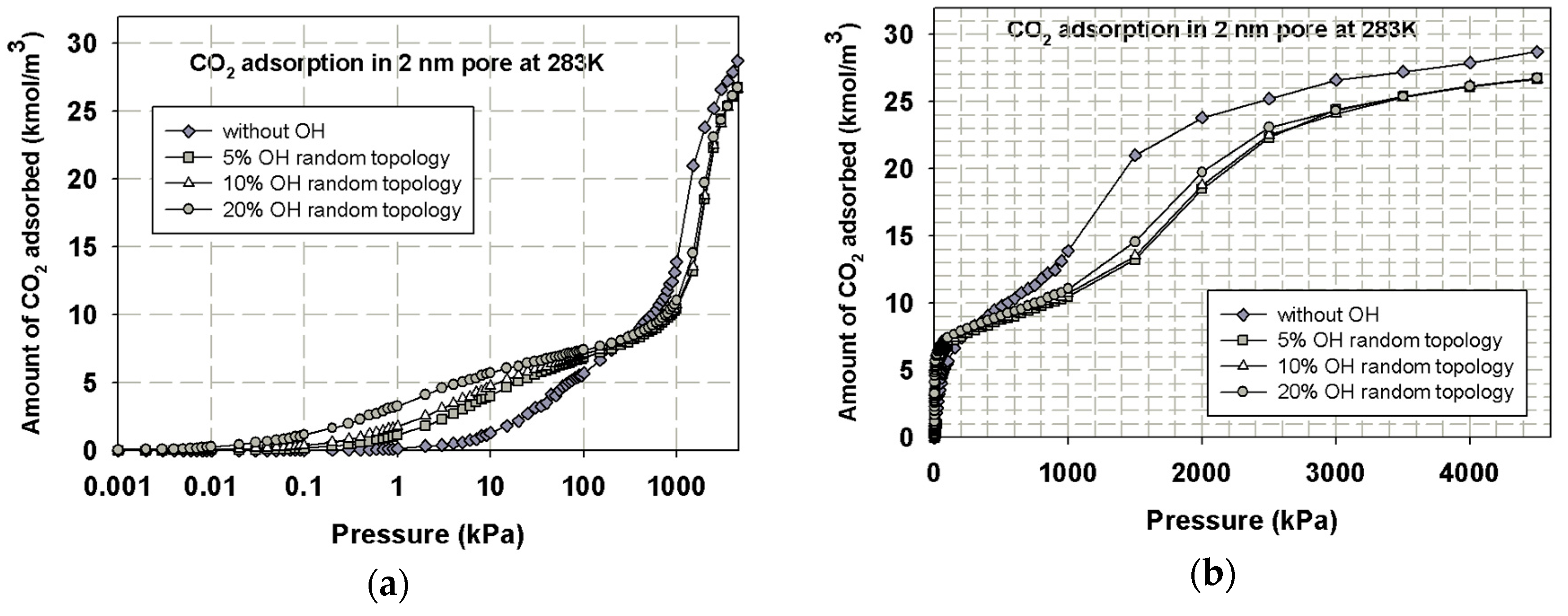
4.2.2. Effects of Functional Group Concentration on CO2 Adsorption Isotherms
4.2.3. Effects of the Functional Group Allocation on the Adsorption of CO2
4.2.4. Adsorption of CO2 on a Defective Surface
4.2.5. Comparison between the Experiment and GCMC Simulation Method
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lopes, F.V.S.; Grande, C.A.; Ribeiro, A.M.; Loureiro, J.M.; Evaggelos, O.; Nikolakis, V.; Rodrigues, A.E. Adsorption of H2, CO2, CH4, CO, N2 and H2O in activated carbon and zeolite for hydrogen production. Sep. Sci. Technol. 2009, 44, 1045–1073. [Google Scholar] [CrossRef]
- Feng, L.; Shen, Y.; Wu, T.; Liu, B.; Zhang, D.; Tang, Z. Adsorption equilibrium isotherms and thermodynami analysis of CH4, CO2, CO, N2, and H2 on NaY Zeolite. Adsorption 2020. [Google Scholar] [CrossRef]
- Kemper, J. Biomass and carbon dioxide capture and storage: A review. Int. J. Greenh. Gas Control 2015, 40, 401–430. [Google Scholar] [CrossRef]
- Khandaker, T.; Hossain, M.S.; Dhar, P.K.; Rahman, M.S.; Hossain, M.A.; Ahmed, M.B. Efficacies of carbon-based adsorbents for carbon dioxide capture. Processes 2020, 8, 654. [Google Scholar]
- Leung, D.Y.C.; Caramanna, G.; Maroto-Valer, M.M. An overview of current status of carbon dioxide capture and storage technologies. Renew. Sustain. Energy Rev. 2014, 39, 426–443. [Google Scholar] [CrossRef] [Green Version]
- Chiang, Y.C.; Juang, R.S. Surface modification of carbonaceous materials for carbon dioxide adsorption: A review. J. Taiwan Inst. Chem. Eng. 2017, 71, 214–234. [Google Scholar] [CrossRef]
- Yazawa, T. Present Status and Future Potential of Preparation of Porous Glass and Its Application in Porous Ceramic Materials; Liu, D.-M., Ed.; Trans. Tech. Publications: Stafa-Zurich, Switzerland, 1995; pp. 125–146. [Google Scholar]
- Nimjaroen, C.; Morimoto, S.; Tangsathitkulchai, C. Preparation and properties of porous glass using fly ash as a raw material. J. Non-Crystalline Solids 2009, 355, 1737–1741. [Google Scholar] [CrossRef]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation; Academic Press: New York, NY, USA, 2002. [Google Scholar]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Clarendon Press: Oxford, UK, 1987. [Google Scholar]
- Ketprasoet, N.; Nimjaroen, C.; Tangsathitkulchai, C.; Wongkoblap, A. Adsorption and isosteric heat studies for adsorption of fluid on porous silica glass using GCMC simulation. In Proceedings of the 9th South East Asian Technical University Consortium (SEATUC) Symposium, Suranaree University of Technology, Nakhon Ratchasima, Thailand, 27–30 July 2015. [Google Scholar]
- Xiaoning, Y.; Xiaopeng, Y. Adsorption and structure of Lennard-Jones model fluid in slit like amorphous silica nanopoes. Colloids Surfaces A Physicochem. Eng. Asp. 2007, 301, 166–173. [Google Scholar]
- Witoon, T.; Chareonpanich, M. Effect of pore size and surface chemistry of porous silica on CO2 adsorption. Songklanakarin J. Sci. Technol. 2012, 34, 403–407. [Google Scholar]
- Kim, J.M.; Chang, S.M.; Kong, S.M.; Kim, K.S.; Kim, J.; Kim, W.S. Control of hydroxyl group in silica particle synthesized by the sol-precipitation process. Ceram. Int. 2005, 35, 1015–1019. [Google Scholar] [CrossRef]
- Ek, S.; Root, A.; Peussa, M.; Niinisto, L. Determination of the hydroxyl group content in silica by thermogravimetry and a comparison with H MAS NMR results. Thermochim. Acta 2001, 379, 201–212. [Google Scholar] [CrossRef]
- Do, D.D. Adsorption Analysis: Equilibria and Kinetics; Imperial College Press: London, UK, 1998. [Google Scholar]
- Harris, J.G.; Yung, K.H. Carbon dioxide’s liquid-vapor coexistence curve and critical properties as predicted by a simple molecular model. J. Phys. Chem. 1995, 99, 12021–12024. [Google Scholar] [CrossRef]
- Burchart, E.D.; Vandegraaf, B.; Vogt, E.T.C. A consistent molecular mechanics force field for aluminophosphates. J. Chem. Soc. Faraday Trans. 1992, 88, 2761–2769. [Google Scholar] [CrossRef]
- He, Y.; Seaton, N.A. Experimental and computer simulation studies of the adsorption of ethane, carbon dioxide, and their binary mixtures in MCM-41. Langmuir 2003, 19, 10132–10138. [Google Scholar] [CrossRef]
- Calero, S.; Dubbeldam, D.; Krishna, R.; Smit, B.; Vlugt, T.J.H.; Denayer, J.F.M.; Martens, J.A.; Maesen, T.L.M. Understanding the role of sodium during adsorption: A force field for alkanes in sodium-exchanged Faujasites. J. Am. Chem. Soc. 2004, 126, 11377–11386. [Google Scholar] [CrossRef] [Green Version]
- Jorge, M.; Schumacher, C.; Seaton, N.A. Simulation study of the effect of the chemical heterogeneity of activated carbon on water adsorption. Langmuir 2002, 18, 9296–9306. [Google Scholar] [CrossRef] [Green Version]
- Bansal, R.C.; Goyal, M. Activated carbon Adsorption; Taylor& Francis: Boca Raton, FL, USA, 2005. [Google Scholar]
- Do, D.D.; Do, H.D. Modeling of adsorption on nongraphitized carbon surface: GCMC simulation studies and comparison with experimental data. J. Phys Chem. B. 2006, 110, 17531–17538. [Google Scholar] [CrossRef]
- Wongkoblap, A.; Do, D.D. Characterization of Cabot non-graphitized carbon blacks with a defective surface model: Adsorption of argon and nitrogen. Carbon 2007, 45, 1527–1534. [Google Scholar] [CrossRef]
- Johnson, J.K.; Zolloweg, J.A.; Gubbins, K.E. The Lennard-Jones equation of state revisited. Mol. Phys. 1993, 78, 591–618. [Google Scholar] [CrossRef]
- Sing, K.S.W.; Everett, D.H.; Haul, R.A.W.; Moscou, L.; Pierotto, R.A.; Rouquerol, J.; Siemieniewska, T. Reporting Physisorption Data for Gas/Solid systems, with special reference to the determination of surface area and porosity, International Union of Pure and Applied Chemistry. Pure Appl. Chem. 1985, 57, 603–619. [Google Scholar] [CrossRef]
- Rouquerol, F.; Rouquerol, J.; Sing, K. Adsorption by Powders and Porous Solids: Principles, Methodology and Applications; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Muñoz-Aguado, M.J.; Gregorkiewitz, M. Preparation of silica-based microporous inorganic gas separation membranes. J. Membr. Sci. 1996, 111, 7–18. [Google Scholar] [CrossRef]
- Wongkoblap, A.; Junpirom, S.; Do, D.D. Adsorption of Lennard-Jones fluids in carbon slit pores of a finite length a computer simulation study. Ads. Sci. Technol. 2005, 23, 1–18. [Google Scholar] [CrossRef]
- Wongkoblap, A.; Do, D.D. The effects of energy sites on adsorption of Lennard–Jones fluids and phase transition in carbon slit pore of finite length: A computer simulation study. J. Colloid Interface Sci. 2006, 297, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Borowko, M. Adsorption Theory, Modeling and Analysis; Toth, J., Ed.; Marcel Dekker Inc.: New York, NY, USA, 2002. [Google Scholar]
- Samios, S.; Stubos, A.K.; Kanellopoulos, N.K.; Cracknell, R.F.; Papadopoulos, G.K.; Nicholson, D. Determination of micropore size distribution from Grand Canonical Monte Carlo simulations and experimental CO2 isotherm data. Langmuir 1997, 13, 2795–2802. [Google Scholar] [CrossRef]












| Site | Collision Diameter σ [Å] | Reduced Well Depth, ε/kb [K] | Point Charge q[e] |
|---|---|---|---|
| C (in CO2) | 2.757 | 28.129 | +0.6512 |
| O (in CO2) | 3.033 | 80.507 | −0.3256 |
| O (in silica) | 2.708 | 185.0 | −0.36 |
| Si (in silica) | +0.18 | ||
| O (in OH) | 3.07 | 78.23 | −0.64 |
| H (in OH) | +0.45 |
| Composition | SiO2 | CaO | TiO2 | Fe2O3 | Others |
|---|---|---|---|---|---|
| wt.% | 99.213 | 0.017 | 0.338 | 0.052 | 0.380 |
| Samples * | Average Pore Size (nm) | BET Surface Area (m2/g) | Micropore Volume (cm3/g) | Mesopore Surface Area (m2/g) | Total Pore Volume (cm3/g) | Mesopore Volume (cm3/g) |
|---|---|---|---|---|---|---|
| SG2-200 | 2.4 | 798 | 0.183 (37.6%) | 719 | 0.487 | 0.304 (62.4%) |
| SG2-500 | 2.2 | 630 | 0.062 (15.9%) | 596 | 0.391 | 0.329 (84.1%) |
| SG3-200 | 5.0 | 778 | 0.062 (7.8%) | 739 | 0.791 | 0.729 (92.2%) |
| SG4-200 | 10.3 | 413 | 0.017 (1.5%) | 399 | 1.105 | 1.088 (98.5%) |
| SG4-500 | 10.9 | 404 | 0.016 (1.6%) | 390 | 1.032 | 1.016 (98.4%) |
| Samples | Geminal and Vicinal Silanols Content (mmol OH/g) | Isolated Silanols Content (mmol OH/g) | Total OH Group Content (mmol/g) |
|---|---|---|---|
| SG2-200 | 4.48 | 3.46 | 7.94 |
| SG2-500 | 3.92 | 0.26 | 4.18 |
| SG3-200 | 4.32 | 1.73 | 6.05 |
| SG4-200 | 3.86 | 0.36 | 4.22 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boonfung, C.; Tangsathitkulchai, C.; Wongkoblap, A. Carbon Dioxide Capture in Homogeneous and Heterogeneous Surfaces of Porous Silica Glass. Processes 2020, 8, 1260. https://doi.org/10.3390/pr8101260
Boonfung C, Tangsathitkulchai C, Wongkoblap A. Carbon Dioxide Capture in Homogeneous and Heterogeneous Surfaces of Porous Silica Glass. Processes. 2020; 8(10):1260. https://doi.org/10.3390/pr8101260
Chicago/Turabian StyleBoonfung, Chontira, Chaiyot Tangsathitkulchai, and Atichat Wongkoblap. 2020. "Carbon Dioxide Capture in Homogeneous and Heterogeneous Surfaces of Porous Silica Glass" Processes 8, no. 10: 1260. https://doi.org/10.3390/pr8101260





