New Aspects on the Modeling of Dithiolactone-Mediated Radical Polymerization of Vinyl Monomers
Abstract
:1. Introduction
2. Experimental
2.1. Polymerization Procedure
2.2. Measurement of Molar Mass Characteristics
3. Modeling
3.1. Polymerization Scheme
3.2. Diffusion-Controlled (DC) Effects
3.3. Parameter Estimation Strategy
4. Results and Discussion
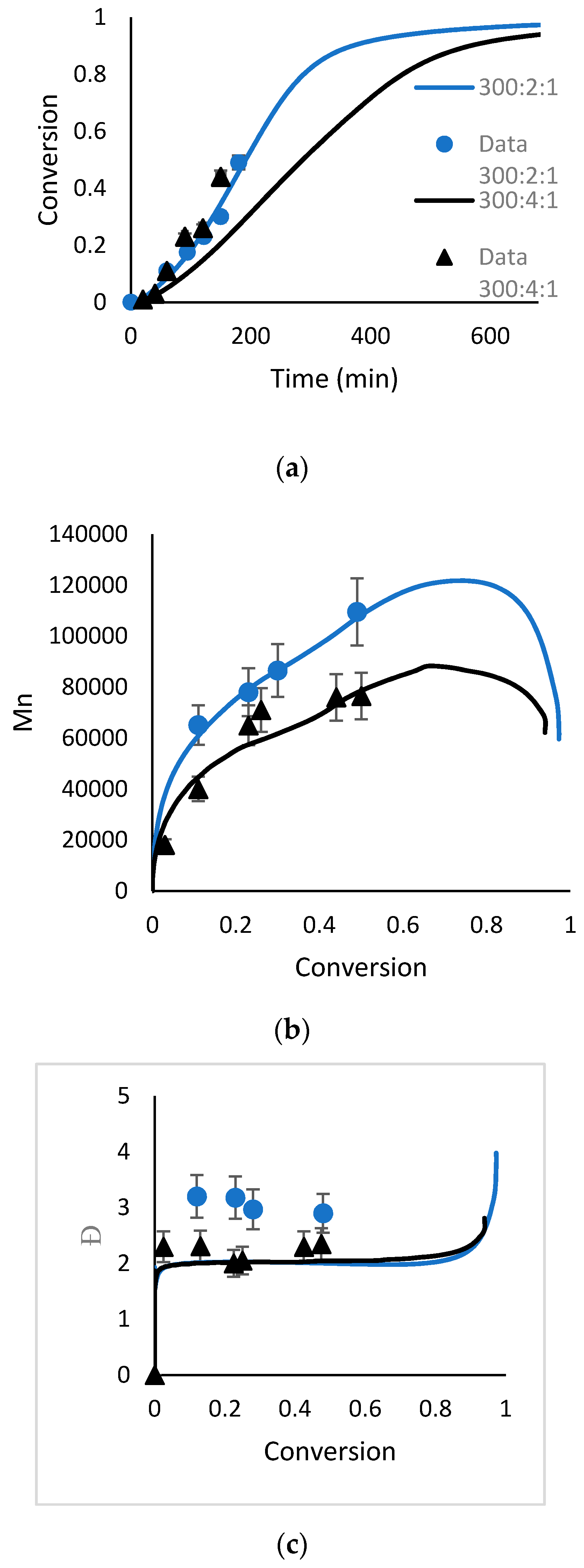
4.1. Polymerization of MMA Using DTL1
4.2. Polymerization of MMA Using DTL2
4.3. Some Thoughts on Future Research Steps
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jenkins, A.D.; Jones, R.G.; Moad, G. Terminology for reversible-deactivation radical polymerization previously called “controlled” radical or “living” radical polymerization (IUPAC Recommendations 2010). Pure Appl. Chem. 2009, 82, 483–491. [Google Scholar] [CrossRef]
- Luo, Y.D.; Chiu, W.Y. Synthesis and kinetic analysis of DPE controlled radical polymerization of MMA. J. Polym. Sci. Polym. Chem. 2009, 47, 6789–6800. [Google Scholar] [CrossRef]
- Vivaldo-Lima, E.; Jaramillo-Soto, G.; Penlidis, A. Nitroxide-Mediated Polymerization (NMP). In Encyclopedia of Polymer Science and Technology, 4th ed.; Mark, H.F., Ed.; John Wiley & Sons: New York, NY, USA, 2016; pp. 1–48. [Google Scholar]
- Kim, K.; Kim, Y.; Ko, N.R.; Choe, S. Effect of molecular weight on the surface morphology of crosslinked polymer particles in the RITP-dispersion polymerization. Polymer 2011, 52, 5439–5444. [Google Scholar] [CrossRef]
- Yamago, S. Development of organotellurium-mediated and organostibine-mediated living radical polymerization reactions. J. Polym. Sci. Part A Polym. Chem. 2016, 44, 1–12. [Google Scholar] [CrossRef]
- Masoumi, S.; Duever, T.A.; Penlidis, A.; Azimi, R.; López-Domínguez, P.; Vivaldo-Lima, E. Model discrimination between RAFT polymerization models using sequential Bayesian methodology. Macromol. Theory Simul. 2018, 27, 1800016. [Google Scholar] [CrossRef]
- Monteiro, M.J.; de Brouwer, H. Intermediate Radical Termination as the Mechanism for Retardation in Reversible Addition-Fragmentation Chain Transfer Polymerization. Macromolecules 2001, 34, 349–352. [Google Scholar] [CrossRef]
- Buback, M.; Vana, P. Mechanism of Dithiobenzoate-Mediated RAFT polymerization: A missing reaction Step. Macromol. Rapid Commun. 2006, 27, 1299. [Google Scholar] [CrossRef]
- Barner-Kowollik, C.; Buback, M.; Charleux, B.; Coote, M.L.; Drache, M.; Fukuda, T.; Goto, A.; Klumperman, B.; Lowe, A.B.; Mcleary, J.B.; et al. Mechanism and Kinetics of Dithiobenzoate-Mediated RAFT Polymerization. I. The Current Situation. J. Polym. Sci. Part A Polym. Chem. 2006, 44, 5809–5831. [Google Scholar] [CrossRef]
- Konkolewicz, D.; Hawkett, B.S.; Gray-Weale, A.; Perrier, S. RAFT Polymerization Kinetics: Combination of Apparently Conflicting Models. Macromolecules 2008, 41, 6400–6412. [Google Scholar] [CrossRef]
- Li, C.; He, J.; Liu, Y.; Zhou, Y.; Yang, Y. Probing the RAFT Process Using a Model Reaction between Alkoxyamine and Dithioester. Aust. J. Chem. 2012, 65, 1077–1089. [Google Scholar] [CrossRef]
- Inuit, T.; Yamanishi, K.; Sato, E.; Matsumoto, A. Organotellurium-Mediated Living Radical Polymerization (TERP) of Acrylates Using Ditelluride Compounds and Binary Azo Initiators for the Synthesis of High-Performance Adhesive Block Copolymers for On-Demand Dismantlable Adhesion. Macromolecules 2013, 46, 8111–8120. [Google Scholar] [CrossRef]
- Soriano-Moro, J.G.; Rico-Valverde, J.C.; Enriquez-Mendrano, F.J.; Maldonado-Textle, H.; Vivaldo-Lima, E.; Acosta-Ortiz, R.; Guerrero-Santos, R. Toward a Living Radical Polymerization of Styrene by Using Dithiolactone as a New Type of Mediating Agent. Macromol. Rapid Commun. 2008, 29, 80–85. [Google Scholar] [CrossRef]
- Soriano-Moro, J.G.; Jaramillo-Soto, G.; Guerrero-Santos, R.; Vivaldo-Lima, E. Kinetics and Molecular Weight Development of Dithiolactone-Mediated Radical Polymerization of Styrene. Macromol. React. Eng. 2009, 3, 178–184. [Google Scholar] [CrossRef]
- Soriano-Moro, J.G. Síntesis y Caracterización de Ditiolactonas y su Empleo Como Agentes de Transferencia en la Polimerización RAFT. Ph.D. Thesis, Programa de Doctorado en Tecnología de Polímeros, CIQA, Saltillo, México, February 2008. [Google Scholar]
- Wulkow, M. Computer Aided Modeling of Polymer Reaction Engineering-The Status of Predici, 1-Simulation. Macromol. React. Eng. 2008, 2, 461–494. [Google Scholar] [CrossRef]
- Hungenberg, K.D.; Wulkow, M. Modeling and Simulation in Polymer Reaction Engineering: A Modular Approach; Wiley-VCH: Weinheim, Germany, 2018; pp. 92, 256. [Google Scholar]
- Beurmann, S.; Buback, M. Rate coefficients of free-radical polymerization deduced from pulsed laser experiments. Prog. Polym. Sci. 2002, 27, 191–254. [Google Scholar] [CrossRef]
- Pallares, J.; Jaramillo-Soto, G.; Flores-Cataño, C.; Vivaldo Lima, E.; Lona, L.M.F.; Penlidis, A. A Comparison of Reaction Mechanisms for Reversible Addition-Fragmentation Chain Transfer Polymerization Using Modeling Tools. J. Macromol. Sci. A Pure Appl. Chem. 2006, 43, 1293. [Google Scholar] [CrossRef]
- Barner-Kowollik, C.; Quinn, J.F.; Nguyen, T.L.U.; Heuts, J.P.A.; Davis, T.P. Kinetic investigations of reversible addition fragmentation chain transfer polymerizations: Cumyl phenyldithioacetate mediated homopolymerizations of styrene and methyl methacrylate. Macromolecules 2001, 34, 7849–7857. [Google Scholar] [CrossRef]
- Jaramillo-Soto, G.; Castellanos-Cardenas, M.L.; García-Moran, P.; Vivaldo-Lima, E.; Luna-Barcenas, G.; Pendilis, A. Simulation of Reversible Addition-Fragmentation Chain Transfer (RAFT) Dispersion Polymerization in Supercritical Carbon Dioxide. Macromol. Theory Simul. 2008, 17, 280–289. [Google Scholar] [CrossRef]
- Jung, W. Mathematical Modeling of Free-Radical Six-Component Bulk and Solution Polymerization. Master’s Thesis, Department of Chemical Engineering, University of Waterloo, Waterloo, ON, Canada, 2008. [Google Scholar]
- Gao, J.; Penlidis, A. A Comprehensive Simulator Database Package for Reviewing Free-Radical Copolymerizations. J. Macromol. Sci. Part C Polym. Rev. 1998, 38, 651–780. [Google Scholar] [CrossRef]
- Vivaldo-Lima, E.; García-Pérez, R.; Celedón-Briones, O.J. Modeling of the Free-Radical Copolymerization Kinetics with Crosslinking of Methyl Methacrylate/Ethylene Glycol Dimethacrylate Up to High Conversions and Considering Thermal Effects. Evista Sociedad Química México 2003, 47, 22–33. [Google Scholar]
- Faldi, A.; Tirrell, M.; Lodge, T.P.; von Meerwall, E. Monomer Diffusion and the Kinetics of Methyl Methacrylate Radical Polymerization at Intermediate to High Conversion. Macromolecules 1994, 27, 4184–4192. [Google Scholar] [CrossRef]
- Gómez-Reguera, J.A.; Vivaldo-Lima, E.; Gabriel, V.A.; Dubé, M.A. Modeling of the Free Radical Copolymerization Kinetics of n-Butyl Acrylate, Methyl Methacrylate and 2-ethylhexyl Acrylate Using PREDICI. Processes 2019, 7, 395. [Google Scholar] [CrossRef]
- Moad, G.; Rizzardo, E.; Thang, S.H. Living Radical Polymerization by the RAFT Process—A Second Update. Aust. J. Chem. 2009, 62, 1402–1472. [Google Scholar] [CrossRef]
- Barner-Kowollik, C.; Quinn, J.F.; Morsley, D.R.; Davis, T.P. Modeling the reversible addition–fragmentation chain transfer process in cumyl dithiobenzoate-mediated styrene homopolymerizations: Assessing rate coefficients for the addition–fragmentation equilibrium. J. Polym. Sci. Part A Polym. Chem. 2001, 39, 1353–1365. [Google Scholar] [CrossRef]
- Wang, A.R.; Zhu, S. Modeling the reversible addition–fragmentation transfer polymerization process. J. Polym. Sci. Part A Polym. Chem. 2003, 41, 1553–1566. [Google Scholar] [CrossRef]












| Reaction | Step Pattern | k (m3 kmol−1 s−1, Unless Otherwise Stated) | DTL1 [Source] | DTL2 [Source] |
|---|---|---|---|---|
| Initiator decomposition | →+ | (s−1) | [21] | [21] |
| First propagation | +→ | 833 [18] | 833 [18] | |
| Propagation | +→ | 685.9 [22,23] | 685.9 [22,23] | |
| First reversible addition | +→ | 2.3 × 103 [this work] | 8.1 [this work] | |
| →+ | 2.622 × 10−2 [this work] | 8.6 × 10−2 [this work] | ||
| Reversible cross-termination | +→ | 5 [14] | [this work] | |
| →+ | 2 [this work] | 2 [this work] | ||
| Irreversible termination | +→+ | 3.40 [22,23] | 3.40 [22,23] | |
| +→ | 9.78 [22,23] | 9.78 [22,23] | ||
| Second reversible addition | +→ | 2 [this work] | 2 [this work] | |
| →+ | 4 [this work] | 4 [this work] |
| Reaction | Mathematical Expression | β Parameters for DC-Expressions [Source] |
|---|---|---|
| Propagation | ] | 0.01 [14] |
| First reversible addition | ] | 0.01 [14] |
| ] | 0.01 [14] | |
| Reversible cross-termination | ] | 0.45 [this work] |
| ] | 0.45 [this work] | |
| Irreversible Termination | ] | 0.45 [14] |
| ] | 0.45 [14] | |
| Second reversible addition | ] | 0.55 [this work] |
| ] | 0.55 [this work] | |
| Fractional Free Volume | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benitez-Carreón, A.J.; Soriano-Moro, J.G.; Vivaldo-Lima, E.; Guerrero-Santos, R.; Penlidis, A. New Aspects on the Modeling of Dithiolactone-Mediated Radical Polymerization of Vinyl Monomers. Processes 2019, 7, 842. https://doi.org/10.3390/pr7110842
Benitez-Carreón AJ, Soriano-Moro JG, Vivaldo-Lima E, Guerrero-Santos R, Penlidis A. New Aspects on the Modeling of Dithiolactone-Mediated Radical Polymerization of Vinyl Monomers. Processes. 2019; 7(11):842. https://doi.org/10.3390/pr7110842
Chicago/Turabian StyleBenitez-Carreón, Anete Joceline, Jesús Guillermo Soriano-Moro, Eduardo Vivaldo-Lima, Ramiro Guerrero-Santos, and Alexander Penlidis. 2019. "New Aspects on the Modeling of Dithiolactone-Mediated Radical Polymerization of Vinyl Monomers" Processes 7, no. 11: 842. https://doi.org/10.3390/pr7110842







