Activation Energy Determination in Case of Independent Complex Kinetic Processes
Abstract
:1. Introduction
2. Theoretical Simulations
2.1. Software
2.2. Complex Process Datasets
2.2.1. First Group of Complex-Process Scenarios
2.2.2. Second Group of Complex-Process Scenarios
3. Results and Discussion
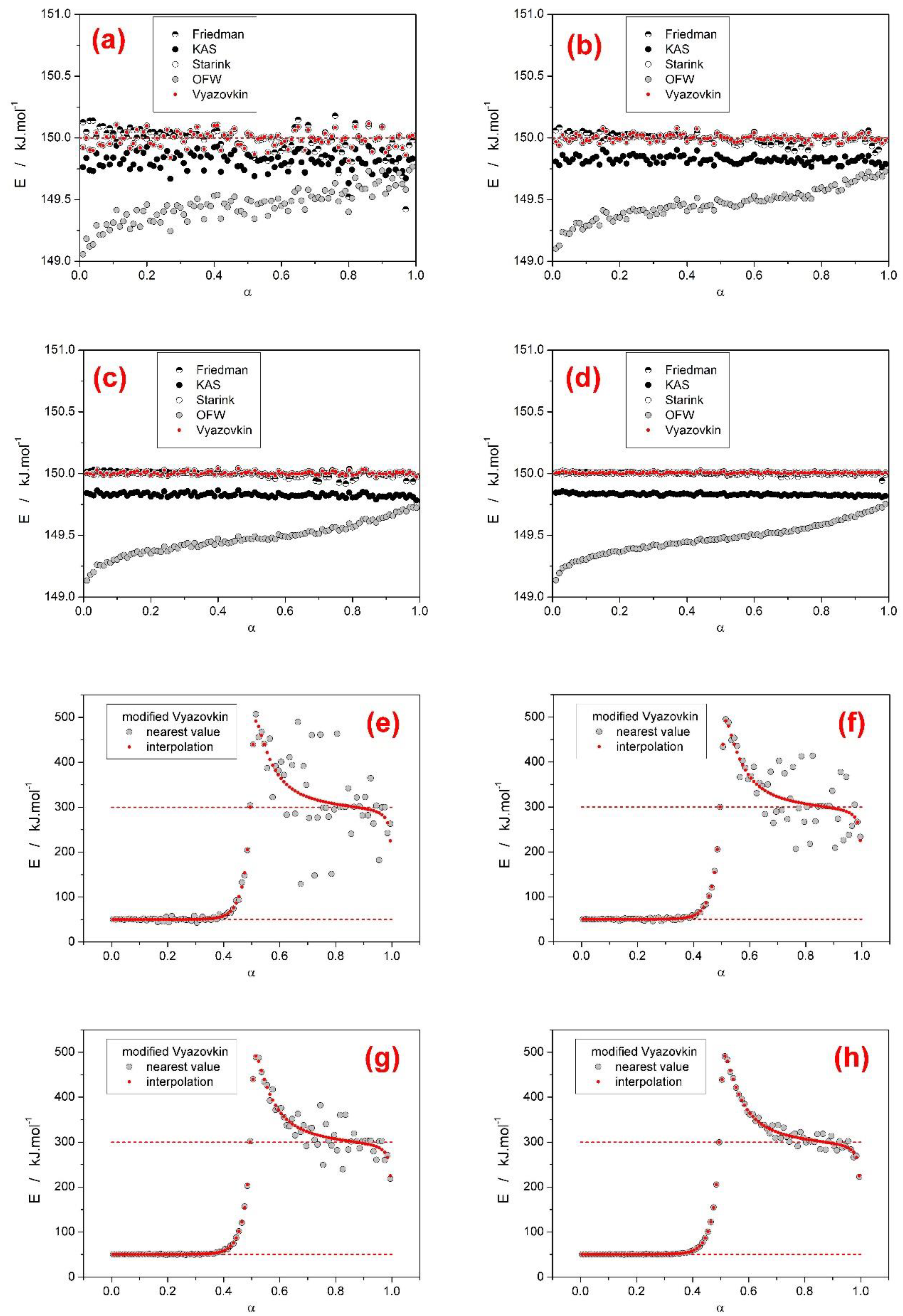
3.1. First Group of Complex-Process Scenarios
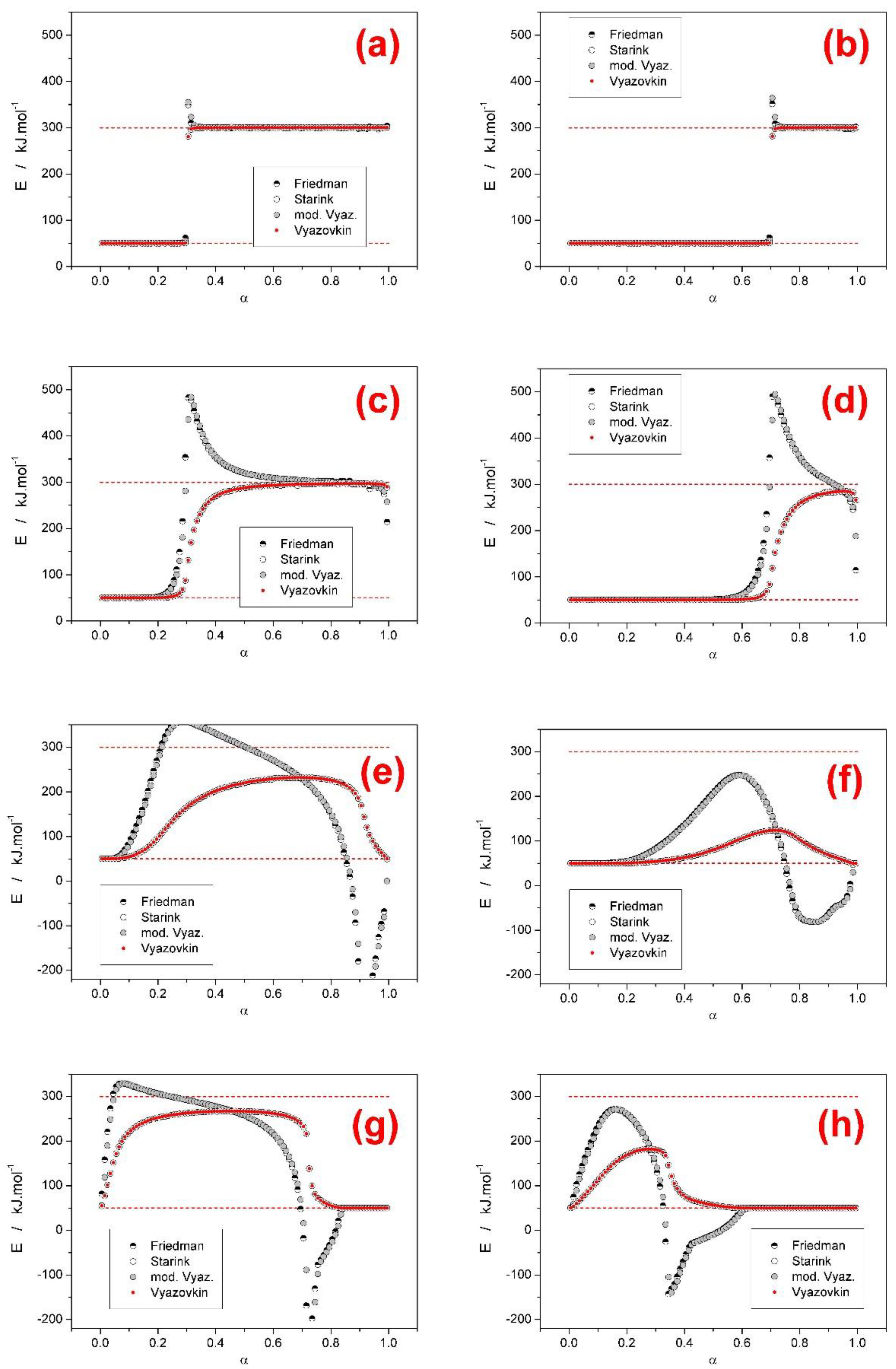
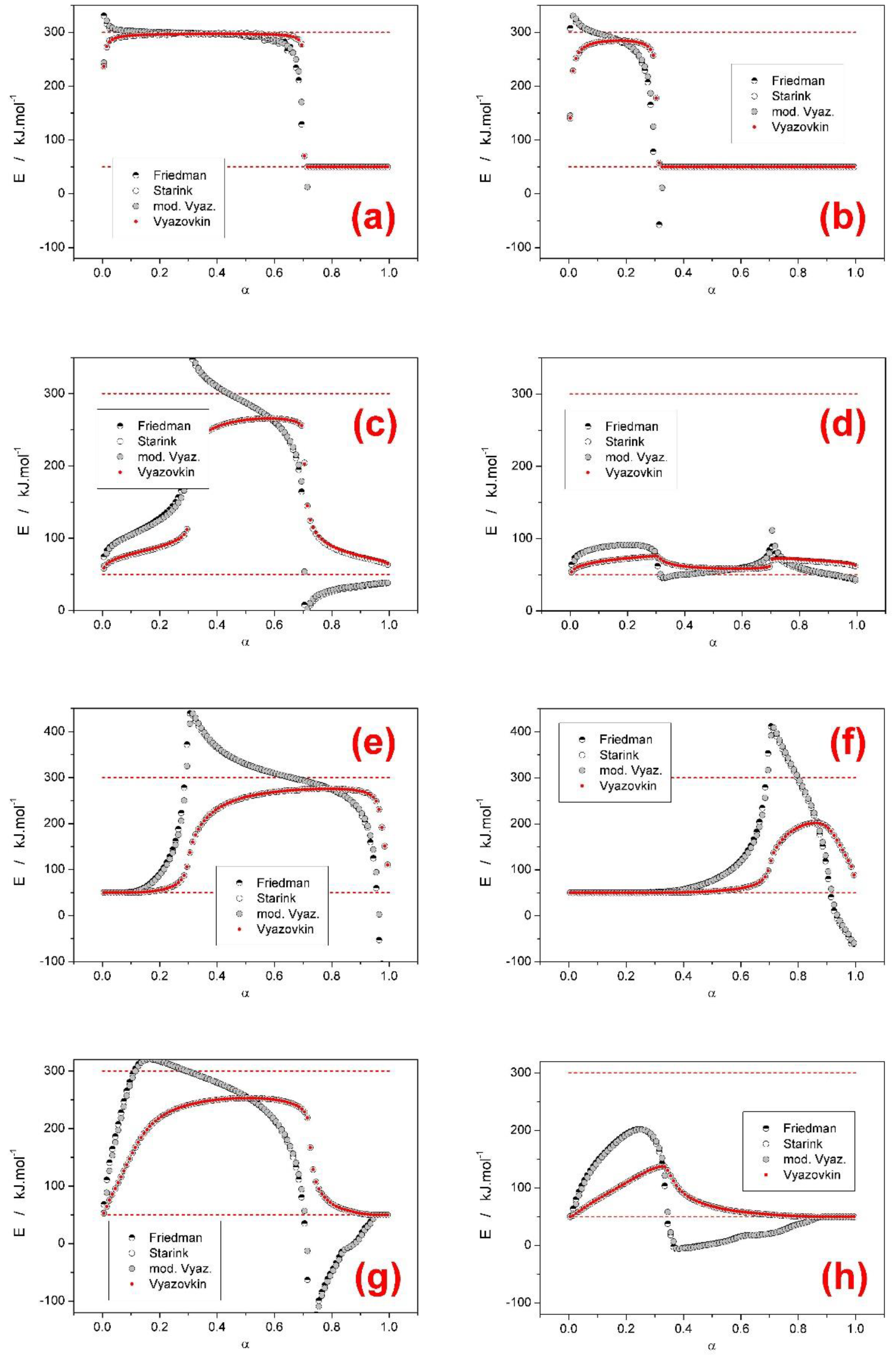
3.2. Second Group of Complex-Process Scenarios
4. Conclusions
- (a)
- Based on theoretical simulations the behavior and performance of the most common isoconversional methods of kinetic analysis were tested in various complex process scenarios. In general situations, when two overlapping sub-processes with different activation energies occurred, most tested methods (KAS, Starink, OFW, and Vyazovkin) performed very similarly and with respect to the E-α outcome (being considered with the general trends or predictive ability in mind) were perfectly interchangeable. On the other hand, the Friedman method and the incremental modified Vyazovkin method provided (as expected) a different course of E-α dependence, which was found to almost always cover the whole E1–E2 range. Similar conclusion was reported also in [28] for overlaps of sub-processes with opposite I values.
- (b)
- Based on the presence and shape of the over- and undershoots manifesting from the integral and differential isoconversional methods, a guide to estimation of the true E1 and E2 values utilizing a combined interpretation of the integral and differential approaches was introduced for the JMA asymmetry and confirmed also for AC model with opposite (positive) asymmetry. The suggested procedure is based on combined interpretation of the positions of the overshoots produced by the differential methods and of the plateaus provided by the integral methods. Development and extensive testing of this methodology is subject of continued research.
- (c)
- In the case of a larger difference between the activation energies of the overlapping sub-processes, the range of applied heating rates was found to drastically influence the course of E-α dependences. The range of applied heating rates should be always optimized with respect to the applied methodology. The Tp-based methods (e.g., Kissinger) generally favor the widest possible ranges of q+. The full-scale non-linear optimization methods (e.g., MKA) usually need to adopt the single-curve-fit approach with fixed E values (see, e.g., [39]) due to the complex kinetics being often T/q+-dependent [40]. On the other hand, the sensitivity of isoconversional methods to the applied q+ range and their consequent performance towards the estimation of the true values of activation energies corresponding to the involved sub-processes depend on two factors: consistence of the shape of the complex kinetic curve (the breakpoint being the complete switch of the positions of the involved kinetic sub-peaks within the range of applied q+) and the weighted (over both n and I) presence of the full overlaps of the involved sub-processes.
- (d)
- With regard to the methods accuracies (tested on datasets D–G from the first group of scenarios, where both sub-processes had the same activation energy), the Friedman, Starink, and Vyazovkin methods provided correct and accurate values of E, the KAS method was off by approximately 0.15%, and the OFW method provided data with error up to 0.8% (contrary to all other methods, the OFW method provided a non-constant E-α dependence). These conclusions confirm the similarity between the single process scenario and complex process situation where all the sub-processes have the same apparent activation energy. Moreover, the two main evaluation algorithms for determining tα/Tα/Φα values (nearest value versus interpolation approach) were compared—most tested methods are insensitive to the way of evaluation. The only exception was the modified incremental Vyazovkin method, which exhibited large scatter in the E-α results, if the latter, less accurate approach (assignment of the nearest tα/Tα/Φα values) was used.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Šesták, J. Thermophysical Properties of Solids, Their Measurements and Theoretical Analysis; Elsevier: Amsterdam, The Netherlands, 1984. [Google Scholar]
- Šesták, J. Science of Heat and Thermophysical Studies: A Generalized Approach to Thermal Analysis; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Kissinger, H.E. Reaction kinetics in differential thermal analysis. Anal. Chem. 1957, 29, 1702–1706. [Google Scholar] [CrossRef]
- Ozawa, T. A new method of analyzing thermogravimetric data. Bull. Chem. Soc. Jpn. 1965, 38, 1881. [Google Scholar] [CrossRef]
- Takhor, R.L.; Hench, L.L.; Freiman, S.W. (Eds.) Advances in Nucleation and Crystallization of Glasses; American Ceramic Society: Columbus, OH, USA, 1971; pp. 166–172. [Google Scholar]
- Mahadevan, S.; Giridhar, A.; Singh, A.K. Calorimetric measurements on as–sb–se glasses. J. Non-Cryst. Solids 1986, 88, 11–34. [Google Scholar] [CrossRef]
- Friedman, H.L. Kinetics of thermal degradation of char-forming plastics from thermogravimetry. Application to a phenolic plastic. J. Polym. Sci. Part C 1964, 6, 183–195. [Google Scholar] [CrossRef]
- Akahira, T.; Sunose, T. Method of determining activation deterioration constant of electrical insulating materials. Res. Rep. Chiba Inst. Technol. (Sci. Technol.) 1971, 16, 22–31. [Google Scholar]
- Starink, M.J. The determination of activation energy from linear heating rate experiments: A comparison of the accuracy of isoconversion methods. Thermochim. Acta 2003, 404, 163–176. [Google Scholar] [CrossRef]
- Flynn, J.H.; Wall, L.A. General treatment of the thermogravimetry of polymers. J. Res. Nat. Bur. Stand. 1966, 70, 487–523. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Dollimore, D. Linear and nonlinear procedures in isoconversionalcomputations of the activation energy of thermally induced reactions in solids. J. Chem. Inf. Comp. Sci. 1996, 36, 42–45. [Google Scholar] [CrossRef]
- Vyazovkin, S. Evaluation of the activation energy of thermally stimulated solidstate reactions under an arbitrary variation of the temperature. J. Comput. Chem. 1997, 18, 393–402. [Google Scholar] [CrossRef]
- Vyazovkin, S. Advanced isoconversional method. J. Therm. Anal. Calorim. 1997, 49, 1493–1499. [Google Scholar] [CrossRef]
- Malek, J. The kinetic-analysis of nonisothermal data. Thermochim. Acta 1992, 200, 257–269. [Google Scholar] [CrossRef]
- Vyazovkin, S. A unified approach to kinetic processing of nonisothermal data. Int. J. Chem. Kinet. 1996, 28, 95–101. [Google Scholar] [CrossRef]
- Perez-Maqueda, L.A.; Criado, J.M.; Sanchez-Jimenez, P.E. Combined kinetic analysis of solid-state reactions: A powerful tool for the simultaneous determination of kinetic parameters and the kinetic model without previous assumptions on the reaction mechanism. J. Phys. Chem. A 2006, 110, 12456–12462. [Google Scholar] [CrossRef] [PubMed]
- Kitabayashi, S.; Koga, N. Thermal Decomposition of Tin(II) Oxyhydroxide and Subsequent Oxidation in Air: Kinetic Deconvolution of Overlapping Heterogeneous Processes. J. Phys. Chem. C 2015, 119, 16188–16199. [Google Scholar] [CrossRef] [Green Version]
- Opfermann, J. Kinetic analysis using multivariate non-linear regression. I. basic concepts. J. Therm. Anal. Calorim. 2000, 60, 641–658. [Google Scholar] [CrossRef]
- Sbirrazuoli, N.; Girault, Y.; Elegant, L. Simulations for evaluation of kinetic methods in differential scanning calorimetry. Part 3. Thermochim. Acta 1997, 293, 25–37. [Google Scholar] [CrossRef]
- Cai, J.; Wu, W.; Liu, R. Isoconversional Kinetic Analysis of Complex Solid-State Processes: Parallel and Successive Reactions. Ind. Eng. Chem. Res. 2012, 51, 16157–16161. [Google Scholar] [CrossRef]
- Vyazovkin, S.V.; Goryachko, V.I.; Lesnikovich, A.I. An approach to the solution of the inverse kinetic problem in the case of complex processes. Part III. Parallel independent reactions. Thermochim. Acta 1992, 197, 41–51. [Google Scholar] [CrossRef]
- Criado, J.M.; Gonzalez, M.; Ortega, A.; Real, C. Discrimination of the kinetic model of overlapping solid-state reactions from non-isothermal data. J. Therm. Anal. 1988, 34, 1387. [Google Scholar] [CrossRef]
- Vaganova, N.I.; Rozenband, V.I.; Barzykin, V.V. Thermoanalytical studies of the kinetic of reversible reactions. J. Therm. Anal. 1988, 34, 949–962. [Google Scholar] [CrossRef]
- Vyazovkin, S.V.; Lesnikovich, A.I. An approach to the solution of the inverse kinetic problem in the case of complex processes 1. Thermochim. Acta 1990, 165, 273–280. [Google Scholar] [CrossRef]
- Criado, J.M.; Sanchez-Jimenez, P.E.; Perez-Maqueda, L.A. Critical study of the isoconversional methods of kinetic analysis. J. Therm. Anal. Calorim. 2008, 92, 199–203. [Google Scholar] [CrossRef] [Green Version]
- Cai, J.M.; Chen, S.Y. A new iterative linear integral isoconversional method for the determination of the activation energy varying with the conversion degree. J. Comput. Chem. 2009, 30, 1986–1991. [Google Scholar] [CrossRef]
- Perejon, A.; Sanchez-Jimenez, P.E.; Criado, J.M.; Perez-Maqueda, L.A. Kinetic analysis of complex solid-state reactions. A new deconvolution procedure. J. Phys. Chem. B 2011, 115, 1780–1791. [Google Scholar] [CrossRef]
- Muravyev, N.V.; Pivkina, A.N.; Koga, N. Critical appraisal of kinetic calculation methods applied to overlapping multistep reactions. Molecules 2019, 24, 2298. [Google Scholar] [CrossRef]
- Johnson, W.A.; Mehl, K.F. Reaction kinetics in processes of nucleation and growth. Trans. Metall. Soc. AIME 1939, 135, 416–442. [Google Scholar]
- Avrami, M. Kinetics of phase change I—General theory. J. Chem. Phys. 1939, 7, 1103–1112. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of phase change. II—Transformation-time relations for random distribution of nuclei. J. Chem. Phys. 1940, 7, 212–224. [Google Scholar] [CrossRef]
- Avrami, M. Granulation, phase change, and microstructure—Kinetics of phase change III. J. Chem. Phys. 1941, 7, 177–184. [Google Scholar] [CrossRef]
- Vyazovkin, S. Modification of the integral isoconversional method to account for variation in the activation energy. J. Comput. Chem. 2001, 22, 178–183. [Google Scholar] [CrossRef]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Veterling, W.T. Numerical Recipes in Pascal; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Brent, R.P. Algorithms for Minimization without Derivatives; Prentice Hall: Englewood Cliffs, NJ, USA, 1973. [Google Scholar]
- Budrugeac, P.; Homentcovschi, D.; Segal, E. Critical considerations on the isoconversional methods III. J. Therm. Anal. Calorim. 2001, 66, 557–565. [Google Scholar] [CrossRef]
- Šimon, P.; Thomas, P.; Dubaj, T.; Cibulková, Z.; Peller, A.; Veverka, M. The mathematical incorrectness of the integral isoconversional methods in case of variable activation energy and the consequences. J. Therm. Anal. Calorim. 2014, 115, 853–859. [Google Scholar] [CrossRef]
- Golikeri, S.V.; Luss, D. Analysis of activation energy of grouped parallel reactions. AIChE J. 1972, 18, 277–282. [Google Scholar] [CrossRef]
- Brandová, D.; Svoboda, R.; Olmrová Zmrhalová, Z.; Chovanec, J.; Bulánek, R.; Romanová, J. Crystallization kinetics of glassy materials—the ultimate complexity? J. Therm. Anal. Calorim. 2018, 134, 825–834. [Google Scholar] [CrossRef]
- Svoboda, R.; Brandová, D. Crystal growth from mechanically induced defects: A phenomenon observed for glassy materials. J. Therm. Anal. Calorim. 2017, 127, 799–808. [Google Scholar] [CrossRef]
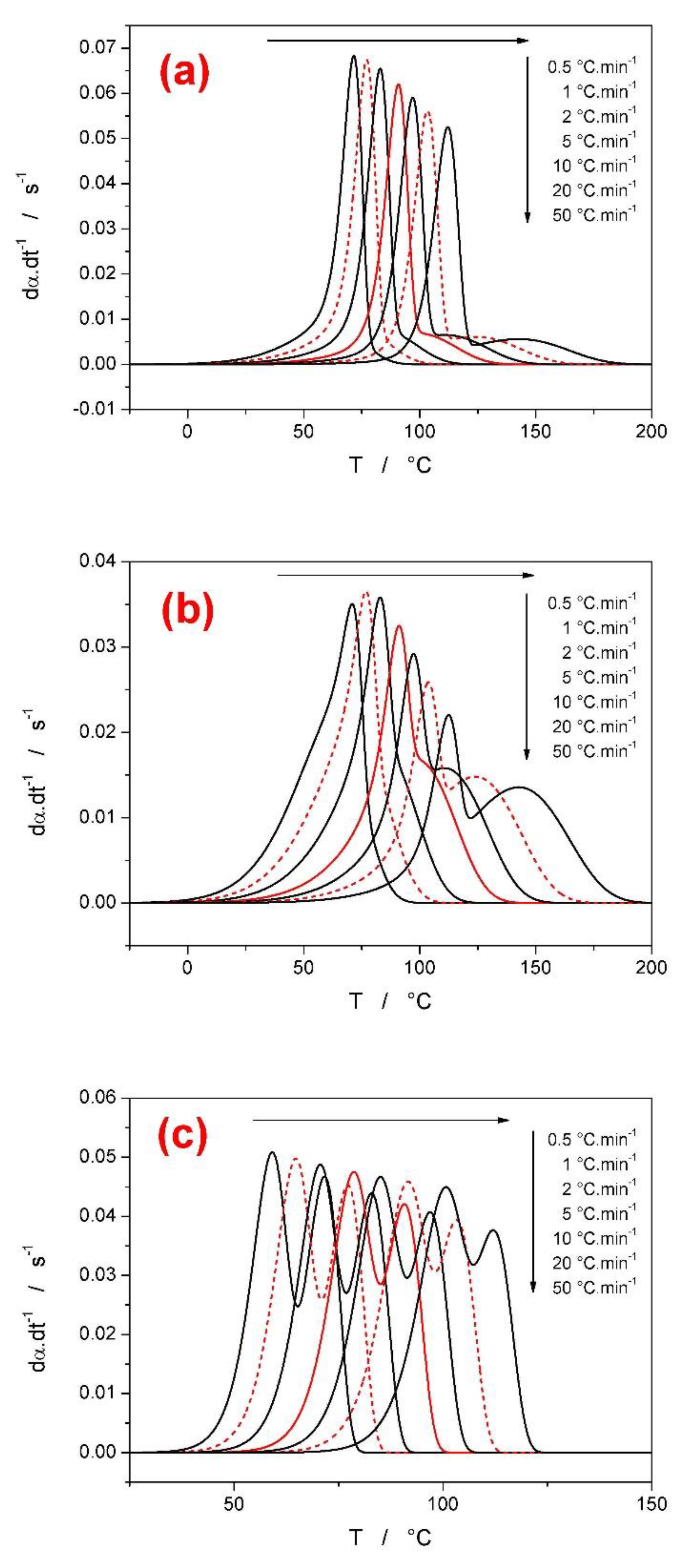
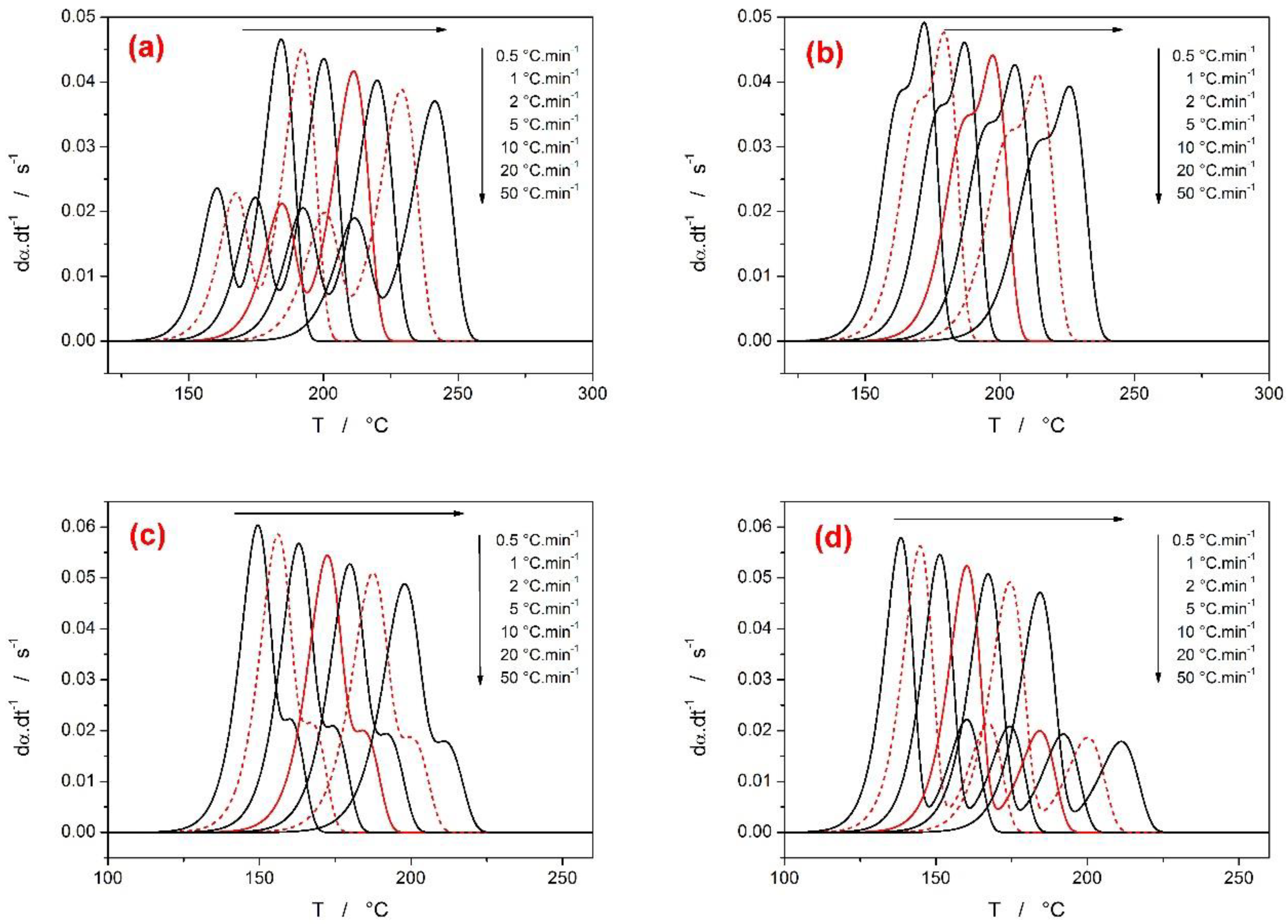
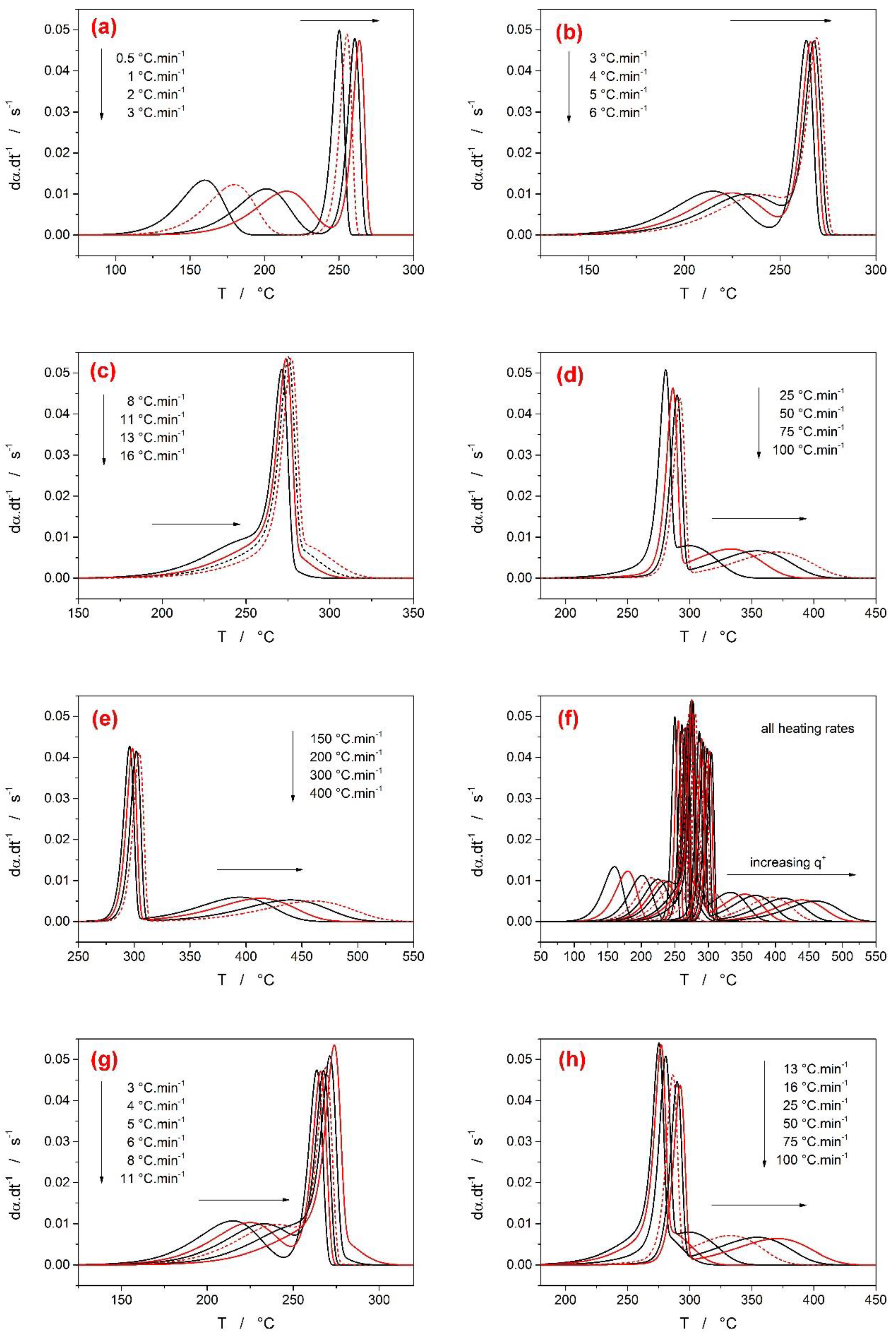
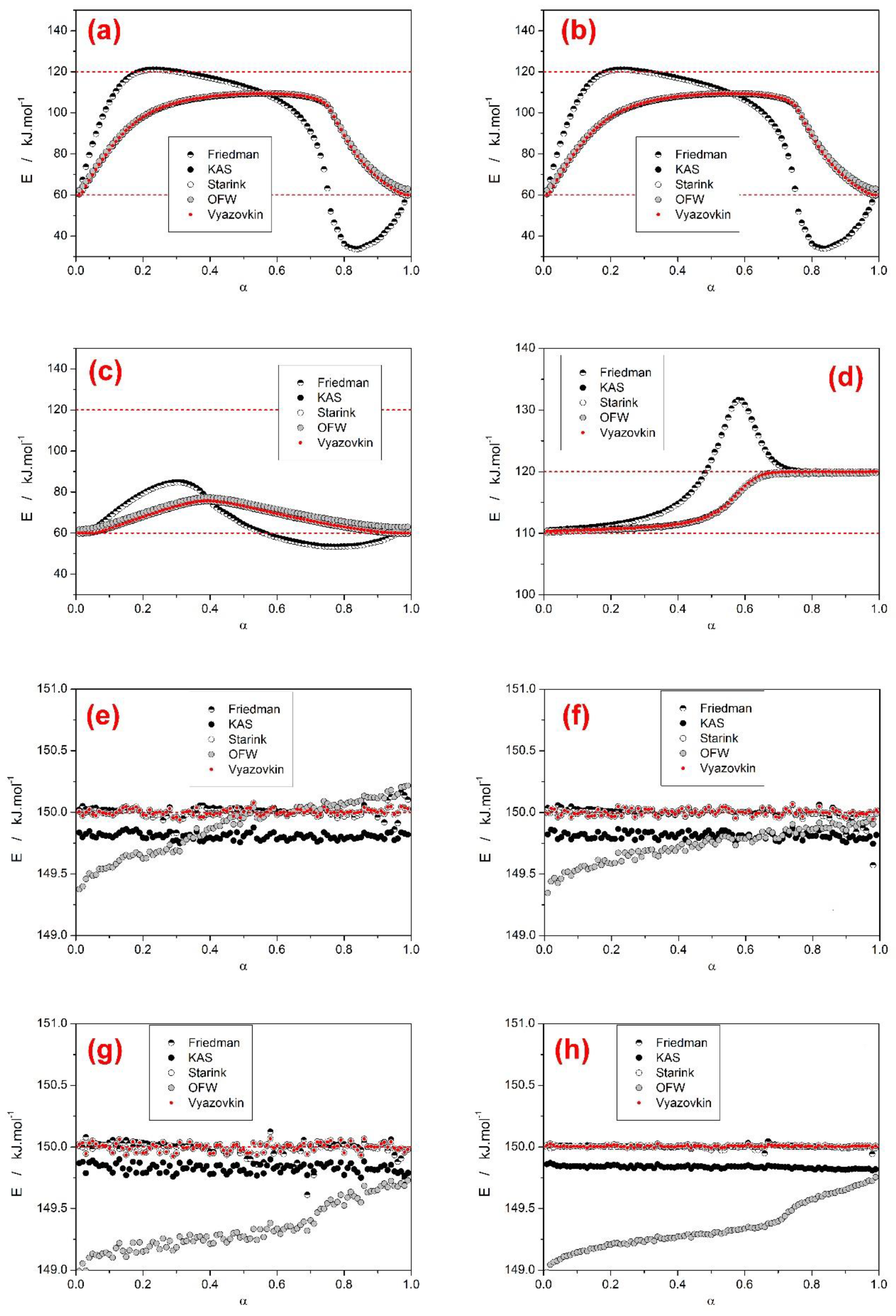

| Set | E1 | A1 | m1 | I1 | E2 | A2 | m2 | I2 |
|---|---|---|---|---|---|---|---|---|
| kJ·mol−1 | s−1 | - | - | kJ·mol−1 | s−1 | - | - | |
| A | 120 | 1015.2 | 2 | 0.66 | 60 | 106.08 | 1 | 0.33 |
| B | 120 | 1015.2 | 2 | 0.20 | 60 | 106.08 | 1 | 0.80 |
| C | 120 | 1015.2 | 2 | 0.50 | 110 | 1014.33 | 2 | 0.50 |
| D | 150 | 1015 | 2 | 0.30 | 150 | 1014 | 2 | 0.70 |
| E | 150 | 1015 | 2 | 0.30 | 150 | 1014.5 | 2 | 0.70 |
| F | 150 | 1015 | 2 | 0.30 | 150 | 1015.5 | 2 | 0.70 |
| G | 150 | 1015 | 2 | 0.30 | 150 | 1016 | 2 | 0.70 |
| Set | Included Heating Rates (in °C·min−1) |
|---|---|
| A | 0.5, 1, 2, 3 |
| B | 3, 4, 5, 6 |
| C | 8, 11, 13, 16 |
| D | 25, 50, 75, 100 |
| E | 150, 200, 300, 400 |
| F | 0.5, 1, 2, 3, 4, 5, 6, 8, 11, 13, 16, 25, 50, 75, 100, 150, 200, 300, 400 |
| G | 3, 4, 5, 6, 8, 11 |
| H | 13, 16, 25, 50, 75, 100 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luciano, G.; Svoboda, R. Activation Energy Determination in Case of Independent Complex Kinetic Processes. Processes 2019, 7, 738. https://doi.org/10.3390/pr7100738
Luciano G, Svoboda R. Activation Energy Determination in Case of Independent Complex Kinetic Processes. Processes. 2019; 7(10):738. https://doi.org/10.3390/pr7100738
Chicago/Turabian StyleLuciano, Giorgio, and Roman Svoboda. 2019. "Activation Energy Determination in Case of Independent Complex Kinetic Processes" Processes 7, no. 10: 738. https://doi.org/10.3390/pr7100738





