Structural Properties of Dynamic Systems Biology Models: Identifiability, Reachability, and Initial Conditions
Abstract
:1. Introduction
2. Background: Nonlinear Observability, Reachability, and Identifiability
2.1. Notation and Differential Geometry Concepts
- is a linearly independent set for each .
- , [17].
2.2. Observability
2.2.1. Linear Observability
2.2.2. Nonlinear Observability
2.3. Controllability and Reachability
2.3.1. Linear Controllability and Reachability
2.3.2. Nonlinear Controllability and Reachability
2.4. Structural Identifiability as Observability
3. Results
3.1. Reachability Is Neither Necessary Nor Sufficient for Identifiability
3.2. The Results of Identifiability Tests Can Be Misleading for Certain State Vectors
3.3. Knowledge of Additional Initial Conditions Can Increase Identifiability
3.4. Guaranteeing the Results of the Structural Identifiability Test
- Check the Observability-Identifiability condition (OIC, Theorem 4) for a generic symbolic augmented vector . If the matrix is not full rank, i.e., , then the model is structurally unidentifiable and no further tests are needed. If, however, it is full rank, i.e., , the model is generically structurally identifiable. However, in this case there may be loss of identifiability for certain states; to assess this we proceed to the next step.
- Check the Observability-Identifiability condition (OIC, Theorem 4) for a particular vector of initial conditions of interest, . If , there has been a loss of rank which indicates loss of local identifiability (as in Example 4), but that may be possible to overcome (as in Example 5). To assess this point, we go to step 3.
- Simulate the model starting from to see if there are any states that remain zero.
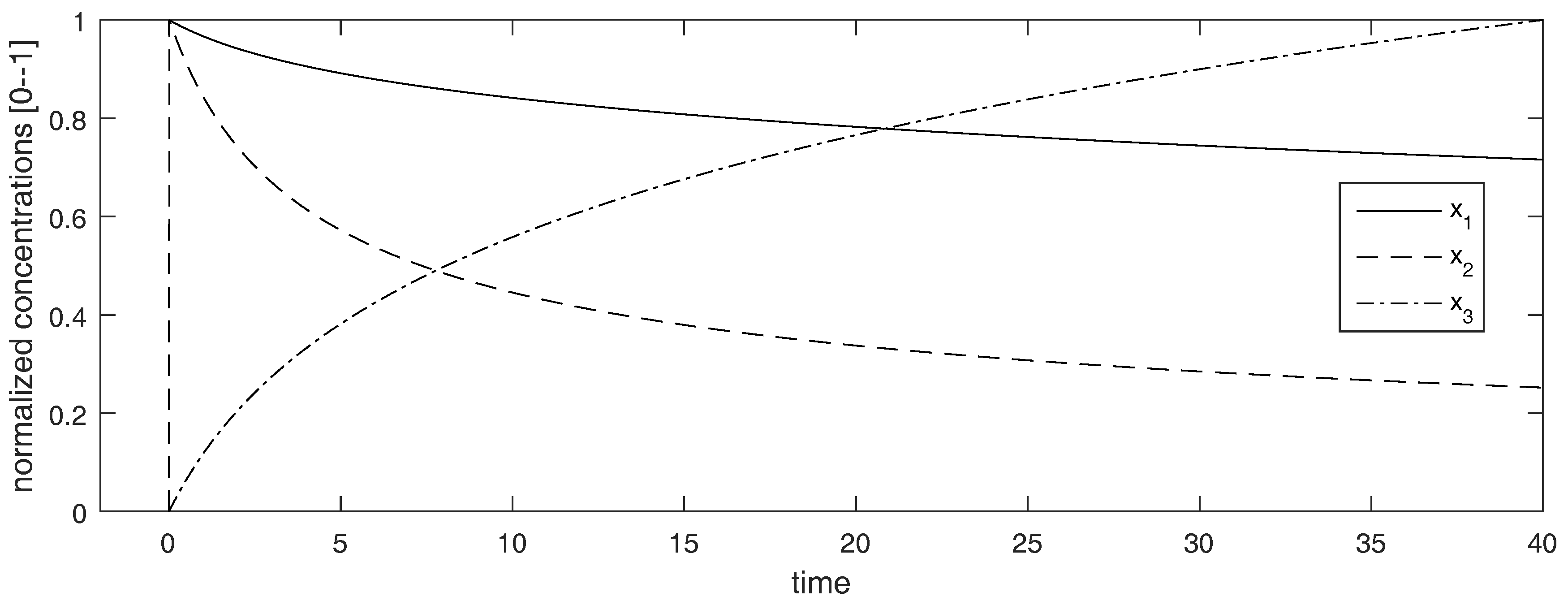
3.5. Finding Specific Initial Conditions That Lead to Loss of Rank in the OIC
3.5.1. Finding Solutions Analytically
3.5.2. Finding Solutions via Optimization
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| ORC | Observability Rank Condition |
| CRC | Controllability Rank Condition |
| OIC | Observability-Identifiability Condition |
| ODE | Ordinary Differential Equation |
| EAR | Exact Arithmetic Rank |
| SI | Structural Identifiability |
References
- Walter, E.; Pronzato, L. Identification of Parametric Models From Experimental Data; Communications and Control Engineering Series; Springer: London, UK, 1997. [Google Scholar]
- DiStefano, J., III. Dynamic Systems Biology Modeling and Simulation; Academic Press: New York, NY, USA, 2015. [Google Scholar]
- Villaverde, A.F.; Barreiro, A. Identifiability of large nonlinear biochemical networks. MATCH Commun. Math. Comput. Chem. 2016, 76, 259–276. [Google Scholar]
- Bellman, R.; Åström, K.J. On structural identifiability. Math. Biosci. 1970, 7, 329–339. [Google Scholar] [CrossRef]
- Chiş, O.T.; Banga, J.R.; Balsa-Canto, E. Structural identifiability of systems biology models: A critical comparison of methods. PLoS ONE 2011, 6, e27755. [Google Scholar] [CrossRef] [PubMed]
- Miao, H.; Xia, X.; Perelson, A.S.; Wu, H. On identifiability of nonlinear ODE models and applications in viral dynamics. SIAM Rev. 2011, 53, 3–39. [Google Scholar] [CrossRef] [PubMed]
- Kalman, R.E. Contributions to the theory of optimal control. Bol. Soc. Mat. Mexicana 1960, 5, 102–119. [Google Scholar]
- Hermann, R.; Krener, A.J. Nonlinear controllability and observability. IEEE Trans. Autom. Control 1977, 22, 728–740. [Google Scholar] [CrossRef]
- Tunali, E.T.; Tarn, T.J. New results for identifiability of nonlinear systems. IEEE Trans. Autom. Control 1987, 32, 146–154. [Google Scholar] [CrossRef]
- Karlsson, J.; Anguelova, M.; Jirstrand, M. An Efficient Method for Structural Identiability Analysis of Large Dynamic Systems. In Proceedings of the 16th IFAC Symposium on System Identification, Brussels, Belgium, 11–13 July 2012; Volume 16, pp. 941–946. [Google Scholar]
- August, E.; Papachristodoulou, A. A new computational tool for establishing model parameter identifiability. J. Comput. Biol. 2009, 16, 875–885. [Google Scholar] [CrossRef] [PubMed]
- Chatzis, M.N.; Chatzi, E.N.; Smyth, A.W. On the observability and identifiability of nonlinear structural and mechanical systems. Struct. Control Health Monit. 2015, 22, 574–593. [Google Scholar] [CrossRef]
- Villaverde, A.F.; Barreiro, A.; Papachristodoulou, A. Structural Identifiability of Dynamic Systems Biology Models. PLOS Comput. Biol. 2016, 12, e1005153. [Google Scholar] [CrossRef] [PubMed]
- Denis-Vidal, L.; Joly-Blanchard, G.; Noiret, C. Some effective approaches to check the identifiability of uncontrolled nonlinear systems. Math. Comput. Simul 2001, 57, 35–44. [Google Scholar] [CrossRef]
- Saccomani, M.P.; Audoly, S.; D’Angiò, L. Parameter identifiability of nonlinear systems: The role of initial conditions. Automatica 2003, 39, 619–632. [Google Scholar] [CrossRef]
- Xia, X.; Moog, C.H. Identifiability of nonlinear systems with application to HIV/AIDS models. IEEE Trans. Autom. Control 2003, 48, 330–336. [Google Scholar] [CrossRef]
- Vidyasagar, M. Nonlinear Systems Analysis; Prentice Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Sontag, E.D. Mathematical Control Theory: Deterministic Finite Dimensional Systems; Springer Science & Business Media: Berlin, Germany, 2013; Volume 6. [Google Scholar]
- Sedoglavic, A. A probabilistic algorithm to test local algebraic observability in polynomial time. J. Symb. Comput. 2002, 33, 735–755. [Google Scholar] [CrossRef]
- DiStefano, J., III. On the relationships between structural identifiability and the controllability, observability properties. IEEE Trans. Autom. Control 1977, 22, 652. [Google Scholar] [CrossRef]
- Cobelli, C.; Lepschy, A.; Romanin-Jacur, G. Comments on “On the relationships between structural identifiability and the controllability, observability properties”. IEEE Trans. Autom. Control 1978, 23, 965–966. [Google Scholar] [CrossRef]
- Jacquez, J. Further comments on “On the relationships between structural identifiability and the controllability, observability properties”. IEEE Trans. Autom. Control 1978, 23, 966–967. [Google Scholar] [CrossRef]
- Balsa-Canto, E. Tutorial on Advanced Model Identification using Global Optimization. In Proceedings of the ICSB 2010 International Conference on Systems Biology, Edinburgh, UK, 11–14 October 2010. [Google Scholar]
- Robertson, H. The solution of a set of reaction rate equations. In Numerical Analysis: An Introduction; Academic Press: London, UK, 1966; pp. 178–182. [Google Scholar]
- Eydgahi, H.; Chen, W.W.; Muhlich, J.L.; Vitkup, D.; Tsitsiklis, J.N.; Sorger, P.K. Properties of cell death models calibrated and compared using Bayesian approaches. Mol. Syst. Biol. 2013, 9, 644. [Google Scholar] [CrossRef] [PubMed]
- Mannakee, B.K.; Ragsdale, A.P.; Transtrum, M.K.; Gutenkunst, R.N. Sloppiness and the geometry of parameter space. In Uncertainty in Biology; Springer: Cham, Switzerland, 2016; pp. 271–299. [Google Scholar]
- Chappell, M.J.; Godfrey, K.R. Structural identifiability of the parameters of a nonlinear batch reactor model. Math. Biosci. 1992, 108, 241–251. [Google Scholar] [CrossRef]
- D’Angiò, L.; Saccomani, M.P.; Audoly, S.; Bellu, G. Identifiability of Nonaccessible Nonlinear Systems. In Positive Systems; Bru, R., Romero-Vivó, Eds.; Springer: Basel, Switzerland, 2009; Volume 389, LNCIS; pp. 269–277. [Google Scholar]
- Bellu, G.; Saccomani, M.P.; Audoly, S.; D’Angio, L. DAISY: A new software tool to test global identifiability of biological and physiological systems. Comput. Methods Programs Biomed. 2007, 88, 52–61. [Google Scholar]
- Egea, J.A.; Henriques, D.; Cokelaer, T.; Villaverde, A.F.; MacNamara, A.; Danciu, D.P.; Banga, J.R.; Saez-Rodriguez, J. MEIGO: An open-source software suite based on metaheuristics for global optimization in systems biology and bioinformatics. BMC Bioinf. 2014, 15, 136. [Google Scholar] [CrossRef] [PubMed]
- Balsa-Canto, E.; Alonso, A.; Banga, J.R. An iterative identification procedure for dynamic modeling of biochemical networks. BMC Syst. Biol. 2010, 4, 11. [Google Scholar] [CrossRef] [PubMed]
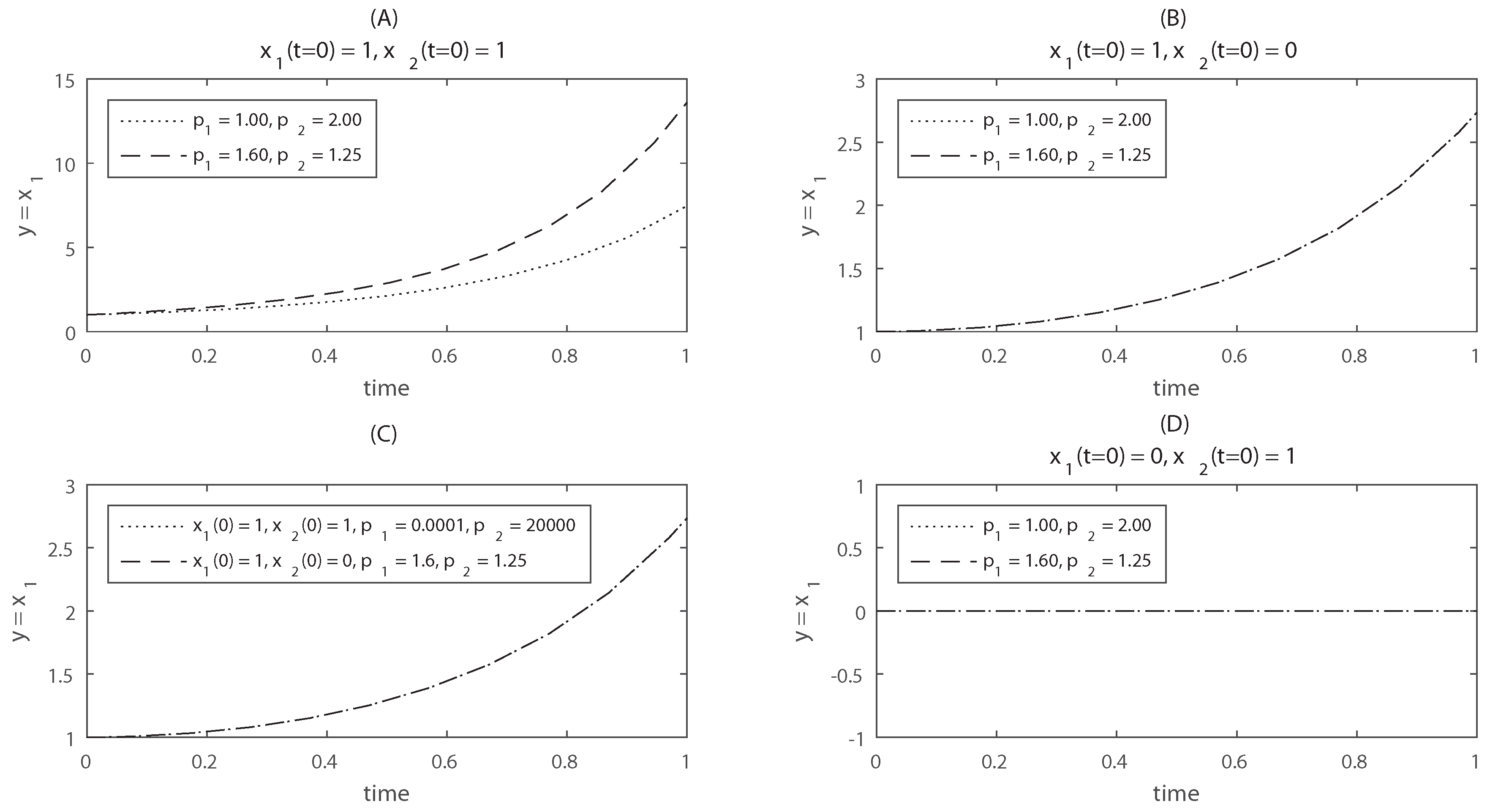
| Example | Ref. | (Generic) | (Generic) | Decrease | Loss | Loss of |
|---|---|---|---|---|---|---|
| SI | Reachability | in rank() | of SI | Reachability | ||
| 1 | This paper | YES | NO | NO | NO | N/A |
| 2 | This paper | NO | YES | N/A | N/A | NO |
| 3 | [23] | NO | YES | N/A | N/A | YES |
| 4 | [11] | YES | NO | YES | YES | N/A |
| 5 | [24] | YES | NO | YES | NO | N/A |
| 6.A | [14] | NO | NO | N/A | N/A | N/A |
| 6.B | [14] | YES | NO | YES | NO | N/A |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Villaverde, A.F.; Banga, J.R. Structural Properties of Dynamic Systems Biology Models: Identifiability, Reachability, and Initial Conditions. Processes 2017, 5, 29. https://doi.org/10.3390/pr5020029
Villaverde AF, Banga JR. Structural Properties of Dynamic Systems Biology Models: Identifiability, Reachability, and Initial Conditions. Processes. 2017; 5(2):29. https://doi.org/10.3390/pr5020029
Chicago/Turabian StyleVillaverde, Alejandro F, and Julio R Banga. 2017. "Structural Properties of Dynamic Systems Biology Models: Identifiability, Reachability, and Initial Conditions" Processes 5, no. 2: 29. https://doi.org/10.3390/pr5020029
APA StyleVillaverde, A. F., & Banga, J. R. (2017). Structural Properties of Dynamic Systems Biology Models: Identifiability, Reachability, and Initial Conditions. Processes, 5(2), 29. https://doi.org/10.3390/pr5020029






