All computational experiments are performed on a DELL OPTIPLEX 790 desktop with an Intel(R) Core(TM) i5-2400 CPU @3.10GHz processor and 8 GB RAM. All of the models and solution procedures are coded in GAMS 24.2.1 (GAMS Development Corporation, Washington, DC, USA) [
44]. The MILP problems within the proposed algorithm are solved with CPLEX 12.6 (IBM, Armonk, NY, USA), and the NLP subproblems are solved using CONOPT 3 (ARKI Consulting & Development A/S, Bagsvaerd, Denmark). The original MINLFP formulation is solved with BARON 14.4.0 (The Optimization Firm, Urbana-Champaign, IL, USA) [
45] with an optimality gap of 10
−2.
3.1. Description of Case Study
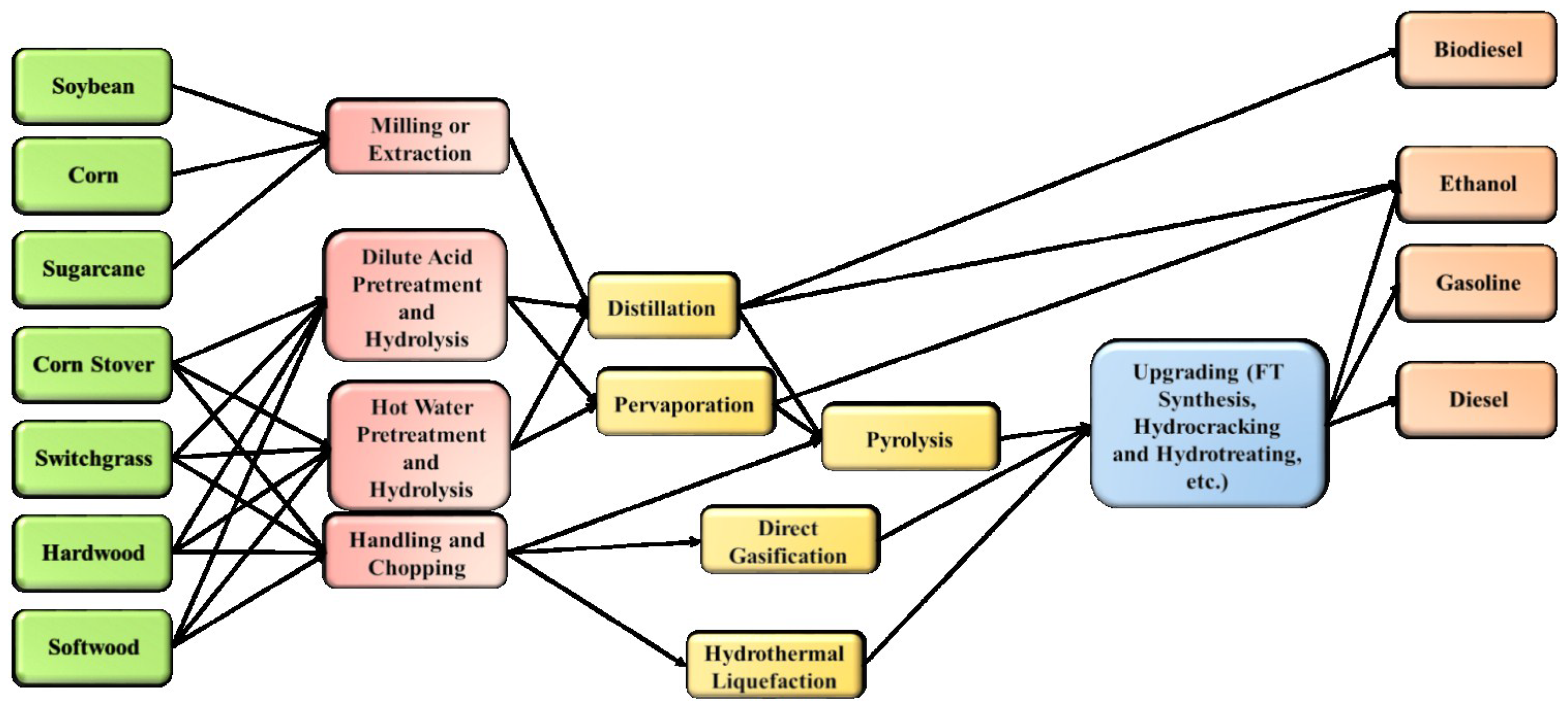
A multiobjective case study concerning optimization of a bioconversion product and process network is performed over the three objectives of minimization of water consumption and maximization of both the energy and economic efficiencies of water. Some of the network is shown in
Figure 1, and an abstract representation of the entire network is shown in
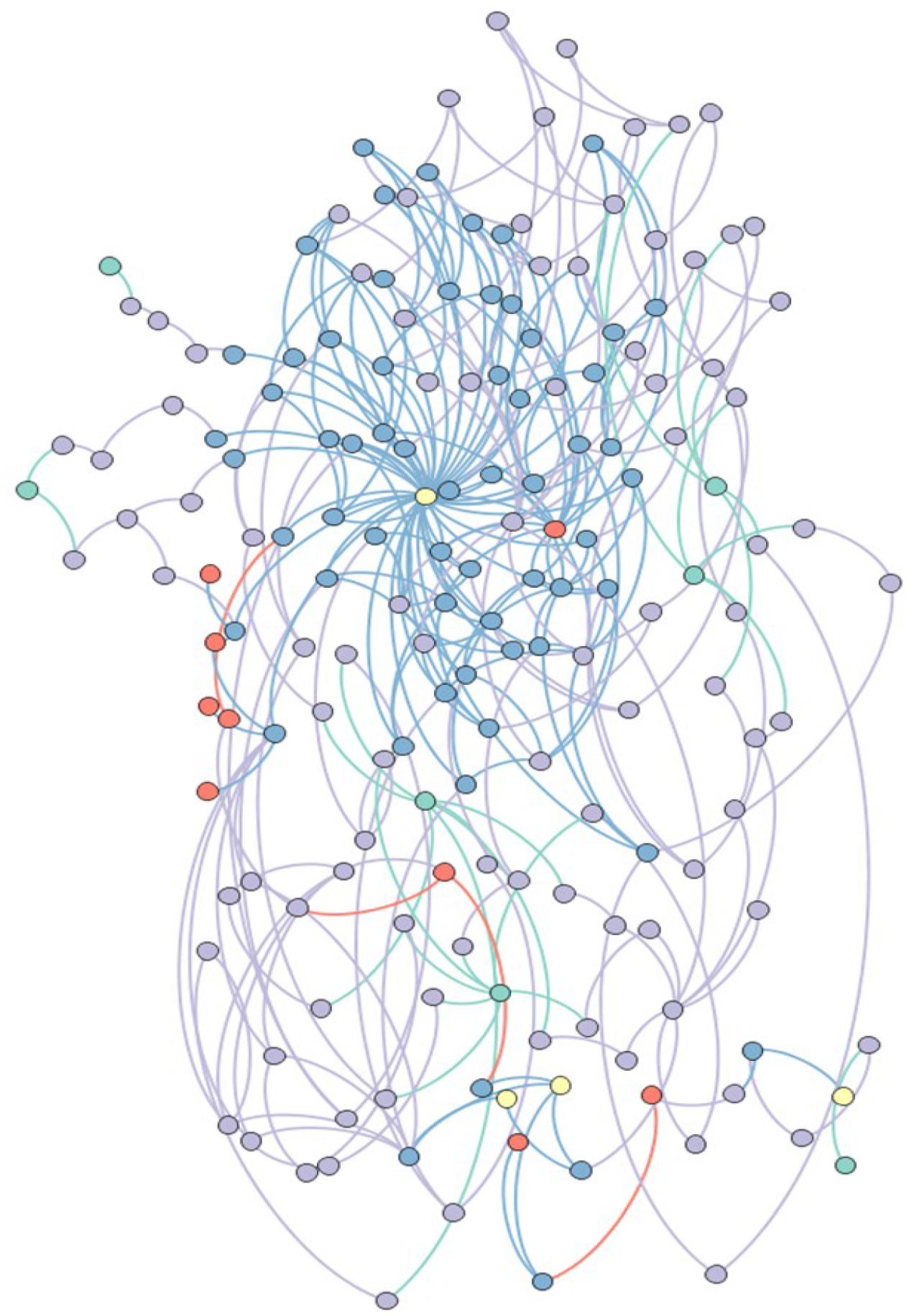
Figure 2.
Much of the data collection strategy can be found in the author’s previous work, including methods for extracting reference operating costs, capital costs, yields, and energy use [
33]. Similar methods are employed to extract water consumption rate data corresponding to each technology’s reference capacity. Extracting water consumption data directly from the literature for the purpose of optimization could provide a novel, concrete lens with which to optimize processing pathways. The reference capacities and corresponding data were retrieved from a variety of sources including technoeconomic analyses and journal articles. While the data included in this particular work is derived from bioconversion process and product technologies, the overall data collection, modeling, and solution strategies presented here hold for a variety of energy-focused process and product networks. Only data from relatively advanced technologies were included in the model; no data collected from investigations at the lab-scale or smaller were included.
Figure 1.
Sample subset of technologies in the model and their possible connections within a processing pathway.
Figure 1.
Sample subset of technologies in the model and their possible connections within a processing pathway.
Figure 2.
Abstract representation of the bioconversion network used in this study. Yellow nodes correspond to biofuel products, orange nodes correspond to byproducts/intermediates, teal nodes correspond to biomass feedstocks, purple nodes correspond to initial/pretreatment technologies, and blue nodes correspond to final upgrading technologies.
Figure 2.
Abstract representation of the bioconversion network used in this study. Yellow nodes correspond to biofuel products, orange nodes correspond to byproducts/intermediates, teal nodes correspond to biomass feedstocks, purple nodes correspond to initial/pretreatment technologies, and blue nodes correspond to final upgrading technologies.
Both indirect and direct process water consumption was retrieved from technoeconomic analyses and design reports (for example, [
34,
35,
36]). Most direct water consumption (e.g., water used for reactions) data were retrieved from analyzing mass flow streams. When direct water consumption was not explicitly provided, the amount of makeup water needed in the process models was used. Indirect water consumption via cooling and heating was taken into account. All input data, including the water consumption rates for each technology, the unit energy consumption rates for each technology, reference capital costs for each technology, reference operating costs for each technology, and yield coefficints for the different technologies and their feeds and products are available as an Excel file in the
Supporting Information.
Direct water consumption stemming from biomass cultivation was retrieved from a variety of sources [
46]. For example, the cultivation water footprints for many biomass feedstocks were compiled by Mekonnen and Hoekstra (2011) [
47], and May
et al. [
48] analyzed water requirements for softwood plantations. These studies and the present one assume that each biomass crop is grown in arable land with typical amounts of rainfall. Furthermore, this study only investigates fresh water consumption that are in addition to typical amounts of rainfall. Overall, water footprints tended to be higher for highly irrigated crops, such as corn, soybeans, and sugarcane. In contrast, water footprints tended to be very low or negligible for energy crops and woody biomass. Similar water consumption analyses can also be performed for general energy product and process networks. The water consumption of each type of biomass during its cultivation is included in
Table 1.
Table 1.
Water consumption rates for cultivation of the biomass feedstocks available in this work.
Table 1.
Water consumption rates for cultivation of the biomass feedstocks available in this work.
| Biomass Feedstock | Water Consumption Rate for Cultivation (L/kg Biomass) |
|---|
| Soybean | 2145 |
| Corn | 1222 |
| Sugarcane | 210 |
| Corn Stover | 1222 |
| Hardwood | 0.357 |
| Softwood | 0.268 |
| Switchgrass | 0 |
Simulated demands of 10.89 ML/year for ethanol, 11.53 ML/year for gasoline, and 10.32 ML/year for diesel are chosen for each bioconversion case study. These demand levels were chosen to represent a pilot-scale processing pathway with approximately half the capacity relative to a recently built, full scale biofuels plant with total capacity of 76 ML/year [
39]. The capital cost of this 76 ML/year plant is also given, providing a basis for a capital cost budget for this work of $250 M. The minimum availability of each biomass type was set to zero, and the maximum availability of each biomass type was set to a large number (100,000 kg/h each) to ensure the solutions would not be constrained by biomass availability. Thus, any amount of biomass between 0 kg/h and 100,000 kg/h could be utilized in the processing pathways. Such an approach was taken to ensure that the chosen pathways of each solution are inherently the most optimal ones. In order to calculate the fixed and variable transportation costs, an average distance of 33.3 miles (approximately 54 km) was chosen as this is the average distance traveled to the center of a circle with a radius of 50 miles, a distance identified to be a maximum viable transportation distance for biofuels [
49]. The fixed transportation cost of each biomass type was assumed to be $0.0000048/kg, and the variable transportation cost of each biomass type was assumed to be $0.0000024/kg. Since this study is primarily concerned with investigating the water-energy nexus of bioconversion technologies, only biofuels technologies were included in the case studies. The energy content of each biofuel was taken as its HHV. No bioproducts (e.g., succinic acid, levulinic acid, biopolymers,
etc.) technologies were included in the model, as there is no straightforward way to analyze the economic and water footprint impacts of their production from a water-energy nexus perspective. This is done not to imply that production of bioproducts is not promising—Indeed, several studies cite bioproducts as key to enhancing the economic viability of biofuels processes [
50,
51,
52]. However, this possibility is not a focus of this work.
An interest rate
r of 10% and a processing pathway lifetime
n of 20 years is assumed. The fixed cost factor
fcfj is taken as 5% of the capital cost of technology
j [
40]. Technology selection, sizing, feedstock selection and quantities purchased, levels of the three fuels produced, capital costs, operating costs, and the water footprint are all decision variables. The HHV for each fuel was used to determine the energy efficiency of water for each processing pathway. The case study has a system boundary of “cradle to grave”, and it is assumed that all biomass that is purchased is processed, and all biofuels produced are sold and consumed. Water consumption is tallied from biomass cultivation to biomass processing and fuel production. Current market prices for feedstocks and fuels are used [
53,
54], and these prices are compiled in
Table 2.
Table 2.
Market prices of all raw materials (biomass feedstocks) and products (biofuels) available in this work.
Table 2.
Market prices of all raw materials (biomass feedstocks) and products (biofuels) available in this work.
| Biomass Feedstock/Biofuel | Market Price ($/kg) |
|---|
| Soybean | 0.1085 |
| Corn | 0.0317 |
| Sugarcane | 0.0925 |
| Corn Stover | 0.0881 |
| Hardwood | 0.0728 |
| Softwood | 0.0728 |
| Switchgrass | 0.0878 |
| Ethanol | 0.61 |
| Gasoline | 0.83 |
| Diesel and Biodiesel | 0.92 |
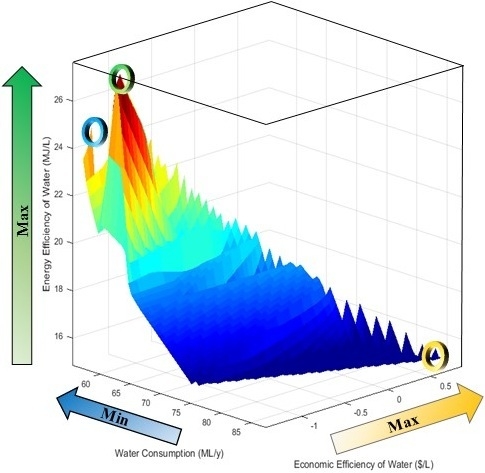
A Pareto-optimal surface displaying the results is shown in
Figure 3. Clear trends and tradeoffs between the objective functions are present. In general, as the economic efficiency of water increases, the total water consumption increases and the energy efficiency of water decreases. There are also three distinct regimes following energy efficiency of water changes relative to changes in water consumption rates along the Pareto-optimal surface: A jagged regime, a smooth regime, and a jagged regime with valleys, as shown on
Figure 3. A more jagged regime could suggest that the energy efficiency of water is more sensitive to changes in water consumption rates in this regime than a smooth regime. A jagged regime with valleys might imply that changes in the energy efficiency of water are more sensitive to changes in the water consumption rate than in a smooth regime, but not as sensitive as in a jagged regime. Interestingly, the maximum energy efficiency of water and the minimum water consumption points are near each other on the Pareto-optimal surface. This implies that there are synergies between maximizing the water efficiency of energy and minimizing water consumption, a relationship that could have important policy implications. For example, since the energy efficiency of water solution has a better economic efficiency of water than the minimum water consumption solution, this solution might be chosen as something of a “good compromise” solution. Overall, the Pareto-optimal surface provides the decision maker with a thorough overview of the economic, energy, and environmental impacts of their decisions. Furthermore, more informed decisions can be made in the biofuels water-energy nexus depending on which regime the decision maker plans to operate within.
Figure 3.
Pareto-optimal surface with key features and extreme points highlighted. The minimum water consumption solution is denoted with a blue circle (far left), the maximum energy efficiency of water solution is denoted with a green circle (middle), and the maximum economic efficiency of water solution is denoted with a yellow circle (right).
Figure 3.
Pareto-optimal surface with key features and extreme points highlighted. The minimum water consumption solution is denoted with a blue circle (far left), the maximum energy efficiency of water solution is denoted with a green circle (middle), and the maximum economic efficiency of water solution is denoted with a yellow circle (right).
Three extreme points exist on the three corners of the Pareto-optimal surface: One denotes the minimum water footprint solution, another denotes the maximum economic efficiency of water solution, and the third point denotes the maximum energy efficiency of water solution. These three solutions are highlighted in
Figure 3 and discussed in the following subsections.
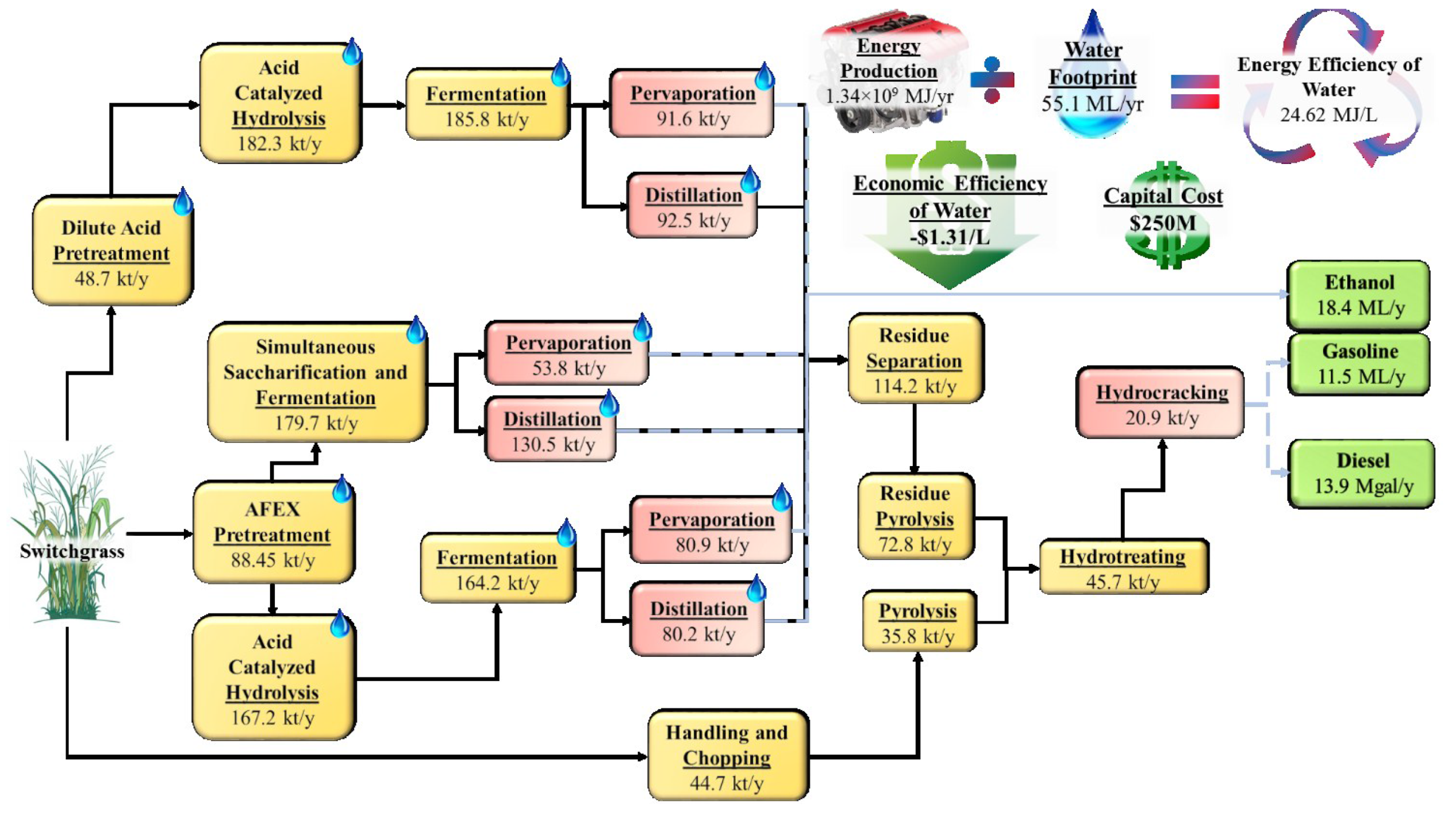
3.3. Maximum Economic Efficiency of Water Solution
The processing pathway with the highest economic efficiency of water is shown in
Figure 5. It has an energy efficiency of water of 15.32 MJ/L, an economic efficiency of water of $0.76/L, a water footprint of 87.6 ML/year, and a capital cost of $250 M. Both switchgrass and softwood are used in this pathway. The overall processing pathway is similar to the pathway for the minimum water footprint solution in that ethanol is produced by pretreatment, saccharification and fermentation of hydrolyzates, and distillation of the resulting broth. Gasoline and diesel are again produced by hydrotreating and hydrocracking of pyrolysis products. However, pervaporation technologies are absent in favor of larger, more cost-effective distillation technologies. Hot water pretreatment is also preferred over dilute acid pretreatment due to lower operating costs, despite larger energy costs and higher rates of water use.
Figure 5.
Optimal processing pathway, water footprint, economic efficiency of water, overall capital cost, and energy efficiency of water of the maximum economic efficiency of water solution.
Figure 5.
Optimal processing pathway, water footprint, economic efficiency of water, overall capital cost, and energy efficiency of water of the maximum economic efficiency of water solution.
Less ethanol is produced in this processing pathway compared to the minimum water footprint solution, implying that producing ethanol is not a profitable venture, even with a myriad of conversion technologies to choose from. Gasoline demand is met exactly, and diesel demand is exceeded as hydrocracking has a higher yield for diesel than gasoline. Interestingly, technologies that employ water recycling are employed extensively in this processing pathway. This selection might appear to work against increasing the economic efficiency of water of the process, as water recycling is expensive. This might be true when maximizing solely the NPV. However, the goal of this solution point is to maximize the economic efficiency of water, or the amount of value the processing pathway can produce from each liter of water consumed. Thus, there is a tradeoff between minimizing the water footprint and maximizing the NPV of the processing pathway. Encouragingly, the economic efficiency of water for this processing pathway is positive, indicating an overall profitable process. Thus, the results show that profits can still be made by producing biofuels while simultaneously considering sustainability impacts such as the water footprint.
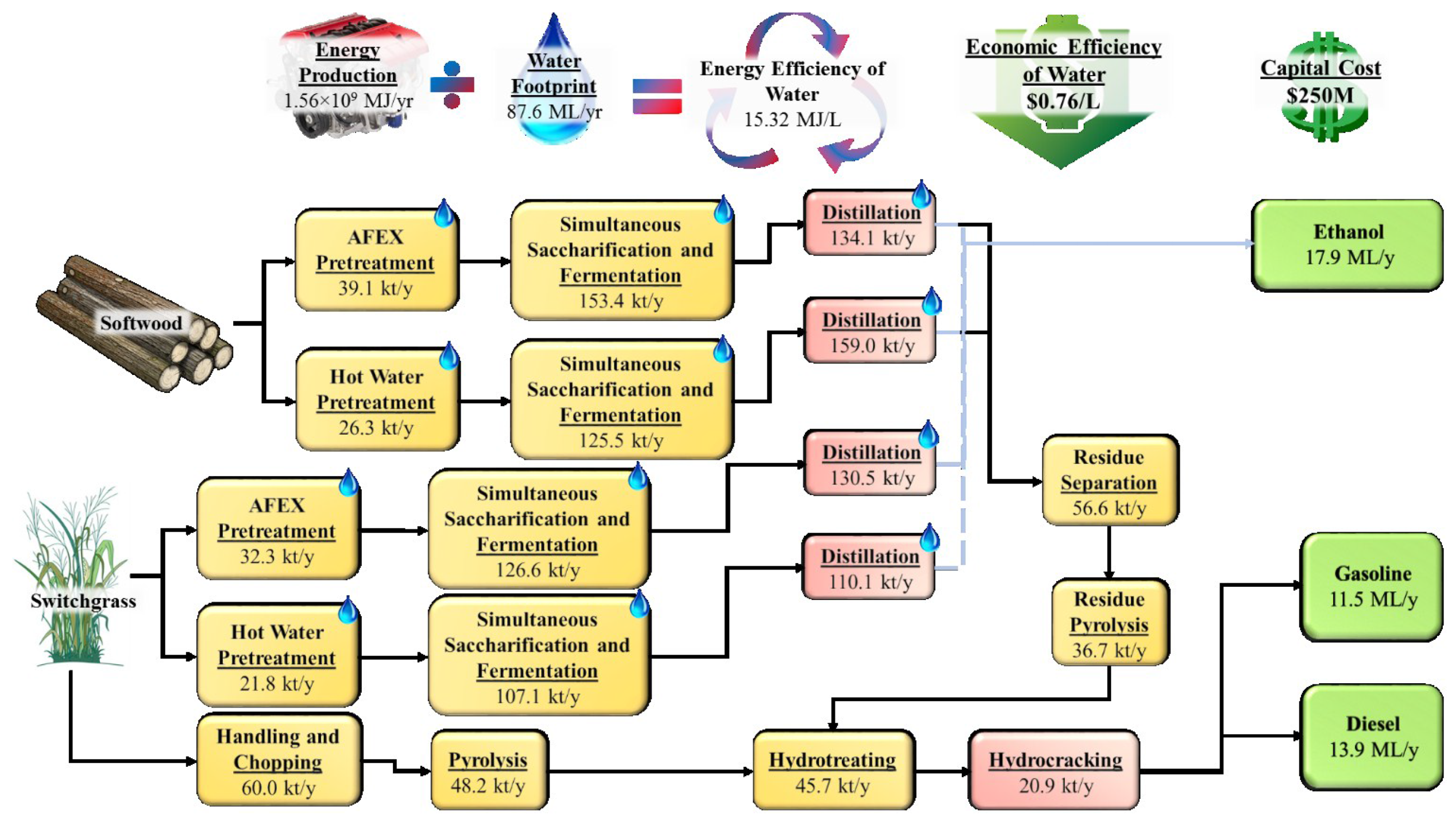
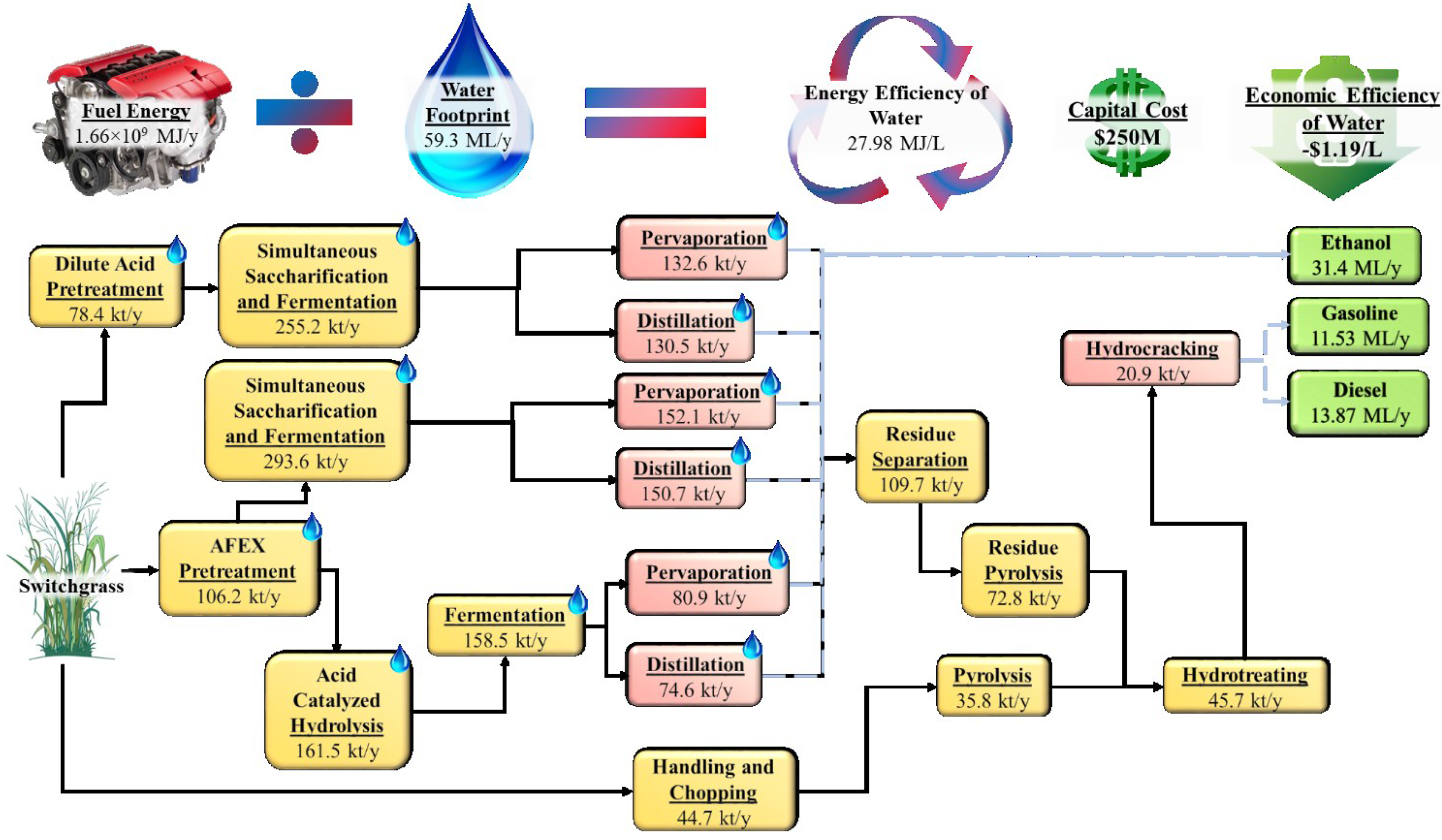
3.4. Maximimum Energy Efficiency of Water Solution
Finally, the processing pathway with the maximum energy efficiency of water is shown in
Figure 6. As in the minimum water footprint solution, only switchgrass is processed, minimizing the amount of cultivation water used in the processing pathway. Indeed, the same technologies are employed as in the minimum water footprint solution with the difference between the two solutions in the capacities of the selected technologies. The amount of ethanol produced is the largest of either of the previous solutions at 31.4 ML/year. Instead of producing the more energy dense fuels of gasoline and diesel to increase the energy efficiency of water, ethanol production is favored. This phenomenon is likely due to high levels of water recycling in the technologies within the ethanol production pathway. Traditionally, ethanol has been essentially the only biofuel produced in the United States. As a result, various technoeconomic analyses of ethanol production processes have been performed that take into account details such as water recycling and process optimization. Detailed technology development and process optimization for more advanced bioconversion technologies has not been performed, so detailed data concerning recycling of water in these advanced technologies do not yet exist.
Figure 6.
Optimal processing pathway, water footprint, economic efficiency of water, overall capital cost, and energy efficiency of water of the maximum energy efficiency of water solution.
Figure 6.
Optimal processing pathway, water footprint, economic efficiency of water, overall capital cost, and energy efficiency of water of the maximum energy efficiency of water solution.
An energy efficiency of water of 27.98 MJ/L is the largest energy efficiency of water across all processing pathways, as expected. An economic efficiency of water of −$1.19/L is achieved, a value intermediate between that of the minimum water footprint solution and that of the maximum economic efficiency of water solution. Furthermore, its water footprint of 59.3 ML/year is intermediate between that of the previous two solutions; however, this value is far closer to that of the minimum water footprint solution than that of the maximum economic efficiency of water solution. Thus, this solution could be seen in several ways as a good compromise solution between the two extremes of the minimum water footprint solution and the maximum economic efficiency of water solution. While this solution has the highest energy efficiency of water and intermediate values of the water footprint and economic efficiency of water, its economic efficiency of water is still negative, implying a non-profitable and, ultimately, unrealistic solution. A comparison in computation time between finding this solution by directly solving the model with BARON 14.4 and the proposed pathway with CPLEX 12.6 is shown in the
Appendix.
Results presented in this work compare favorably to previous literature on estimated water footprints of biofuels production processes. The energy efficiencies of water in this work ranged from 15.32 MJ/L to 27.98 MJ/L. Wu
et al. assessed the water footprints of ethanol production from switchgrass and found that between 1.9 and 9.8 liters of water were required to produce one liter of ethanol [
55]. These results correspond to energy efficiencies of water ranging from 0.62 MJ/L to 3.18 MJ/L. Since the results presented in this work are optimal processing solutions, they are larger than the non-optimal results reported in the literature by up to two orders of magnitude. We note that on a liter of water consumed per liter of fuel produced basis (not adjusting for energy content of the fuel), our results range from 1.04 to 2.02, which are similar to the lower range of the results of Wu
et al. They also found that using corn to produce ethanol with traditional methods requires 10–17 liters of water per liter of ethanol produced, a far less efficient method than using switchgrass. Other sources state more optimistic results of approximately three liters of water per liter of ethanol, a water footprint that is still higher than the values found in our work [
56]. Our results reflect these estimates: Only switchgrass is used to produce ethanol when considering the processing pathway’s water footprint, and corn is not used in any of the optimal solutions. This result has been found elsewhere in the literature; Kantas
et al. found that converting switchgrass to ethanol was the most profitable and preferred option when considering water consumption of the process [
27].
All results for each extreme point are compiled in
Table 3 for convenience and clarity. Each pathway reaches the maximum allowable capital cost of $250 M, and all have similar amounts of produced energy in the form of biofuels per year. The largest differences between the solutions are in their respective economic efficiencies of water, highlighting how critical it still is to further optimize and develop bioconversion technologies to be simultaneously economically competitive and sustainable.
Table 3.
Compilation of results for the three optimization scenarios.
Table 3.
Compilation of results for the three optimization scenarios.
| Metric | Minimum Water Footprint | Maximum Economic Efficiency of Water | Maximum Energy Efficiency of Water |
|---|
| Energy Produced (in Biofuel Form) (MJ/year) | 1.34 × 109 | 1.56 × 109 | 1.66 × 109 |
| Water Footprint (ML/year) | 55.1 | 87.6 | 59.3 |
| Energy Efficiency of Water (MJ/L) | 24.62 | 15.32 | 27.98 |
| Capital Cost ($M) | 250 | 250 | 250 |
| Economic Efficiency of Water ($/L) | −1.31 | 0.76 | −1.19 |
Overall, modeling and optimization of biofuels product and process networks was shown to provide meaningful insight to the water-energy nexus of biofuels. The results herein could also have significant policy implications. For example, it is immediately apparent that feedstocks that require minimal water for cultivation should be utilized for energy production compared to highly irrigated crops, such as corn or soybeans. Thus, decision makers should consider using feedstocks such as switchgrass or woody biomass to produce biofuels. Results obtained from the case study with maximizing the energy efficiency of water as the objective resulted in a relatively low water footprint paired with the best use of water resources in the context of energy production. Furthermore, while still economically unviable, it is less unprofitable than minimizing the water footprint directly. Thus, policymakers and other decision makers might look to use the energy efficiency of water as a metric to create policies for the water-energy nexus of both biofuels systems and other energy systems. Consideration must be given, however, to the economics of the system. In this case study, if the solution with the maximum energy efficiency of water is chosen by policymakers or other decision makers, then some sort of economic subsidy would also be required for successful implementation.