Experimental Study on Pressure Oscillations of Direct-Contact Condensation between Saturated Steam and Droplets at Sub-Atmospheric Pressure
Abstract
:1. Introduction
2. Experimental Apparatus and Procedure
3. Results and Discussion
3.1. The RMS of the Pressure Oscillation
3.2. The Time-Domain Characteristics of the Pressure Oscillation
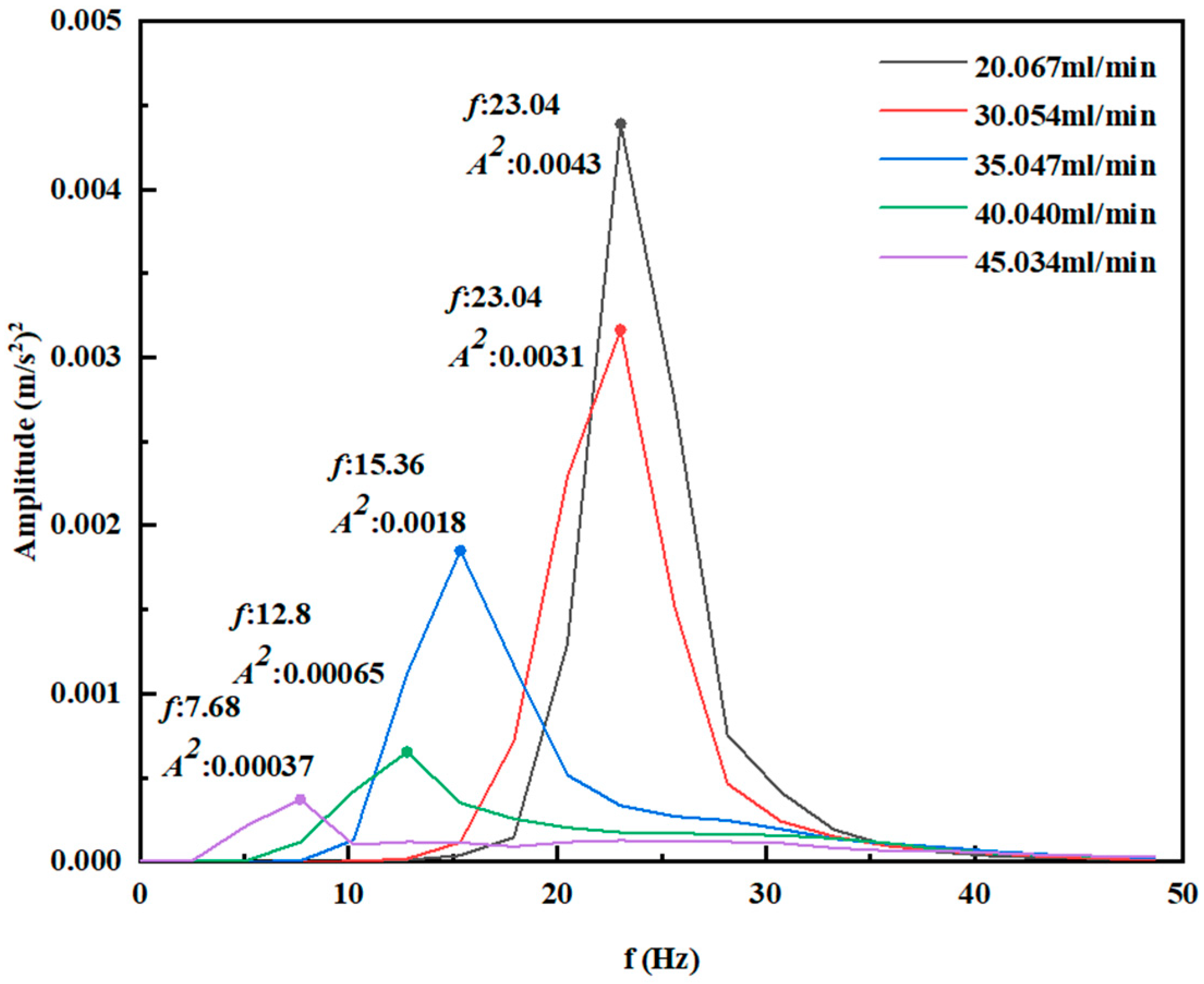
3.3. The Frequency-Domain Characteristics of the Pressure Oscillation
4. Conclusions
- (1)
- The peak value of the oscillation in the condenser shows pulse fluctuations when pure steam condenses in direct contact with droplets. The energy of the condenser is maximum in the Z direction, and the acceleration RMS value can reach 0.08 m/s2.
- (2)
- When the flow rate is constant, the peak value of the oscillation signal decreases gradually with the increase in absolute pressure, and the time-domain periodic waveform becomes fluctuating. When the absolute pressure is constant, the peak value of the condensation oscillation signal mainly occurs at a low mass flow rate. When the flow rate continues to increase, there is no obvious peak value change.
- (3)
- In the spectrum waterfall diagram, the energy contribution decreases in the range of 20–30 Hz but increases in the range of 5–20 Hz. The range of 0–50 Hz is where the oscillation frequency changes the most in the process of steam condensation. At a low mass flow rate, the RMS of pressure oscillation does not change significantly, and the peak frequency moves towards a high frequency. As the flow rate gradually increases, frequencies with high energy become unconcentrated. The peak frequency decreases continuously from 23.68 Hz to 7.16 Hz, and the oscillation amplitude decreases in a parabolic pattern.
- (4)
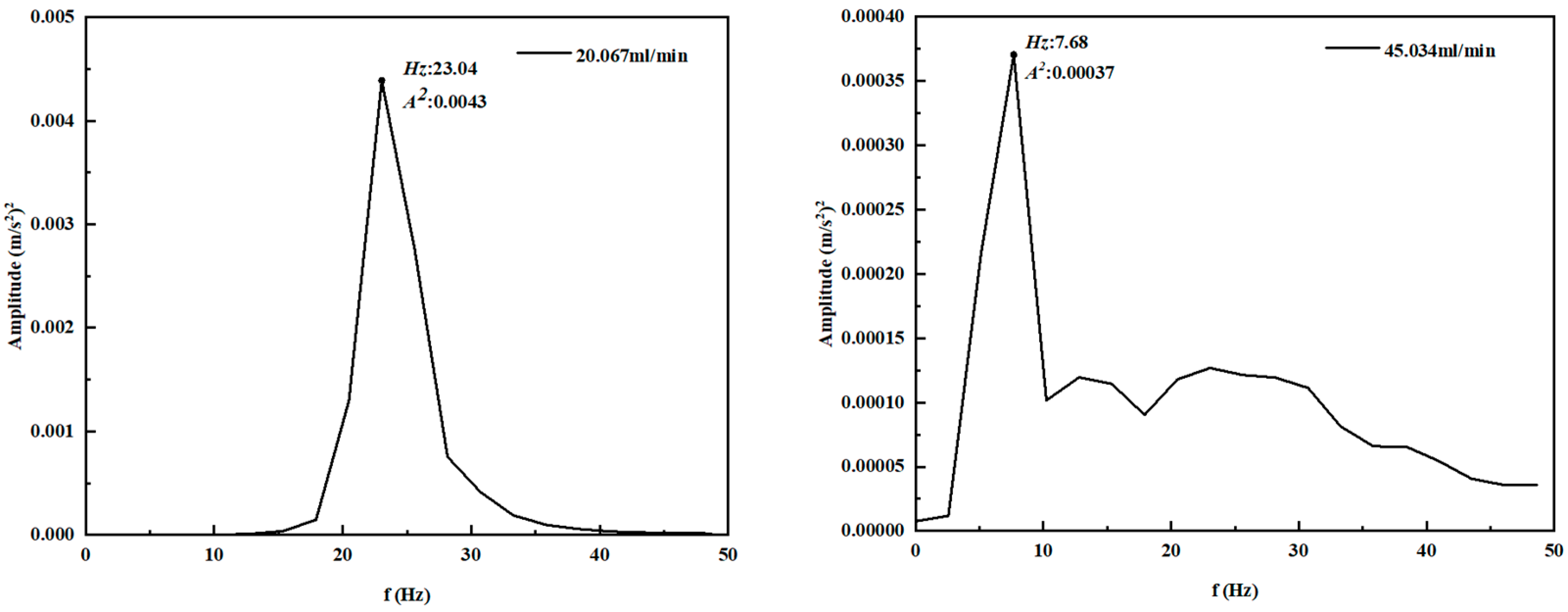
- The auto power spectrum of the oscillation shows that the main frequency of oscillation is maintained at 23.04 Hz at a low flow velocity, and gradually decreases to 7.68 Hz when the flow velocity continues to increase.
- (5)
- As the flow rate increases, the main frequency of oscillation is no longer stable and its energy continues to decrease. The auto power spectrum changes from a single peak to a fluctuating characteristic. The amplitude of the first main frequency is approximately 0.00037 (m/s2)2, while the amplitude of other dominant frequencies is between 0.00010 (m/s2)2 and 0.00015 (m/s2)2. Other dominant frequencies may be caused by the formation, aggregation, and rupture of non-condensable gas layers on the surface of droplets.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Miró, L.; Gasia, J.; Cabeza, L.F. Thermal energy storage (TES) for industrial waste heat (IWH) recovery: A review. Appl. Energ. 2016, 179, 284–301. [Google Scholar] [CrossRef]
- Zhao, S.; Zhihua, G.; Jie, H.; Chunlan, W.; Yongping, Y.; Peifeng, L. A novel mechanism for exhaust steam waste heat recovery in combined heat and power unit. Appl. Energ. 2017, 204, 596–606. [Google Scholar] [CrossRef]
- Celata, G.P.; Cumo, M.; D’annibale, F.; Farello, G.E. Direct contact condensation of steam on droplets. Int. J. Multiphase Flow 1991, 17, 191–211. [Google Scholar] [CrossRef]
- Lekic, A.; Ford, J.D. Direct contact condensation of vapour on a spray of subcooled liquid droplets. Int. J. Heat Mass Tran. 1980, 11, 1531–1537. [Google Scholar] [CrossRef]
- Gumruk, S.; Aktas, M.K.; Kasap, F. Experimental investigation of spray dehumidification process in moist air. Int. Commun. Heat Mass Transf. 2018, 97, 163–171. [Google Scholar] [CrossRef]
- Khabeyev, N.S.; Shagapov, V.S.; Yumagulova, Y.A. The reduction in the vapour pressure in a closed volume due to condensation at the contact interface with a cold liquid. J. Appl. Math. Mech. 2013, 77, 33–38. [Google Scholar] [CrossRef]
- Qiu, B.; Yan, J.; Chong, D.; Revankar, S.T. Experimental investigation on the mechanism of pressure oscillation for steam jet in stable condensation region. Exp. Therm. Fluid Sci. 2017, 82, 1–7. [Google Scholar] [CrossRef]
- Zhao, X. Mathematical Simulation Research on Steam Ejection System of Aircraft Carrier Carrier-based aircraft. Shipborne Weapons 1996, 3, 45–53. (In Chinese) [Google Scholar]
- Arinobu, M. Studies on the Dynamic Phenomena Caused by Steam Condensation in Water; International Atomic Energy Agency: Vienna, Austria, 1980; pp. 293–297. [Google Scholar]
- Aya, I.; Nariai, H. Boundaries between regimes of pressure oscillation induced by steam condensation in pressure suppression containment. Nucl. Eng. Des. 1987, 99, 31–40. [Google Scholar] [CrossRef]
- Chun, M.H.; Kim, Y.S.; Park, J.W. An investigation of direct condensation of steam jet in subcooled water. Int. Commun. Heat Mass Transf. 1996, 23, 947–958. [Google Scholar] [CrossRef]
- Cho, S.; Song, C.H.; Park, C.K.; Yang, S.K.; Chung, M.K. Experimental study on dynamic pressure pulse in direct contact condensation of steam jets discharging into subcooled water. In Proceedings of the 1st Korea-Japan Symposium on Nuclear Thermal Hydraulics, Pusan, Republic of Korea, 21–24 October 1998; pp. 291–298. [Google Scholar]
- Ren, H.; Liang, D.; Lu, T.; Wang, J.; Yu, P.; Li, J.; Zhao, J.; Xiong, P. Experimental investigation on pressure oscillation induced by steam injection into subcooled water through an opposite nozzle. Ann. Nucl. Energy 2023, 184, 109698. [Google Scholar] [CrossRef]
- Kozeki, M.; Nakanishi, T.; Kuwahara, S. Experimental Studies on Pressure-Suppression Containment for Nuclear Ships; Mitsui Shipbuilding and Engineering: Tokyo, Japan, 1971. [Google Scholar]
- Saito, T.; Uchida, H.; Morita, T.; Oishi, T.; Saito, S. Unsteady Phenomena Relating to Vapor Suppression; ASME United States: New York, NY, USA, 1974. [Google Scholar]
- Yang, Q.; Qiu, B.; Chen, W.; Chong, D.; Liu, J.; Yan, J. Experimental investigation on the condensation regime and pressure oscillation characteristics of vertical upward steam jet condensation with low mass flux. Exp. Therm. Fluid Sci. 2020, 111, 109983. [Google Scholar] [CrossRef]
- Wang, K. Analysis of oscillation and oscillation frequency caused by steam condensation in supercooled water. Therm. Power Eng. 1992, 7, 69–73. (In Chinese) [Google Scholar]
- Cong, Y.; Wang, Y.; Chen, W.; Chong, D.; Yan, J. Effect of non-condensable gas on pressure oscillation of submerged steam jet. J. Univ. Chin. Acad. Sci. 2017, 34, 135–140. (In Chinese) [Google Scholar]
- Li, S.Q.; Lu, T.; Wang, L.; Chen, H.S. Experiment study on steam-water direct contact condensation in water flow in a Tee junction. Appl. Therm. Eng. 2017, 120, 99–106. [Google Scholar] [CrossRef]
- Li, S.Q.; Wang, P.; Lu, T. CFD based approach for modeling steam–water direct contact condensation in subcooled water flow in a tee junction. Prog. Nucl. Energy 2015, 85, 729–746. [Google Scholar] [CrossRef]
- Hong, S.J.; Park, G.C.; Cho, S.; Song, C.H. Condensation dynamics of submerged steam jet in subcooled water. Int. J. Multiph. Flow 2012, 39, 66–77. [Google Scholar] [CrossRef]
- Aya, I.; Kobayashi, M.; Nariai, H. Pressure and fluid oscillations in vent system due to steam condensation(II). Nucl. Sci. Technol. 1983, 20, 213–227. [Google Scholar] [CrossRef]
- Wang, J.; Chen, C.; Liang, D.; Lu, T.; Bai, S. Temperature and pressure oscillations induced by steam direct contact condensation in a T-junction with porous inner-structures. Int. J. Heat Mass Trans. 2021, 168, 120863. [Google Scholar] [CrossRef]
- Frano, R.L.; Forasassi, G. Preliminary evaluation of seismic isolation effects in a Generation IV reactor. Energy 2011, 36, 2278–2284. [Google Scholar] [CrossRef]
- Qiu, B.; Yang, Q.; Yu, X.; Ma, T.; Liu, J. Experimental study on the correlation between bubble heat transfer coefficient and pressure oscillation frequency in the bubbling regime of steam jet. Prog. Nucl. Energy 2023, 161, 104757. [Google Scholar] [CrossRef]
- Ding, Z.; Xu, L.; Liu, D.; Yang, Y.; Yang, J.; Tang, D. Influence of support gap on flow induced oscillation of heat exchange tube. Ann. Nucl. Energy 2023, 180, 109443. [Google Scholar] [CrossRef]
- Ji, J.D.; Ge, P.Q.; Bi, W.B. Numerical investigation on the flow and heat transfer performance of horizontal spiralcoil pipes. J. Hydrodyn. 2016, 28, 576–584. [Google Scholar] [CrossRef]
- Duan, D.; Ge, P.; Bi, W.; Ji, J. Numerical investigation on the heat transfer enhancement mechanism of planarelastic tube bundle by flow induced oscillation. Int. J. Therm. Sci. 2017, 112, 450–459. [Google Scholar] [CrossRef]
- Ji, J.; Ge, P.; Bi, W.; Liu, P. Shell-side flow induced oscillation responses of elastic tube bundle based on different tube combination. J. Xi’an Jiaotong Univ. 2018, 52, 69–75. (In Chinese) [Google Scholar]
- Jing, Y.; Wang, Y.; Huang, Q. Experimental and Simulation Study on the Direct Contact Condensation of Saturated Steam on Moving Droplets at Sub-Atmospheric Pressure. Processes 2023, 11, 1097. [Google Scholar] [CrossRef]
- Li, X.; Liu, S.; Cui, X.; Li, H. Experimental study of direct contact steam condensation in structured packing. Asia-Pac. J. Chem. Eng. 2013, 8, 657–664. [Google Scholar] [CrossRef]
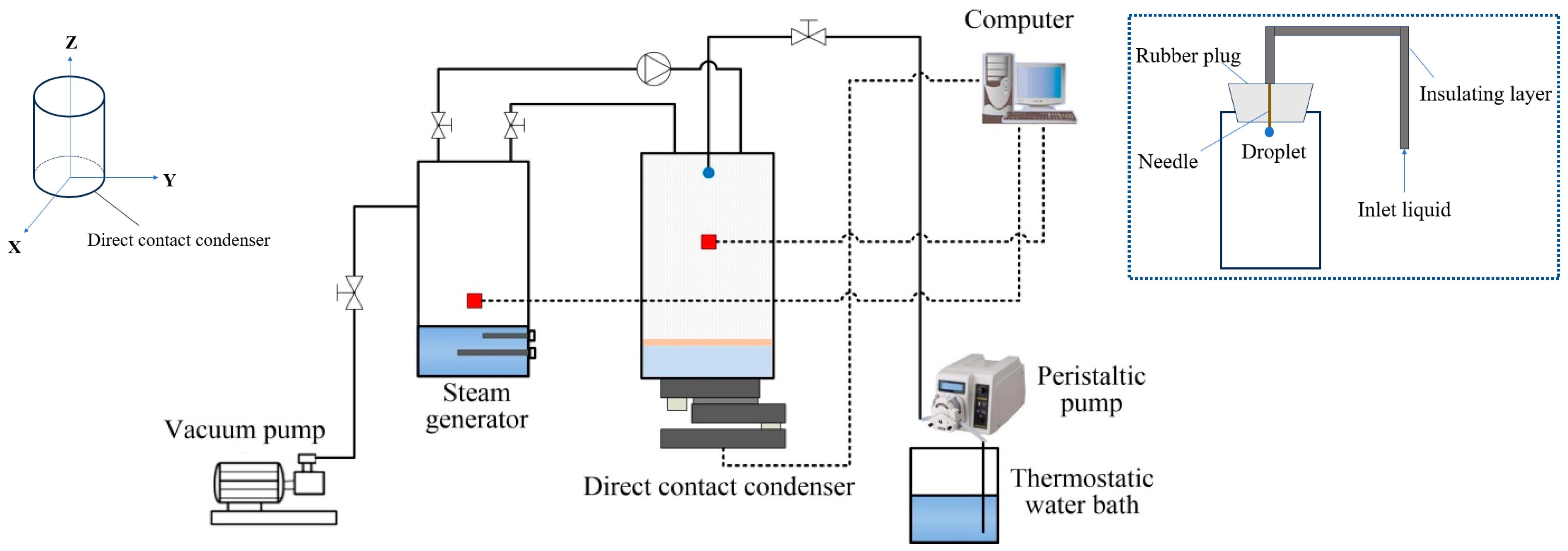




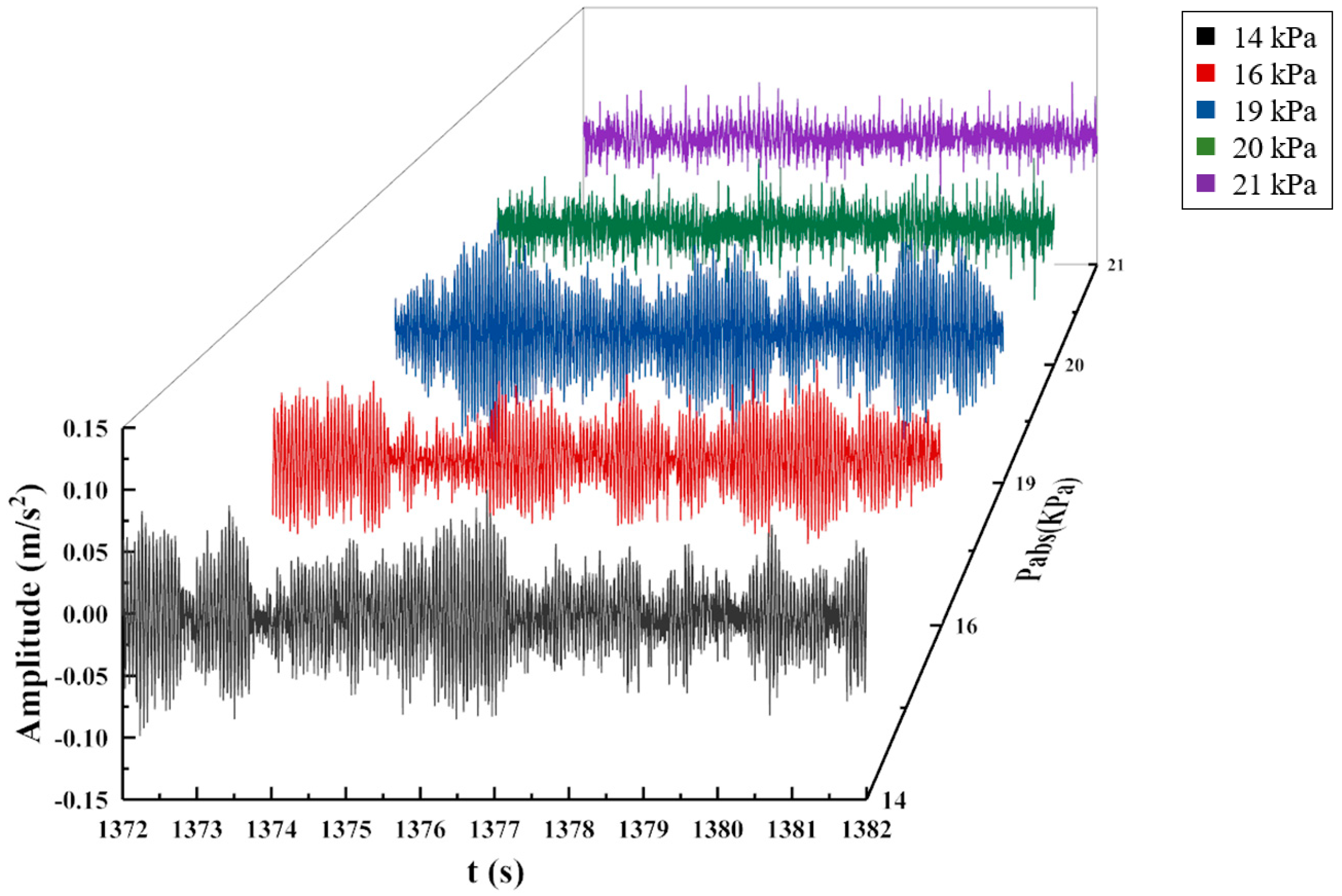
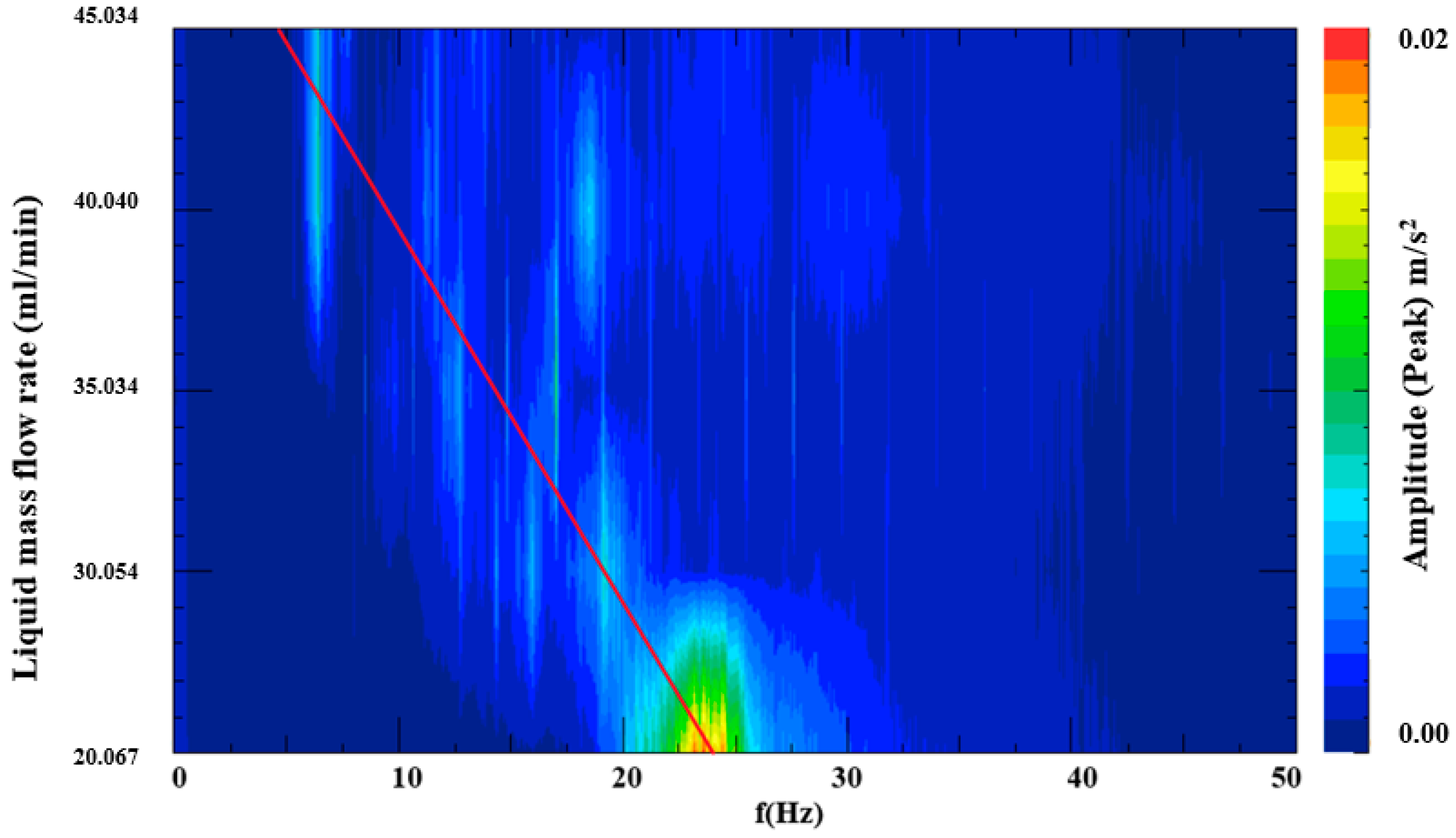
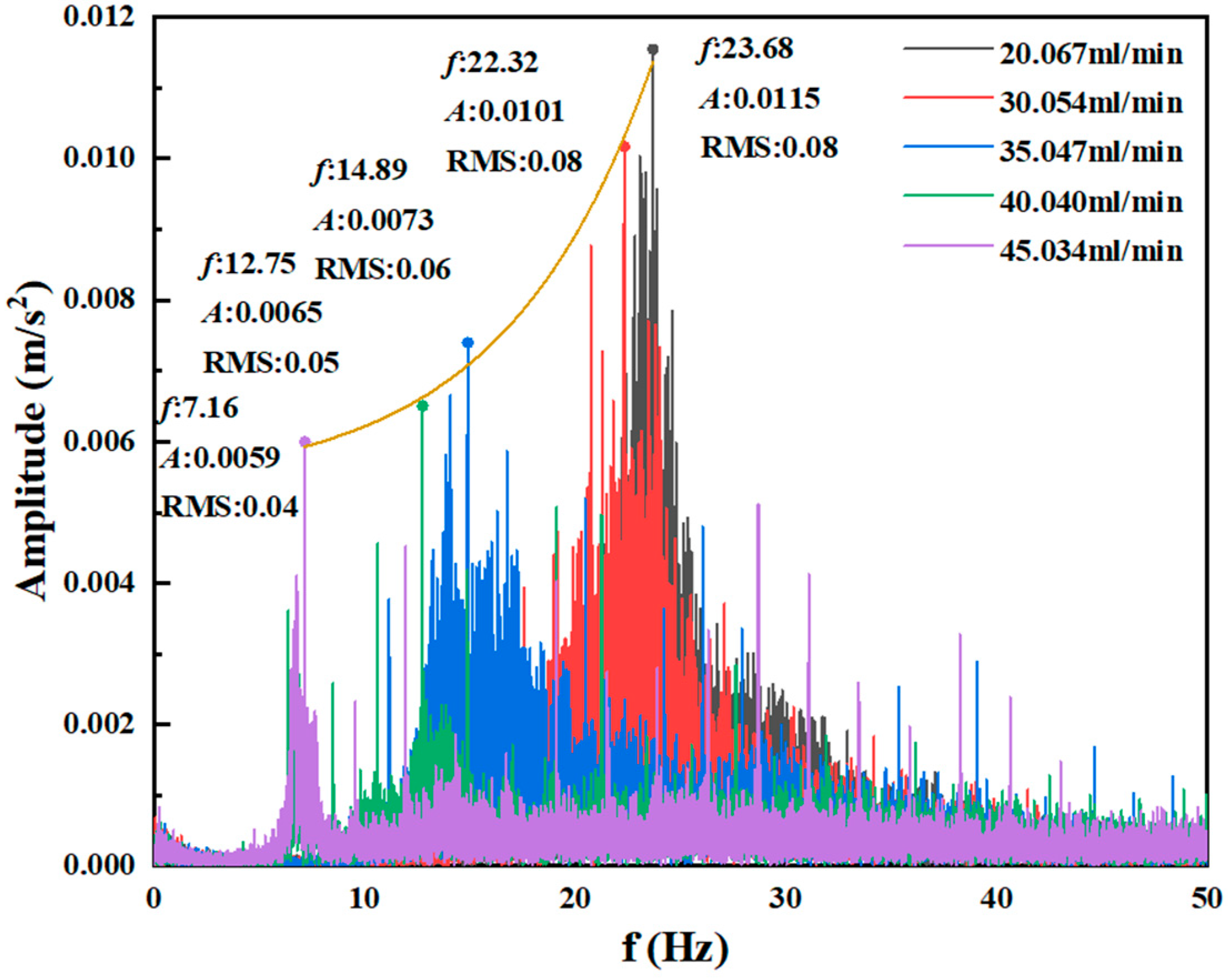
| Parameter | Parameter Symbol | Value | Error |
|---|---|---|---|
| Pressure, kPa | P | 14–21 | ±0.2% |
| Inlet mass flow rate, mL/min | V | 20.067/30.054/35.047/40.040/45.034 | ±0.1% |
| Droplet temperature, °C | Ti | 25 | ±0.05% |
| Oscillation amplitude, m/s2 | A | ±5% |
| V, mL/min | |||||
|---|---|---|---|---|---|
| 20.067 | 30.054 | 35.047 | 40.040 | 45.034 | |
| X | 0.05 | 0.04 | 0.03 | 0.03 | 0.04 |
| Y | 0.02 | 0.04 | 0.02 | 0.02 | 0.02 |
| Z | 0.08 | 0.08 | 0.06 | 0.05 | 0.04 |
| P, kPa | |||||
|---|---|---|---|---|---|
| 14 | 16 | 19 | 20 | 21 | |
| X | 0.05 | 0.05 | 0.04 | 0.04 | 0.03 |
| Y | 0.02 | 0.03 | 0.03 | 0.02 | 0.02 |
| Z | 0.08 | 0.06 | 0.05 | 0.04 | 0.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, Y.; Wang, C.; Huang, Q.; Wang, Y.; Yu, Y. Experimental Study on Pressure Oscillations of Direct-Contact Condensation between Saturated Steam and Droplets at Sub-Atmospheric Pressure. Processes 2024, 12, 516. https://doi.org/10.3390/pr12030516
Jing Y, Wang C, Huang Q, Wang Y, Yu Y. Experimental Study on Pressure Oscillations of Direct-Contact Condensation between Saturated Steam and Droplets at Sub-Atmospheric Pressure. Processes. 2024; 12(3):516. https://doi.org/10.3390/pr12030516
Chicago/Turabian StyleJing, Yuanlin, Chenhao Wang, Qunwu Huang, Yiping Wang, and Yangyang Yu. 2024. "Experimental Study on Pressure Oscillations of Direct-Contact Condensation between Saturated Steam and Droplets at Sub-Atmospheric Pressure" Processes 12, no. 3: 516. https://doi.org/10.3390/pr12030516




