Vortex of a Symmetric Jet Structure in a Natural Gas Pipeline via Proper Orthogonal Decomposition
Abstract
1. Introduction
2. Numerical Simulation Method
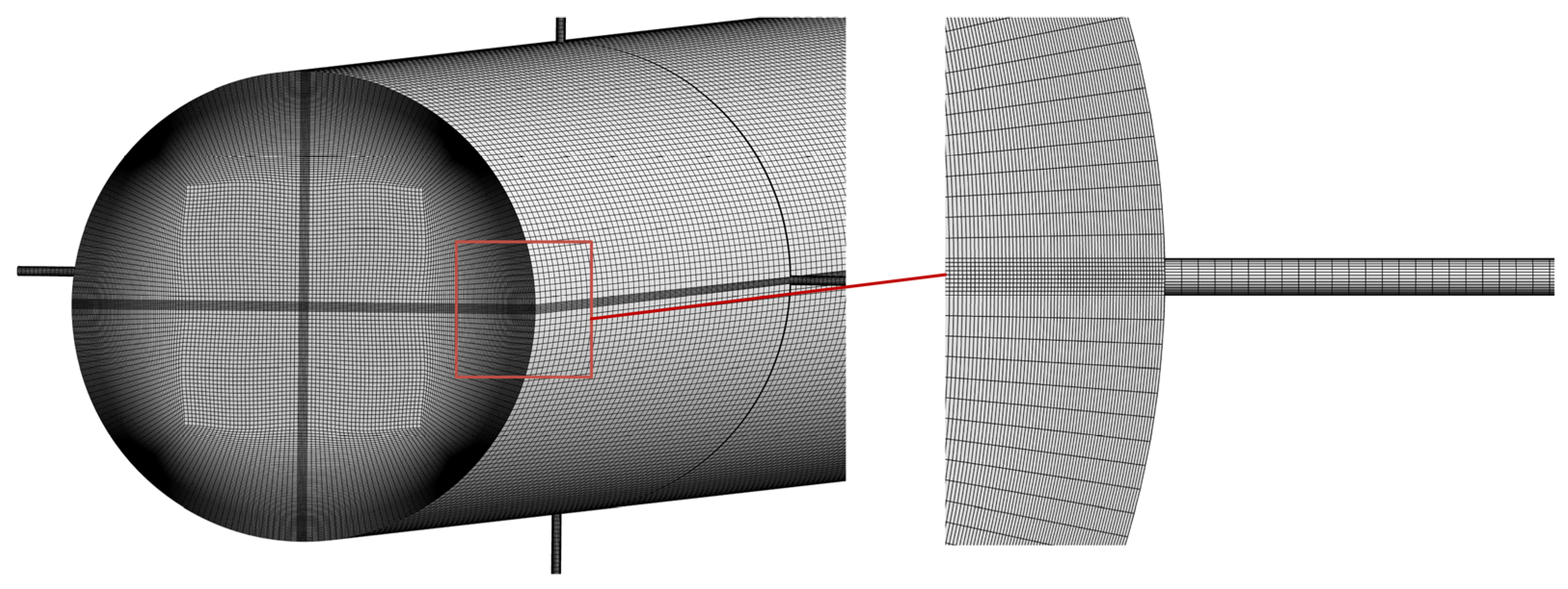
2.1. Numerical Model
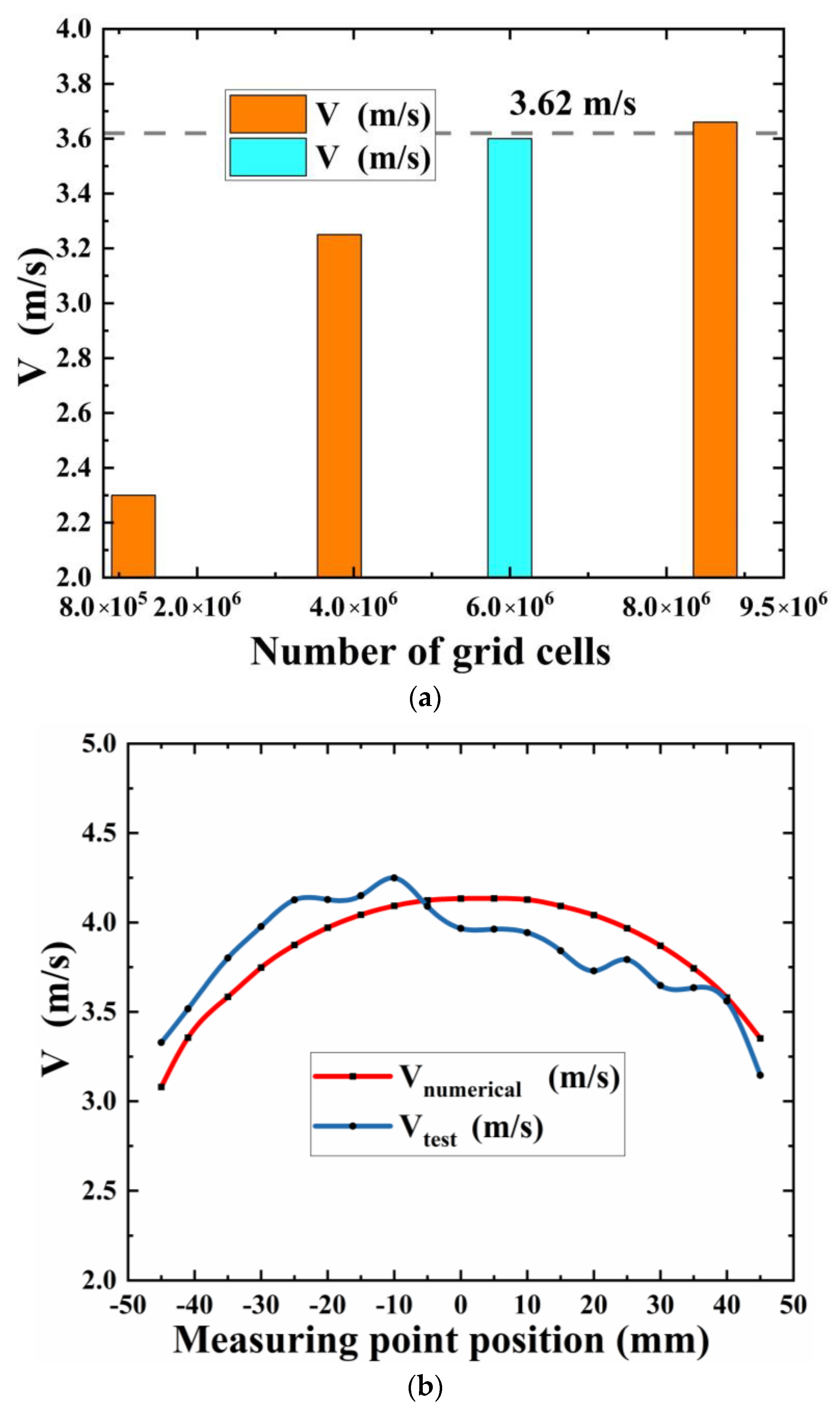
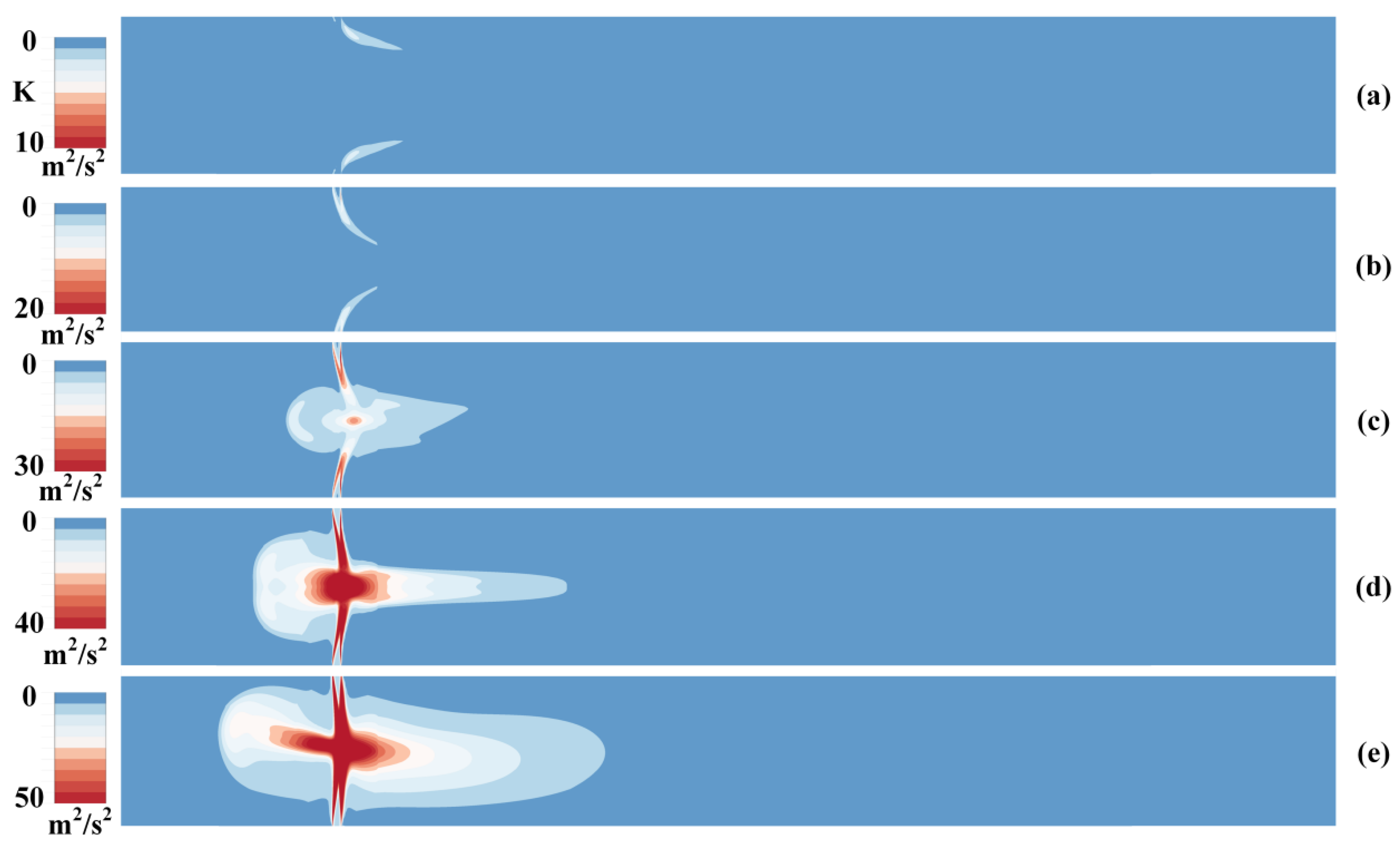
2.2. Analysis of the Numerical Result
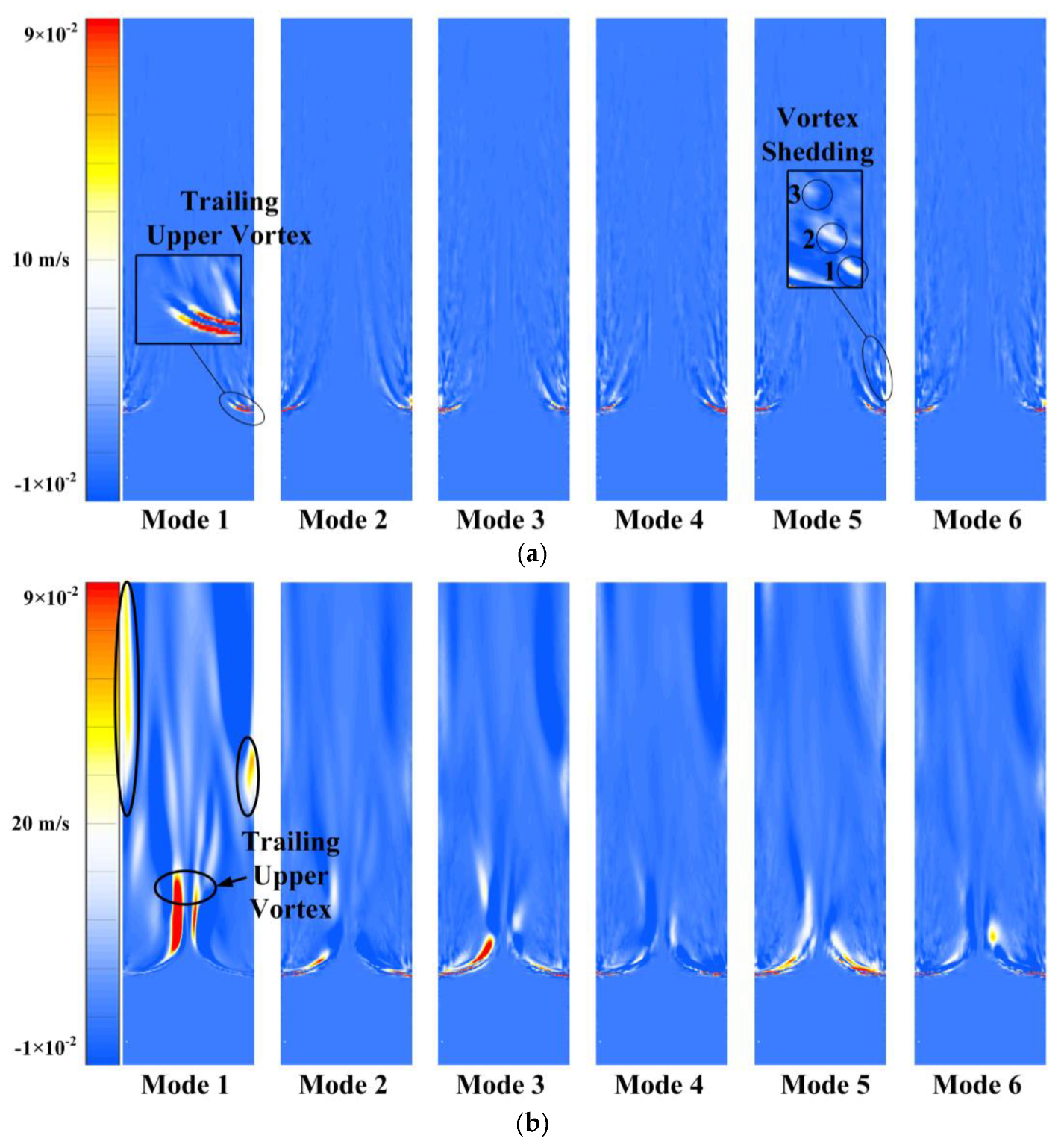
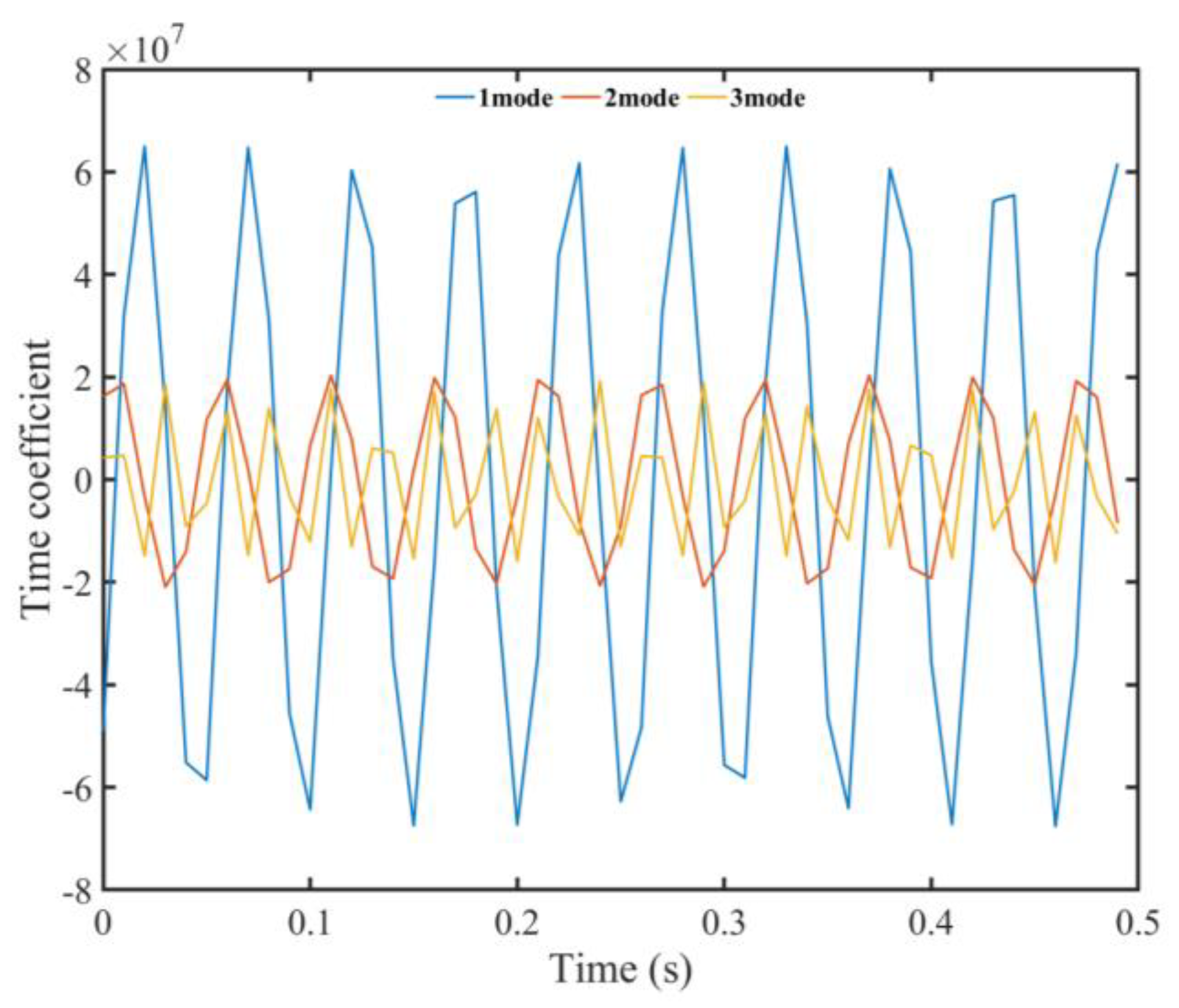
3. Proper Orthogonal Decomposition
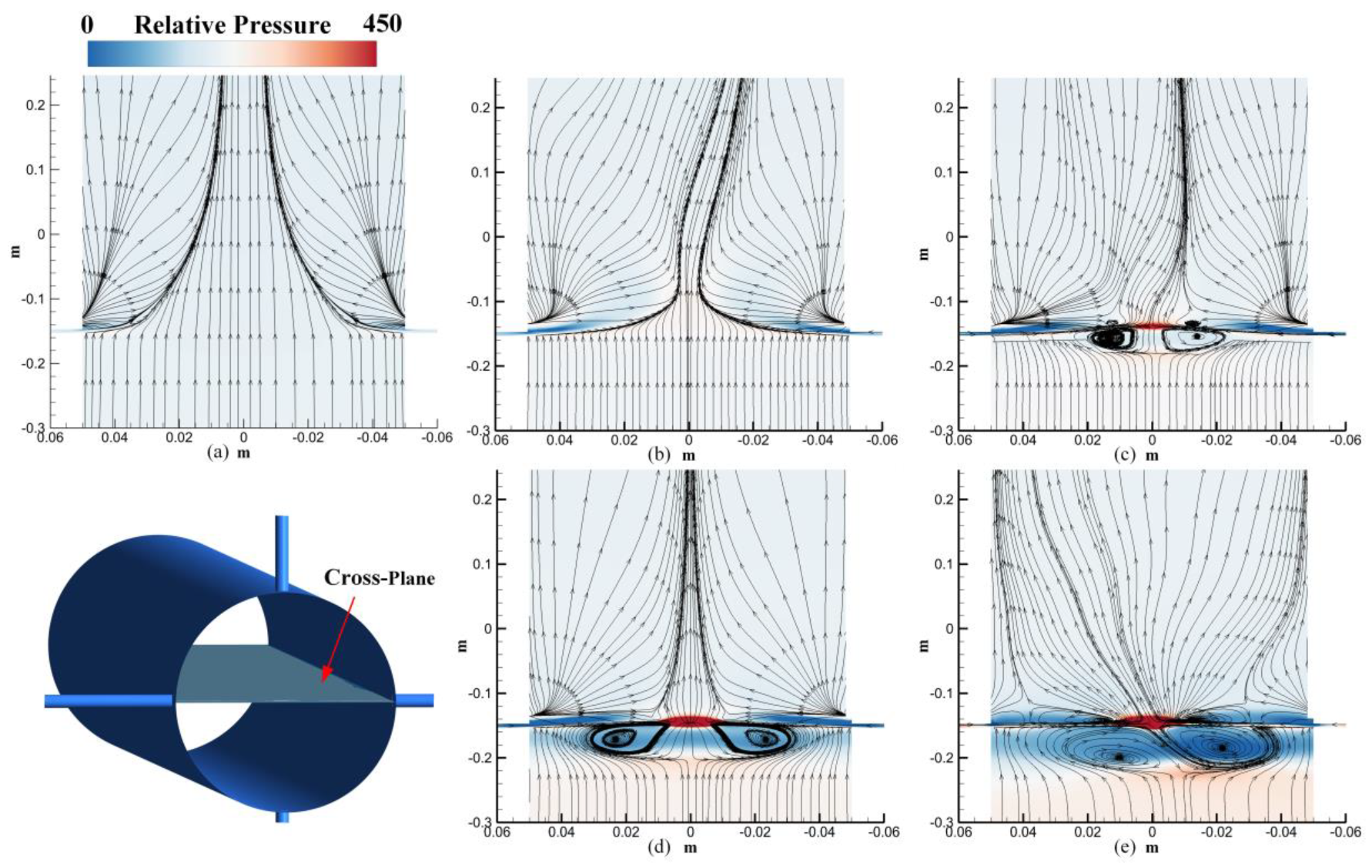
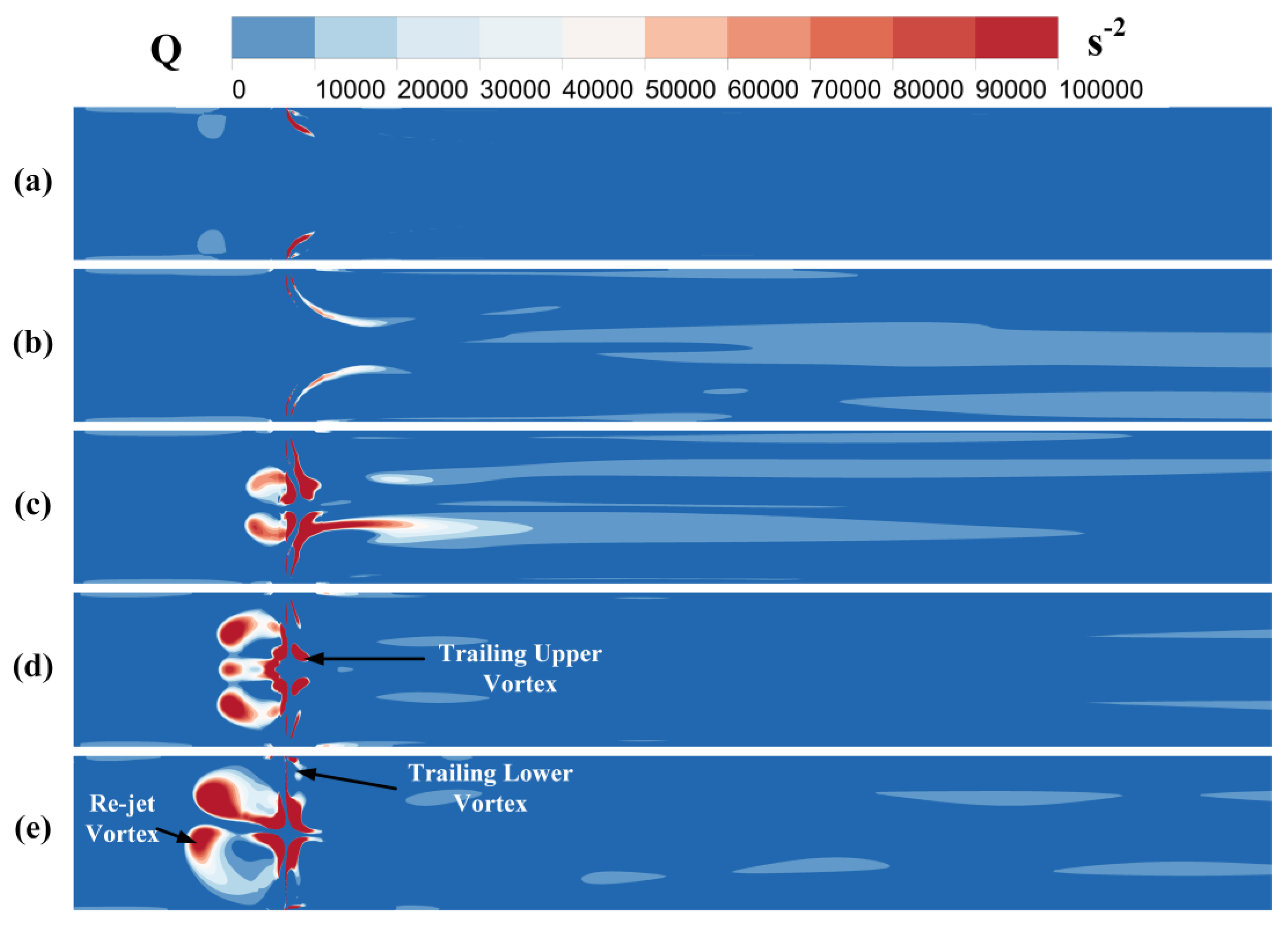
3.1. Vortex Distribution Characteristics
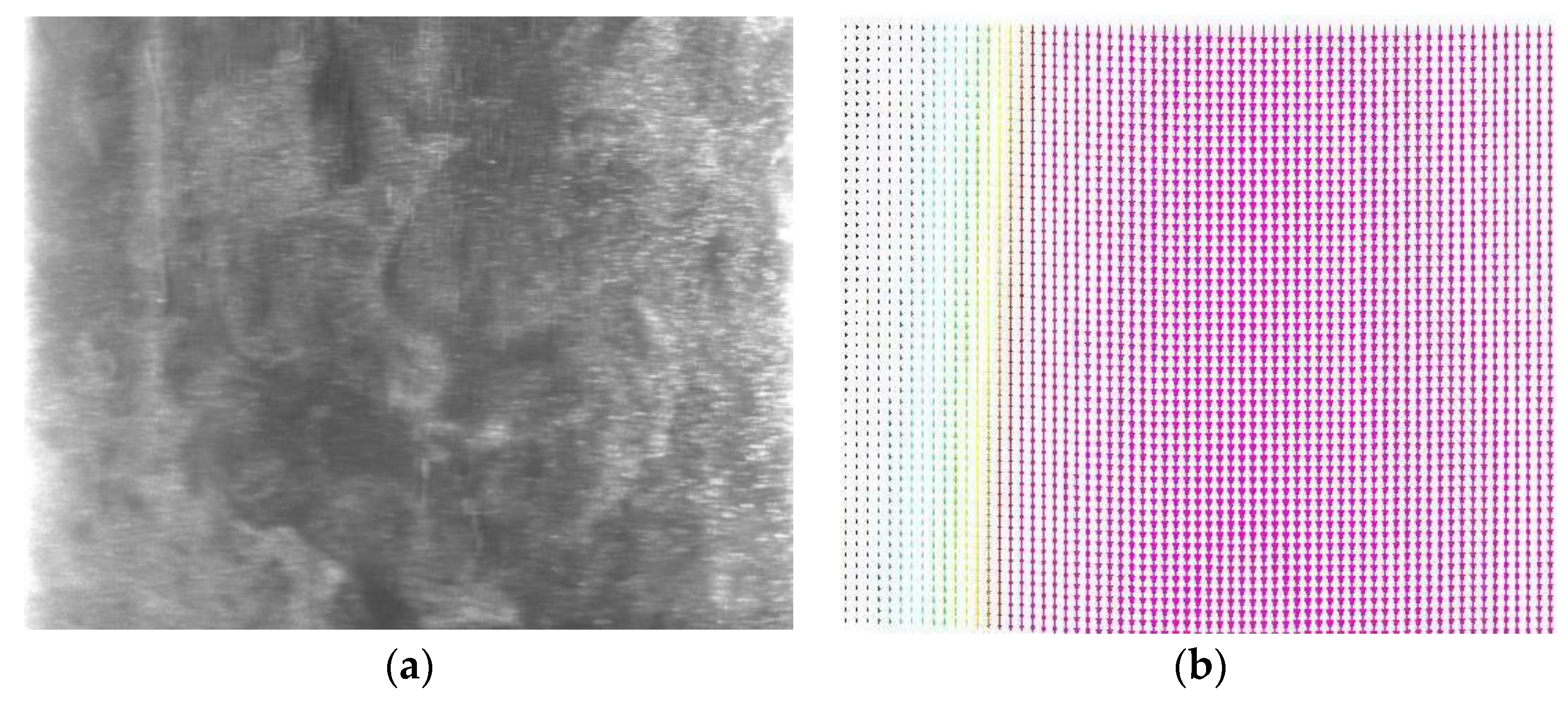
3.2. The Result of PIV
4. Conclusions
- The jet flow interacts with the crossflow, resulting in the formation of trailing upper and lower vortices. At lower jet flow rates, the trailing upper and lower vortices are located above and below the nozzle, respectively.
- As the velocity of the jet flow increases, the trailing upper vortices begin to interfere with each other and gradually merge, forming a re-jet vortex. This observation highlights the complex dynamics and interactions between the jet flow and the surrounding crossflow within the pipeline.
- The POD method is employed to analyze the coherent vortex structure in different modes. The first and second order modes exhibit relatively high energy, enabling them to accurately capture the coherent vortex structure of the jet.
- Higher order modes are useful for observing and studying the growth and shedding of small-scale vortex structures.
- The vortex structure formed by symmetrical jet is conducive to PIV flowmeter measurements.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Neumann, A.; Hirschhausen, C.V. Natural Gas: An Overview of a Lower-Carbon Transformation Fuel. Rev. Environ. Econ. Policy 2015, 9, 64–84. [Google Scholar] [CrossRef]
- Wu, X.; Wang, Z.; Dong, M.; Dong, L.F.; Ge, Q. A Critical Analysis of Natural Gas Liquefaction Technology. Fluids Dyn. Mater. Process. 2022, 18, 145–158. [Google Scholar] [CrossRef]
- Kuang, Y.; Lin, B. Unwatched Pollution Reduction: The Effect of Natural Gas Utilization On Air Quality. Energy 2023, 273, 127247. [Google Scholar] [CrossRef]
- Kuang, Y.M.; Lin, B.Q. Natural Gas Resource Utilization, Environmental Policy and Green Economic Development: Empirical Evidence From China. Resour. Policy 2022, 79, 102992. [Google Scholar] [CrossRef]
- Li, W.; Lu, C. The Multiple Effectiveness of State Natural Gas Consumption Constraint Policies for Achieving Sustainable Development Targets in China. Appl. Energy 2019, 235, 685–698. [Google Scholar] [CrossRef]
- Jia, A.; Cheng, G.; Chen, W.; Li, Y. Forecast of natural gas supply and demand in China under the background of “Dual Carbon Targets”. Pet. Explor. Dev. 2023, 50, 492–504. [Google Scholar] [CrossRef]
- Liu, H.; Liu, Y.; Wang, C.; Song, Y.; Jiang, W.; Li, C.; Zhang, S.; Hong, B. Natural Gas Demand Forecasting Model Based On Lasso and Polynomial Models and its Application: A Case Study of China. Energies 2023, 16, 4268. [Google Scholar] [CrossRef]
- Ou, J.; Chen, Y. A Novel Dynamic Parameter Discrete Grey Model and its Application. Energy Rep. 2023, 9, 4941–4950. [Google Scholar] [CrossRef]
- Jenkins, C.M.; Horie, Y.; Wu, C.Y. Particle Velocity and Structures in Blast Waves Imaged Using Particle Image Velocimetry. Int. J. Multiph. Flow 2010, 36, 88–91. [Google Scholar] [CrossRef]
- Gao, Q.; Wang, H.; Shen, G. Review On Development of Volumetric Particle Image Velocimetry. Chin. Sci. Bull. 2013, 58, 4541–4556. [Google Scholar] [CrossRef]
- Liu, S.; Xu, J.; Gong, H.; Yu, K. Experimental Comparison of Piv-Based Pressure Measurements in Supersonic Flows with Shock Waves. Meas. Sci. Technol. 2019, 30, 105201. [Google Scholar] [CrossRef]
- Li, W.; Li, Z.; Deng, W.; Ji, L.; Qiu, Y.; Chen, H. Particle Image Velocimetry Flowmeter for Natural Gas Applications. Flow Meas. Instrum. 2021, 82, 102072. [Google Scholar]
- Ranz, W.E. Some Experiments On Orifice Sprays. Can. J. Chem. Eng. 1958, 36, 175–181. [Google Scholar] [CrossRef]
- Atmaca, M.; Cetin, B.; Ezgi, C.; Kosa, E. CFD Analysis of Jet Flows Ejected From Different Nozzles. Int. J. Low-Carbon Technol. 2021, 16, 940–945. [Google Scholar] [CrossRef]
- Muhammad, N.; Alharbi, K.A.M. OpenFOAM for Computational Hydrodynamics Using Finite Volume Method. Int. J. Mod. Phys. B 2023, 37, 2350026. [Google Scholar] [CrossRef]
- Rehman, S.; Muhammad, N. Mathematical Analysis of Nonlinear Models and their Role in Dynamics. Mod. Phys. Lett. B 2023. [Google Scholar] [CrossRef]
- Cao, W.; Altoum, S.H.; Othman, H.A.; Alzubaidi, A.M.; Alghawli, A.S. Numerical Modeling for Thermal Behavior of Nanomaterial Laminar Flow and Convective Heat Transfer in Appearance of Magnetic Field. Case Stud. Therm. Eng. 2023, 42, 102727. [Google Scholar] [CrossRef]
- Upadhyay, P.; Valentich, G.; Kumar, R.; Alvi, F. Flow and Acoustic Characteristics of Non-Axisymmetric Jets at Subsonic Conditions. Exp. Fluids 2017, 58, 52. [Google Scholar] [CrossRef]
- Xiao, S.; Ge, Z.; Ren, Q.; Liu, J.; Wang, H. Numerical Analysis On the Flow Field Structure and Deflection Characteristics of Water Jets Under Nozzle Moving Conditions. Eng. Appl. Comp. Fluids 2020, 14, 1279–1301. [Google Scholar] [CrossRef]
- Cai, C.; Ren, K.; Li, Q. Numerical Simulation of the Flow Field Structure of Liquid Nitrogen Jet. Therm. Sci. 2019, 23, 1337–1343. [Google Scholar] [CrossRef]
- Bi, R.; Ali, S.; Savory, E.; Zhang, C. A Numerical Modelling Investigation of the Development of a Human Cough Jet. Eng. Comput. 2022, 39, 773–791. [Google Scholar] [CrossRef]
- Hou, R.; Huang, C.; Zhu, H. Numerical Simulation Ultrahigh Waterjet (Wj) Flow Field with the High-Frequency Velocity Vibration at the Nozzle Inlet. Int. J. Adv. Manuf. Tech. 2014, 71, 1087–1092. [Google Scholar] [CrossRef]
- Lee, C.; Ozawa, Y.; Haga, T.; Nonomura, T.; Asai, K. Comparison of Three-Dimensional Density Distribution of Numerical and Experimental Analysis for Twin Jets. J. Vis. 2021, 24, 1173–1188. [Google Scholar] [CrossRef]
- Hart, J.T.; Karim, M.R.; Bhuiyan, A.A.; Witt, P.; Naser, J. Numerical Modelling of Unsteady Flow Behaviour in the Rectangular Jets with Oblique Opening. Alex. Eng. J. 2016, 55, 2309–2320. [Google Scholar] [CrossRef]
- Miltner, M.; Jordan, C.; Harasek, M. CFD Simulation of Straight and Slightly Swirling Turbulent Free Jets Using Different Rans-Turbulence Models. Appl. Therm. Eng. 2015, 89, 1117–1126. [Google Scholar] [CrossRef]
- Zheng, J.X.; Wang, X.K.; Tan, D.S.; Tan, S.K. Experimental Investigation of Interactions of Three Co-Planar and Converging Jets. Exp. Fluids 2014, 55, 1733. [Google Scholar] [CrossRef]
- Afzal, A.; Ansari, Z.; Faizabadi, A.R.; Ramis, M.K. Parallelization Strategies for Computational Fluid Dynamics Software: State of the Art Review. Arch. Comput. Methods Eng. 2017, 24, 337–363. [Google Scholar] [CrossRef]
- Dai, Y.; Zhang, Y.; Li, X. Numerical and Experimental Investigations On Pipeline Internal Solid-Liquid Mixed Fluid for Deep Ocean Mining. Ocean Eng. 2021, 220, 108411. [Google Scholar] [CrossRef]
- Kang, H.; Tian, Z.; Chen, G.; Li, L.; Wang, T. Application of Pod Reduced-Order Algorithm On Data-Driven Modeling of Rod Bundle. Nucl. Eng. Technol. 2022, 54, 36–48. [Google Scholar] [CrossRef]
- Lee, S.J. Pod Analysis of Near-Wake Structures of an Elliptic Cylinder Adjacent to a Free Surface. J. Vis. 2004, 7, 179–186. [Google Scholar]
- Sakai, M.; Sunada, Y.; Imamura, T.; Rinoie, K. Experimental and Numerical Studies on Flow behind a Circular Cylinder Based on POD and DMD. Trans. Jpn. Soc. Aeronaut. Space Sci. 2015, 58, 100–107. [Google Scholar] [CrossRef]
- El-Adawy, M.; Heikal, M.R.; Aziz, A.R.A.; Adam, I.K.; Ismael, M.A.; Babiker, M.E.; Baharom, M.B.; Firmansyah; Abidin, E.Z.Z. On the Application of Proper Orthogonal Decomposition (Pod) for in-Cylinder Flow Analysis. Energies 2018, 11, 2261. [Google Scholar] [CrossRef]
- Zhang, Y.; Vanierschot, M. Proper Orthogonal Decomposition Analysis of Coherent Motions in a Turbulent Annular Jet. Appl. Math. Mech. 2021, 42, 1297–1310. [Google Scholar] [CrossRef]
- Jang, Y.I.; Lee, S.J. Pod Analysis On the Sphere Wake at a Subcritical Reynolds Number. J. Vis. 2010, 13, 311–318. [Google Scholar] [CrossRef]
- Deep, D.; Sahasranaman, A.; Senthilkumar, S. POD Analysis of the Wake Behind a Circular Cylinder with Splitter Plate. Eur. J. Mech. B Fluids 2022, 93, 1–12. [Google Scholar] [CrossRef]
- Wang, M.; Cao, S.; Cao, J. POD-Based Analysis of Time-Resolved Tornado-Like Vortices. Wind Struct. 2021, 33, 13–27. [Google Scholar]
- Wu, W.; Zhou, C. A Numerical Study of the Tip Wake of a Wind Turbine Impeller Using Extended Proper Orthogonal Decomposition. Fluid Dyn. Mater. Process. 2020, 16, 883–901. [Google Scholar] [CrossRef]
- Apacoglu, B.; Paksoy, A.; Aradag, S. CFD Analysis and Reduced Order Modeling of Uncontrolled and Controlled Laminar Flow Over a Circular Cylinder. Eng. Appl. Comput. Fluid Mech. 2011, 5, 67–82. [Google Scholar] [CrossRef]
- Sen, U.; Mukhopadhyay, A.; Sen, S. Effects of Fluid Injection on Dynamics of Flow Past a Circular Cylinder. Eur. J. Mech. B Fluids 2017, 61, 187–199. [Google Scholar] [CrossRef]
- Chen, H.; Qiu, Y.; Wang, H. Numerical and Experimental Investigation of Flow Characteristics in Natural Gas Pipe. AIP Adv. 2023, 13, 045017. [Google Scholar] [CrossRef]
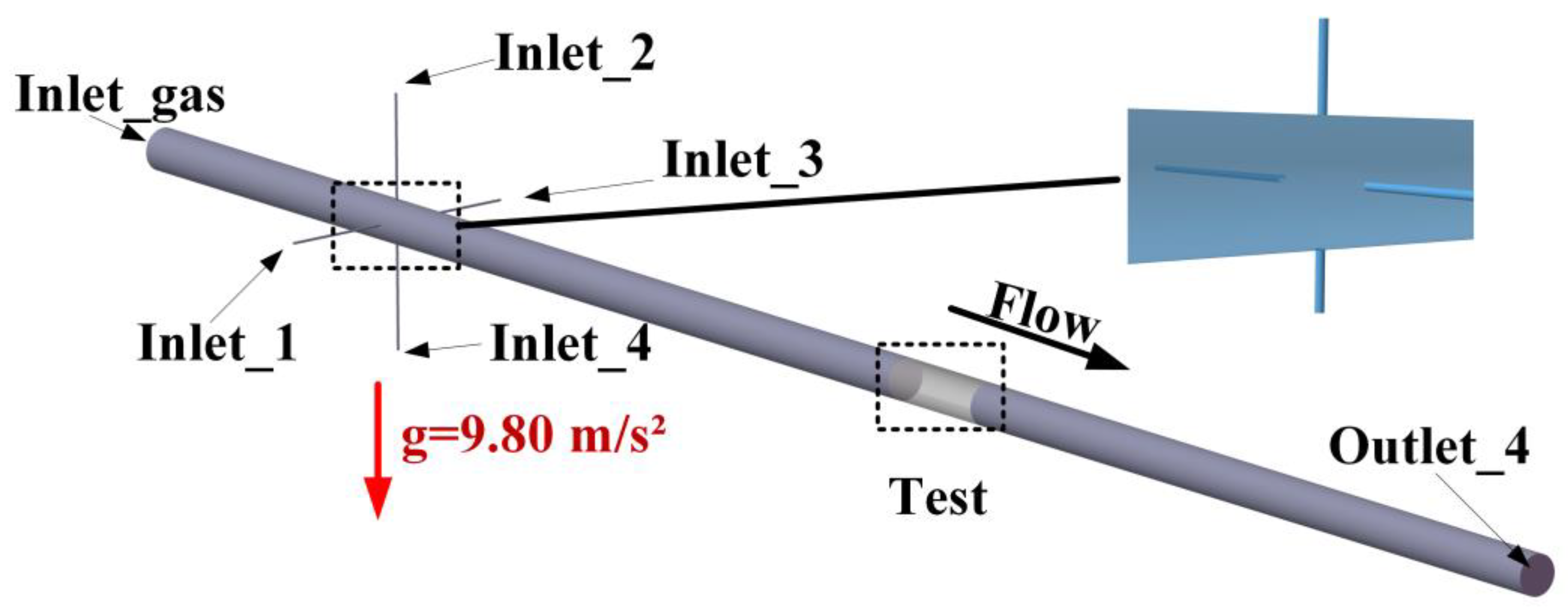





| Diameter of Main Pipe (mm) | Main Length (mm) | Length of Bypass Pipe (mm) | Diameter of Bypass Pipe (mm) | Number of Bypass Pipes |
|---|---|---|---|---|
| 100 | 5000 | 200 | 6 | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Lu, J.; Zhao, H.; Qiu, Y. Vortex of a Symmetric Jet Structure in a Natural Gas Pipeline via Proper Orthogonal Decomposition. Processes 2024, 12, 418. https://doi.org/10.3390/pr12020418
Li L, Lu J, Zhao H, Qiu Y. Vortex of a Symmetric Jet Structure in a Natural Gas Pipeline via Proper Orthogonal Decomposition. Processes. 2024; 12(2):418. https://doi.org/10.3390/pr12020418
Chicago/Turabian StyleLi, Lihao, Jiaxing Lu, Haoyu Zhao, and Yilong Qiu. 2024. "Vortex of a Symmetric Jet Structure in a Natural Gas Pipeline via Proper Orthogonal Decomposition" Processes 12, no. 2: 418. https://doi.org/10.3390/pr12020418
APA StyleLi, L., Lu, J., Zhao, H., & Qiu, Y. (2024). Vortex of a Symmetric Jet Structure in a Natural Gas Pipeline via Proper Orthogonal Decomposition. Processes, 12(2), 418. https://doi.org/10.3390/pr12020418











