The Splitter Blade Pump–Turbine in Pump Mode: The Hump Characteristic and Hysteresis Effect Flow Mechanism
Abstract
:1. Introduction
2. Entropy Theory
2.1. Turbulent Entropy Production
2.2. Entropy Wall Function
3. Numerical Model and Schemes
3.1. Pump–Turbine Model
3.2. Numerical Schemes and Boundary Conditions
3.3. Grid Independence Validation
4. Analysis of Numerical Results
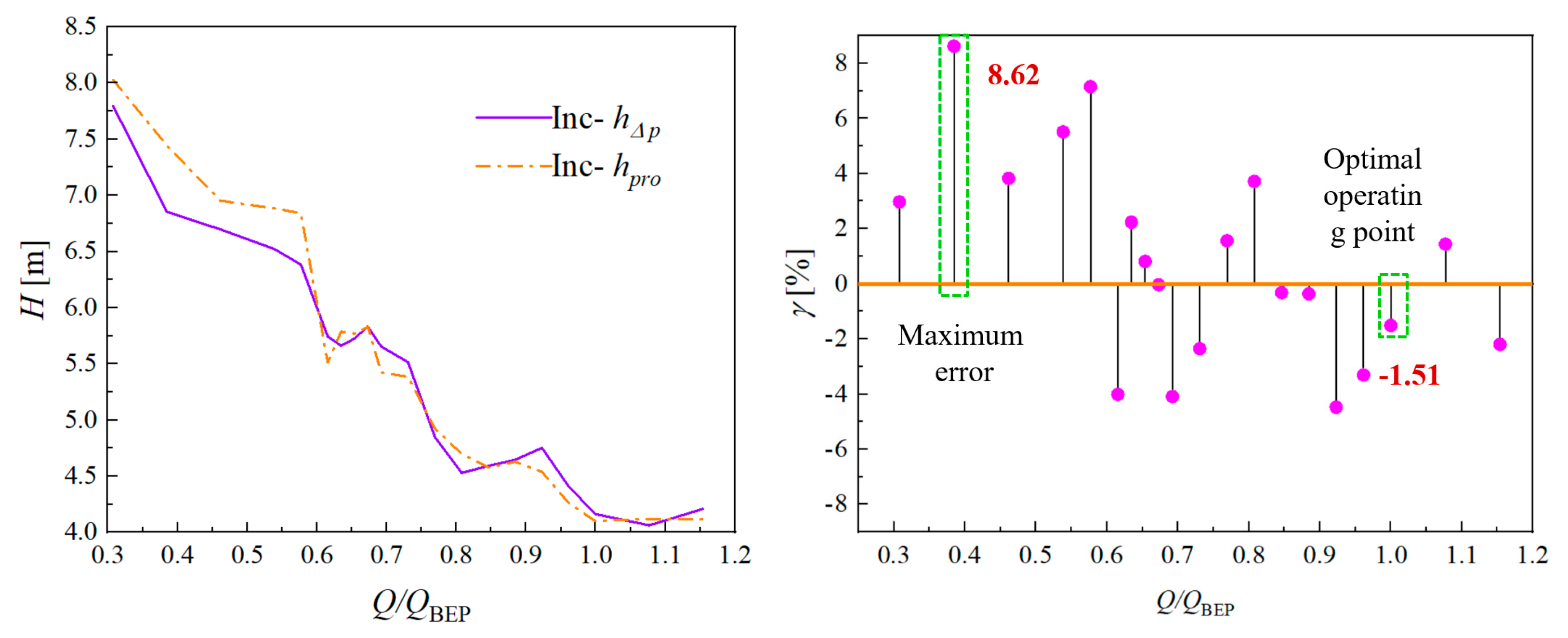
4.1. Characteristic Curve of Flow Head
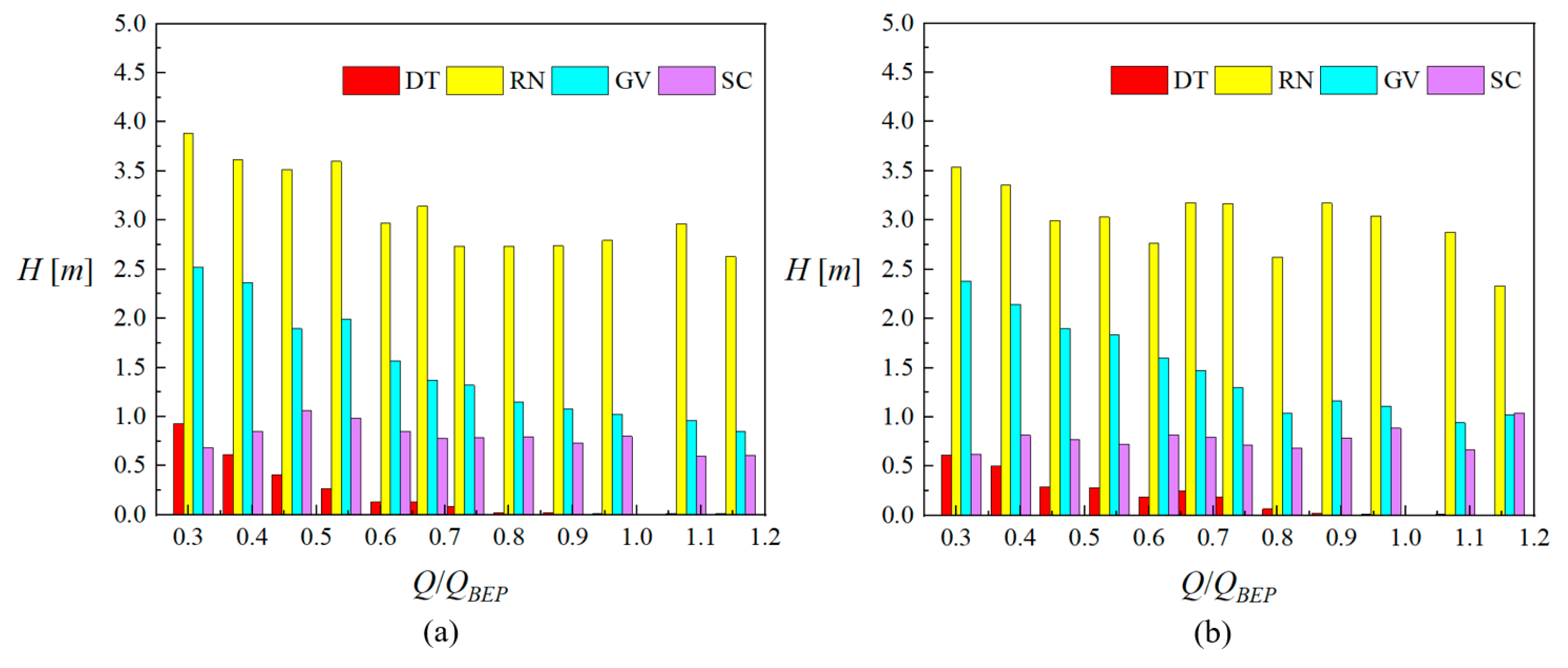
4.2. Calculation of Hydraulic Losses
5. Detailed Distribution of Local Entropy Production Rate
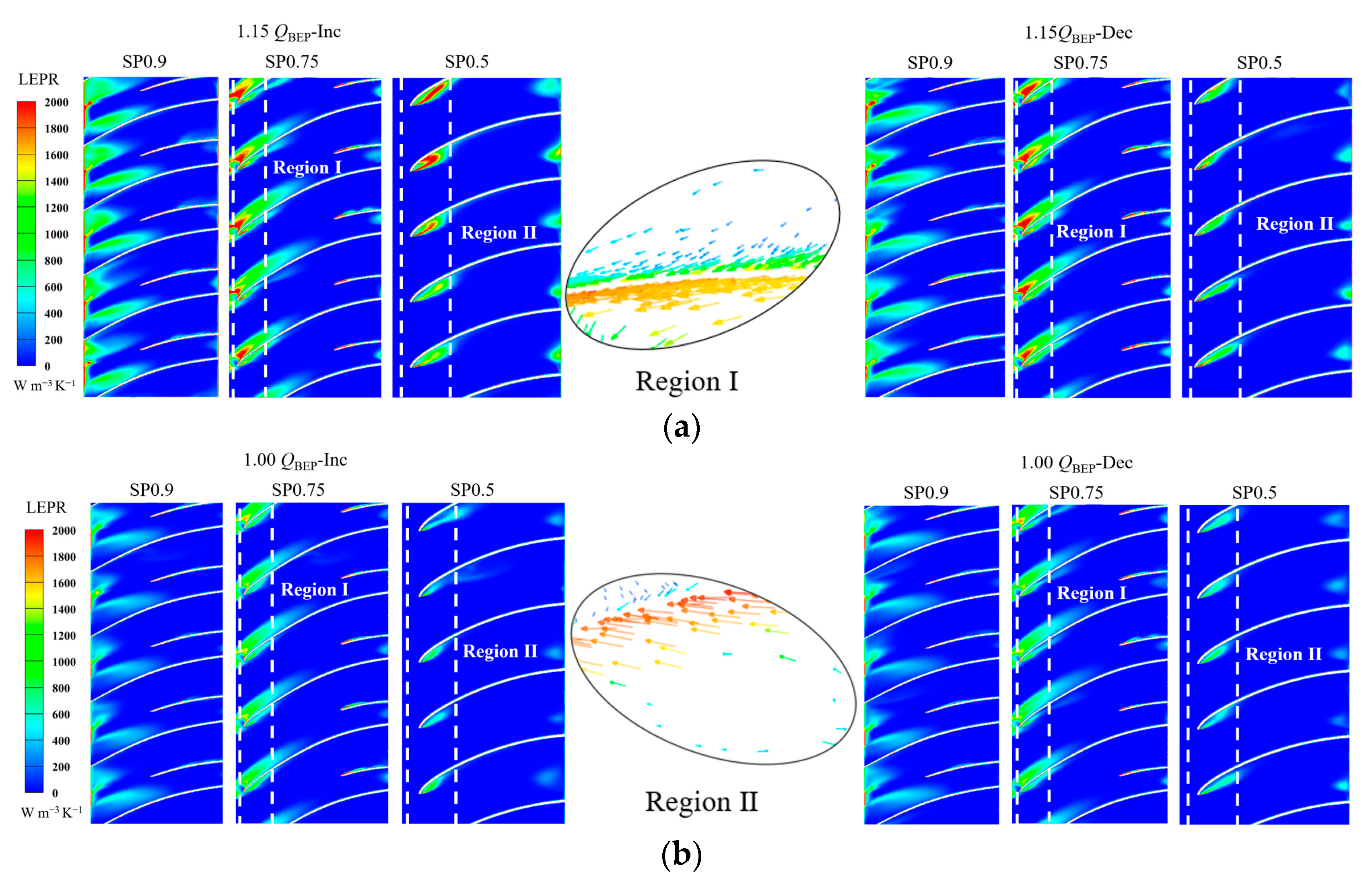
5.1. LEPR Distribution in the Runner
5.2. LEPR Distribution in the Guide/Stay Vanes
5.3. LEPR Distribution in the Draft Tube
5.4. LEPR Distribution on the Wall
6. Conclusions
- As with the traditional pump–turbine, the pump–turbine with diverter vanes also has hump characteristics and hysteresis effects in the pumping condition.
- The hydraulic losses of the runner are mainly distributed in the leading and trailing edges of the long blades and the suction surface area, while the energy loss near the short blades is very low. This is mainly due to the energy loss caused by the high velocity gradient at the wall surface and the resulting flow disturbance.
- Compared with the traditional runner [40], the pumping condition of the vortex of the impeller in the pump–turbine with the splitter blade in was significantly reduced. It was found that in the pumping condition, the hydraulic loss at the outlet of the runner was concentrated in the vicinity of the trailing edge of the long blades, whereas there was no such phenomenon in the case of the short blades. This indicates that the use of a combination of splitter blades contributes to the energy performance of the pump–turbine.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| H | head of pump–turbine [m] |
| Q | discharge [m3·s−1] |
| GVO | guide vane opening [mm] |
| EnD | energy factor |
| TnD | torque factor |
| QnD | discharge factor |
| T | temperature [K] |
| ρ | density [kg/m3] |
| u | velocity [m·s−1] |
| Fx | body force [N] |
| μ | hydrodynamic viscosity [Pa·s] |
| entropy production rate of time-averaged movement [kW m−3 K−1] | |
| entropy production rate of velocity fluctuation [kW m−3 K−1] | |
| β | Constant = 0.09 |
| μeff | effective dynamic viscosity [kg m−1 s−1] |
| μt | turbulent dynamic viscosity [kg m−1 s−1] |
| ε | turbulent dissipation rate [m2·s−3] |
| ω | turbulent eddy frequency [s−1] |
| k | turbulent energy [m2/s2] |
| y+ | Dimensionless distance |
| η | efficiency [%] |
| γ | relative error [%] |
| δij | Crowe dick symbol |
| Dec | the direction of decreasing discharge |
| Inc | the direction of increasing discharge |
| BEP | best efficiency point |
| h∆P | Head loss computed by differential pressure method |
| hpro | Head loss computed by entropy production method |
References
- Feng, C. Study on System Identification and Control Law under Complex Conditions of Pumped Law under Complex Conditions of Pumped. Ph.D. Thesis, Huazhong University of Science & Technology, Wuhan, China, May 2020. [Google Scholar]
- Lu, G.C. Investigations on the Influence of the Flow Separation in Guide Vane Channels on the Positive Slope on the Pump Performance Curve in a Pump-Turbine. Ph.D. Thesis, Tsinghua University, Beijing, China, June 2018. [Google Scholar]
- Jese, U.; Fortes-Patella, R.; Dular, M. Numerical study of Pump-turbine instabilities under pumping mode off-design conditions. In Proceedings of the ASME-JSME-KSME Joint Fluids Engineering Conference, Seoul, Republic of Korea, 26–31 July 2015. [Google Scholar] [CrossRef]
- Yang, J.; Pavesi, G.; Yuan, S.; Cavazzini, G.; Ardizzon, G. Experimental Characterization of a Pump-Turbine in Pump Mode at Hump Instability Region. J. Fluids Eng.-Trans. ASME 2015, 137, 051109. [Google Scholar] [CrossRef]
- Li, D.Y.; Han, L.; Wang, H.; Gong, R.; Wei, X.; Qin, D. Flow characteristics prediction in pump mode of a pump turbine using large eddy simulation. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2017, 231, 961–977. [Google Scholar] [CrossRef]
- Braun, O.; Kueny, J.L.; Avellan, F. Numerical analysis of flow phenomena related to the unstable energy-discharge characteristic of a pump-turbine in pump mode. In Proceedings of the ASME Fluids Engineering Division Summer Conference, Houston, TX, USA, 19–23 June 2005; pp. 1075–1080. [Google Scholar] [CrossRef]
- Liu, J.; Liu, S.; Wu, Y.; Jiao, L.; Wang, L.; Sun, Y. Numerical investigation of the hump characteristic of a pump–turbine based on an improved cavitation model. Comput. Fluids 2012, 68, 105–111. [Google Scholar] [CrossRef]
- Lu, G.; Zuo, Z.; Sun, Y.; Liu, D.; Tsujimoto, Y.; Liu, S. Experimental evidence of cavitation influences on the positive slope on the pump performance curve of a low specific speed model pump-turbine. Renew. Energy 2017, 113, 1539–1550. [Google Scholar] [CrossRef]
- Li, D.; Zhu, Y.; Lin, S.; Gong, R.; Wang, H.; Luo, X. Cavitation effects on pressure fluctuation in pump-turbine hump region. J. Energy Storage 2022, 47, 103936. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Y.; Liu, C.; Han, W. Study on Unsteady internal flow characteristics in hump zone of mixed flow pump turbine. J. Gansu Sci. 2017, 29, 54–58. [Google Scholar] [CrossRef]
- Qin, Y.L. Investigation on the Influence of Geometric Factors at Runner Outlet on the Hump Characteristics of a Pump-Turbine. Master’s Thesis, Harbin Institute of Technology, Harbin, China, June 2020. [Google Scholar] [CrossRef]
- Ciocan, G.; Desvignes, V.; Combes, J.; Parkinson, E.; Kueny, J. Experimental and numerical unsteady analysis of rotor-stator interaction in a pump-turbine. In Proceedings of the XIX IAHR International Symposium on Hydraulic Machinery and Cavitation, Singapore, 9–11 September 1998; pp. 210–219. [Google Scholar]
- Li, X.; Zhu, Z.; Li, Y.; Chen, X. Experimental and numerical investigations of head-flow curve instability of a single-stage centrifugal pump with volute casing. Proc. Inst. Mech. Eng. Part A J. Power Energy 2016, 230, 633–647. [Google Scholar] [CrossRef]
- Xiao, Y.; Yao, Y.; Wang, Z.; Zhang, J.; Luo, Y.; Zeng, C.; Zhu, W. Hydrodynamic mechanism analysis of the pump hump district for a pump-turbine. Eng. Comput. 2016, 33, 957–976. [Google Scholar] [CrossRef]
- Ye, W.X.; Ikuta, A.; Chen, Y.N.; Miyagawa, K.; Luo, X.W. Numerical simulation on role of the rotating stall on the hump characteristic in a mixed flow pump using modified partially averaged Navier-Stokes model. Renew. Energy 2020, 166, 91–107. [Google Scholar] [CrossRef]
- Ran, H.J.; Zhang, Y.; Luo, X.W.; Xu, H. Numerical simulation of the positive-slope performance curve of a reversible hydro-turbine in pumping mode. J. Hydroelectr. Eng. 2011, 30, 175–179. [Google Scholar] [CrossRef]
- Guedes, A.; Kueny, J.L.; Ciocan, G.D.; Avellan, F. Unsteady Rotor-Stator Analysis of A Hydraulic Pump-Turbine—CFD and Experimental Approach. In Proceedings of the 21st IAHR Symposium on Hydraulic Machinery and Systems, Lausanne, Switzerland, 9–12 September 2002. [Google Scholar]
- Shibata, A.; Hiramatsu, H.; Komaki, S.; Miyagawa, K.; Maeda, M.; Kamei, S.; Hazama, R.; Sano, T.; Iino, M. Study of flow instability in off design operation of a multistage centrifugal pump. J. Mech. Sci. Technol. 2016, 30, 493–498. [Google Scholar] [CrossRef]
- Wang, L.Q.; Liu, J.T.; Zhang, L.F.; Qin, D.Q.; Jiao, L. Low flow s fluctuation characteristics in pump-turbine s pump mode. J. Zhejiang Univ. Eng. Sci. 2011, 45, 1239–1243. [Google Scholar] [CrossRef]
- Sun, Y.K. Instability Characteristics and Instability Characteristics and Pump Performance Curves of a Low-Specific-Speed Pump-Turbine. Ph.D. Thesis, Tsinghua University, Beijing, China, May 2016. [Google Scholar]
- Chen, J.X. Experimental Investigation of Hysteresis Characteristics in the Hump and S-Shaped Region of a Pump-Turbine. Master’s Thesis, Harbin Institute of Technology, Harbin, China, September 2017. [Google Scholar]
- Li, D.Y.; Chang, H.; Zuo, Z.G.; Wang, H.J.; Li, Z.G.; Wei, X.Z. Experimental investigation of hysteresis on pump performance characteristics of a model pump-turbine with different guide vane openings. Renew. Energy 2020, 149, 652–663. [Google Scholar] [CrossRef]
- Li, D.Y.; Wang, H.J.; Chen, J.X.; Nielsen, T.K.; Qin, D.Q. Hysteresis Characteristic in the Hump Region of a Pump-Turbine Model. Energies 2016, 9, 620. [Google Scholar] [CrossRef]
- Li, D.Y.; Wang, H.J.; Qin, Y.L.; Han, L.; Wei, X.Z.; Qin, D.Q. Entropy production analysis of hysteresis characteristic of a pump-turbine model. Energy Convers. Manag. 2017, 149, 175–191. [Google Scholar] [CrossRef]
- Li, D.Y.; Gong, R.Z.; Wang, H.J.; Fu, W.W.; Wei, X.Z.; Liu, Z.S. Fluid flow analysis of drooping phenomena in pump mode for a given guide vane setting of a pump-turbine model. J. Zhejiang Univ. Sci. A 2015, 16, 851–863. [Google Scholar] [CrossRef]
- Tao, R.; Xiao, R.F.; Yang, W.; Liu, W.C. Hump characteristic of reversible pump-turbine in pump mode. J. Drain. Irrig. Mach. Eng. 2014, 32, 936. [Google Scholar] [CrossRef]
- Kock, F.; Herwig, H. Local entropy production in turbulent shear flows: A high-Reynolds number model with wall functions. Int. J. Heat Mass Transf. 2004, 7, 2205–2215. [Google Scholar] [CrossRef]
- Li, D.Y.; Gong, R.Z.; Wang, H.J.; Xiang, G.M.; Wei, X.Z.; Qin, D.Q. Entropy production analysis for hump characteristics of a pump turbine model. Chin. J. Mech. Eng. 2016, 29, 803–812. [Google Scholar] [CrossRef]
- Lu, J.L.; Wang, L.K.; Liao, W.L.; Zhao, Y.P.; Ji, Q.F. Entropy production analysis for vortex rope of a turbine model. J. Hydraul. Eng. 2019, 50, 233–241. [Google Scholar] [CrossRef]
- Zeng, H.J.; Li, Z.G.; Li, D.Y.; Li, Q.F. Relationship between flow pulsation and entropy production rate of pump turbine. J. Drain. Irrig. Mach. Eng. 2022, 40, 777–784. [Google Scholar]
- Li, D.Y. Investigation on Flow Mechanism and Transient Characteristics in Hump Region of A Pump-Turbine. Ph.D, Thesis, Harbin Institute of Technology, Harbin, China, June 2017. [Google Scholar]
- Li, D.K.; Gui, Z.H.; Yan, X.T.; Zheng, Y.; Kan, K. Hydraulic loss distribution of pump-turbine operated in pump mode based on entropy production method. South North Water Transf. Water Sci. Technol. 2023, 21, 390–397. [Google Scholar]
- Chen, H.Y. Application of Long-and Short-Blade Runner in Qingyuan Pumped Storage Power Station. Mech. Electr. Tech. Hydropower Stn. 2016, 39, 5–8. [Google Scholar] [CrossRef]
- Du, R.X.; Wang, Q.; Enomoto, Y.; Chen, H.Y. Application of Splitter Blades Runner Pump Turbine in Qingyuan Pump Storage Station. Hydropower Pumped Storage 2016, 2, 39–44. [Google Scholar] [CrossRef]
- Mathieu, J.; Scott, J. An Introduction to Turbulent Flow; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Herwig, H.; Kock, F. Direct and indirect methods of calculating entropy generation rates in turbulent convective heat transfer problems. Heat Mass Transf. 2007, 43, 207–215. [Google Scholar] [CrossRef]
- Melzer, S.; Pesch, A.; Schepeler, S.; Kalkkuhl, T.; Skoda, R. Three-Dimensional Simulation of Highly Unsteady and Isothermal Flow in Centrifugal Pumps for the Local Loss Analysis Including a Wall Function for Entropy Production. J. Fluids Eng.-Trans. ASME 2020, 142, 111209. [Google Scholar] [CrossRef]
- Li, D.; Wang, H. Numerical simulation of hysteresis characteristic in the hump region of a pump-turbine model. Renew. Energy 2018, 115, 433–447. [Google Scholar] [CrossRef]
- Li, Z.; Liu, X.; Xu, L. A Review of Research on Hump Characteristics of High-head Pump-turbine. Hydropower Pumped Storage 2023, 9, 39–47. [Google Scholar] [CrossRef]
- Li, D.; Zuo, Z.; Wang, H.; Liu, S.; Wei, X.; Qin, D. Review of positive slopes on pump performance characteristics of pump-turbines. Renew. Sustain. Energy Rev. 2019, 112, 901–916. [Google Scholar] [CrossRef]


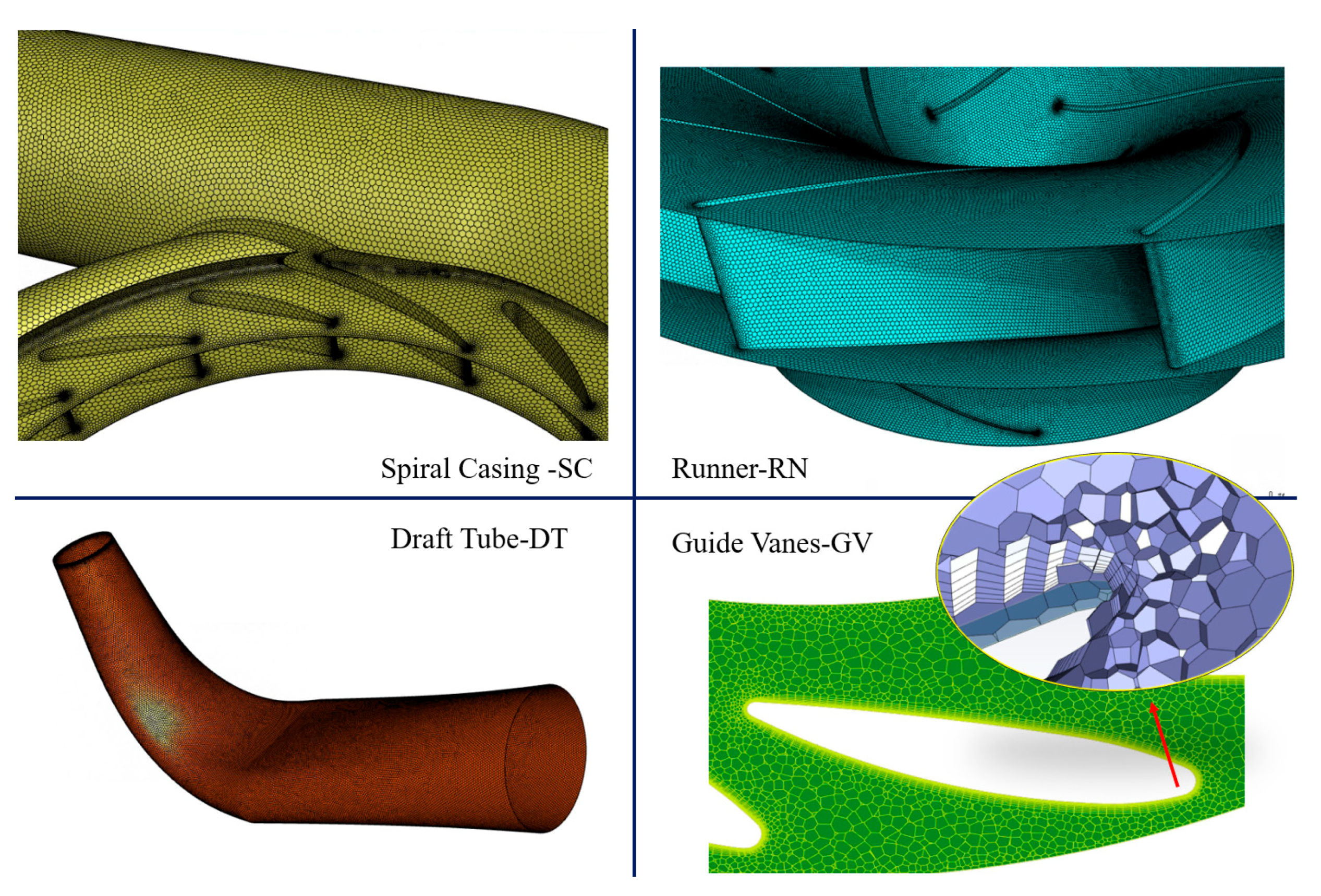









| Parameter | Symbol | Value |
|---|---|---|
| Specific speed | nq | 31.633 |
| Runner blade number (long) | Zr1 | 5 |
| Runner blade number (short) | Zr2 | 5 |
| Guide vane number | Zg | 16 |
| Stay vane number | Zs | 16 |
| Runner outlet | D1m | 540.5 mm |
| Runner inlet | D2m | 287.5 mm |
| Guide vane height | B0 | 52 mm |
| Component | Case1 | Case2 | Case3 |
|---|---|---|---|
| Draft tube | 499,451 | 931,463 | 1,107,572 |
| Runner | 2,576,221 | 3,636,685 | 5,997,393 |
| Guide vane | 887,352 | 1,357,038 | 1,840,524 |
| Stay vane and volute | 1,874,117 | 2,372,530 | 2,563,200 |
| Total | 5,837,141 | 8,297,716 | 11,508,689 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, G.; Luo, Z.; Guo, T.; Zhang, X.; Shan, R.; Dai, L. The Splitter Blade Pump–Turbine in Pump Mode: The Hump Characteristic and Hysteresis Effect Flow Mechanism. Processes 2024, 12, 324. https://doi.org/10.3390/pr12020324
Dong G, Luo Z, Guo T, Zhang X, Shan R, Dai L. The Splitter Blade Pump–Turbine in Pump Mode: The Hump Characteristic and Hysteresis Effect Flow Mechanism. Processes. 2024; 12(2):324. https://doi.org/10.3390/pr12020324
Chicago/Turabian StyleDong, Guanghe, Zhumei Luo, Tao Guo, Xiaoxu Zhang, Rong Shan, and Linsheng Dai. 2024. "The Splitter Blade Pump–Turbine in Pump Mode: The Hump Characteristic and Hysteresis Effect Flow Mechanism" Processes 12, no. 2: 324. https://doi.org/10.3390/pr12020324





