Discrete-Element-Method-Based Determination of Particle-Level Inputs for the Continuum Theory of Flows with Moderately Cohesive Particles
Abstract
:1. Introduction
2. Methods
2.1. Extraction of Inputs to the Continuum Theory for Cohesive Particles
2.1.1. System Overview: Oscillating Shear Flow
2.1.2. DEM Simulation of Oscillating Shear Flow
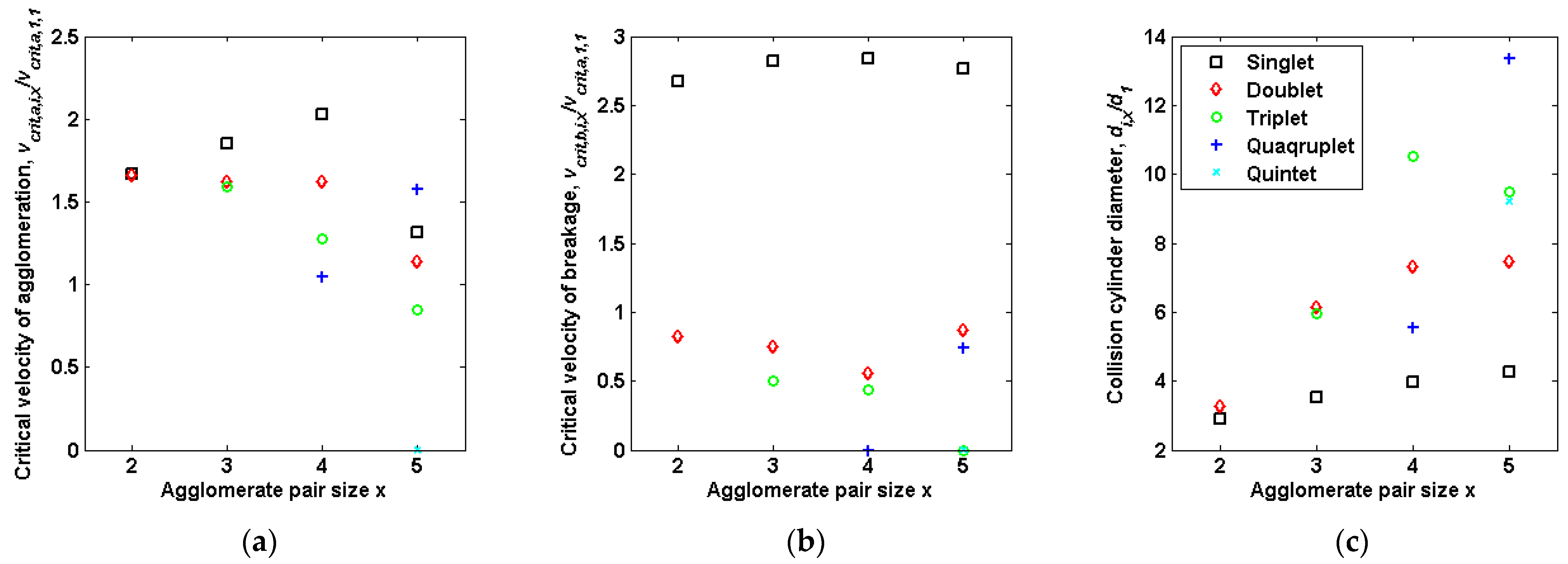
2.1.3. DEM Extraction of Cohesion-Specific Inputs for Continuum Theory
2.2. Testing of the Continuum Theory for Cohesive Particles and DEM-Based Inputs
2.2.1. System Description: Unbounded Riser
2.2.2. Continuum Theory Simulations
2.2.3. DEM Simulations
3. Results and Discussion
3.1. Extraction of Continuum (Population Balance) Inputs from the DEM of Oscillating Shear Flow
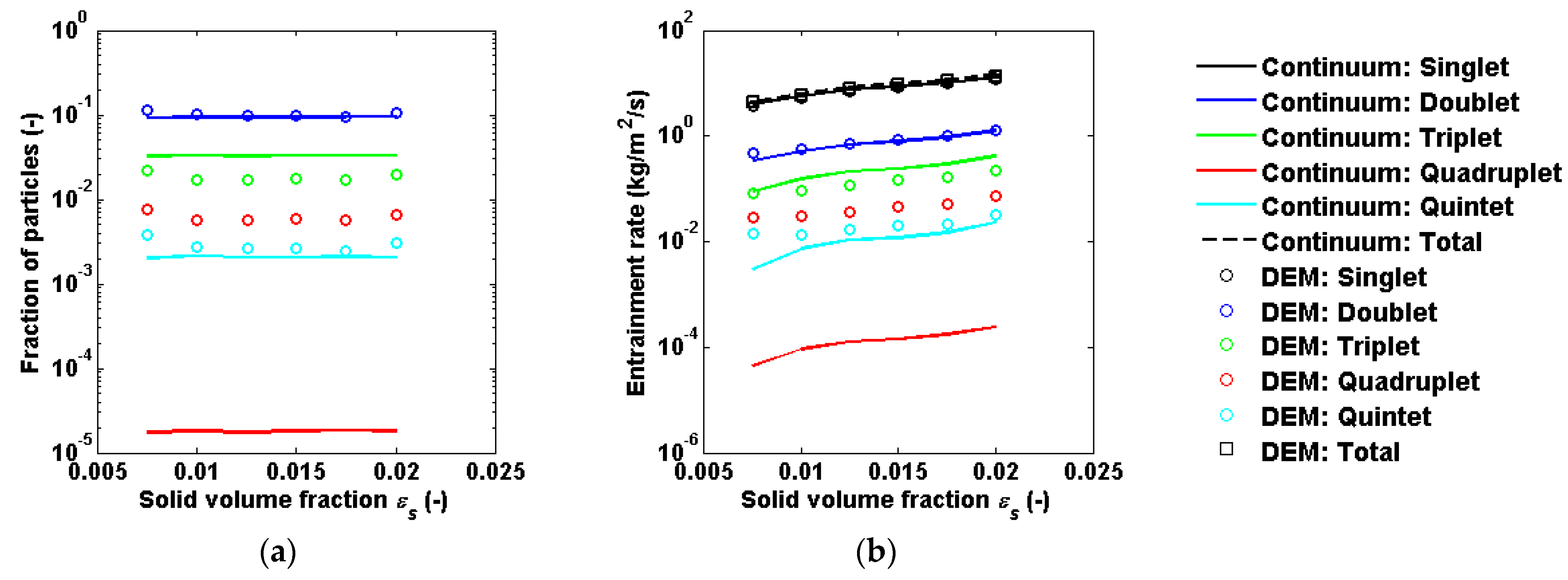
3.2. Testing of the Continuum Theory in the Unbounded Riser
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A. Drag Closures from Extension [53] of Koch–Hill–Ladd [54]
Appendix B. Continuum Theory Closures from Iddir and Arastoopour [52]
References
- Visser, J. Van der Waals and other cohesive forces affecting powder fluidization. Powder Technol. 1989, 58, 1–10. [Google Scholar] [CrossRef]
- Henthorne, K.; Hrenya, C. Particle cohesion. In Particle Theory and Applications; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Galvin, J.E.; Benyahia, S. The effect of cohesive forces on the fluidization of aeratable powders. AIChE J. 2013, 60, 473–484. [Google Scholar] [CrossRef]
- Castellanos, A.; Valverde, J.M.; Quintanilla, M.A.S. Aggregation and sedimentation in gas-fluidized beds of cohesive powders. Phys. Rev. E 2001, 64, 041304. [Google Scholar] [CrossRef] [PubMed]
- Geldart, D.; Harnby, N.; Wong, A. Fluidization of cohesive powders. Powder Technol. 1984, 37, 25–37. [Google Scholar] [CrossRef]
- Tomas, J. Fundamentals of cohesive powder consolidation and flow. Granul. Matter 2004, 6, 75–86. [Google Scholar] [CrossRef]
- Calvert, G.; Ghadiri, M.; Tweedie, R. Aerodynamic dispersion of cohesive powders: A review of understanding and technology. Adv. Powder Technol. 2009, 20, 4–16. [Google Scholar] [CrossRef]
- Chew, J.W.; Cahyadi, A.; Hrenya, C.M.; Karri, R.; Cocco, R.A. Review of entrainment correlations in gas–solid fluidization. Chem. Eng. J. 2015, 260, 152–171. [Google Scholar] [CrossRef]
- Shabanian, J.; Jafari, R.; Chaouki, J. Fluidization of Ultrafine Powders. Int. Rev. Chem. Eng. 2012, 4, 16–50. [Google Scholar]
- Mikami, T.; Kamiya, H.; Horio, M. Numerical simulation of cohesive powder behavior in a fluidized bed. Chem. Eng. Sci. 1998, 53, 1927–1940. [Google Scholar] [CrossRef]
- Chaudhuri, B.; Mehrotra, A.; Muzzio, F.J.; Tomassone, M.S. Cohesive effects in powder mixing in a tumbling blender. Powder Technol. 2006, 165, 105–114. [Google Scholar] [CrossRef]
- Anand, A.; Curtis, J.S.; Wassgren, C.R.; Hancock, B.C.; Ketterhagen, W.R. Predicting discharge dynamics of wet cohesive particles from a rectangular hopper using the discrete element method (DEM). Chem. Eng. Sci. 2009, 64, 5268–5275. [Google Scholar] [CrossRef]
- Figueroa, I.; Li, H.; McCarthy, J. Predicting the impact of adhesive forces on particle mixing and segregation. Powder Technol. 2009, 195, 203–212. [Google Scholar] [CrossRef]
- Hou, Q.; Zhou, Z.; Yu, A. Micromechanical modeling and analysis of different flow regimes in gas fluidization. Chem. Eng. Sci. 2012, 84, 449–468. [Google Scholar] [CrossRef]
- Liu, P.; LaMarche, C.Q.; Kellogg, K.M.; Hrenya, C.M. Fine-particle defluidization: Interaction between cohesion, Young’s modulus and static bed height. Chem. Eng. Sci. 2016, 145, 266–278. [Google Scholar] [CrossRef]
- Gu, Y.; Ozel, A.; Sundaresan, S. A modified cohesion model for CFD–DEM simulations of fluidization. Powder Technol. 2016, 296, 17–28. [Google Scholar] [CrossRef]
- Ucgul, M.; Fielke, J.M.; Saunders, C. Three-dimensional discrete element modelling (DEM) of tillage: Accounting for soil cohesion and adhesion. Biosyst. Eng. 2015, 129, 298–306. [Google Scholar] [CrossRef]
- Hou, Q.; Dong, K.; Yu, A. DEM study of the flow of cohesive particles in a screw feeder. Powder Technol. 2014, 256, 529–539. [Google Scholar] [CrossRef]
- van der Hoef, M.; Annaland, M.v.S.; Deen, N.; Kuipers, J. Numerical Simulation of Dense Gas-Solid Fluidized Beds: A Multiscale Modeling Strategy. Annu. Rev. Fluid Mech. 2008, 40, 47–70. [Google Scholar] [CrossRef]
- Fullmer, W.D.; Hrenya, C.M. The Clustering Instability in Rapid Granular and Gas-Solid Flows. Annu. Rev. Fluid Mech. 2017, 49, 485–510. [Google Scholar] [CrossRef]
- Cocco, R.; Fullmer, W.; Liu, P.; Hrenya, C. CFD-DEM: Modeling the small to understand the large. Chem. Eng. Prog. 2017, 113, 38–45. [Google Scholar]
- van Wachem, B.; Sasic, S. Derivation, simulation and validation of a cohesive particle flow CFD model. AIChE J. 2008, 54, 9–19. [Google Scholar] [CrossRef]
- Motlagh, A.; Grace, J.; Salcudean, M.; Hrenya, C. New structure-based model for Eulerian simulation of hydrodynamics in gas–solid fluidized beds of Geldart group “A” particles. Chem. Eng. Sci. 2014, 120, 22–36. [Google Scholar] [CrossRef]
- Cameron, I.; Wang, F.; Immanuel, C.; Stepanek, F. Process systems modelling and applications in granulation: A review. Chem. Eng. Sci. 2005, 60, 3723–3750. [Google Scholar] [CrossRef]
- Kellogg, K.M.; Liu, P.; LaMarche, C.Q.; Hrenya, C.M. Continuum theory for rapid cohesive-particle flows: General balance equations and discrete-element-method-based closure of cohesion-specific quantities. J. Fluid Mech. 2017, 832, 345–382. [Google Scholar] [CrossRef]
- Goldschmidt, M.J.V. Hydrodynamic Modelling of Fluidised Bed Spray Granulation. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2001. [Google Scholar]
- Fan, R.; Marchisio, D.L.; Fox, R.O. Application of the direct quadrature method of moments to polydisperse gas–solid fluidized beds. Powder Technol. 2004, 139, 7–20. [Google Scholar] [CrossRef]
- Costa, A.; Folch, A.; Macedonio, G. A model for wet aggregation of ash particles in volcanic plumes and clouds: 1. Theoretical formulation. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Rabinovich, Y.I.; Adler, J.J.; Ata, A.; Singh, R.K.; Moudgil, B.M. Adhesion between Nanoscale Rough Surfaces. J. Colloid Interface Sci. 2000, 232, 17–24. [Google Scholar] [CrossRef]
- Gantt, J.A.; Gatzke, E.P. A stochastic technique for multidimensional granulation modeling. AIChE J. 2006, 52, 3067–3077. [Google Scholar] [CrossRef]
- Fadda, S.; Cincotti, A.; Concas, A.; Pisu, M.; Cao, G. Modelling breakage and reagglomeration during fine dry grinding in ball milling devices. Powder Technol. 2009, 194, 207–216. [Google Scholar] [CrossRef]
- Le, P.; Avontuur, P.; Hounslow, M.; Salman, A. The kinetics of the granulation process: Right from the early stages. Powder Technol. 2009, 189, 149–157. [Google Scholar] [CrossRef]
- Braumann, A.; Kraft, M.; Mort, P.R. Parameter estimation in a multidimensional granulation model. Powder Technol. 2010, 197, 196–210. [Google Scholar] [CrossRef]
- Seville, J.; Willett, C.; Knight, P. Interparticle forces in fluidisation: A review. Powder Technol. 2000, 113, 261–268. [Google Scholar] [CrossRef]
- Donahue, C.M.; Davis, R.H.; Kantak, A.A.; Hrenya, C.M. Mechanisms for agglomeration and deagglomeration following oblique collisions of wet particles. Phys. Rev. E 2012, 86, 021303. [Google Scholar] [CrossRef] [PubMed]
- Donahue, C.M.; Hrenya, C.M.; Davis, R.H.; Nakagawa, K.J.; Zelinskaya, A.P.; Joseph, G.G. Stokes’ cradle: Normal three-body collisions between wetted particles. J. Fluid Mech. 2010, 650, 479–504. [Google Scholar] [CrossRef]
- Davis, R.H.; Rager, D.A.; Good, B.T. Elastohydrodynamic rebound of spheres from coated surfaces. J. Fluid Mech. 2002, 468, 107–119. [Google Scholar] [CrossRef]
- Ennis, G.B.J.; Pfeffer, R. A microlevel-based characterization of granular phenomena. Powder Technol. 1991, 65, 257–272. [Google Scholar] [CrossRef]
- Weber, M.W.; Hoffman, D.K.; Hrenya, C.M. Discrete-particle simulations of cohesive granular flow using a square-well potential. Granul. Matter 2004, 6, 239–354. [Google Scholar] [CrossRef]
- Liu, P.; Kellogg, K.M.; LaMarche, C.Q.; Hrenya, C.M. Dynamics of singlet-doublet collisions of cohesive particles. Chem. Eng. J. 2017, 324, 380–391. [Google Scholar] [CrossRef]
- Kafui, K.D.; Thornton, C. Numerical simulations of impact breakage of a spherical crystalline agglomerate. Powder Technol. 2000, 109, 113–132. [Google Scholar] [CrossRef]
- Ringl, C.; Bringa, E.M.; Bertoldi, D.S.; Urbassek, H.M. Collisions of porous clusters: A granular-mechanics study of compaction and fragmentation. Astrophys. J. 2012, 752, 151. [Google Scholar] [CrossRef]
- Liu, P.; LaMarche, C.Q.; Kellogg, K.M.; Leadley, S.; Hrenya, C.M. Cohesive grains: Bridging microlevel measurements to macrolevel flow behavior via surface roughness. AIChE J. 2016, 62, 3529–3537. [Google Scholar] [CrossRef]
- Liu, P.; LaMarche, C.Q.; Kellogg, K.M.; Hrenya, C.M. A square-force cohesion model and its extraction from bulk measurements. AIChE J. 2018, 64, 2329–2339. [Google Scholar] [CrossRef]
- Frungieri, G.; Boccardo, G.; Buffo, A.; Karimi-Varzaneh, H.A.; Vanni, M. CFD-DEM characterization and population balance modelling of a dispersive mixing process. Chem. Eng. Sci. 2022, 260, 117859. [Google Scholar] [CrossRef]
- Kellogg, K.; Liu, P.; Hrenya, C. Continuum predicton of entrainment rates and agglomeration of gas-fluidized, lightly cohesive particles. Chem. Eng. J. 2019, 199, 249–257. [Google Scholar] [CrossRef]
- Liu, P.; Hrenya, C.M. Cluster-Induced Deagglomeration in Dilute Gravity-Driven Gas-Solid Flows of Cohesive Grains. Phys. Rev. Lett. 2018, 121, 238001. [Google Scholar] [CrossRef]
- Lees, A.W.; Edwards, S.F. The computer study of transport processes under extreme conditions. J. Phys. C Solid State Phys. 1972, 5, 1921–1928. [Google Scholar] [CrossRef]
- Antypov, D.; Elliott, J.A. On an analytical solution for the damped Hertzian spring. Europhys. Lett. 2011, 94, 50004. [Google Scholar] [CrossRef]
- Orr, F.M.; Scriven, L.E.; Rivas, A.P. Pendular rings between solids: Meniscus properties and capillary force. J. Fluid Mech. 1975, 67, 723–742. [Google Scholar] [CrossRef]
- LaMarche, C.Q.; Miller, A.W.; Liu, P.; Hrenya, C.M. Linking micro-scale predictions of capillary forces to macro-scale fluidization experiments in humid environments. AIChE J. 2016, 62, 3585–3597. [Google Scholar] [CrossRef]
- Iddir, H.; Arastoopour, H. Modeling of multitype particle flow using the kinetic theory approach. AIChE J. 2005, 51, 1620–1632. [Google Scholar] [CrossRef]
- Benyahia, S.; Syamlal, M.; O’Brien, T.J. Extension of Hill–Koch–Ladd drag correlation over all ranges of Reynolds number and solids volume fraction. Powder Technol. 2006, 162, 166–174. [Google Scholar] [CrossRef]
- Hill, R.J.; Koch, D.L.; Ladd, A.J.C. Moderate-Reynolds-number flows in ordered and random arrays of spheres. J. Fluid Mech. 2001, 448, 243–278. [Google Scholar] [CrossRef]
- Gollwitzer, F.; Rehberg, I.; Kruelle, C.A.; Huang, K. Coefficient of restitution for wet particles. Phys. Rev. E 2012, 86, 011303. [Google Scholar] [CrossRef] [PubMed]
- Murphy, E.; Subramaniam, S. Freely cooling granular gases with short-ranged attractive potentials. Phys. Fluids 2015, 27, 043301. [Google Scholar] [CrossRef]
- Syamlal, M.; Rogers, W.; OBrien, T.J. MFIX Documentation Theory Guide; National Energy Techonology Laboratory, Department of Energy: Morgantown, WV, USA, 1993. [Google Scholar]
- Cahyadi, A.; Neumayer, A.H.; Hrenya, C.M.; Cocco, R.A.; Chew, J.W. Comparative study of Transport Disengaging Height (TDH) correlations in gas–solid fluidization. Powder Technol. 2015, 275, 220–238. [Google Scholar] [CrossRef]


| Property | Symbol | Value | Units |
|---|---|---|---|
| Young’s modulus | E | 10 | MPa |
| Poisson ratio | 0.3 | - | |
| Primary particle diameter | d1 | 64 | μm |
| Particle density | ρs | 2500 | kg/m3 |
| Intrinsic coefficient of restitution | eint | 0.97 | - |
| Small-scale wavelength | λS | 369 | nm |
| Small-scale roughness | rmsS | 2.411 | nm |
| Minimum separation distance | Dmin | 0.15 | nm |
| Relative humidity | RH | 0.1 | - |
| System side length | L/d | 13.51 | - |
| Solid volume fraction | εs | 0.1 | - |
| Number of particles | - | 471 | - |
| Shear rate | 75, 200 | 1/s | |
| Ideal gas constant | Rg | 8.314 | J/(mol∙K) |
| Thermodynamic temperature | T | 300 | K |
| Molar density of water | 5.56 × 104 | mol/m3 | |
| Surface tension of water | σ | 72 × 10−3 | N/m |
| Asperity geometric constant | k1 | 1.817 | - |
| Property | Symbol | Value | Units |
|---|---|---|---|
| Gas (air) density | ρg | 0.97 | kg/m3 |
| Gas (air) viscosity | μg | 1.8335 × 10−5 | Pa∙s |
| Target gas velocity | ug,y | 0.515 | m/s |
| System width and depth | W = L | 0.3234375 | cm |
| System height | H | 1.4375 | cm |
| Grid size | ∆x/d1 | 2 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kellogg, K.M.; Liu, P.; Hrenya, C.M. Discrete-Element-Method-Based Determination of Particle-Level Inputs for the Continuum Theory of Flows with Moderately Cohesive Particles. Processes 2023, 11, 2553. https://doi.org/10.3390/pr11092553
Kellogg KM, Liu P, Hrenya CM. Discrete-Element-Method-Based Determination of Particle-Level Inputs for the Continuum Theory of Flows with Moderately Cohesive Particles. Processes. 2023; 11(9):2553. https://doi.org/10.3390/pr11092553
Chicago/Turabian StyleKellogg, Kevin M., Peiyuan Liu, and Christine M. Hrenya. 2023. "Discrete-Element-Method-Based Determination of Particle-Level Inputs for the Continuum Theory of Flows with Moderately Cohesive Particles" Processes 11, no. 9: 2553. https://doi.org/10.3390/pr11092553







