Decentralized Control Strategy for Participation of Electric Vehicles in Distribution Voltage Control
Abstract
:1. Introduction
- Existing voltage control schemes are mainly based on the active charging power scheduling of EVs without fully exploiting the reactive power compensation capability of EVCSs;
- The EV-battery-SoC constraints and the uncertainties of EV charging demands indicate that the EV charging scheduling has to be conducted at multiple time steps, whereas current studies consider snapshot operations only;
- The distribution network partitioning method is not integrated into the current decentralized distribution voltage schemes.
2. Materials and Methods
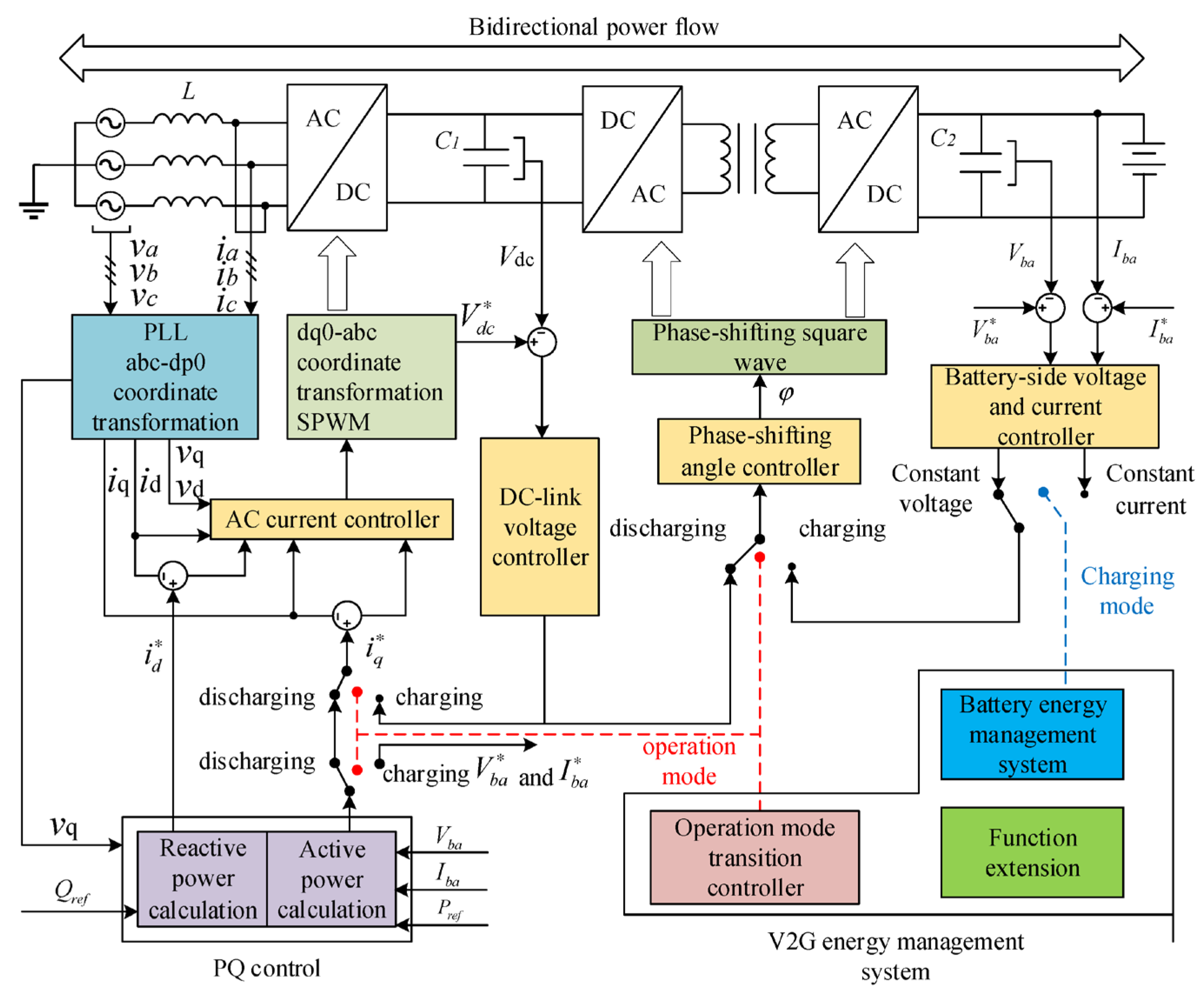
2.1. The Grid Voltage Support Mechanism of EVs and EVCSs
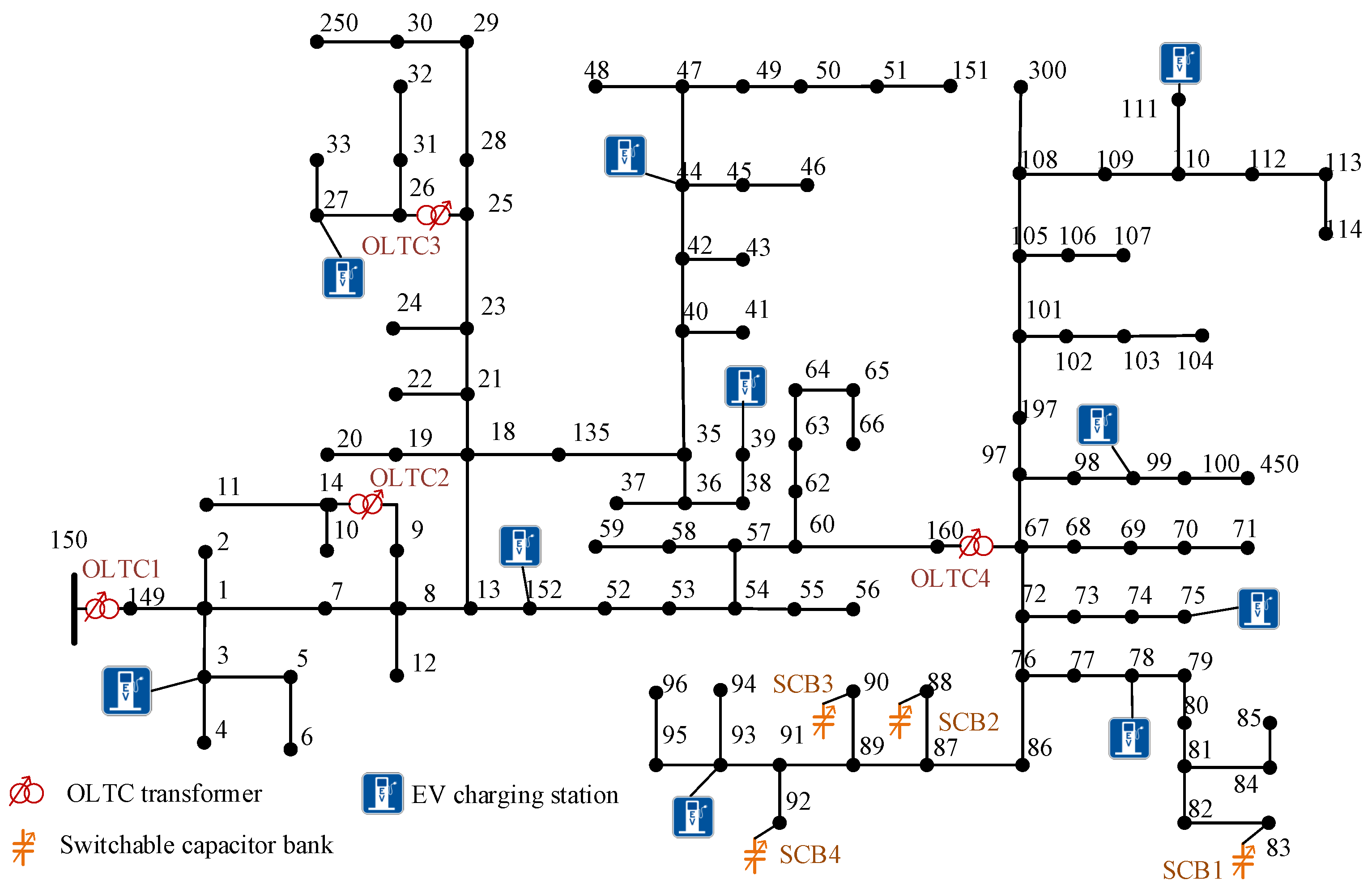
2.2. The Partitioning Method and Index for Distribution Networks Integrated with EVs
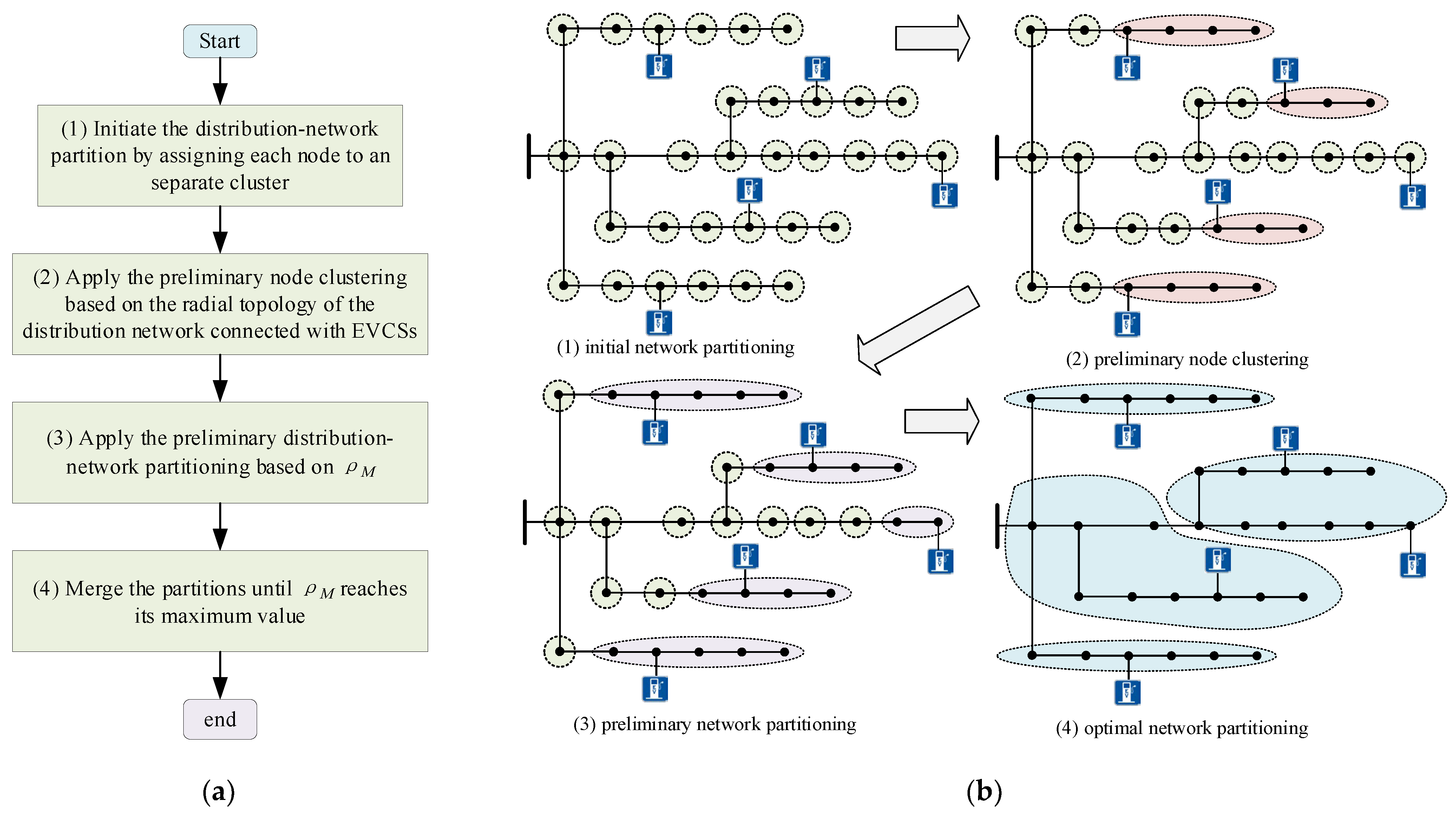
2.2.1. Principles of the Distribution Network Partitioning Method
2.2.2. The Distribution Network Partitioning Method
- (1)
- Initiate the distribution network partitioning by making each node an individual cluster;
- (2)
- Apply the preliminary node clustering based on the radial topology of the distribution network. Specifically, if a feeder branch has an EVCS connected and it is not located at the feeder end, the grid-integration point of EVCS and its downstream nodes are assigned into one cluster (named an EV cluster). If a feeder branch has no EVCSs connected, the feeder branch source node and all its downstream nodes are assigned to one cluster (named a load cluster). The preliminary node-clustering process is illustrated in Figure 4;
- (3)
- Apply the preliminary distribution network partitioning based on . For any EV cluster, find its adjacent isolated nodes and temporarily assign each of them to the cluster. Assign the isolated node with the highest to the EV cluster to form the updated cluster. Repeat the process until there is no isolated node in the distribution network;
- (4)
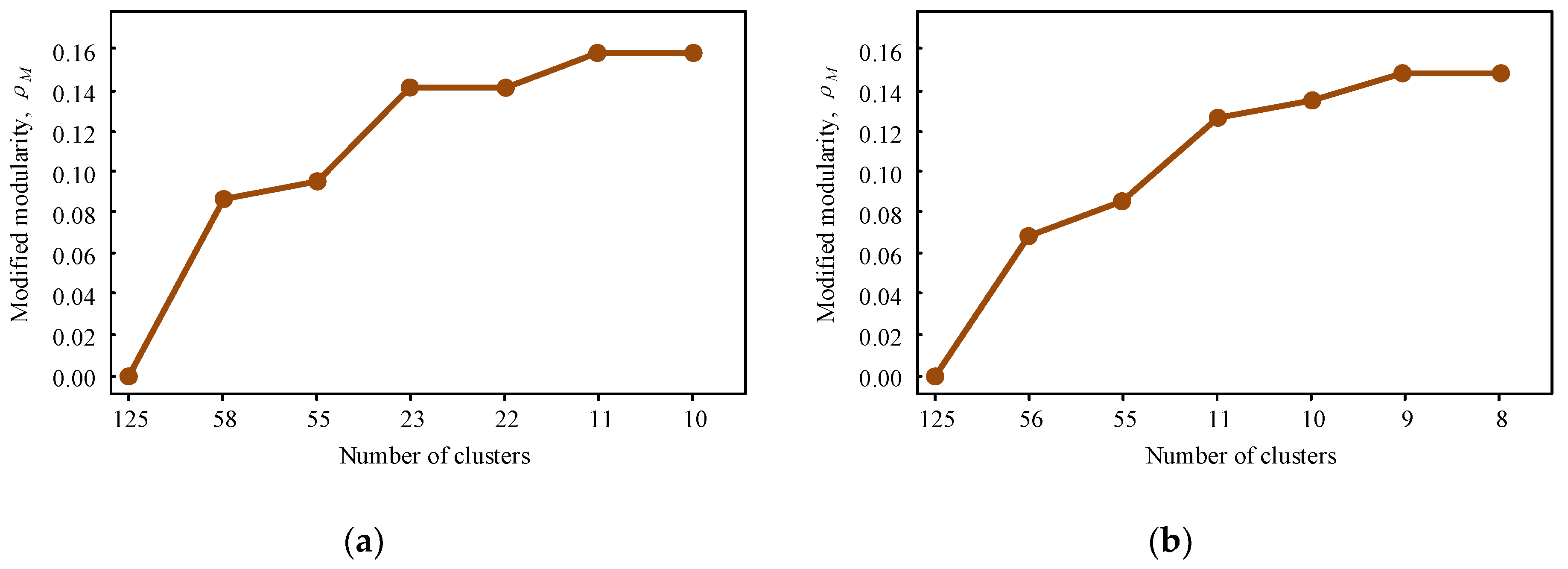
- Merge the clusters based on the objective function (24) until reaches its maximum value.
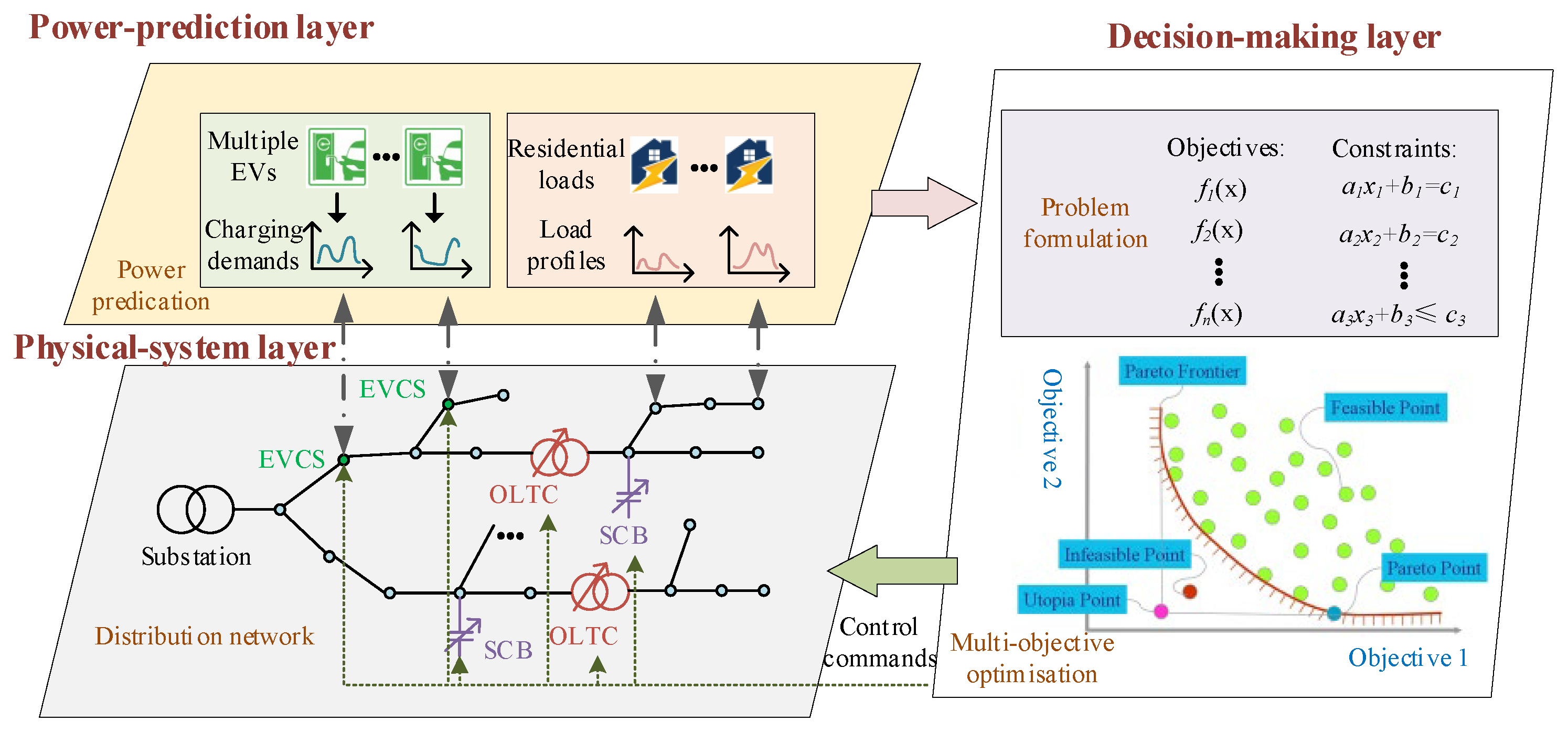
2.3. Decentralized Distribution Voltage Control with the Involvement of EVs and EVCSs
2.3.1. Principles of the Decentralized Voltage Control Scheme
2.3.2. Modeling of Distribution Voltage Control with Conventional Voltage-Support Resources
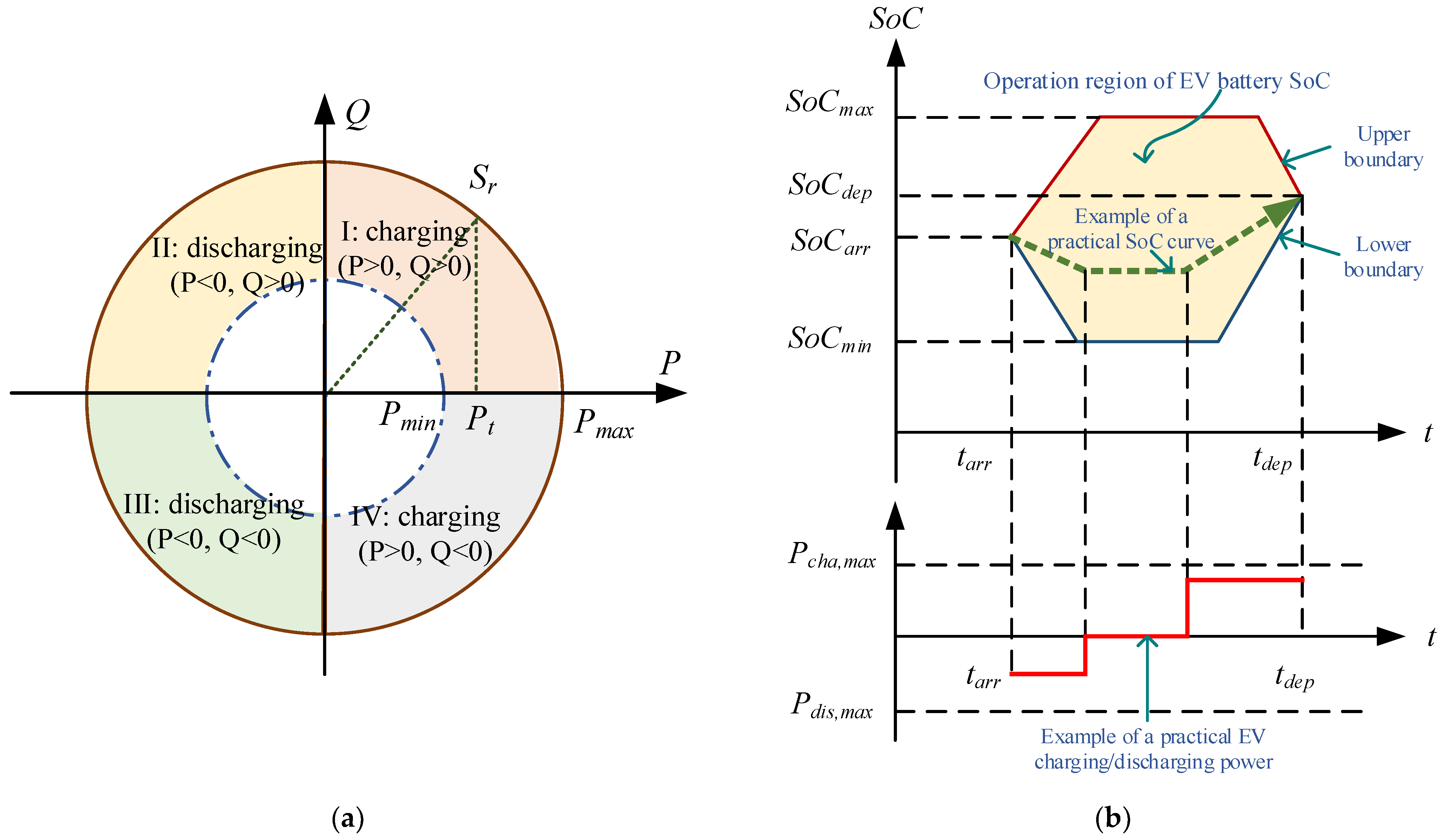
2.3.3. Modeling of Distribution Voltage Regulation with the Four-Quadrant Power Control of EVs and EVCSs
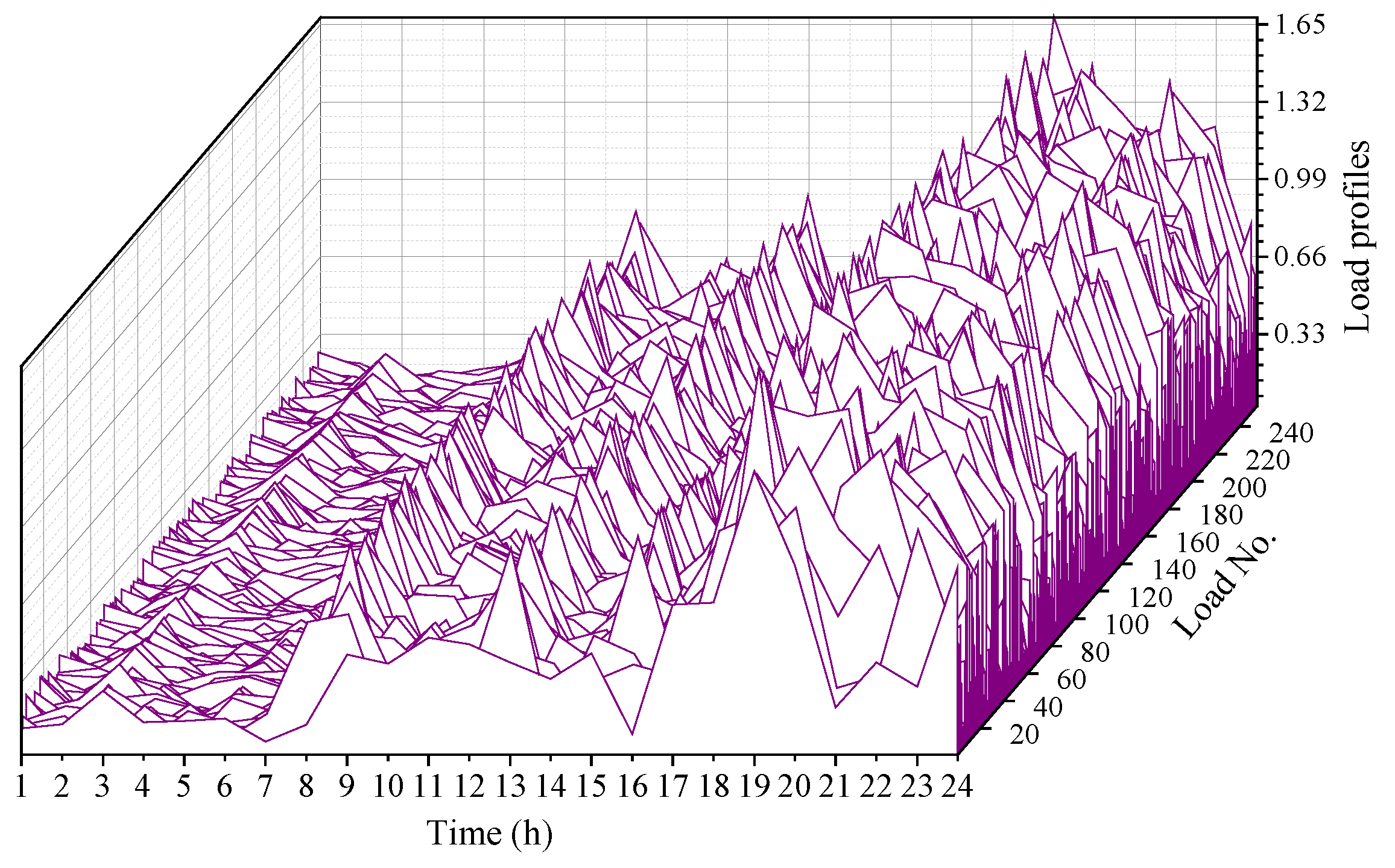
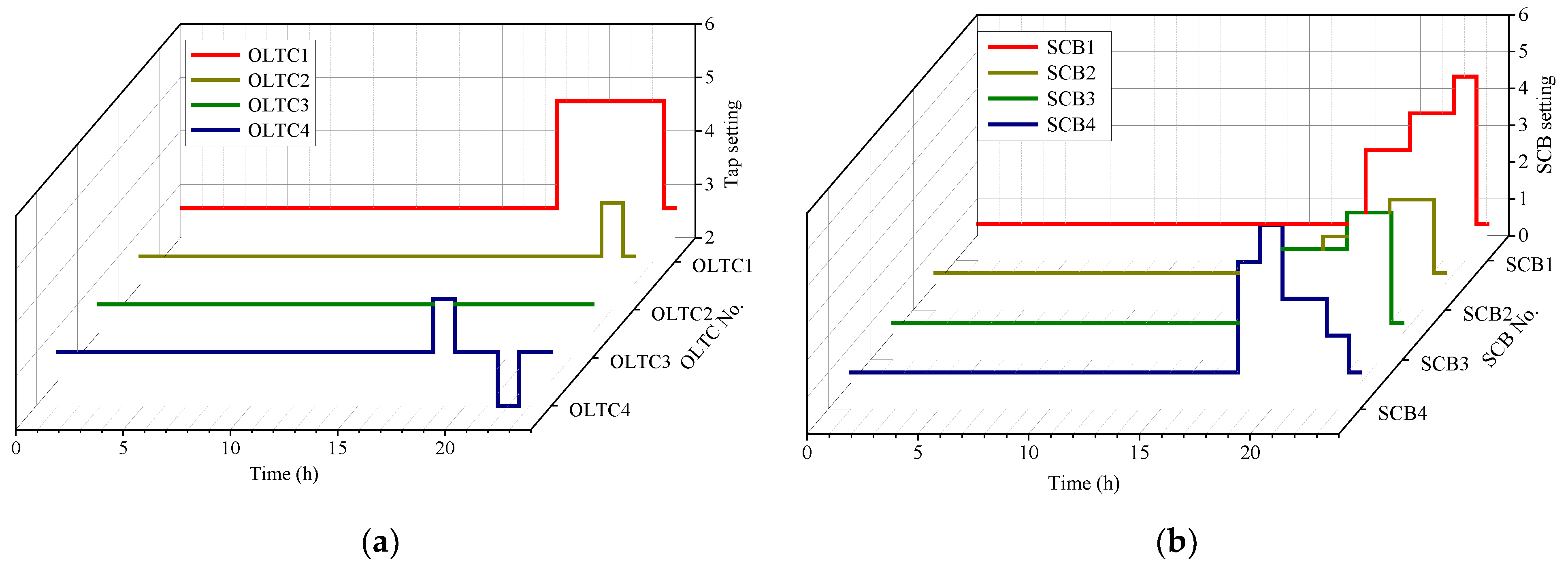
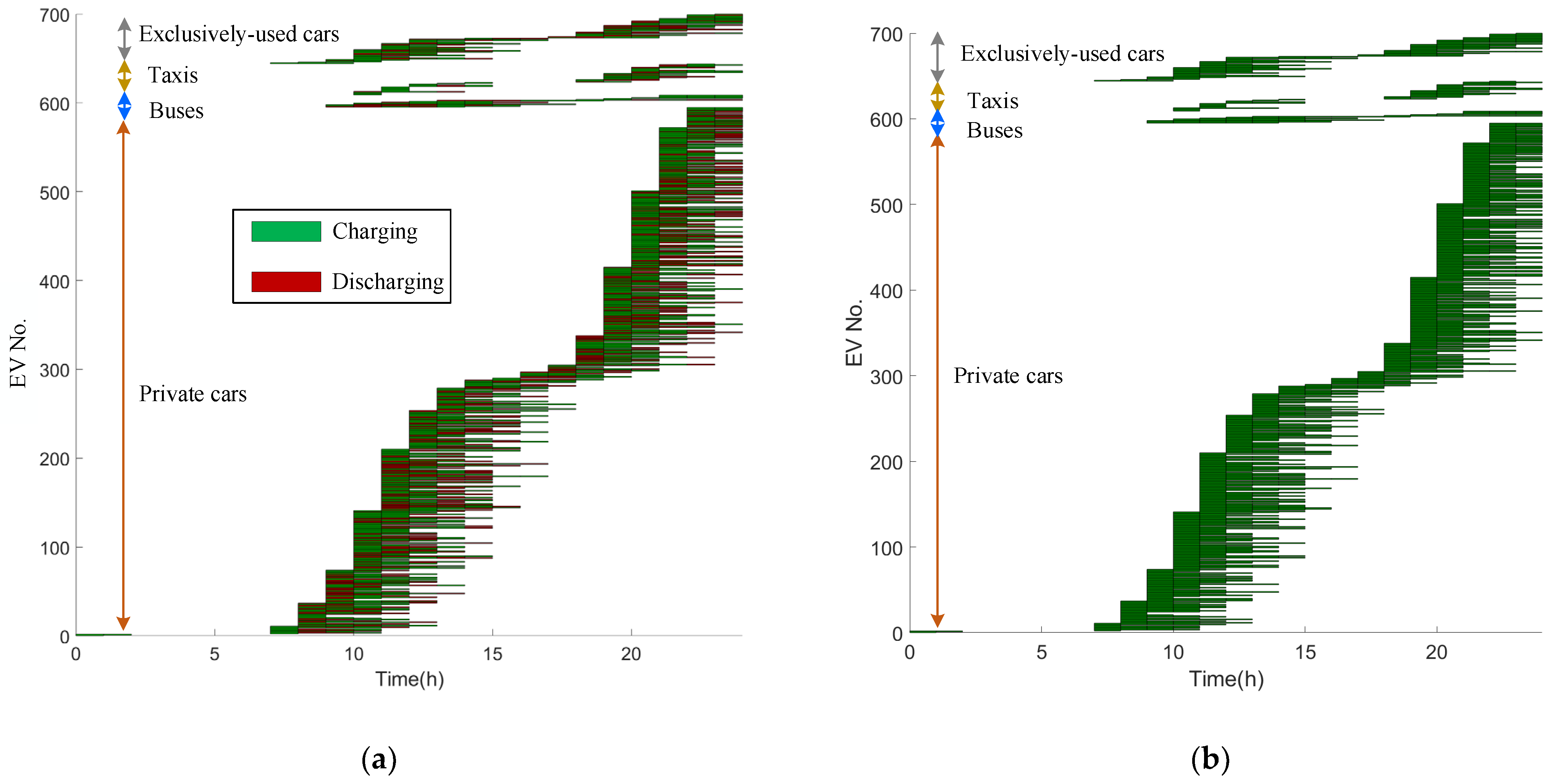
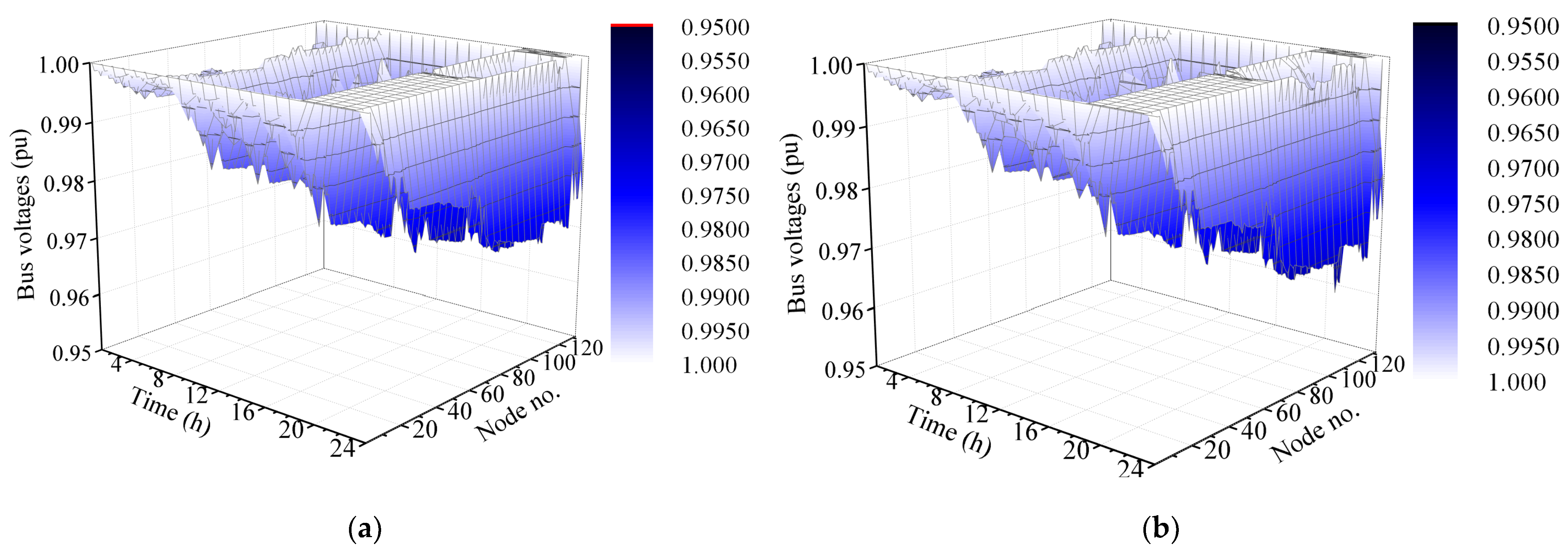
3. Case Studies
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- The Global EV Outlook. Available online: https://www.iea.org/reports/global-ev-outlook-2021 (accessed on 6 August 2021).
- Vagropoulos, S.I.; Balaskas, G.A.; Bakirtzis, A.G. An investigation of plug-in electric vehicle charging impact on power systems scheduling and energy costs. IEEE Trans. Power Syst. 2017, 32, 1902–1912. [Google Scholar] [CrossRef]
- Chukwu, U.C.; Mahajan, S.M. V2G electric power capacity estimation and ancillary service market evaluation. In Proceedings of the IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011; pp. 1–8. [Google Scholar]
- Leou, R.; Su, C.; Lu, C. Stochastic analyses of electric vehicle charging impacts on distribution network. IEEE Trans. Power Syst. 2014, 29, 1055–1063. [Google Scholar] [CrossRef]
- Yang, H.; Yang, S.; Xu, Y.; Cao, E.; Lai, M.; Dong, Z. Electric vehicle route optimization considering time-of-use electricity price by learnable partheno-genetic algorithm. IEEE Trans. Smart Grid 2015, 6, 657–666. [Google Scholar] [CrossRef]
- De Hoog, J.; Alpcan, T.; Brazil, M.; Thomas, D.A.; Mareels, I. Optimal charging of electric vehicles taking distribution network constraints into account. IEEE Trans. Power Syst. 2015, 30, 365–375. [Google Scholar] [CrossRef]
- Hu, W.; Su, C.; Chen, Z.; Bak-Jensen, B. Optimal operation of plug-in electric vehicles in power systems with high wind power penetrations. IEEE Trans. Sustain. Energy 2013, 4, 577–585. [Google Scholar]
- Chen, T.; Zhang, B.; Pourbabak, H.; Kavousi-Fard, A.; Su, W. Optimal routing and charging of an electric vehicle fleet for high-efficiency dynamic transit systems. IEEE Trans. Smart Grid 2018, 9, 3563–3572. [Google Scholar] [CrossRef]
- Mansouri, S.A.; Jordehi, A.R.; Marzband, M.; Tostado-Véliz, M.; Jurado, F.; Aguado, J.A. An IoT-enabled hierarchical decentralized framework for multi-energy microgrids market management in the presence of smart prosumers using a deep learning-based forecaster. Appl. Energy 2023, 333, 120560. [Google Scholar] [CrossRef]
- Liu, H.; Wu, W. Federated Reinforcement Learning for Decentralized Voltage Control in Distribution Networks. IEEE Trans. Smart Grid 2022, 13, 3840–3843. [Google Scholar] [CrossRef]
- Zhang, M.; Xu, Q.; Magnússon, S.; Pilawa-Podgurski, R.C.; Guo, G. Multi-Agent Deep Reinforcement Learning for Decentralized Voltage-Var Control in Distribution Power System. In Proceedings of the 2022 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 9–13 October 2022. [Google Scholar]
- Jafari, M.R.; Parniani, M.; Ravanji, M.H. Decentralized Control of OLTC and PV Inverters for Voltage Regulation in Radial Dis-tribution Networks with High PV Penetration. IEEE Trans. Power Deliv. 2022, 37, 4827–4837. [Google Scholar] [CrossRef]
- Luo, X.; Chan, K.W. Real-time scheduling of electric vehicles charging in low-voltage residential distribution systems to minimise power losses and improve voltage profile. IET Gener. Transm. Distrib. 2014, 8, 516–529. [Google Scholar] [CrossRef]
- Dutta, A.; Ganguly, S.; Kumar, C. Coordinated Volt/Var Control of PV and EV Interfaced Active Distribution Networks Based on Dual-Stage Model Predictive Control. IEEE Syst. J. 2022, 16, 4291–4300. [Google Scholar] [CrossRef]
- Li, H.; Azzouz, M.A.; Hamad, A.A. Cooperative Voltage Control in MV Distribution Networks with Electric Vehicle Charging Stations and Photovoltaic DGs. IEEE Syst. J. 2021, 15, 2989–3000. [Google Scholar] [CrossRef]
- Zhou, K.; Cai, L. Randomized PHEV Charging under Distribution Grid Constraints. IEEE Trans. Smart Grid 2014, 5, 879–887. [Google Scholar] [CrossRef]
- Beaude, O.; He, Y.; Hennebel, M. Introducing Decentralized EV Charging Coordination for the Voltage Regulation. In Proceedings of the IEEE PES ISGT Europe 2013, Lyngby, Denmark, 6–9 October 2013; pp. 1–5. [Google Scholar]
- Kriukov, A.; Gavrilas, M.; Ivanov, O.; Grigoras, G.; Neagu, B.-C.; Scarlatache, F. Novel Decentralized Voltage-Centered EV Charging Control Algorithm Using DSRC System in Low Voltage Distribution Networks. IEEE Access 2021, 9, 164779–164800. [Google Scholar] [CrossRef]
- Hu, J.; Ye, C.; Ding, Y.; Tang, J.; Liu, S. A Distributed MPC to Exploit Reactive Power V2G for Real-Time Voltage Regulation in Distribution Networks. IEEE Trans. Smart Grid 2022, 13, 576–588. [Google Scholar] [CrossRef]
- Sawalha, H.F.; Batarseh, M.G. An Improved Two-Stage Bidirectional Converter for Electric Vehicles to Grid Applications. In Proceedings of the 2022 International Conference on Electrical, Computer and Energy Technologies (ICECET), Prague, Czech Republic, 20–22 July 2022; pp. 1–6. [Google Scholar]
- Zhao, B.; Xu, Z.; Xu, C.; Wang, C.; Lin, F. Network Partition-Based Zonal Voltage Control for Distribution Networks with Distributed PV Systems. IEEE Trans. Smart Grid 2018, 9, 4087–4098. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M.E. Community structure in social and biological networks. Proc. Nat. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef] [PubMed]
- Electricity North West. Low Voltage Network Solutions Closedown Report. 2014. Available online: https://www.enwl.co.uk/go-net-zero/innovation/smaller-projects/low-carbon-networks-fund/low-voltage-network-solutions/low-voltage-networksolutions-closedown-report/ (accessed on 6 August 2023).
- IEEE. PES Distribution Systems Analysis Subcommittee Radial Test Feeders. Available online: https://cmte.ieee.org/pestestfeeders/resources/ (accessed on 6 August 2023).
- Xu, X.; Li, Q.; Sheng, M.; Gao, H. An Optimization-based Approach for the Distribution Network Electric Vehicle Hosting Capacity Assessment. In Proceedings of the 2022 China Automation Congress (CAC), Xiamen, China, 25–27 November 2022; pp. 3795–3800. [Google Scholar]
- Vyas, A.; Santini, D. Use of National Surveys for Estimating ‘Full’ PHEV Potential for Oil Use Reduction [EB/OL]. 21 July 2008. Available online: http://www.transportation.anl.gov/pdfs/HV/525.pdf (accessed on 6 August 2023).
- Li, D.; Zheng, J.; Shi, M.; Li, T.; Shao, H.; Liang, X. Prediction of time and space distribution of electric vehicle charging load. Electr. Power Eng. Technol. 2019, 38, 75–83. [Google Scholar]
- Zou, D.; Chen, G.; Xu, X. Architecture design of automatic voltage control system for active distribution network. Electr. Power Eng. Technol. 2019, 38, 42–47. [Google Scholar]












| Types of the Voltage Controllers | Advantages | Disadvantages |
|---|---|---|
| Centralized control [13,14,15] | Proven robustness; straight-forward decision-making process; enhanced control capability due to single authority. | Computational expensive for large systems; require extensive investment in communication infrastructures; potential privacy issue due to data transparency. |
| Decentralized control [16,17,18,19] | Work well with a sparse communication infrastructure; good scalability for large-scale distribution networks with complex operation conditions; low computational burdens; preserved privacy of EV users. | Complex decision-making process; may suffer from convergence issues; performance is determined by the structure design of the controller. |
| Proposed decentralized control | Advantages of conventional decentralized control; dynamic partitioning good scalability for large-scale distribution networks with complex operation conditions; low computational burdens; preserved privacy of EV users. | Complex decision-making process; applicable to the radial network topology only. |
| EV Type | Expected Charging Period | Arrival Time Battery SoC | Battery Capacity (kWh) | Rated Power of EVBC (kW) | EV Arrival Time to the EVCS |
|---|---|---|---|---|---|
| EVT1 * | 7:00 a.m.~5:00 p.m. 6:00 p.m.~7:00 a.m. | N(0.69, 0.12) | 35 | 7 | N * (11.3, 3.12) N * (20.9, 1.72) |
| EVT2 * | 11:00 p.m.~5:30 a.m. | N(0.5, 0.12) | 100 | 7 | U * |
| EVT3 * | 4:00 a.m.~7:00 a.m. 4:30 pm~7:00 p.m. | N(0.3, 0.12) | 80 | 30 | N * (5.6, 1.22) N * (17.1, 1.22) |
| EVT4 * | 5:00 p.m.~8:00 a.m. | N(0.48, 0.22) | 50 | 7 | N * (18.3, 3.92) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, X.; Li, J.; Yuan, Y.; Yuan, X. Decentralized Control Strategy for Participation of Electric Vehicles in Distribution Voltage Control. Processes 2023, 11, 2552. https://doi.org/10.3390/pr11092552
Fang X, Li J, Yuan Y, Yuan X. Decentralized Control Strategy for Participation of Electric Vehicles in Distribution Voltage Control. Processes. 2023; 11(9):2552. https://doi.org/10.3390/pr11092552
Chicago/Turabian StyleFang, Xin, Juan Li, Yubo Yuan, and Xiaodong Yuan. 2023. "Decentralized Control Strategy for Participation of Electric Vehicles in Distribution Voltage Control" Processes 11, no. 9: 2552. https://doi.org/10.3390/pr11092552




