Study on Adaptive Parameter Internal Mode Control Method for Argon–Oxygen Refining Ferrochrome Alloy
Abstract
1. Introduction
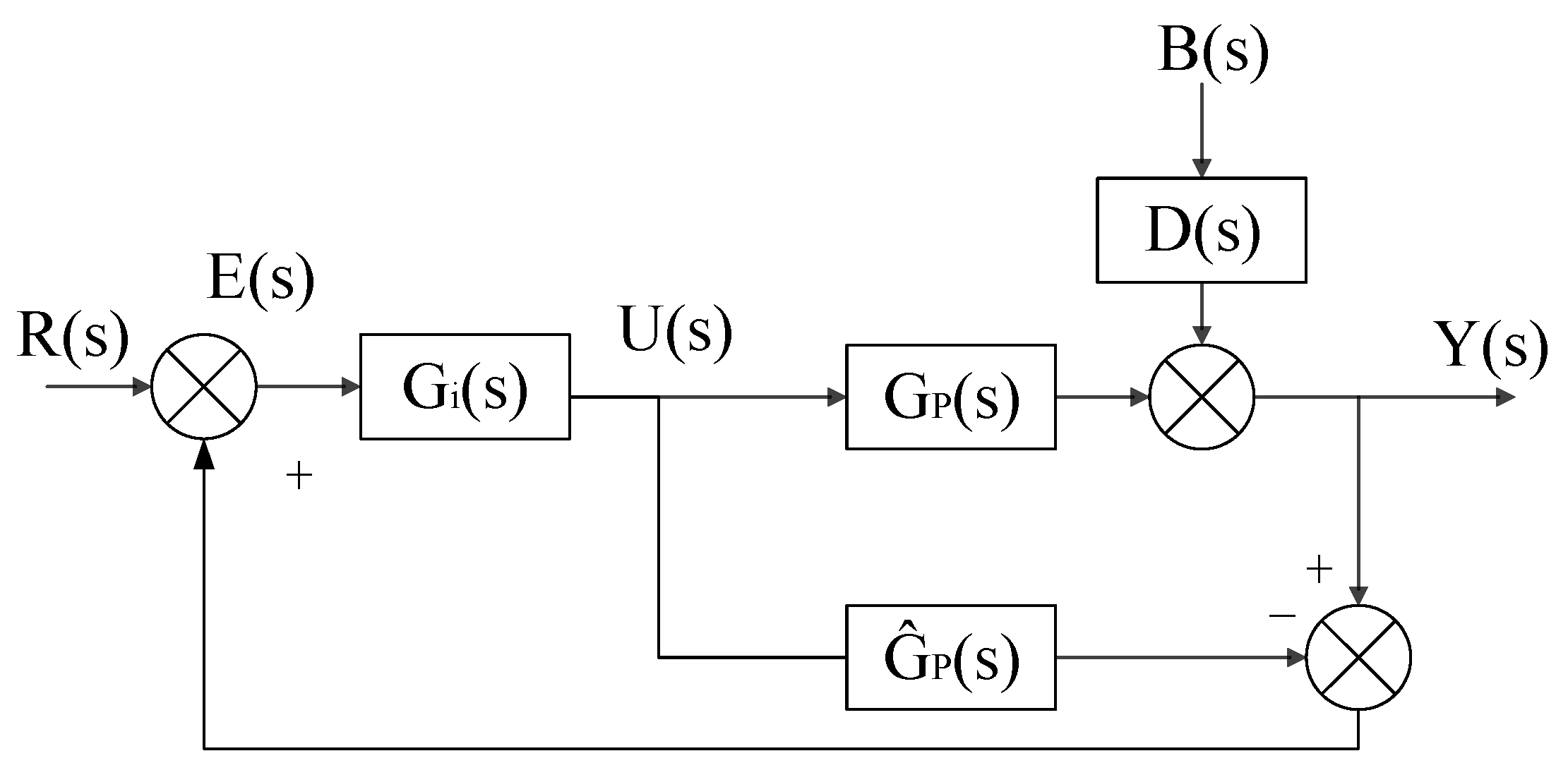
2. Internal Mode Control with Adaptive Fuzzy Regulator
2.1. Internal Model Control
2.2. Adaptive Fuzzy Regulator
3. Metallurgical Modeling
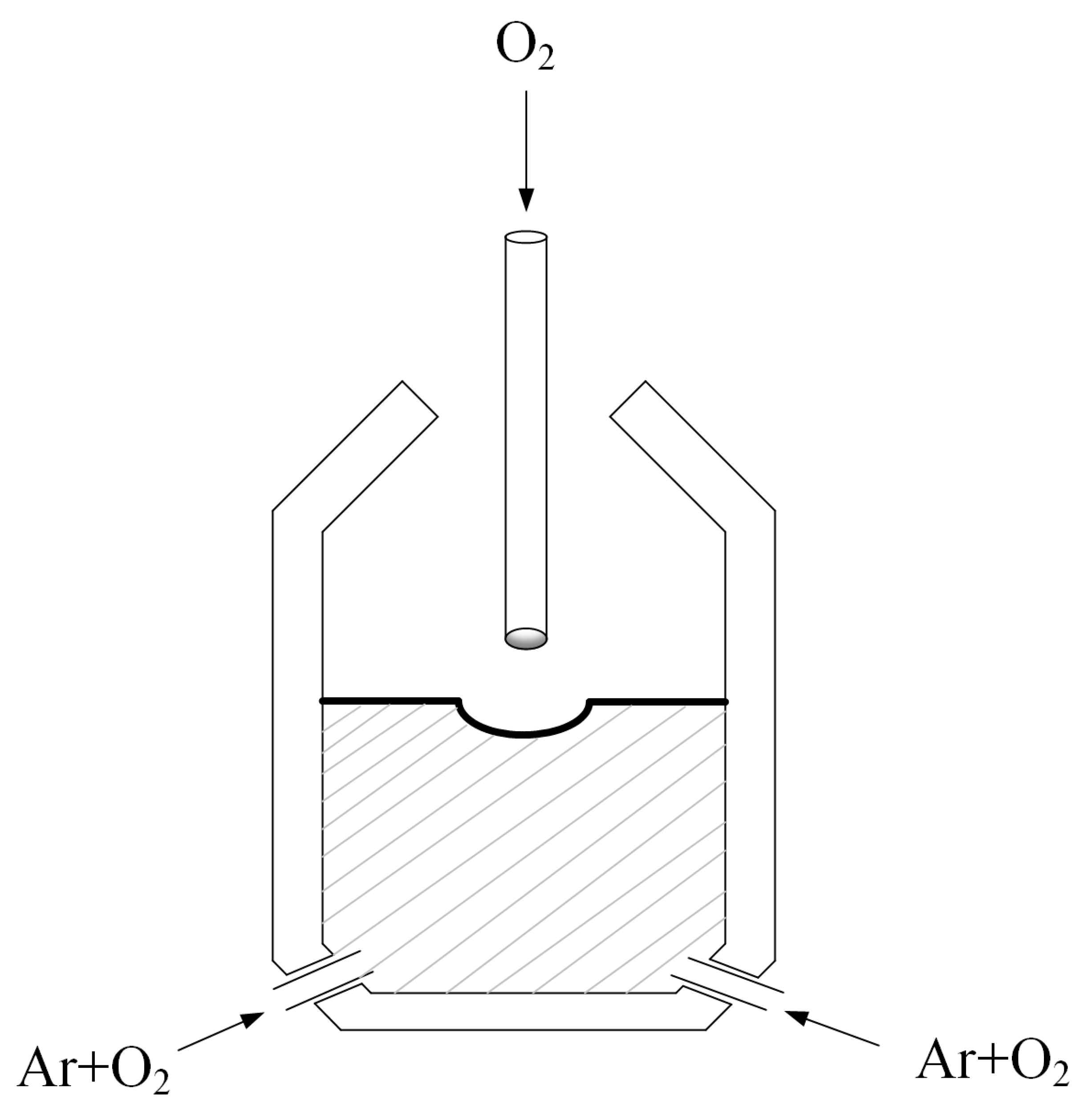
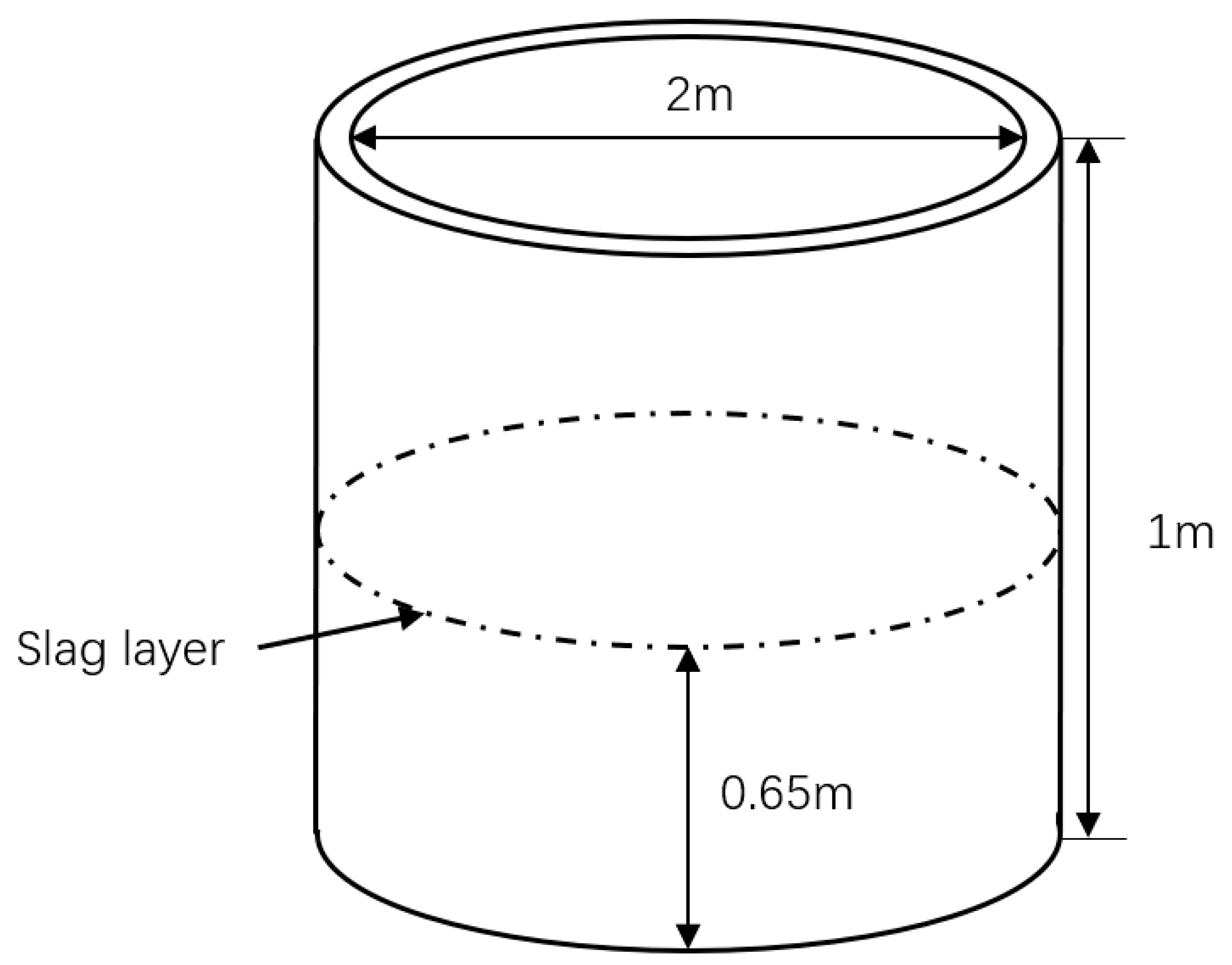
3.1. Mechanistic Model Assumptions
- Throughout the smelting process, the chemical reactions of all elements occur simultaneously in the converter and are able to reach a dynamic equilibrium in competition. During the stop-oxygen stirring process, the oxides stop reacting and reach a new equilibrium state [30].
- It is assumed that the entire smelting process is fully carried out. The oxygen blown into the AOD converter is not directly dissolved in the ferrochrome alloy. The CO produced will be changed to CO2 and discharged [31].
- It is assumed that Fe is always involved in the oxidation reaction during the smelting process and that FeO is always involved in the reduction reaction to produce Fe. Both processes are always in dynamic equilibrium.
- It is assumed that the relationship between the rate of oxygen blown in and the rate of oxidation during the smelting process is linear. Only C, Fe, Cr and Si are considered in the smelting process. Other elements are ignored.
- The coupling between the rate of decarburization and the rate of temperature change is linear. The carbon content composition and temperature are continuously varied and uniformly distributed in the transient state.
3.2. Smelting Model Building and Transfer Function Finding
3.2.1. Model of the Relationship between Decarbonization Rate and Oxygen Supply Rate
3.2.2. Model of the Relationship between the Rate of Temperature Change and the Rate of Gas Supply
3.3. Mechanistic Model Transfer Function Finding
3.3.1. Carbon Content and Oxygen Supply Rate Transfer Function
3.3.2. Temperature and Gas Supply Rate Transfer Function
4. Controller Design
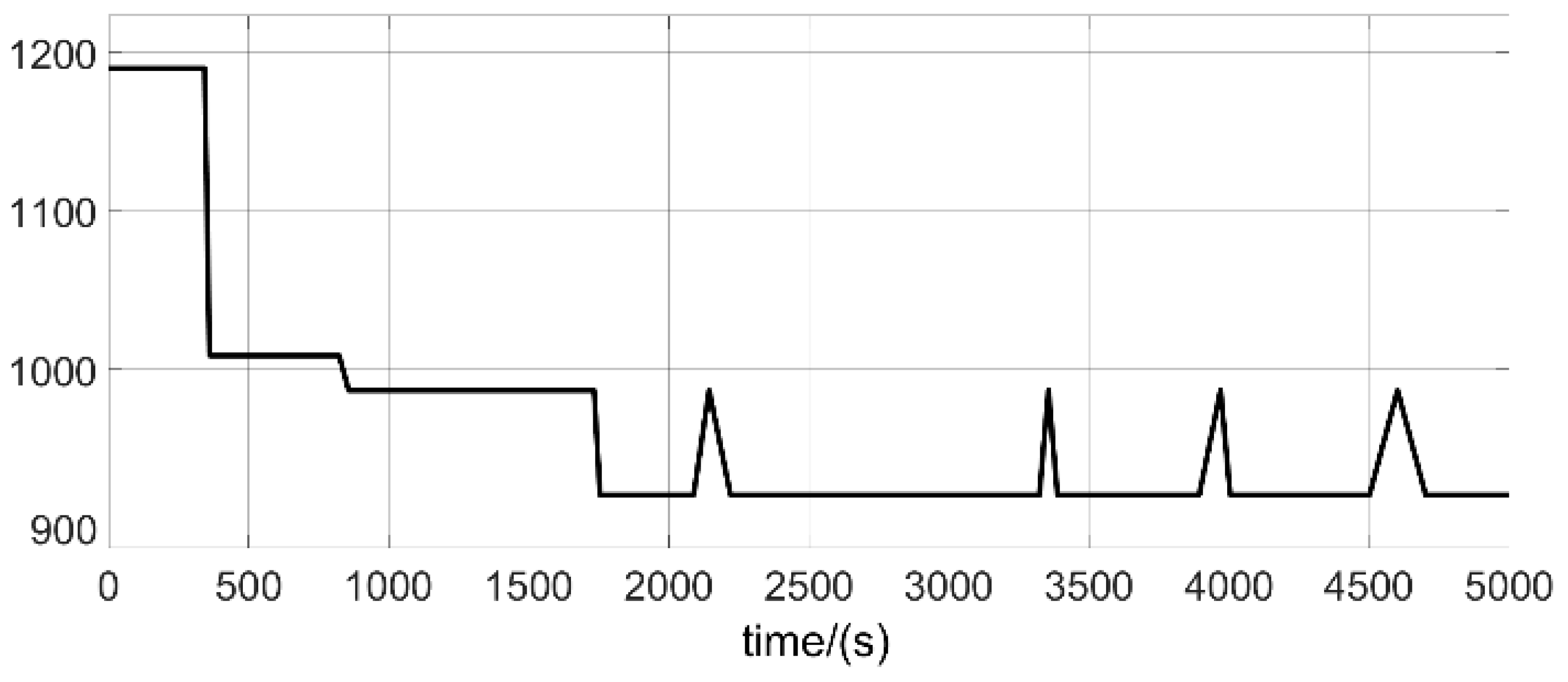
5. Simulation and Analysis
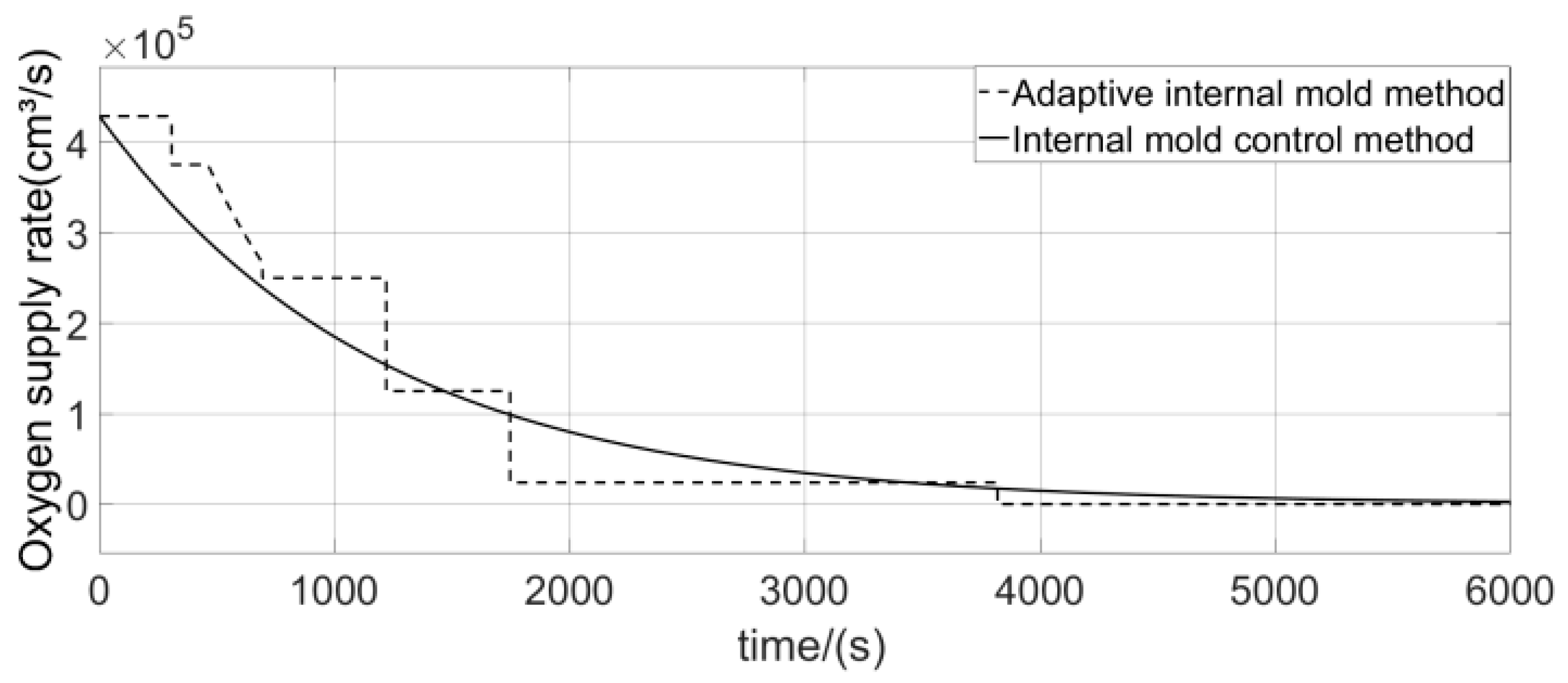
5.1. Simulation Design and Curves
5.2. Analysis of Measured Data
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kulkarni, V.R.; Jagannath, N.; Dabhade, V.V. Effect of chromium addition on properties of sinter-forged Fe–Cu–C alloy steel. Int. J. Mod. Phys. B 2018, 32, 1840040. [Google Scholar] [CrossRef]
- Dwarapudi, S.; Tathavadkar, V.; Rao, B.C.; Kumar, T.K.S.; Ghosh, T.K.; Denys, M. Development of Cold Bonded Chromite Pellets for Ferrochrome Production in Submerged Arc Furnace. ISIJ Int. 2013, 53, 533–539. [Google Scholar] [CrossRef]
- Peng, C.; Fan, J.F. Rotary hearth furnace process development in Baosteel. Iron Steel 2019, 54, 97–100. [Google Scholar] [CrossRef]
- Wei, T.; Shen, Q.H.; Zhan, H.W. The Development Thinking of Lance Life of Top-blown Melting Furnace. Sci. Technol. Eng. 2009, 9, 5778–5782+5791. [Google Scholar] [CrossRef]
- Byrne, G. Duplex Stainless Steels—Alloys for the 21st Century. Metals 2021, 11, 836. [Google Scholar] [CrossRef]
- Liu, Z.; Jones, P.T.; Kendall, M.; Blanpain, B.; Guo, M. On the CO Desorption and Absorption in Liquid Low-carbon Steel. ISIJ Int. 2021, 61, 510. [Google Scholar] [CrossRef]
- Kärnä, A.; Visuri, V.-V.; Heikkinen, E.-P.; Sulasalmi, P.; Torvinen, P.; Koskinen, J.; Fabritius, T. Numerical Modeling of Argon-Oxygen Decarburization Slag Cooling. Steel Res. Int. 2020, 91, 1134–1141. [Google Scholar] [CrossRef]
- Järvinen, M.; Visuri, V.V.; Heikkinen, E.P.; Kärnä, A.; Sulasalmi, P.; De Blasio, C.; Fabritius, T. Law of Mass Action Based Kinetic Approach for the Modelling of Parallel Mass Transfer Limited Reactions: Application to Metallurgical Systems. ISIJ Int. 2016, 56, 1543–1552. [Google Scholar] [CrossRef]
- Shi, G.M.; Wei, J.H.; Zhu, H.L.; Shu, J.H.; Jiang, Q.Y.; Chi, H.B. Preliminary Investigation of Mathematical Modeling of Stainless Steelmaking in an AOD Converter: Application of the Model and Results. Steel Res. Int. 2016, 78, 311–317. [Google Scholar] [CrossRef]
- Illarionov, A.G.; Kosmatskii, Y.I.; Filyaeva, E.A.; Vodolazskii, F.V.; Barannikova, N.A. Experimental Determination of Temperature Parameters for Evaluating the Possibility of Manufacturing Alloy Ti-3Al-2.5V Hot-Extruded Tubes. Metallurgist 2017, 60, 983–988. [Google Scholar] [CrossRef]
- Wei, J.H.; Li, Y. Study on Mathematical Modeling of Combined Top and Bottom Blowing VOD Refining Process of Stainless Steel. Steel Res. Int. 2015, 86, 189–211. [Google Scholar] [CrossRef]
- Wuppermann, C.; Rückert, A.; Pfeifer, H.; Odenthal, H.J. Physical and Mathematical Modeling of the Vessel Oscillation in the AOD Process. ISIJ Int. 2013, 53, 441–449. [Google Scholar] [CrossRef]
- Ternstedt, P.; Ni, P.; Lundqvist, N.; Tilliander, A.; Jönsson, P.G. A physical modelling study to determine the influence of slag on the fluid flow in the AOD converter process. Ironmak. Steelmak. 2018, 45, 944–950. [Google Scholar] [CrossRef]
- You, J.; Wang, S.C.; Li, X.S.; Han, Y.P. Determination of blowing end point of oxygen top blown converter by flame texture analysis of converter mouth. J. Beijing Univ. Sci. Technol. 2000, 6, 524–528. [Google Scholar] [CrossRef]
- Fei, H.; Zhang, L. Prediction model of end-point phosphorus content in BOF steelmaking process based on PCA and BP neural network. J. Process Control 2018, 66, 51–58. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, H.; Yang, C. Hybrid Model Based Intelligent Optimization of Ironmaking Process. IEEE Trans. Ind. Electron. 2019, 67, 2469–2479. [Google Scholar] [CrossRef]
- Yu, F.-P.; Lin, J.-J.; Lin, X.-M.; Li, L. Dual pulse laser induced spectroscopy combined with multivariate GA-BP-ANN detection of C element in alloy steel. Spectrosc. Spectr. Anal. 2022, 42, 197–202. [Google Scholar] [CrossRef]
- Li, L.; Niu, H.-F.; Lin, J.-J.; Che, C.-J.; Lin, X.-M. Quantitative Analysis of Carbon Elements in Collinear DP-LIBS Low Carbon Alloy Steel. Spectrosc. Spectr. Anal. 2018, 38, 2951–2956. [Google Scholar] [CrossRef]
- Chen, G.-H.; Zhang, D.-J.; Lin, X.-M. AOD furnace bottom gun infrared colorimetric temperature measurement system based on gray temperature compensation model. Metall. Ind. Autom. 2013, 37, 62–67. [Google Scholar] [CrossRef]
- Wei, J.H. Physical and Mathematical Modeling of the Argon-Oxygen Decarburization Refining Process of Stainless Steel. J. Shanghai Univ. 2002, 1, 1–23. [Google Scholar] [CrossRef]
- Wei, J.H.; Zeng, L. Numerical Simulation of Fluid Flow in Bath during Combined Top and Bottom Blowing VOD Refining Process of Stainless Steel. Steel Res. Int. 2012, 83, 1053–1070. [Google Scholar] [CrossRef]
- Wei, J.H.; Yuan, H.E.; Shi, G.M. Mathematical Modeling of Fluid Flow in an AOD Converter Bath under Conditions of Combined Side and Top Blowing: Application of the Model to Combined Side and Top Blowing Process and Results. Chin. J. Process Eng. 2011, 11, 40–43. [Google Scholar] [CrossRef]
- Wei, J.H.; Zhu, H.L.; Chi, H.B.; Wang, H.J. Physical Modeling Study on Combined Side and Top Blowing AOD Refining Process of Stainless Steel: Fluid Mixing Characteristics in Bath. ISIJ Int. 2010, 50, 26–34. [Google Scholar] [CrossRef]
- Li, B.; Wei, J.H.; Jiang, X. A simulating investigation into the characteristics of the mass transfer between molten steel and particles in the 150 t RH-IJ refining. Baosteel Technol. Res. 2010, 4, 6. [Google Scholar] [CrossRef]
- Ma, H. Mathematical Model and Control Strategy of Argon-Oxygen Refining Low-Carbon Ferrochrome Production Process; University of Chinese Academy of Sciences: Beijing, China, 2011. [Google Scholar]
- Wei, B.K.; You, W.; Guan, C.J. Endpoint Predictive Control System for Argon-Oxygen Refining of Low Carbon Ferrochrome Based on Internal Model Control. Metall. Ind. Autom. 2020, 44, 55–59+66. [Google Scholar] [CrossRef]
- Moon, E.J.; Choi, Y.C. Development of carbon-capture binder using stainless steel argon oxygen decarburization slag activated by carbonation. J. Clean. Prod. 2018, 180, 642–654. [Google Scholar] [CrossRef]
- Song, Z.; Ersson, M.; Jnsson, P. A Study of Post-Combustion in an AOD Flue. Steel Res. Int. 2014, 85, 1173–1184. [Google Scholar] [CrossRef]
- Rout, B.K.; Brooks, G.; Akbar Rhamdhani, M.; Li, Z.; Schrama, F.N.; van der Knoop, W. Dynamic Model of Basic Oxygen Steelmaking Process Based on Multizone Reaction Kinetics: Modeling of Manganese Removal. Metall. Mater. Trans. B 2018, 49, 2191–2208. [Google Scholar] [CrossRef]
- Gao, C.; Shen, M.G.; Liu, X.P.; Zhao, N.N.; Chu, M.X. End-point dynamic control of basic oxygen furnace steelmaking based on improved unconstrained twin support vector regression. J. Iron Steel Res. Int. 2020, 27, 42–54. [Google Scholar] [CrossRef]
- Wu, S.; Xu, A. Calculation Method of Energy Saving in Process Engineering: A Case Study of Iron and Steel Production Process. Energies 2021, 14, 5756. [Google Scholar] [CrossRef]



| Carbon Content | Oxygenation Rate |
|---|---|
| 8–1% | 444,444 cm3/s |
| 1–0.25% | 55,555 cm3/s |
| Component | Cr | C | S | P | Si |
|---|---|---|---|---|---|
| Content | >55% or >65% | C < 8% | <0.02% | <0.03% | 2~4% |
| Component | Cr | C | S | P | Si |
|---|---|---|---|---|---|
| Content | 60~65% | C < 0.25% | <0.02% | <0.03% | 2~4% |
| Serial No. | End Point Carbon Content | End Point Temperature | Time |
|---|---|---|---|
| 1# | 0.25% | 1923 K | 74.6 min |
| 2# | 0.25% | 1906 K | 73.5 min |
| 3# | 0.25% | 1910 K | 73.9 min |
| 4# | 0.25% | 1889 K | 77.2 min |
| 5# | 0.25% | 1925 K | 72.3 min |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, N.; Han, S.; You, W.; Wang, Y. Study on Adaptive Parameter Internal Mode Control Method for Argon–Oxygen Refining Ferrochrome Alloy. Processes 2023, 11, 1461. https://doi.org/10.3390/pr11051461
Qu N, Han S, You W, Wang Y. Study on Adaptive Parameter Internal Mode Control Method for Argon–Oxygen Refining Ferrochrome Alloy. Processes. 2023; 11(5):1461. https://doi.org/10.3390/pr11051461
Chicago/Turabian StyleQu, Na, Shunjie Han, Wen You, and Yifan Wang. 2023. "Study on Adaptive Parameter Internal Mode Control Method for Argon–Oxygen Refining Ferrochrome Alloy" Processes 11, no. 5: 1461. https://doi.org/10.3390/pr11051461
APA StyleQu, N., Han, S., You, W., & Wang, Y. (2023). Study on Adaptive Parameter Internal Mode Control Method for Argon–Oxygen Refining Ferrochrome Alloy. Processes, 11(5), 1461. https://doi.org/10.3390/pr11051461






