Investigation on the Dynamics of a Flexible Multi-Body System of a Three-Cylinder Gasoline Engine Crankshaft
Abstract
:1. Introduction
2. Simulation Modeling of a Crankshaft Flexible Multi-Body System of a Three-Cylinder Gasoline Engine
2.1. Engine Crankshaft Finite Element Modeling
2.2. Analysis of the Crankshaft Meshing Results
2.3. Adams-Based Crankshaft Flexible Multi-Body Dynamics Modeling
3. Simulation Analysis of the Kinematic Dynamics of the Crankshaft Connecting Rod System of the Three-Cylinder Engine
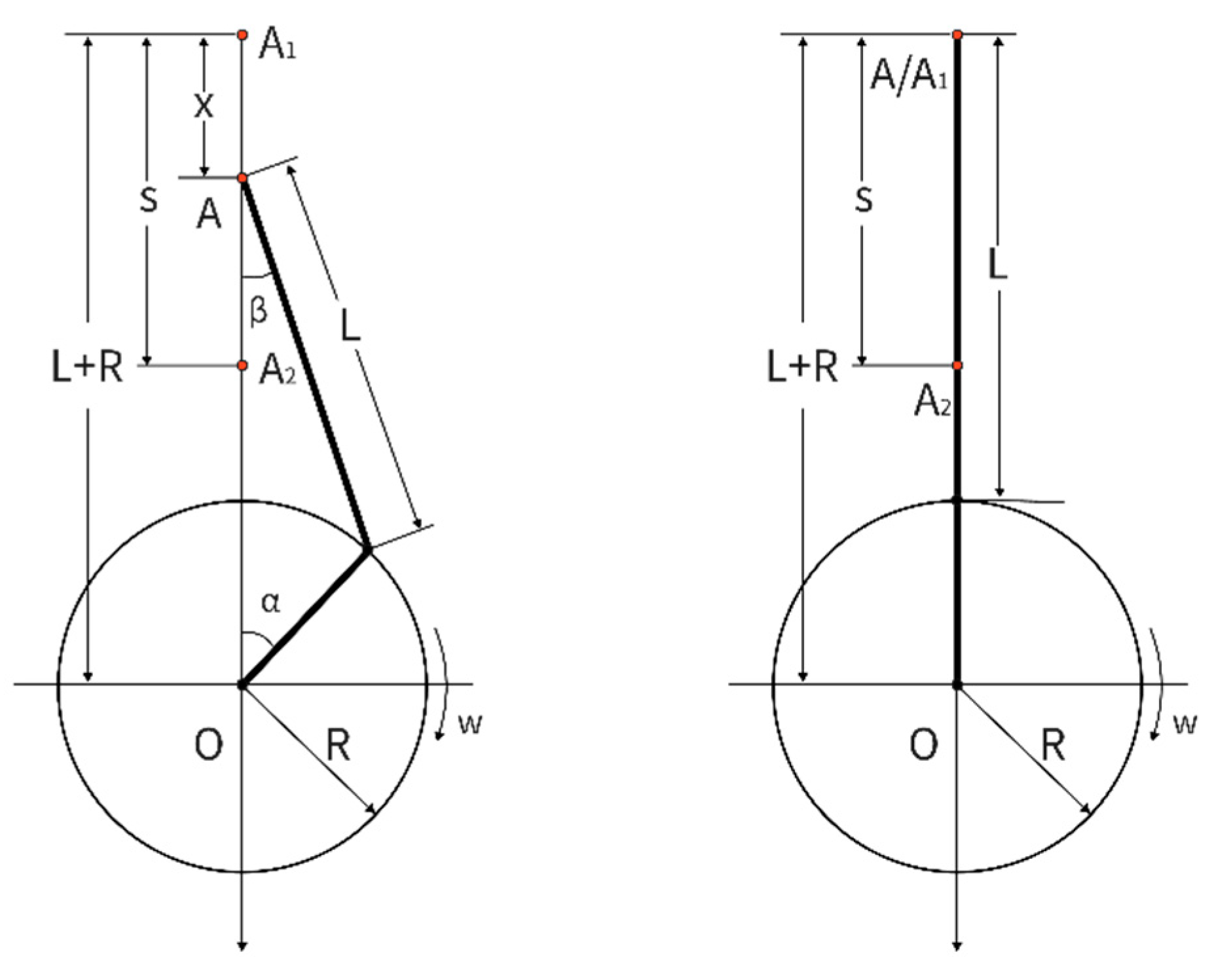
3.1. Kinematic Analysis
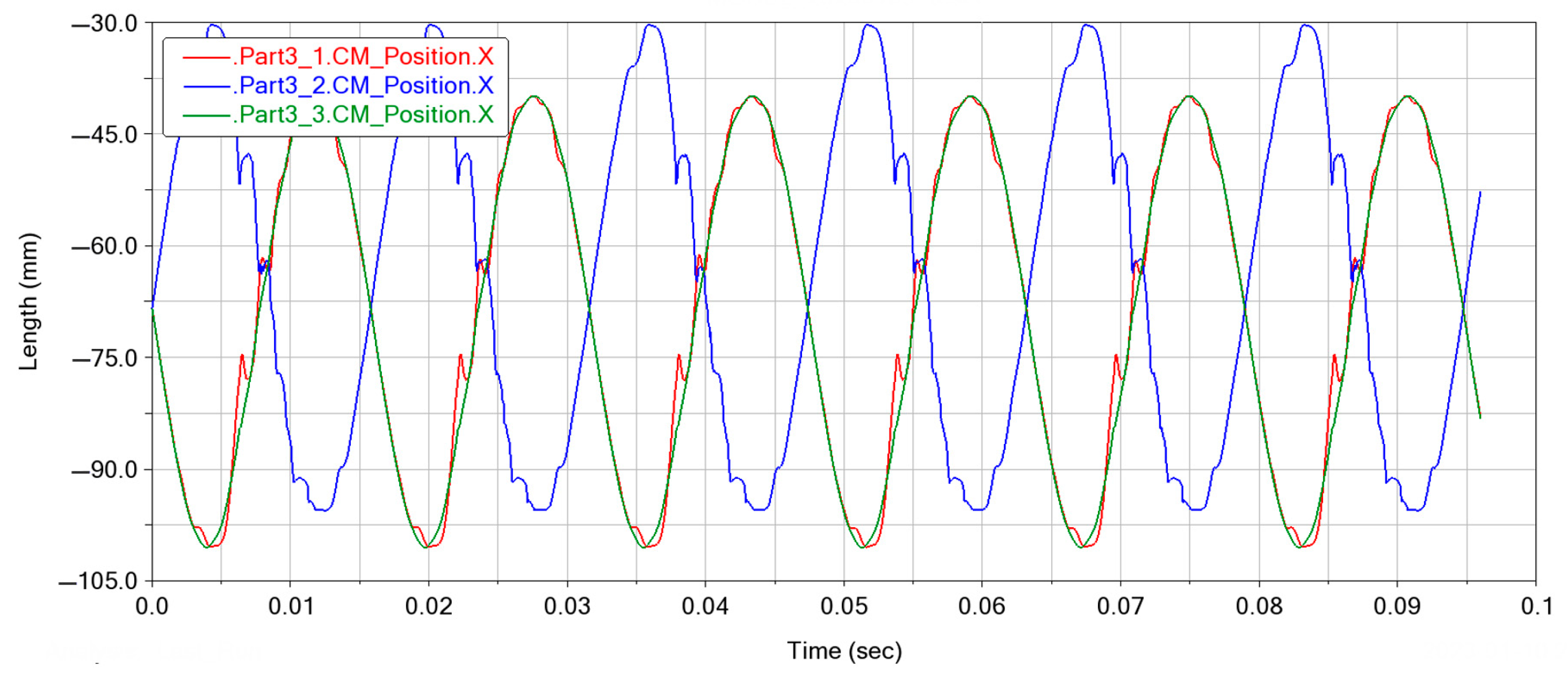
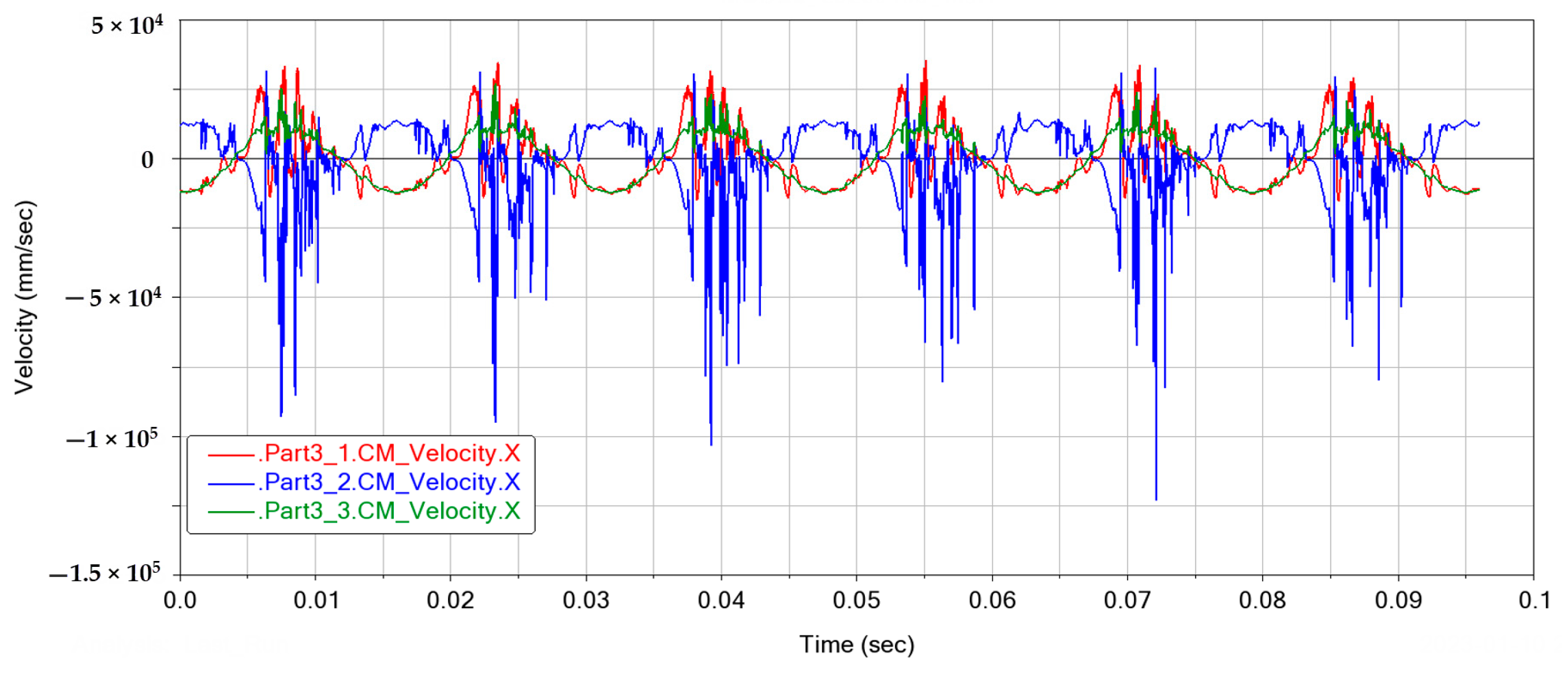
3.2. Piston Kinematics Simulation
3.3. Linkage Kinematics Simulation
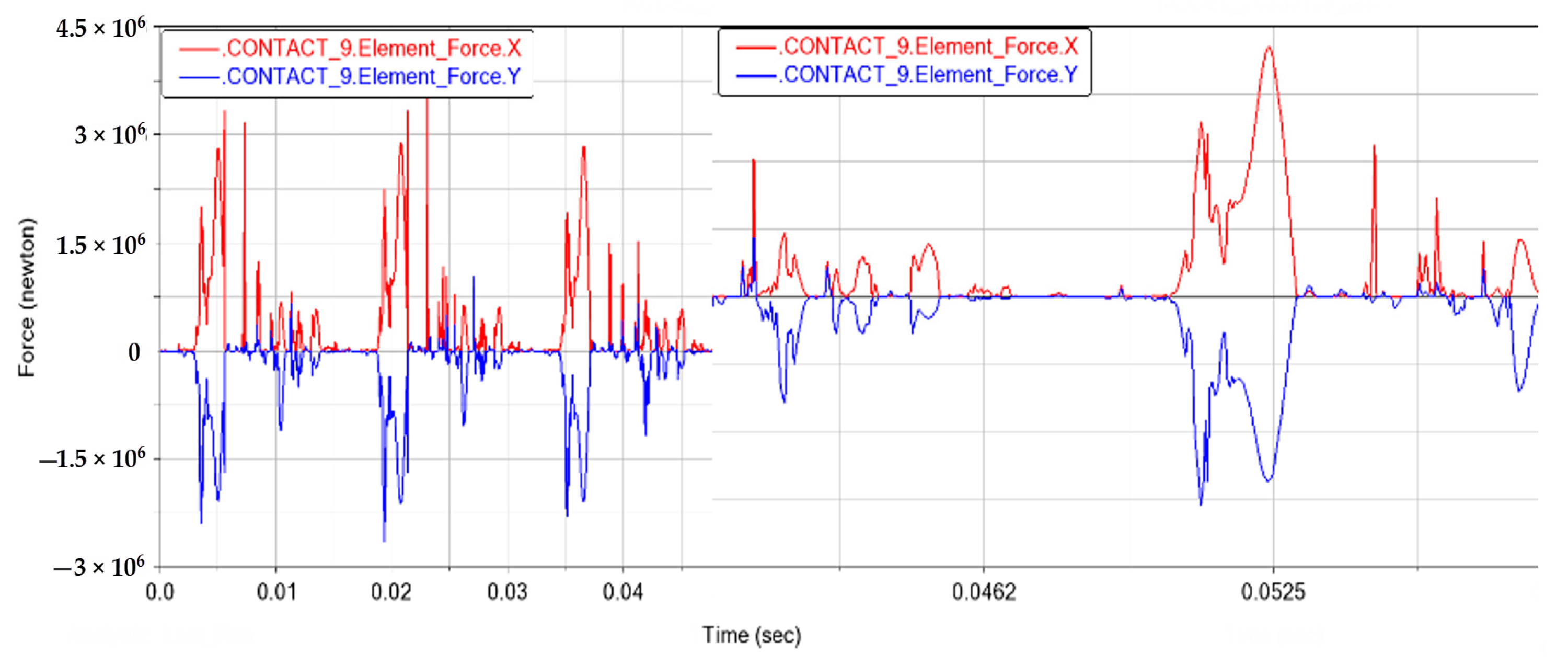
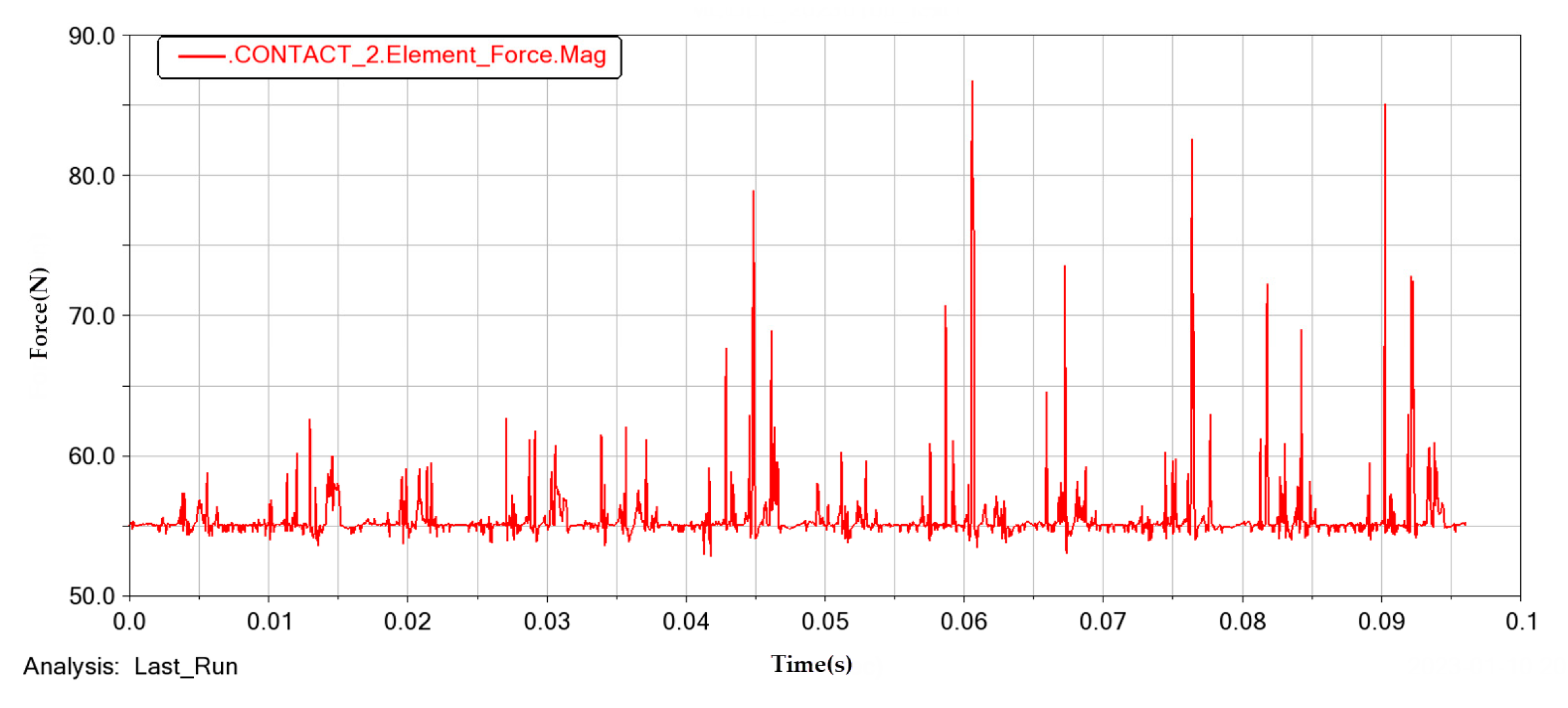
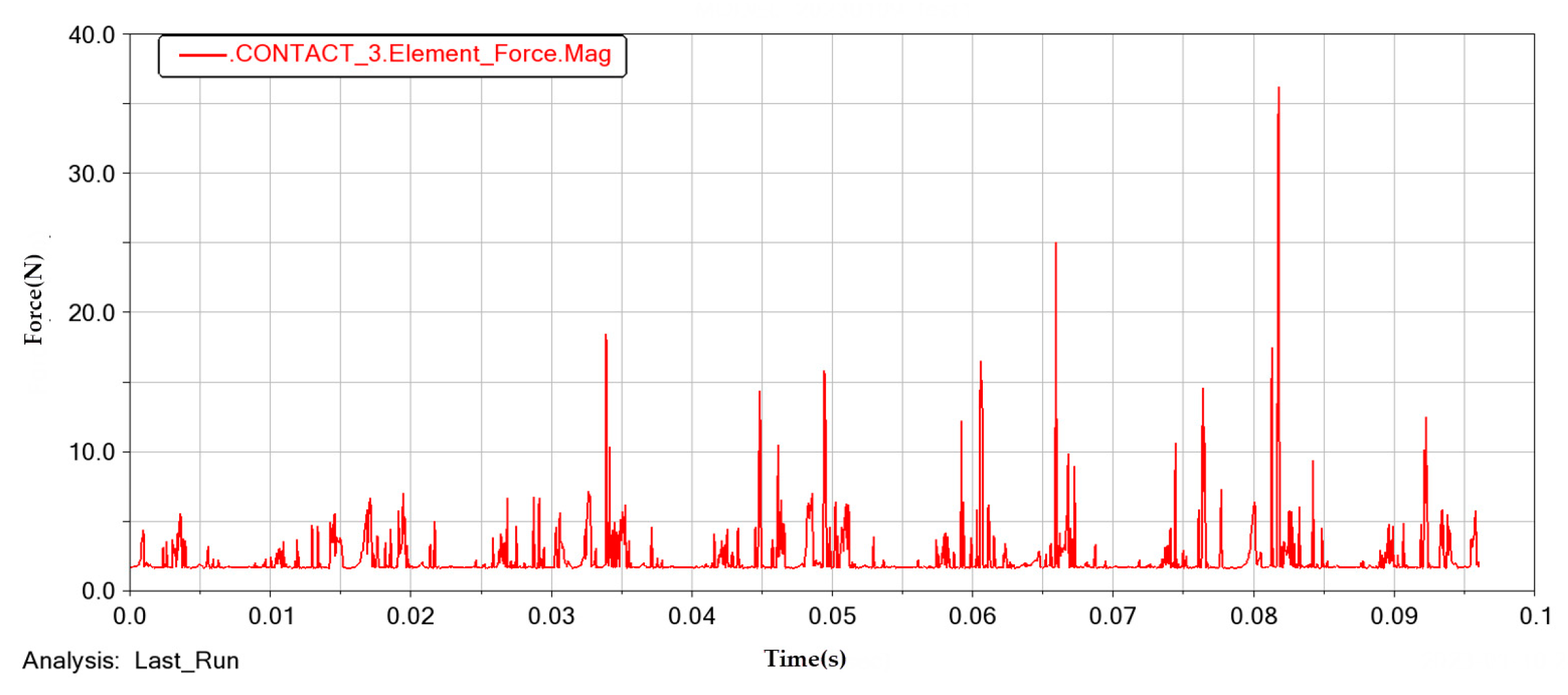
3.4. Force Analysis of the Crankshaft System
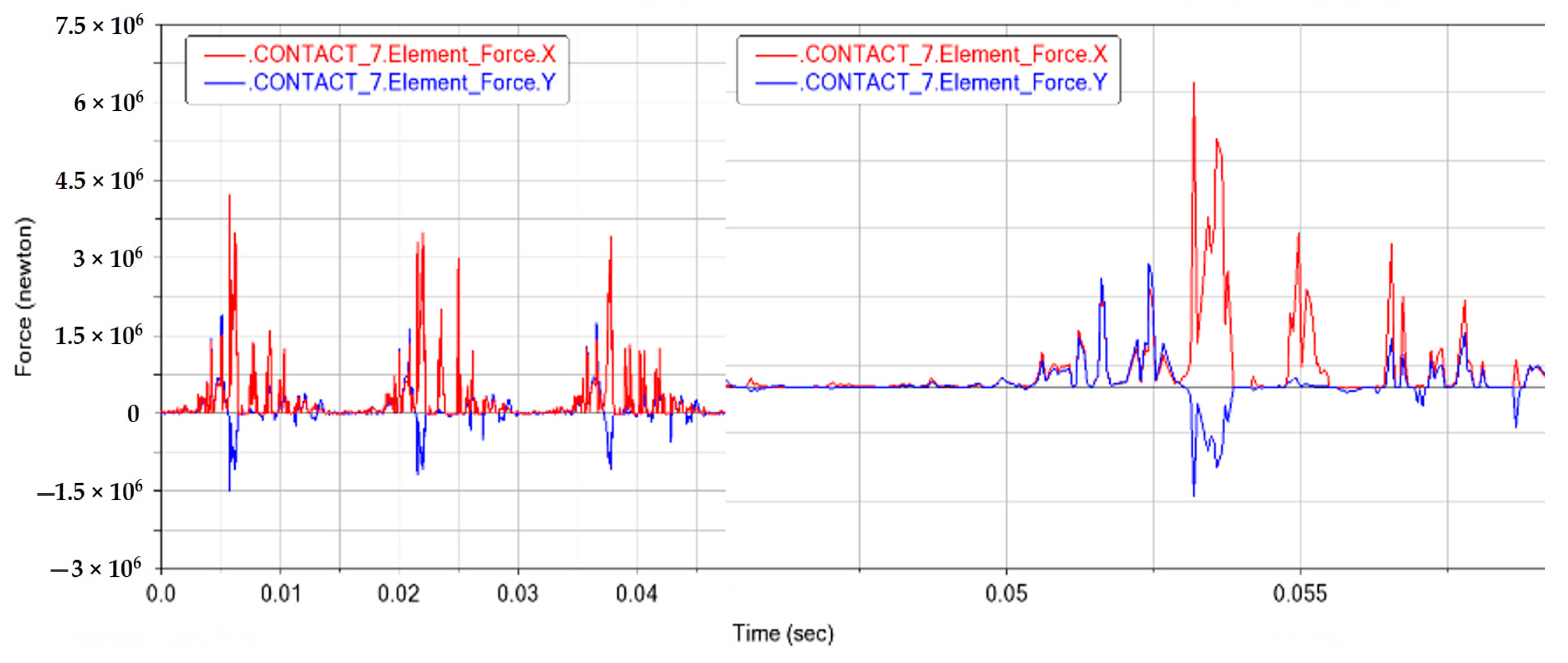
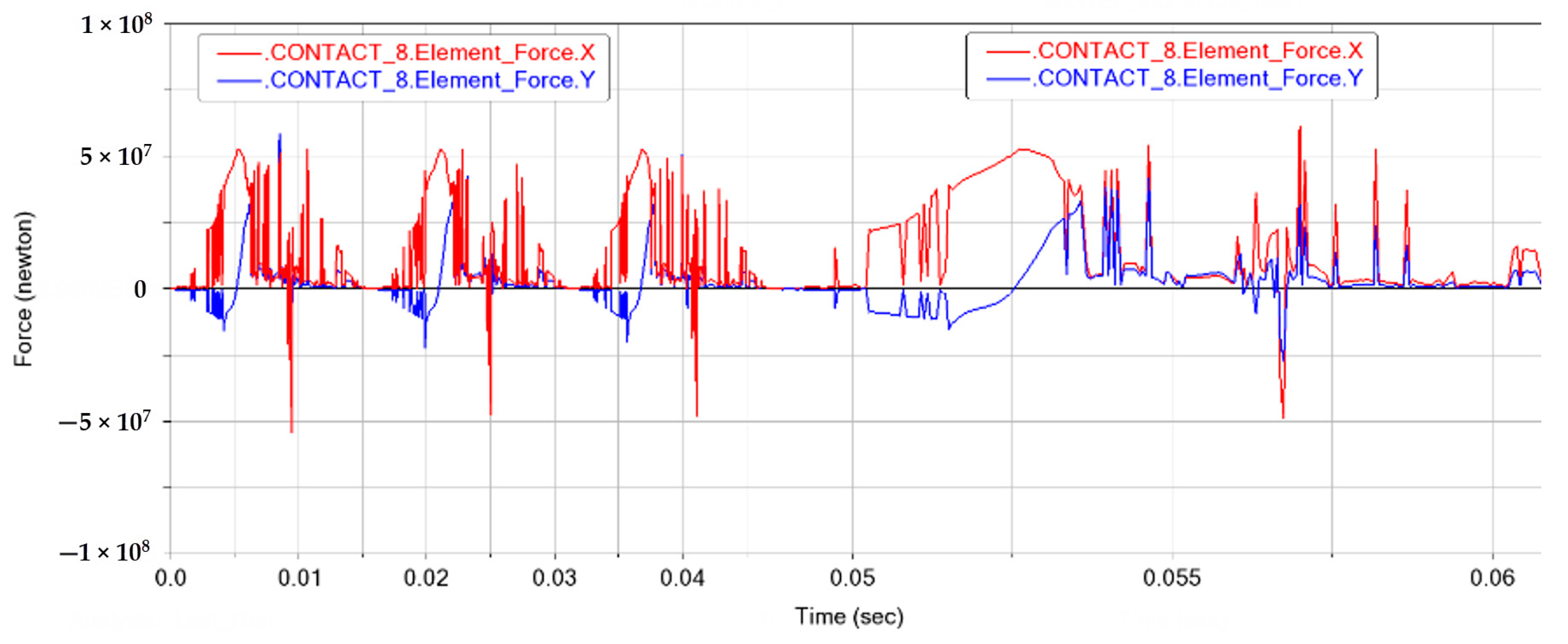
3.5. Force Analysis of the Crank Pin
3.6. Piston Pin Force Analysis
3.7. Torsional Vibration Analysis of the Crankshaft
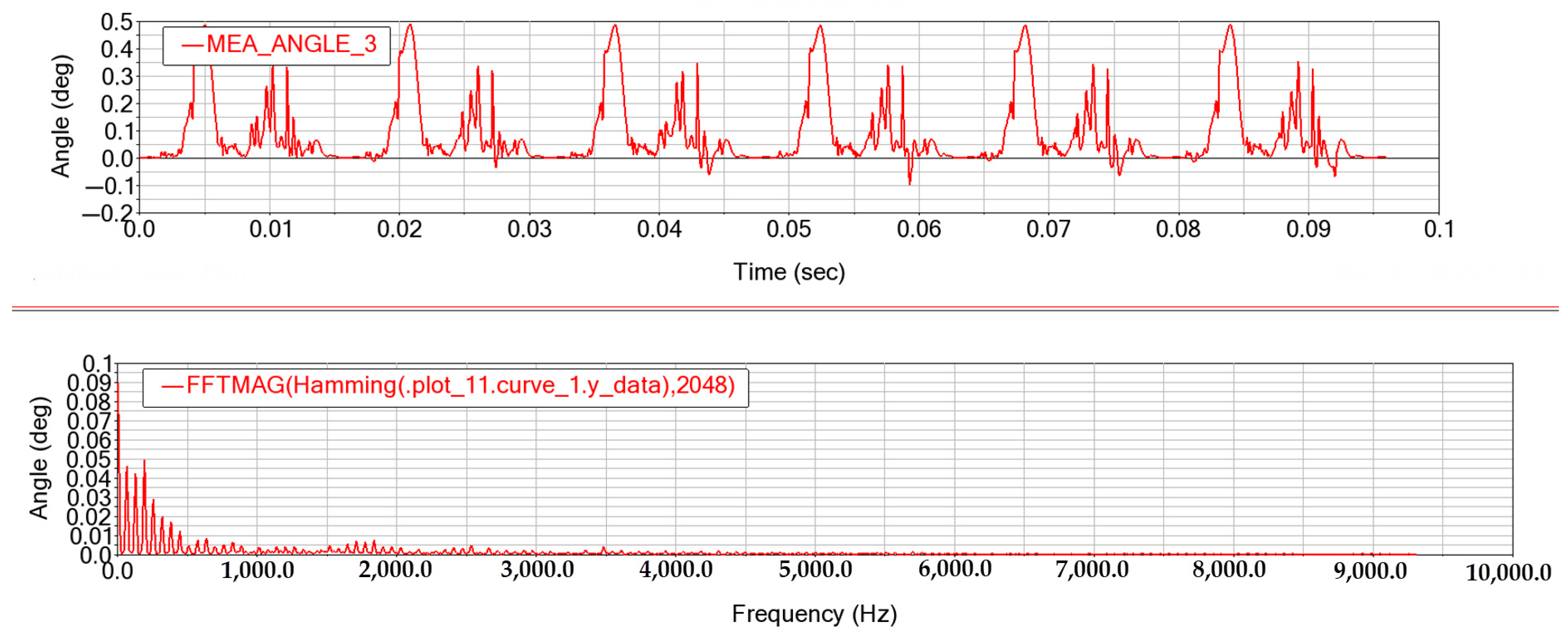
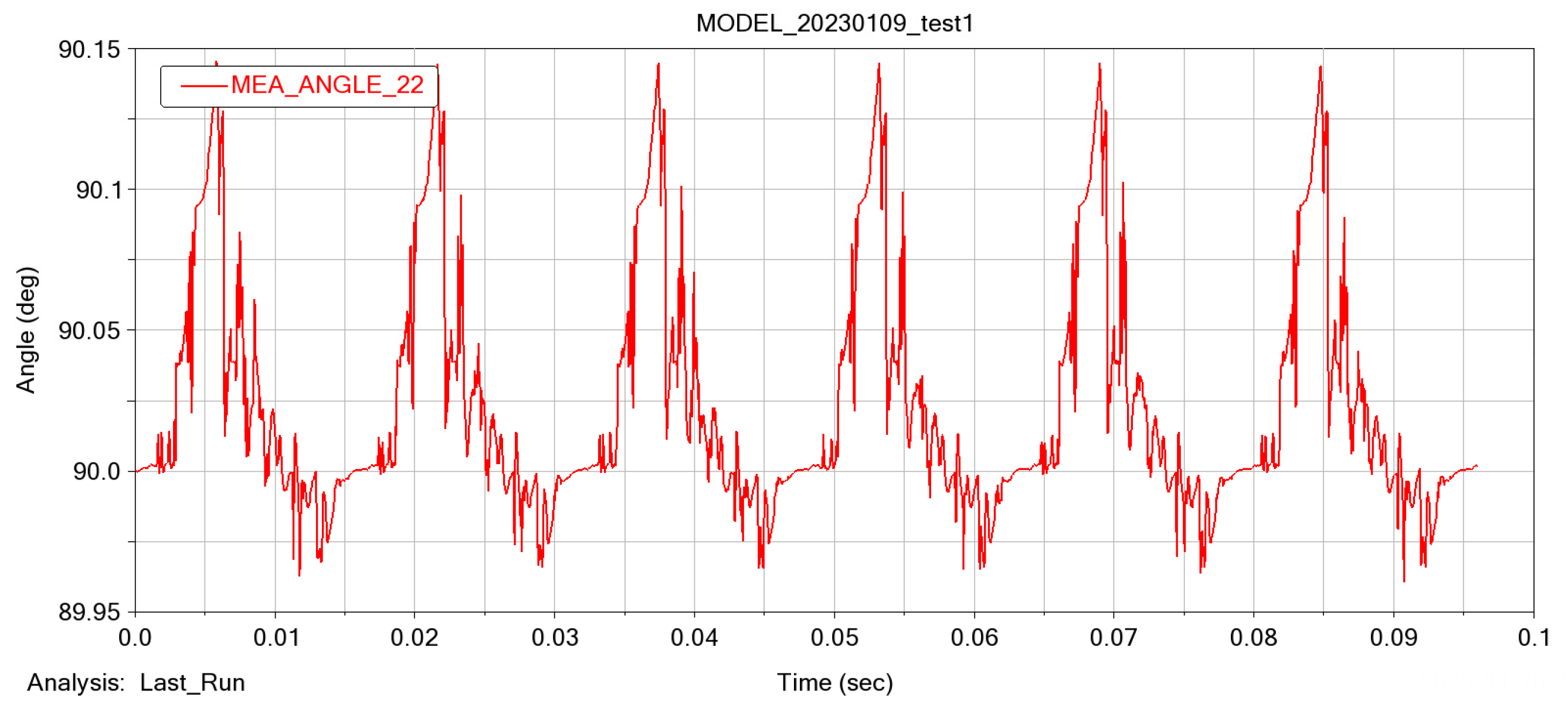
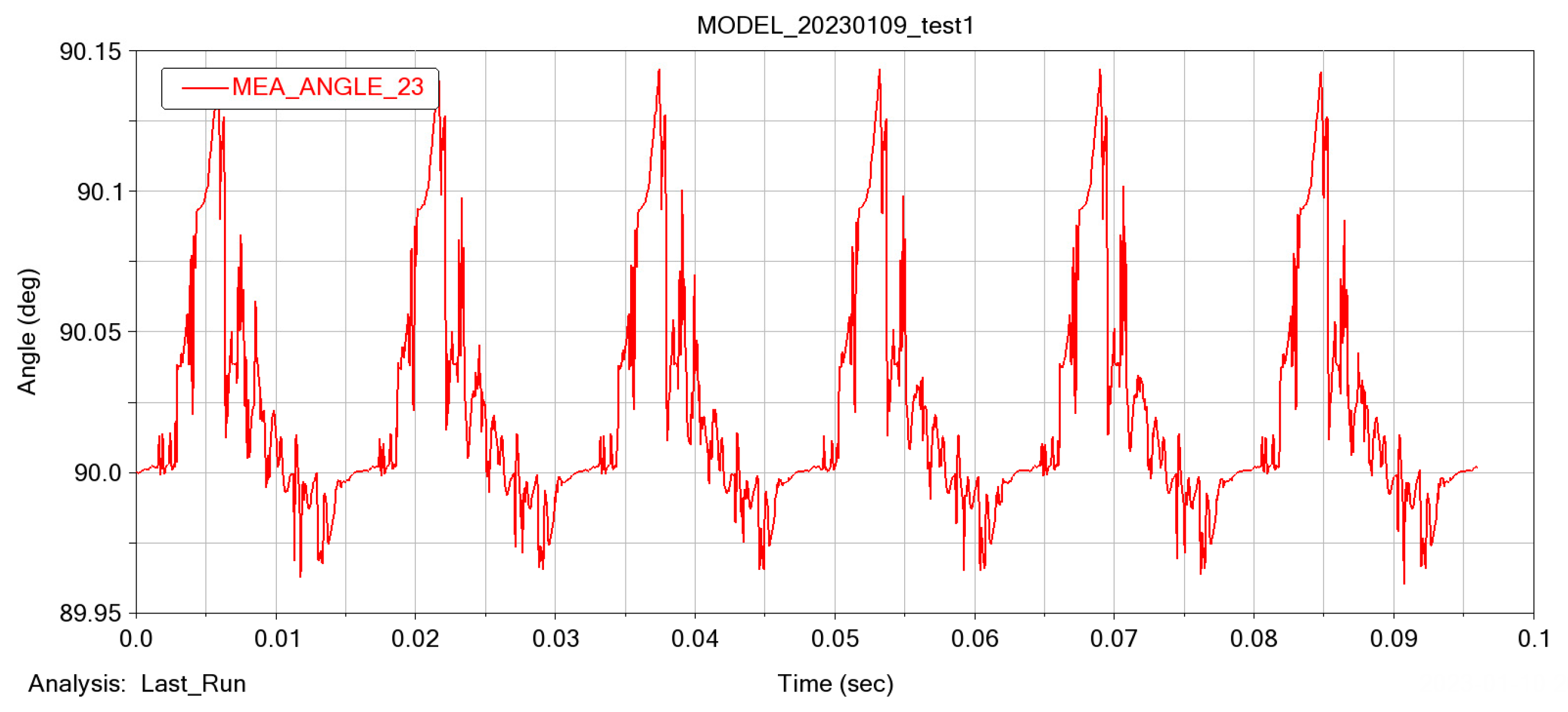
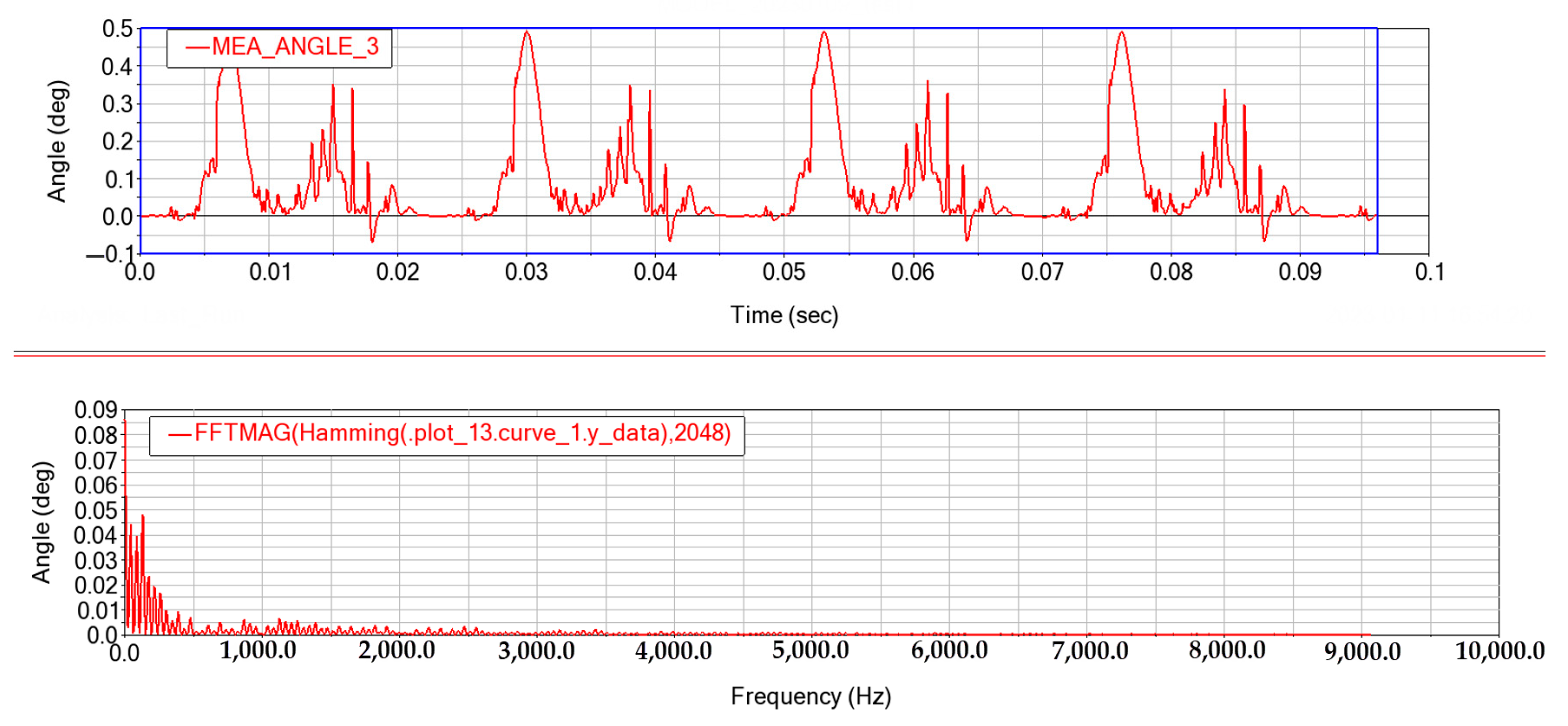
3.7.1. Test Point Arrangement
3.7.2. Analysis of the Crankshaft Torsional Vibration
4. Conclusions
- The modal and torsional vibration analyses of the crankshaft can help guide the study of engine dynamics to a certain extent. The first 20~30 orders of the modal analysis for the crankshaft are proposed for the simulation calculation. The crankshaft vibration patterns of different orders mainly show the superimposed combination of the bending vibration and torsional vibration around the X/Y/Z axis;
- The dynamic model of the crankshaft flexible multi-body system of the three-cylinder engine is established by analyzing the kinematics and dynamics of the engine crankshaft connecting rod mechanism and considering the attribute values and operating characteristics of each component. The simulation analysis of the multi-body system dynamics of the shafting system is completed under the rated speed condition, and the kinematics and dynamics characteristics of the crankshaft system are obtained;
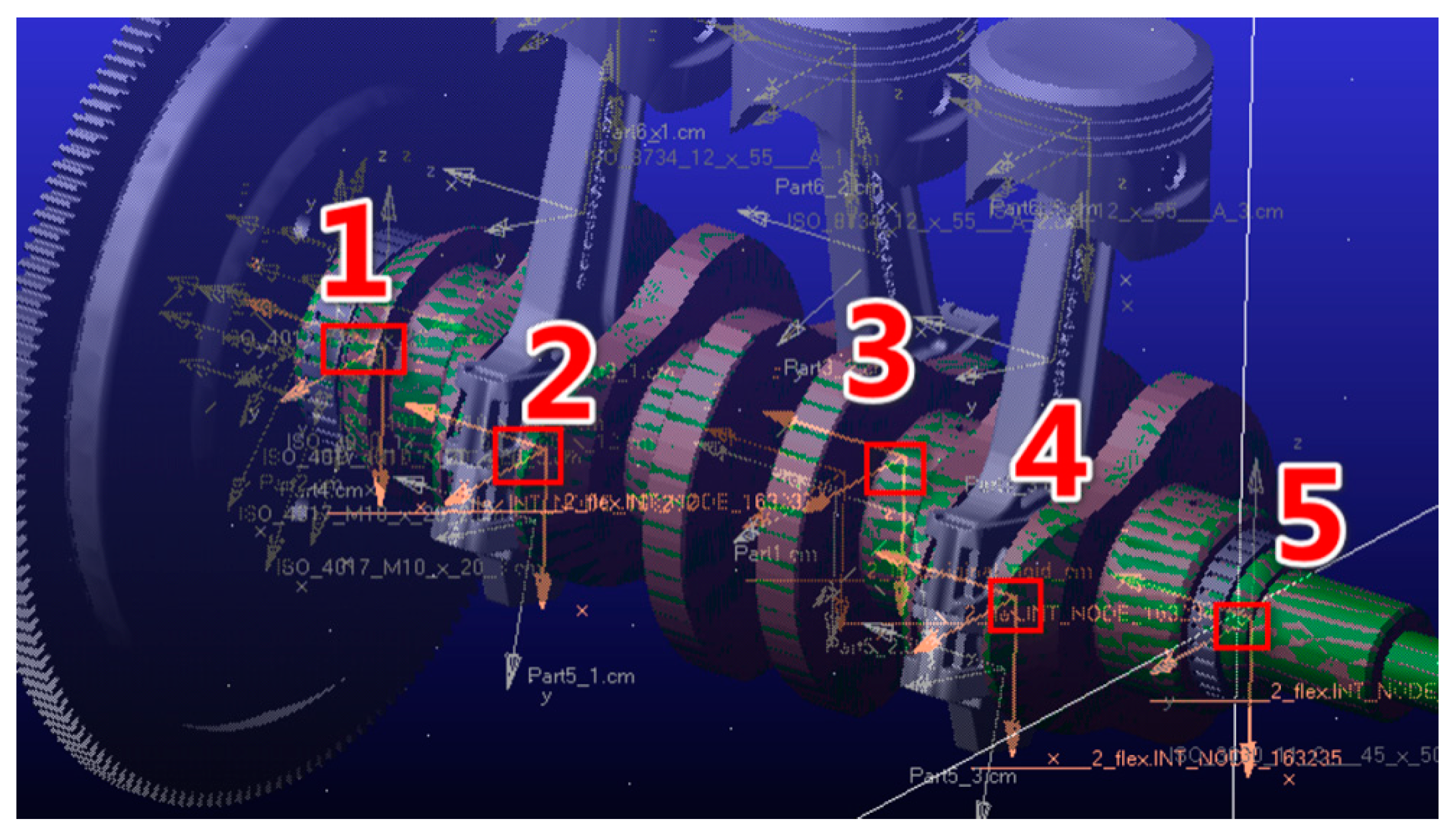
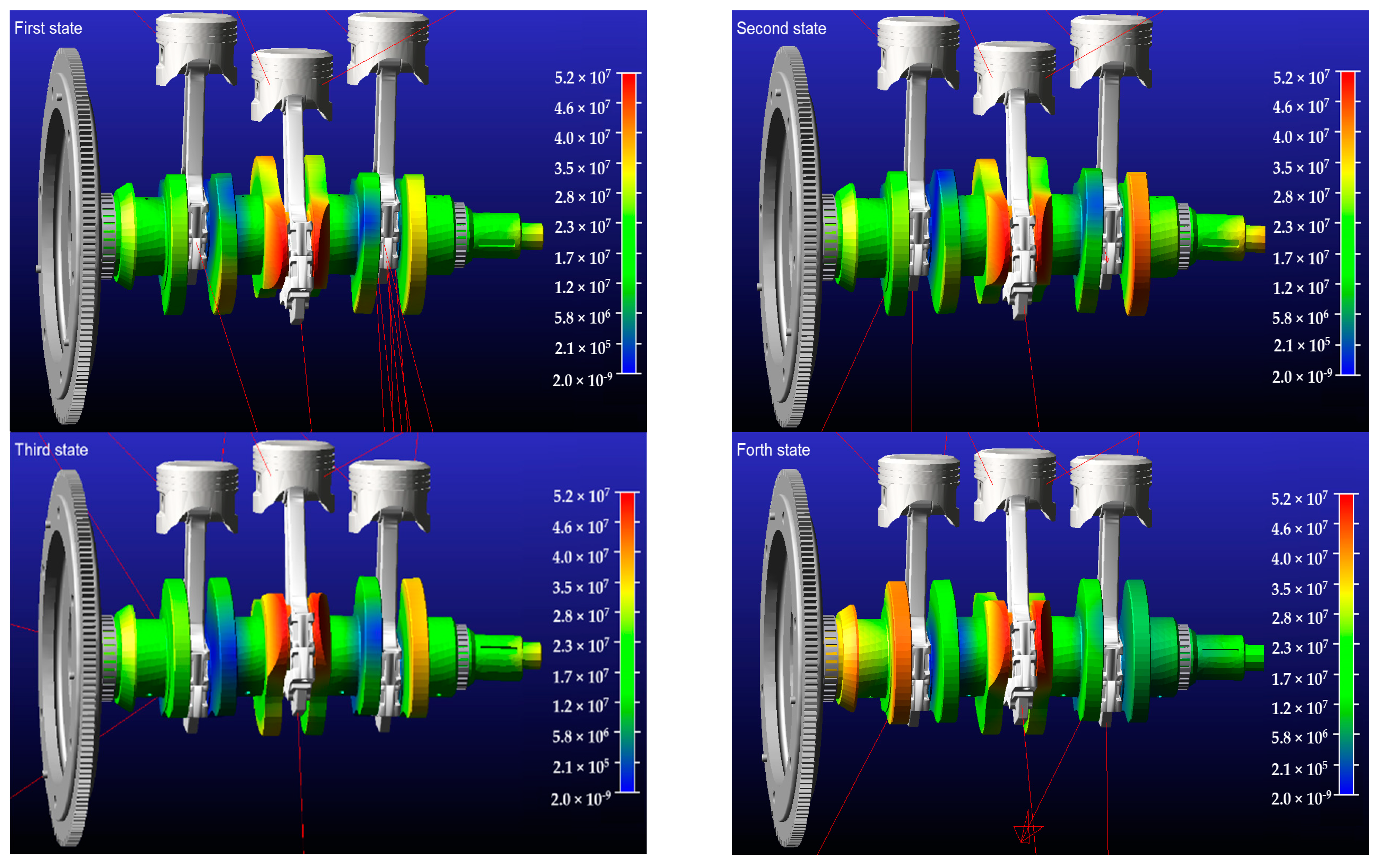
- The largest bending and torsional vibration deformation can be found at the second crank. This can affect the movement of the moving parts connected to it, resulting in varying forces on these various components, which can lead to premature fatigue failure of these components. In addition, the vibration deformation around the first and third cranks is smaller than that of the second crank, which can lead to stress concentration to the second crank and related parts, which can be confirmed by analyzing the force, displacement, velocity, and acceleration between the parts connected to the first, second and third cranks;
- The kinematic analysis can accurately obtain the kinematic response, such as the stress distribution and maximum stress for one working cycle. The natural frequency of the crankshaft system can be obtained through the constrained modal analysis of the engine crankshaft system, and engine resonance can be avoided by optimizing the operating speed and crankshaft size, thereby improving the engine life.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hoen, K.M.R.; Tan, T.; Fransoo, J.C.; van Houtum, G.J. Effect of carbon emission regulations on transport mode selection under stochastic demand. Flex. Serv. Manuf. J. 2014, 26, 170–195. [Google Scholar] [CrossRef]
- Toptal, A.; Özlü, H.; Konur, D. Joint decisions on inventory replenishment and emission reduction investment under different emission. Int. J. Prod. Res. 2014, 52, 243–269. [Google Scholar] [CrossRef]
- Hirose, K.; Matsumura, T. A comparison between emission intensity and emission cap regulations. Energy Policy 2020, 137, 111115. [Google Scholar] [CrossRef]
- Kastanaki, E.; Giannis, A. Dynamic estimation of end-of-life electric vehicle batteries in the EU-27 considering reuse, remanufacturing and recycling options. J. Clean. Prod. 2023, 393, 136349. [Google Scholar] [CrossRef]
- Friedfeldt, R.; Zenner, T.; Ernst, R.; Fraser, A. Three-cylinder gasoline engine with direct injection. MTZ Worldw. 2012, 73, 4–11. [Google Scholar] [CrossRef]
- Flierl, R.; Hannibal, W.; Schurr, A.; Neugä, J. Turbocharged three-cylinder engine with activation of a cylinder. MTZ Worldw. 2014, 75, 22–27. [Google Scholar] [CrossRef]
- Guo, R.; Zhou, Z. Influence of mass unbalancing of three-cylinder engine on idle vibration based on powertrain model. Vibroeng. Procedia 2019, 9, 81–86. [Google Scholar] [CrossRef]
- Liu, X.A.; Shangguan, W.B.; Lv, Z.P.; Ahmed, W.; Zhu, W. A study on optimization method of a powertrain mounting system with a three-cylinder engine. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 2235–2252. [Google Scholar] [CrossRef]
- Hooper, P.R. Low noise, vibration and harshness solutions for in-line three-cylinder range extender and hybrid electric vehicles. Int. J. Engine Res. 2021, 2, 581–591. [Google Scholar] [CrossRef]
- Eichler, F.; Demmelbauer-Ebner, W.; Persigehl, K.; Wendt, W. The 1.0-l Three-Cylinder TSI Engine in Volkswagen’s Modular. MTZ Worldw. 2014, 75, 18–23. [Google Scholar]
- Li, L.-B.; Wang, C.; Yin, J.-D.; Shen, Y.; Wang, R.-P. Kinematic analysis of crank-link mechanism. Intern. Combust. Engine 2017, 4, 49–52. [Google Scholar]
- Liu, J.; Lu, Q.x. Research on optimization of engine crankshaft structure based on finite element analysis. Agric. Mech. Res. 2022, 44, 241–252. [Google Scholar]
- Bai, B.Q.; Wang, Y. Modal analysis and structural optimization of V-type engine crankshaft based on Abaqus. Model. Simul. 2022, 11, 636–647. [Google Scholar] [CrossRef]
- Li, X.M.; Cui, C.Q.; Xu, H.L. Modal analysis of crankshaft of a four-cylinder engine. Hebei Agric. Mach. 2015, 9, 60–61. [Google Scholar]
- Zhao, J.S.; Li, B.C.; Li, H.; Baibin, L.; Zhang, C.D. Study of crankshaft three-dimensional coupled vibration characteristics with the influence of nonlinear parameters. Vib. Shock. 2020, 39, 198–205. [Google Scholar]
- Inagaki, M.; Kawamoto, T.; Yamamoto, K. Prediction of structural and kinematic coupled vibration on internal combustion engine. RD Rev. Toyota CRDL 2002, 37, 2. [Google Scholar]
- Mourelatos, Z.P. An efficient crankshaft dynamic analysis using substructuring with Ritz vectors. J. Sound Vib. 2000, 238, 495–527. [Google Scholar] [CrossRef]
- Nozdrzykowski, K.; Grządziel, Z.; Nozdrzykowska, M.; Grzejda, R.; Stępień, M. Eliminating the Influence of Support Conditions on Geometric Shape Measurements of Large Crankshafts of Marine Engines. Energies 2023, 16, 16. [Google Scholar] [CrossRef]
- Sestieri, A. SDM applications to machine tools and engines. Sadhana 2000, 25, 305–317. [Google Scholar] [CrossRef]
- Zhang, Q.; Zuo, Z.; Liu, J. Failure analysis of a diesel engine cylinder head based on finite element method. Eng. Fail. Anal. 2013, 34, 51–58. [Google Scholar] [CrossRef]

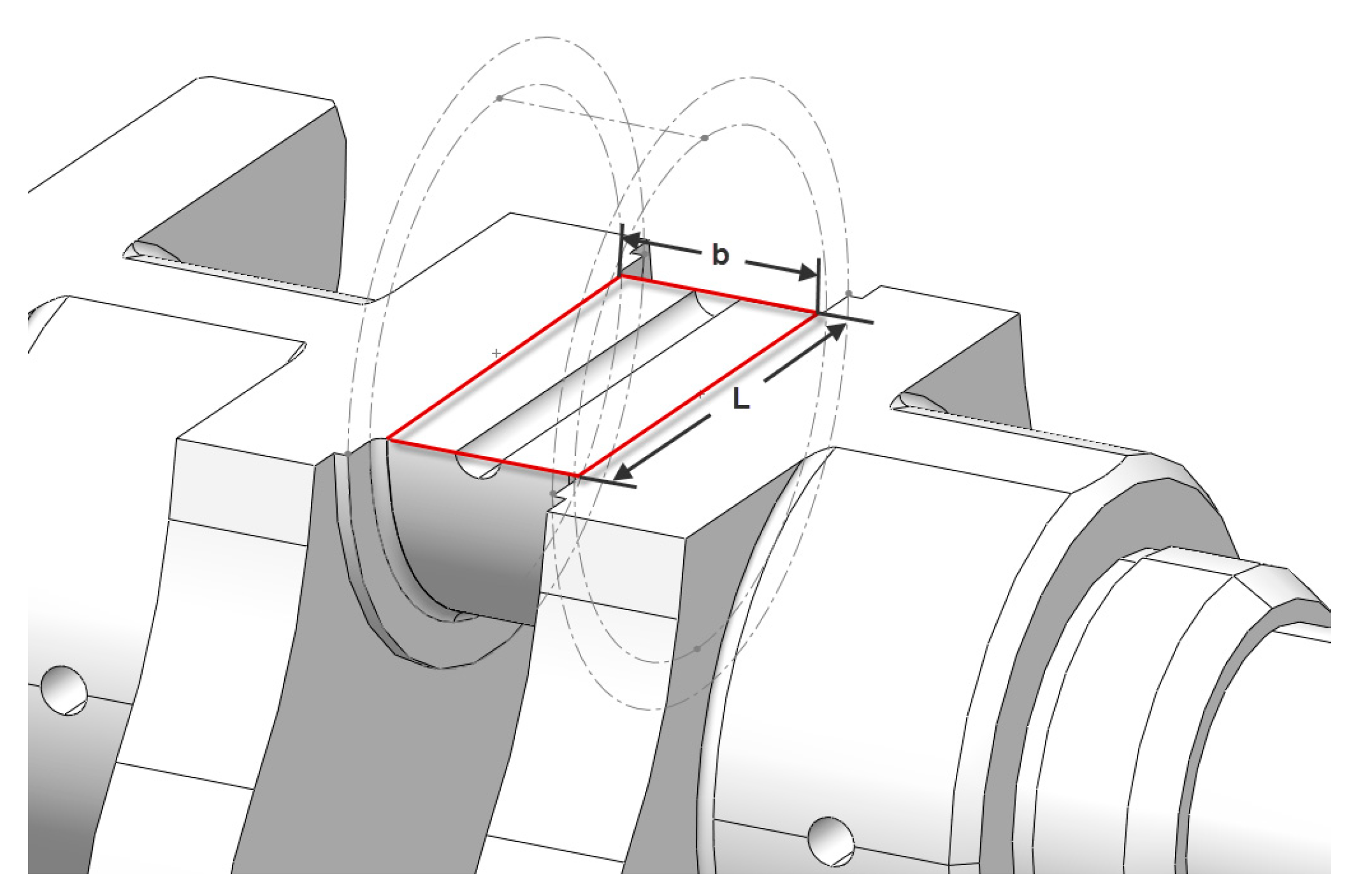

















| Symbol | Corresponding Meaning |
|---|---|
| The contact stress on the crankshaft | |
| The combined force applied to the crankshaft | |
| The idealized rectangular contact surface length | |
| The idealized rectangular contact surface width | |
| Poisson’s ratio of material 1 | |
| Poisson’s ratio of material 2 | |
| The modulus of elasticity of material 1 | |
| The modulus of elasticity of material 2 |
| Name | Unit Size | Grid Nodes | Grid Cells | Average Mass | Average Deformation |
|---|---|---|---|---|---|
| DP 0 | 1 | 4,956,547 | 3,400,246 | 0.827769 | 7.544466 |
| DP 1 | 1.5 | 1,830,357 | 1,228,602 | 0.814675 | 7.576838 |
| DP 2 | 2 | 1,006,786 | 673,009 | 0.815887 | 7.655221 |
| DP 3 | 2.5 | 606,452 | 399,819 | 0.805338 | 7.814621 |
| DP 4 | 3 | 395,230 | 257,287 | 0.795004 | 7.758828 |
| DP 5 | 3.5 | 291,525 | 188,933 | 0.790261 | 7.478033 |
| DP 6 | 4 | 219,903 | 140,967 | 0.773641 | 7.476684 |
| DP 7 | 4.5 | 167,588 | 106,517 | 0.766163 | 7.474908 |
| DP 8 | 4.8 | 149,001 | 94,094 | 0.746741 | 7.476052 |
| DP 9 | 6 | 109,232 | 64,782 | 0.741255 | 7.342311 |
| DP 10 | 8 | 46,893 | 28,300 | 0.734225 | 7.162736 |
| Mode | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|
| Inherent frequency | 850.23 | 1083.3 | 1773.1 | 1785.8 | 1809.8 | 2544.3 |
| 13 | 14 | 15 | 16 | 17 | 18 | |
| Inherent frequency | 3164.5 | 3840.3 | 3982.4 | 5013.3 | 5312.2 | 5750.4 |
| 19 | 20 | 21 | 22 | 23 | 24 | |
| Inherent frequency | 5785.3 | 6009.4 | 6287.9 | 6671.3 | 6905.2 | 7094.5 |
| 25 | 26 | 27 | 28 | 29 | 30 | |
| Inherent frequency | 7469.8 | 7559.3 | 7605.5 | 7615.4 | 8489.1 | 8868.1 |
| Serial Number | Parts | Material Name | Modulus of Elasticity (Gpa) | Poisson’s Ratio | Material Density (kg/m3) |
|---|---|---|---|---|---|
| 1 | Crankshaft | 45 gauge steel | 2.06 | 0.3 | 7850 |
| 2 | Connecting rod | 45 Mn manganese steel | 2.1 | 0.28 | 8000 |
| 3 | Piston | Eutectic aluminum alloy | 1.23 | 0.33 | 4650 |
| 4 | Piston pin | 15 Cr chromium steel | 2.12 | 0.284 | 7800 |
| 5 | Flywheel | Ductile iron | - | - | 7200 |
| Serial Number | Parts 1 | Part 2 | Constraint Name |
|---|---|---|---|
| 1 | Cylindrical roller bearings | Crankshaft | Rotating sub |
| 2 | Flywheel | Crankshaft | Fixed sub |
| 3 | Connecting rod (big end) | Crankshaft | Rotating sub |
| 4 | Piston pin | Connecting rod (small end) | Rotating sub |
| 5 | Piston | Piston pin | Rotating sub |
| 6 | Piston | - | Panning |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Zheng, L. Investigation on the Dynamics of a Flexible Multi-Body System of a Three-Cylinder Gasoline Engine Crankshaft. Processes 2023, 11, 1248. https://doi.org/10.3390/pr11041248
Zhang X, Zheng L. Investigation on the Dynamics of a Flexible Multi-Body System of a Three-Cylinder Gasoline Engine Crankshaft. Processes. 2023; 11(4):1248. https://doi.org/10.3390/pr11041248
Chicago/Turabian StyleZhang, Xiao, and Lu Zheng. 2023. "Investigation on the Dynamics of a Flexible Multi-Body System of a Three-Cylinder Gasoline Engine Crankshaft" Processes 11, no. 4: 1248. https://doi.org/10.3390/pr11041248




