Intelligent Diagnosis Model of Working Conditions in Variable Torque Pumping Unit Wells Based on an Electric Power Diagram
Abstract
:1. Introduction
2. Materials and Methods
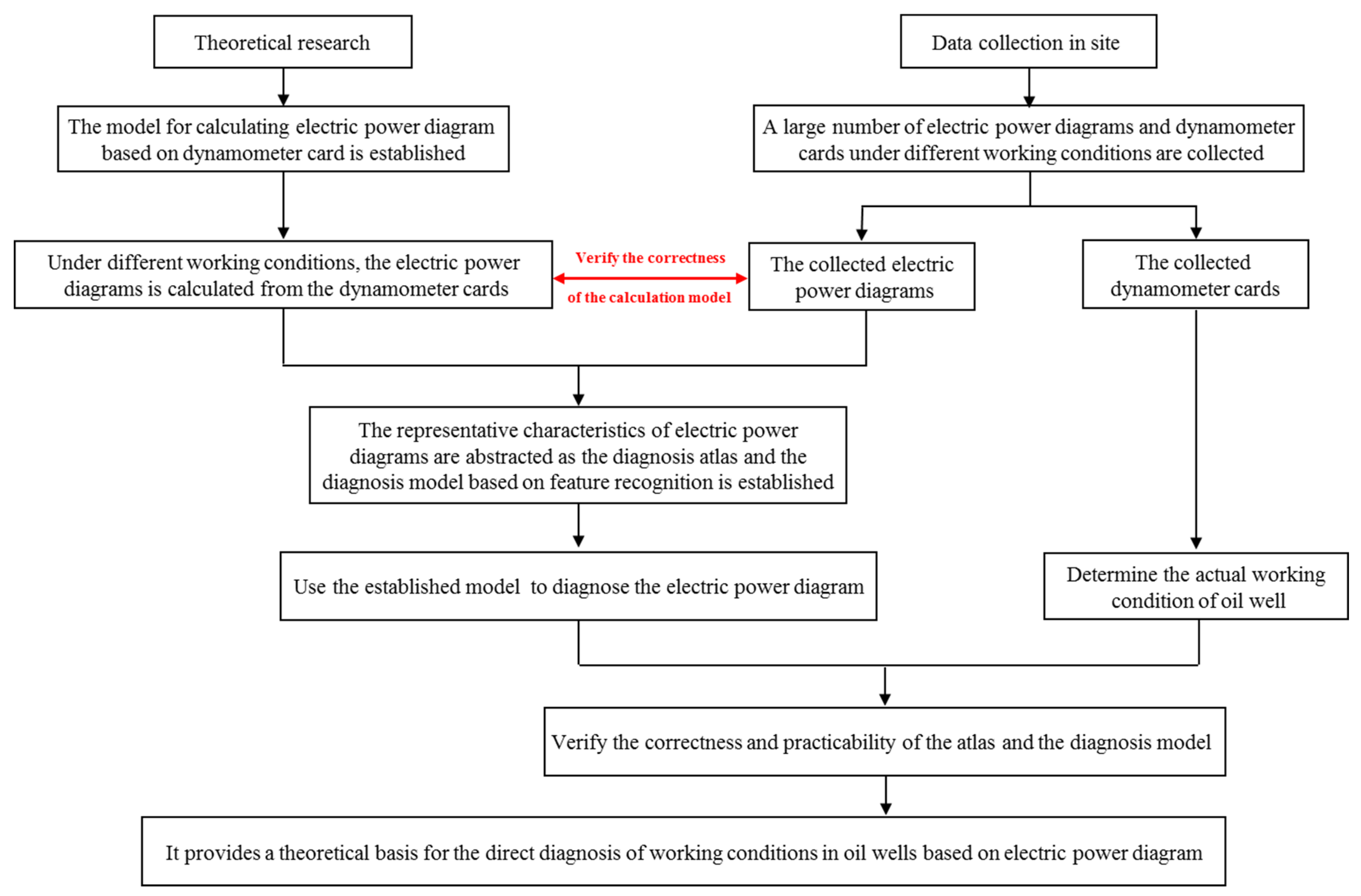
2.1. Technical Ideas
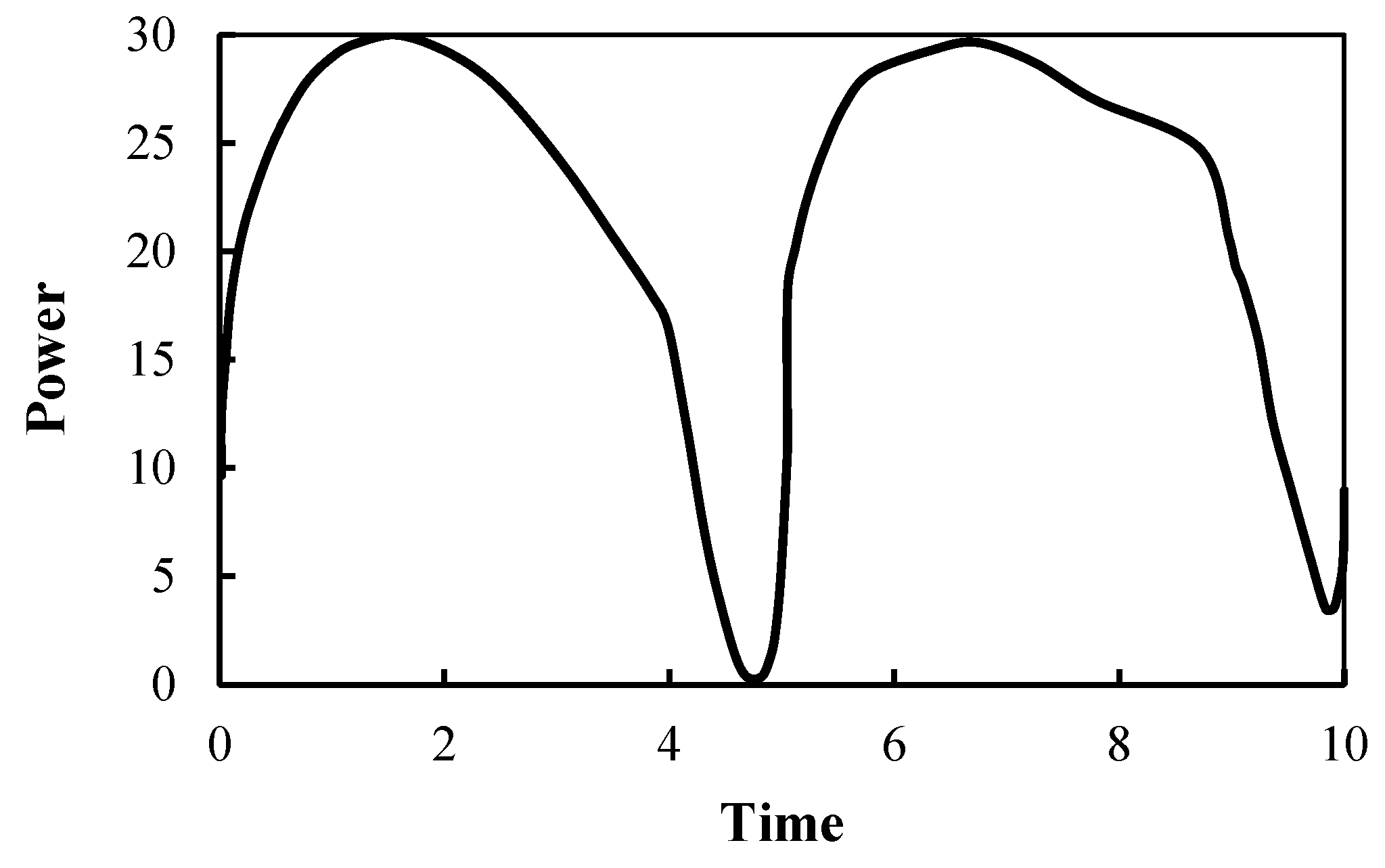
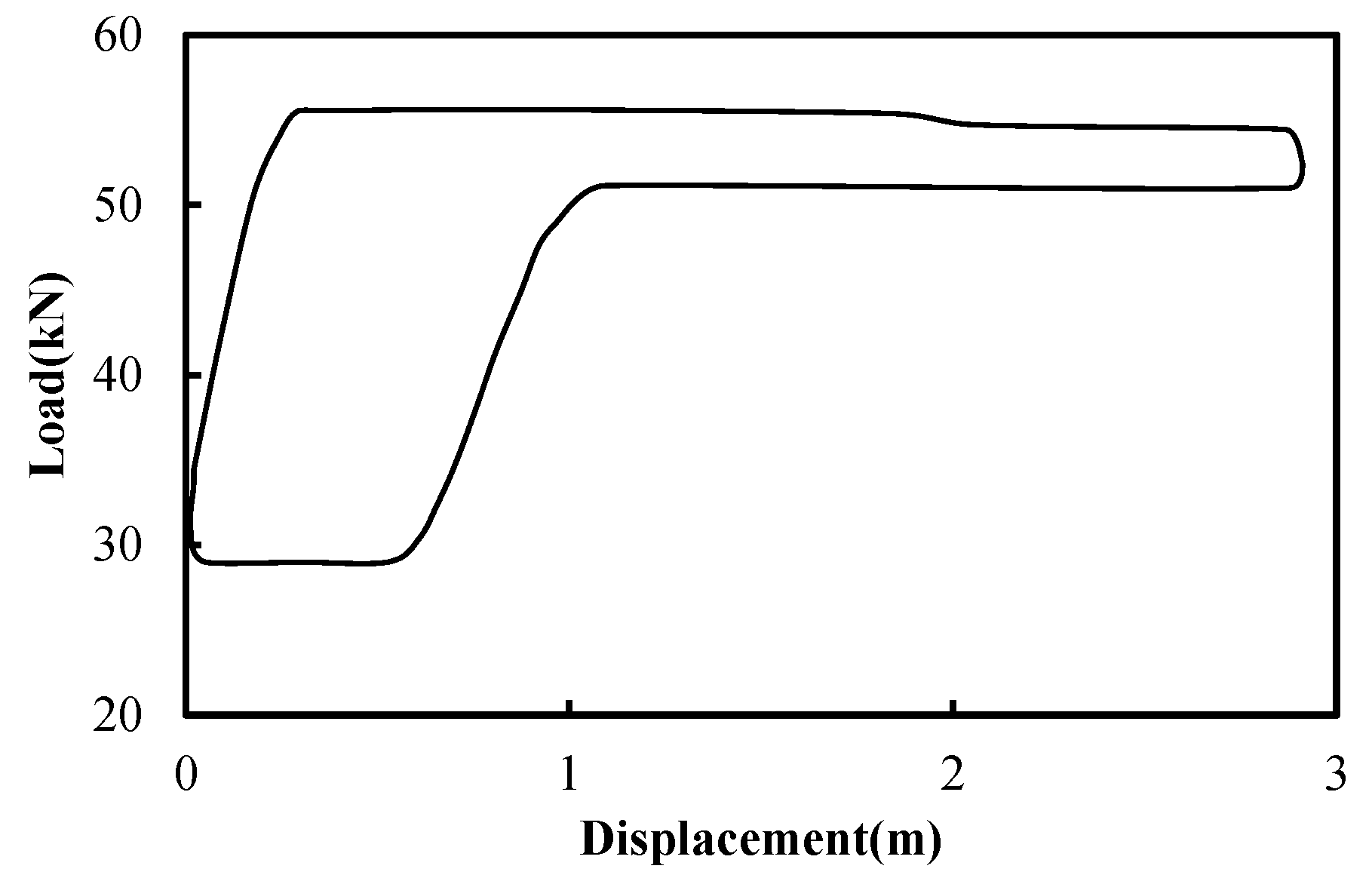
2.2. Model for Calculating Electric Power Diagram Based on Dynamometer Card
2.3. Diagnosis Model on Working Condition
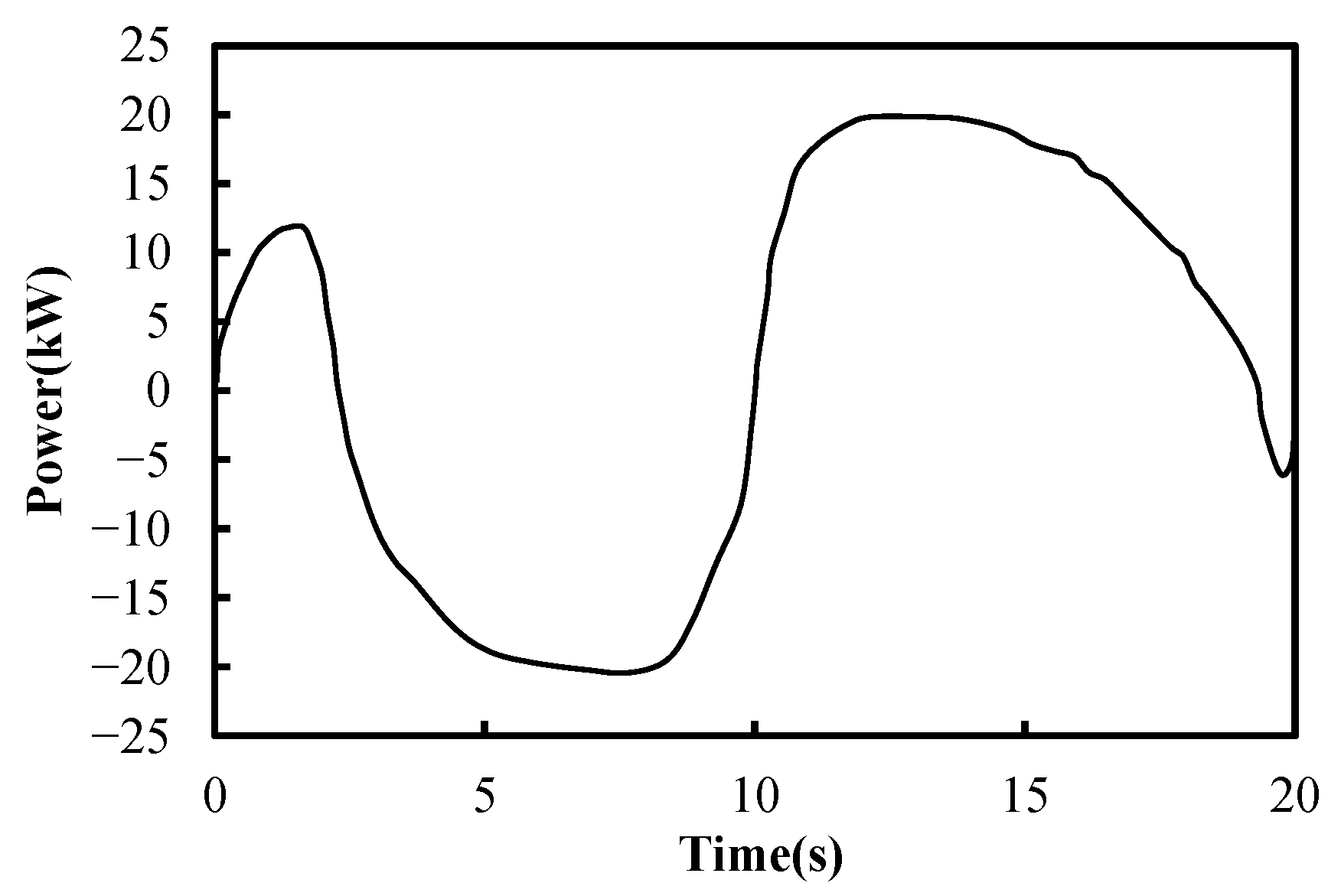
2.3.1. Electric Power Diagram Atlas under Different Working Conditions
2.3.2. Feature Analysis and Eigenvalue Extraction
3. Results and Analysis
3.1. Accuracy Test of Model
3.2. Application and Analysis in the Field
4. Limitations and Future Scope of the Research
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, Z.; Lin, C.; Du, D.; Bi, H.; Ren, H. Application of seismic architecture interpretation in enhancing oil recovery in late development stage—Taking meandering river reservoir in dongying depression as an example. J. Pet. Sci. Eng. 2019, 187, 106769. [Google Scholar]
- Qin, G.; Dai, X.; Wu, M.; Zheng, Y.; Li, W. Study of massive water huff-n-puff technology in tight oil field and its field application. J. Pet. Sci. Eng. 2020, 196, 107514. [Google Scholar] [CrossRef]
- Han, D. Discussions on concepts, countermeasures and technical routes for the secondary development of high water-cut oilfields. Pet. Explor. Dev. 2010, 37, 583–591. [Google Scholar]
- Zhang, R.; Wang, Z.; Wang, X.; Chen, D.; Bao, B.; Li, Y. Preparation and application of macroscopic behavior chart of pumping unit in high-water-cut oil wells under the constraint of multiple factors. Oil Drill. Prod. Technol. 2018, 40, 94–101. [Google Scholar]
- Chen, D.; Yao, Y.; Fu, G.; Meng, H.; Xie, S. A new model for predicting liquid loading in deviated gas wells. J. Nat. Gas Sci. Eng. 2016, 34, 178–184. [Google Scholar] [CrossRef]
- Deng, J. Uniformed model for energy conservation and optimization of rod-pumped wells. Oil Drill. Prod. Technol. 2016, 38, 842–847. [Google Scholar]
- Zhang, R.; Yin, Y.; Xu, L.; Chen, D.; Xiao, L.; Yang, K. A new intelligent diagnosis method for working conditions in electric submersible pump well based on feature recognition. J. Shengli Coll. China Univ. Pet. 2018, 32, 41–45. [Google Scholar]
- Wu, F.; Li, F.; Zhao, X.; Bolan, N.S.; Fu, P.; Lam, S.S.; Mašek, O.; Ong, H.C.; Pan, B.; Qiu, X.; et al. Meet the challenges in the “Carbon Age”. Carbon Res. 2022, 1, 1. [Google Scholar] [CrossRef]
- Cao, L.; Sun, J.; Zhang, B.; Lu, N.; Xu, Y. Sensitivity analysis of the temperature profile changing law in the production string of a high-pressure high-temperature gas well considering the coupling relation among the gas flow friction, gas properties, temperature, and pressure. Front. Phys. 2022, 10, 1050229. [Google Scholar] [CrossRef]
- Li, K.; Han, Y.; Wang, T. A novel prediction method for down-hole working conditions of the beam pumping unit based on 8-directions chain codes and online sequential extreme learning machine. J. Pet. Sci. Eng. 2018, 160, 285–301. [Google Scholar] [CrossRef]
- Bello, O.; Dolberg, E.P.; Teodoriu, C.; Karami, H.; Devegowdva, D. Transformation of academic teaching and research: Development of a highly automated experimental sucker rod pumping unit. J. Pet. Sci. Eng. 2020, 190, 107087. [Google Scholar] [CrossRef]
- Zhang, R.; Xiao, L.; Chen, D.; Peng, Y.; Qin, Y.; Zhao, T. Balance diagnosis and adjustment of pumping unit based on indicator diagram. China Pet. Mach. 2018, 46, 88–93. [Google Scholar]
- Chen, D.; Xiao, L.; Zhang, R.; Yao, Y.; Peng, Y.; Yang, K. A diagnosis model on working condition of pumping unit in oil wells based on electrical diagrams. J. China Univ. Pet. (Ed. Nat. Sci.) 2017, 41, 108–115. [Google Scholar]
- Feng, K.; Jiang, Z.; He, W.; Bo, M. A recognition and novelty detection approach based on Curvelet transform, nonlinear PCA and SVM with application to indicator diagram diagnosis. Expert Syst. Appl. 2011, 38, 12721–12729. [Google Scholar] [CrossRef]
- Lv, X.; Wang, H.; Liu, Y.; Yan, X.; Sheng, S.; Wen, J.; Bing, Y. A novel method of output metering with dynamometer card for SRPS under fault conditions. J. Pet. Sci. Eng. 2020, 192, 107098. [Google Scholar] [CrossRef]
- Xu, P.; Xu, S.; Yin, H. Application of self-organizing competitive neural network in fault diagnosis of suck rod pumping system. J. Pet. Sci. Eng. 2007, 58, 43–48. [Google Scholar] [CrossRef]
- Hua, L.; Li, X. Accurate extraction of valve opening and closing points based on the physical meaning of surface dynamometer card. Pet. Explor. Dev. 2011, 38, 109–115. [Google Scholar] [CrossRef]
- Zheng, B.; Gao, X. Sucker rod pumping diagnosis using valve working position and parameter optimal continuous hidden Markov model. J. Process Control 2017, 59, 1–12. [Google Scholar] [CrossRef]
- Zheng, B.; Gao, X.; Li, X. Diagnosis of Sucker Rod Pump based on generating dynamometer cards. J. Process Control 2019, 77, 76–88. [Google Scholar] [CrossRef]
- Sun, D. Research on the technology of remote intelligent fault diagnosis based on electrical parameters of pumping unit. Process Autom. Instrum. 2012, 33, 22–24. [Google Scholar]
- Li, J.; Zhi, L. Predicting dynamometer cards by actual motor power curves. Pet. Geol. Oilfield Dev. Daqing 1991, 10, 63–67. [Google Scholar]
- Tan, C.; Feng, Z.; Liu, X.; Fan, J.; Cui, W.; Sun, R.; Ma, Q. Review of variable speed drive technology in beam pumping units for energy-saving. Energy Rep. 2020, 6, 2676–2688. [Google Scholar] [CrossRef]
- Zhang, D. Study of Power Balance Technology on Beam Pumping Unit. In Proceedings of the 2nd International Conference on Measurement, Information and Control (ICMIC), Harbin, China, 16–18 August 2013. [Google Scholar]
- Lea, J.; Bowen, J. Dynamic measurements of beam-pump parameters. SPE Prod. Eng. 1992, 7, 113–120. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, Q.; Wang, L.; Zhang, H.; Zhang, L.; Yao, J.; Yang, Y. Fault diagnosis method for sucker rod well with few shots based on meta-transfer learning. J. Pet. Sci. Eng. 2022, 212, 110295. [Google Scholar] [CrossRef]
- Zhang, R.; Wang, Z.; Wang, X.; Wang, J.; Zhang, G.; Chen, D. Integrated Diagnostics Method and Application of Ground and Downhole Working Condition in Rod Pumping Well. J. Appl. Sci. Eng. 2018, 24, 615–624. [Google Scholar]
- Desai, J.N.; Pandian, S.; Vij, R.K. Big data analytics in upstream oil and gas industries for sustainable exploration and development: A review. Environ. Technol. Innov. 2020, 21, 101186. [Google Scholar] [CrossRef]

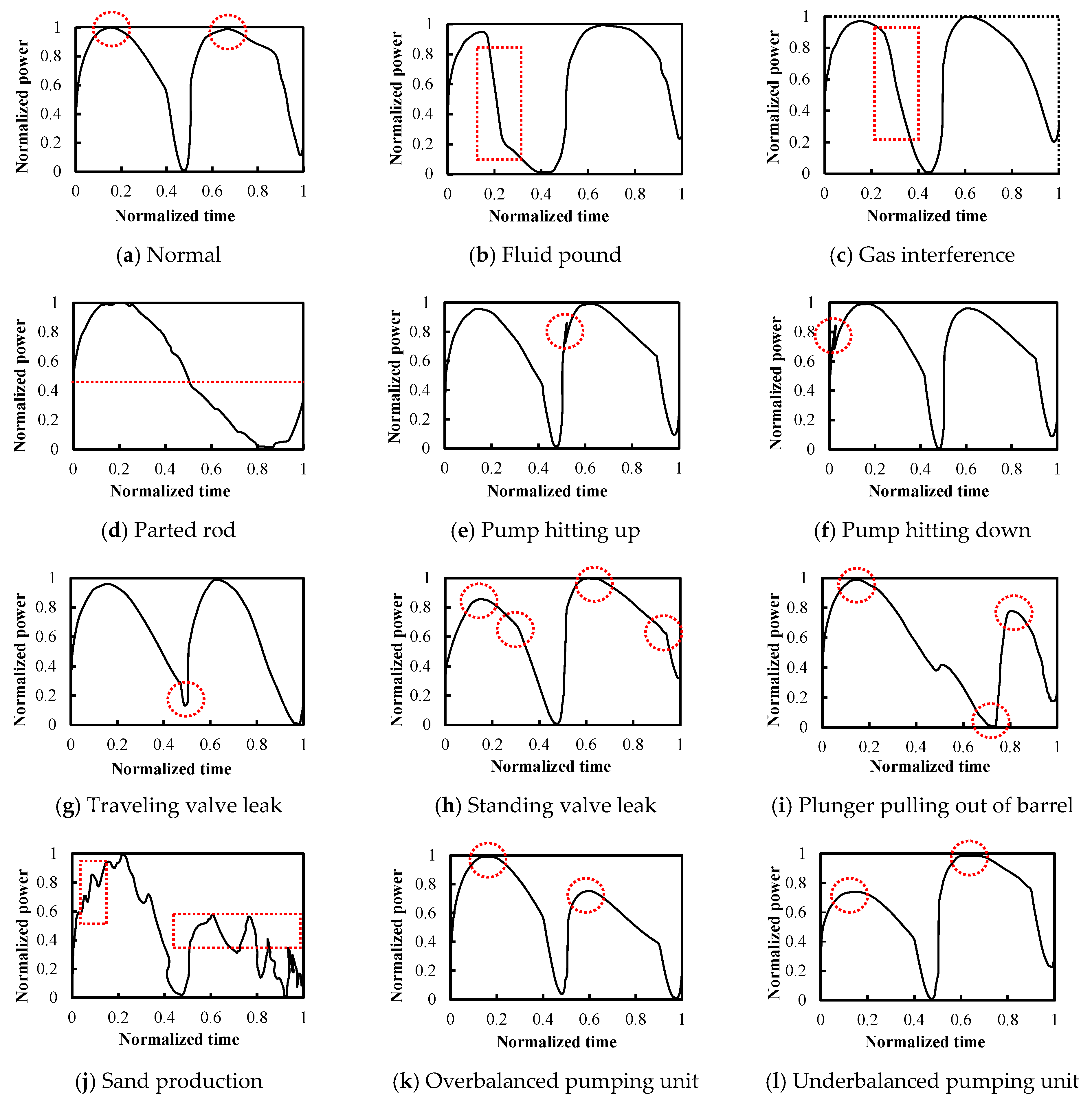

| Type of Equipment | Number | Type of Working Conditions | Number | Type of Working Conditions |
|---|---|---|---|---|
| Wellbore conditions | 1 | Normal | 2 | Fluid pound |
| 3 | Gas interference | 4 | Parted rod | |
| 5 | Pump hitting up | 6 | Pump hitting down | |
| 7 | Traveling valve leak | 8 | Standing valve leak | |
| 9 | Plunger pulling out of barrel | 10 | Sand production | |
| Surface conditions | 11 | Overbalanced pumping unit | 12 | Underbalanced pumping unit |
| Type of Pumping Unit | Type of Motor | Angle between Beam and Boom (°) | Counterweight of Boom (kN) | Structural Unbalance Weight (kN) | Stroke (m) | Stroke Frequency (min−1) |
|---|---|---|---|---|---|---|
| CYJT8-3-37HY | Y200L-8 | 42.8 | 4.79 | −0.97 | 3 | 3 |
| Relative Error Name | Calculated Value/kW | Measured Value/kW | Relative Error Value/% |
|---|---|---|---|
| The relative error of the power peak in the upstroke Er(u max) | 19.803 | 19.847 | 0.22 |
| The relative error of the power peak in the downstroke Er(d max) | 12.817 | 12.427 | 3.14 |
| The relative error of the difference between the maximum power and the minimum power Er(ΔPmax) | 40.123 | 40.267 | 0.36 |
| The relative error of average power | 11.287 | 10.607 | 6.41 |
| Well Name | Dynamometer Card | Electric Power Diagram | Er(u max) | Er(d max) | Diagnosis of Dynamometer Card | Diagnosis of Electric Power Diagram | |
|---|---|---|---|---|---|---|---|
| X2 | 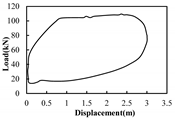 |  | 0.45% | 0.32% | 2.38% | Traveling valve leak | Traveling valve leak; Underbalanced pumping unit |
| X3 | 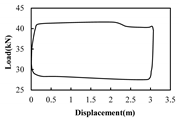 | 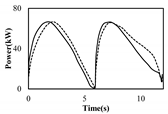 | 6.72% | 1.72% | 5.22% | Normal condition | Normal condition; Pumping unit well balanced |
| X4 | 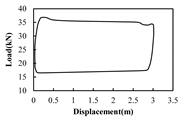 | 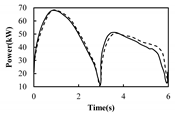 | 4.86% | 2.45% | 1.81% | Normal condition | Normal condition; Overbalanced pumping unit |
| X5 | 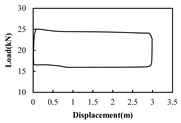 |  | 3.58% | 2.12% | 6.91% | Normal condition | Normal condition; Underbalanced pumping unit |
| X6 |  | 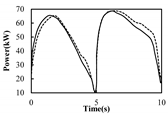 | 5.28% | 2.94% | 2.03% | Normal condition | Normal condition; Pumping unit well balanced |
| Average of relative error | 4.18% | 1.91% | 3.67% | ----- | |||
| Wellbore Conditions | Well Count | Proportion | Electric Power Diagram Diagnosis Results | |
|---|---|---|---|---|
| Accurate Diagnosis Well Count | Accuracy | |||
| Normal | 163 | 54.3% | 151 | 91.6% |
| Fluid pound | 32 | 10.7% | 30 | 93.8% |
| Gas interference | 24 | 8.0% | 23 | 95.8% |
| Parted rod | 10 | 3.3% | 9 | 90.0% |
| Pump hitting up | 13 | 4.3% | 11 | 84.6% |
| Pump hitting down | 8 | 2.7% | 8 | 100% |
| Traveling valve leak | 15 | 5.0% | 14 | 93.3% |
| Standing valve leak | 18 | 6.0% | 16 | 88.9% |
| Plunger pulling out of barrel | 4 | 1.4% | 4 | 100% |
| Sand production | 13 | 4.3% | 12 | 92.3% |
| Total | 300 | 100% | 278 | 92.6% |
| Surface Conditions | Number of Wells | Proportion | Electric Power Diagram Diagnosis Results | |
|---|---|---|---|---|
| Number of Wells Accurately Diagnosed | Accuracy | |||
| Well balanced pumping unit | 178 | 59.3% | 175 | 98.3% |
| Overbalanced pumping unit | 59 | 19.7% | 57 | 96.6% |
| Underbalanced pumping unit | 63 | 21.0% | 60 | 95.2% |
| Total | 300 | 100% | 292 | 97.3% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Chen, D.; Lu, N.; Zhang, B.; Yang, Y. Intelligent Diagnosis Model of Working Conditions in Variable Torque Pumping Unit Wells Based on an Electric Power Diagram. Processes 2023, 11, 1166. https://doi.org/10.3390/pr11041166
Zhang R, Chen D, Lu N, Zhang B, Yang Y. Intelligent Diagnosis Model of Working Conditions in Variable Torque Pumping Unit Wells Based on an Electric Power Diagram. Processes. 2023; 11(4):1166. https://doi.org/10.3390/pr11041166
Chicago/Turabian StyleZhang, Ruichao, Dechun Chen, Nu Lu, Bo Zhang, and Yanjie Yang. 2023. "Intelligent Diagnosis Model of Working Conditions in Variable Torque Pumping Unit Wells Based on an Electric Power Diagram" Processes 11, no. 4: 1166. https://doi.org/10.3390/pr11041166






