Adsorption of As and Pb by Stone Powder/Chitosan/Maghemite Composite Beads (SCM Beads): Kinetics and Column Study
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Preparation of SCM Beads
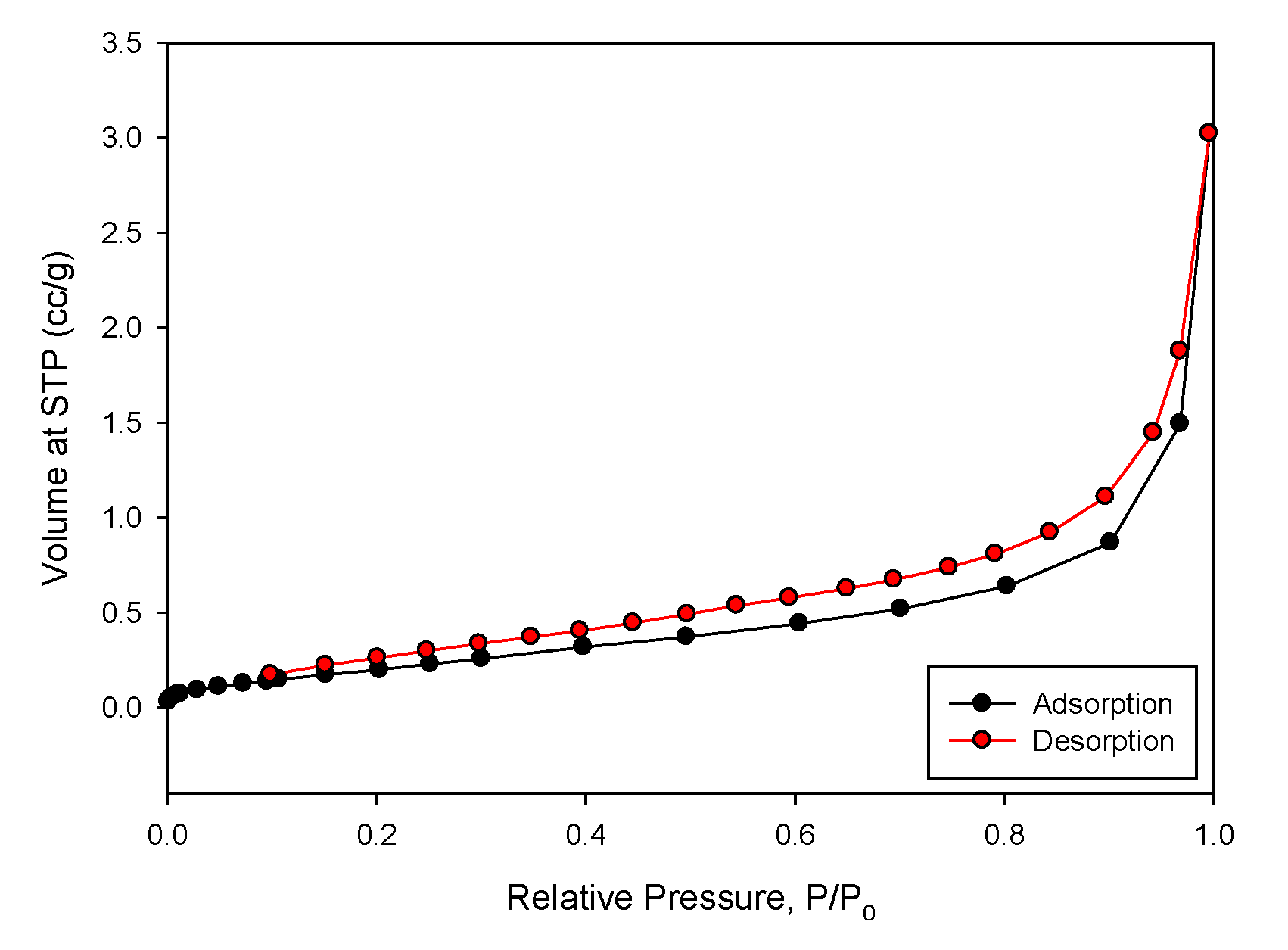
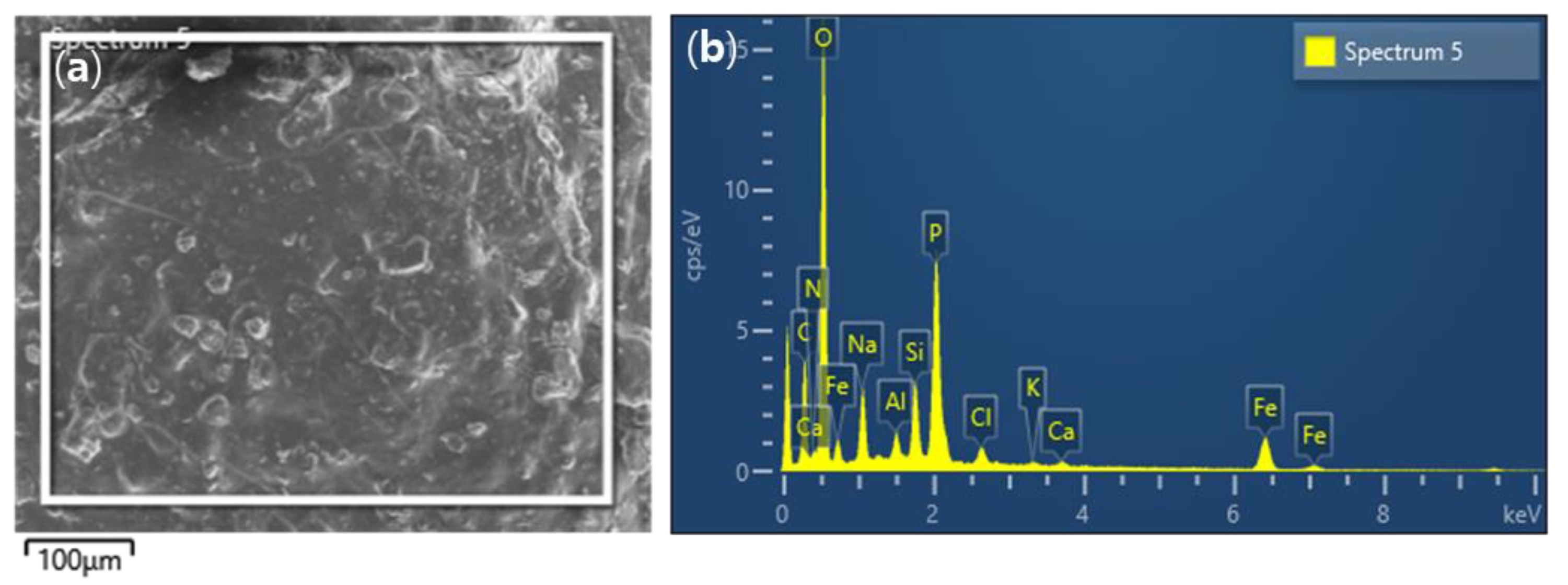
2.3. Characterization of SCM Beads
2.4. Adsorption Kinetic Experiments
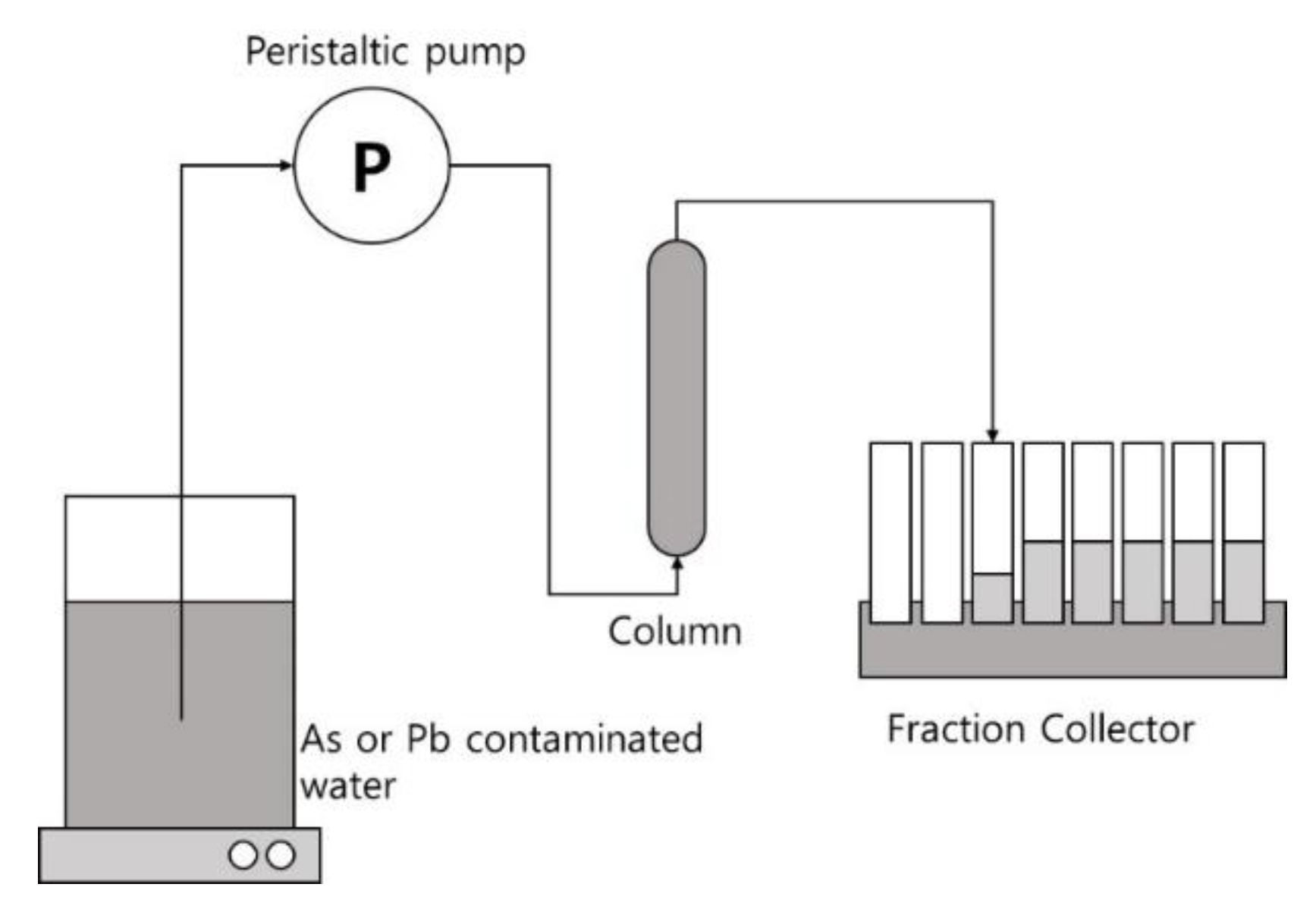
2.5. Continuous-Flow Column Experiments
2.6. Model Analysis
2.6.1. Kinetic Models
2.6.2. Column Models
3. Results and Discussion
3.1. Adsorption Batch Studies
The Adsorption Kinetics of As and Pb onto the SCM Beads
3.2. The Column Studies
3.2.1. CXTFIT Analysis
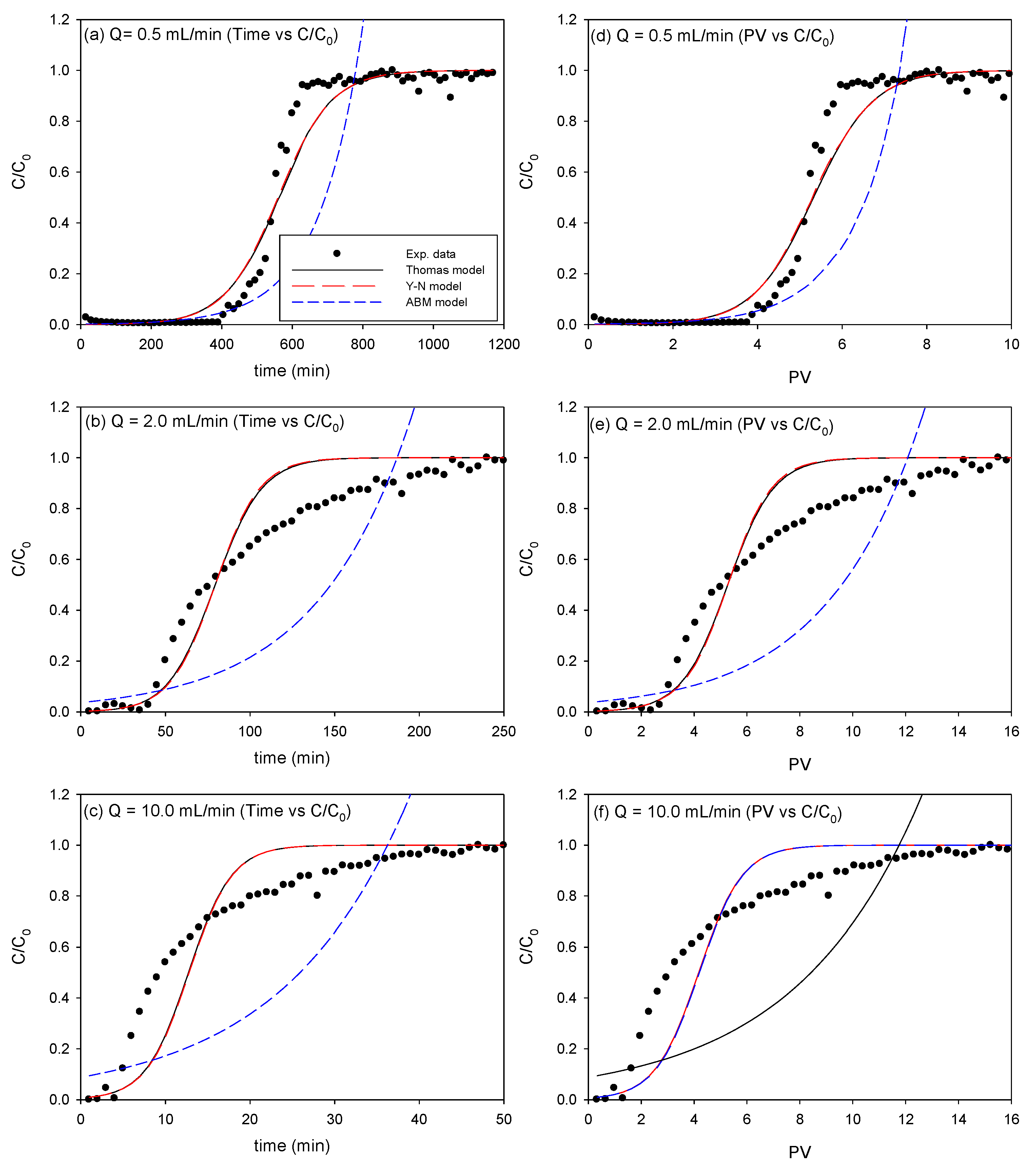
3.2.2. Effect of Flow Rate for As Removal via Model Analysis
3.2.3. Effect of Flow Rate for Pb Removal
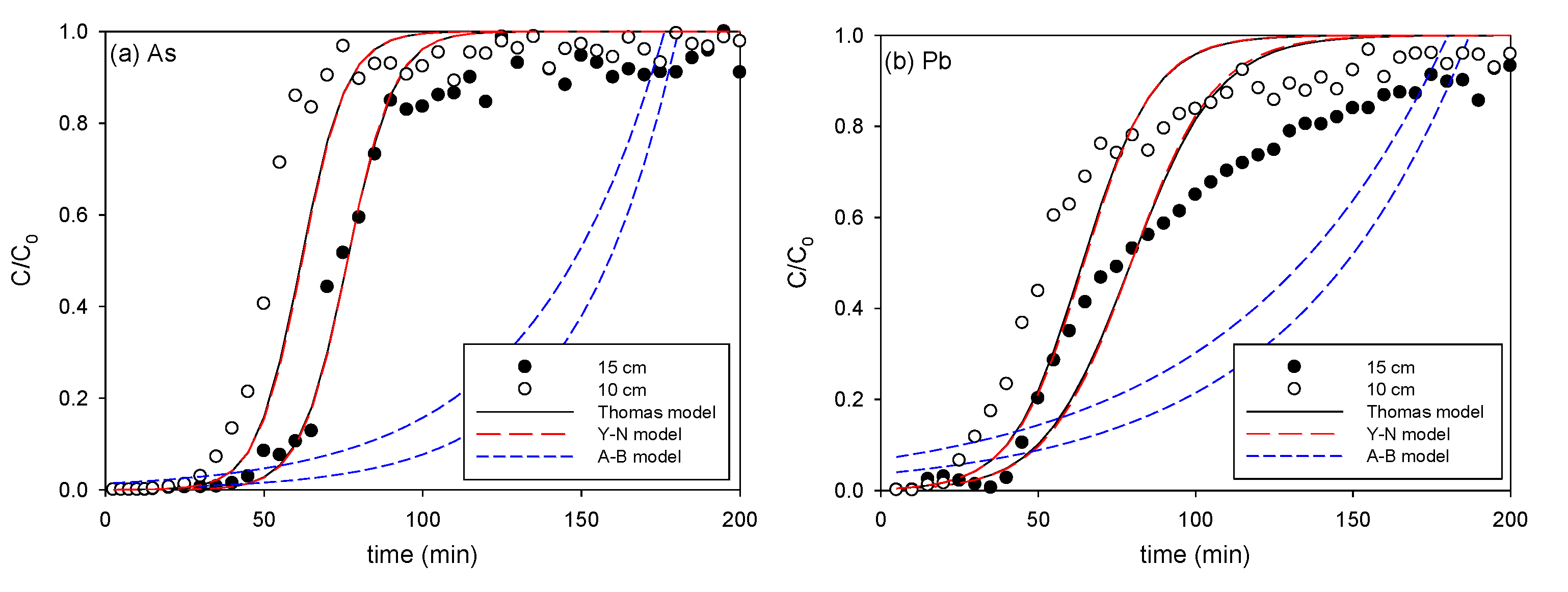
3.2.4. Effect of Bed Height
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, W.; Singh, P.; Issa, T.B. The effect of Cl-, PO43−, and SiO32− on the adsorption of As(V) and As(III) on bauxite in water. Int. J. Eng. Sci. Technol. 2015, 7, 30–36. [Google Scholar] [CrossRef]
- Karrari, P.; Mehrpour, O.; Abdollahi, M. A systematic review on status of lead pollution and toxicity in Iran; Guidance for preventive measures. DARU J. Pharma. Sci. 2012, 20, 2–17. [Google Scholar] [CrossRef] [PubMed]
- Postma, D.; Mai, N.T.H.; Lan, V.M.; Trang, P.T.K.; So, H.U.; Nhan, P.Q.; Larsen, F.; Viet, P.H.; Jakobsen, R. Fate of arsenic during red river water infiltration into aquifers beneath Hanoi, Vietnam. Environ. Sci. Technol. 2017, 51, 838–845. [Google Scholar] [CrossRef] [PubMed]
- Clausen, J.L.; Bostick, B.; Korte, N. Migration of lead in surface water, pore water, and groundwater with a focus on firing ranges. Crit. Rev. Environ. Sci. Technol. 2011, 41, 1397–1448. [Google Scholar] [CrossRef]
- Komarek, M.; Vanek, A.; Ettler, V. Chemical stabilization of metals and arsenic in contaminate soils using oxides-a review. Environ. Pollut. 2013, 172, 9–22. [Google Scholar] [CrossRef]
- Trancoso, M.A.; Dos Santos, C.; Gonsalves, M.L.S. Lead sorption to selected Portuguese soils. Eur. J. Soil Sci. 2007, 58, 854–863. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, J.; Li, N.; Wang, W.; Nan, J.; Zhao, Z.; Cui, F. Highly efficient removal of bivalent heavy metals from aqueous systems by magnetic porous Fe3O4-MnO2: Adsorption behavior and process. Chem. Eng. J. 2016, 304, 737–746. [Google Scholar] [CrossRef]
- Cantu, J.; Gonzalez, L.E.; Goodship, J.; Contreras, M.; Joseph, M.; Garza, C.; Eubanks, T.M.; Parsons, J.G. Removal of arsenic from water using synthetic Fe7S8 nanoparticles. Chem. Eng. J. 2016, 290, 428–437. [Google Scholar] [CrossRef]
- Siddiqui, S.I.; Chaudhry, S.A. Iron oxide and its modified forms as an adsorbent for arsenic removal: A comprehensive recent advancement. Proc. Safety Environ. Protect. 2017, 111, 592–626. [Google Scholar] [CrossRef]
- Adhikari, T.; Singh, M.V. Sorption characteristics of lead and cadmium in some soils of India. Geoderma 2003, 114, 81–92. [Google Scholar] [CrossRef]
- Manindy-Pajany, Y.; Hurel, C.; Marmier, N.; Romeo, M. Arsenic (V) adsorption from aqueous solution onto goethite, hematite, magnetite and zero-valent iron: Effects of pH, concentration and reversibility. Desalination 2011, 281, 93–99. [Google Scholar] [CrossRef]
- Cho, D.W.; Jeon, B.H.; Chon, C.M.; Schwartz, F.W.; Jeong, Y.; Song., H. Magnetic chitosan composite for adsorption of cationic and anionic dyes in aqueous solution. J. Ind. Eng. Chem. 2015, 28, 60–66. [Google Scholar] [CrossRef]
- Podder, M.S.; Majumder, C.B. Application of granular activated carbon/MnFe2O4 composite immobilized on C. glutamicum MTCC 2745 to remove As(III) and As(V): Kinetic, mechanistic and thermodynamic studies. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2016, 153, 298–314. [Google Scholar] [CrossRef]
- Ngah, W.S.W.; Fatinathan, S. Adsorption characterization of Ph(II) and Cu(II) ions onto chitosan-tripolyphosphate beads: Kinetic, equilibrium and thermodynamic studies. J. Environ. Manag. 2010, 91, 958–969. [Google Scholar] [CrossRef]
- Pak, H.; Phiri, J.; We, J.H.; Jung, K.; Oh, S. Adsorptive removal of arsenic and lead by stone-powder/chitosan/maghemite composite beads. Int. J. Environ. Res. Pub. Health 2021, 20, 8808. [Google Scholar] [CrossRef]
- Zafar, M.N.; Parveen, A.; Nadeem, R. A pretreated green biosorbent based on neem leaves biomass for the removal of lead from wastewater. Desal. Water Treat. 2013, 51, 4459–4466. [Google Scholar] [CrossRef]
- Batool, M.; Nazar, M.F.; Awan, A.; Tahir, M.B.; Rahdar, A.; Shalan, A.E.; Lanceros-Mendez, S.; Zafar, M.N. Bismuth-based heterojunction nanocomposites for photocatalysis and heavy metal detection applications. Nano Struct Nano Object. 2021, 27, 100762. [Google Scholar] [CrossRef]
- Jung, G.H. Adsorptive Removal of Arsenic and Lead by Using Stone Powder-Chitosan-Magnetic Beads. Ph.D. Dissertation, Kyungpook National University, Daegu, Republic of Korea, 2019. [Google Scholar]
- Sureshkumar, M.K.; Das, D.; Mallia, M.B.; Gupta, P.C. Adsorption of uranium from aqueous solution using chitosan-tripolyphosphate (CTPP) beads. J. Hazard. Mater. 2010, 184, 65–72. [Google Scholar] [CrossRef]
- Oh, S. Analysis of sorption kinetics of ibuprofen on sediment using modified two-compartment first order kinetic model (MTCFOKM). KSWST J. Water Treat. 2015, 23, 161–171. [Google Scholar] [CrossRef]
- Brion-Roby, R.; Gagnon, J.; Deschenes, J.S.; Chabot, B. Investigation of fixed bed adsorption column operation parameters using a chitosan material for treatment of arsenate contaminated water. J. Environ. Chem. Eng. 2018, 6, 505–511. [Google Scholar] [CrossRef]
- Song, G.H. Column study on the characteristics of As and Pb adsorption onto stone powder-based magnetic beads. Ph.D. Dissertation, Kyungpook National University, Daegu, Republic of Korea, 2020. [Google Scholar]
- Massart, R. Preparation of aqueous magnetic liquids in alkaline and acidic media. IEEE Trans. Magn. 1981, 17, 1247–1248. [Google Scholar] [CrossRef]
- Bee, A.; Obeid, L.; Mbolantenaina, R.; Welschbillig, M.; Talbot, D. Magnetic chitosan/clay beads: A magsorbent for the removal of cationic dye from water. J. Magnetism Magnet. Mater. 2017, 421, 59–64. [Google Scholar] [CrossRef]
- Ghosh, M.K.; Poinern, G.E.J.; Issa, T.B.; Singh, P. Arsenic adsorption on goethite nanoparticles produced through hydrazine sulfate assisted synthesis method. Korean J. Chem. Eng. 2012, 29, 95–102. [Google Scholar] [CrossRef]
- Oh, S.; Wang, Q.; Shin, W.S.; Song, D.I. Sorption and desorption kinetics of PAHs in coastal sediment. Korean J. Chem. Eng. 2013, 30, 145–153. [Google Scholar] [CrossRef]
- Pan, M.; Lin, X.; Xie, J.; Huang, X. Kinetic, equilibrium and thermodynamic studies for phosphate adsorption on aluminum hydroxide modified palygorskite nano-composites. RSC Adv. 2017, 7, 4492–4500. [Google Scholar] [CrossRef]
- Chowdhury, Z.Z.; Zain, S.M.; Rashid, A.K.; Rafique, R.f.; Khalid, K. Breakthrough curve analysis for column dynamics sorption of Mn(II) ions from wastewater by using Mangostana garcinia peel-based granular-activated carbon. J. Chem. 2013, 2013, 959761. [Google Scholar] [CrossRef]
- Jang, J.S.; Lee, D.S. Enhanced adsorption of cesium on PVA-alginate encapsulated Prussian blue-graphene oxide hydrogel beads in a fixed-bed column system. Biores. Technol. 2016, 218, 294–300. [Google Scholar] [CrossRef]
- Mu, W.; Bao, D.; Chang, C.; Lian, F. Adsorption of methyl blue by maize waste based biochar: Adsorption kinetics and isotherms. J. Phys. Conf. Ser. 2020, 1622, 012081. [Google Scholar] [CrossRef]
- Kiwaan, H.A.; Mohamed, F.S.; El-Bindary, A.A.; El-Ghamaz, N.A.; Abo-Yassin, H.R.; El-Bindary, M.A. Synthesis, identification and application of metal organic framework for removal of industrial cationic dyes. J. Mol. Liq. 2021, 342, 117435. [Google Scholar] [CrossRef]
- Nadeem, R.; Zafar, M.N.; Afzal, A.; Hanif, M.A.; Saeed, R. Potential of NaOH pretreated Mangifera indica waste biomass for the mitigation of Ni(II) and Co(II) from aqueous solutions. J. Taiwan Inst. Chem. Eng. 2014, 45, 967–972. [Google Scholar] [CrossRef]
- Banerjee, K.; Amy, G.L.; Prevost, M.; Nour, S.; Jekel, M.; Gallagher, P.M.; Blumenschein, C.D. Kinetic and thermodynamic aspects of adsorption of arsenic onto granular ferric hydroxide (GFH). Water Res. 2008, 42, 3371–3378. [Google Scholar] [CrossRef]
- Idris, A.; Ismail, N.S.M.; Hassan, N.; Misran, E. Synthesis of magnetic alginate beads based on maghemite nanoparticles for Pb(II) removal in aqueous solution. J. Ind. Eng. Chem. 2012, 18, 1582–1589. [Google Scholar] [CrossRef]
- Kim, J.H.; Shin, W.S.; Kim, Y.H.; Choi, S.J.; Jo, W.K.; Song, D.I. Sorption and desorption kinetics of chlorophenols in hexadecyltrimethyl ammonium-montmorillonites and their model analysis. Korean J. Chem. Eng. 2005, 22, 857–864. [Google Scholar] [CrossRef]
- Kwak, M.Y.; Shin, W.S.; Ko, S.O.; Park, J.W.; Jeong, Y.K. Modeling on the sorption kinetics of lead and cadmium onto natural sediments. Korean J. Limnol. 2006, 39, 450–461. [Google Scholar]
- Oh, S.; Wu, Q.; Song, D.I.; Shin, W.S. Sorption and desorption kinetics of naphthalene and phenanthrene on black carbon in sediment. J. Soil Groundwater Environ. 2011, 16, 79–94. [Google Scholar] [CrossRef]
- Iram, M.; Guo, G.; Guan, Y.P.; Ishfaq, A.; Liu, H.Z. Adsorption and magnetic removal of neutral red dye from aqueous solution using Fe3O4 hollow nanospheres. J. Hazard. Mater. 2010, 181, 1039–1050. [Google Scholar] [CrossRef]
- Toride, N.; Leji, F.J.; van Genuchten, M.T. The CXTFIT Code for Estimating Transport Parameters from Laboratory or Field Tracer Experiments. Version 2.1. U.S. Salinity Laboratory Agricultural Research Service; U.S. Department of Agriculture: Riverside, CA, USA.
- El-Sadek, A. Comparison between numerical and analytical solution of solute transport models. J. African Earth Sci. 2009, 55, 63–68. [Google Scholar] [CrossRef]
- Patel, H. Fixed-bed column adsorption study: A comprehensive review. Appl. Water Sci. 2019, 9, 45. [Google Scholar] [CrossRef]
- Juela, D.; Vera, M.; Cruzat, C.; Alvarez, X.; Vanegas, E. Mathematical modeling and numerical simulation of sulfamethoxazole adsorption onto sugarcane bagasse in a fixed-bed column. Chemosphere 2021, 280, 130687. [Google Scholar] [CrossRef]


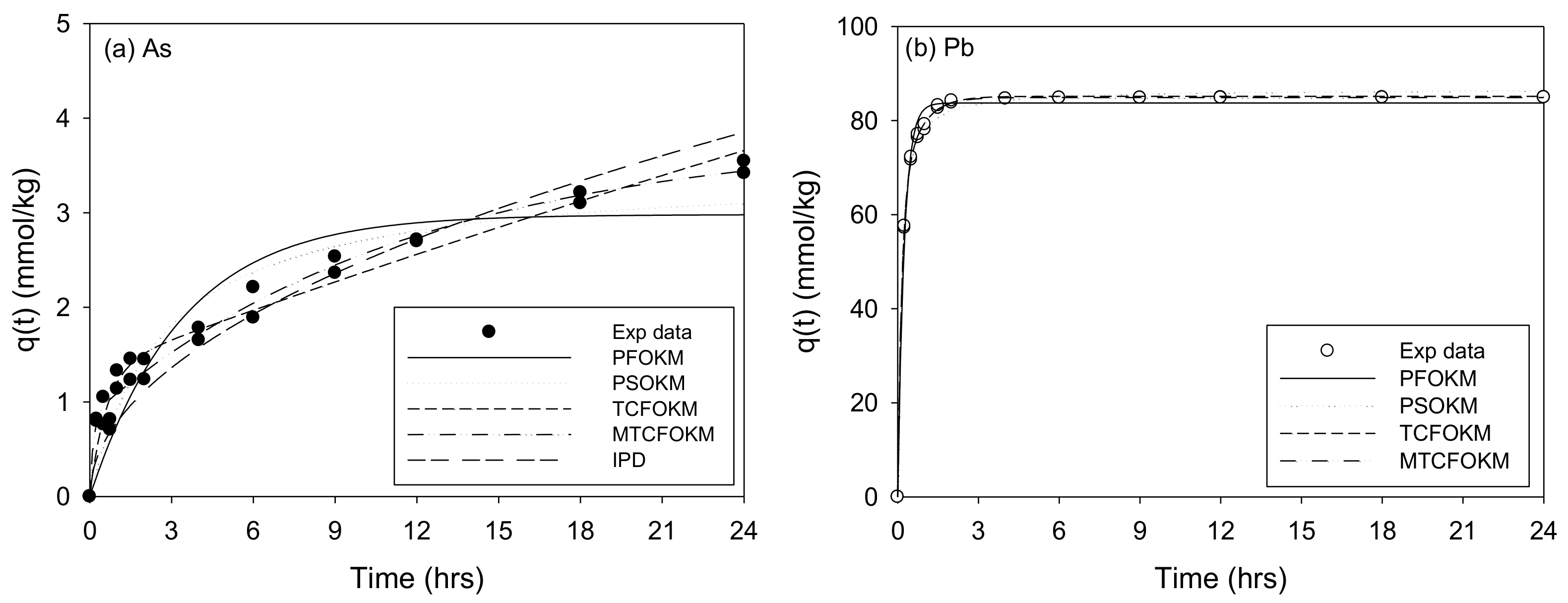
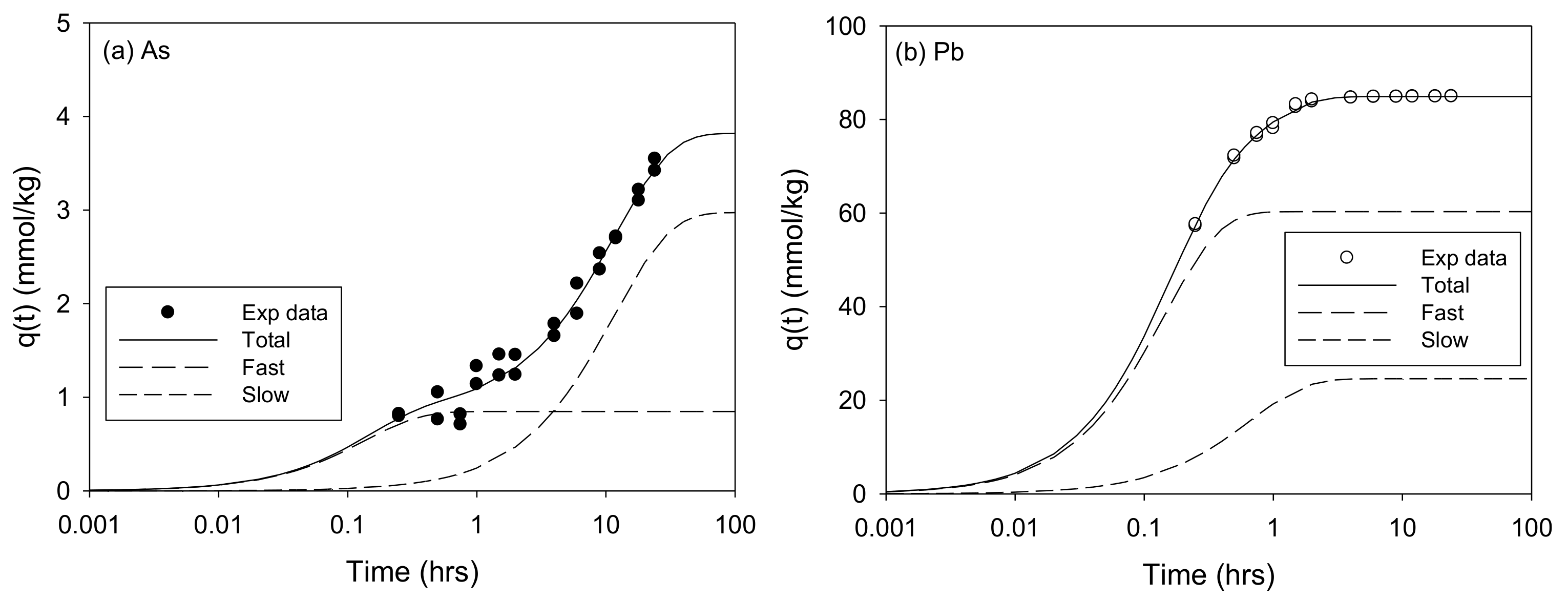
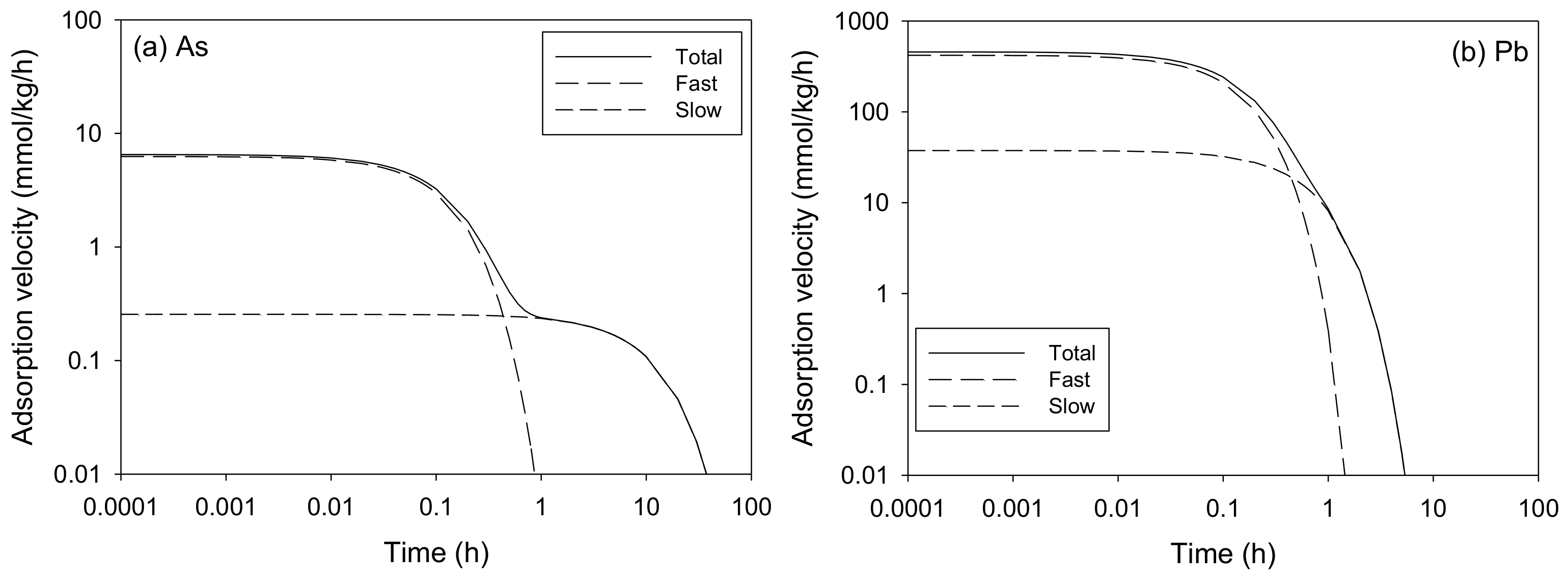

| Model | qe (mmol/kg) | f1 (or f1′) (-) | k1(or k1′) (1/h) | f2 (or f2′) (-) | k2 (or k2′) (1/h) | teq (h) | v0 (mmol/kg/h) | R2 | SSE |
|---|---|---|---|---|---|---|---|---|---|
| As | |||||||||
| PFOKM | 2.980 ± 0.157 | - | 0.295 ± 0.048 | - | - | 15.63 | 0.878 | 0.862 | 3.523 |
| PSOKM | 3.447 ± 0.184 | - | - | - | 0.107 ± 0.024 | 268.3 | 1.272 | 0.916 | 2.138 |
| TCFOKM | - | 0.096 ± 0.007 | 1.673 ± 0.351 | 0.904 | 0.008 ± 0.001 | - | 2.360 | 0.967 | 0.836 |
| MTCFOKM | 3.820 ± 0.221 | 0.222 ± 0.016 | 7.398 ± 3.538 | 0.778 | 0.086 ± 0.014 | 42.63 | 6.521 | 0.983 | 0.443 |
| Pb | |||||||||
| PFOKM | 83.72 ± 0.46 | - | 4.199 ± 0.162 | - | - | 1.10 | 351.6 | 0.993 | 91.38 |
| PSOKM | 86.72 ± 0.41 | - | - | - | 0.104 ± 0.005 | 11.0 | 778.8 | 0.996 | 48.72 |
| TCFOKM | - | 0.722 ± 0.030 | 6.842 ± 0.361 | 0.278 | 1.436 ± 0.115 | - | 454.6 | 1.000 | 4.572 |
| MTCFOKM | 84.89 ± 0.12 | 0.710 ± 0.032 | 6.958 ± 0.382 | 0.290 | 1.526 ± 0.128 | 1.75 | 457.1 | 1.000 | 3.821 |
| Q (mL/min) | Thomas Model | Yoon-Nelson Model | Adams-Bohart Model | ||||||
|---|---|---|---|---|---|---|---|---|---|
| kTH (L/mg/min) | q0 (mg/kg) | R2 | kYN (L/min) | τ (min) | R2 | kAB (L/mg/min) | N0 (mg/L) | R2 | |
| 0.5 | 0.040 | 2.47 | 0.927 | 0.036 | 255.2 | 0.927 | 0.012 | 4.99 | 0.300 |
| 2.0 | 0.143 | 2.94 | 0.989 | 0.137 | 76.31 | 0.989 | 0.036 | 6.79 | 0.172 |
| 10.0 | 1.184 | 1.82 | 0.732 | 1.678 | 6.617 | 0.731 | 0.050 | 10.39 | 0.124 |
| Q (mL/min) | Thomas Model | Yoon-Nelson Model | Adams-Bohart Model | ||||||
|---|---|---|---|---|---|---|---|---|---|
| kTH (L/mg/min) | q0 (mg/kg) | R2 | kYN (L/min) | τ (min) | R2 | kAB (L/mg/min) | N0 (mg/L) | R2 | |
| 0.5 | 2.7 × 10−5 | 2655 | 0.953 | 0.011 | 590.5 | 0.951 | 8.0 × 10−6 | 7461 | 0.354 |
| 2.0 | 1.0 × 10−4 | 2399 | 0.953 | 0.076 | 79.6 | 0.949 | 2.3 × 10−5 | 6013 | 0.483 |
| 10.0 | 5.3 × 10−4 | 1862 | 0.908 | 0.396 | 12.8 | 0.906 | 8.1 × 10−5 | 6366 | 0.444 |
| Bed Height (cm) | Thomas Model | Yoon-Nelson Model | Adams-Bohart Model | ||||||
|---|---|---|---|---|---|---|---|---|---|
| kTH (L/mg/min) | q0 (mg/kg) | R2 | kYN (L/min) | τ (min) | R2 | kAB (L/mg/min) | N0 (mg/L) | R2 | |
| As | |||||||||
| 10 | 0.153 | 3.375 | 0.934 | 0.142 | 62.00 | 0.931 | 0.028 | 9.59 | 0.153 |
| 15 | 0.143 | 2.940 | 0.989 | 0.137 | 76.31 | 0.989 | 0.036 | 6.79 | 0.172 |
| Pb | |||||||||
| 10 | 1.2 × 10−4 | 2938 | 0.944 | 0.090 | 64.55 | 0.940 | 1.9 × 10−5 | 8847 | 0.355 |
| 15 | 1.0 × 10−4 | 2399 | 0.953 | 0.076 | 79.60 | 0.949 | 2.3 × 10−5 | 6013 | 0.483 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, G.; Oh, S. Adsorption of As and Pb by Stone Powder/Chitosan/Maghemite Composite Beads (SCM Beads): Kinetics and Column Study. Processes 2023, 11, 581. https://doi.org/10.3390/pr11020581
Song G, Oh S. Adsorption of As and Pb by Stone Powder/Chitosan/Maghemite Composite Beads (SCM Beads): Kinetics and Column Study. Processes. 2023; 11(2):581. https://doi.org/10.3390/pr11020581
Chicago/Turabian StyleSong, Gunho, and Sanghwa Oh. 2023. "Adsorption of As and Pb by Stone Powder/Chitosan/Maghemite Composite Beads (SCM Beads): Kinetics and Column Study" Processes 11, no. 2: 581. https://doi.org/10.3390/pr11020581
APA StyleSong, G., & Oh, S. (2023). Adsorption of As and Pb by Stone Powder/Chitosan/Maghemite Composite Beads (SCM Beads): Kinetics and Column Study. Processes, 11(2), 581. https://doi.org/10.3390/pr11020581







