A Thermal-Fluid-Solid Coupling Computation Model of Initiation Pressure Using Supercritical Carbon Dioxide Fracturing
Abstract
:1. Introduction
2. Theoretical Model
2.1. Tangential Stress Model around Well
2.2. Reservoir Temperature and Pore Pressure Model
3. Model Solving and Verification
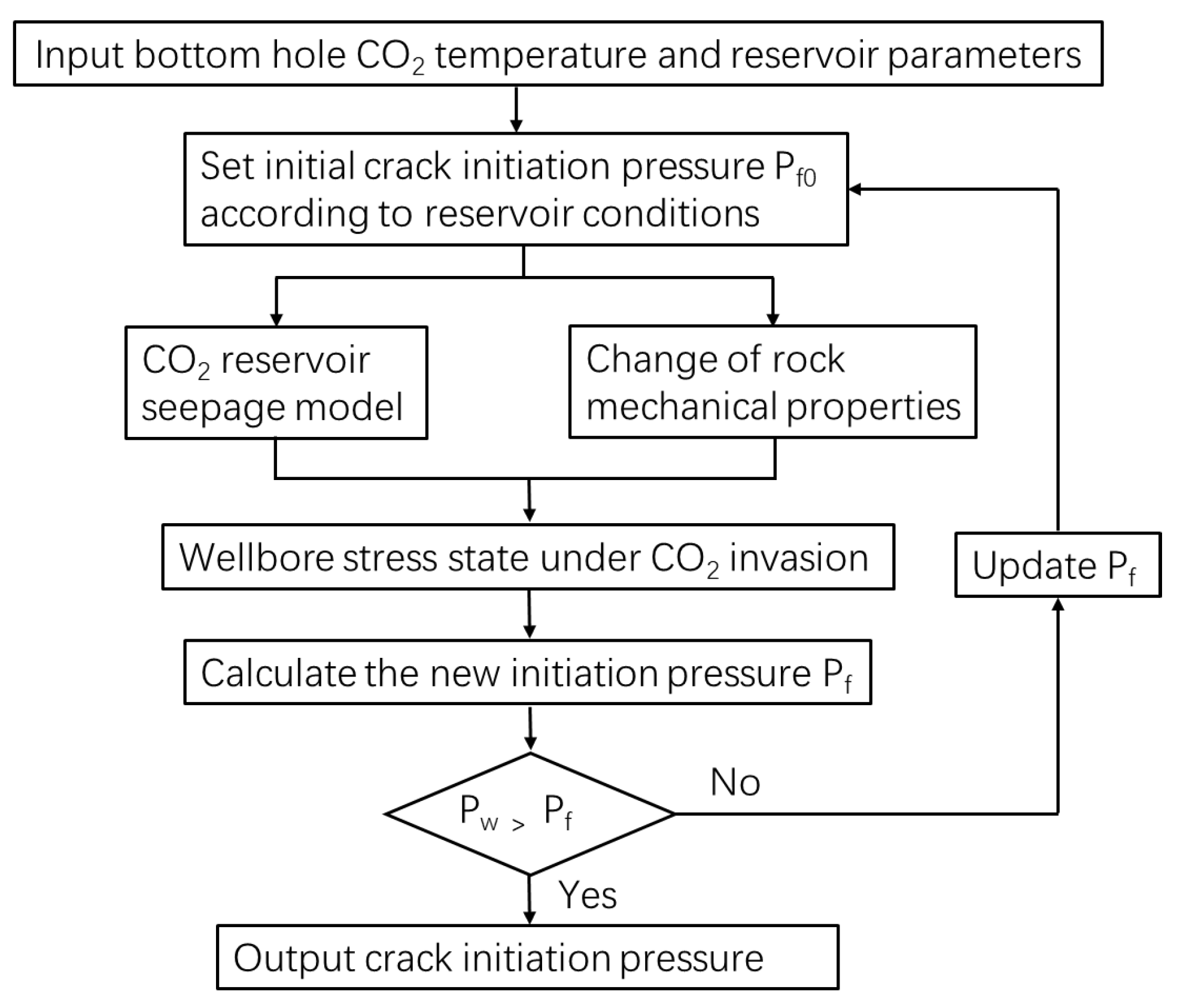
3.1. Model Solving Method
3.2. Model Validation
4. Results
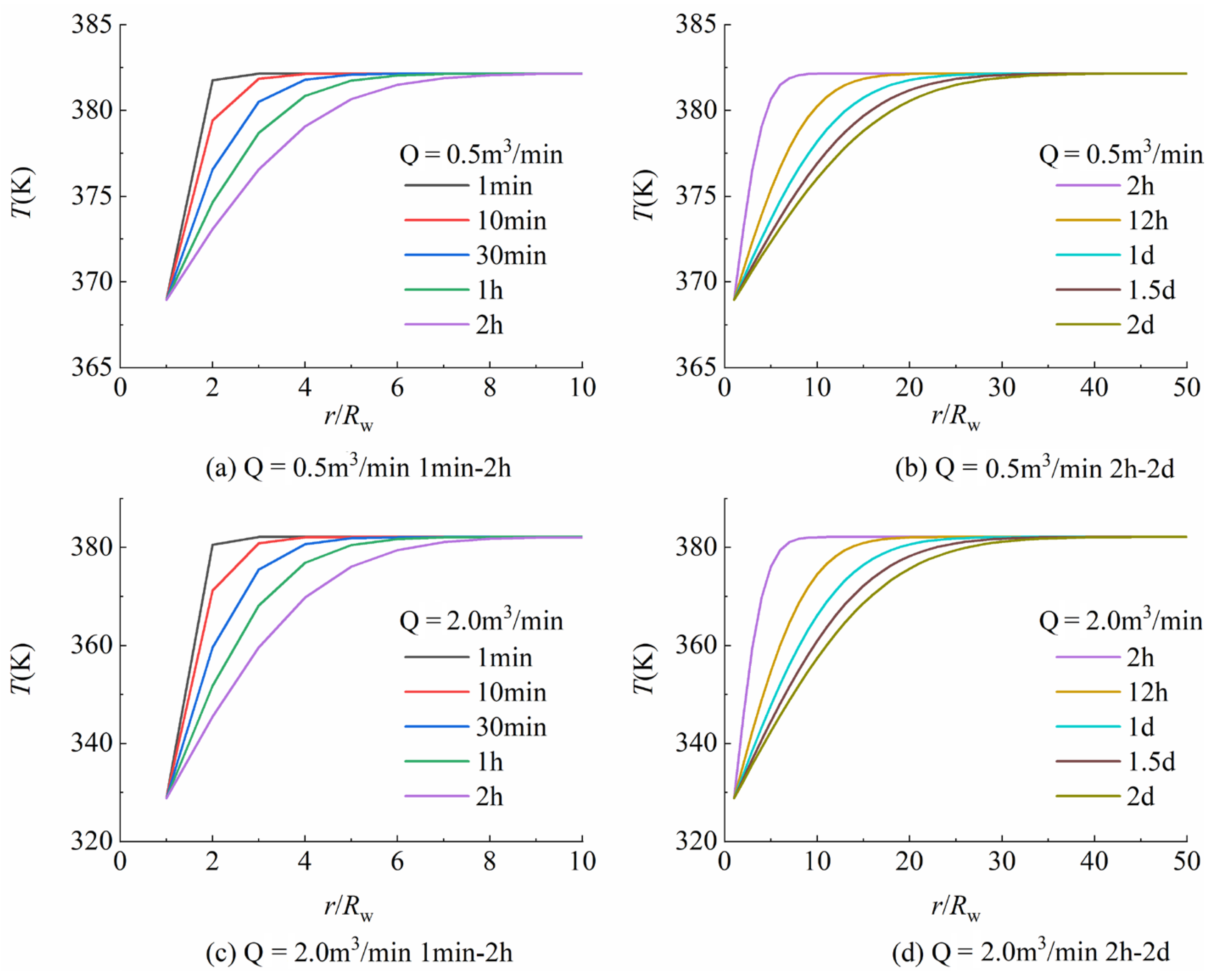
4.1. Distribution of Formation Temperature and Pressure
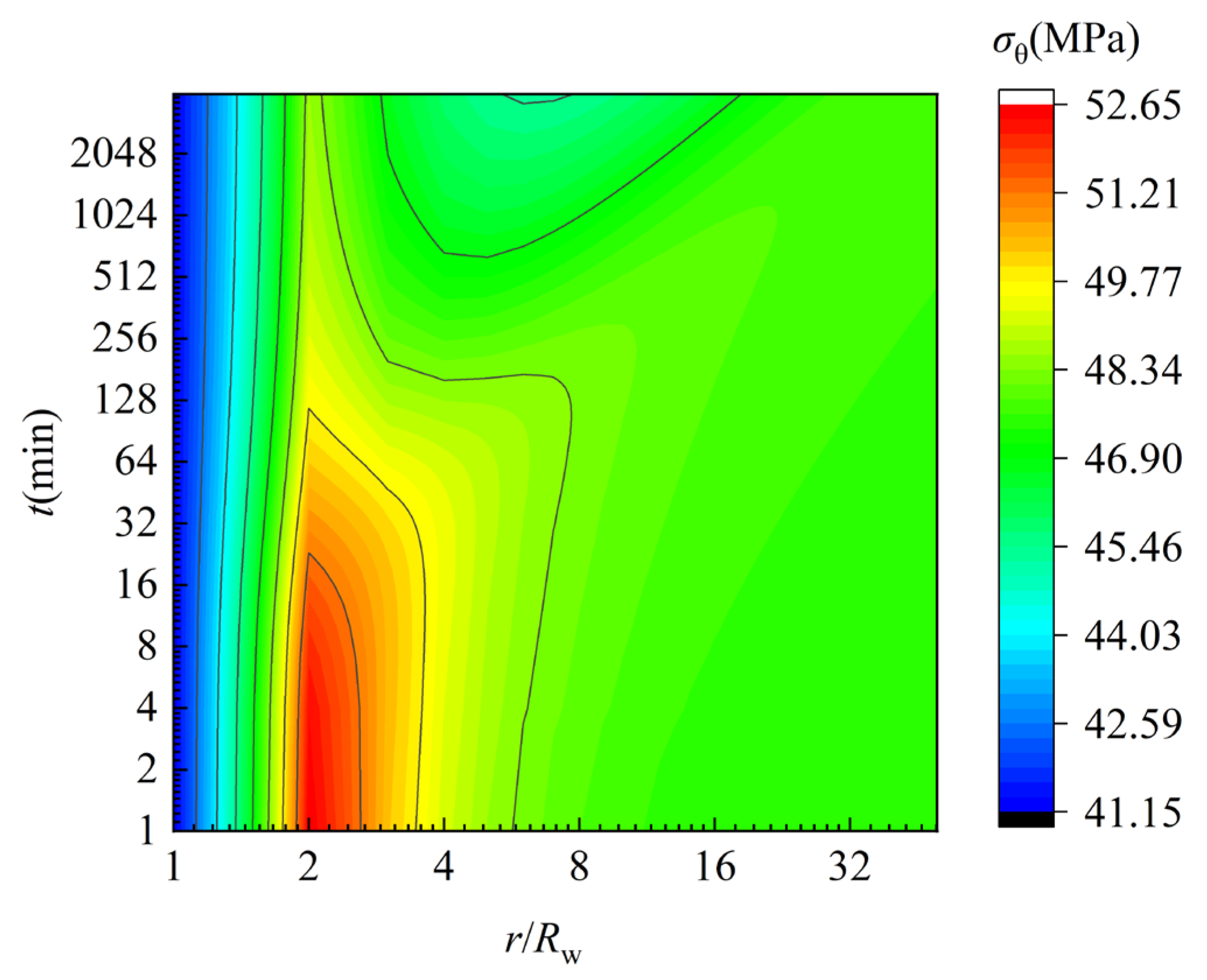
4.2. Distribution of In Situ Stress
4.3. Influencing Factors of Fracture Initiation Pressure
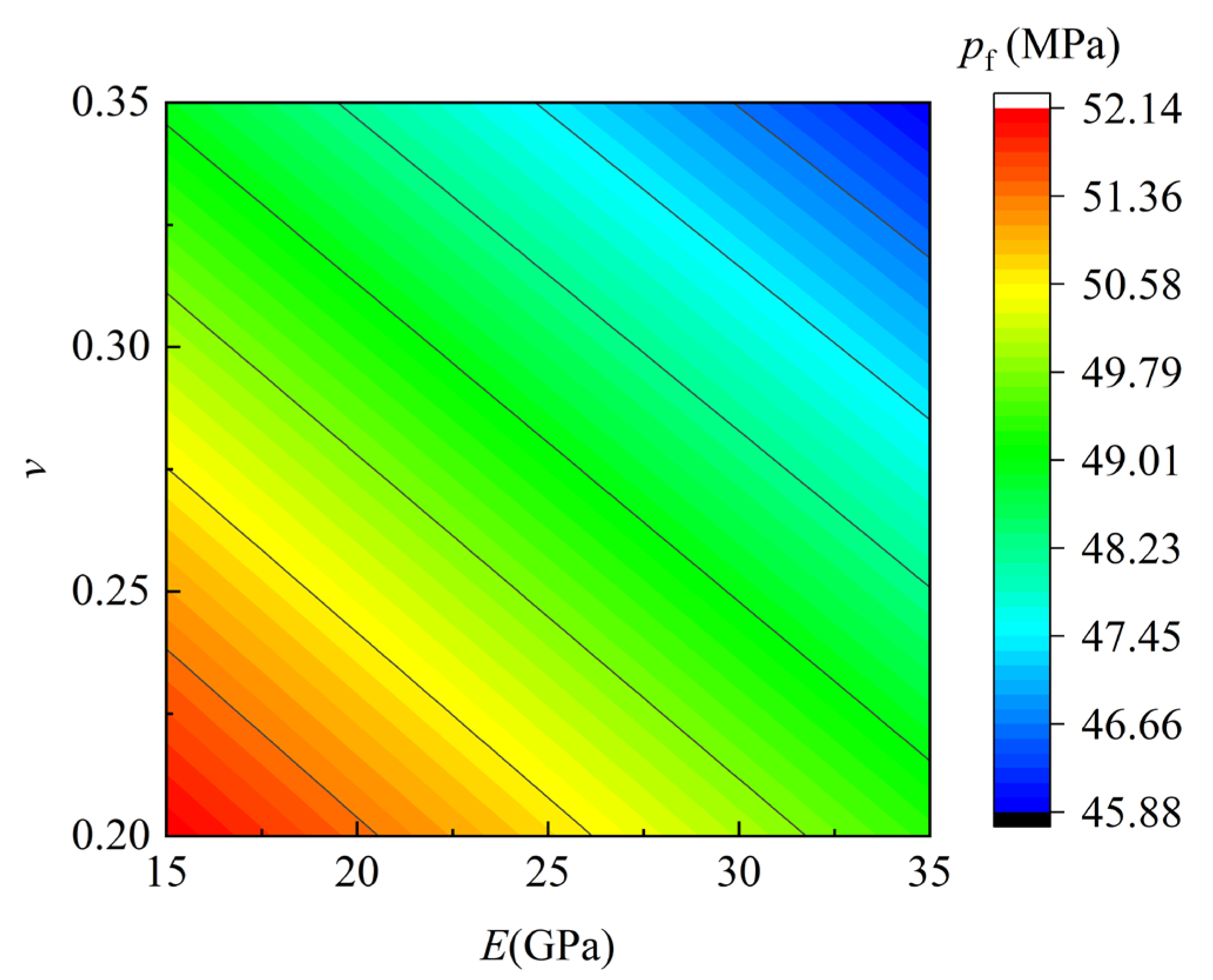
4.3.1. Poisson’s Ratio
4.3.2. Elastic Modulus
4.3.3. Bottom Hole Temperature
5. Application Example
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, J.; Xia, X.; Li, W. Rapid development of unconventional oil and gas: Status, challenges and prospects of shale oil extraction technology. Front. Energy Res. 2022, 10, 1–4. [Google Scholar] [CrossRef]
- Li, Q.; Wang, F.; Forson, K.; Zhang, J.; Zhang, C.; Chen, J.; Xu, N.; Wang, Y. Affecting analysis of the rheological characteristic and reservoir damage of CO2 fracturing fluid in low permeability shale reservoir. Environ. Sci. Pollut. Res. 2022, 29, 37815–37826. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Shi, X.; Jiang, S.; Cao, Q.; Wang, F.; Wang, Z.; Ge, Y.; Du, Y. Experimental study of hydraulic fracture initiation and propagation in highly saturated methane-hydrate-bearing sands. J. Nat. Gas Sci. Eng. 2020, 79, 1–12. [Google Scholar] [CrossRef]
- Li, Q.; Wu, J. Factors affecting the lower limit of the safe mud weight window for drilling operation in hydrate-bearing sediments in the Northern South China Sea. Geomech. Geophys. Geo-Energy Geo-Resour. 2022, 82, 1–21. [Google Scholar] [CrossRef]
- Xue, M.; Cheng, Y.; Yan, C.; Li, Y.; Li, Q.; Han, S. Optimization of multistage hydraulic fracturing method of horizontal wells in shale gas reservoirs. Pet. Geol. Oilfield Dev. Daqing 2020, 39, 152–159. [Google Scholar]
- Chen, Z.; Li, S.; Chen, Z.; Wang, H. Hydraulic fracture initiation and extending tests in deep shale gas formations and fracturing design optimization. Pet. Drill. Tech. 2020, 48, 70–76. [Google Scholar]
- Valder, J.F.; McShane, R.R.; Barnhart, T.B.; Wheeling, S.L.; Carter, J.M.; Macek-Rowland, K.M.; Delzer, G.C.; Thamke, J.N. Analytical Framework to Estimate Water Use Associated with Continuous Oil and Gas Development; US Geological Survey: Reston, VA, USA, 2019; pp. 1–17.
- Zhang, C.P.; Liu, S.; Ma, Z.Y.; Ranjith, P.G. Combined micro-proppant and supercritical carbon dioxide (SC-CO2) fracturing in shale gas reservoirs: A review. Fuel 2021, 305, 121431. [Google Scholar] [CrossRef]
- Li, X.J.; Li, G.; Wang, H.; Tian, S. A wellbore flow model and coupling solution for supercritical CO2 fracturing. J. China Univ. Pet. 2018, 42, 87–94. [Google Scholar]
- Xiao, C.; Ni, H.; Shi, X. Unsteady model for wellbore pressure transmission of carbon dioxide fracturing considering limited-flow outlet. Energy 2021, 239, 122289. [Google Scholar] [CrossRef]
- Lu, Y.; Liao, Y.; Tang, J.; Zhang, X.; Han, S.; Ling, Y. Experimental study on fracture initiation pressure and morphology in shale using supercritical CO2 fracturing. J. China Coal Soc. 2018, 43, 175–180. [Google Scholar]
- Chen, H.; Hu, Y.; Liu, J.; Liu, F.; Liu, Z.; Kang, Y.; Wang, X. Surface characteristics analysis of fractures induced by supercritical CO2 and water through three-dimensional scanning and scanning electron micrography. J. Rock Mech. Geotech. Eng. 2021, 13, 1047–1058. [Google Scholar] [CrossRef]
- Wang, H.; Li, G.; He, Z.; Shen, Z.; Li, X.; Zhang, Z.; Wang, M.; Yang, B.; Zheng, Y.; Shi, L. Analysis of mechanisms of supercritical CO2 fracturing. Rock Soil Mech. 2018, 39, 3589–3596. [Google Scholar]
- Hubbert, M.K.; Willis, D.G. Mechanics of hydraulic fracturing. Trans. AIME 1957, 210, 153–168. [Google Scholar] [CrossRef]
- Haimson, B.; Fairhurst, C. Initiation and extension of hydraulic fractures in rocks. Soc. Pet. Eng. J. 1967, 7, 310–318. [Google Scholar] [CrossRef]
- Haimson, B.; Fairhurst, C. In-situ stress determination at great depth by means of hydraulic fracturing. In Proceedings of the 11th U.S. Symposium on Rock Mechanics (USRMS), Berkeley, CA, USA, 16–19 June 1969; pp. 559–584. [Google Scholar]
- Huang, R. Fracture initiation and propagation in hydraulic fracturing. Pet. Explor. Dev. 1981, 8, 62–74. [Google Scholar]
- Hossain, M.; Rahman, M.; Rahman, S. Hydraulic fracture initiation and propagation: Roles of wellbore trajectory, perforation and stress regimes. J. Pet. Sci. Eng. 2000, 27, 129–149. [Google Scholar] [CrossRef]
- Chen, M.; Chen, Z.; Huang, R. Hydraulic fracturing of highly deviated wells. J. Univ. Pet. 1995, 19, 30–35. [Google Scholar]
- Li, G.; Liu, L.; Huang, Z.; Niu, J. Study of effect of hydraulic perforating on formation fracturing pressure. J. China Univ. Pet. 2006, 30, 42–45. [Google Scholar]
- Fallahzadeh, S.A.H.; Shadizadeh, R.S.; Pourafshary, P. Dealing with the challenges of hydraulic fracture initiation in deviated-cased perforated boreholes. In Proceedings of the SPE Trinidad and Tobago Energy Resources Conference, Port of Spain, Trinidad and Tobago, 27–30 June 2010; pp. 1–15. [Google Scholar]
- Ma, T.; Zhang, Q.B.; Chen, P.; Yang, C.; Zhao, J. Fracture pressure model for inclined wells in layered formations with anisotropic rock strengths. J. Pet. Sci. Eng. 2017, 149, 393–408. [Google Scholar] [CrossRef]
- Liang, C.; Yi-Yu, L.; Zhao-Long, G.; Hong, D.; Ding-Yun, Z. Initiation pressure calculation model and judgment criterion for hydraulic fracturing of inclined coal seam. Rock Soil Mech. 2015, 36, 444–450. [Google Scholar]
- Jin, Y.; Chen, M.; Zhang, Z. Hydraulic fracturing initiation pressure models for directional wells in naturally fractured formation. Acta Pet. Sin. 2006, 27, 124–126. [Google Scholar]
- Zhao, J.; Ren, L.; Hu, Y.; Wang, L. A calculation model of breakdown pressure for perforated wells in fractured formations. Acta Pet. Sin. 2012, 33, 841–845. [Google Scholar]
- Liu, G.-J.; Xian, X.-F.; Ping, Z.; Zhang, L.; Liu, Q.-L.; Zhao, Y.; Zhang, S. Experimental study on the supercritical CO2 fracturing of shale. J. China Coal Soc. 2017, 42, 694–701. [Google Scholar]
- Zhang, X.; Lu, Y.; Tang, J.; Zhou, Z.; Liao, Y. Experimental study on fracture initiation and propagation in shale using supercritical carbon dioxide fracturing. Fuel 2017, 190, 370–378. [Google Scholar] [CrossRef]
- Chen, L.; Tian, S.; Li, G.; Xin, F. Initiation pressure models for supercritical CO2 fracturing and sensitivity analysis. Rock Soil Mech. 2015, 36, 125–131. [Google Scholar]
- Xiao, C.; Ni, H.; Shi, X.; Wang, R. A fracture initiation model for carbon dioxide fracturing considering the bottom hole pressure and temperature condition. J. Pet. Sci. Eng. 2020, 184, 106541. [Google Scholar] [CrossRef]
- Zhong, G.; Zuo, L.; Jiang, T.; Wang, H.; Li, S.; Song, W. Fracture initiation pressure prediction for shale gas well fracturing with super-critical carbon dioxide. Fault-Block Oil Gas Field 2020, 27, 710–714. [Google Scholar]
- Sun, X.; Sun, B.; Wang, Z. Fissure temperature field model of supercritical CO2 fracturing. Acta Pet. Sin. 2015, 36, 1586–1592. [Google Scholar]
- Li, M.; Ni, H.; Wang, R.; Song, W. The effect of thermal stresses on the relation between rock failure and temperature and pressure of supercritical carbon dioxide jet. Greenh. Gases Sci. Technol. 2018, 8, 218–237. [Google Scholar] [CrossRef]
- Li, X.; Li, G.; Yu, W.; Wang, H.; Sepehrnoori, K.; Chen, Z.; Sun, H.; Zhang, S. Thermal effects of liquid/supercritical carbon dioxide arising from fluid expansion in fracturing. SPE J. 2018, 23, 2026–2040. [Google Scholar] [CrossRef]
- Ding, L.; Ni, H.; Li, M.; Li, W.; Song, W.; Guo, X. Wellbore collapse pressure analysis under supercritical carbon dioxide drilling condition. J. Pet. Sci. Eng. 2018, 161, 458–467. [Google Scholar] [CrossRef]
- Viete, D.R.; Ranjith, P.G. The effect of CO2 on the geomechanical and permeability behaviour of brown coal: Implications for coal seam CO2 sequestration. Int. J. Coal Geol. 2006, 66, 204–216. [Google Scholar] [CrossRef]
- Sun, X.; Ni, H.; Qiao, H.; Wang, X.; Ma, B.; Wang, R.; Shen, Z.; Zhao, M. Experimental study on the mechanism of carbon dioxide removing formation paraffin deposits. J. Nat. Gas Sci. Eng. 2016, 32, 59–65. [Google Scholar] [CrossRef]
- Span, R.; Wagner, W. A new equation of state for carbon dioxide covering the fluid region from the triple-point temperature to 1100 K at pressures up to 800 MPa. J. Phys. Chem. Ref. Data 1996, 25, 1509–1596. [Google Scholar] [CrossRef]
- Vesovic, V.; Wakeham, W.A.; Olchowy, G.A.; Sengers, J.V.; Watson, J.T.R.; Millat, J. The transport properties of carbon dioxide. J. Phys. Chem. Ref. Data 1990, 19, 763–808. [Google Scholar] [CrossRef]
- Fenghour, A.; Wakeham, W.A.; Vesovic, V. The viscosity of carbon dioxide. J. Phys. Chem. Ref. Data 1998, 27, 31–44. [Google Scholar] [CrossRef]
- Song, W.; Ni, H.; Wang, R.; Sun, B.; Shen, Z. Pressure transmission in the tubing of supercritical carbon dioxide fracturing. J. CO2 Util. 2017, 21, 467–472. [Google Scholar] [CrossRef]
- Li, X.; Li, G.; Wang, H.; Tian, S.; Song, X.; Lu, P.; Wang, M. A unified model for wellbore flow and heat transfer in pure CO2 injection for geological sequestration, EOR and fracturing operations. Int. J. Greenh. Gas Control. 2017, 57, 102–115. [Google Scholar] [CrossRef]





| Parameter | Value |
|---|---|
| Well depth/m | 3 250 |
| Borehole diameter/mm | 121.36 |
| Formation pressure/MPa | 28.16 |
| Inlet temperature/K | 258 |
| Wellhead pressure/MPa | 8 |
| Ground temperature gradient/(K·100 m−1) | 2.8 |
| Formation thermal expansion coefficient/K−1 | 3 × 10−5 |
| Thermal permeability coefficient/(m2·(s·K)−1) | 6.0 × 10−11 |
| Original fracture initiation pressure/MPa | 66.02 |
| Formation tensile strength/MPa | 11.256 |
| Elastic modulus/GPa | 22.04 |
| Poisson’s ratio | 0.312 |
| Porosity | 0.05 |
| Maximum horizontal stress gradient/(g·cm−3) | 1.9 |
| Minimum horizontal stress gradient/(g·cm−3) | 1.5 |
| Vertical stress gradient/(g·cm−3) | 2.3 |
| Coupling coefficient | 1.2375 × 10−3 |
| Q /(m3·min−1) | Bottom Hole Temperature /K | Initiation Pressure /MPa | Original Initiation Pressure /MPa | Reduction Rate /% |
|---|---|---|---|---|
| 0.5 | 368.97 | 48.94 | 66.02 | 25.87 |
| 2.0 | 328.83 | 40.99 | 66.02 | 37.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Kang, Z.; Kang, Y.; Chen, X.; Chen, X.; Fan, Q.; Du, Y.; Wang, J. A Thermal-Fluid-Solid Coupling Computation Model of Initiation Pressure Using Supercritical Carbon Dioxide Fracturing. Processes 2023, 11, 437. https://doi.org/10.3390/pr11020437
Chen Y, Kang Z, Kang Y, Chen X, Chen X, Fan Q, Du Y, Wang J. A Thermal-Fluid-Solid Coupling Computation Model of Initiation Pressure Using Supercritical Carbon Dioxide Fracturing. Processes. 2023; 11(2):437. https://doi.org/10.3390/pr11020437
Chicago/Turabian StyleChen, Yi, Zhihong Kang, Yuzhu Kang, Xiaocheng Chen, Xiaohong Chen, Qingteng Fan, Yukun Du, and Jinguang Wang. 2023. "A Thermal-Fluid-Solid Coupling Computation Model of Initiation Pressure Using Supercritical Carbon Dioxide Fracturing" Processes 11, no. 2: 437. https://doi.org/10.3390/pr11020437





