Experimental and Numerical Investigation on Effects of Pin Diameter on Multi-Point Forming
Abstract
:1. Introduction
2. Experimental Study and Finite Element Simulations
2.1. Experimental Setup Design
2.2. Finite Element Modeling
3. Results and Discussion
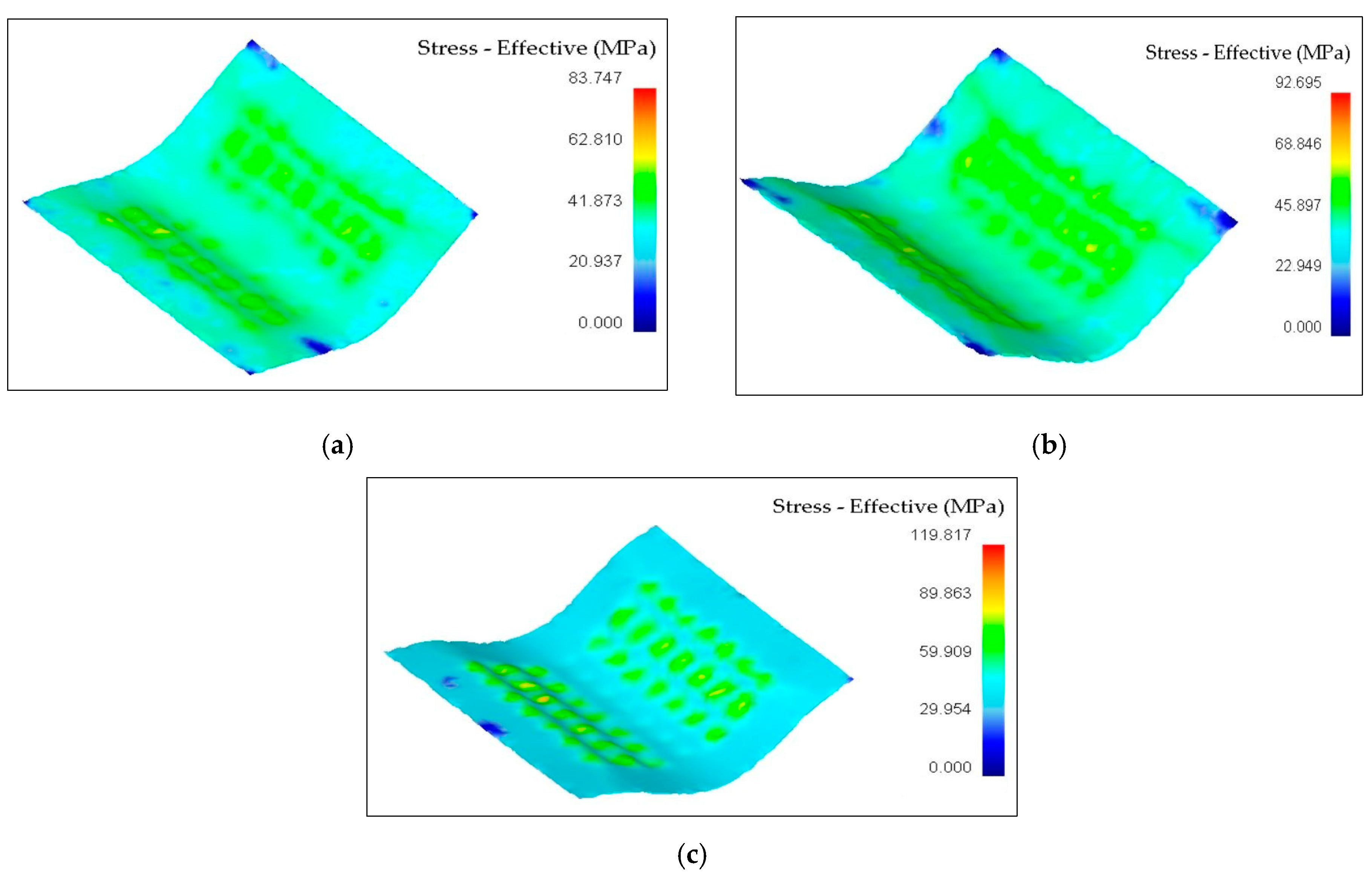
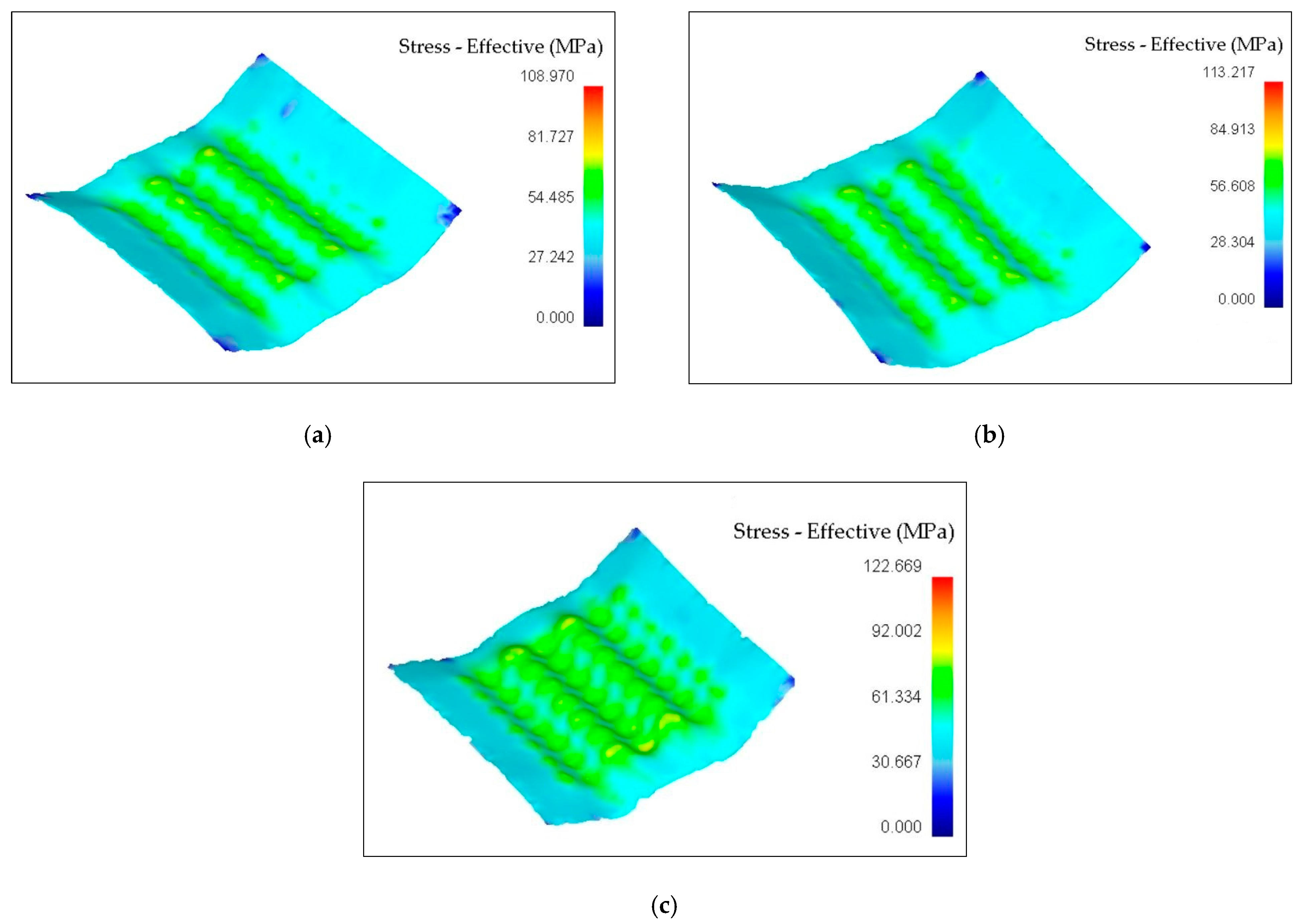
3.1. Effective Stress Distribution
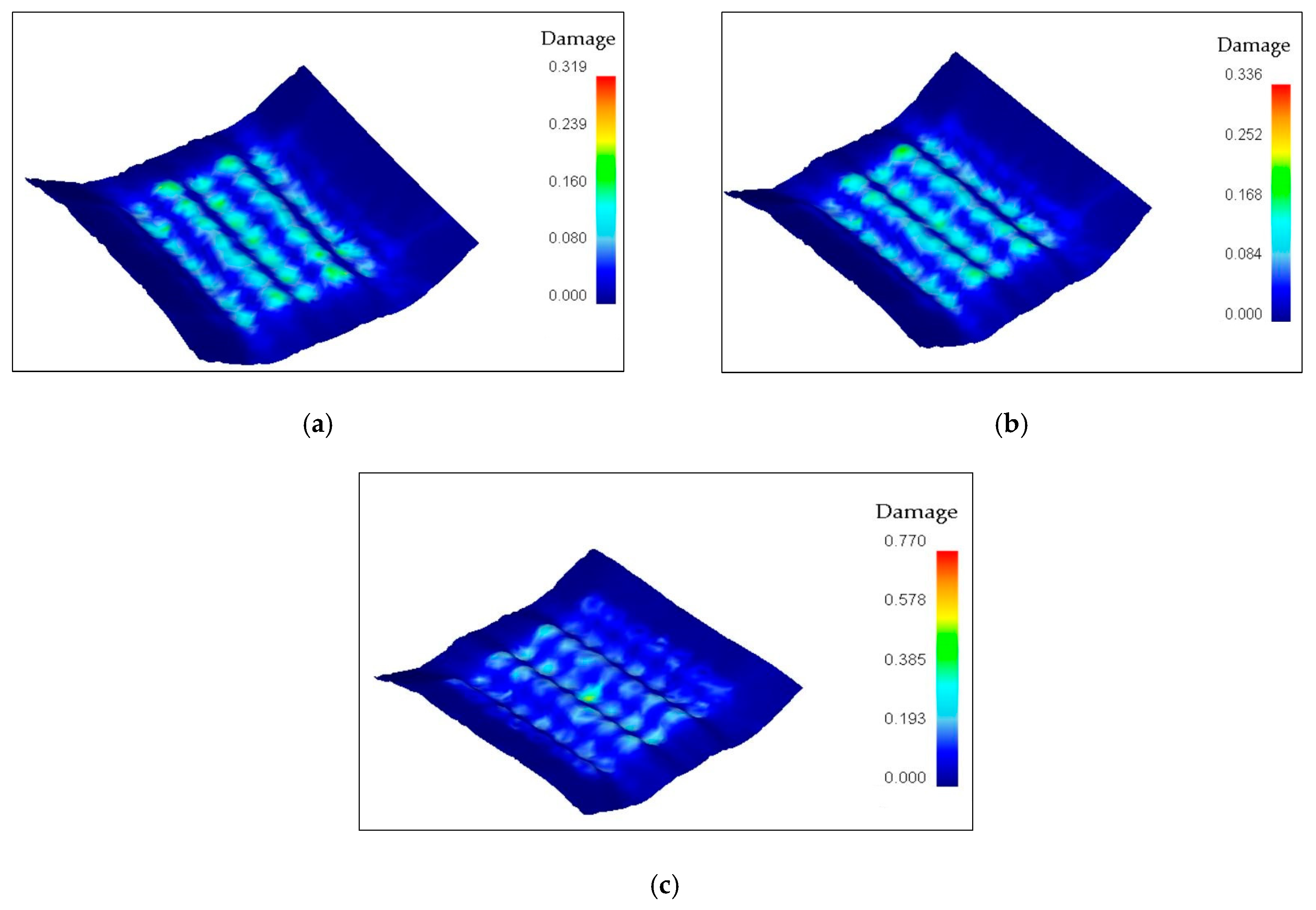
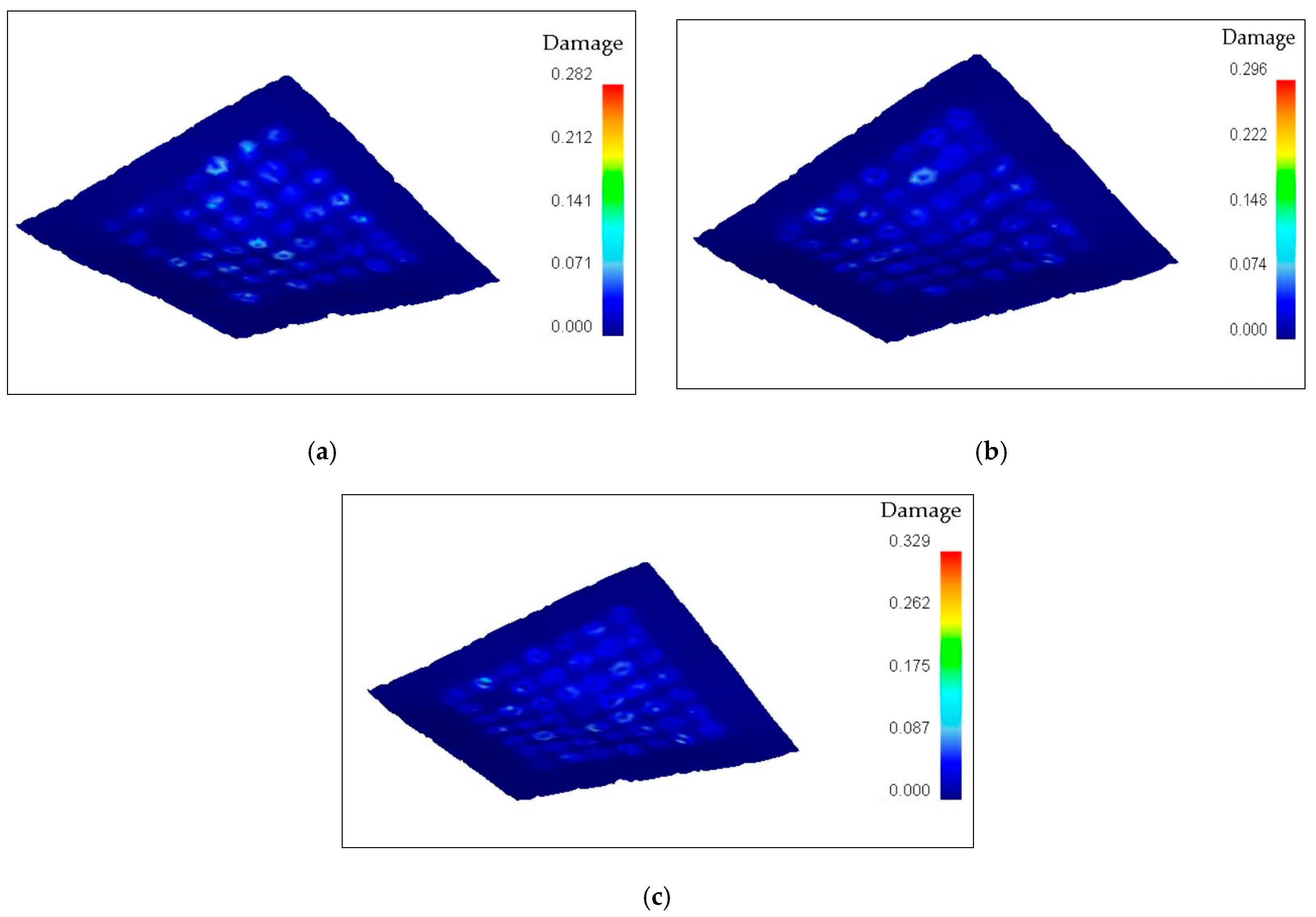
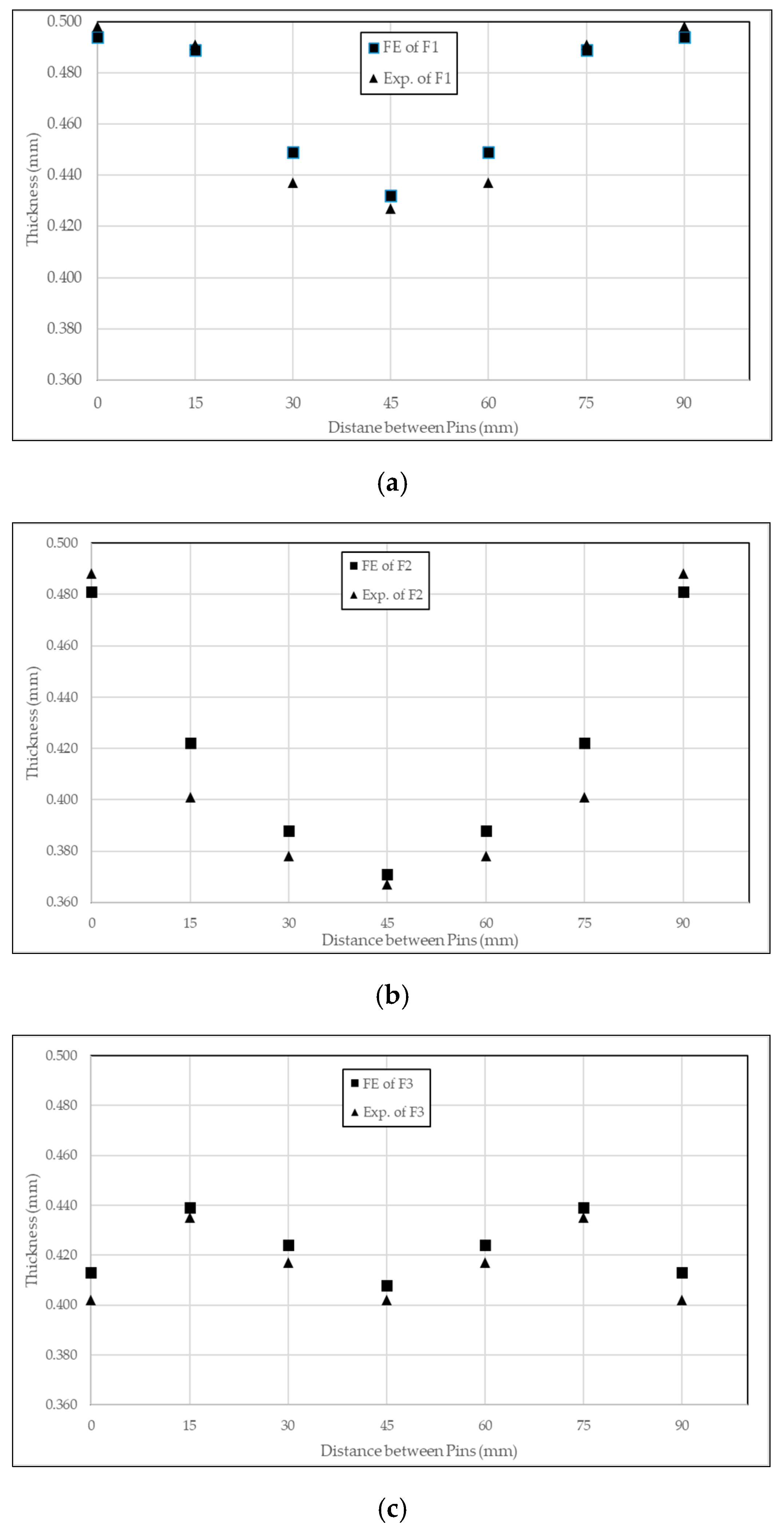
3.2. Damage on the Sheets
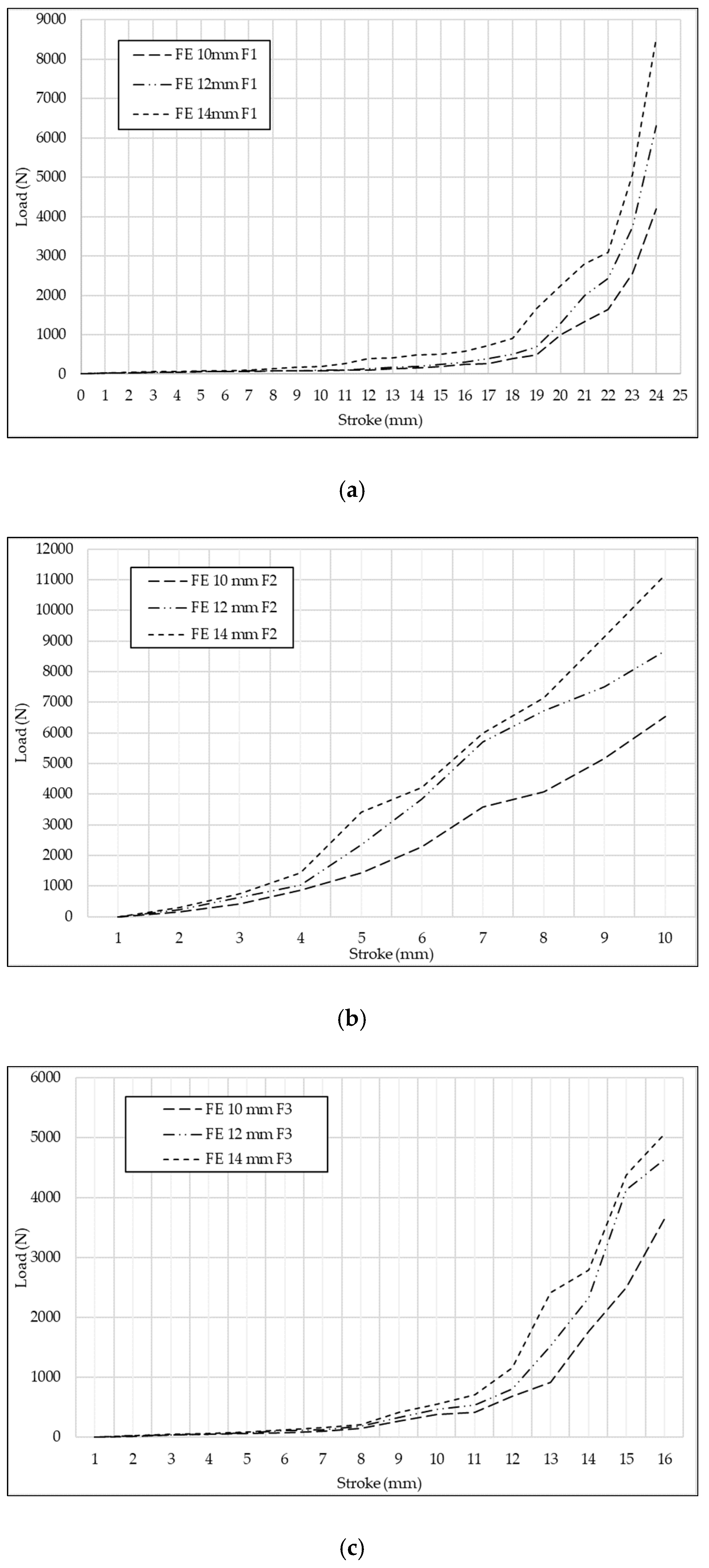
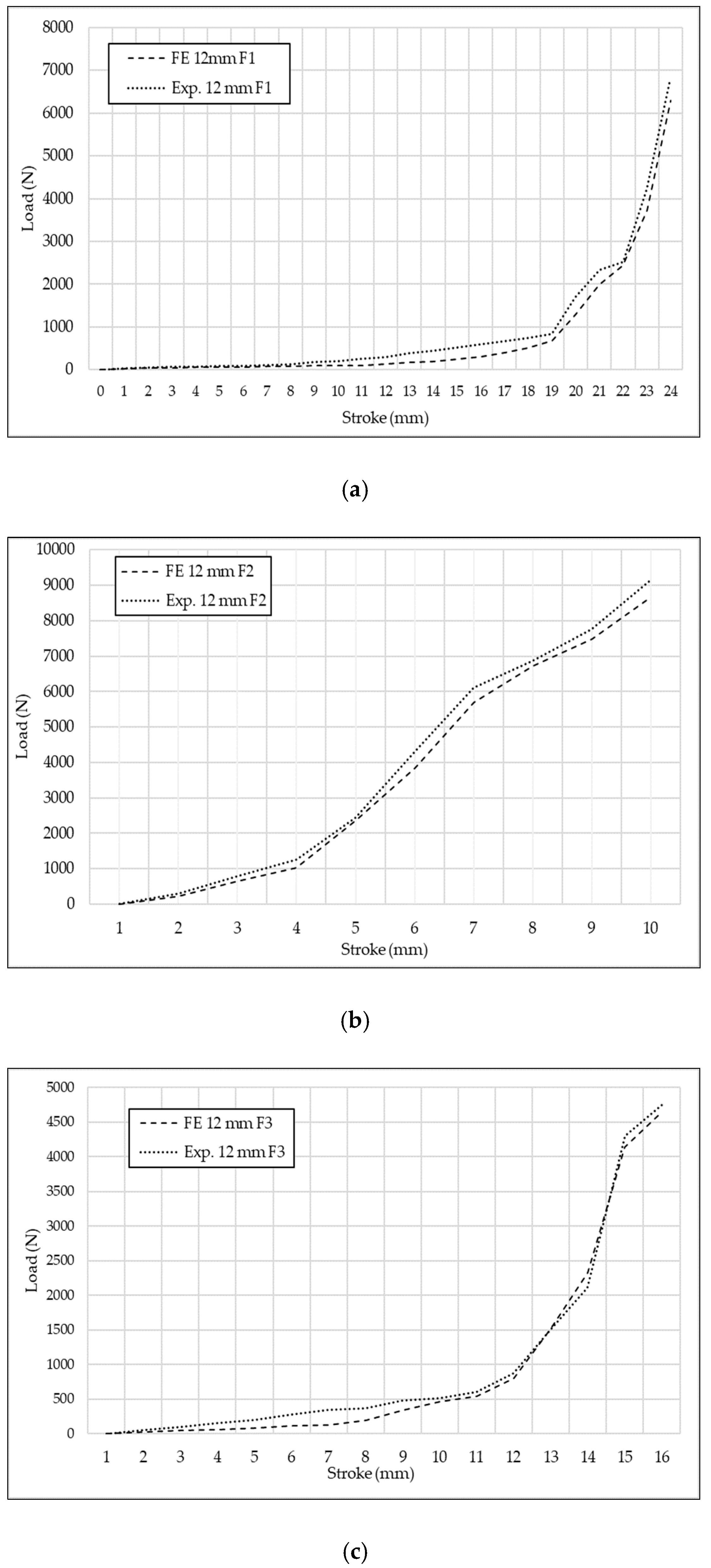
3.3. Forming Load
4. Conclusions
- Different forms of parts were formed in one MPF die by changing the length of pins according to the required part geometry. Thanks to this, it can be said that MPF is cost- and time-effective.
- It was observed that the effect of diameter was directly related to the forming of sheets. The larger diameter of the pin results in higher loads and stress on sheet metal parts.
- In complexly shaped parts, as the pin diameter increases, the material flow is more difficult. This situation showed that a higher load, hence a higher capacity press was required.
- Dimples and thinning of the sheet are unwanted defects but they cannot be completely eliminated in multi-point forming if the workpiece and punch are in contact.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, M.Z.; Nakamura, K.; Watanabe, S. Study of the basic principles (first report research on multi-point forming for sheet metal). In Proceedings of the Japanese Spring Conference for Technology of Plasticity, May 1992; pp. 519–522. [Google Scholar]
- Walczyk, D.F.; Hardt, D.E. Design and analysis of reconfigurable discrete dies for sheet metal forming. J. Manuf. Syst. 1998, 17, 436–454. [Google Scholar] [CrossRef]
- Li, M.; Liu, Y.; Su, S.; Li, G. Multi-point forming: A flexible manufacturing method for a 3-d surface sheet. J. Mater. Process. Technol. 1999, 87, 277–280. [Google Scholar] [CrossRef]
- Li, M.Z.; Cai, Z.Y.; Sui, Z.; Yan, Q.G. Multi-point forming technology for sheet metal. J. Mater. Process. Technol. 2002, 129, 333–338. [Google Scholar] [CrossRef]
- Cai, Z.Y.; Li, M.Z. Finite element simulation of multi-point sheet forming process based on implicit scheme. J. Mater. Process. Technol. 2005, 161, 449–455. [Google Scholar] [CrossRef]
- Liu, C.; Li, M.; Fu, W. Principles and apparatus of multi-point forming for sheet metal. Int. J. Adv. Manuf. Technol. 2008, 35, 1227–1233. [Google Scholar] [CrossRef]
- Qian, Z.R.; Li, M.Z.; Tan, F.X. The analyse on the process of multi-point forming for dish head. J. Mater. Process. Technol. 2007, 187, 471–475. [Google Scholar] [CrossRef]
- Liu, Y.; Li, M.; Ju, F. Research on the process of flexible blank holder in multi-point forming for spherical surface parts. Int. J. Adv. Manuf. Technol. 2017, 89, 2315–2322. [Google Scholar] [CrossRef]
- Abebe, M.; Lee, K.; Kang, B.S. Surrogate-based multi-point forming process optimization for dimpling and wrinkling reduction. Int. J. Adv. Manuf. Technol. 2016, 85, 391–403. [Google Scholar] [CrossRef]
- Zhu, L.; Liang, Q.; Yu, T.; Yuan, P.; Hu, Y. Experimental and theoretical study of constant curvature multi-square punch forming process of strips under follower load. Int. J. Mech. Sci. 2019, 156, 462–473. [Google Scholar] [CrossRef]
- Li, Y.; Shi, Z.; Rong, Q.; Zhou, W.; Lin, J. Effect of pin arrangement on formed shape with sparse multi-point flexible tool for creep age forming. Int. J. Mach. Tools Manuf. 2019, 140, 48–61. [Google Scholar] [CrossRef]
- Xinqi, L.; Shicheng, H. Numerical Simulation and Experimental Research on Multi-Point Forming of Aluminum Alloy Sheets Based on Ultrasonic Vibration. Math. Probl. Eng. 2022, 2022, 7688376. [Google Scholar] [CrossRef]
- Teng, F.; Liang, J.; Wang, S.; Han, Q. Effect of Axial Normal Stress and Bending Moment between Contact and Non-Contact Zone on Forming Accuracy for Flexible Stretch Bending Formation. Metals 2022, 12, 1168. [Google Scholar] [CrossRef]
- Moheen, M.; Abdel-Wahab, A.; Hassanin, H.; Essa, K. Reconfigurable Multipoint Forming Using Waffle-Type Elastic Cushion and Variable Loading Profile. Materials 2020, 13, 4506. [Google Scholar] [CrossRef]
- Tolipov, A.; Hassanin, H.; El-Sayed, M.A.; Eldessouky, H.M.; Alsaleh, N.A.; Alfozan, A.K.; Essa, K.; Ahmadein, M. Multipoint Forming Using Hole-Type Rubber Punch. Metals 2022, 12, 491. [Google Scholar] [CrossRef]
- Borchers, F.; Clausen, B.; Ehle, L.C.; Eich, M.; Epp, J.; Frerichs, F.; Hettig, M.; Klink, A.; Kohls, E.; Lu, Y.; et al. The Influence of Former Process Steps on Changes in Hardness, Lattice and Micro Structure of AISI 4140 Due to Manufacturing Processes. Metals 2021, 11, 1102. [Google Scholar] [CrossRef]
- Engin, K.; Eyercioglu, O. The Effect of the Thickness-to-Die Diameter Ratio on the Sheet Metal Blanking Process. Stroj. Vestn. J. Mech. Eng. 2017, 63, 501–509. [Google Scholar] [CrossRef] [Green Version]
- Semiatin, S.L. Forming and Forging ASM Handbook, 9th ed.; ASM International: Phoenix, AZ, USA, 1996; pp. 796–814. [Google Scholar]
- Smith, L.M.; Averill, R.C.; Lucas, J.P.; Stoughton, T.B.; Matin, P.H. Influence of transverse normal stress on sheet metal formability. Int. J. Plast. 2003, 19, 1567–1583. [Google Scholar] [CrossRef]
- Dib, M.; Ribeiro, B.; Prates, P. Model Prediction of Defects in Sheet Metal Forming Processes. In Proceedings of the Engineering Applications of Neural Networks 19th International Conference, Bristol, UK, 3–5 September 2018; pp. 169–180. [Google Scholar] [CrossRef]
- Jia, B.B.; Chen, G.; Wang, W.W.; Shen, Y.; Gu, Y. Deformation characteristics and forming force limits of multi-point forming with individually controlled force–displacement. Int. J. Adv. Manuf. Technol. 2022, 123, 1565–1576. [Google Scholar] [CrossRef]


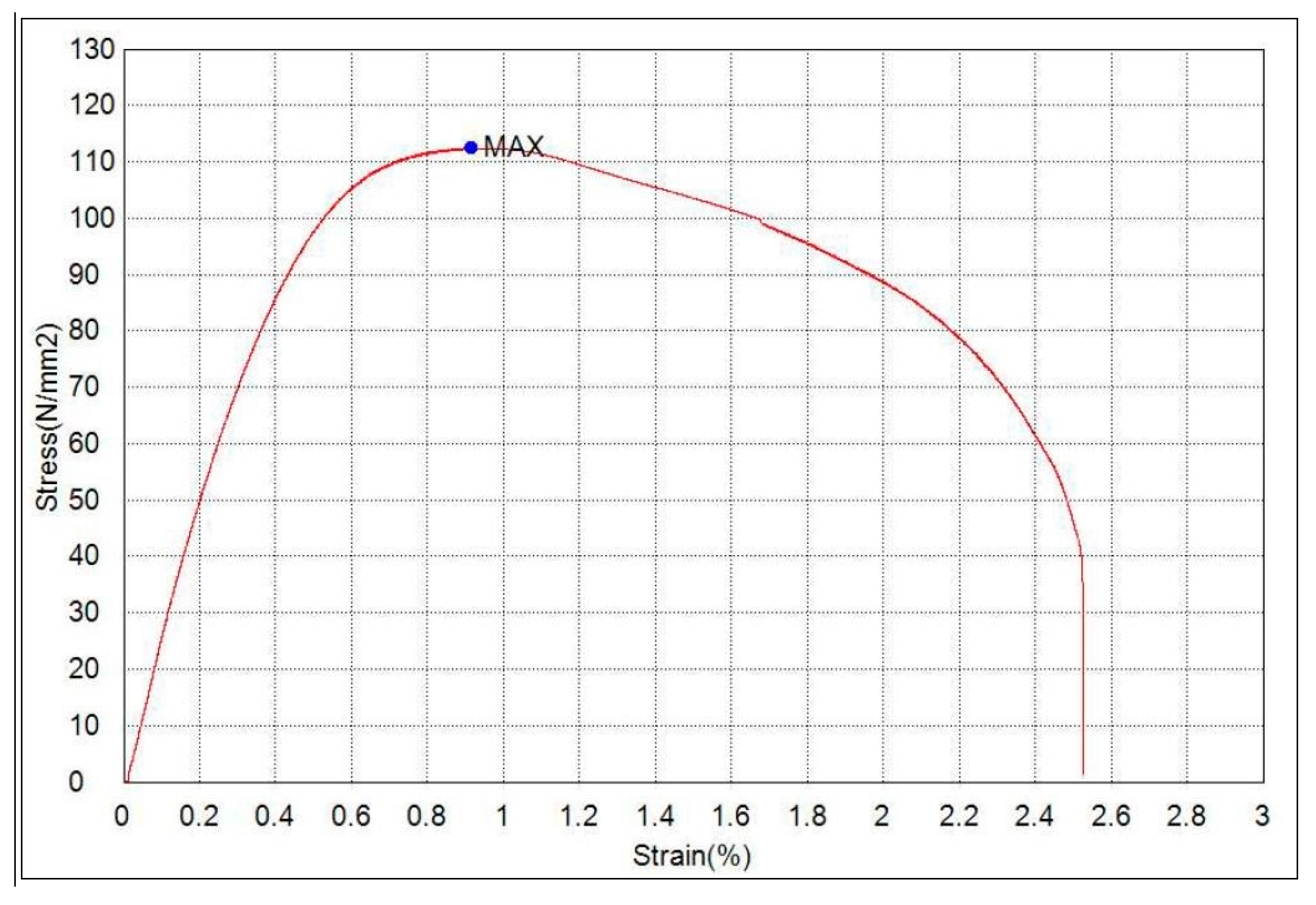

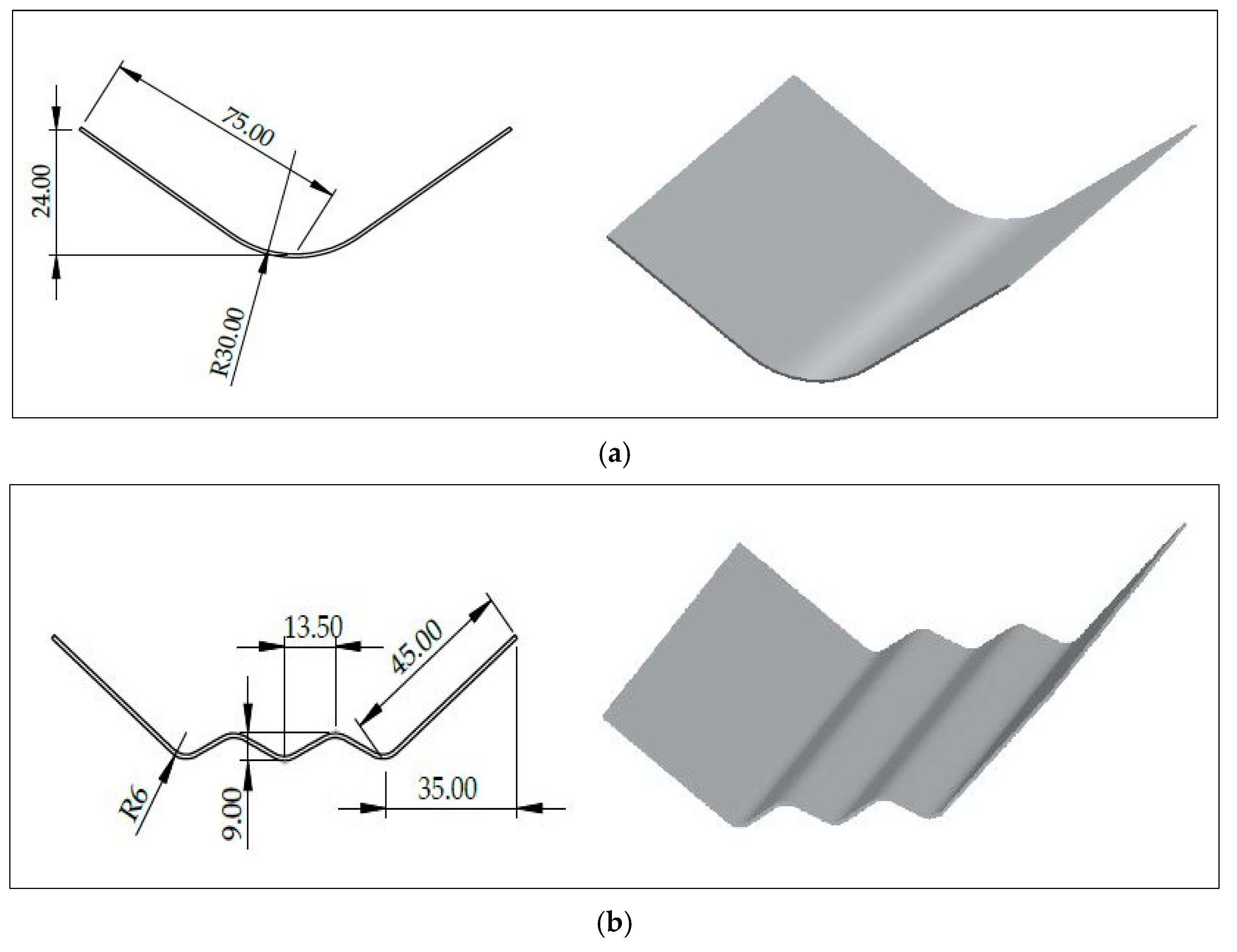
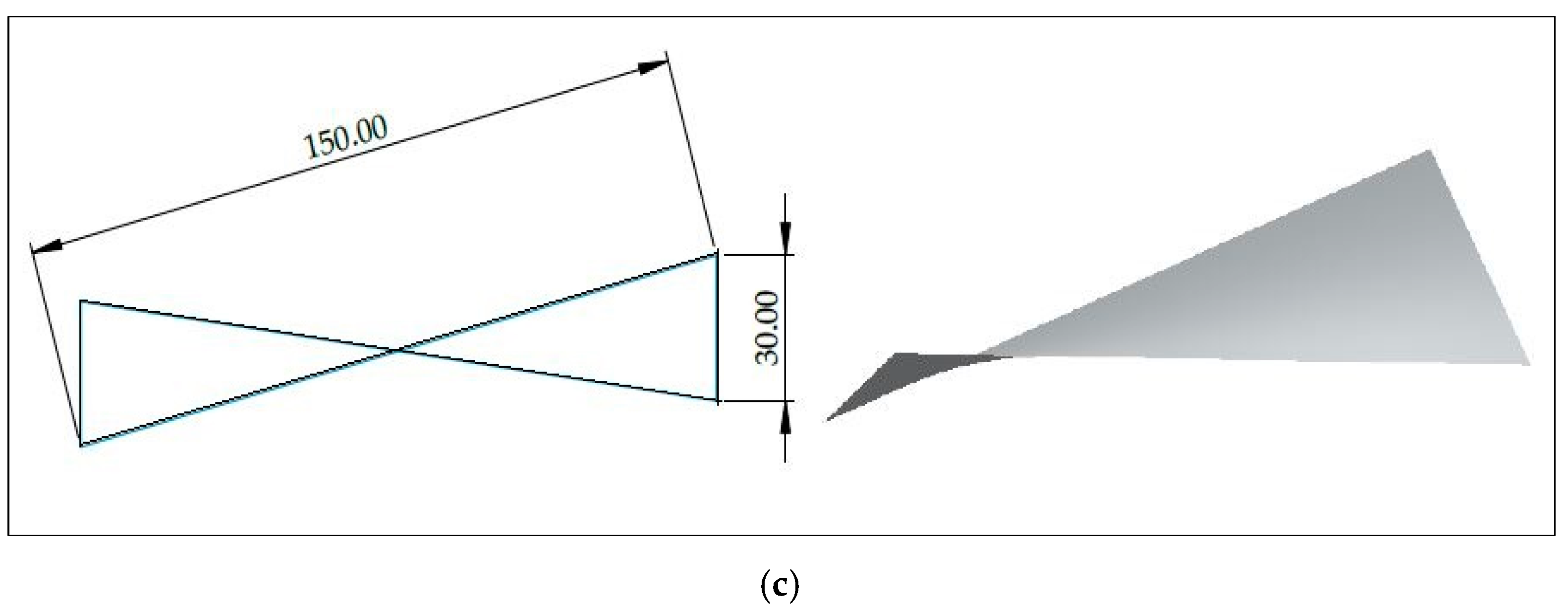

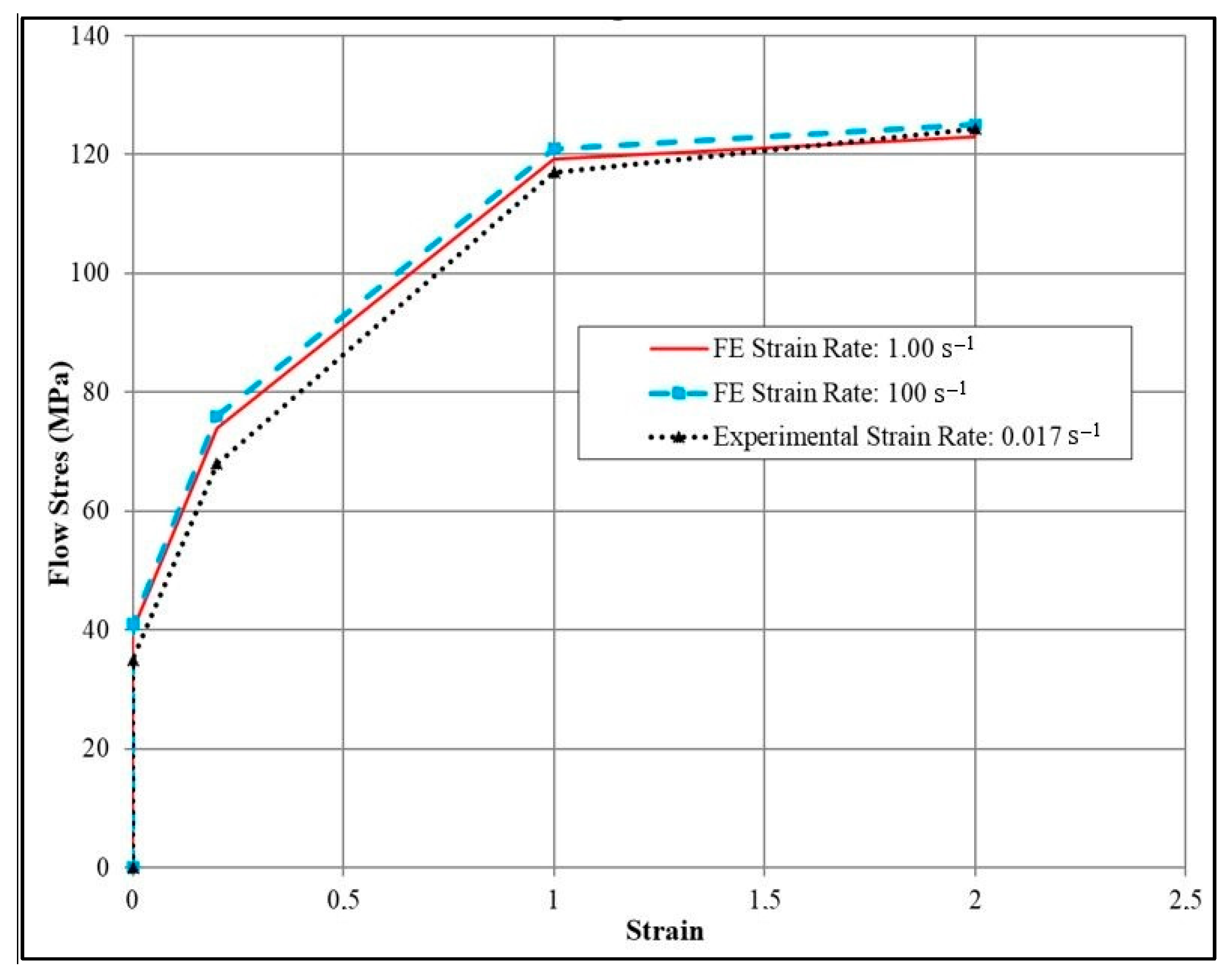



| Si | Cu | Mn | Zn | Fe | Al |
|---|---|---|---|---|---|
| 0.081 | 0.117 | 0.049 | 0.72 | 0.09 | Balance |
| Pin Diameter | Forms | No. of Elements | No. of Nodes |
|---|---|---|---|
| 10 mm | Form1 Form2 Form3 | 17,683 | 6037 |
| 12 mm | Form1 Form2 Form3 | 17,683 | 6037 |
| 14 mm | Form1 Form2 Form3 | 17,683 | 6037 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tandogan, M.; Eyercioglu, O.; Engin, K.E. Experimental and Numerical Investigation on Effects of Pin Diameter on Multi-Point Forming. Processes 2023, 11, 387. https://doi.org/10.3390/pr11020387
Tandogan M, Eyercioglu O, Engin KE. Experimental and Numerical Investigation on Effects of Pin Diameter on Multi-Point Forming. Processes. 2023; 11(2):387. https://doi.org/10.3390/pr11020387
Chicago/Turabian StyleTandogan, Mahmut, Omer Eyercioglu, and Kaan Emre Engin. 2023. "Experimental and Numerical Investigation on Effects of Pin Diameter on Multi-Point Forming" Processes 11, no. 2: 387. https://doi.org/10.3390/pr11020387





