Modelling and Optimization of Methylene Blue Adsorption Process on Leonurus cardiaca L. Biomass Powder

Abstract

The main objective of this study was to optimize the adsorption process of methylene blue on a natural, low-cost adsorbent, Leonurus cardiaca L. biomass powder, in order to maximize dye removal efficiency from aqueous solutions. For this purpose, the Taguchi method was used based on an L₂₇ orthogonal array design considering six controllable factors at three levels. The percentage contribution of each factor was computed using analysis of variance (ANOVA). The optimal adsorption conditions were established. The experimental data from equilibrium and kinetic studies were modelled using specific equilibrium isotherms and kinetic models. Thermodynamic parameters were calculated in order to determine the main adsorption mechanism. The obtained results showed that the ionic strength is the factor that most influences dye adsorption (percentage contribution 72.33%), whereas the adsorbent dose had the least impact. The Sips isotherm and the general kinetic model most accurately characterized the process. The maximum adsorption capacity 103.21 (mg g⁻¹) indicated by the Sips isotherm and the equilibrium time (40 min) were better compared to the values obtained for other bio-adsorbents used for methylene blue adsorption. The main mechanism involved in the adsorption is physisorption, while chemisorption only contributes marginally to the process.

1. Introduction

The widespread presence of harmful substances in the natural environment is frequently associated with the expansion of human populations and their activities. Global water quality degradation represents a highly contentious problem with significant and lasting impacts on ecosystems, including loss of life. Of notable concern are the dyes found in waste effluent, which can have serious consequences for a variety of living organisms. The pollution caused by dye products combines both danger to health and environmental unattractiveness [1,2,3,4,5].

Over the past decade, adsorption has emerged as a highly effective physico-chemical treatment method for eliminating dye pollutants. The adsorption technique is a simple process that uses a variety of cheap and abundant adsorbents and provides high yields of dye removal from water. Moreover, it prevents the formation of secondary contaminants; thus, this process has attracted the attention of a large number of researchers [1,5,6,7,8,9,10].

Types of environmentally friendly sorbents, such as organic waste materials derived from plant biomass as well as microbial biomass are increasingly being recognized as viable alternatives to commercial-activated carbon, which is the best-known adsorbent on the market. The use of nonliving biomass as bio-adsorbents is environmentally safe and has demonstrated effective removal of dyes from colored effluent. The ability of these adsorbents to remove dyes depends on the presence of alcohol, aldehyde, ketone, carboxylic, ether, and phenolic compounds in their structure, as these compounds have functional groups capable of bounding dye molecules [6,9,11,12,13,14,15,16].

In addition to the various cost-effective available bio-adsorbents, another significant advantage of using the adsorption process is its ease of optimization and modeling [17,18,19,20].

Modeling the data obtained in the process using adsorption isotherms and specific kinetic model are a fundamental aspect of the study of adsorption. These isotherms illustrate the correlation between the amount of solute adsorbed onto the adsorbent surface and the solute concentration in the solution. Researchers rely on various equations to model and depict adsorption isotherms, which provide key insights into the properties and behavior of adsorbent materials [21,22,23,24,25].

The use of adsorption kinetics models is essential in assessing the capabilities and nature of adsorbents, as well as exploring the mass transfer in the adsorption process. These models offer a comprehensive evaluation of the changes in sorption behavior over time, thereby providing critical insight into the degree and rate of surface coverage [10,13,26,27].

The establishment of the parameters of the adsorption isotherms and the kinetic models together with the determination of the specific thermodynamic parameters provides important information regarding the interaction mechanisms, surface properties, and the affinity degree of adsorbent. Ultimately, these parameters provide a vital basis for the development of efficient, cost-effective and environmentally friendly solutions for the removal of pollutants of various types [10,13,22,26,27].

The efficiency of the dye adsorption process is influenced by a series of parameters, such as the solution pH, contact time, temperature, adsorbent dose, dye initial concentration and ionic strength. In order to obtain a maximum efficiency of dye removal from water, these parameters should be optimized [28,29].

The utilization of statistical techniques through Design of Experiment (DOE) methods has been proven to be very useful for process optimization. DOE methods, such as Full factorial design, Fractional factorial design, Taguchi method, Response surface methodology and Box–Behnken design, can evaluate the individual contribution of controlling parameters to objective functions. The Taguchi technique is an effective optimization method that requires fewer experiments than other methods, leading to cost reduction, quality improvement, and reliable design solutions [17,18,19,20,30,31,32].

The aim of the work was to optimize and model the adsorption process of methylene blue on Leonurus cardiaca L. biomass powder, a natural, cheap and environmentally friendly material. Current scientific literature lacks any documented research or investigation into the effectiveness of this adsorbent material in removing methylene blue from aqueous solutions. The study represents an opportunity to explore this new approach and evaluate its potential as an effective strategy for the removal of this dye. To optimize the process and to establish the influence of each controllable factor on the process, the Taguchi method and one-way ANOVA analysis were used. Equilibrium, kinetic and thermodynamic studies were performed and the modeling of the experimental data was carried out using specific equilibrium isotherms and kinetic models.

2. Materials and Methods

The adsorbent material was obtained from the aerial parts of mature Leonurus cardiaca L. plants, which were purchased from StefMar (Ramnicu Valcea, Romania). The process, which did not involve a chemical or thermal treatment, is described in detail in a previously published study [33]. The point of zero charge (pH_PZC) for the material was 6.58 [33].

For SEM analysis and color analysis, performed before and after the methylene blue dye adsorption process, an FEI Inspect S model microscope (FEI, Eindhoven, The Netherlands) and a Cary-Varian 300 Bio UV-VIS colorimeter (Varian Inc., Mulgrave, Australia) were used, respectively.

The batch system was used to study how various factors affect the efficiency of dye removal during the adsorption process, using the Taguchi approach with a standard orthogonal array L₂₇ as the experimental design. The experiments were conducted in three independent replicates for each experiment at a constant mixing intensity. Merck’s analytical grade chemicals were utilized throughout the experimental procedures. Dilute solutions of HCl and NaOH (0.1 N) were utilized to regulate pH, while NaCl was used as a background electrolyte to study the influence of ionic strength. The Specord 200 PLUS UV-VIS spectrophotometer (Analytik Jena, Jena, Germany) was used to determine methylene blue concentration at a wavelength of 664 nm.

The methylene blue removal percentage, R(%), and the adsorption capacity at equilibrium, (qe), were calculated with equations presented in

Table 1. The calculation equations for dye removal percentage and adsorption capacity at equilibrium.

Parameters	Equation
Dye removal percentage	$R(\%)=\frac{\left(C_0-C_e\right)}{C_0}·100$
Adsorption capacity	$q_e=\frac{\left(C_0-C_e\right)·V}{m}$

C₀—initial and equilibrium dye concentration; V—solution volume; m—mass of adsorbent [5,17].

[5,17].

To enhance the efficiency of the dye removal process, the Taguchi method was used. An experimental design utilizing an L₂₇ orthogonal array (six factors at three levels) was employed to determine the optimal adsorption conditions. The percentage contribution of each factor to the dye removal efficiency was computed using analysis of variance (ANOVA) with a general linear model. Minitab 19 software (version 19.1.1, Minitab LLC, State College, PA, USA) was used to carry out the necessary mathematical computations.

In order to model the experimental data obtained in the adsorption process and to find out information regarding the interaction mechanisms, surface properties, and the affinity degree of adsorbent, several equilibrium isotherms and kinetic models were tested. The nonlinear equations of these adsorption isotherms [21,25,26] and kinetic models [22,27] used in data processing are illustrated in

Table 2. The nonlinear equations of the tested adsorption isotherms.

Equilibrium Isotherm	Equation
Langmuir	$q_e=\frac{q_m·K_L·C_e}{1+K_L·C_e}$
Freundlich	$q_e=K_F·C_e^{1/n_F}$
Temkin	$q_e=\frac{R·T}{b}ln\left(K_T·C_e\right)$
Redlich–Peterson	$q_e=\frac{K_{RP}·C_e}{1+a_{RP}·C_e^{{\beta }_{RP}}}$
Sips	$q_e=\frac{Q_{sat}·K_S·C_e^n}{1+K_S·C_e^n}$

q_m, Q_sat—maximum absorption capacities; K_L, K_F, K_T, K_S, K_RP—Langmuir, Freundlich, Temkin, Sips, Redlich–Peterson isotherm constants; 1/n_F—empirical constant indicating the intensity of adsorption; R—universal gas constant; T—absolute temperature; b—Temkin constant, which is related to the adsorption heat; a_RP—Redlich–Peterson isotherm constant; β_RP—Redlich–Peterson exponent (vary between 0 and 1); n—Sips isotherm exponent [21,25,26].

and

Table 3. The nonlinear equations of the tested kinetic models.

Kinetic Models	Equation
Pseudo-first-order	$q_t=q_e\left(1-{exp}^{-k_{1·}t}\right)$
Pseudo-second-order	$q_t=\frac{k_2·t·q_e^2}{1+k_2·{t·q}_e}$
Elovich	$q_t=\frac{1}{a}ln\left(1+a·b·t\right)$
Avrami	$q_t=q_{AV}\left[1-exp{\left(-k_{AV}·t\right)}^{n_{AV}}\right]$
General order	$q_t=q_n-\frac{q_n}{{\left[k_n·{\left(q_n\right)}^{n-1}·t·\left(n-1\right)+1\right]}^{1/1-n}}$

q_t—dye amount adsorbed at time t; k₁, k₂, k_AV, k_n—rate constants of pseudo-first-order, pseudo-second-order, Avrami and general order models; q_e, q_n, q_AV—theoretical values for the adsorption capacity; a—desorption constant of Elovich model; b—initial velocity; n_AV—fractional exponent; n—general order exponent [22,27].

.

To determine the most suitable isotherm and kinetic models, values for determination coefficient (R²), adjusted determination coefficient (R²_adj), sum of square error (SSE), chi-square (χ²), average relative error (ARE) and hybrid fractional error function (HYBRID) were calculated [22]. The applicability of these parameters was evaluated based on a higher R² and R²_adj value and lower values of SSE, χ², ARE and HYBRID. The calculation equations for these error parameters are described in

Table 4. The calculation equations for determination coefficient (R²), adjusted determination coefficient (R_adj²), sum of square error (SSE), chi-square (χ²), average relative error (ARE) and hybrid fractional error function (HYBRID).

Error Parameter	Equation
R2	$R^2=1-\frac{{\sum }_{i=1}^n{\left(y_{i,exp}-y_{i,mod}\right)}^2}{{\sum }_{i=1}^n{\left(y_{i,mod}-\overline{y_{i,exp}}\right)}^2}$
R2adj	$R_{adj}^2=1-\left(\frac{n-1}{1-(n_p+1)}\right)\left(1+R^2\right)$
SSE	$SSE={\sum }_{i=1}^n{\left(y_{i,exp}-y_{i,mod}\right)}^2$
χ2	${\chi }^2={\sum }_{i=1}^n\frac{{\left(y_{i,exp}-y_{i,mod}\right)}^2}{y_{i,mod}}$
ARE	$ARE=\frac{100}{n}{\sum }_{i=1}^n\left|\frac{y_{i,exp}-y_{i,mod}}{y_{i,mod}}\right|$
HYBRID	$HYBRID=\frac{100}{n-n_p}{\sum }_{i=1}^n\frac{{\left(y_{i,exp}-y_{i,mod}\right)}^2}{y_{i,mod}}$

y_i,exp—experimental value; y_i,mod—modeled value; $\overline{y_{i,\exp }}$—mean values, n—total amount of information, n_p—model parameters number [22].

.

The values of the thermodynamic parameters are standard Gibbs free energy change (ΔG⁰), standard enthalpy change (ΔH⁰) and standard entropy change (ΔS⁰), which were calculated with the equations from

Table 5. The calculation equations for thermodynamic parameters (ΔG⁰, ΔH⁰, ΔS⁰).

Thermodynamic Parameters	Equation
Standard Gibbs free energy change	$∆G^0=-R·T·ln{K}_L$
Standard enthalpy change	$ln{K}_L=\frac{∆S^0}{R}-\frac{∆H^0}{R·T}$
Standard entropy change

R—universal gas constant; K_L—Langmuir constant; T—absolute temperature [26].

[26].

3. Results and Discussion

3.1. SEM and Color Analyzes for Adsorbent Material

SEM and color analyses for adsorbent material performed before and after adsorption indicate the retention of methylene blue dye on the surface of the adsorbent material. The SEM analysis of the adsorbent (Figure 1A) revealed a porous surface, with voids and cavities of various shapes and sizes. After adsorption, the adsorbent material has a smooth and homogeneous surface (Figure 1B), suggesting that the pores were filled with methylene blue molecules. This conclusion is supported by the color analysis in the CIEL*a*b* system (Figure 2). Before adsorption, the color of the adsorbent is described by the point (LCPB). After adsorption, the color of the adsorbent is described by the point (LCPB + MB), which is in the domain color where there is also the point that characterizes the color of the dye (MB).

3.2. Dye Adsorption Process Optimization Using Taguchi Methods

The optimal conditions for dye removal by adsorption were established using a Taguchi (L₂₇) orthogonal array. Six factors at three levels were studied to evaluate their effect on dye removal efficiency (

Table 6. The six three-level factors used to evaluate the effect on dye removal efficiency.

Factor	Level 1	Level 2	Level 3
pH	2	6	10
Time (min)	5	30	60
Adsorbent dose (g·L−1)	1	3	5
Initial dye concentration (mg·L−1)	25	100	200
Temperature (K)	281	291	305
Ionic strength (mol L−1)	0	0.15	0.25

). The Taguchi approach was used to convert the experimental data into a signal-to-noise (S/N) ratio, which was analyzed to determine the quality of the experiment and the validity of the results. The terms “signal” and “noise” referred to the desirable value (mean) and undesirable value (standard deviation), respectively, for the output characteristic [20,28,29,30]. The highest adsorption efficiency was considered for evaluating the experimental outcomes; consequently, the “larger-the-better” option was selected to analyze the signal-to-noise ratio of the Taguchi method. The equation corresponding to this option is:

$$\frac{S}{N}=-{log}_{10}\left[\frac{1}{n}{\sum }_{i=1}^n{\left(\frac{1}{y_i}\right)}^2\right]$$

where n—number of repetitions under similar experimental conditions; and y_i—experimental response [20,29].

Table 7. Controllable factors and their levels used in L₂₇ orthogonal array.

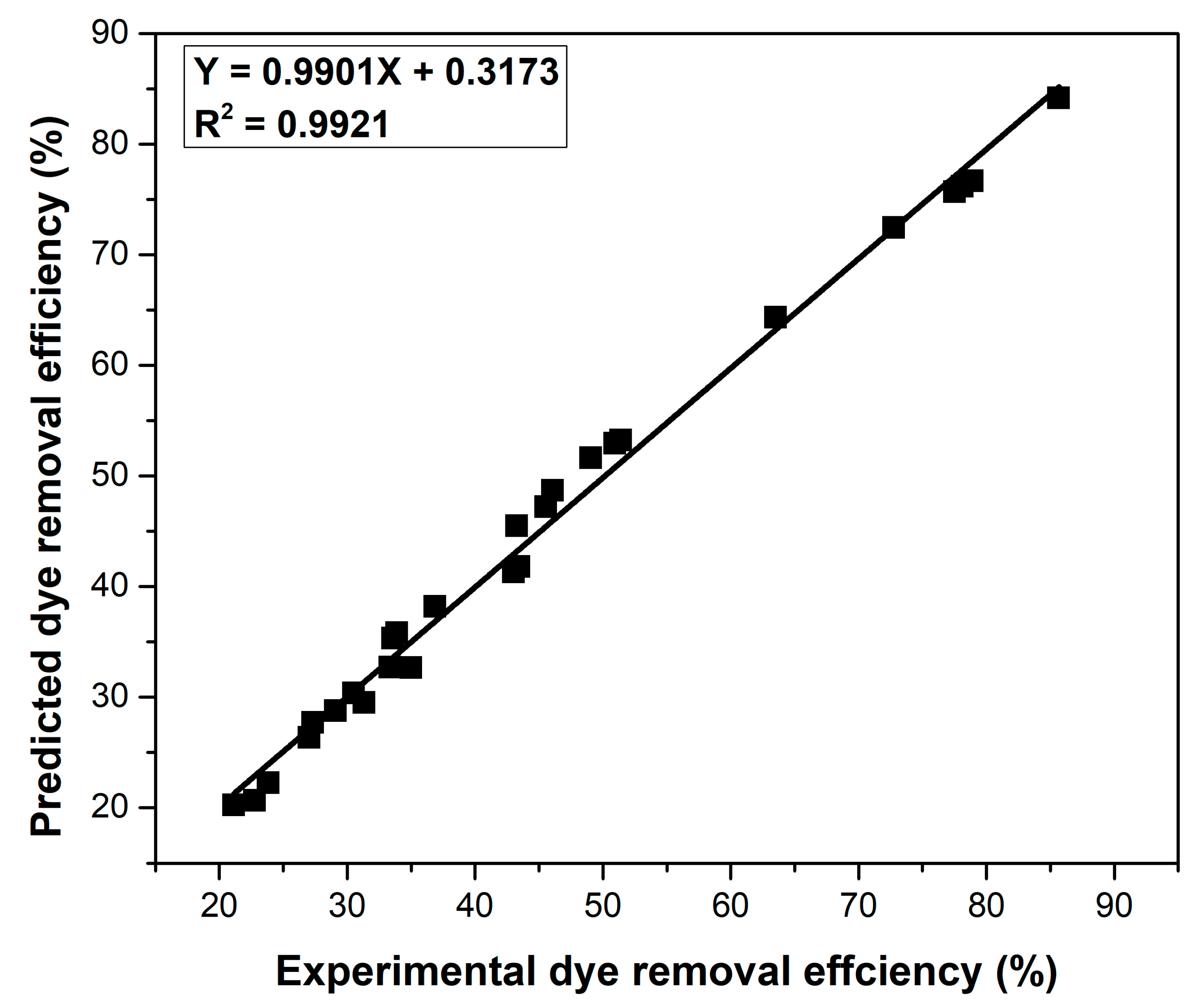
pH	Time (min)	Adsorbent Dose (g L−1)	Initial Dye Concentration (mg L−1)	Temperature (K)	Ionic Strength (mol L−1)	Dye Removal Efficiency (%)	S/N Ratio
2	5	1	25	281	0.00	45.56	33.17
2	5	1	25	291	0.15	27.04	28.64
2	5	1	25	305	0.25	21.14	26.50
2	30	3	100	281	0.00	51.39	34.21
2	30	3	100	291	0.15	30.50	29.68
2	30	3	100	305	0.25	23.85	27.55
2	60	5	200	281	0.00	49.05	33.81
2	60	5	200	291	0.15	29.11	29.28
2	60	5	200	305	0.25	22.76	27.14
6	5	3	200	281	0.15	34.98	30.87
6	5	3	200	291	0.25	27.30	28.72
6	5	3	200	305	0.00	63.54	36.06
6	30	5	25	281	0.15	43.43	32.75
6	30	5	25	291	0.25	33.90	30.60
6	30	5	25	305	0.00	78.90	37.94
6	60	1	100	281	0.15	43.01	32.67
6	60	1	100	291	0.25	33.57	30.52
6	60	1	100	305	0.00	78.12	37.85
10	5	5	100	281	0.25	33.37	30.46
10	5	5	100	291	0.00	77.52	37.78
10	5	5	100	305	0.15	46.09	33.27
10	30	1	200	281	0.25	31.32	29.91
10	30	1	200	291	0.00	72.76	37.23
10	30	1	200	305	0.15	43.26	32.72
10	60	3	25	281	0.25	36.87	31.33
10	60	3	25	291	0.00	85.67	38.65
10	60	3	25	305	0.15	50.93	34.14

describes the L₂₇ orthogonal array built with the controllable factors from Table 6 and results obtained in each of the experiments performed after each run. The S/N ratio response curves for the individual effects of dye adsorption parameters on the S/N ratio and dye removal efficiency are comparatively shown in Figure 3.

Analyzing the obtained data, we can observe the positive effect of increasing pH, contact time, adsorbent dose and temperature on the dye removal efficiency from water by adsorption. The initial concentration and the ionic strength have a negative influence on the process. The dye removal efficiency of methylene blue varies, depending on the values and the combination of controllable factors, from 21.14% to 85.67%.

Table 8. Response table for signal-to-noise ratios (the underlined values of S/N ratio indicate the optimum condition).

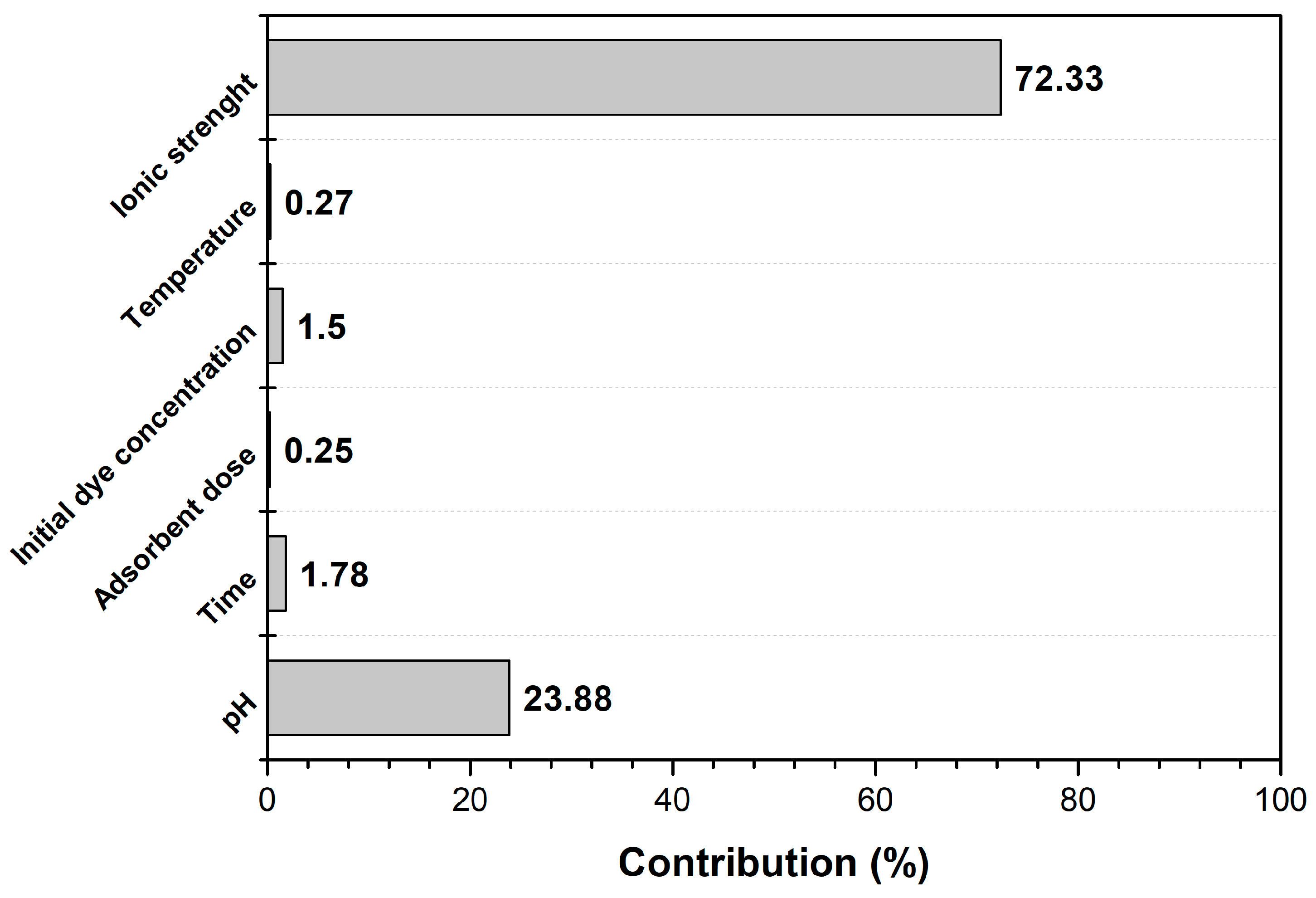
Level	pH	Time	Adsorbent Dose	Initial Dye Concentration	Temperature	Ionic Strength
1	30.00	31.72	32.14	32.64	32.14	36.31
2	33.11	32.52	32.36	32.67	32.35	31.56
3	33.95	32.82	32.56	31.75	32.58	29.20
Delta	3.95	1.10	0.43	0.92	0.44	7.11
Rank	2	3	6	4	5	1

displays the interaction effects of different factors based on the S/N ratio and the factors’ significance ranks. The ionic strength is the controllable factor that had the most impact on the process, while the adsorbent dose had the lowest impact. Correlating the data from Table 6 with those from Table 8, the optimal conditions for the adsorption process can be established: pH = 10, contact time = 60 min, adsorbent dose = 5 (g L⁻¹), initial dye concentration = 25 (mg L⁻¹), temperature = 305 K and ionic strength = 0 (mol L⁻¹).

Comparing the results with those reported in the scientific literature regarding the adsorption of methylene blue on similar bio-adsorbent materials, it is found that the controllable factor that had the most impact on the process differs depending on the adsorbent used. Thus, for the adsorbent material obtained from bilberry leaves, the factor with the greatest influence was the pH [12], while for the adsorbents obtained from dry bean pods husks and raspberry leaves, it was the adsorbent dose [17] and the contact time [34], respectively.

The order of controllable factor influence obtained with the Taguchi method was verified by ANOVA analysis, which also determined the percentage contribution of each factor (Figure 4). The results confirm the order of controllable factor impact obtained by the Taguchi approach. The ionic strength is the controllable factor that had the most impact on the process, while the adsorbent dose had the lowest impact.

The accuracy of the predictions indicated by the Taguchi optimization method was also verified. A strong correlation between the experimental and predicted values for dye removal efficiency was observed, with the coefficient of determination (R²) value being close to 1, indicating high prediction accuracy (Figure 5).

3.3. Equilibrium Isotherms

Equilibrium isotherms indicate the relationship between the concentration of solute in a solution and the amount of solute adsorbed onto the adsorbent material surface [21,22,23,24,25]. Some of the most-used isotherms to model the experimental data obtained in adsorption processes are Langmuir, Freundlich, Temkin, Redlich–Peterson and Sips. The fitted curves of these isotherms are shown in Figure 6 and their specific constant and error parameters are depicted in

Table 9. The adsorption isotherm models specific constants and error parameters.

Isotherm Model	Parameters	Value
Langmuir	KL (L mg−1)	0.023 ± 0.003
	qmax (mg g−1)	109.5 ± 5.24
	R2	0.9916
	Radj2	0.9891
	SSE	81.96
	χ2	2.59
	ARE (%)	7.66
	HYBRID	37.06
Freundlich	Kf (mg g−1)	9.37 ± 1.84
	1/n	0.44 ± 0.03
	R2	0.9424
	Radj2	0.9381
	SSE	513.45
	χ2	13.86
	ARE (%)	15.40
	HYBRID	190.97
Temkin	KT (L mg−1)	0.227 ± 0.029
	b (kJ g−1)	100.96 ± 5.13
	R2	0.9877
	Radj2	0.9860
	SSE	106.02
	χ2	2.54
	ARE (%)	8.36
	HYBRID	36.37
Redlich–Peterson	KRP (L g−1)	2.59 ± 0.18
	aRP (L mg−1)	0.024 ± 0.006
	βRP	0.93 ± 0.05
	R2	0.9915
	Radj2	0.9972
	SSE	82.45
	χ2	2.62
	ARE (%)	7.72
	HYBRID	37.56
Sips	Qsat (mg g−1)	103.2 ± 4.21
	KS (L mg−1)	0.014 ± 0.003
	n	1.17
	R2	0.9992
	Radj2	0.9990
	SSE	6.99
	χ2	0.24
	ARE (%)	2.46
	HYBRID	2.82

.

The information provided indicates that the Freundlich and Temkin isotherms are not suitable for characterizing the methylene blue retention process on Leonorus cardiaca biomass powder, having the lowest values for determination coefficient R² (0.9424 and 0.9877, respectively), and adjusted determination coefficient R²_adj (0.9381 and 0.9860, respectively). For the Langmuir and Redlich–Peterson isotherms, good values were obtained for the determination coefficient (0.9916 and 0.9915, respectively), and adjusted determination coefficient (0.9891 and 0.9972, respectively). The highest values for these parameters were obtained for the Sips isotherm (R² = 0.9992, R²_adj = 0.9973). In addition, the Sips isotherms have the lower values of SSE (6.99), χ² (0.24), ARE (2.46) and HYBRID (2.82); therefore, this isotherm best describes the process.

The scientific literature reported that the Sips isotherm most accurately characterized the adsorption process of methylene blue on bilberry leaves [12], raspberry leaves [34], lemon peel [35], Canola residues [36], date stones-based activated carbon [37] and carbon nanotubes [38].

The maximum adsorption capacity 103.21 (mg g⁻¹) indicated by the Sips isotherm is higher than maximum adsorption capacity of some other similar bio-adsorbents used for methylene blue adsorption such as: Ficcus Palmata leaves 6.89 (mg g⁻¹) [39], Neem leaf powder 19.6 (mg g⁻¹) [40], Ginkgo biloba leaves 48.07 (mg g⁻¹) [41], Solanum tuberosum leaves 52.60 (mg g⁻¹) [42], Salix babylonica leaves 60.9 (mg g⁻¹) [13], carrot leaves 66.5 (mg g⁻¹) [43], phoenix tree’s leaves 80.9 (mg g⁻¹) [44], Acer tree leaves 97.07 (mg g⁻¹) [45] and Elaeis guineensis leaves 103.0 (mg g⁻¹) [10].

3.4. Adsorption Kinetic

To evaluate the mass transfer rate during the adsorption process, it is crucial to use adsorption kinetic models. These patterns provide valuable information on the extent and rate of surface coverage [10,13,26,27]. Several kinetic models, including pseudo-first order, pseudo-second order, Elovich, Avrami and general order, are commonly applied in modeling experimental data from adsorption processes. These kinetic models fitted curves are illustrated in Figure 7, and

Table 10. The kinetic models specific constants and error parameters.

Kinetic Model	Parameters	Value
Pseudo-first order	k1 (min−1)	0.461 ± 0.041
	qe,calc (mg g−1)	18.67 ± 0.32
	R2	0.9919
	Radj2	0.9858
	SSE	2.46
	χ2	0.13
	ARE (%)	13.44
	HYBRID	1.90
Pseudo-second order	k2 (min−1)	0.065 ± 0.007
	qe,calc (g mg−1 min−1)	19.31 ± 0.16
	R2	0.9979
	Radj2	0.9973
	SSE	0.62
	χ2	0.03
	ARE (%)	12.43
	HYBRID	0.52
Elovich	a (g mg−1)	0.641 ± 0.052
	b (mg g−1 min−1)	9407 ± 374
	R2	0.9932
	Radj2	0.9914
	SSE	2.28
	χ2	0.83
	ARE (%)	13.01
	HYBRID	11.94
Avrami	kAV (min−1)	0.819 ± 0.078
	qAV (mg g−1)	18.67 ± 0.25
	nAV	0.56 ± 0.07
	R2	0.9919
	Radj2	0.9893
	SSE	2.46
	χ2	0.13
	ARE (%)	2.33
	HYBRID	1.89
General order	kN (min−1 (g mg−1)n–1)	0.065 ± 0.012
	qn (mg g−1)	19.31 ± 0.18
	n	2.01 ± 0.16
	R2	0.9992
	Radj2	0.9987
	SSE	0.21
	χ2	0.01
	ARE (%)	0.70
	HYBRID	0.17

displays their specific constant and error parameters.

Analyzing the data in Figure 7, it can be concluded that the adsorption equilibrium was reached after approximately 40 min. This equilibrium time is lower than that obtained for other similar adsorbent materials, such as Salix babylonica leaves 45 min [13], pineapple leaf 60 min [14], Platanus orientalis leaf 70 min [16], Ficcus Palmata leaves 80 min [39], Ginkgo biloba leaves 100 min [41], banana leaves 120 min [46], and phoenix tree leaves 150 min [44].

All kinetic models tested show good values for the determination coefficient, R², (0.9919–0.9992) and adjusted determination coefficient, R²_adj, (0.9858–0.9987). The highest values for these parameters and lower values of SSE (0.21), χ² (0.01), ARE (0.70%) and HYBRID (0.17) were obtained for the general order model. In conclusion, this model best characterizes the process.

According to the scientific literature, in other previous studies, the general order kinetic model described the adsorption of the methylene blue dye on bilberry leaves [12], ultrasonic surface modified chitin [47], cassava bagasse [48], comminuted raw avocado seeds [49] and golden trumpet tree bark [50].

3.5. Thermodynamic Study

The thermodynamic parameters for methylene blue adsorption process on Leonurus cardiaca L. biomass powder are shown in

Table 11. The thermodynamic parameters used to assess the dye adsorption process.

ΔG0 (kJ mol−1)			ΔH0 (kJ mol−1)	ΔS0 (J mol−1 K−1)
281 K	291 K	305 K
−20.05	−20.85	−21.97	0.29	9.62

. The standard Gibbs energy change (ΔG⁰) has a negative value and the standard enthalpy change (ΔH⁰) has a positive value; therefore, the dye adsorption process is spontaneous, favorable and exothermic. At the solid-liquid interface, an increased degree in randomness is highlighted by the positive value of the standard entropy change (ΔS⁰) [9,10].

The main mechanism involved in the adsorption is physisorption, with van der Waals forces having an important role in the process. This observation is indicated by the value of ΔH⁰ lower than 20 (kJ mol⁻¹) [17,34,51]. The values for ΔG⁰ lower but close to −20 (kJ mol⁻¹) may suggest that the involvement of chemisorption in the process is limited, physical adsorption playing the main role in the dye retaining [12,14,34].

4. Conclusions

In order to maximize the methylene blue removal efficiency from aqueous solutions using Leonurus cardiaca L. biomass powder, the Taguchi method was performed. SEM and color analyses for adsorbent material, before and after adsorption, indicate the retention of dye on the adsorbent surface. The dye removal efficiency of methylene blue varies, depending on the values and the combination of controllable factors, from 21.14% to 85.67%. The optimal conditions of the adsorption established using a Taguchi (L₂₇) orthogonal array were pH = 10, contact time = 60 min, adsorbent dose = 5 (g L⁻¹), initial dye concentration = 25 (mg L⁻¹), temperature = 305 K and ionic strength = 0 (mol L⁻¹). The ionic strength is the controllable factor that had the most impact on the process (72.33% contribution), while the adsorbent dose had the lowest impact. The accuracy of the predictions indicated by the Taguchi optimization method was very high. The Sips isotherm and general order kinetic model most accurately characterized the adsorption process. The main mechanism involved in the adsorption is physisorption, while chemisorption only contributes marginally to the process. The adsorption process is spontaneous, favorable and exothermic.