Evaluating Industry 4.0 Manufacturing Configurations: An Entropy-Based Grey Relational Analysis Approach
Abstract
:1. Introduction
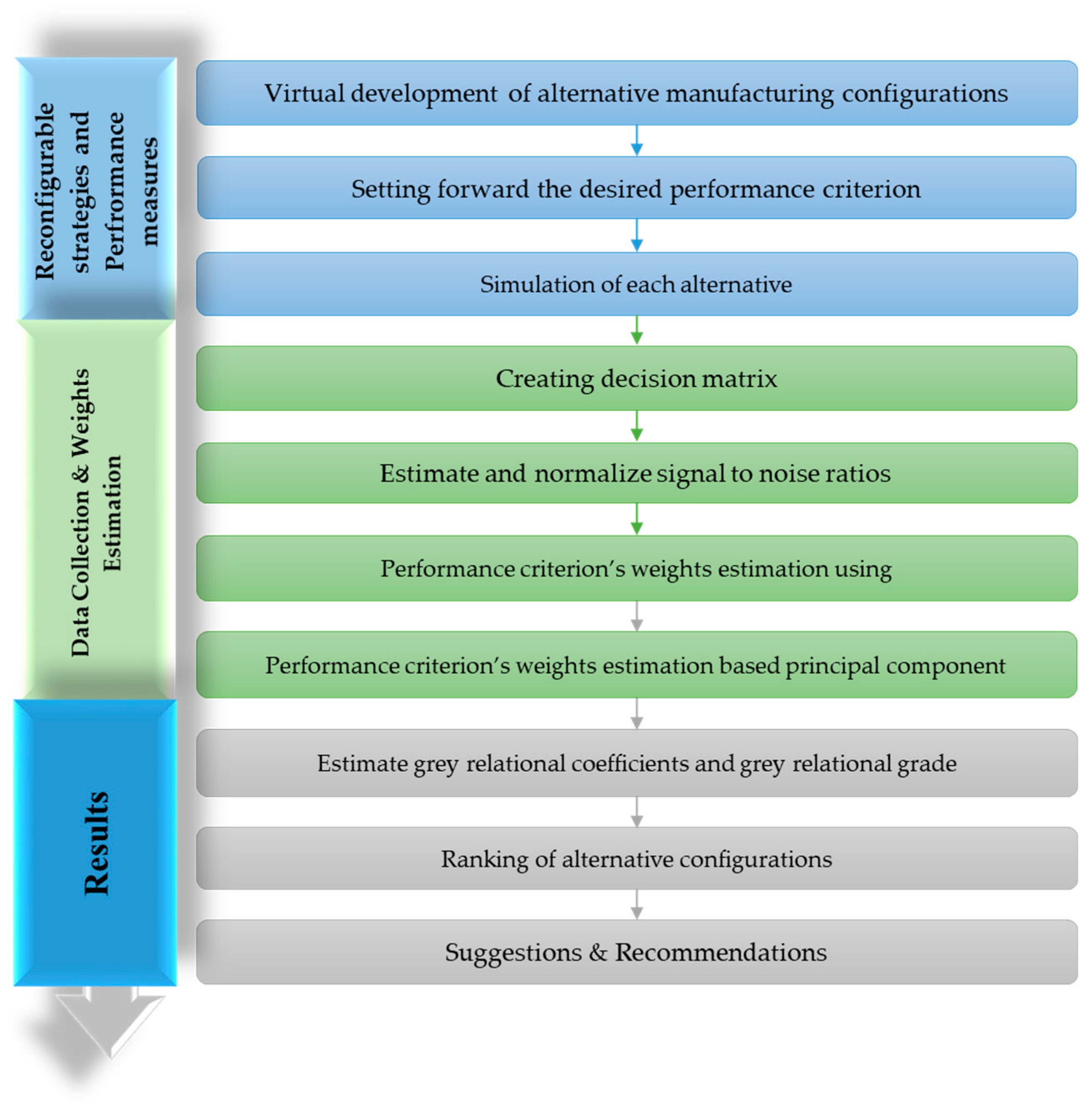
2. Research Methodology and the Problem on Hand
3. Adopted Approach and Its Application
3.1. Estimate and Normalize Signal to Noise Ratios
3.2. Estimate Grey Relational Coefficients and Grey Relational Grade
3.3. Performance Criterion’s Weight Estimation
3.4. Ranking of Alternative Configurations for Industry 4.0
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Spenhoff, P.; Wortmann, J.C.; Semini, M. EPEC 4.0: An Industry 4.0-Supported Lean Production Control Concept for the Semi-Process Industry. Prod. Plan. Control 2022, 33, 1337–1354. [Google Scholar] [CrossRef]
- A.T. Kearney Man Sees Future of Saudi Arabia in 3-D Vision|Arab News. Available online: https://www.arabnews.com/node/1319326/business-economy (accessed on 23 August 2023).
- Pech, M.; Vrchota, J. The Product Customization Process in Relation to Industry 4.0 and Digitalization. Processes 2022, 10, 539. [Google Scholar] [CrossRef]
- Mourtzis, D.; Angelopoulos, J.; Panopoulos, N. A Literature Review of the Challenges and Opportunities of the Transition from Industry 4.0 to Society 5.0. Energies 2022, 15, 6276. [Google Scholar] [CrossRef]
- Konstantinidis, F.K.; Myrillas, N.; Mouroutsos, S.G.; Koulouriotis, D.; Gasteratos, A. Assessment of Industry 4.0 for Modern Manufacturing Ecosystem: A Systematic Survey of Surveys. Machines 2022, 10, 746. [Google Scholar] [CrossRef]
- Hallioui, A.; Herrou, B.; Santos, R.S.; Katina, P.F.; Egbue, O. Systems-Based Approach to Contemporary Business Management: An Enabler of Business Sustainability in a Context of Industry 4.0, Circular Economy, Competitiveness and Diverse Stakeholders. J. Clean. Prod. 2022, 373, 133819. [Google Scholar] [CrossRef]
- Petrisor, I.; Cozmiuc, D. Global Supply Chain Management Organization at Siemens in the Advent of Industry 4.0. Available online: https://www.igi-global.com/chapter/global-supply-chain-management-organization-at-siemens-in-the-advent-of-industry-40/www.igi-global.com/chapter/global-supply-chain-management-organization-at-siemens-in-the-advent-of-industry-40/239318 (accessed on 19 March 2023).
- Leng, J.; Wang, D.; Shen, W.; Li, X.; Liu, Q.; Chen, X. Digital Twins-Based Smart Manufacturing System Design in Industry 4.0: A Review. J. Manuf. Syst. 2021, 60, 119–137. [Google Scholar] [CrossRef]
- Lin, Y.-J.; Hsieh, Y.-Y.; Huang, C.-Y. Ontology-Based Manufacturing Control Systems (MCS). Procedia Manuf. 2019, 39, 1906–1912. [Google Scholar] [CrossRef]
- Saboor, A.; Imran, M.; Agha, M.H.; Ahmed, W. Flexible Cell Formation and Scheduling of Robotics Coordinated Dynamic Cellular Manufacturing System: A Gateway to Industry 4.0. In Proceedings of the 2019 International Conference on Robotics and Automation in Industry (ICRAI), Montreal, QC, Canada, 20–24 May 2019; pp. 1–6. [Google Scholar]
- Ivanov, D.; Tang, C.S.; Dolgui, A.; Battini, D.; Das, A. Researchers’ Perspectives on Industry 4.0: Multi-Disciplinary Analysis and Opportunities for Operations Management. Int. J. Prod. Res. 2021, 59, 2055–2078. [Google Scholar] [CrossRef]
- Ding, B.; Ferràs Hernández, X.; Agell Jané, N. Combining Lean and Agile Manufacturing Competitive Advantages through Industry 4.0 Technologies: An Integrative Approach. Prod. Plan. Control 2023, 34, 442–458. [Google Scholar] [CrossRef]
- Morgan, J.; Halton, M.; Qiao, Y.; Breslin, J.G. Industry 4.0 Smart Reconfigurable Manufacturing Machines. J. Manuf. Syst. 2021, 59, 481–506. [Google Scholar] [CrossRef]
- Gruber, F.E. Industry 4.0: A Best Practice Project of the Automotive Industry. In Proceedings of the Digital Product and Process Development Systems IFIP TC 5 International Conference, Dresden, Germany, 10–11 October 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 36–40. [Google Scholar]
- Tsaramirsis, G.; Kantaros, A.; Al-Darraji, I.; Piromalis, D.; Apostolopoulos, C.; Pavlopoulou, A.; Alrammal, M.; Ismail, Z.; Buhari, S.M.; Stojmenovic, M.; et al. A Modern Approach towards an Industry 4.0 Model: From Driving Technologies to Management. J. Sens. 2022, 2022, e5023011. [Google Scholar] [CrossRef]
- Butt, J. Exploring the Interrelationship between Additive Manufacturing and Industry 4.0. Designs 2020, 4, 13. [Google Scholar] [CrossRef]
- Guo, D.; Ling, S.; Li, H.; Ao, D.; Zhang, T.; Rong, Y.; Huang, G.Q. A Framework for Personalized Production Based on Digital Twin, Blockchain and Additive Manufacturing in the Context of Industry 4.0. In Proceedings of the 2020 IEEE 16th International Conference on Automation Science and Engineering (CASE), Hong Kong, China, 20–21 August 2020; pp. 1181–1186. [Google Scholar]
- Shah, K.; Patel, N.; Thakkar, J.; Patel, C. Exploring Applications of Blockchain Technology for Industry 4.0. Mater. Today Proc. 2022, 62, 7238–7242. [Google Scholar] [CrossRef]
- Hegedűs, C.; Frankó, A.; Varga, P. Asset and Production Tracking through Value Chains for Industry 4.0 Using the Arrowhead Framework. In Proceedings of the 2019 IEEE International Conference on Industrial Cyber Physical Systems (ICPS), Taipei, Taiwan, 6–9 May 2019; pp. 655–660. [Google Scholar]
- Frankó, A.; Vida, G.; Varga, P. Reliable Identification Schemes for Asset and Production Tracking in Industry 4.0. Sensors 2020, 20, 3709. [Google Scholar] [CrossRef]
- Singh, A.; Gupta, P.; Asjad, M. Reconfigurable Manufacturing System (RMS): Accelerate towards Industries 4.0. In Proceedings of the International Conference on Sustainable Computing in Science, Technology and Management (SUSCOM), Jaipur, India, 26–28 February 2019. [Google Scholar]
- Jandyal, A.; Chaturvedi, I.; Wazir, I.; Raina, A.; Ul Haq, M.I. 3D Printing—A Review of Processes, Materials and Applications in Industry 4.0. Sustain. Oper. Comput. 2022, 3, 33–42. [Google Scholar] [CrossRef]
- Evjemo, L.D.; Gjerstad, T.; Grøtli, E.I.; Sziebig, G. Trends in Smart Manufacturing: Role of Humans and Industrial Robots in Smart Factories. Curr. Robot. Rep. 2020, 1, 35–41. [Google Scholar] [CrossRef]
- Chen, B.; Wan, J.; Shu, L.; Li, P.; Mukherjee, M.; Yin, B. Smart Factory of Industry 4.0: Key Technologies, Application Case, and Challenges. IEEE Access 2018, 6, 6505–6519. [Google Scholar] [CrossRef]
- Khan, M.; Wu, X.; Xu, X.; Dou, W. Big Data Challenges and Opportunities in the Hype of Industry 4.0. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, Italy, 21–25 May 2017; pp. 1–6. [Google Scholar]
- Xu, L.D.; Xu, E.L.; Li, L. Industry 4.0: State of the Art and Future Trends. Int. J. Prod. Res. 2018, 56, 2941–2962. [Google Scholar] [CrossRef]
- Pech, M.; Vrchota, J. Classification of Small- and Medium-Sized Enterprises Based on the Level of Industry 4.0 Implementation. Appl. Sci. 2020, 10, 5150. [Google Scholar] [CrossRef]
- Oztemel, E.; Gursev, S. Literature Review of Industry 4.0 and Related Technologies. J. Intell. Manuf. 2020, 31, 127–182. [Google Scholar] [CrossRef]
- Milisavljevic-Syed, J.; Li, J.; Xia, H. Realisation of Responsive and Sustainable Reconfigurable Manufacturing Systems. Int. J. Prod. Res. 2023, 1–22. [Google Scholar] [CrossRef]
- Koren, Y.; Gu, X.; Guo, W. Reconfigurable Manufacturing Systems: Principles, Design, and Future Trends. Front. Mech. Eng. 2018, 13, 121–136. [Google Scholar] [CrossRef]
- Juliet, A.V.; Suresh, S.; Viswanathan, T. Design of a Cost-Effective Material Handling System. AIP Conf. Proc. 2023, 2427, 020030. [Google Scholar] [CrossRef]
- Dibb, S.; Wensley, R. Segmentation Analysis for Industrial Markets: Problems of Integrating Customer Requirements into Operations Strategy. Eur. J. Mark. 2002, 36, 231–251. [Google Scholar] [CrossRef]
- Xing, B.; Nelwamondo, F.V.; Battle, K.; Gao, W.; Marwala, T. Application of Artificial Intelligence (AI) Methods for Designing and Analysis of Reconfigurable Cellular Manufacturing System (RCMS). In Proceedings of the 2009 2nd International Conference on Adaptive Science & Technology (ICAST), Accra, Ghana, 14–16 January 2009; pp. 402–409. [Google Scholar]
- Eguia, I.; Racero, J.; Guerrero, F.; Lozano, S. Cell Formation and Scheduling of Part Families for Reconfigurable Cellular Manufacturing Systems Using Tabu Search. Simulation 2013, 89, 1056–1072. [Google Scholar] [CrossRef]
- Hagag, A.M.; Yousef, L.S.; Abdelmaguid, T.F. Multi-Criteria Decision-Making for Machine Selection in Manufacturing and Construction: Recent Trends. Mathematics 2023, 11, 631. [Google Scholar] [CrossRef]
- Fattoruso, G. Multi-Criteria Decision Making in Production Fields: A Structured Content Analysis and Implications for Practice. J. Risk Financ. Manag. 2022, 15, 431. [Google Scholar] [CrossRef]
- Madzík, P.; Falát, L. State-of-the-Art on Analytic Hierarchy Process in the Last 40 Years: Literature Review Based on Latent Dirichlet Allocation Topic Modelling. PLoS ONE 2022, 17, e0268777. Available online: https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0268777 (accessed on 23 August 2023). [CrossRef]
- Patalas-Maliszewska, J.; Losyk, H. An Approach to Maintenance Sustainability Level Assessment Integrated with Industry 4.0 Technologies Using Fuzzy-TOPSIS: A Real Case Study. Adv. Prod. Eng. Manag. 2022, 17, 455–468. [Google Scholar] [CrossRef]
- Das, S.C. Prasenjit Chatterjee, Partha Protim Elimination Et Choice Translating Reality (Electre). In Multi-Criteria Decision-Making Methods in Manufacturing Environments; Apple Academic Press: Ontario, CA, USA, 2023; ISBN 978-1-00-337703-0. [Google Scholar]
- Zayat, W.; Kilic, H.S.; Yalcin, A.S.; Zaim, S.; Delen, D. Application of MADM Methods in Industry 4.0: A Literature Review. Comput. Ind. Eng. 2023, 177, 109075. [Google Scholar] [CrossRef]
- Raj, A.; Dwivedi, G.; Sharma, A.; Lopes de Sousa Jabbour, A.B.; Rajak, S. Barriers to the Adoption of Industry 4.0 Technologies in the Manufacturing Sector: An Inter-Country Comparative Perspective. Int. J. Prod. Econ. 2020, 224, 107546. [Google Scholar] [CrossRef]
- Caiado, R.G.G.; Scavarda, L.F.; Gavião, L.O.; Ivson, P.; Nascimento, D.L.d.M.; Garza-Reyes, J.A. A Fuzzy Rule-Based Industry 4.0 Maturity Model for Operations and Supply Chain Management. Int. J. Prod. Econ. 2021, 231, 107883. [Google Scholar] [CrossRef]
- Ding, X.; Chen, Y.; Li, M.; Liu, N. Booster or Killer? Research on Undertaking Transferred Industries and Residents’ Well-Being Improvements. Int. J. Environ. Res. Public Health 2022, 19, 15422. [Google Scholar] [CrossRef]
- Yang, G.; Zhang, J.; Zhang, J. Can Central and Local Forces Promote Green Innovation of Heavily Polluting Enterprises? Evidence from China. Front. Energy Res. 2023, 11, 1194543. [Google Scholar] [CrossRef]
- Ding, X.; Cai, Z.; Fu, Z. Does the New-Type Urbanization Construction Improve the Efficiency of Agricultural Green Water Utilization in the Yangtze River Economic Belt? Environ. Sci. Pollut. Res. 2021, 28, 64103–64112. [Google Scholar] [CrossRef] [PubMed]
- Urdinez, C.L. Francisco Principal Component Analysis. In R for Political Data Science; Chapman and Hall/CRC: Boca Raton, FL, USA, 2020; ISBN 978-1-00-301062-3. [Google Scholar]
- Zhu, Y.; Tian, D.; Yan, F. Effectiveness of Entropy Weight Method in Decision-Making. Math. Probl. Eng. 2020, 2020, e3564835. [Google Scholar] [CrossRef]
- Parmar, H.; Khan, T.; Tucci, F.; Umer, R.; Carlone, P. Advanced Robotics and Additive Manufacturing of Composites: Towards a New Era in Industry 4.0. Mater. Manuf. Process. 2022, 37, 483–517. [Google Scholar] [CrossRef]
- Wu, R.M.; Zhang, Z.; Yan, W.; Fan, J.; Gou, J.; Liu, B.; Gide, E.; Soar, J.; Shen, B.; Fazal-e-Hasan, S.; et al. A Comparative Analysis of the Principal Component Analysis and Entropy Weight Methods to Establish the Indexing Measurement. PLoS ONE 2022, 17, e0262261. Available online: https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0262261 (accessed on 23 August 2023). [CrossRef]
- Lotfi, F.H.; Fallahnejad, R. Imprecise Shannon’s Entropy and Multi Attribute Decision Making. Entropy 2010, 12, 53–62. [Google Scholar] [CrossRef]

| Performance Criterion (j) → Alternative (i) ↓ | 1 | 2 | … | n |
|---|---|---|---|---|
| 1 | X11k | X12k | … | X1nk |
| 2 | X21k | X22k | … | X2nk |
| . | . | . | … | . |
| m | Xm1k | Xm2k | … | Xmnk |
| Criterion weight → | W1k | W2k | … | Wnk |
| Market Scenario: k | Alternative: i | Performance Criteria: j | ||||
|---|---|---|---|---|---|---|
| Performance Criterion 1 | Performance Criterion 2 | Performance Criterion 3 | Performance Criterion 4 | Performance Criterion 5 | ||
| Market Scenario: 1 Market Demand: High Product Variety: Low | Alternative: 1 | X111 = 87.72 | X121 = 236.25 | X131 = 325.38 | X141 = 27.11 | X151 = 545.04 |
| Alternative: 2 | X211 = 84.60 | X221 = 416.82 | X231 = 211.72 | X241 = 103.85 | X251 = 374.15 | |
| Alternative: 3 | X311 = 86.21 | X321 = 566.62 | X331 = 156.73 | X341 = 194.53 | X351 = 521.10 | |
| Alternative: 4 | X411 = 65.01 | X421 = 509.64 | X431 = 186.90 | X441 = 161.59 | X451 = 469.28 | |
| Alternative: 5 | X511 = 61.94 | X521 = 445.11 | X531 = 208.25 | X541 = 117.40 | X551 = 391.36 | |
| Market Scenario: 2 Market Demand: Low Product Variety: Low | Alternative: 1 | X112 = 64.79 | X122 = 183.38 | X132= 376.58 | X142 = 15.36 | X152 = 406.30 |
| Alternative: 2 | X212 = 70.24 | X222 = 274.68 | X232= 304.50 | X242 = 45.70 | X252 = 239.77 | |
| Alternative: 3 | X312 = 77.06 | X322 = 360.64 | X332= 254.39 | X342 = 78.30 | X352 = 315.98 | |
| Alternative: 4 | X412 = 63.26 | X422 = 331.99 | X432= 272.72 | X442 = 59.80 | X452 = 297.91 | |
| Alternative: 5 | X512 = 60.32 | X522 = 300.54 | X532 = 287.77 | X542 = 42.39 | X552 = 266.17 | |
| Market Scenario: 3 Market Demand: High Product Variety: Medium | Alternative: 1 | X113 = 92.93 | X123 = 692.41 | X133 = 157.22 | X143 = 301.51 | X153 = 1690.42 |
| Alternative: 2 | X213 = 89.31 | X223 = 1132.45 | X233 = 116.65 | X243 = 711.53 | X253 = 1084.61 | |
| Alternative: 3 | X313 = 90.14 | X323= 1534.96 | X333 = 81.53 | X343 = 718.11 | X353 = 1297.11 | |
| Alternative: 4 | X413 = 69.84 | X423= 1160.99 | X433 = 115.04 | X443 = 727.81 | X453 = 1113.32 | |
| Alternative: 5 | X513 = 71.04 | X523 = 1059.74 | X533 = 117.77 | X543 = 628.13 | X553 = 963.02 | |
| Market Scenario: 4 Market Demand: Low Product Variety: Medium | Alternative: 1 | X114= 80.21 | X124= 266.73 | X134 = 314.28 | X144 = 25.08 | X154 = 620.56 |
| Alternative: 2 | X214 = 81.78 | X224 = 464.44 | X234 = 215.22 | X244 = 136.70 | X254 = 432.62 | |
| Alternative: 3 | X314 = 83.60 | X324 = 574.05 | X334 = 183.76 | X344 = 207.47 | X354 = 528.20 | |
| Alternative: 4 | X414 = 67.45 | X424 = 495.62 | X434 = 217.26 | X444 = 156.69 | X454 = 462.08 | |
| Alternative: 5 | X514 = 64.93 | X524 = 449.30 | X534 = 230.45 | X544 = 122.52 | X554 = 395.75 | |
| Market Scenario: 5 Market Demand: Low Product Variety: High | Alternative: 1 | X115 = 96.78 | X125 = 1162.72 | X135 = 73.79 | X145 = 700.89 | X155 = 2871.57 |
| Alternative: 2 | X215 = 88.44 | X225 = 1676.26 | X235 = 58.29 | X245 = 1208.01 | X255 = 1543.52 | |
| Alternative: 3 | X315 = 89.64 | X325 = 1993.89 | X335 = 44.00 | X345 = 1511.55 | X355 = 1807.63 | |
| Alternative: 4 | X415 = 66.93 | X425 = 1746.08 | X435 = 56.78 | X445 = 1266.71 | X455 = 1641.52 | |
| Alternative: 5 | X515 = 67.31 | X525 = 1621.92 | X535 = 56.14 | X545 = 1140.46 | X555 = 1394.66 | |
| Market Scenario: 6 Market Demand: High Product Variety: High | Alternative: 1 | X116 = 93.93 | X126 = 711.83 | X136 = 123.62 | X146 = 300.14 | X156 = 1728.41 |
| Alternative: 2 | X216 = 84.71 | X226 = 1056.70 | X236 = 85.51 | X246 = 617.61 | X256 = 1008.13 | |
| Alternative: 3 | X316 = 87.28 | X326 = 1287.48 | X336 = 64.56 | X346 = 824.13 | X356 = 1221.62 | |
| Alternative: 4 | X416 = 65.59 | X426 = 1149.35 | X436 = 91.50 | X446 = 704.92 | X456 = 1085.18 | |
| Alternative: 5 | X516 = 61.68 | X526 = 1061.38 | X536 = 88.10 | X546 = 612.57 | X556 = 931.75 | |
| Set of Weights | Rankings of Alternative Configurations for Each Scenarios | |||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Scenario:1 # | Scenario:2 | Scenario:3 | Scenario:4 | Scenario:5 | Scenario:6 | |||||||||||||||||||||||||
| Alternative: 1 | Alternative: 2 | Alternative: 3 | Alternative: 4 | Alternative: 5 | Alternative: 1 | Alternative: 2 | Alternative: 3 | Alternative: 4 | Alternative: 5 | Alternative: 1 | Alternative: 2 | Alternative: 3 | Alternative: 4 | Alternative: 5 | Alternative: 1 | Alternative: 2 | Alternative: 3 | Alternative: 4 | Alternative: 5 | Alternative: 1 | Alternative: 2 | Alternative: 3 | Alternative: 4 | Alternative: 5 | Alternative: 1 | Alternative: 2 | Alternative: 3 | Alternative: 4 | Alternative: 5 | |
| Set 1: equal weights for all performance measures | 2 | 4 | 1 | 3 | 5 | 3 | 4 | 1 | 2 | 5 | 3 | 2 | 1 | 4 | 5 | 2 | 4 | 1 | 3 | 5 | 2 | 3 | 1 | 4 | 5 | 2 | 4 | 1 | 3 | 5 |
| Set 2: entropy weight | 2 | 4 | 1 | 3 | 5 | 3 | 4 | 1 | 2 | 5 | 3 | 2 | 1 | 4 | 5 | 3 | 2 | 1 | 4 | 5 | 2 | 3 | 1 | 4 | 5 | 2 | 3 | 1 | 4 | 5 |
| Set 3: principal component weight | 2 | 4 | 1 | 3 | 5 | 3 | 4 | 1 | 2 | 5 | 3 | 2 | 1 | 4 | 5 | 2 | 4 | 1 | 3 | 5 | 2 | 3 | 1 | 4 | 5 | 2 | 4 | 1 | 3 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rehman, A.U.; AlFaify, A.Y. Evaluating Industry 4.0 Manufacturing Configurations: An Entropy-Based Grey Relational Analysis Approach. Processes 2023, 11, 3151. https://doi.org/10.3390/pr11113151
Rehman AU, AlFaify AY. Evaluating Industry 4.0 Manufacturing Configurations: An Entropy-Based Grey Relational Analysis Approach. Processes. 2023; 11(11):3151. https://doi.org/10.3390/pr11113151
Chicago/Turabian StyleRehman, Ateekh Ur, and Abdullah Yahia AlFaify. 2023. "Evaluating Industry 4.0 Manufacturing Configurations: An Entropy-Based Grey Relational Analysis Approach" Processes 11, no. 11: 3151. https://doi.org/10.3390/pr11113151






