Research on Open Circuit Fault Modeling and Fault Tolerant Control Strategy of Five-Phase Induction Motor
Abstract
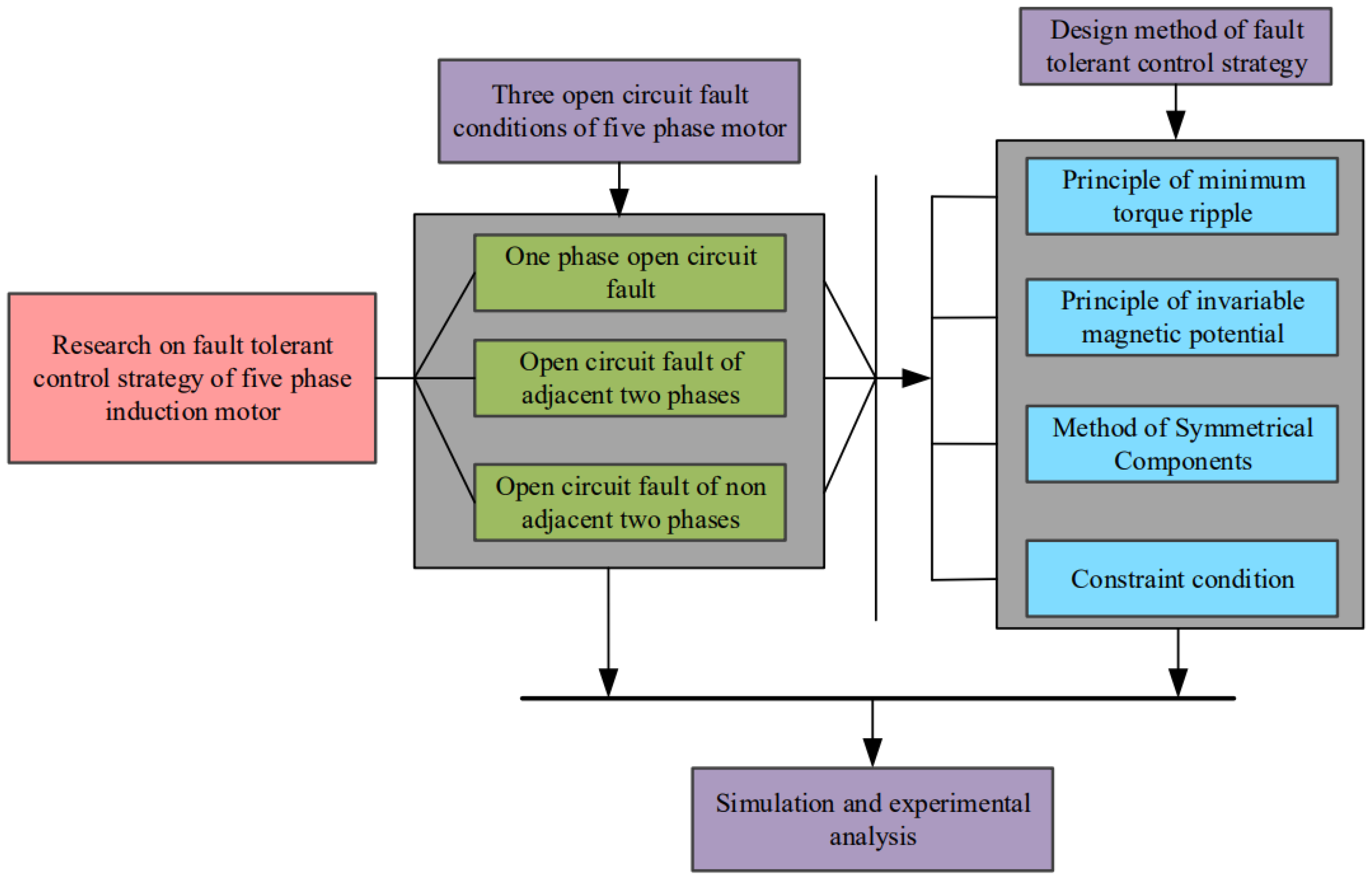
:1. Introduction
2. Establishment of Mathematical Model for Open-Circuit Fault of Five-Phase Induction Motor
2.1. Mathematical Model of Normal Operation of Five-Phase Induction Motor
- (1)
- The matrix form of the stator and rotor flux linkage equation is [27]:where:
- is the stator flux linkage equation;
- is the rotor flux linkage equation;
- is the stator current equation;
- is the rotor current equation.
- (2)
- The voltage equation of the stator and rotor is [27]:where, is the voltage vector in the rotating coordinate system.
- (3)
- The electromagnetic torque equation is [27]:
2.2. Mathematical Model of One-Phase Open-Circuit Fault
2.3. Mathematical Model of Two-Phase Open-Circuit Fault
3. Fault Tolerant Strategy Analysis of Open-Circuit Fault of Five-Phase Induction Motor
3.1. Fault Tolerant Control Model of Five-Phase Motor Based on Magnetomotive Force Balance
3.2. Fault Tolerant Strategy Analysis of One-Phase Open-Circuit Fault
3.3. Mathematical Model Establishment and Fault Tolerance Strategy Analysis of Adjacent Two-Phase Open-Circuit Fault
3.4. Mathematical Model Establishment and Fault Tolerance Strategy Analysis of Non-Adjacent Two-Phase Open-Circuit Fault
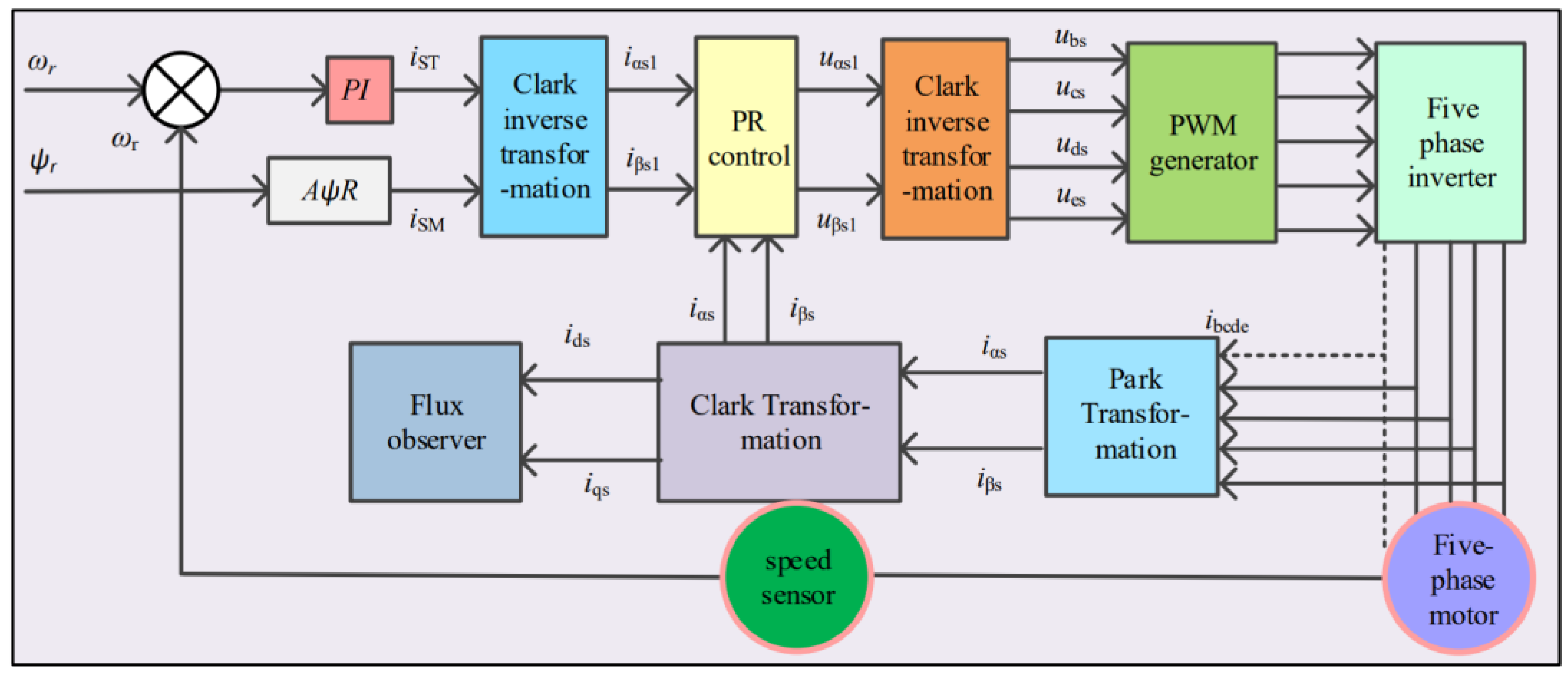
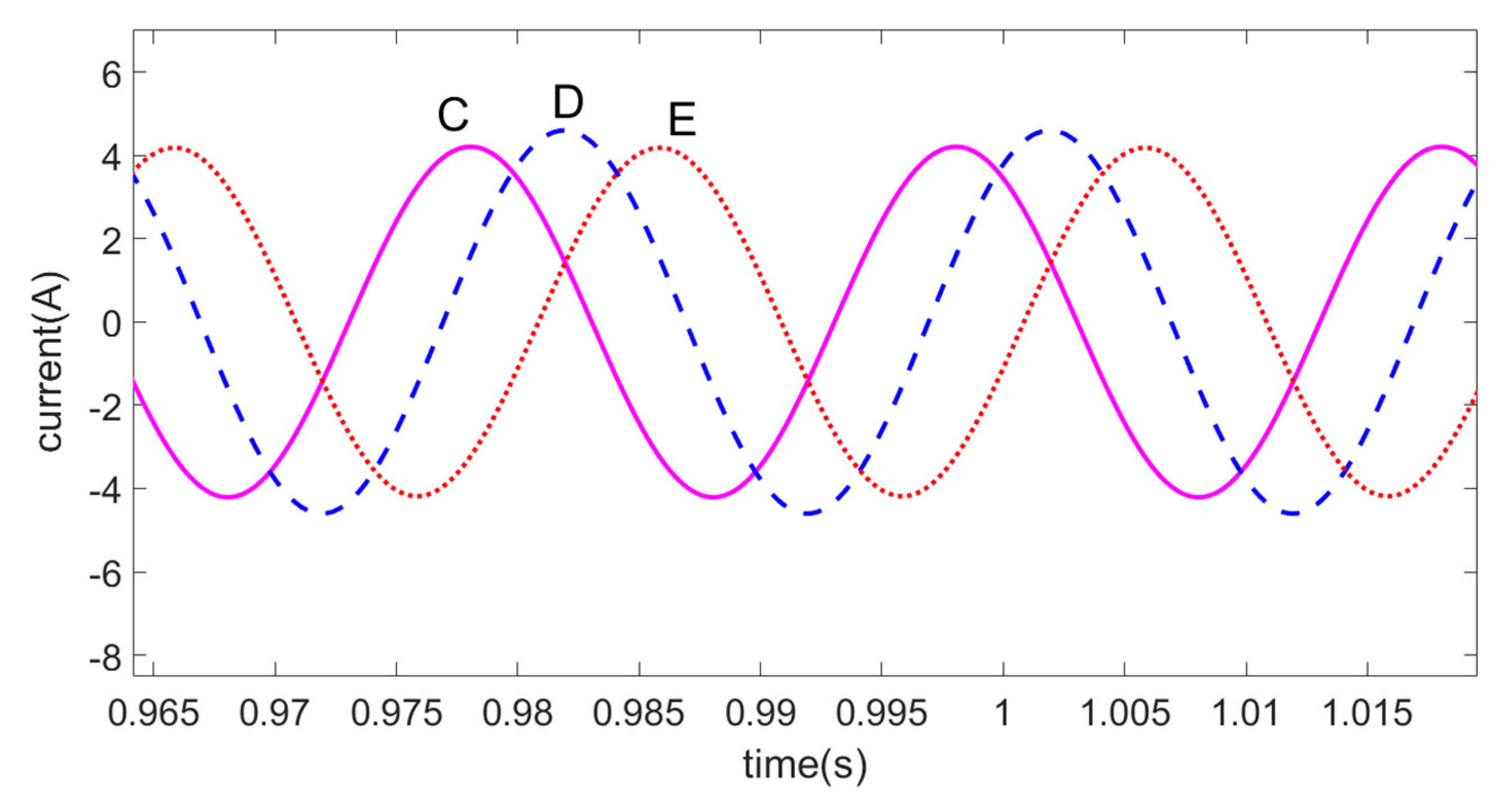
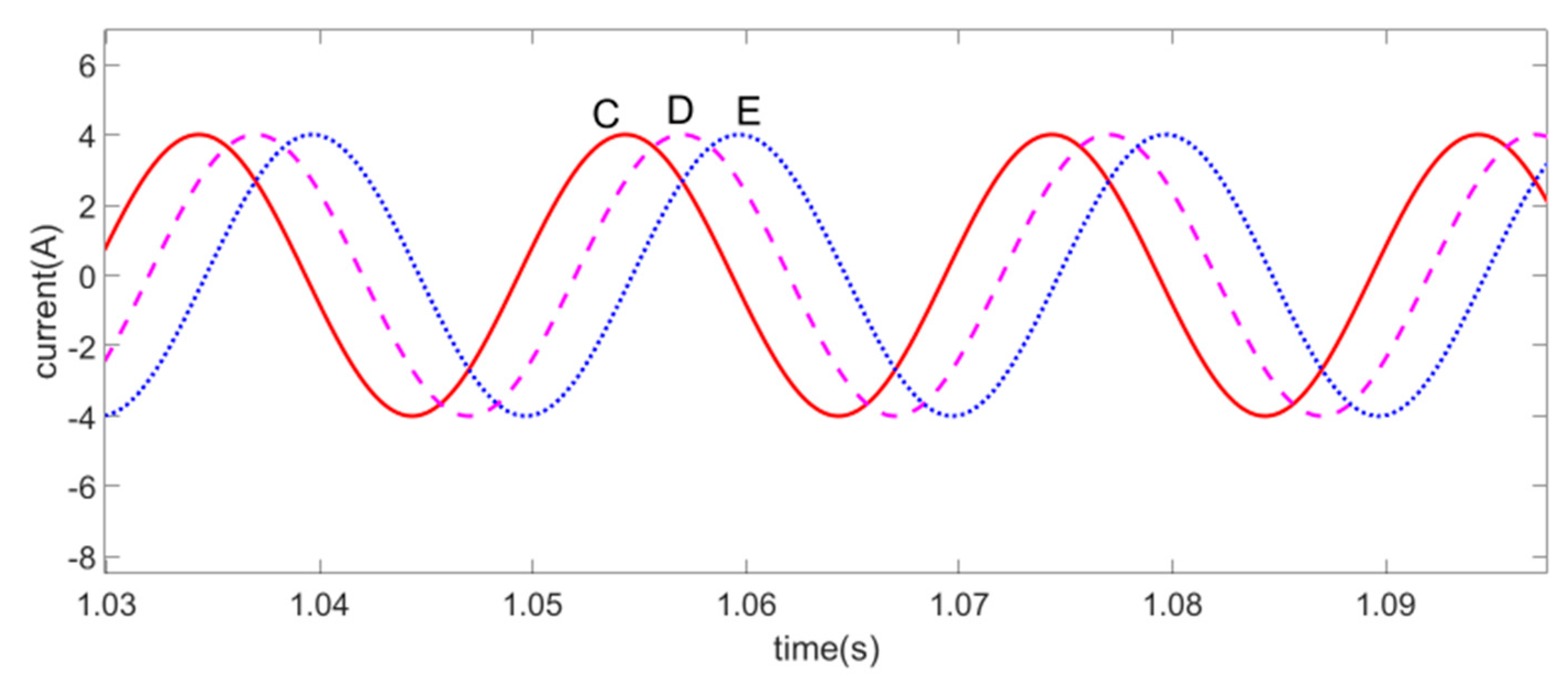
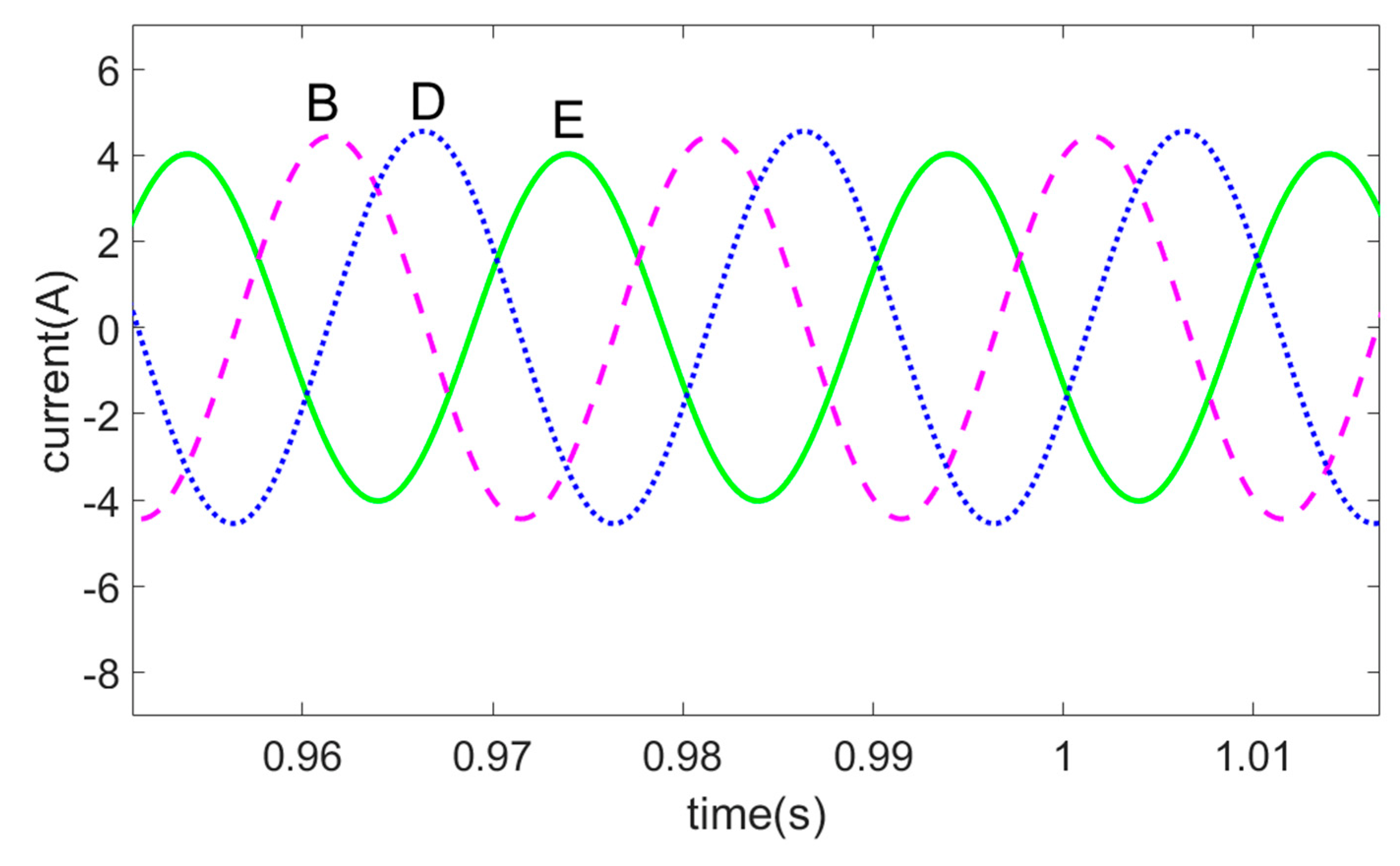
4. Simulation and Experimental Discussion
4.1. Simulation Discussion
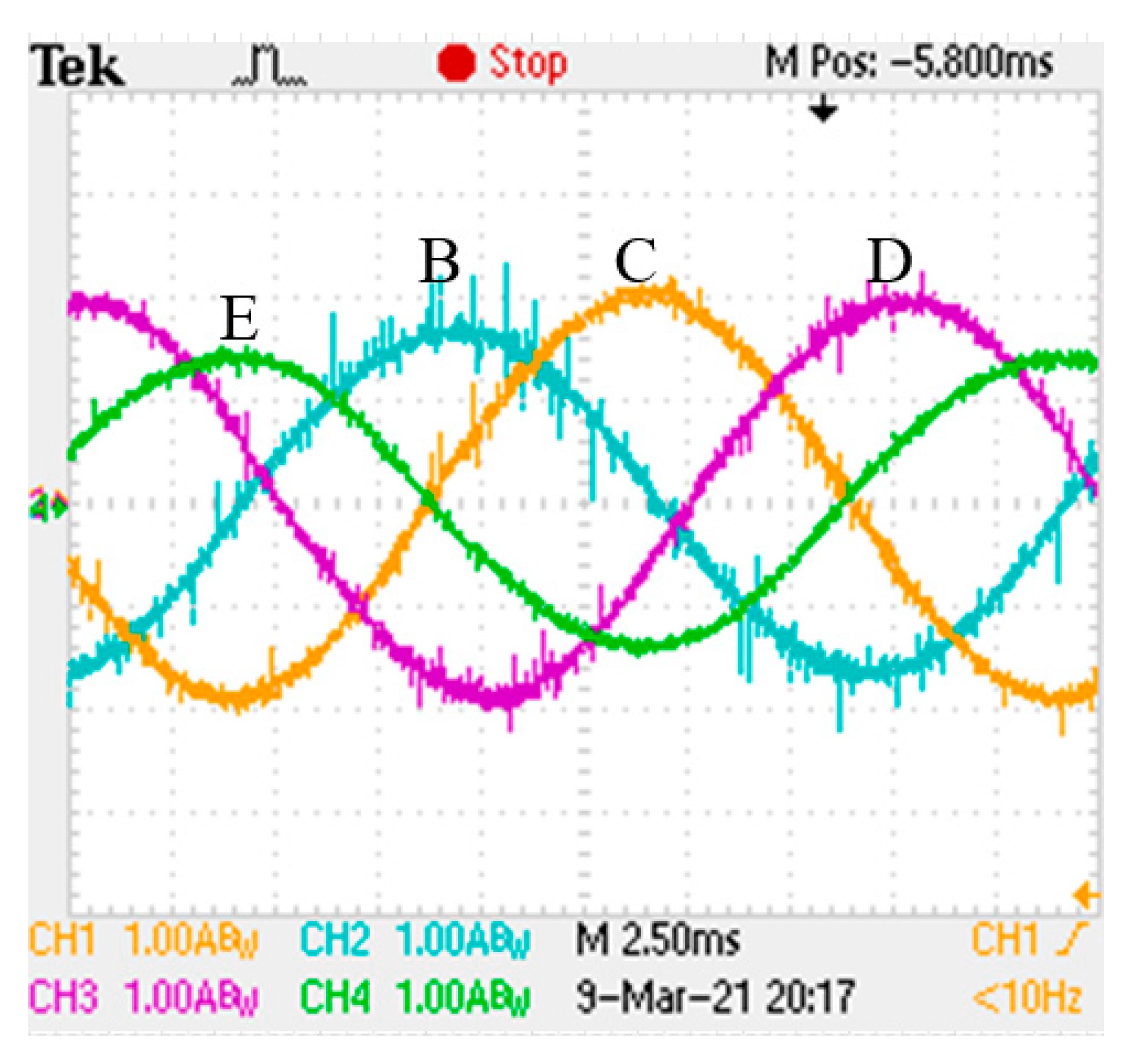
4.2. Experimental Discussion
- (1)
- When the motor operates normally, the motor speed is increased with the increase of input voltage, and when it reaches 80 V, the motor works at the rated speed.
- (2)
- After the open-circuit fault of phase A occurs, the motor speed is increased for a certain time and cannot reach the expected value. However, after fault-tolerant control, the speed increases significantly faster and gradually reaches the rated value.
- (3)
- After the open-circuit fault of phase A and B occurs, the basic speed of the motor is extremely small. At this time, it is difficult to make up for the disturbance caused by the open-circuit fault and provide sufficient power to the motor. After fault-tolerant control, when the input voltage reaches 70 V, the motor speed is rapidly increased. It can be seen that the adjacent two-phase open-circuit fault has a great impact on the motor. When the input voltage reaches 110 V, the rotation speed of the motor tends to be stable. At this time, the motor does not reach the rated speed, but maintains low-speed operation at 1200 r/min.
- (4)
- After the open-circuit fault of phase A and C occurs, the speed of the motor is decreased. After fault-tolerant control, the speed of the motor is increased rapidly and operates at a stable speed of 1500 r/min. The two-phase open-circuit fault of A and C is more stable than that of A and B.
- (5)
- During normal operation, the motor vibration can be ignored. When an open-circuit fault occurs to the motor, the vibration is increased significantly. After fault-tolerant control, motor vibration is as follows: (a) The vibration is significantly reduced when a phase open-circuit fault occurs. (b) The motor vibration is small, and the operation is relatively stable when two non-adjacent phases fail. (c) The motor vibration is significantly reduced but still strong after fault-tolerant control when two adjacent phases of the motor fail.
- (6)
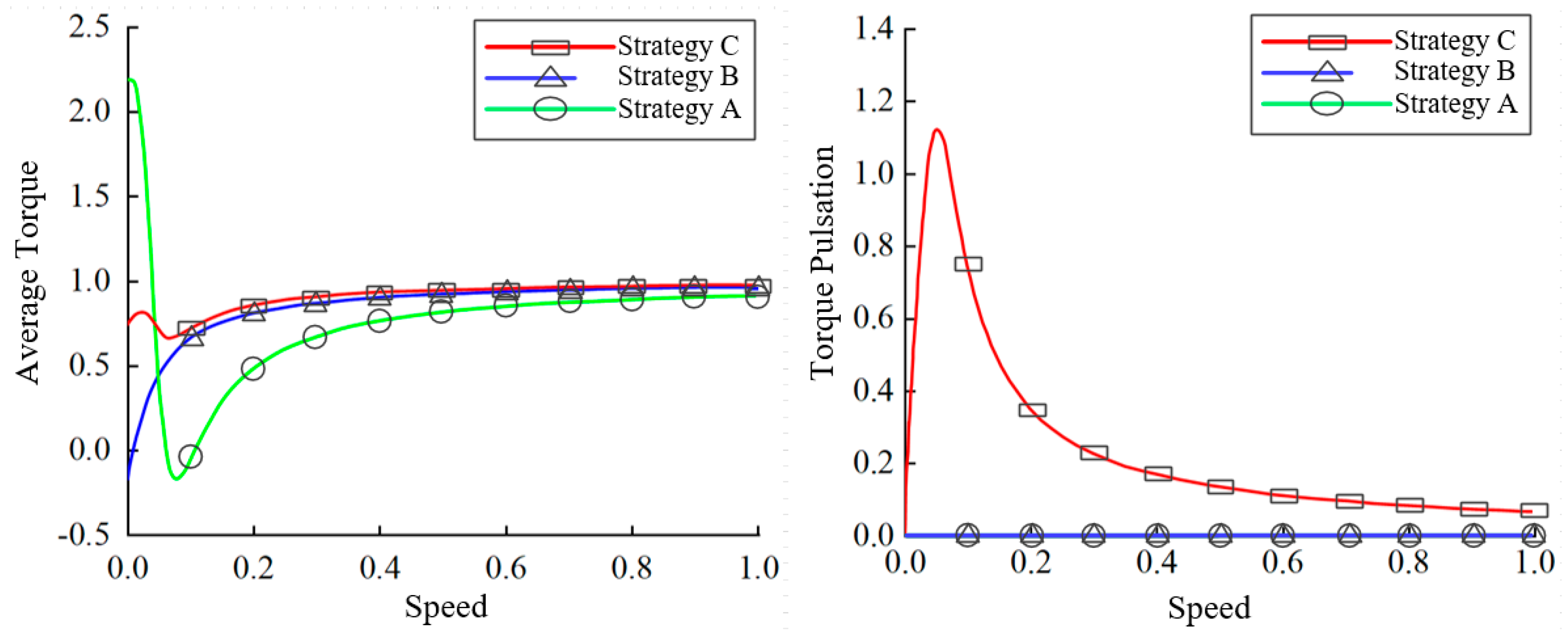
- The fault-tolerant control strategy proposed in this paper has the advantages of simple calculation, constant magnetomotive force, low loss, and small current fluctuation. The strategy takes the minimum torque ripple as the constraint condition and controls the amplitude and phase of the remaining healthy phase current to realize the normal operation of the five-phase induction motor in the event of an open-circuit fault. Compared with vector pulse width modulation technology, this strategy has less computations and simpler control [24]; Compared with the fault-tolerant control strategy in [28], which takes the balance of the magnetomotive force after the motor is out-of-phase as the constraint condition, this strategy can maintain the stability of the motor torque and has high working reliability. Compared with the full torque range efficiency optimization fault-tolerant control strategy, the control efficiency of this strategy is higher [14].
5. Conclusions
- (1)
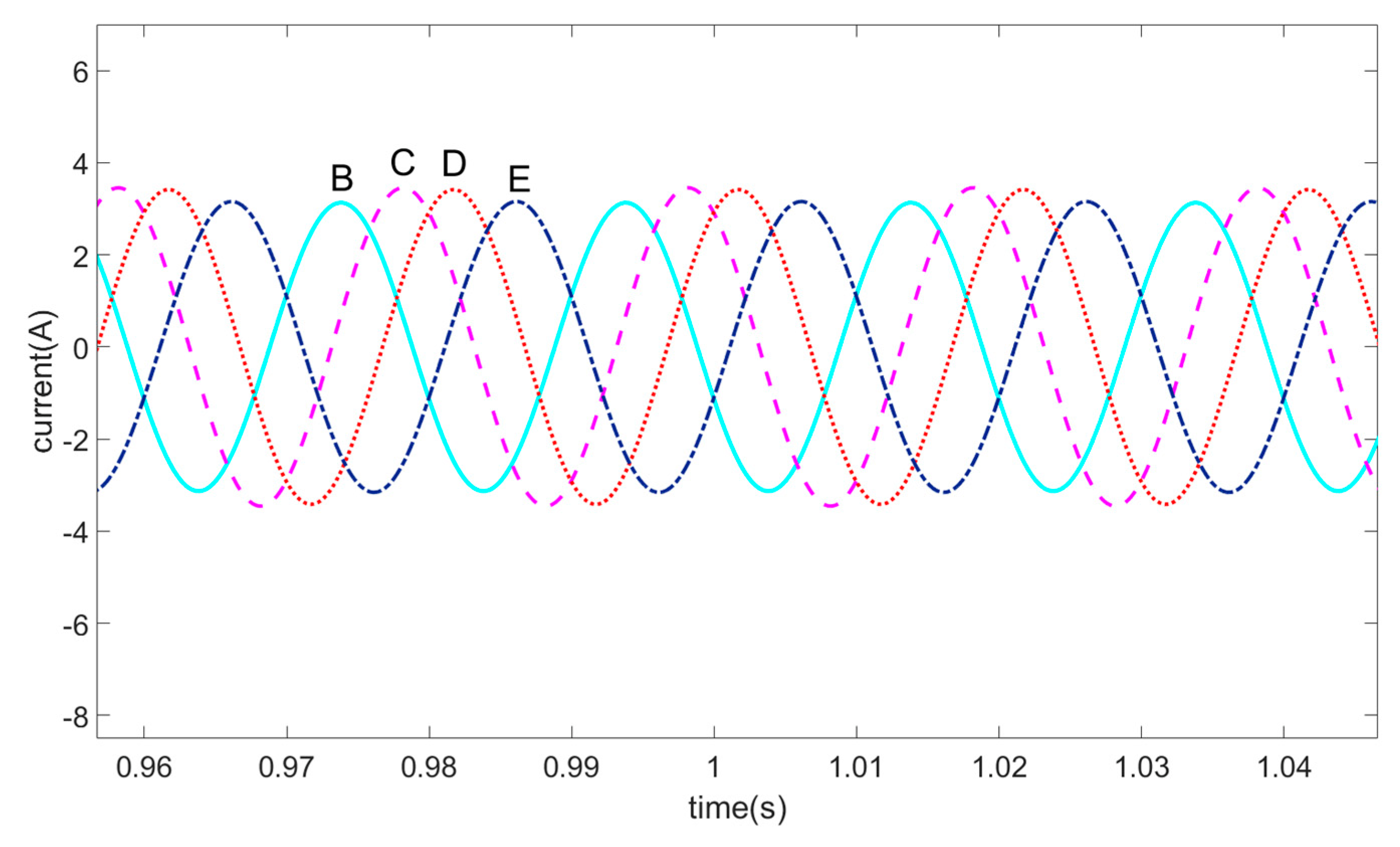
- When the five-phase motor has an open-circuit fault, the residual phase current is no longer balanced. After fault-tolerant control, the residual phase current is balanced again.
- (2)
- When the five-phase motor has an open-circuit fault, the motor speed decreases, so the rated speed cannot be reached. When the two adjacent phases of the motor have an open-circuit fault, the motor speed is almost zero, and the low-speed operation can be maintained after fault-tolerant control. When one phase or two non-adjacent phases of the motor have open-circuit faults, the rated speed can be reached after fault-tolerant control.
- (3)
- When the motor has an open-circuit fault, the vibration increases significantly. After fault-tolerant control, the vibration of the motor is reduced and the motor runs smoothly. However, when two adjacent phases fail, even after fault-tolerant control, the vibration of the motor is reduced, but it is still strong.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Barrero, F.; Duran, M.J. Recent Advances in the Design, Modeling, and Control of Multiphase Machines—Part I. IEEE Trans. Ind. Electron. 2016, 63, 449–458. [Google Scholar] [CrossRef]
- Duran, M.J.; Barrero, F. Recent Advances in the Design, Modeling, and Control of Multiphase Machines—Part II. IEEE Trans. Ind. Electron. 2015, 63, 459–468. [Google Scholar] [CrossRef]
- Levi, E. Multiphase electric machines for variable-speed applications. IEEE Trans. Ind. Electron. 2008, 55, 1893–1909. [Google Scholar] [CrossRef]
- Banu, J.B.; Jeyashanthi, J.; Ansari, A.T. DTC-IM drive using adaptive neuro fuzzy inference strategy with multilevel inverter. J. Ambient. Intell. Humaniz. Comput. 2021, 1–23. [Google Scholar] [CrossRef]
- Fan, Z.; Yi, H.; Xu, J.; Xie, K.; Qi, Y.; Ren, S.; Wang, H. Performance Study and Optimization Design of High-Speed Amorphous Alloy Induction Motor. Energies 2021, 14, 2468. [Google Scholar] [CrossRef]
- Abdel-Khalik, A.S.; Masoud, M.I.; Williams, B.W. Improved Flux Pattern with Third Harmonic Injection for Multiphase Induction Machines. IEEE Trans. Power Electron. 2012, 27, 1563–1578. [Google Scholar] [CrossRef]
- Liu, W.; Xing, J.; Zhao, X.; Zhou, D. Hybrid direct torque control strategy for dual three-phase and multi-phase permanent magnet synchronous motor drives. Sci. Technol. Eng. 2022, 22, 3564–3575. [Google Scholar]
- Kellner, J.; Kaák, S.; Praenica, M.; Resutík, P. A Comprehensive Investigation of the Properties of a Five-Phase Induction Motor Operating in Hazardous States in Various Connections of Stator Windings. Electronics 2021, 10, 609. [Google Scholar] [CrossRef]
- Muduli, U.R.; Behera, R.K. Virtual Vector based SVPWM-DTC for Five-Phase Two-Level VSI fed Induction Motor Drive. In Proceedings of the 2021 1st International Conference on Power Electronics and Energy (ICPEE-2021), Bhubaneswar, India, 2–3 January 2021. [Google Scholar]
- Zheng, X. Research on Phase Failure Operation of Polyphase Induction Motor. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2017. [Google Scholar]
- Bai, H.; Zhu, J.; Qin, J. Study of Fault-tolerant Control Strategies for a Fault-tolerant Permanent Magnet Motor. In Proceedings of the 2016 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016. [Google Scholar]
- Ibitoye, M.O.; Estigoni, E.H.; Hamzaid, N.A.; Wahab, A.K.A.; Davis, G.M. The Effectiveness of FES-Evoked EMG Potentials to Assess Muscle Force and Fatigue in Individuals with Spinal Cord Injury. Sensors 2014, 14, 12598–12622. [Google Scholar] [CrossRef]
- Zhu, P.; Zhang, X.; Qiao, M.; Cai, W.; Liang, J. Air gap magnetic field indirect vector control of five phase induction motor based on biplane synchronous rotation transformation. Chin. J. Electr. Eng. 2013, 33, 112–119+16. [Google Scholar]
- Liu, H.; Yi, X.; Wang, D.; Zheng, X.; Meng, F. Efficiency optimization control strategy for full torque range of five phase induction motor without compatible and staggered operation. Chin. J. Electr. Eng. 2020, 40, 1642–1653. [Google Scholar]
- Mossa, M.A.; Echeikh, H. A novel fault tolerant control approach based on backstepping controller for a five phase induction motor drive: Experimental investigation. ISA Trans. 2021, 112, 373–385. [Google Scholar] [CrossRef]
- Shuting, F.; Dawei, M.; Mengmeng, A. Comparative analysis of the performance of five phase induction motors with different stator winding structures under open circuit fault. J. Electr. Technol. 2022, 37, 1679–1688. [Google Scholar]
- Yepes, A.G.; Doval-Gandoy, J. Overmodulation Method with Adaptive x-y Current Limitation for Five-Phase Induction Motor Drives. IEEE Trans. Ind. Electron. 2021, 69, 2240–2251. [Google Scholar] [CrossRef]
- Fengxiang, L.; Juncheng, J.; Jun, T. Fault tolerant control strategy for flux linkage correction of five phase permanent magnet synchronous motor. Electr. Drive 2022, 52, 40–45. [Google Scholar]
- Wang, T.; Wang, A.; Sun, J.; Jin, Y. Research on phase failure fault-tolerant control of six phase permanent magnet synchronous motor based on model predictive current control. Micromotor 2020, 53, 73–77+104. [Google Scholar]
- Guzman, H.; Durán, M.J.; Barrero, F.; Toral, S. Fault-tolerant Current Predictive Control of Five-phase Induction Motor Drives with an Open Phase. In Proceedings of the IECON 2011—37th Annual Conference of the IEEE Industrial Electronics Society, Melbourne, VIC, Australia, 7–10 November 2011; pp. 3680–3685. [Google Scholar]
- Tao, X.; Peng, X. Five phase induction motor finite control set model predictive fault-tolerant control. Electr. Drive 2019, 49, 17–21+74. [Google Scholar]
- Kang, X.; Li, J. Research on load current control performance of three-phase inverter based on predictive control. Invert. World 2019, 10, 63–66. [Google Scholar]
- Wang, Y.; Zhang, C.; Hao, W. Overview of fault tolerance technology for permanent magnet motors and their drive systems. Chin. J. Electr. Eng. 2022, 42, 351–372. [Google Scholar]
- Liu, G.; Song, C.; Xu, L.; Du, K. Fault tolerant control strategy for two-phase open circuit fault of five phase permanent magnet synchronous motor based on SVPWM. J. Electrotech. 2019, 34, 23–32. [Google Scholar]
- Liu, G.; Qu, L.; Zhao, W.; Chen, Q.; Xie, Y. Comparison of Two Svpwm Control Strategies of Five-phase Fault-tolerant Permanent-magnet Motor. IEEE Trans. Power Electron. 2016, 31, 6621–6630. [Google Scholar] [CrossRef]
- Liu, R.; Wang, X.; Zou, M. Fault tolerant control of electric vehicle five phase permanent magnet brushless motor based on asymmetric SVPWM. Mot. Control Appl. 2018, 6, 95–101. [Google Scholar]
- Cao, Z. Design Analysis and Fault Tolerant Control of Five Phase Induction Motor. Master’s Thesis, Harbin University of Technology, Harbin, China, 2021. [Google Scholar]
- Zhu, P.; Qiao, M.; Yu, F.; Wei, Y. Fault tolerant control of polyphase induction motors based on magnetomotive force balance analysis. J. Electrotech. 2019, 34, 62–69. [Google Scholar]



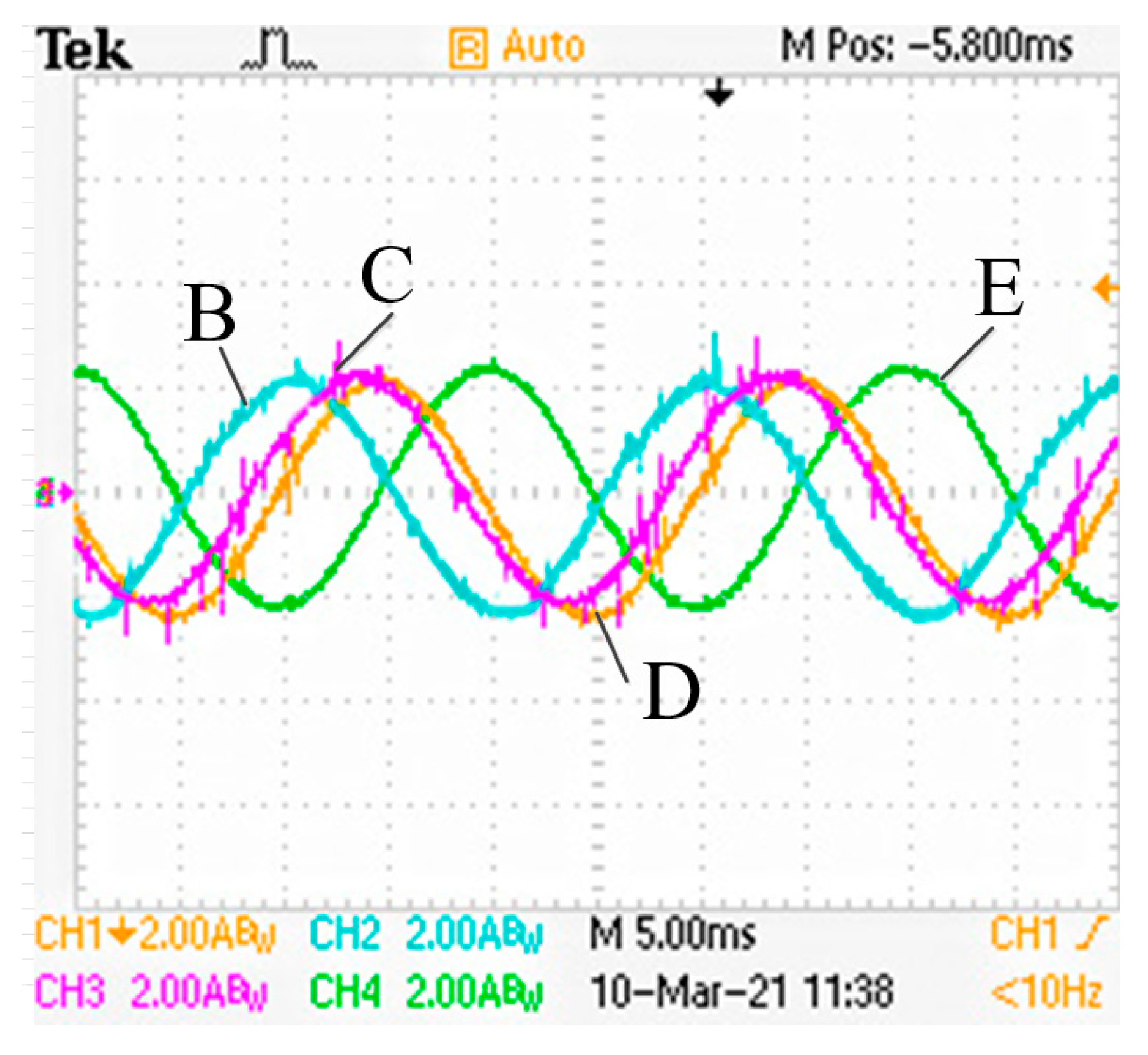
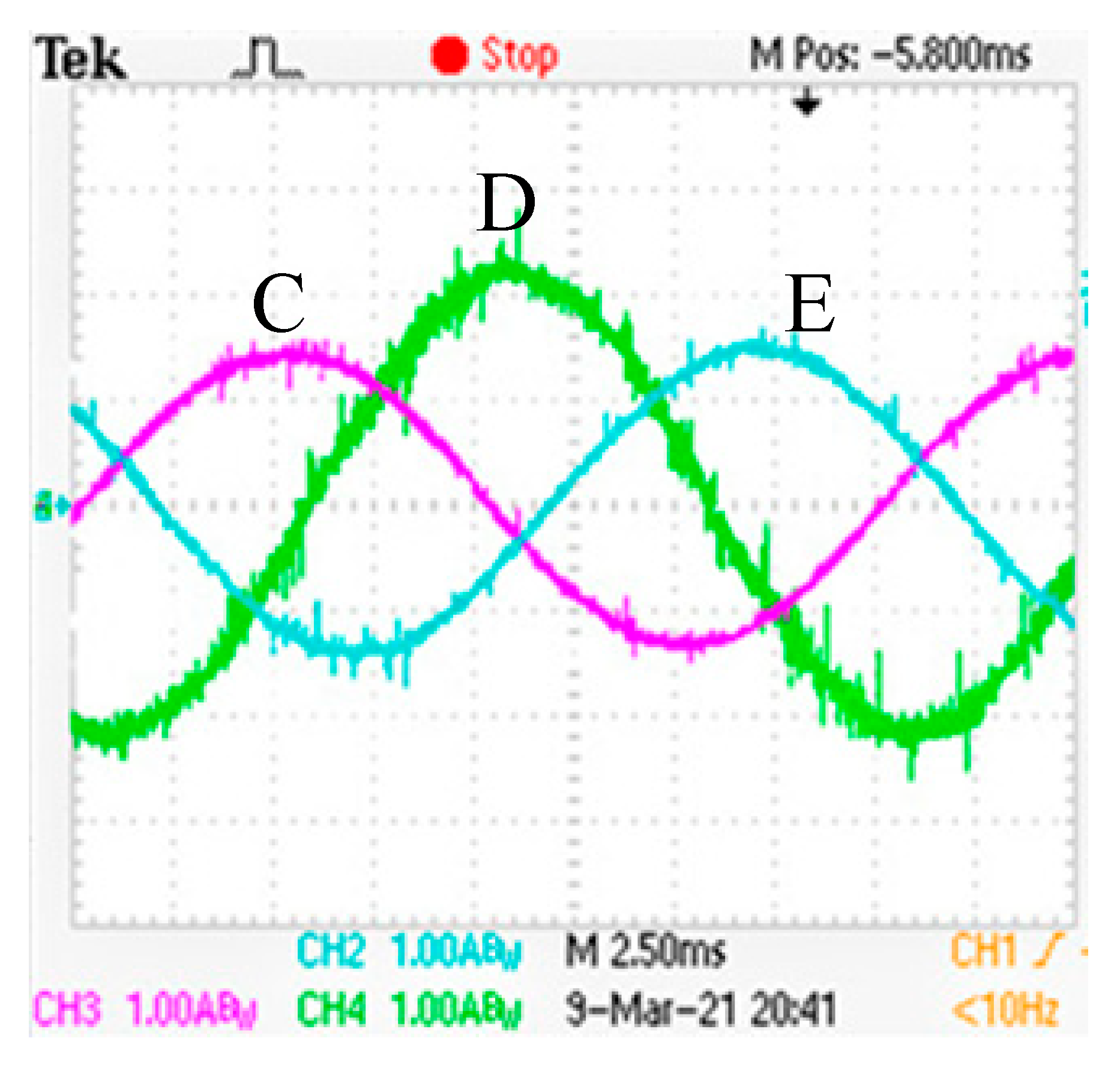
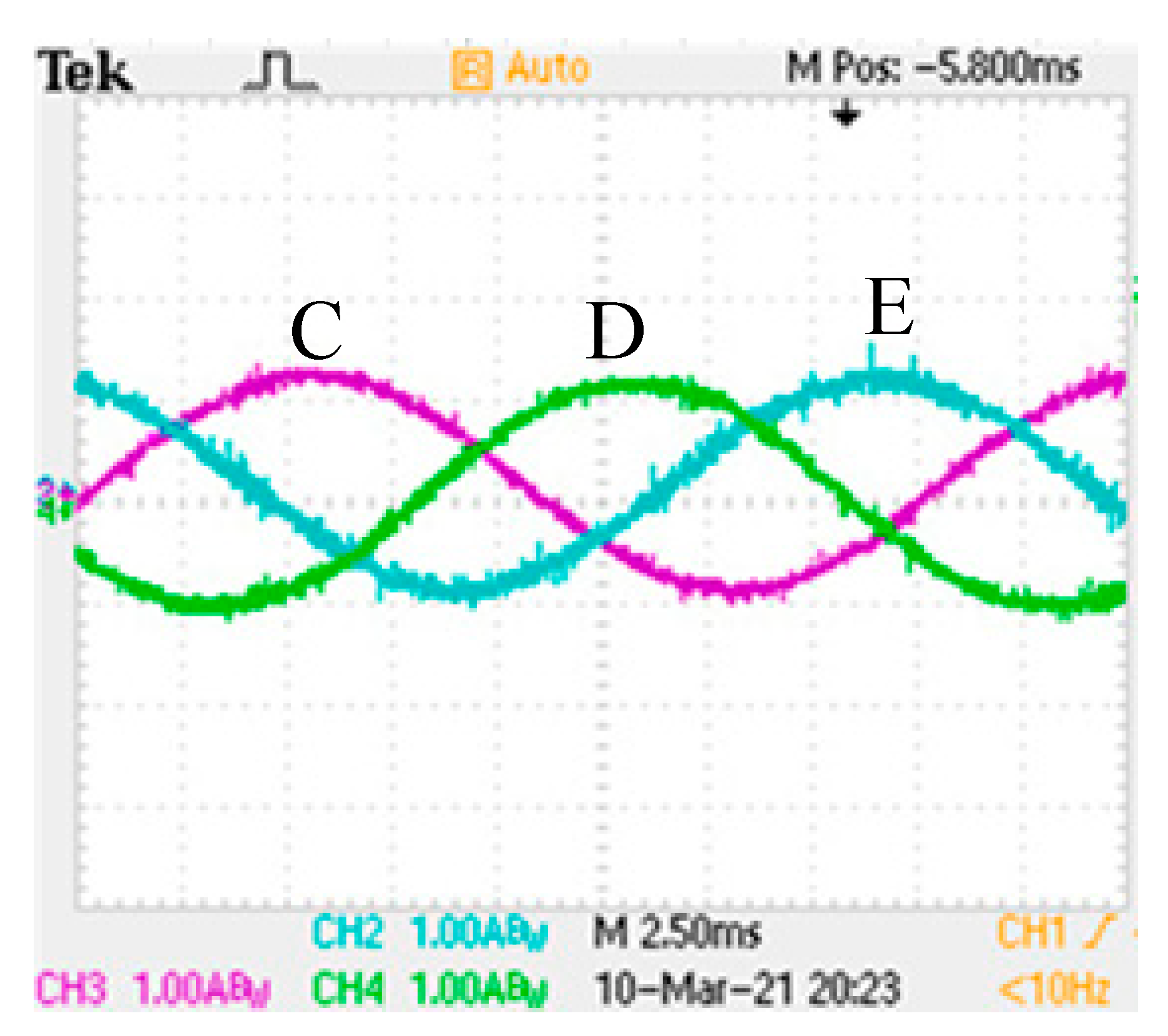


| Parameter | Unit | Value |
|---|---|---|
| Rated voltage | V | 220 |
| Stator resistance | Ω | 4.3845 |
| Rotor resistance | Ω | 5.8266 |
| Stator leakage inductance | H | 0.0185 |
| Excitation inductance | H | 0.6575 |
| Rotor leakage inductance | H | 0.0319 |
| Moment of inertia | 0.0178 |
| Parameter | Unit | Value |
|---|---|---|
| Stator inner diameter | mm | 98 |
| Stator outer diameter | mm | 175 |
| Rotor inner diameter | mm | 38 |
| Rotor outer diameter | mm | 97.5 |
| Core length | mm | 130 |
| Number of stator slots | 30 | |
| Number of slots of squirrel cage rotor | 26 | |
| Number of conductors per slot of stator winding | 57 | |
| Polar logarithm | 1 |
| Input Voltage (V) | Normal Operation (r/min) | Open Circuit Fault (r/min) | Fault Tolerant Control (r/min) |
|---|---|---|---|
| 30 V | 97 | 67 | 105 |
| 40 V | 108 | 80 | 180 |
| 50 V | 216 | 200 | 220 |
| 60 V | 463 | 458 | 564 |
| 70 V | 1385 | 588 | 600 |
| 80 V | 1430 | 686 | 1356 |
| 90 V | 1447 | 1273 | 1361 |
| 100 V | 1465 | 1308 | 1459 |
| 110 V | 1475 | 1259 | 1470 |
| Input Voltage (V) | Normal Operation (r/min) | Open Circuit Fault (r/min) | Fault Tolerant Control (r/min) |
|---|---|---|---|
| 30 V | 97 | 0 | 0 |
| 40 V | 108 | 0 | 0 |
| 50 V | 216 | 0 | 0 |
| 60 V | 463 | 0 | 50 |
| 70 V | 1385 | 66 | 230 |
| 80 V | 1430 | 105 | 588 |
| 90 V | 1447 | 130 | 988 |
| 100 V | 1465 | 149 | 1059 |
| 110 V | 1475 | 150 | 1189 |
| Input Voltage (V) | Normal Operation (r/min) | Open Circuit Fault (r/min) | Fault Tolerant Control (r/min) |
|---|---|---|---|
| 30 V | 97 | 60 | 80 |
| 40 V | 108 | 90 | 110 |
| 50 V | 216 | 108 | 189 |
| 60 V | 463 | 220 | 260 |
| 70 V | 1385 | 503 | 539 |
| 80 V | 1430 | 514 | 917 |
| 90 V | 1447 | 726 | 1262 |
| 100 V | 1465 | 710 | 1436 |
| 110 V | 1475 | 719 | 1466 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Zhao, J.; Yang, L.; Chen, H.; Luo, X.; Zhang, S. Research on Open Circuit Fault Modeling and Fault Tolerant Control Strategy of Five-Phase Induction Motor. Processes 2022, 10, 1891. https://doi.org/10.3390/pr10091891
Xu H, Zhao J, Yang L, Chen H, Luo X, Zhang S. Research on Open Circuit Fault Modeling and Fault Tolerant Control Strategy of Five-Phase Induction Motor. Processes. 2022; 10(9):1891. https://doi.org/10.3390/pr10091891
Chicago/Turabian StyleXu, Hao, Jinghong Zhao, Lv Yang, Hansi Chen, Xiangyu Luo, and Shuheng Zhang. 2022. "Research on Open Circuit Fault Modeling and Fault Tolerant Control Strategy of Five-Phase Induction Motor" Processes 10, no. 9: 1891. https://doi.org/10.3390/pr10091891





