Comprehensive Analysis and Targeting of Distillation Integrated into Overall Process Considering Operating Pressure Change
Abstract
:1. Introduction
- A comprehensive analysis for heat integration of distillation into the overall process.
- The rules to identify the best operating pressure of a distillation column.
2. Impacts of Lowering Distillation Column Pressure
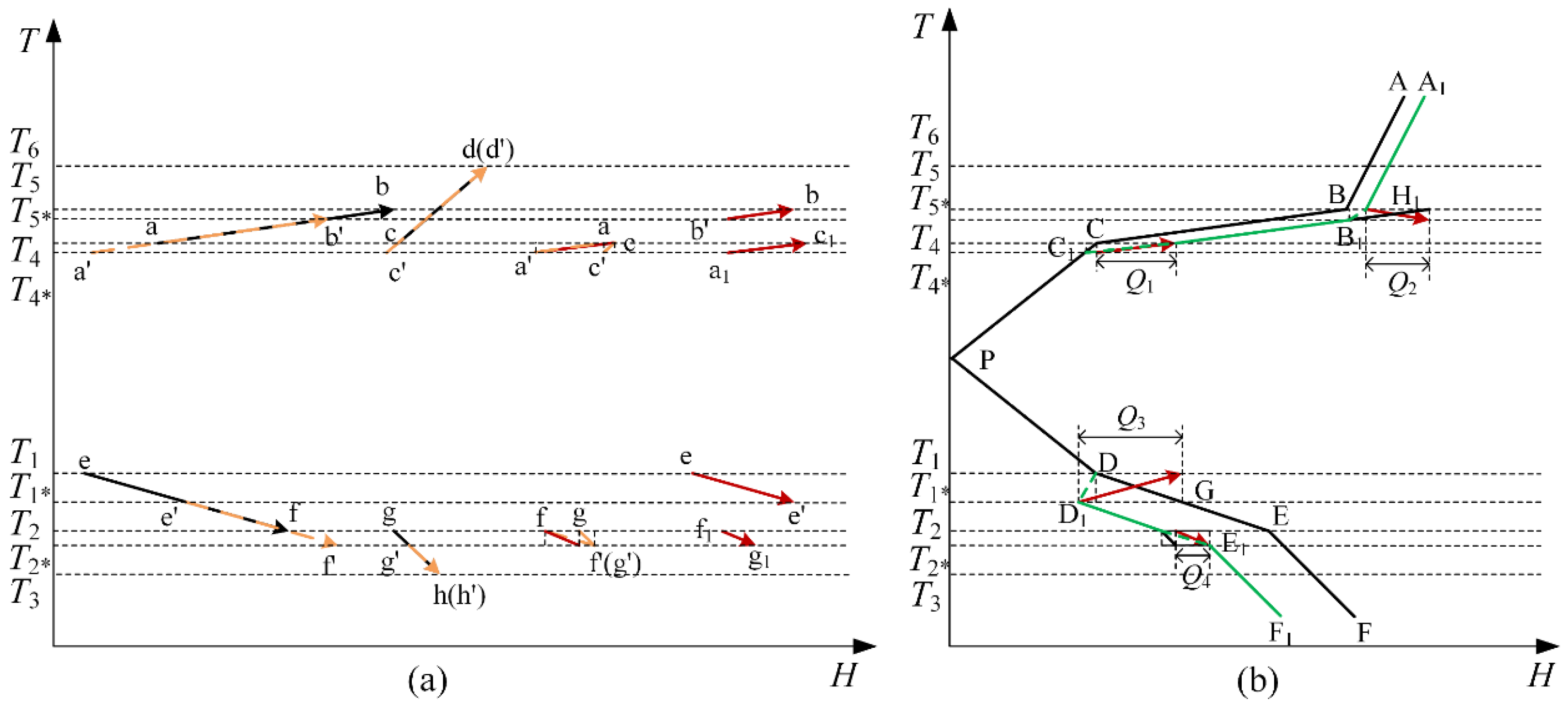
2.1. Streams Related to a Distillation Column
2.2. Changes of GCC and Pinch Temperature
2.2.1. Case 1: A Heat Source below the Pinch and a Heat Sink above the Pinch
- (1)
- If the heat flux of a point above the pinch is negative that increases the pinch temperature, the cold utility is also increased after moving the GCC to the right. If the heat flux of a point below the pinch is negative that decreases the pinch temperature, the hot utility is also increased after moving the GCC to the right. The utility increment is equal to the offset value of the GCC.
- (2)
- If there exist two points with negative heat fluxes above and below the pinch point, the heat fluxes of these two points should be compared. The point with the smaller heat flux becomes the new pinch point. The offset value of the GCC is equal to the absolute value of the heat flux at this point.
2.2.2. Case 2: Two Heat Sources
2.2.3. Case 3: Two Heat Sinks
2.2.4. Case 4: A Heat Sink below the Pinch and a Heat Source above the Pinch
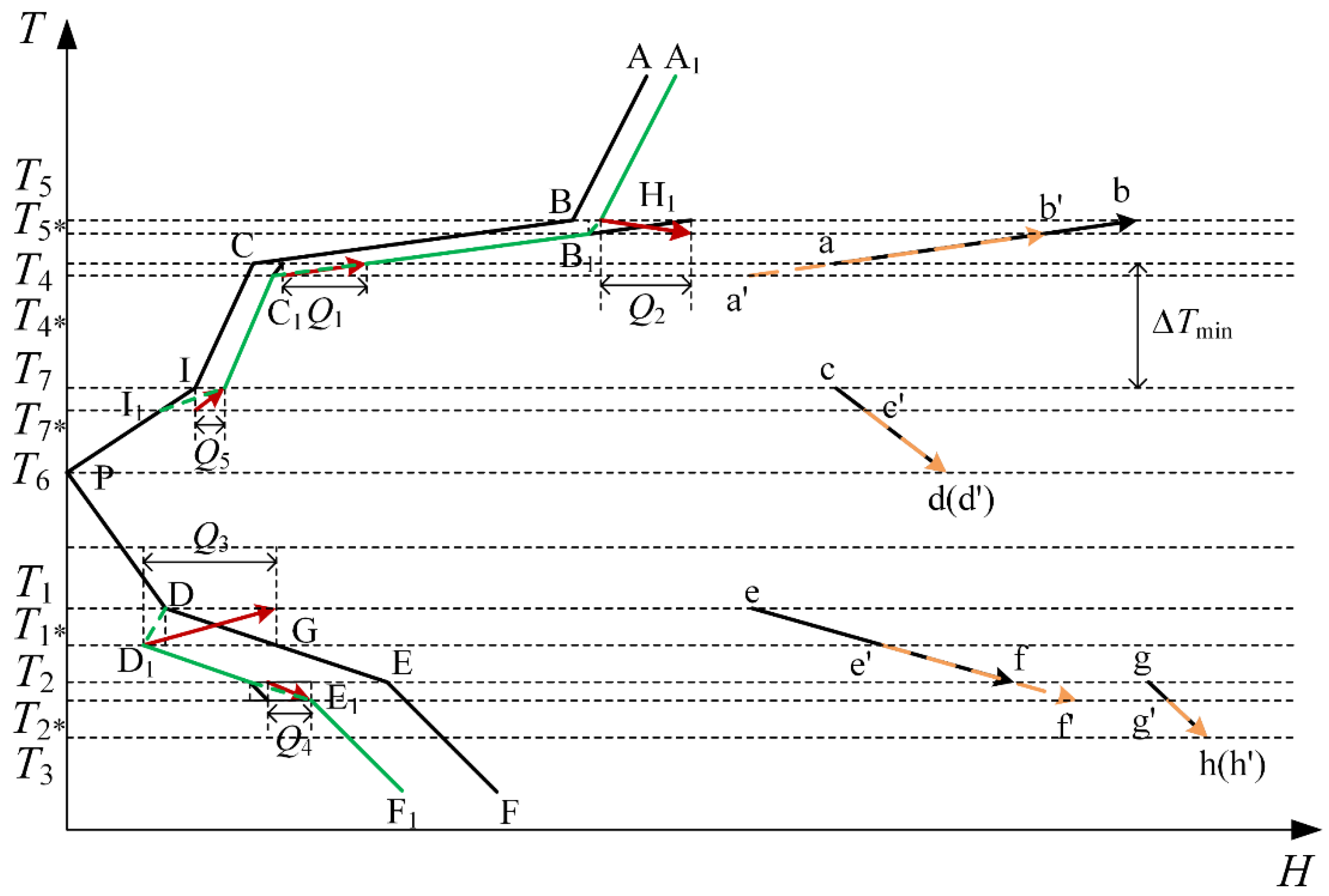
2.3. Identify the Best Operating Pressure
3. Case Study
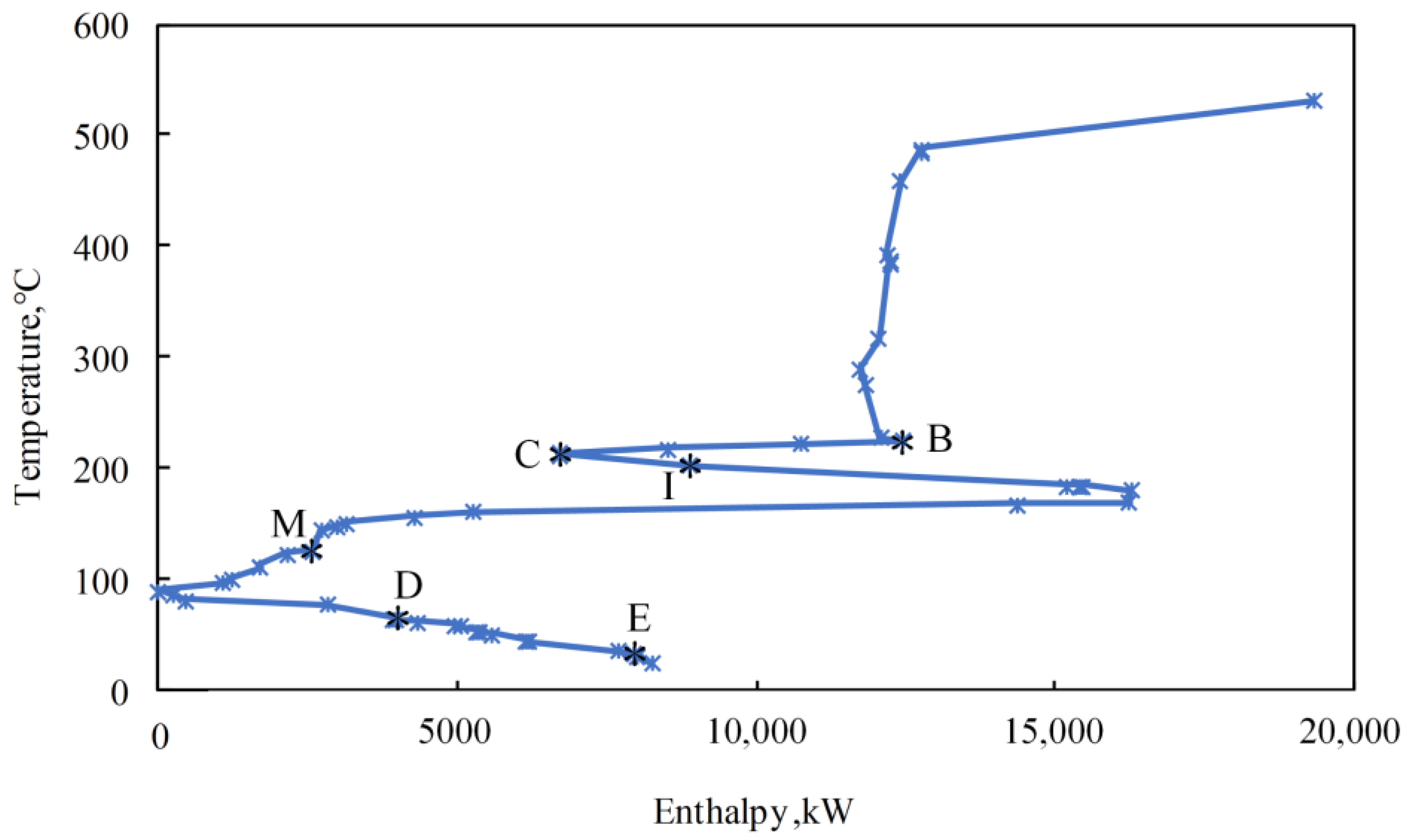
3.1. Process Description and Pinch Analysis
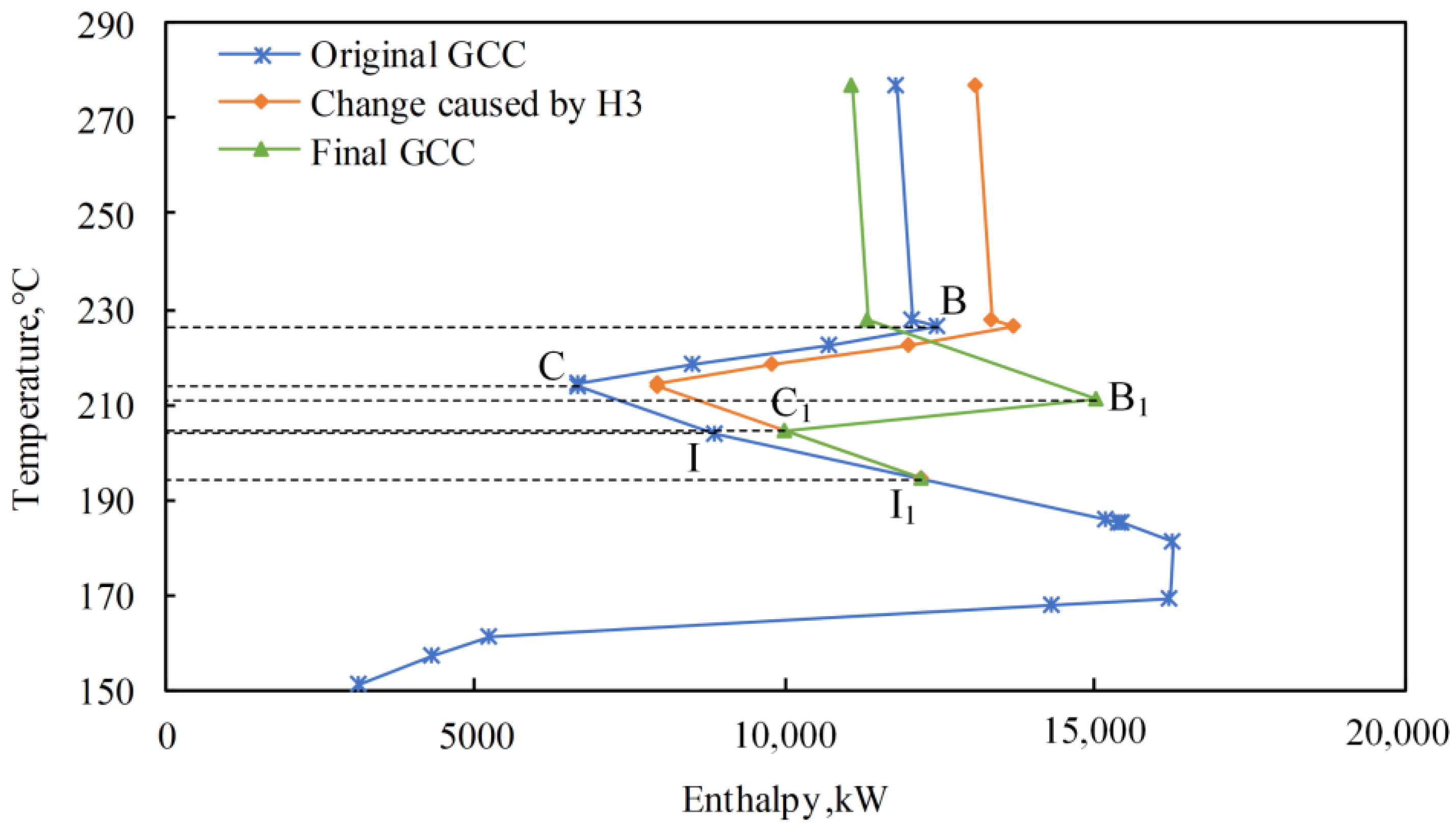
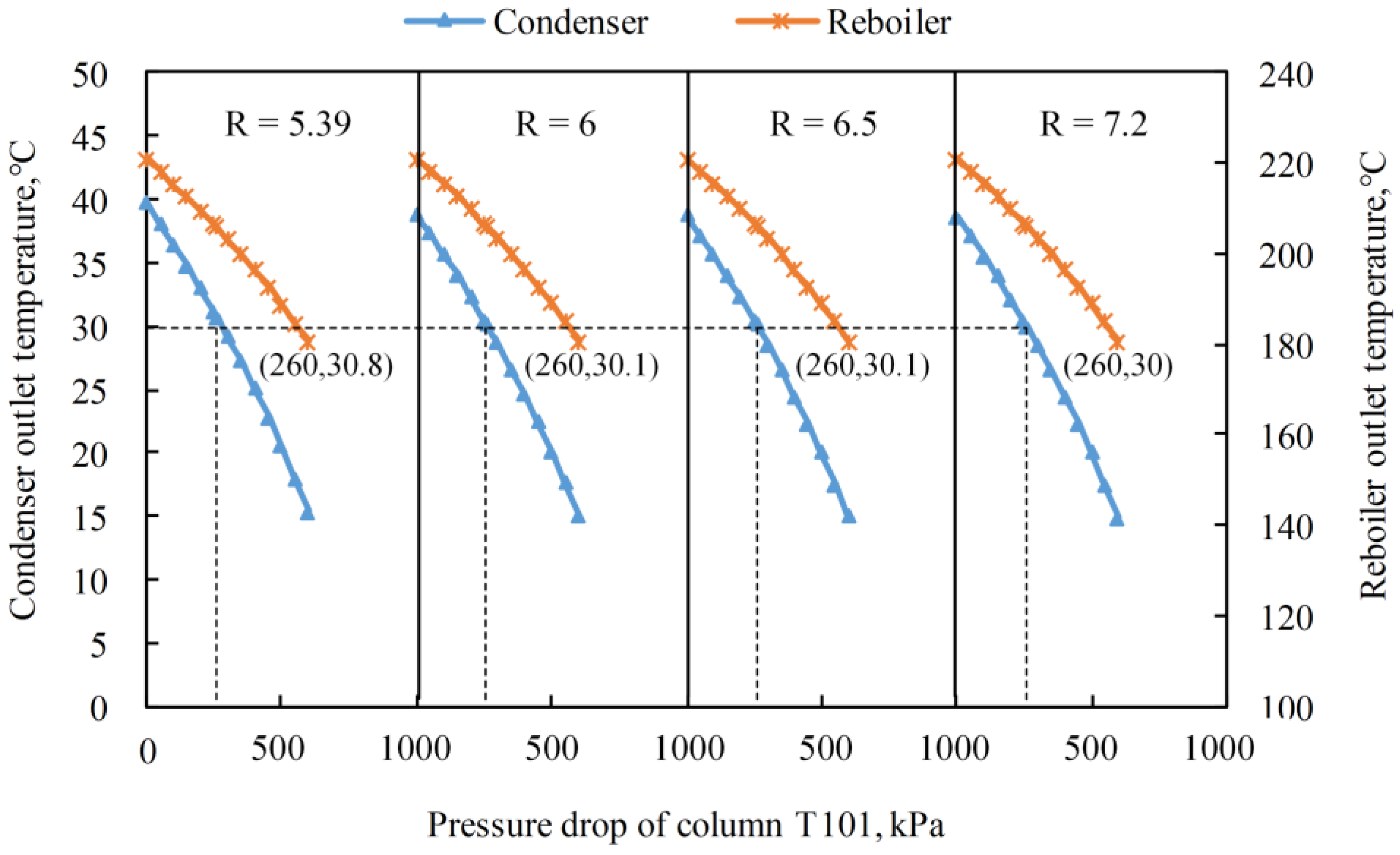
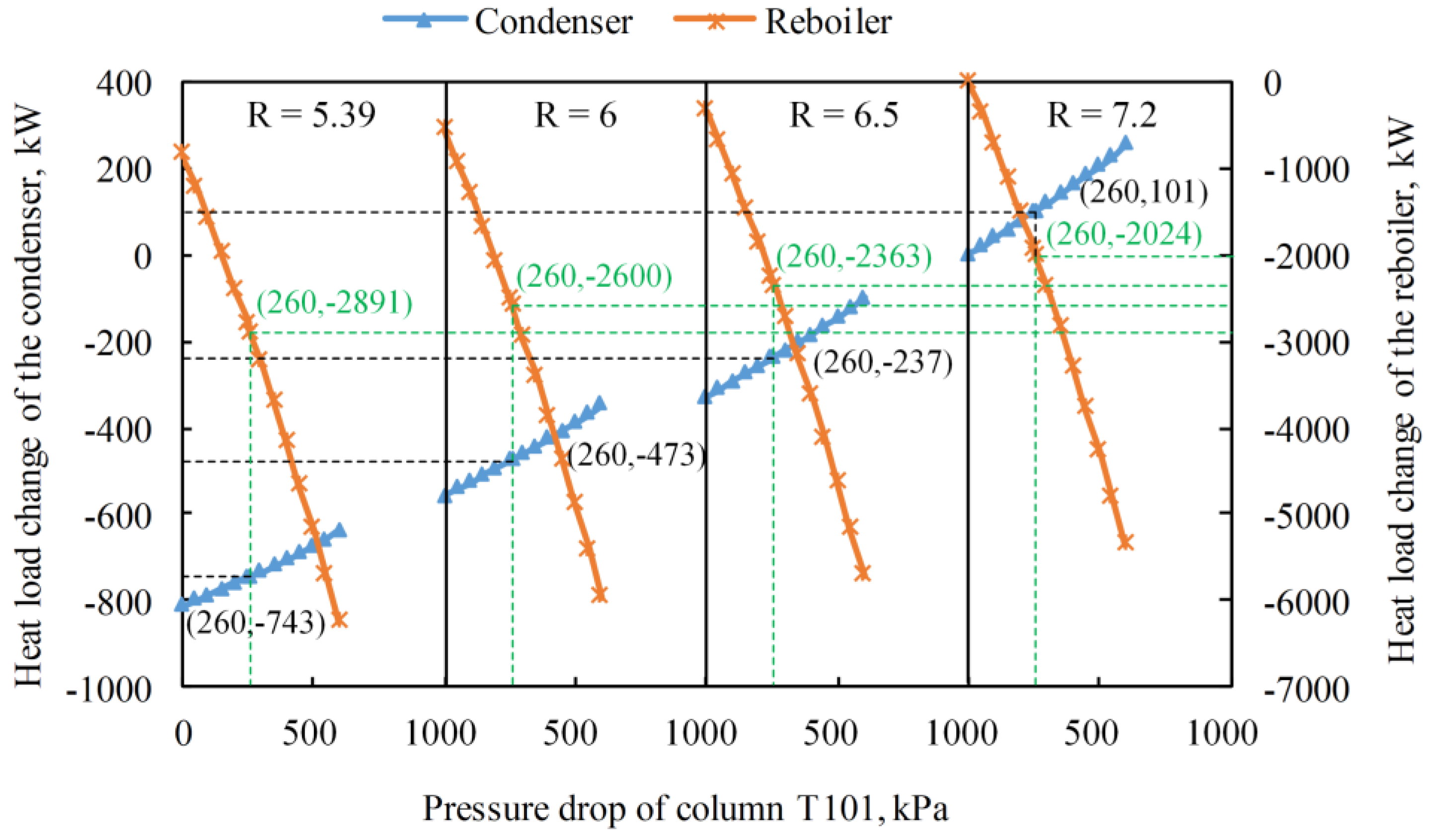
3.2. Effects of Lowering Operating Pressure
3.3. Comparison and Discussion
4. Conclusions
- (1)
- Above the pinch point, no matter whether the bottom outlet stream is a heat source or a heat sink, it always increases the hot utility if lowering the operating pressure. At this point, when the decrease in hot utility caused by the reboiled stream is greater than the increase caused by the bottom outlet stream, the total hot utility of the overall process can be reduced.
- (2)
- Below the pinch point, no matter whether the overhead outlet stream is a heat source or a heat sink, it always reduces the cold utility. In this case, when the increase in cold utility caused by the condensed stream is less than the decrease caused by the overhead outlet stream, the total cold utility of the overall process can be reduced. When the overhead outlet stream is a heat source, at most one new pinch point occurs. When it is a heat sink, two new pinch points may occur.
- (3)
- When the pinch temperature remains unchanged, the changes of GCC and utilities above and below the pinch point are independent from each other.
- (4)
- When the pinch temperature changes, the subsections of GCC above and below the pinch point are interactional. The heat and cold utilities of the overall process are affected by the offset value of GCC.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fang, J.; Cheng, X.; Li, Z.; Li, H.; Li, C. A review of internally heat integrated distillation column. Chin. J. Chem. Eng. 2019, 27, 1272–1281. [Google Scholar] [CrossRef]
- Markowski, M.; Alabrudzinski, S.; Storczyk, S. Heat and mass exchanger model for hybrid heat integrated distillation systems (HHIDiS). Appl. Therm. Eng. 2020, 174, 115249. [Google Scholar] [CrossRef]
- Walk, M.; Hamacher, J.; Downs, J.J.; Miller, S.M.; Owens, S.; Eldridge, R.B. Validation of Differential Temperature Control for a Dividing Wall Distillation Column. Ind. Eng. Chem. Res. 2021, 60, 1341–1355. [Google Scholar] [CrossRef]
- García-García, J.C.; Marmolejo-Correa, D.; Cárdenas-Guerra, J.C.; Morales-Rodriguez, R. Exergy Analysis of an Extractive Distillation Column for Reducing Energy Consumption in a Bioethanol Production Process. Comput. Aided Chem. Eng. 2018, 43, 513–518. [Google Scholar]
- Zhang, S.; Luo, Y.; Ma, Y.; Yuan, X. Simultaneous optimization of nonsharp distillation sequences and heat integration networks by simulated annealing algorithm. Energy 2018, 162, 1139–1157. [Google Scholar] [CrossRef]
- Manyele, S. Analysis of the effect of feed composition and thermal conditions on distillation plant performance using a computer model. J. Chem. Eng. Mater. Sci. 2021, 12, 40–63. [Google Scholar]
- Yang, J.; Yang, M.; Feng, X.; Wang, Y. A Hybrid Method for Integration of Heat Pump Assisted Distillation System with Intermediate Reboiler/condenser. Comput. Aided Chem. Eng. 2020, 48, 1861–1866. [Google Scholar]
- An, R.; Chen, S.; Hou, S.; Zhu, Y.; Li, C.; Zhu, X.; Liu, R.; An, W. Simulation and design of a heat-integrated double-effect reactive distillation process for propylene glycol methyl ether production. Chin. J. Chem. Eng. 2022, in press. [CrossRef]
- Wang, N.; Ye, Q.; Chen, L.; Zhang, H.; Zhong, J. Application of heat pump technology to recover 1,4-dioxane and acetonitrile from wastewater via triple-column distillation. Appl. Therm. Eng. 2021, 190, 116802. [Google Scholar] [CrossRef]
- Zin, R.M.; Abidin, M.A.; Shahruddin, M.Z. Energy Analysis and Remixing Effect of Thermal Coupling Petlyuk Column for Natural Gas Liquid (NGL) Fractionation Train. Int. J. Renew. Energy Dev. 2021, 10, 459–469. [Google Scholar] [CrossRef]
- Caballero, J.A.; Grossmann, I.E. Optimal synthesis of thermally coupled distillation sequences using a novel MILP approach. Comput. Chem. Eng. 2014, 61, 118–135. [Google Scholar] [CrossRef]
- Caballero, J.A.; Javaloyes-Anton, J.; Labarta, J.A. Structural Considerations in Zeotropic Distillation Sequences with Multiple Feeds. Comput. Chem. Eng. 2021, 154, 107475. [Google Scholar] [CrossRef]
- Smith, R. Chemical Process Design and Integration, 2nd ed.; John Wiley & Sons Inc.: Chichester, UK, 2005. [Google Scholar]
- Linnhoff, B.; Dunford, H.; Smith, R. Heat integration of distillation columns into overall processes. Chem. Eng. Sci. 1983, 38, 1175–1188. [Google Scholar] [CrossRef]
- Smith, R.; Linnhoff, B. The Design of Separators in the Context of Overall Processes. Chem. Eng. Res. Des. 1988, 66, 195–228. [Google Scholar]
- Bandyopadhyay, S. Thermal Integration of a Distillation Column Through Side-Exchangers. Chem. Eng. Res. Des. 2007, 85, 155–166. [Google Scholar] [CrossRef]
- Sun, M.; Fu, D.; Sun, L. Heat exchanger network retrofit for optimization of crude distillation unit using pinch analysis. China Pet. Process. Petrochem. Technol. 2021, 23, 31–40. [Google Scholar]
- Kravanja, P.; Modarresi, A.; Friedl, A. Heat integration of biochemical ethanol production from straw—A case study. Appl. Energy 2013, 102, 32–43. [Google Scholar] [CrossRef]
- Yang, M.; Feng, X.; Liu, G. Heat integration of heat pump assisted distillation into the overall process. Appl. Energy 2016, 162, 1–10. [Google Scholar] [CrossRef]
- Zhang, D.; Li, Y.; Sun, H.; Liu, G. Energy recovery enhancement of heat exchanger network by mixing and azeotrope formation—ScienceDirect. Chem. Eng. Sci. 2020, 228, 115992. [Google Scholar] [CrossRef]
- Aggarwal, A.; Floudast, C.A. Synthesis of heat integrated nonsharp distillation sequences. Comput. Chem. Eng. 1992, 16, 89–108. [Google Scholar] [CrossRef]
- Wang, K.; Qian, Y.; Yuan, Y.; Yao, P. Synthesis and optimization of heat integrated distillation systems using an improved genetic algorithm. Comput. Chem. Eng. 1998, 23, 125–136. [Google Scholar] [CrossRef]
- Lashkajani, K.H.; Ghorbani, B.; Amidpour, M.; Hamedi, M.H. Superstructure optimization of the olefin separation system by harmony search and genetic algorithms. Energy 2016, 99, 288–303. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, M.; Zhao, L.; Du, W.; Zhong, W.; Qian, F. Simultaneous Optimization and Heat Integration of an Aromatics Complex with a Surrogate Model. Ind. Eng. Chem. Res. 2021, 60, 3633–3647. [Google Scholar] [CrossRef]
- Fan, Y.; Ye, Q.; Cen, H.; Chen, J.; Liu, T. Design and optimization of reactive distillation processes for synthesis of isopropanol based on self-heat recuperation technology. Chem. Eng. Res. Des. 2019, 147, 171–186. [Google Scholar] [CrossRef]
- Van, D.; Kjelstrup, S. Improving the Heat Integration of Distillation Columns in a Cryogenic Air Separation Unit. Ind. Eng. Chem. Res. 2011, 50, 9324–9338. [Google Scholar]
- Zhao, F.; Xu, Z.; Zhao, J.; Wang, J.; Hu, M.; Li, X.; Zhu, Z.; Cui, P.; Wang, Y.; Ma, Y. Process design and multi-objective optimization for separation of ternary mixtures with double azeotropes via integrated quasi-continuous pressure-swing batch distillation. Sep. Purif. Technol. 2021, 276, 119288. [Google Scholar] [CrossRef]
- Pyrgakis, K.A.; Ioannis, K.P.; Kokossis, A.C. A MILP Transshipment Model to Integrate and Re-Engineer Distillation Columns into Overall Processes. Comput. Aided Chem. Eng. 2015, 37, 2015–2020. [Google Scholar]
- Zhang, D.; Liu, G. Integration of heat exchanger network considering the pressure variation of distillation column. Appl. Therm. Eng. 2017, 116, 777–783. [Google Scholar] [CrossRef]






| Location | Variations of Heat Flux at Each Point | Pinch Temperature | Variations of Utilities |
|---|---|---|---|
| Above the pinch | Q2 < Q1 | Unchanged | (increase) |
| Q2 = Q1 | Unchanged | (unchanged) | |
| Q2 > Q1 and Q2 − Q1 < QB | Unchanged | (decrease) | |
| Q2 > Q1 and Q2 − Q1 = QB | Double pinch points | ||
| Q2 > Q1 and Q2 − Q1 > QB | Raised | (decrease) | |
| Below the pinch | Q3 < QG | Unchanged | |
| Q3 = QG | Double pinch points | ||
| Q3 > QG | Reduced |
| Location | Variations of Heat Flux at Each Point | Pinch Temperature | Variations of Hot Utility |
|---|---|---|---|
| Above the pinch | Q2 < Q1 + Q5 | Unchanged | (increase) |
| Q2 = Q1 + Q5 | Unchanged | (unchanged) | |
| Q2 > Q1 + Q5 and Q2 − (Q1 + Q5) < QB | Unchanged | (decrease) | |
| Q2 > Q1 + Q5 and Q2 − (Q1 + Q5) = QB | Double pinch points | ||
| Q2 > Q1 + Q5 and Q2 − (Q1 + Q5) > QB | Raised | (decrease) |
| Location | Variations of Heat Flux at Each Point | Pinch Temperature | Variations of Cold Utility | |
|---|---|---|---|---|
| Below the pinch | Q6 < QK and Q3 + Q6 < QL | Unchanged | ||
| Q6 < QK and Q3 + Q6 = QL | Double pinch points (the original and the second) | |||
| Q6 < QK and Q3 + Q6 > QL | Reduced (the second pinch point) | |||
| Q6 = QK and Q3 + Q6 < QL | Double pinch points (the original and the first) | |||
| Q6 = QK and Q3 + Q6 = QL | Three pinch points | |||
| Q6 = QK and Q3 + Q6 > QL | Reduced (the second pinch point) | |||
| Q6 > QK and Q3 + Q6 < QL | Reduced (the first pinch point) | |||
| Q6 > QK and Q3 + Q6 = QL | ||||
| Q6 > QK and Q3 + Q6 > QL | ∆QS4 > ∆QS5 | Reduced (the first pinch point) | ||
| ∆QS4 = ∆QS5 | Double pinch points (the first and the second) | |||
| ∆QS4 < ∆QS5 | Reduced (the second pinch point) | |||
| Stream Number | Heat Exchanger | Initial Temperature/°C | Final Temperature/°C | Heat Load/kW |
|---|---|---|---|---|
| H1 | E–201 | 493.4 | 117.0 | 58,300 |
| H2 | E–202 | 490.8 | 190.0 | 42 |
| H3 | E–105 | 208.5 | 132.3 | 9914 |
| H4 | E–102 | 156.3 | 102.6 | 6031 |
| H5 | E–100 | 150.0 | 70.0 | 4692 |
| H6 | A–201 | 117.2 | 42.0 | 7863 |
| H7 | A–103 | 87.4 | 30.5 | 4052 |
| H8 | E–104 | 69.1 | 59.4 | 2152 |
| A–102 | 59.4 | 38.7 | 1376 | |
| C1 | E–201 | 85.5 | 453.9 | 58,300 |
| F–201 | 453.9 | 525.9 | 11,070 | |
| C2 | F–102 | 208.5 | 221.1 | 8539 |
| C3 | E–202 | 27.0 | 180.6 | 42 |
| C4 | E–102 | 48.7 | 102.0 | 6031 |
| E–105 | 102.0 | 179.8 | 9914 | |
| C5 | F–103 | 156.3 | 164.4 | 9437 |
| C6 | E–104 | 40.0 | 58.0 | 2152 |
| T101 | T102 | ||
|---|---|---|---|
| Number of Stages | 40 | 40 | |
| Feed location | 21 | 21 | |
| Feed | Naphtha | Gasoline | |
| Overhead product | Light components | Light naphtha | |
| Bottom product | Gasoline | Refined naphtha | |
| Product specifications | Overhead liquid | C5 ≤ 3.0 vol% | C4 ≤ 12.5 wt % C6 ≤ 45 wt % benzene ≤ 3.6 wt % |
| Overhead waste gas | H2S ≤ 0.1 vol% | - | |
| Bottom product | - | Initial boiling point in 85–89 °C | |
| Stream Number | Change | Initial Temperature/°C | Initial Temperature on the GCC/°C | Final Temperature/°C | Final Temperature on the GCC/°C | Pressure/kPa | Heat Load/kW |
|---|---|---|---|---|---|---|---|
| H3 | Before | 208.5 | 203.5 | 132.3 | 127.3 | 1241 | 9914 |
| After | 199.3 | 194.3 | 132.3 | 127.3 | 981 | 8648 | |
| H8 | Before | 69.1 | 64.1 | 38.7 | 33.7 | 1187 | 3528 |
| After | 59.4 | 54.4 | 30.0 | 25.0 | 927 | 3630 | |
| C2 | Before | 208.5 | 213.5 | 221.1 | 226.1 | 1241 | 8539 |
| After | 199.3 | 204.3 | 206.1 | 211.1 | 981 | 6515 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, W.; Yang, M.; Feng, X. Comprehensive Analysis and Targeting of Distillation Integrated into Overall Process Considering Operating Pressure Change. Processes 2022, 10, 1861. https://doi.org/10.3390/pr10091861
Duan W, Yang M, Feng X. Comprehensive Analysis and Targeting of Distillation Integrated into Overall Process Considering Operating Pressure Change. Processes. 2022; 10(9):1861. https://doi.org/10.3390/pr10091861
Chicago/Turabian StyleDuan, Wenting, Minbo Yang, and Xiao Feng. 2022. "Comprehensive Analysis and Targeting of Distillation Integrated into Overall Process Considering Operating Pressure Change" Processes 10, no. 9: 1861. https://doi.org/10.3390/pr10091861





