Research on Position Control of an Electro–Hydraulic Servo Closed Pump Control System
Abstract
:1. Introduction
2. Principle of Pump Control System
3. Mathematical Model
3.1. Servo Motor
3.2. Fixed Displacement Pump
3.3. Double-Acting Symmetrical Hydraulic Cylinder
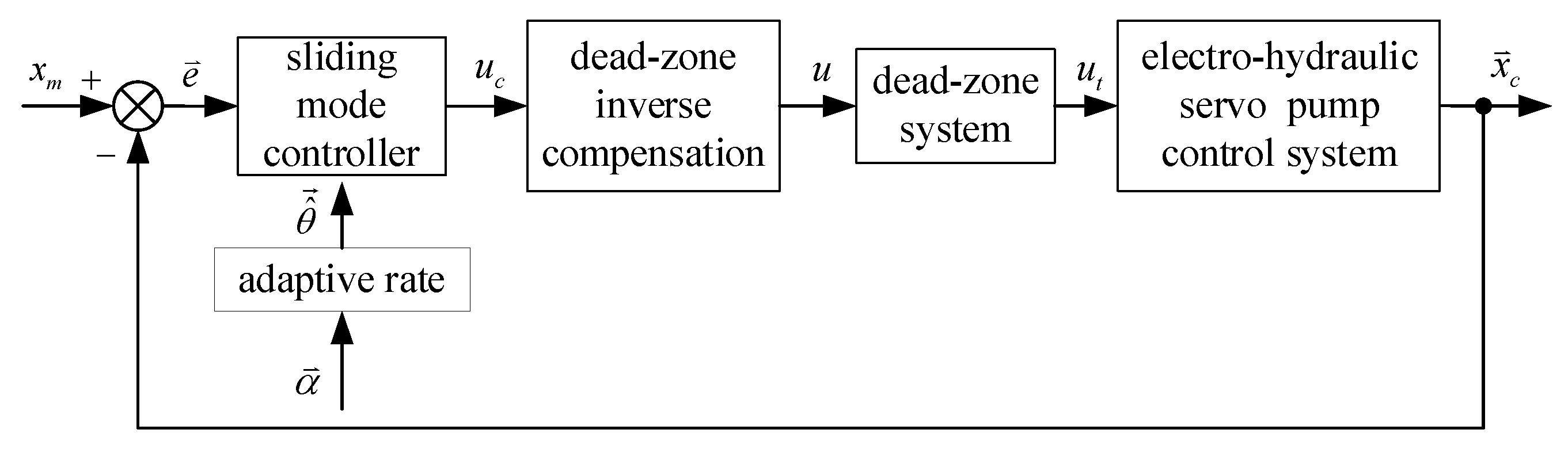
4. Controller Design
4.1. Adaptive Backstepping Sliding Mode Controller
- 1.
- Step 1
- 2.
- Step 2
- 3.
- Step 3
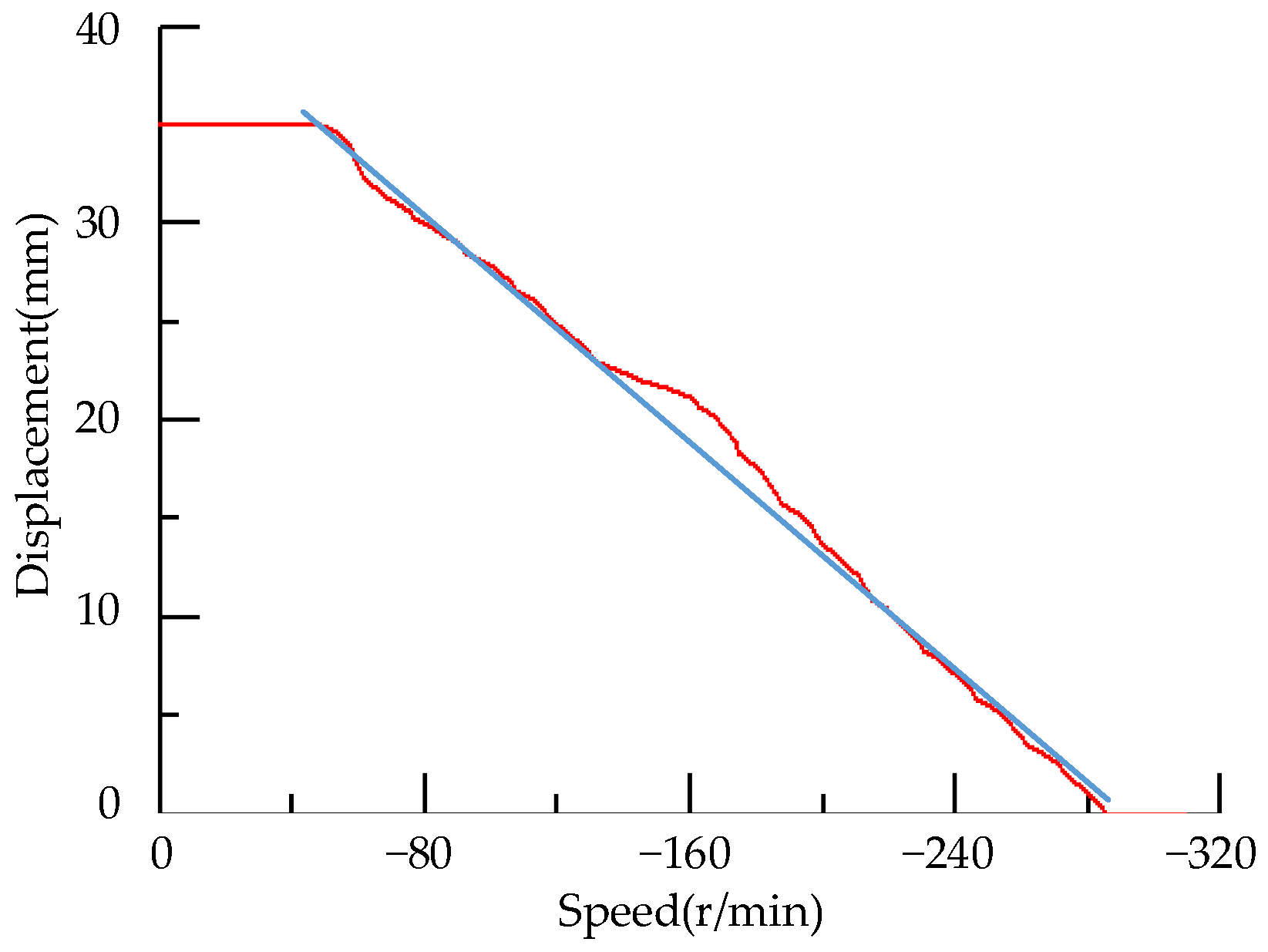
4.2. Dead-Zone Inverse Compensation Controller
- 1.
- Compensation principle
- 2.
- Design process
5. Engineering Experiment Results and Analysis
5.1. Engineering Experiment Elatform
5.2. Experiment Analysis
6. Conclusions
- The mathematical model of the electro–hydraulic servo pump control system was established, and the position output transfer function of the system was deduced.
- Based on the backstepping recursion criterion, an adaptive backstepping sliding mode controller was designed by introducing the sliding mode control principle, and the dead-zone inverse compensation controller was designed by constructing a smooth dead-zone inverse function. Then the two controllers formed a system series controller and were applied to the position control of the pump control system.
- Experimental analysis shows that the control strategy proposed in this paper yields good control performance in practical applications. Compared with the traditional PID control, there is no excessive overshoot before the steady state, the steady-state control accuracy can reach ±0.002 mm, and the time required to reach the steady state is 1–2 s shorter.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hong, W.; Wang, S.; Tomovic, M.M.; Liu, H.; Shi, J.; Wang, X. A Novel Indicator for Mechanical Failure and Life Prediction Based on Debris Monitoring. IEEE Trans. Reliab. 2017, 66, 161–169. [Google Scholar] [CrossRef]
- Lu, C.; Wang, S.; Makis, V. Fault Severity Recognition of Aviation Piston Pump Based on Feature Extraction of EEMD Paving and Optimized Support Vector Regression Model. Aerosp. Sci. Technol. 2017, 67, 105–117. [Google Scholar] [CrossRef]
- Guo, S.; Chen, J.; Lu, Y.; Wang, Y.; Dong, H. Hydraulic piston pump in civil aircraft: Current status future directions and critical technologies. Chin. J. Aeronaut. 2020, 33, 16–30. [Google Scholar] [CrossRef]
- Xu, C.; Liu, G.; Xu, G.; Li, F.; Zhai, Y. The depth and pitch control of submarines based on the pump-hydraulic servo. Chin. J. Ship Res. 2017, 12, 116–123. [Google Scholar]
- Li, Y.; Fan, R.; Yang, L.; Zhao, B.; Quan, L. Research status and development trend of intelligent excavators. Mech. Eng. 2020, 56, 165–178. [Google Scholar]
- Lee, J.; Oh, K.; Yi, K. A novel approach to design and control of an active suspension using linear pump control-based hydraulic system. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 234, 1224–1248. [Google Scholar] [CrossRef]
- Grimminger, F.; Meduri, A.; Khadiv, M.; Viereck, J.; Wüthrich, M.; Naveau, M.; Righetti, L. An open torque-controlled modular robot architecture for legged locomotion research. IEEE Robot. Autom. Lett. 2020, 5, 3650–3657. [Google Scholar] [CrossRef]
- Chaudhuri, A.; Wereley, N. Compact hybrid electro–hydraulic actuators using smart materials: A review. J. Intell. Mater. Syst. Struct. 2012, 23, 597–634. [Google Scholar] [CrossRef]
- Song, Y.; Tai, M.; Wang, R.; Chen, L.; Zhu, Y. Experimental research on a dual magnetostrictive axial plunger pumps-based electro-hydrostatic actuator. Chin. Hydraul. Pneum. 2020, 7, 36–41. [Google Scholar]
- Jing, C.; Xu, H.; Jiang, J. Dynamic Surface Disturbance Rejection Control for Electro–Hydraulic Load Simulator. Mech. Syst. Signal Process. 2019, 134, 106293–106306. [Google Scholar] [CrossRef]
- Sani, S.; Chaji, A. Output Feedback Nonlinear Control of Double-Rod Hydraulic Actuator using Extended Kalman Filter. In Proceedings of the IEEE 4th International Conference on Knowledge-Based Engineering and Innovation (KBEI), Tehran, Iran, 22–22 December 2017; pp. 0349–0354. [Google Scholar]
- Zad, H.S.; Ulasyar, A.; Zohaib, A. Robust Model Predictive Position Control of Direct Drive Electro–Hydraulic Servo System. In Proceedings of the 2016 International Conference on Intelligent Systems Engineering (ICISE), Islamabad, Pakistan, 15–17 January 2016. [Google Scholar]
- Ji, X.; Wang, C.; Chen, S.; Zhang, Z. Sliding mode backstepping control method for valve-controlled electro–hydraulic Position Servo System. J. Cent. South Univ. Sci. Technol. 2020, 51, 1518–1525. [Google Scholar]
- Ji, X.; Wang, C.; Zhang, Z.; Chen, S.; Guo, X. Nonlinear adaptive position control of hydraulic servo system based on sliding mode back-stepping design method. Proc. Inst. Mech. Eng. 2021, 235, 0349–0354. [Google Scholar] [CrossRef]
- Han, S.; Jiao, Z.; Wang, C.; Shang, Y.; Shi, Y. Fractional integral sliding mode nonlinear control of electro–hydraulic flight turntable. J. Beijing Univ. Aeronaut. Astronaut. 2014, 40, 1411–1416. [Google Scholar]
- Helian, B.; Chen, Z.; Yao, B.; Yu, L.; Li, C. Accurate Motion Control of a Direct-drive Hydraulic System with an Adaptive Nonlinear Pump Flow Compensation. IEEE ASME Trans. Mechatron. 2020, 26, 2593–2603. [Google Scholar] [CrossRef]
- Tri, N.M.; Nam, D.N.C.; Park, H.G.; Ahn, K.K. Trajectory control of an electro hydraulic actuator using an iterative backstepping control scheme. Mechatronics 2015, 29, 96–102. [Google Scholar] [CrossRef]
- Shang, X.; Zhou, H.; Yang, H. Research Status of Active Control Method for Fluid Pulsation in Hydraulic System. J. Mech. Eng. 2019, 55, 216–226. [Google Scholar]
- Zhu, Y.; Sun, Y.; Chen, G. Simulation Research on Hydraulic Loading System of Wind Turbine Based on Particle Swarm PID Control. In Proceedings of the IEEE Conference on Telecommunications, Optics and Computer Science (TOCS), Shenyang, China, 11–13 December 2020; pp. 385–388. [Google Scholar]
- Liem, D.T.; Truong, D.Q.; Park, H.G.; Ahn, K.K. A Feedforward Neural Network Fuzzy Grey Predictor-based Controller for Force Control of an Electro–hydraulic Actuator. Int. J. Precision Eng. Manuf. 2016, 17, 309–321. [Google Scholar] [CrossRef]
- Guo, P.; Li, Y.; Li, J.; Zhang, B.; Wu, X. Design of primary mirror position control system for large aperture telescope. Acta Opt. Sin. 2020, 40, 122–128. [Google Scholar]
- Maghareh, A.; Silva, C.E.; Dyke, S.J. Parametric model of servo-hydraulic actuator coupled with a nonlinear system: Experimental validation. Mech. Syst. Signal Process. 2018, 104, 663–672. [Google Scholar] [CrossRef]
- Hao, Y.; Xia, L.; Gem, L.; Wang, X.; Quan, L. Research on position control characteristics of hybrid linear drive system. Trans. Chin. Soc. Agric. Mach. 2020, 51, 379–385. [Google Scholar]
- Kaddissi, C.; Kenne, J.P.; Saad, M. Indirect Adaptive Control of an Electrohydraulic Servo System Based on Nonlinear Backstepping. IEEE/ASME Trans. Mechatron. 2011, 16, 1171–1177. [Google Scholar] [CrossRef]
- Ba, D.X.; Ahn, K.K.; Truong, D.Q.; Park, H.G. Integrated model-based backstepping control for an electro–hydraulic system. Int. J. Precis. Eng. Manuf. 2016, 17, 565–577. [Google Scholar] [CrossRef]
- Chen, G.; Liu, H.; Jia, P.; Qiu, G.; Yu, H.; Yan, G.; Zhang, J. Position Output Adaptive Backstepping Control of Electro–Hydraulic Servo Closed-Pump Control System. Processes 2021, 9, 2209. [Google Scholar] [CrossRef]
- Yin, X.; Zhang, W.; Jiang, Z.; Pan, L. Adaptive robust integral sliding mode pitch angle control of an electro–hydraulic servo pitch system for wind turbine. Mech. Syst. Signal Process. 2019, 133, 105704. [Google Scholar] [CrossRef]
- Yang, R.; Fu, Y.; Zhang, L.; Qi, H.; Han, X.; Fu, J. A Novel Sliding Mode Control Framework for Electrohydrostatic Position Actuation System. Math. Probl. Eng. 2018, 2018, 7159891. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, R. Analysis and Compensation for Nonlinear Systems with Dead-zone. Ind. Control Appl. 2006, 4, 64–66. [Google Scholar]
- Tao, G.; Kokotovic, P.V. Adaptive control of plants with unknown dead-zones. IFAC Proc. Vol. 1994, 39, 59–68. [Google Scholar]
- Mohanty, A.; Yao, B. Integrated Direct/Indirect Adaptive Robust Control of Hydraulic Manipulators with Valve Deadband. IEEE/ASME Trans. Mechatron. 2011, 16, 707–715. [Google Scholar] [CrossRef]
- dos Santos Coelho, L.; Cunha, M.A.B. Adaptive Cascade Control of a Hydraulic Actuator with an Adaptive Dead-Zone Compensation and Optimization Based on Evolutionary Algorithms. Expert Syst. Appl. 2011, 38, 12262–12269. [Google Scholar] [CrossRef]
- Zhou, J.; Wen, C.; Zhang, Y. Adaptive Output Control of Nonlinear Systems with Uncertain Dead-Zone Nonlinearity. IEEE Trans. Autom. Control 2006, 51, 504–511. [Google Scholar] [CrossRef]
- Gu, W.; Yao, J.; Yao, Z.; Zheng, J. Robust Adaptive Control of Hydraulic System with Input Saturation and Valve Dead-Zone. IEEE Access 2018, 6, 53521–53532. [Google Scholar] [CrossRef]
- Chowdhury, F.N.; Wahi, P.; Raina, R.; Kaminedi, S. A Survey of Neural Networks Applications in Automatic Control. In Proceedings of the 33rd Southeastern Symposium on System Theory, Athens, OH, USA, 20–20 March 2001; pp. 349–353. [Google Scholar]
- Li, Y.; Mao, Z.Z.; Wang, F.L.; Wang, Y. Adaptive dead zone compensation control of electrode regulating system of electric arc furnace. Control Decis. 2010, 25, 1474–1478. [Google Scholar]
- Wang, L.; Zhao, D.; Liu, F.; Liu, Q.; Zhang, Z. ADRC for Electro–hydraulic Position Servo Systems Based on Dead-zone Compensation. China Mech. Eng. 2021, 32, 1432–1442. [Google Scholar]











| Parameter | Symbol | Units | Value |
|---|---|---|---|
| Total compression volume | 9.15 × 10−4 | ||
| Efficient working area cylinder | 0.1134 | ||
| Total mass converted from the load to the piston | 500 | ||
| Viscous damping coefficient | N/(m/s) | 150 | |
| Equivalent spring stiffness of the load | N/m | 9 × 107 | |
| Total leakage coefficient of hydraulic system | (m3/s)/Pa | 9 × 10−11 | |
| Effective volume modulus of oil | N/m2 | 6.5 × 108 | |
| Control gain | (r/min)/V | 200 | |
| Displacement of fixed displacement pump | L/r | 8 × 10−3 | |
| External disturbance and unmodeled friction | 4× 104 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Chen, G.; Liu, H.; Yan, G.; Zhang, T.; Liu, K.; Liu, Y.; Ai, C. Research on Position Control of an Electro–Hydraulic Servo Closed Pump Control System. Processes 2022, 10, 1674. https://doi.org/10.3390/pr10091674
Wang F, Chen G, Liu H, Yan G, Zhang T, Liu K, Liu Y, Ai C. Research on Position Control of an Electro–Hydraulic Servo Closed Pump Control System. Processes. 2022; 10(9):1674. https://doi.org/10.3390/pr10091674
Chicago/Turabian StyleWang, Fei, Gexin Chen, Huilong Liu, Guishan Yan, Tiangui Zhang, Keyi Liu, Yan Liu, and Chao Ai. 2022. "Research on Position Control of an Electro–Hydraulic Servo Closed Pump Control System" Processes 10, no. 9: 1674. https://doi.org/10.3390/pr10091674




