Determination of Gas Extraction Borehole Parameters in Fractured Zone on ‘Borehole in Place of Roadway’ Based on RSM-GRA-GA
Abstract
:1. Introduction
2. Mechanism of Gas Extraction by ‘Borehole in Place of Roadway’
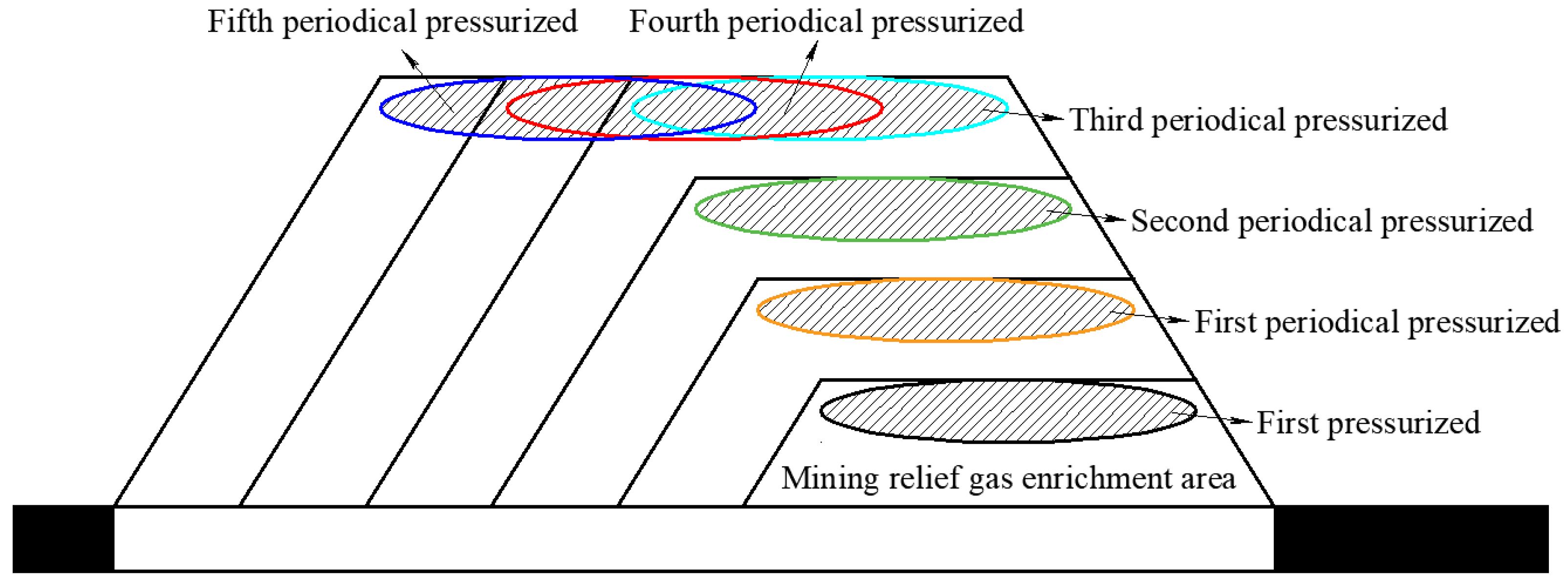
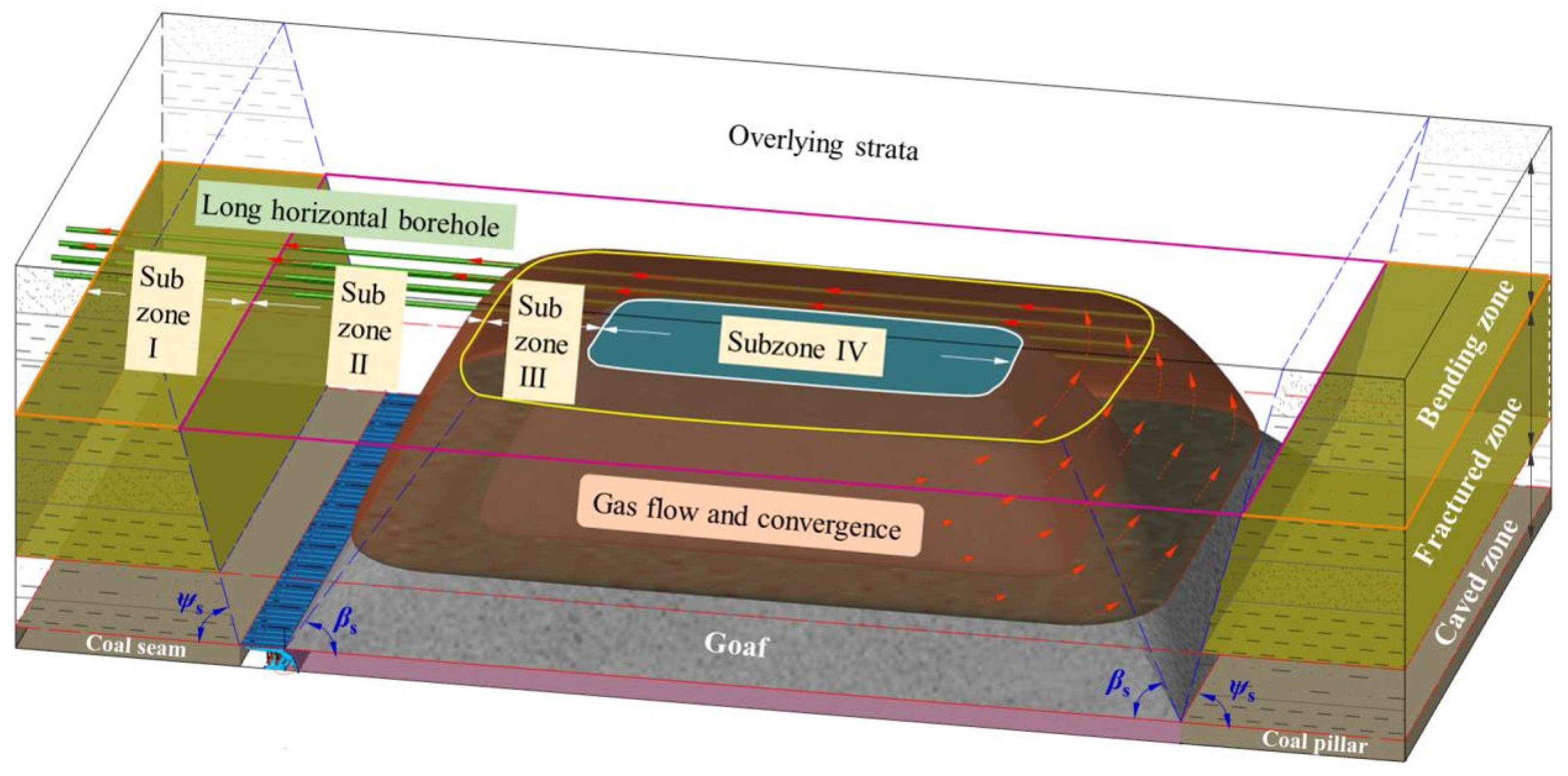
2.1. Formation Mechanism and Migration Law of Dominant Channels for Gas Extraction
2.2. Spatio-Temporal Evolution of Gas Migration in Goaf
2.3. Mathematical Model of Gas Seepage in Roof Fracture Field
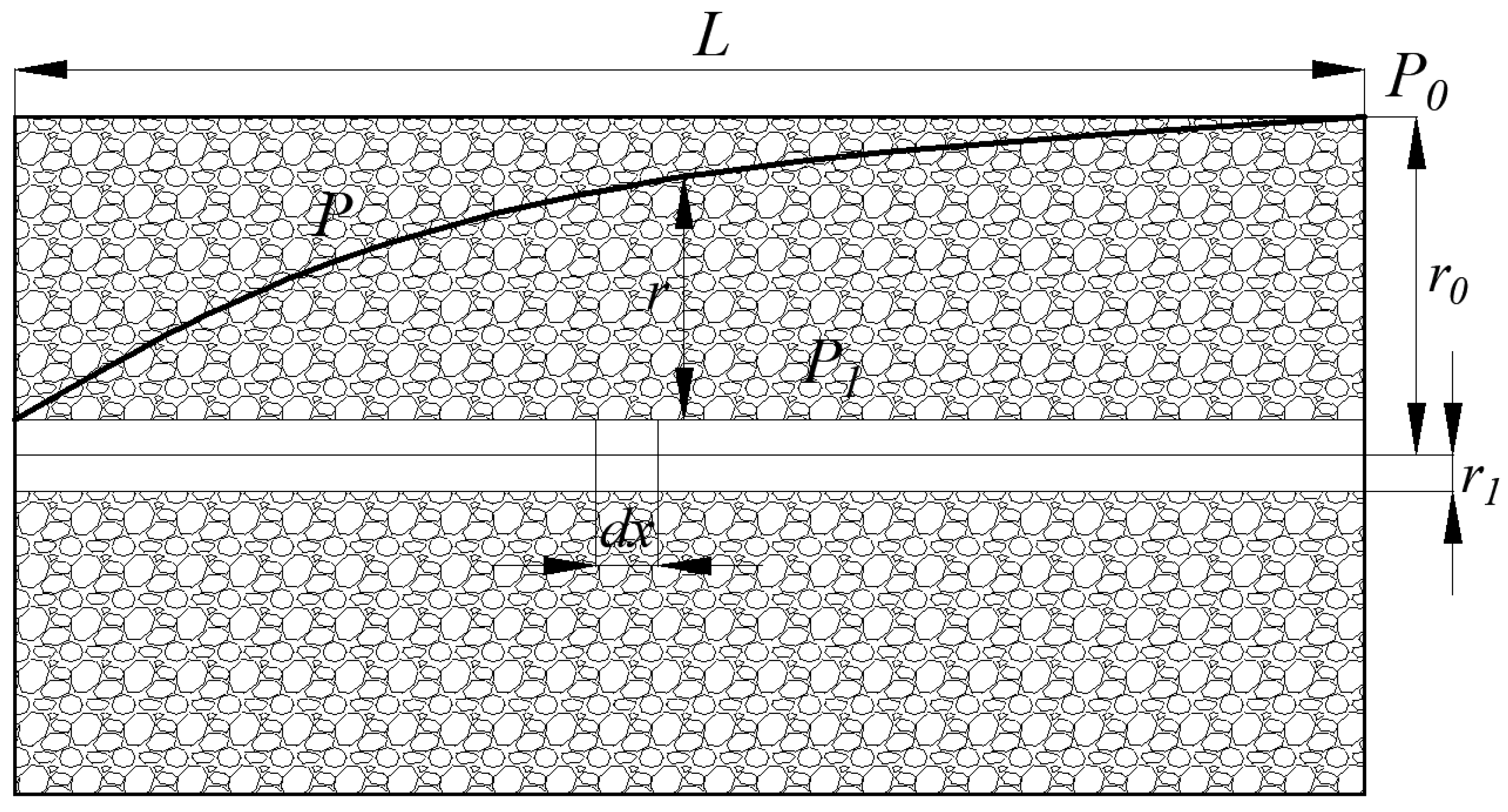
2.3.1. Equation of Gas Extraction from Single Borehole
2.3.2. Analysis of Influencing Factors of Gas Extraction Effect by ‘Borehole in Place of Roadway’
- (1)
- Borehole horizon
- (2)
- Borehole diameter
- (3)
- Borehole spacing
3. Regression Experimental Design
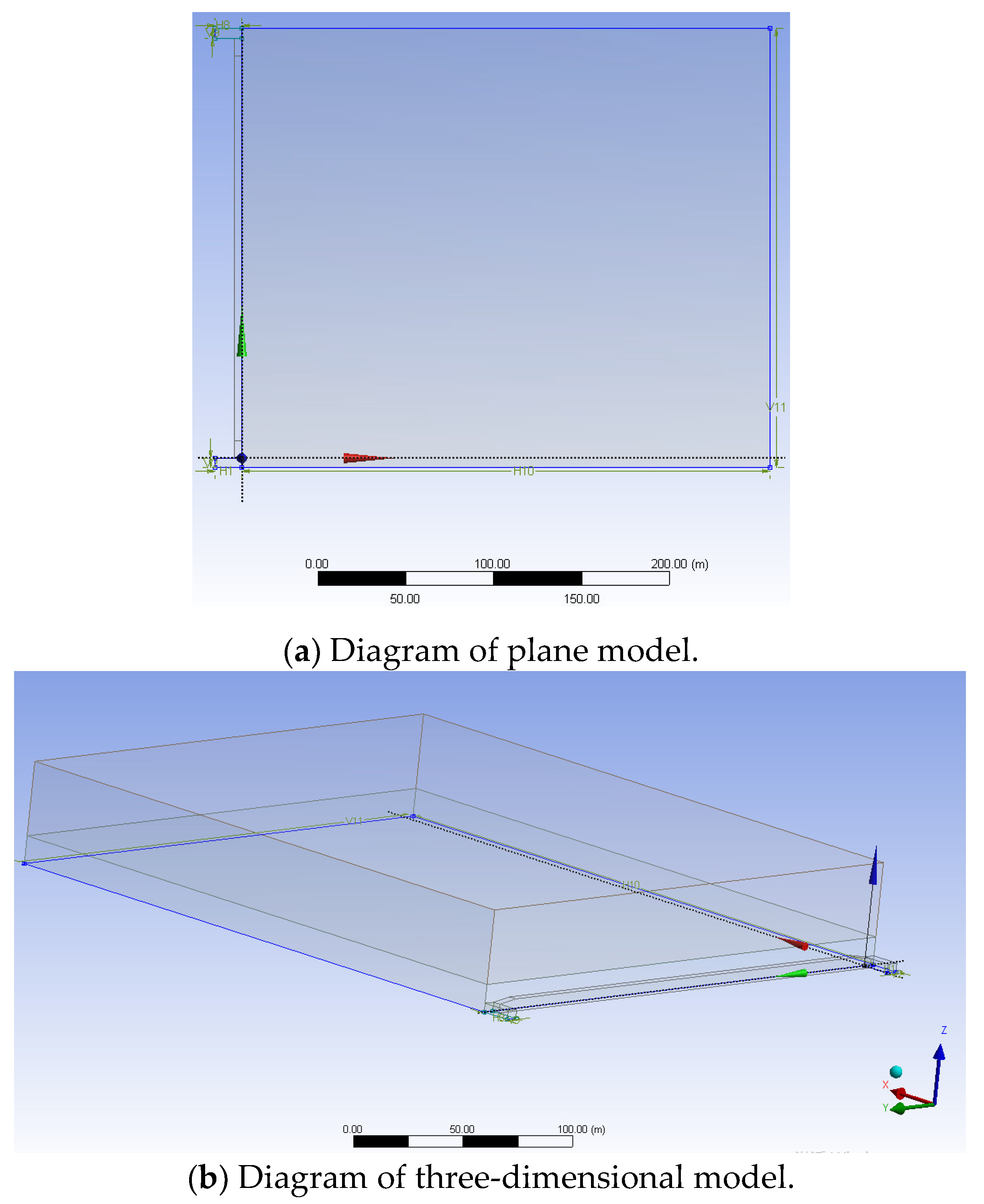
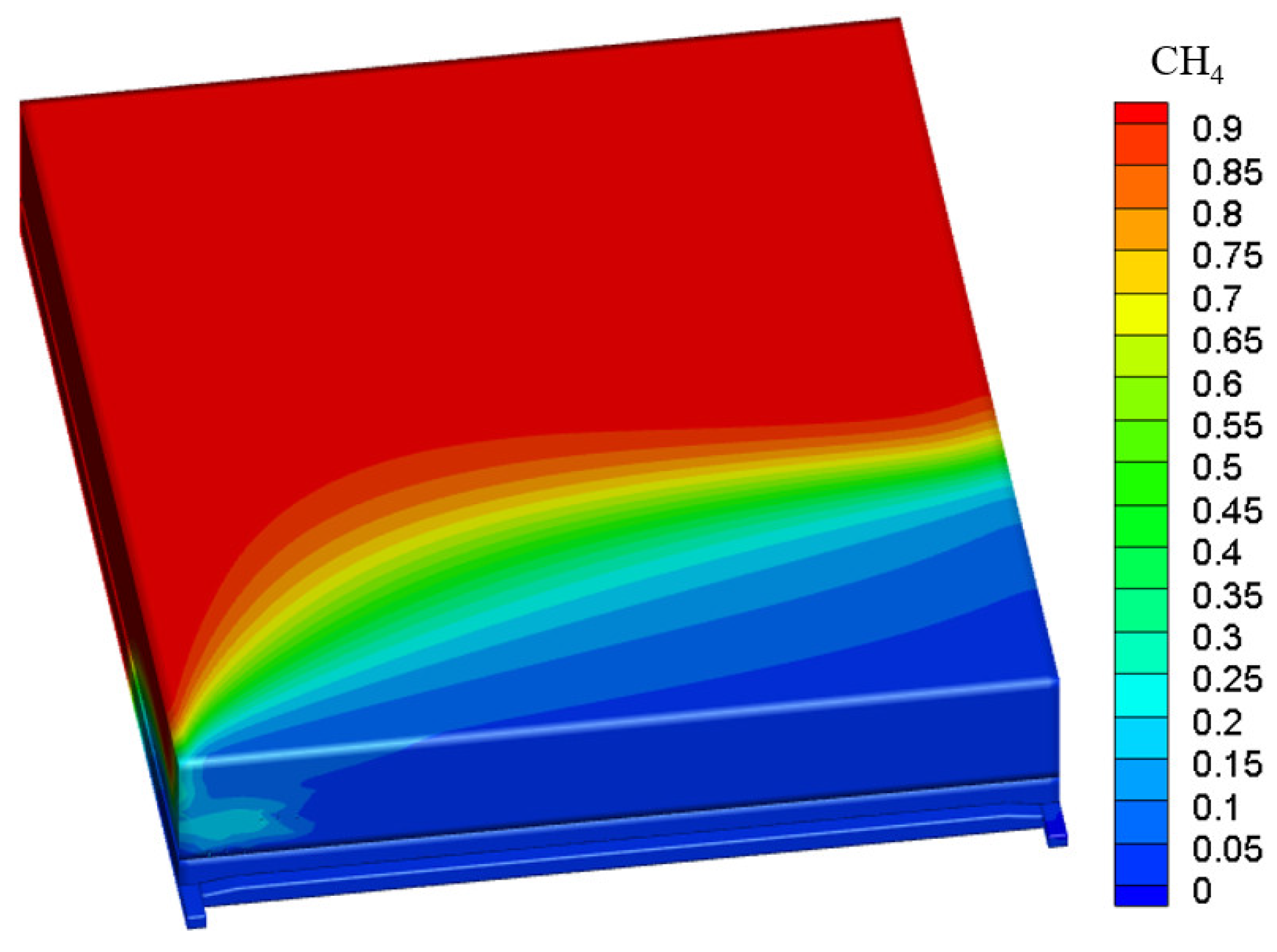
3.1. Computational Fluid Dynamics (CFD) Geometric Model Establishment
- (1)
- Steady-state seepage field—the initial process of gas extraction from the borehole can be regarded as an unsteady seepage state; however, after a long-enough time of gas extraction, the seepage field around the borehole will reach a relatively stable state.
- (2)
- The fracture field formed by the fractured zone of the extracted overburden is regarded as a uniform and continuous porous medium, and the seepage process is not affected by temperature changes and is isothermal seepage.
- (3)
- The process of gas extraction from the boreholes is considered as a planar radial seepage, and the flow line is a set of straight lines from around the borehole into the center of the borehole. Since gas seepage in the overburden fracture field is a complex process, the main influencing factors of borehole extraction are simplified and analyzed according to the above assumptions.
3.2. RSM Experimental Design
3.3. Comprehensive Evaluation Value of Gas Extraction Effect
- (1)
- Data normalization
- (2)
- Building decision matrix
- (3)
- Gray relational coefficient of all factors
- (4)
- Comprehensive evaluation value of the model
3.4. Comparative Analysis
4. RSM Model Predictive Analysis
4.1. Model Establishment
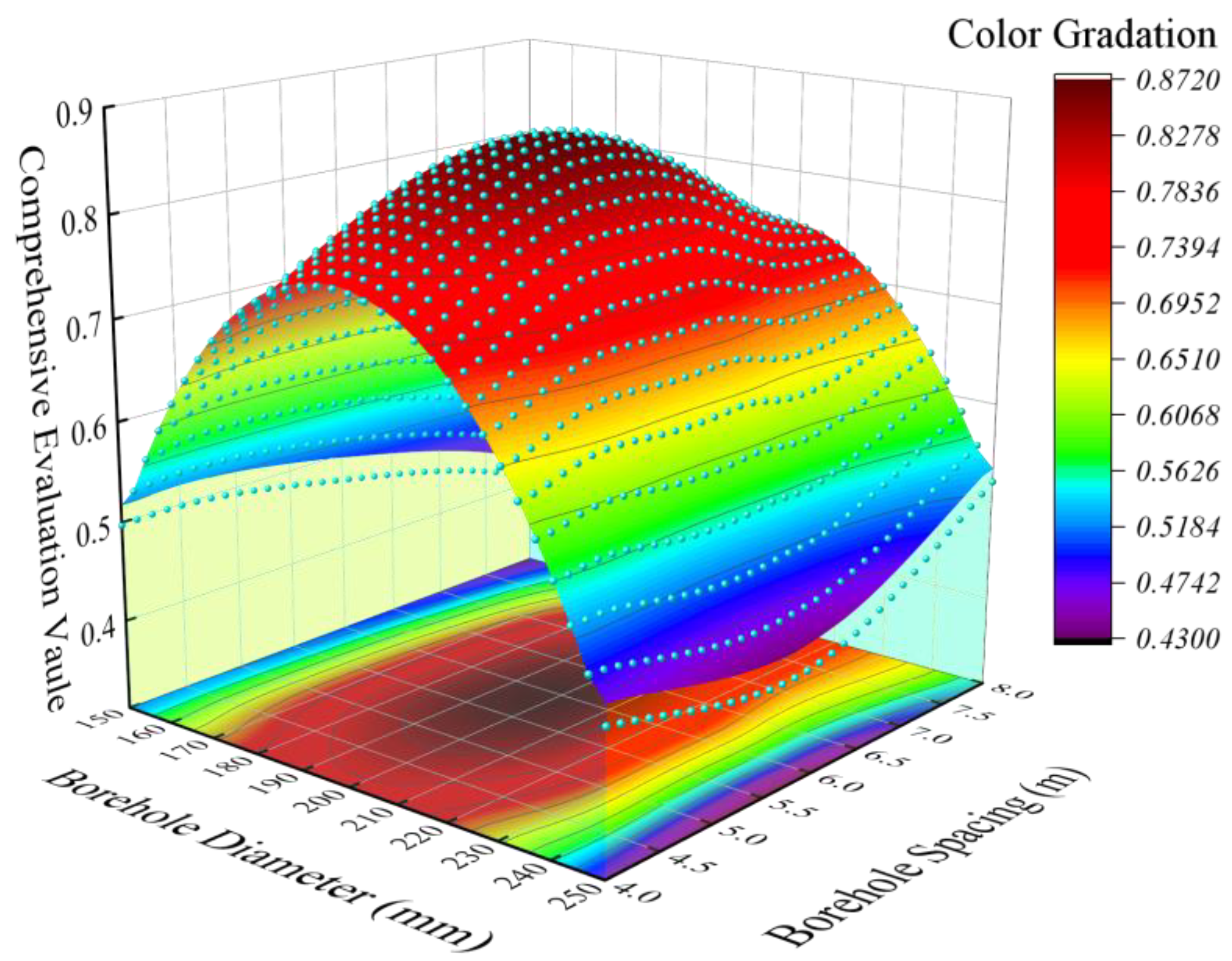
4.2. Interaction Relationship of Various Influencing Factors
5. Analysis of Genetic Algorithm Prediction Model
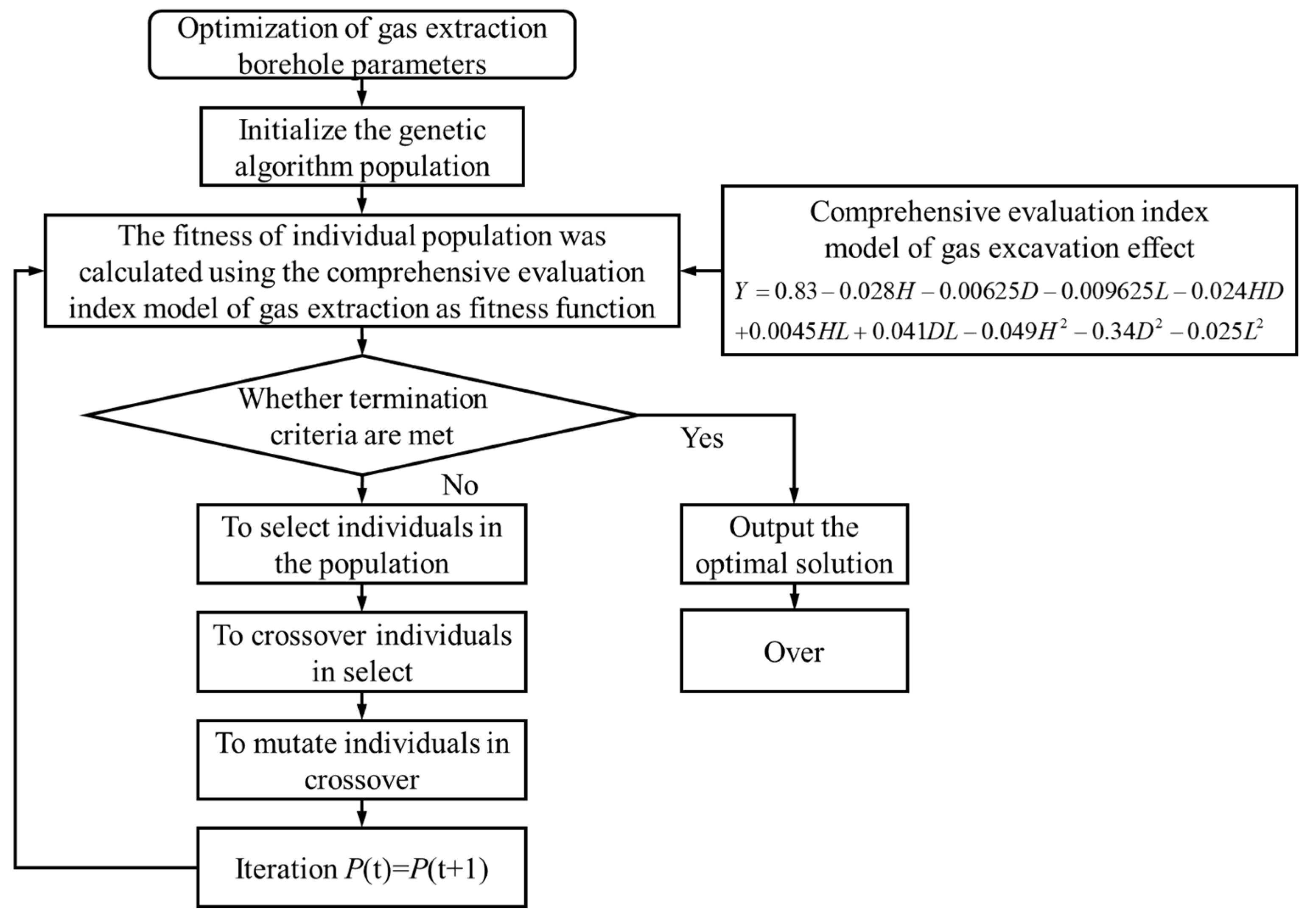
5.1. Genetic Algorithm (GA)
- (1)
- Initialization
- (2)
- Individual evaluation
- (3)
- Selection operation
- (4)
- Crossover operation
- (5)
- Mutate operation
- (6)
- Termination condition judgment
5.2. Genetic Algorithm Model Optimization Results
6. Discussion
7. Conclusions
- (1)
- Among the four objective weighting methods, the weighting results of PCA were 0.385, 0.285 and 0.33; the weighting results of CRITIC were 0.235, 0.325, 0.44; the weighting results of CVM were 0.353, 0.317, 0.33; the weighting results of EWM were 0.33, 0.336, 0.334.
- (2)
- The PCA takes into account the volatility of the data and the correlation between the data and, at the same time, has the effect of information concentration. This paper adopted the PCA. The results of the response surface analysis showed that the optimal solution of the model existed when the borehole horizon was 28–30 m, the borehole diameter was 190–210 mm, and the borehole spacing was 5.5–6.5 m.
- (3)
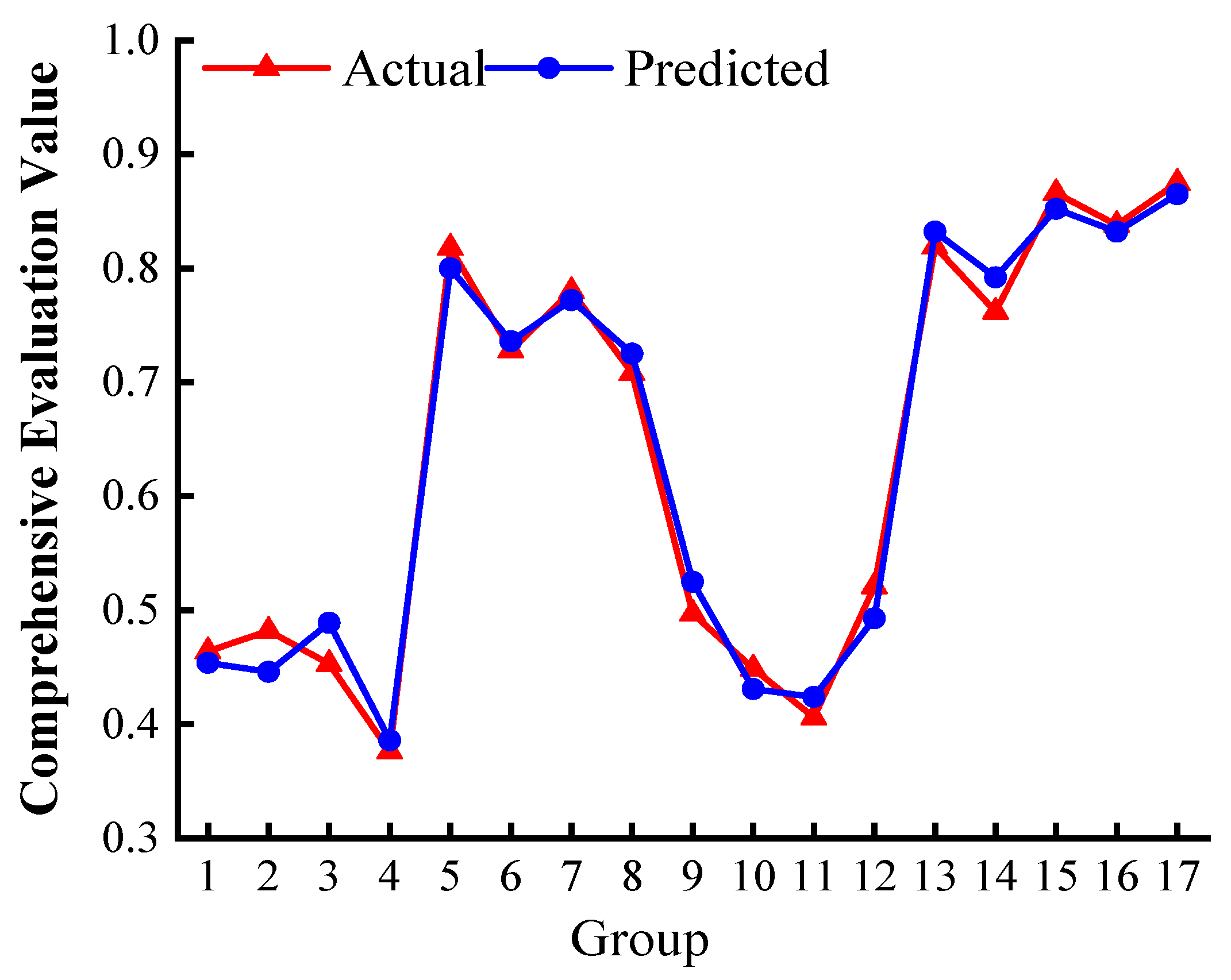
- Through the genetic algorithm, most of this objective function solved and finally determined the borehole horizon as 28.79 m, the borehole diameter as 199.89 mm, the borehole spacing as 5.76 m. This parameter under the borehole gas extraction had great results. The extraction mixed volume was 129.8 m3/min, extraction pure volume was 9.16 m3/min, the upper corner concentration was 0.52%, the prediction accuracy of the model was 97.8%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.; Shao, S.; Wang, X.; Chang, L.; Cui, G.; Zhou, G. Gas flow analysis for the impact of gob gas ventholes on coalbed methane drainage from a longwall gob. J. Nat. Gas Sci. Eng. 2016, 36, 1312–1325. [Google Scholar] [CrossRef]
- Ke, W.; Wang, K. Impact of Gas Control Policy on the Gas Accidents in Coal Mine. Processes 2020, 8, 1405. [Google Scholar] [CrossRef]
- Chen, Z.; Yuan, Y.; Wang, W.; Zhu, C.; Qin, Z.; Yan, C. Pressure Relief and Permeability Enhancement with Carbon Dioxide Phase Transition Blasting: Fracture, Seepage, and Practice. Lithosphere 2021, 2021, 4983754. [Google Scholar] [CrossRef]
- Zhou, F.; Xia, T.; Wang, X.; Zhang, Y.; Sun, Y.; Liu, J. Recent developments in coal mine methane extraction and utilization in China: A review. J. Nat. Gas Sci. Eng. 2016, 31, 437–458. [Google Scholar] [CrossRef]
- Shakib, M.F.; Detournay, E.; van de Wouw, N. Nonlinear dynamic modeling and analysis of borehole propagation for directional drilling. Int. J. Non-Linear Mech. 2019, 113, 178–201. [Google Scholar] [CrossRef]
- Gao, J.; Yang, M.; Li, X. Research on the Parameters of Gas Extraction from the Gob of a Fully Mechanized Working Face. Disaster Adv. 2013, 6, 156–165. [Google Scholar]
- Zhao, E.; Li, K.; Yang, X.; Deng, N. Speculum Observation and Trajectory Measurement in Gas Extraction Drilling: A Case Study of Changling Coal Mine. Geofluids 2021, 2021, 5545067. [Google Scholar] [CrossRef]
- Huang, B.; Cheng, Q.; Zhao, X.; Kang, C. Hydraulic fracturing of hard top coal and roof for controlling gas during the initial mining stages in longwall top coal caving: A case study. J. Geophys. Eng. 2018, 15, 2492–2506. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Y.; Zuo, L.; Chen, Z.; Meng, C.; Yan, C.; Gong, Z. Improvement of coalbed methane recovery rate by carbon dioxide phase transition blast fracturing. Energy Sources Part A-Recovery Util. Environ. Eff. 2022, 44, 3659–3672. [Google Scholar] [CrossRef]
- Wang, H.; Wang, E.; Li, Z.; Wang, X.; Zhang, Q.; Li, B.; Ali, M. Study on sealing effect of pre-drainage gas borehole in coal seam based on air-gas mixed flow coupling model. Process Saf. Environ. Prot. 2020, 136, 15–27. [Google Scholar] [CrossRef]
- Jia, L.; Peng, S.; Xu, J.; Yan, F.; Chen, J.; Wu, B. Investigation on gas drainage effect under different borehole layout via 3D monitoring of gas pressure. J. Nat. Gas Sci. Eng. 2022, 101, 104522. [Google Scholar] [CrossRef]
- Wu, K.; Shi, S.; Lu, Y.; Li, H.; Li, M. Optimization of the Plastic Area of a Borehole Based on the Gas Extraction Effect and Its Engineering Application. Geofluids 2021, 2021, 8147366. [Google Scholar] [CrossRef]
- Yan, Z.; Wang, Y.; Fan, J.; Huang, Y.; He, Y. Study on Key Parameters of Directional Long Borehole Layout in High-Gas Working Face. Shock Vib. 2021, 2021, 5579967. [Google Scholar] [CrossRef]
- Li, T.; Wu, B.; Lei, B. Study on the Optimization of a Gas Drainage Borehole Drainage Horizon Based on the Evolution Characteristics of Mining Fracture. Energies 2019, 12, 4499. [Google Scholar] [CrossRef] [Green Version]
- Fu, G.; Zhao, Z.; Hao, C.; Wu, Q. The Accident Path of Coal Mine Gas Explosion Based on 24Model: A Case Study of the Ruizhiyuan Gas Explosion Accident. Processes 2019, 7, 73. [Google Scholar] [CrossRef] [Green Version]
- An, F.; Wang, Z.; Yang, H.; Yang, S.; Pan, F.; Chen, T.; Xie, C. Application of directional boreholes for gas drainage of adjacent seams. Int. J. Rock Mech. Min. Sci. 2016, 90, 35–42. [Google Scholar] [CrossRef]
- Cheng, C.; Cheng, X.; Yu, R.; Yue, W.; Liu, C. The Law of Fracture Evolution of Overlying Strata and Gas Emission in Goaf under the Influence of Mining. Geofluids 2021, 2021, 2752582. [Google Scholar] [CrossRef]
- Li, H.; Liu, Y.; Wang, W.; Liu, M.; Ma, J.; Guo, X.; Guo, H. The integrated drainage technique of directional high-level borehole of super large diameter on roof replacing roof extraction roadway: A case study of the underground Zhaozhuang Coal Mine. Energy Rep. 2020, 6, 2651–2666. [Google Scholar] [CrossRef]
- Ji, M.; Sun, Z.; Sun, W. A Case Study on the Gas Drainage Optimization Based on the Effective Borehole Spacing in Sima Coal Mine. Geofluids 2021, 2021, 5510566. [Google Scholar] [CrossRef]
- Wang, W.; Li, Z.; Zhao, G.; Chen, Y. Coal and Gas Comining in the High-Gas Detong Mine, China: Analytical and Numerical Parameter Optimization of Gas Extraction Boreholes. Adv. Civ. Eng. 2022, 2022, 9552620. [Google Scholar] [CrossRef]
- Luo, M.; Yang, L.; Wen, H.; Zhao, D.; Wang, K. Numerical Optimization of Drilling Parameters for Gas Predrainage and Excavating-Drainage Collaboration on Roadway Head. Geofluids 2022, 2022, 3241211. [Google Scholar] [CrossRef]
- Liu, J.; Gao, J.; Yang, M.; Wang, D.; Wang, L. Numerical Simulation of Parameters Optimization for Goaf Gas Boreholes. Adv. Civ. Eng. 2019, 2019, 3891080. [Google Scholar] [CrossRef]
- Yang, H.; Qian, Z.; IOP. The Research of Coordination Extraction from the Stope Gas with Partition and Time-sharing. In Proceedings of the 6th International Conference on Advances in Energy, Environment and Chemical Engineering (AEECE), Dalizhou, China, 24–26 June 2020; p. 546. [Google Scholar]
- Zhao, P.; Zhuo, R.; Li, S.; Shu, C.M.; Laiwang, B.; Jia, Y.; Shi, Y.; Suo, L. Analysis of advancing speed effect in gas safety extraction channels and pressure-relief gas extraction. Fuel 2020, 265, 116825. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, L. Application of Desirability Based Multiresponse Optimization for Reciprocating Pump Design: Mechanical, Industrial, And Manufacturing Engineering. In Proceedings of the International Conference on Mechanical, Industrial, and Manufacturing Engineering, Singapore, 28–30 September 2011. [Google Scholar]
- Moore, T.; Friederich, M. Defining Uncertainty: Comparing Resource/Reserve Classification Systems for Coal and Coal Seam Gas. Energies 2021, 14, 6245. [Google Scholar] [CrossRef]
- Yuan, Y.; Chen, Z.; Yuan, C.; Zhu, C.; Wei, H.; Zhang, X. Numerical Simulation Analysis of the Permeability Enhancement and Pressure Relief of Auger Mining. Nat. Resour. Res. 2020, 29, 931–948. [Google Scholar] [CrossRef]
- Zhu, C.; Yuan, Y.; Wang, W.; Chen, Z.; Wang, S.; Zhong, H. Research on the “three shells” cooperative support technology of large-section chambers in deep mines. Int. J. Min. Sci. Technol. 2021, 31, 665–680. [Google Scholar] [CrossRef]
- Guo, M.; Guo, W.; Yuan, R.; Jiao, Z.; Enbing, Y.I. Spatial Location Determination of Directional Boreholes based on Regional Distribution Characteristics of mining-induced overburden fractures. J. Min. Saf. Eng. 2021, 1, 1–10. [Google Scholar]
- Alipour, A.; Mokhtarian, M. RSM-Based Model to Estimate the V-Cut Drill and Blast Pattern Specific Charge in Rock Tunneling. Int. J. Geomech. 2021, 21, 06021030. [Google Scholar] [CrossRef]
- Cancan, P.; Xiaodong, Z.; Zhiguang, G.; Ju, W.; Yan, G. Research on cooperative optimization of multiphase pump impeller and diffuser based on adaptive refined response surface method. Adv. Mech. Eng. 2022, 14, 16878140211072944. [Google Scholar] [CrossRef]
- Hu, Q.; Yuan, K.; Peng, W.; He, S.; Zhao, G.; Wang, J. Flow pattern analysis and multi-objective optimization of helically corrugated tubes used in the intermediate heat exchanger for nuclear hydrogen production. Int. J. Hydrogen Energy 2022, 47, 4885–4902. [Google Scholar] [CrossRef]
- Meng, D.; Gan, H.; Wang, H. Modeling and Optimization of the Flue Gas Heat Recovery of a Marine Dual-Fuel Engine Based on RSM and GA. Processes 2022, 10, 674. [Google Scholar] [CrossRef]
- Mangaraj, S.; Bagal, D.; Parhi, N.; Panda, S.; Barua, A.; Jeet, S. Experimental study of a portable plasma arc cutting system using hybrid RSM-nature inspired optimization technique: Materials Today-Proceedings. In Proceedings of the 2nd International Conference on Functional Material, Manufacturing and Performances, Xi’an, China, 21–23 October 2022; pp. 867–878. [Google Scholar]
- Wang, J.; Wan, W. Optimization of fermentative hydrogen production process using genetic algorithm based on neural network and response surface methodology. Int. J. Hydrogen Energy 2009, 34, 255–261. [Google Scholar] [CrossRef]
- Balasubramanian, V.; Lakshminarayanan, A.K.; Varahamoorthy, R.; Babu, S. Application of Response Surface Methodolody to Prediction of Dilution in Plasma Transferred Arc Hardfacing of Stainless Steel on Carbon Steel. J. Iron Steel Res. Int. 2009, 16, 44–53. [Google Scholar] [CrossRef]
- Mostafa, J.J.; Mohammad, M.A.; Ehsan, M. A hybrid response surface methodology and simulated annealing algorithm: Computer Communication and Management. In Proceedings of the International Conference on Computer Communication and Management, Sydney, Australia, 1 January 2011; pp. 570–576. [Google Scholar]
- Guo, P.; Wang, X.; Han, Y. The Enhanced Genetic Algorithms for the Optimization Design. In Proceedings of the 3rd International Conference on Biomedical Engineering and Informatics (BMEI 2010), Yantai, China, 16–18 October 2010; pp. 2990–2994. [Google Scholar]
- Wen, F.; Zhang, D.; Han, C.; Zhang, G.; Li, G.; Zhang, X.; Ma, J.; Yao, Z.; Yu, K. Anti-offset performance optimization of coupling coils in wireless power transfer system based on genetic algorithm. Energy Rep. 2022, 8, 1–9. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Y.; Shuai, K.; Zhu, W.; Chen, B.; Chen, K. Multi-objective Trajectory Planning Method based on the Improved Elitist Non-dominated Sorting Genetic Algorithm. J. Mec. Eng. 2022, 35, 7. [Google Scholar] [CrossRef]




| Name of the Border | Type of the Border |
|---|---|
| Inlet | Velocity inlet |
| Out | Pressure outlet |
| Wall | Wall |
| Model | Define |
|---|---|
| Solver | Pressure Based |
| Viscous Model | k-epsilon |
| Energy | On |
| Material | Methane–Air |
| Code | H/m | D/mm | S/m |
|---|---|---|---|
| −1 | 24 | 150 | 4 |
| 0 | 30 | 200 | 6 |
| 1 | 36 | 250 | 8 |
| Component | Initial Eigenvalue | Sum of Squares of Loads | Sum of Squares of Rotational Loads | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Total | Percentage of Variance | Accumulation | Total | Percentage of Variance | Accumulation | Total | Percentage of Variance | Accumulation | |
| 1 | 2.955 | 52.372 | 57.372 | 1.571 | 52.372 | 57.372 | 1.564 | 52.126 | 57.126 |
| 2 | 0.039 | 35.382 | 91.755 | 1.061 | 35.382 | 91.755 | 1.069 | 35.628 | 91.755 |
| 3 | 0.367 | 12.245 | 100.000 | ||||||
| Component | 1 |
|---|---|
| the mixed amount of gas extraction | 0.997 |
| the pure amount of gas extraction | 0.992 |
| upper corner concentration | 0.988 |
| Number | Evaluation Index | Weight Distribution | |||
|---|---|---|---|---|---|
| PCA | CRITIC | CVM | EWM | ||
| 1 | the mixed amount of gas extraction | 0.385 | 0.235 | 0.353 | 0.33 |
| 2 | the pure amount of gas extraction | 0.285 | 0.325 | 0.317 | 0.336 |
| 3 | upper corner concentration | 0.33 | 0.44 | 0.33 | 0.334 |
| Number | Parameter of Borehole | Gray Regulation Coefficient | Comprehensive Evaluation Value | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| H | D | L | M | P | C | PCA | CRITIC | CVM | EWM | |
| 1 | 30 | 150 | 4 | 0.424 | 0.526 | 0.556 | 0.497 | 0.515 | 0.500 | 0.502 |
| 2 | 30 | 200 | 6 | 0.851 | 0.906 | 0.875 | 0.875 | 0.879 | 0.876 | 0.877 |
| 3 | 36 | 200 | 8 | 0.664 | 0.899 | 0.596 | 0.708 | 0.710 | 0.716 | 0.720 |
| 4 | 30 | 250 | 4 | 0.458 | 0.535 | 0.364 | 0.449 | 0.442 | 0.451 | 0.452 |
| 5 | 24 | 200 | 4 | 0.806 | 1 | 0.676 | 0.818 | 0.812 | 0.825 | 0.828 |
| 6 | 24 | 250 | 6 | 0.398 | 0.533 | 0.45 | 0.453 | 0.465 | 0.458 | 0.461 |
| 7 | 30 | 250 | 8 | 0.456 | 0.532 | 0.589 | 0.521 | 0.539 | 0.524 | 0.526 |
| 8 | 30 | 200 | 6 | 0.744 | 0.785 | 0.762 | 0.762 | 0.765 | 0.763 | 0.764 |
| 9 | 30 | 150 | 8 | 0.402 | 0.492 | 0.335 | 0.406 | 0.402 | 0.408 | 0.410 |
| 10 | 30 | 200 | 6 | 0.798 | 0.846 | 0.819 | 0.819 | 0.823 | 0.820 | 0.821 |
| 11 | 36 | 250 | 6 | 0.378 | 0.406 | 0.347 | 0.376 | 0.373 | 0.377 | 0.377 |
| 12 | 24 | 150 | 6 | 0.485 | 0.485 | 0.42 | 0.464 | 0.456 | 0.464 | 0.463 |
| 13 | 36 | 150 | 6 | 0.428 | 0.561 | 0.476 | 0.482 | 0.492 | 0.486 | 0.489 |
| 14 | 30 | 200 | 6 | 0.869 | 0.897 | 0.836 | 0.959 | 0.950 | 0.957 | 0.955 |
| 15 | 30 | 200 | 6 | 0.784 | 0.849 | 0.892 | 0.943 | 0.936 | 0.940 | 0.939 |
| 16 | 36 | 200 | 4 | 0.873 | 0.751 | 0.537 | 0.728 | 0.686 | 0.723 | 0.720 |
| 17 | 24 | 200 | 8 | 0.667 | 0.887 | 0.819 | 0.780 | 0.805 | 0.787 | 0.792 |
| Name | Data Volatility | Correlation between Data | Information of Number | Other |
|---|---|---|---|---|
| PCA | Yes | Yes | No | Information enrichment |
| CRITIC | Yes | Yes | No | |
| CVM | Yes | No | No | |
| EWM | No | No | No |
| Parameter | Sum of Squares | Degree of Freedom | Mean Square | F-Value | p-Value | Significance |
|---|---|---|---|---|---|---|
| Model | 0.53 | 9 | 0.059 | 29.67 | <0.0001 | ** |
| H | 0.006105 | 1 | 0.006105 | 3.08 | 0.1225 | - |
| D | 0.0003125 | 1 | 0.0003125 | 0.16 | 0.7030 | - |
| L | 0.0007411 | 1 | 0.0007411 | 0.37 | 0.5600 | - |
| HD | 0.002256 | 1 | 0.002256 | 1.14 | 0.3212 | - |
| HL | 0.000081 | 1 | 0.000081 | 0.041 | 0.8455 | - |
| DL | 0.006642 | 1 | 0.006642 | 3.36 | 0.1097 | - |
| H2 | 0.01 | 1 | 0.02 | 5.11 | 0.0584 | - |
| D2 | 0.48 | 1 | 0.54 | 244.77 | <0.0001 | ** |
| L2 | 0.008263 | 1 | 0.008263 | 1.28 | 0.2958 | - |
| Residual | 0.033 | 7 | 0.004754 | |||
| Lack of Fit | 0.005748 | 3 | 0.001916 | 0.95 | 0.4984 | - |
| Pure Error | 0.00811 | 4 | 0.002027 | |||
| Cor Total | 0.54 | 16 |
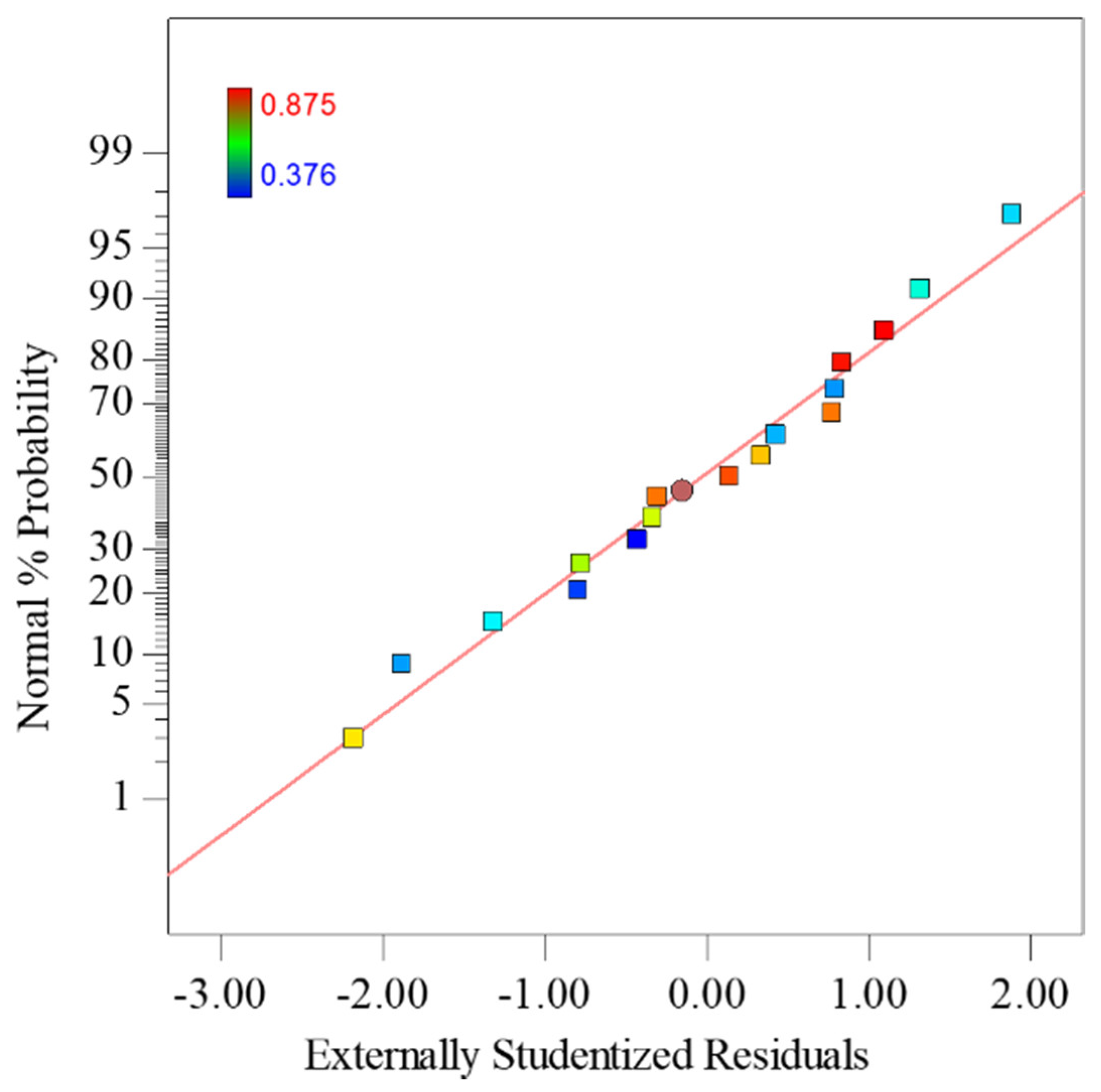
| Model | Std. Dev. | Mean | R-Squared | Adj R-Squared | Pred R-Squared | PRESS | C.V. % | Adeq Precision |
|---|---|---|---|---|---|---|---|---|
| Y | 0.044 | 0.64 | 0.9745 | 0.9416 | 0.8071 | 0.1 | 6.98 | 13.066 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, Z.; Shen, H.; Yuan, Y.; Gong, Z.; Chen, Z.; Xia, Y. Determination of Gas Extraction Borehole Parameters in Fractured Zone on ‘Borehole in Place of Roadway’ Based on RSM-GRA-GA. Processes 2022, 10, 1421. https://doi.org/10.3390/pr10071421
Qin Z, Shen H, Yuan Y, Gong Z, Chen Z, Xia Y. Determination of Gas Extraction Borehole Parameters in Fractured Zone on ‘Borehole in Place of Roadway’ Based on RSM-GRA-GA. Processes. 2022; 10(7):1421. https://doi.org/10.3390/pr10071421
Chicago/Turabian StyleQin, Zhenghan, Haisheng Shen, Yong Yuan, Zhixiong Gong, Zhongshun Chen, and Yongqi Xia. 2022. "Determination of Gas Extraction Borehole Parameters in Fractured Zone on ‘Borehole in Place of Roadway’ Based on RSM-GRA-GA" Processes 10, no. 7: 1421. https://doi.org/10.3390/pr10071421
APA StyleQin, Z., Shen, H., Yuan, Y., Gong, Z., Chen, Z., & Xia, Y. (2022). Determination of Gas Extraction Borehole Parameters in Fractured Zone on ‘Borehole in Place of Roadway’ Based on RSM-GRA-GA. Processes, 10(7), 1421. https://doi.org/10.3390/pr10071421







