Evaluation of Hydrodynamic Performance of New Random Packing Structure Using CFD
Abstract
:1. Introduction
2. CFD Modeling Approach
2.1. Governing Models Selection
2.2. Packing Structures and Properties
2.3. Flow Fields of Packing Columns
2.4. Convergence and Termination
2.5. Calculations of Hydraulic Properties
3. Experiments
4. Results and Discussions
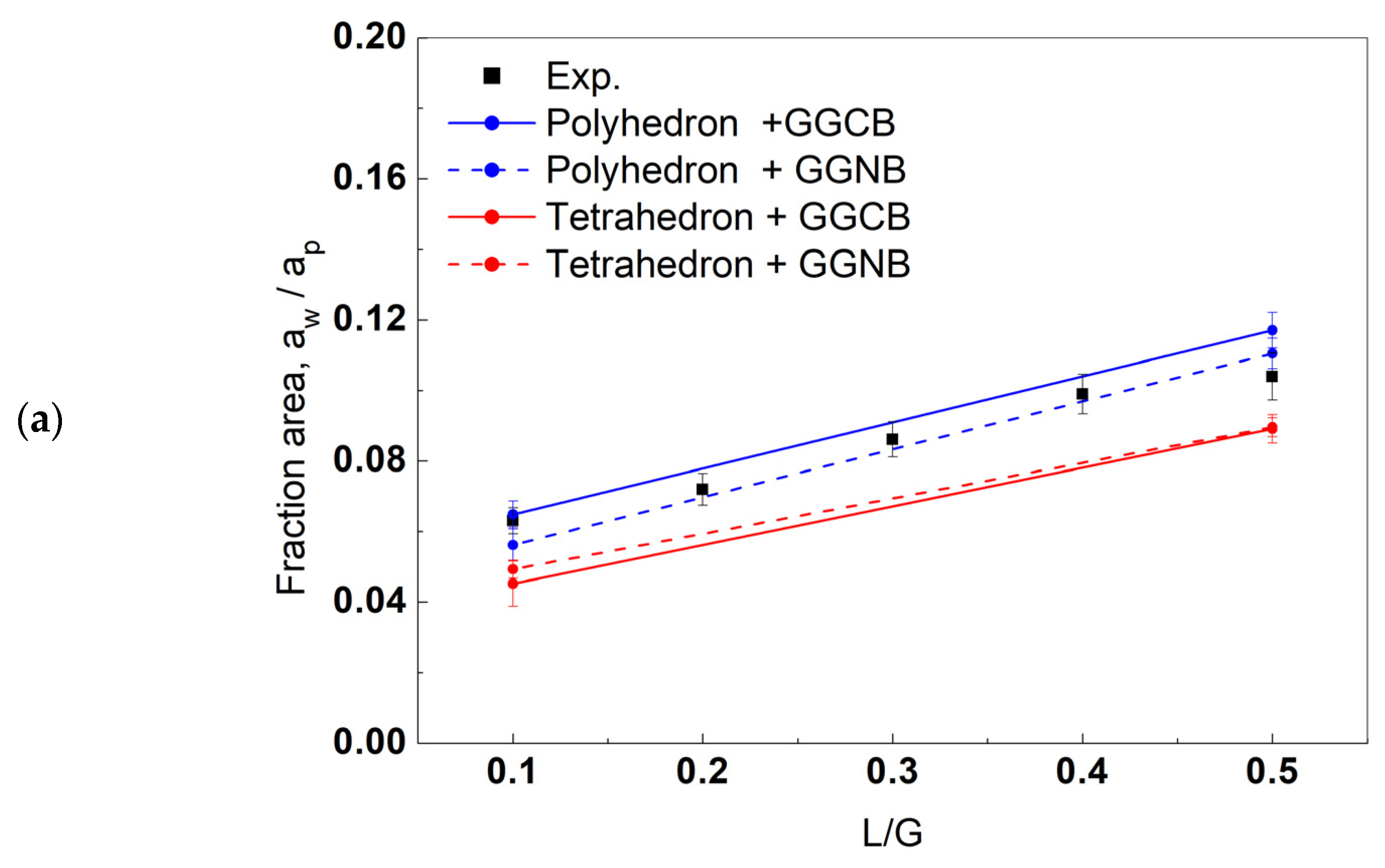
4.1. Gradient Calculations between GGCB and GGNB
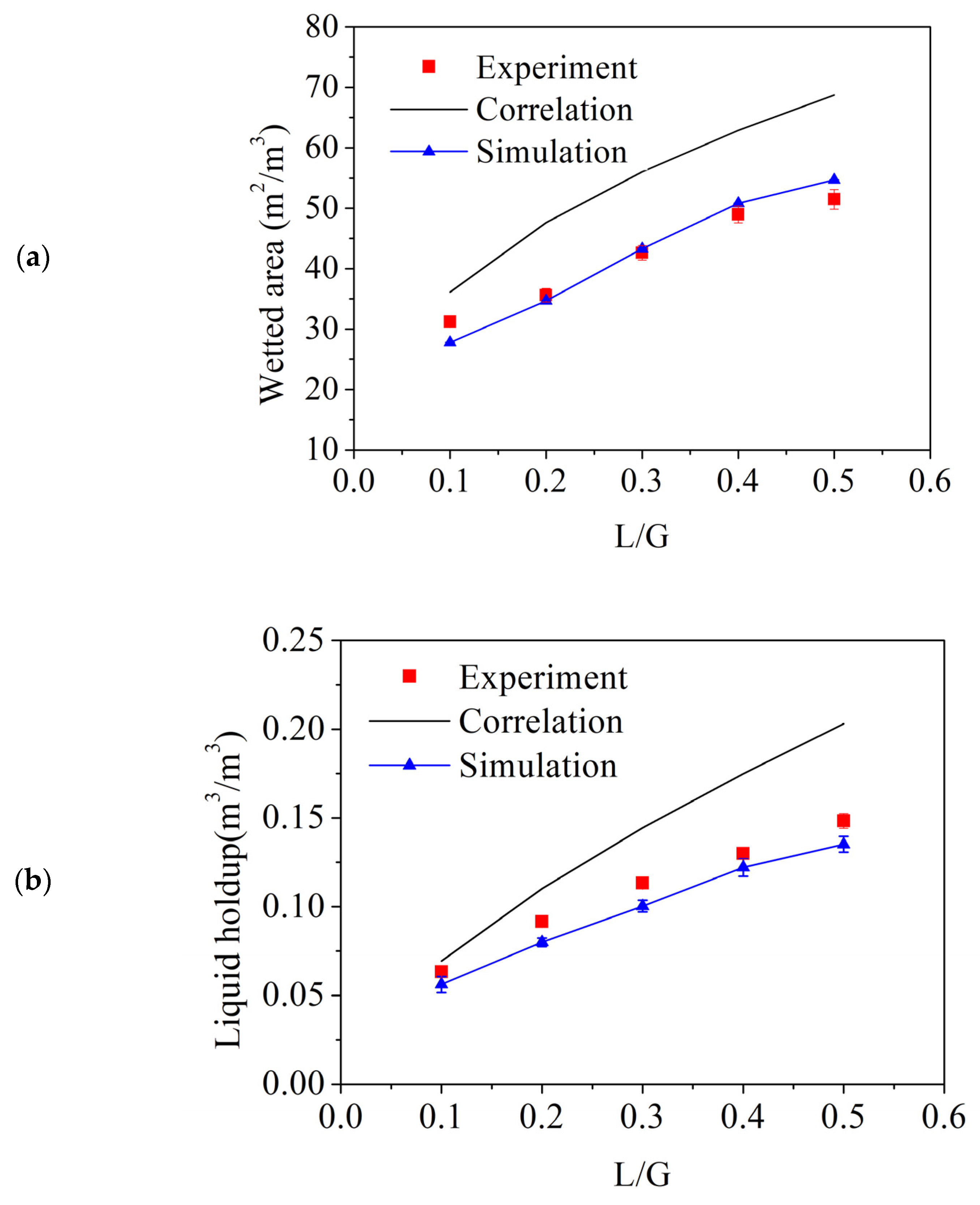
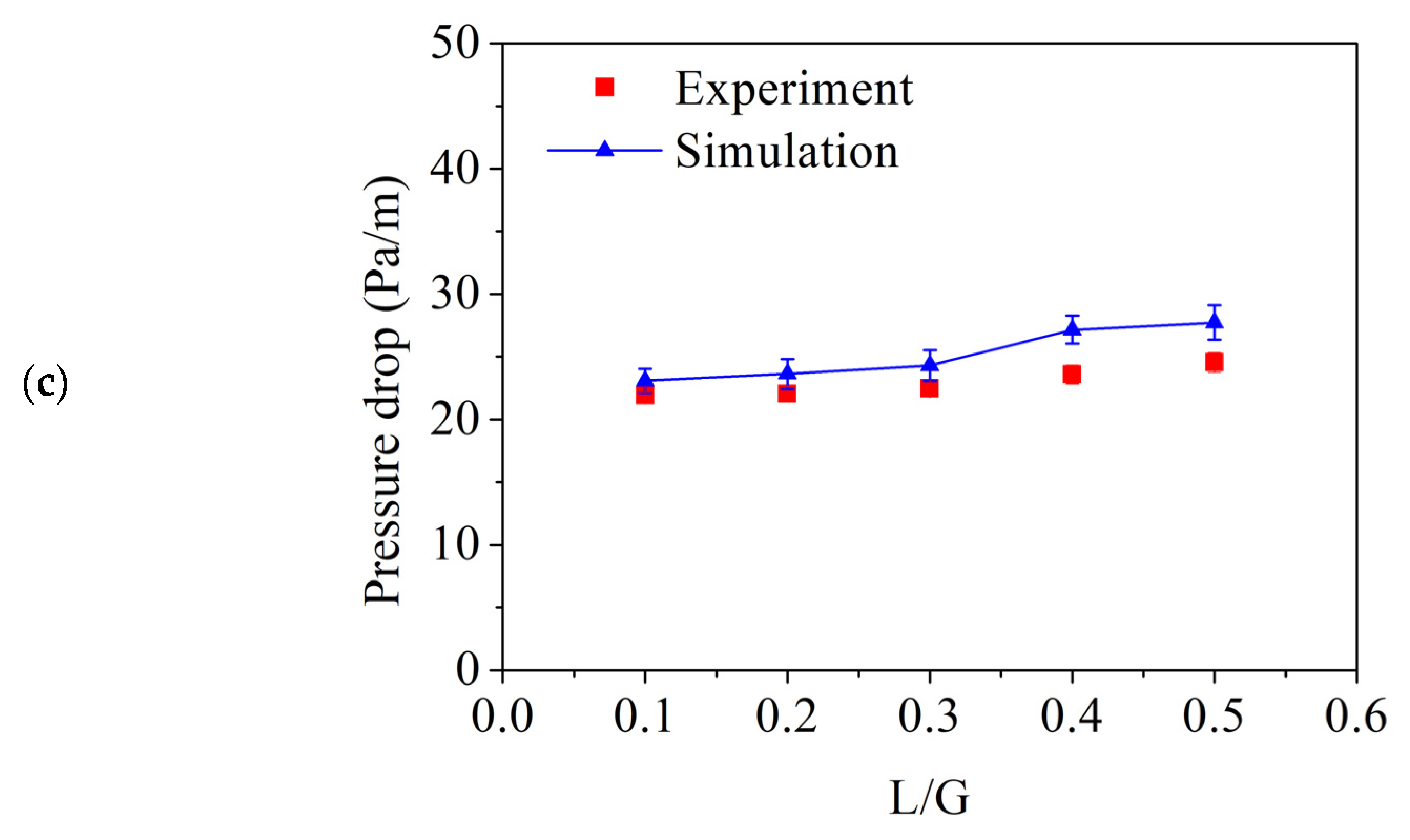
4.2. Validation of Combination of Polyhedral Mesh and GGNB
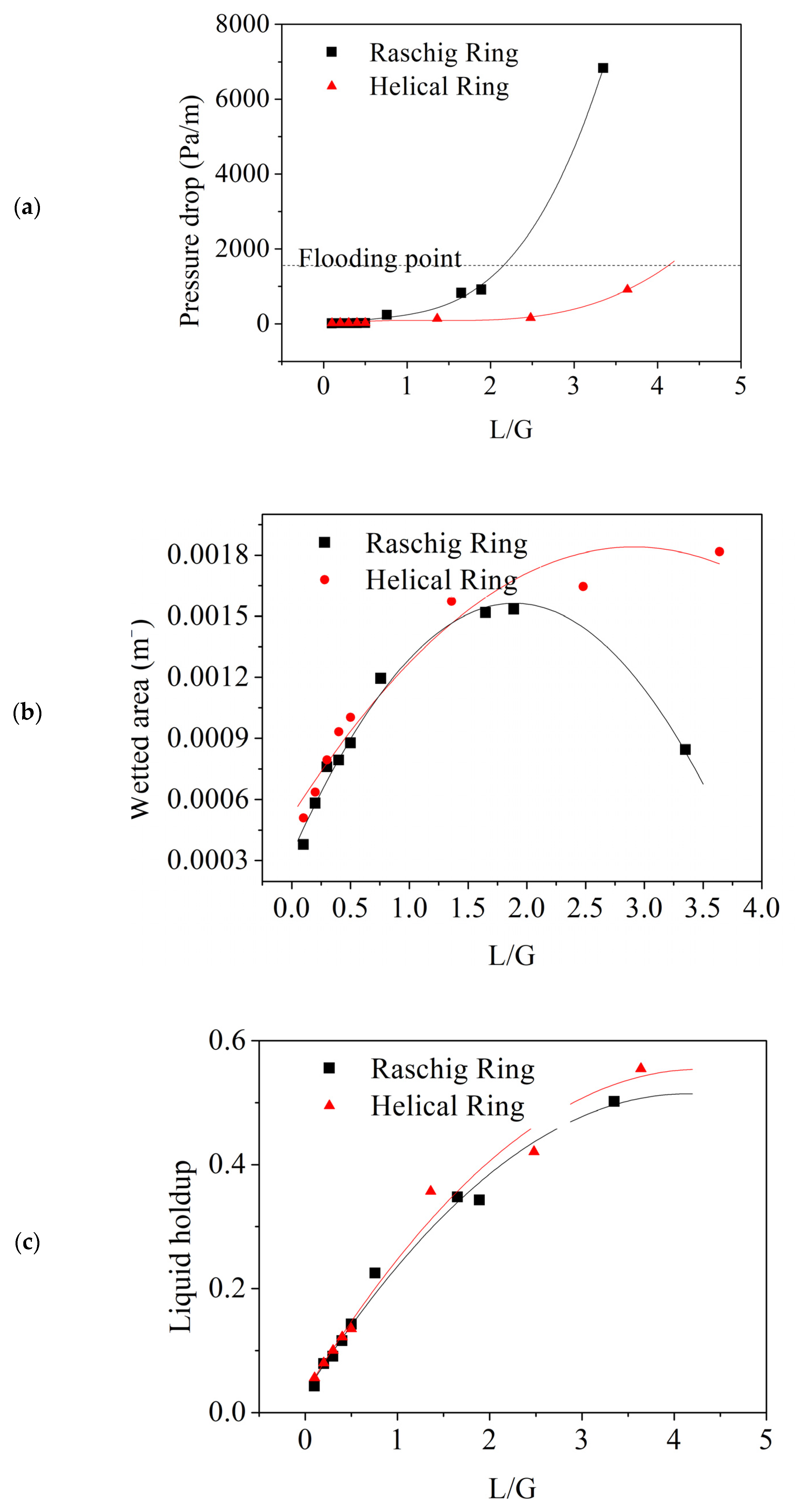
4.3. Hydrodynamic Evaluation for Raschig and Helical Rings
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Humphrey, J.L.; Keller, G.E. Separation Process Technology; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Jalili, B.; Aghaee, N.; Jalili, P.; Ganji, D.D. Novel usage of the curved rectangular fin on the heat transfer of a double-pipe heat exchanger with a nanofluid. Case Stud. Therm. Eng. 2022, 35, 102086. [Google Scholar] [CrossRef]
- Jalili, B.; Jalili, P.; Sadighi, S.; Ganji, D.D. Effect of magnetic and boundary parameters on flow characteristics analysis of micropolar ferrofluid through the shrinking sheet with effective thermal conductivity. Chin. J. Phys. 2021, 71, 136–150. [Google Scholar] [CrossRef]
- Jalili, B.; Sadighi, S.; Jalili, P.; Ganji, D.D. Characteristics of ferrofluid flow over a stretching sheet with suction and injection. Case Stud. Therm. Eng. 2019, 14, 100470. [Google Scholar] [CrossRef]
- Jalili, P.; Ganji, D.D.; Jalili, B.; Ganji, D.R.M. Evaluation of electro-osmotic flow in a nanochannel via semi-analytical method. Therm. Sci. 2012, 16, 1297–1302. [Google Scholar] [CrossRef]
- Hodson, J. Computational Fluid Dynamical Studies of Structured Distillation Packings. Ph.D. Thesis, Aston University, Birmingham, UK, April 1997. [Google Scholar]
- Shojaee, S.; Hosseini, S.H.; Razavi, B.S. Computational fluid dynamics simulation of multiphase flow in structured packings. J. Appl. Math. 2012, 2012, 917650. [Google Scholar] [CrossRef]
- Bai, H., Jr.; Theuerkauf, J.; Gillis, P.A.; Witt, P.M. A coupled DEM and CFD simulation of flow field and pressure drop in fixed bed reactor with randomly packed catalyst particles. Ind. Eng. Chem. Res. 2009, 48, 4060–4074. [Google Scholar] [CrossRef]
- Eppinger, T.; Seidler, K.; Kraume, M. DEM-CFD simulations of fixed bed reactors with small tube to particle diameter ratios. Chem. Eng. J. 2011, 166, 324–331. [Google Scholar] [CrossRef]
- Dixon, A.G.; Nijemeisland, M. CFD as a design tool for fixed-bed reactors. Ind. Eng. Chem. Res. 2001, 40, 5246–5254. [Google Scholar] [CrossRef]
- Lopes, R.J.; Quinta-Ferreira, R.M. CFD modelling of multiphase flow distribution in trickle beds. Chem. Eng. J. 2009, 147, 342–355. [Google Scholar] [CrossRef] [Green Version]
- Lopes, R.J.; Quinta-Ferreira, R.M. Numerical simulation of trickle-bed reactor hydrodynamics with RANS-based models using a volume of fluid technique. Ind. Eng. Chem. Res. 2009, 48, 1740–1748. [Google Scholar] [CrossRef]
- Wen, T.; Lu, L.; He, W.; Min, Y. Fundamentals and applications of CFD technology on analyzing falling film heat and mass exchangers: A comprehensive review. Appl. Energy 2020, 261, 114473. [Google Scholar] [CrossRef]
- Wagner, I.; Stichlmair, J.; Fair, J.R. Mass transfer in beds of modern, high-efficiency random packings. Ind. Eng. Chem. Res. 1997, 36, 227–237. [Google Scholar] [CrossRef]
- Gupta, R.; Fletcher, D.F.; Haynes, B.S. On the CFD modelling of Taylor flow in microchannels. Chem. Eng. Sci. 2009, 64, 2941–2950. [Google Scholar] [CrossRef]
- Kim, S.-E.; Makaro, B.; Caraen, D. A multi-dimensional linear reconstruction scheme for arbitrary unstructured mesh. In Proceedings of the 16th AIAA Computational Fluid Dynamics Conference, Orlando, FL, USA, 23–26 June 2003; p. 3990. [Google Scholar]
- Holmes, D.; Connell, S. Solution of the 2D Navier-Stokes equations on unstructured adaptive grids. In Proceedings of the 9th Computational Fluid Dynamics Conference, Buffalo, NY, USA, 13–15 June 1989; p. 1932. [Google Scholar]
- Haddadi, B.; Jordan, C.; Norouzi, H.R.; Harasek, M. Investigation of the pressure drop of random packed bed adsorbers. Chem. Eng. Trans. 2016, 52, 439–444. [Google Scholar]
- Kang, J.-L.; Ciou, Y.-C.; Lin, D.-Y.; Wong, D.S.-H.; Jang, S.-S. Investigation of hydrodynamic behavior in random packing using CFD simulation. Chem. Eng. Res. Des. 2019, 147, 43–54. [Google Scholar] [CrossRef]
- Brackbill, J.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Mishriky, F.; Walsh, P. Towards understanding the influence of gradient reconstruction methods on unstructured flowsimulations. Trans. Can. Soc. Mech. Eng. 2017, 41, 169–179. [Google Scholar] [CrossRef]
- Ataki, A.; Bart, H.J. Experimental and CFD simulation study for the wetting of a structured packing element with liquids. Chem. Eng. Technol. 2006, 29, 336–347. [Google Scholar] [CrossRef]
- Billet, R.; Schultes, M. Prediction of mass transfer columns with dumped and arranged packings: Updated summary of the calculation method of Billet and Schultes. Chem. Eng. Res. Des. 1999, 77, 498–504. [Google Scholar] [CrossRef]
- McCabe, W.L.; Smith, J.C.; Harriott, P. Unit Operations of Chemical Engineering; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]




| Number of Packing Elements | Specific Surface Area | Porosity | |
|---|---|---|---|
| Exp. helical ring | 30.6 ± 1.3 | 874 ± 37 | 0.869 ± 0.006 |
| Exp. Raschig ring | 24.2 ± 1.1 | 493 ± 23 | 0.789 ± 0.009 |
| Boundaries | Type | Materials | Backflow Phase | Specification |
|---|---|---|---|---|
| Liquid inlet | Velocity | Water | 0.021–0.106 m/s | |
| Top outlet | Pressure | Air | 0 kPa-g | |
| Bottom outlet | Pressure | Air | Adjusted by PID control to obtain the correct gas inlet flow rate of 1 L/min |
| Raschig Ring | Tetrahedral Mesh | Polyhedral Mesh |
|---|---|---|
| Mesh number | 494,937 | 196,116 |
| Min orthogonal quality | 0.1 | 0.129 |
| Max skewness | 0.955 | 0.871 |
| Helical Ring | Tetrahedral Mesh | Polyhedral Mesh |
|---|---|---|
| Mesh number | 4,567,277 | 3,939,130 |
| Min orthogonal quality | 0.128 | 0.156 |
| Max skewness | 0.856 | 0.769 |
| Diameter (mm) | 25.4 |
| Height (mm) | 600 |
| Operating pressure (atm) | 1 |
| Specific surface area (m2/m3) | 869 (helical ring) 495 (Raschig ring) |
| Porosity | 0.87 (helical ring) 0.79 (Raschig ring) |
| Gas flow rate (G) (L/min) | 1 |
| Liquid flow rate (L) (L/min) | 0.1~0.5 |
| Method | Interfacial Area | Liquid Holdup | Pressure Drop |
|---|---|---|---|
| Polyhedron + GGCB | 15.9% | 28.9% | 39.9% |
| Polyhedron + GGNB | 7.1% | 9.9% | 9.1% |
| Tetrahedron + GGCB | 21.3% | 34.8% | 43.1% |
| Tetrahedron + GGNB | 17.8% | 28.6% | 38.5% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, J.-L.; Huang, S.-H.; Jang, S.-S. Evaluation of Hydrodynamic Performance of New Random Packing Structure Using CFD. Processes 2022, 10, 1276. https://doi.org/10.3390/pr10071276
Kang J-L, Huang S-H, Jang S-S. Evaluation of Hydrodynamic Performance of New Random Packing Structure Using CFD. Processes. 2022; 10(7):1276. https://doi.org/10.3390/pr10071276
Chicago/Turabian StyleKang, Jia-Lin, Siao-Han Huang, and Shi-Shang Jang. 2022. "Evaluation of Hydrodynamic Performance of New Random Packing Structure Using CFD" Processes 10, no. 7: 1276. https://doi.org/10.3390/pr10071276






