Integration of an Absorption Chiller to a Process Applying the Pinch Analysis Approach
Abstract
:1. Introduction
2. Methods
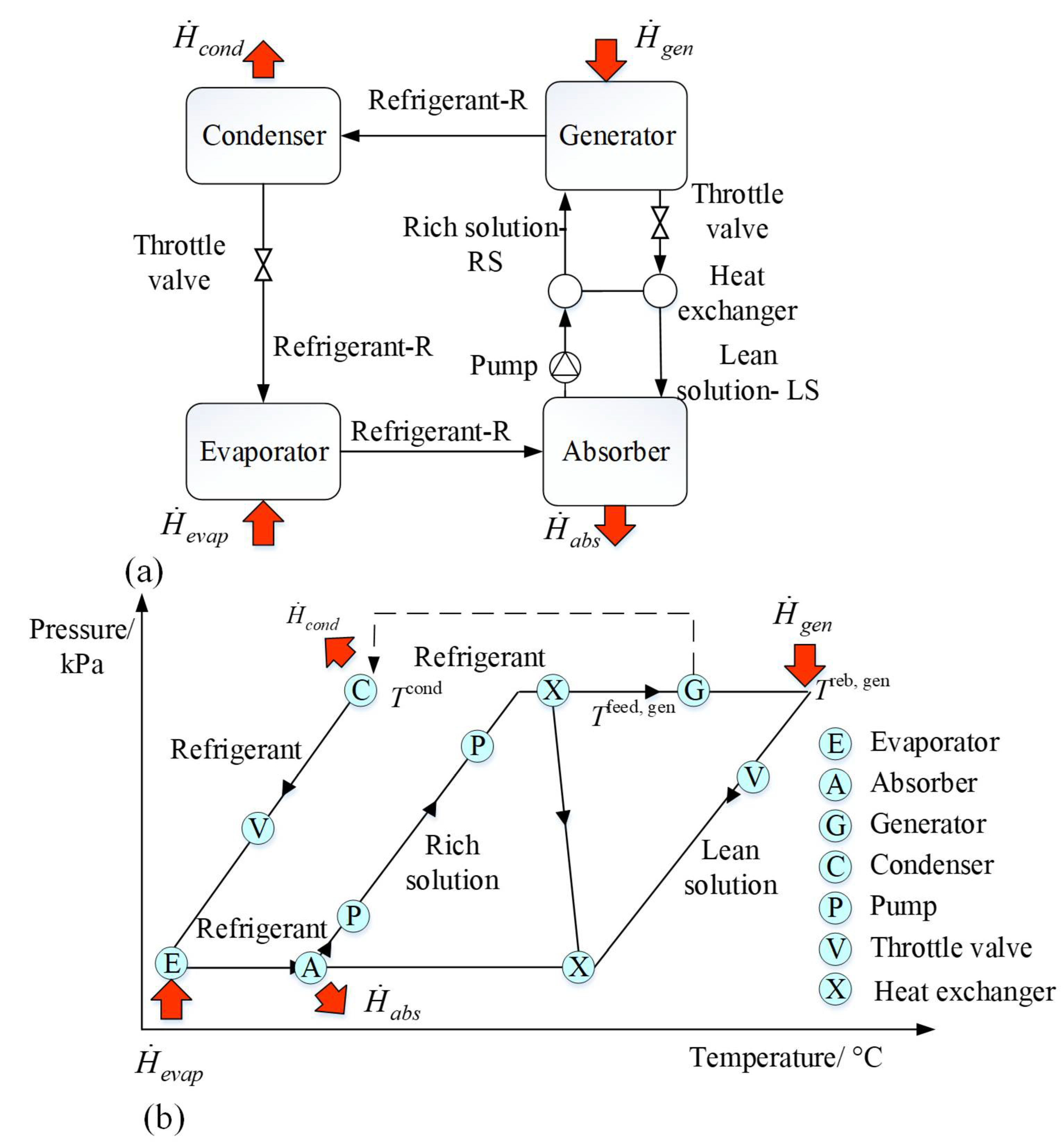
2.1. Absorption Chilling
2.2. Deriving the Representative Streams for Each Unit of Absorption Chilling
2.2.1. Evaporator
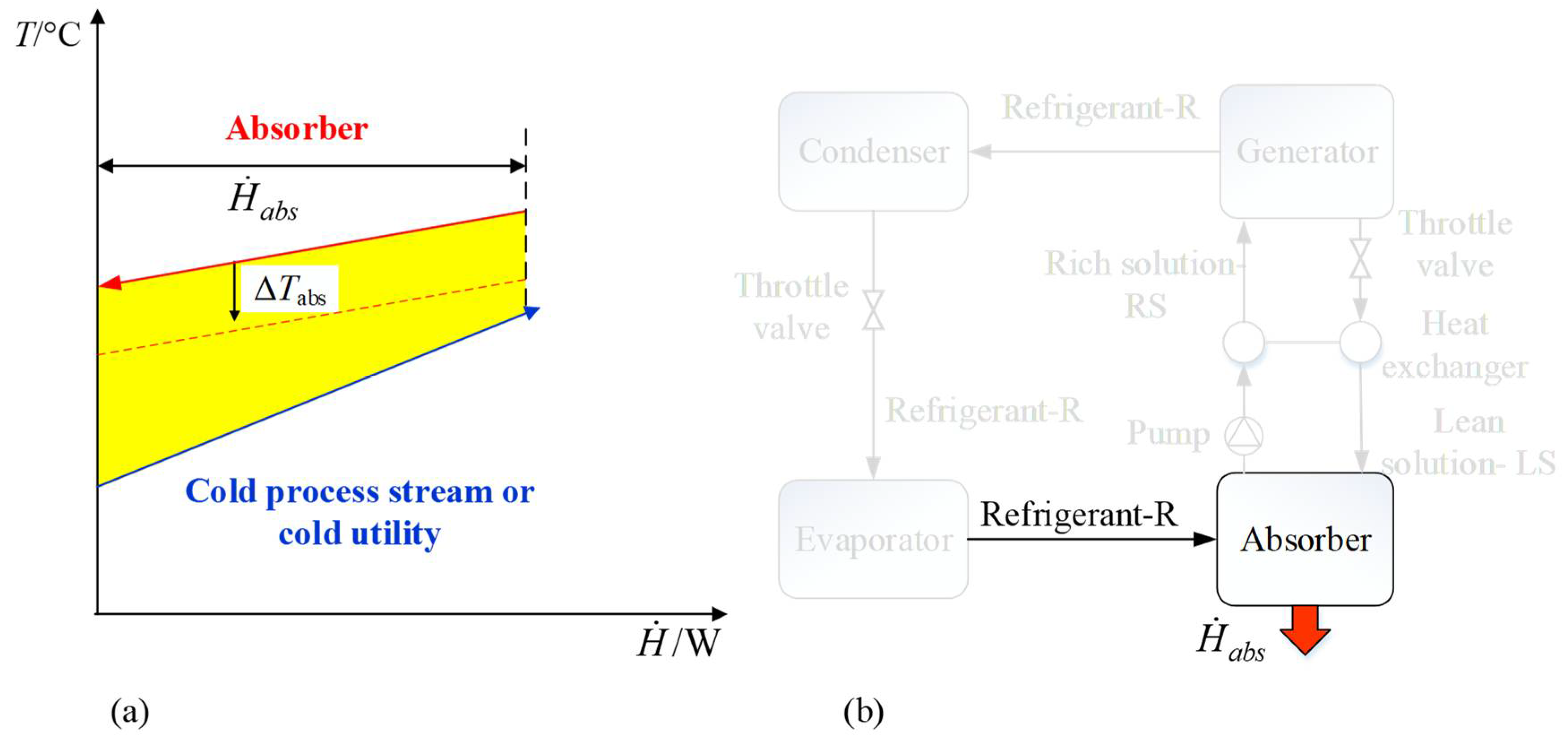
2.2.2. Absorber
2.2.3. Rich and Lean Solutions
2.2.4. Generator
2.2.5. Condenser
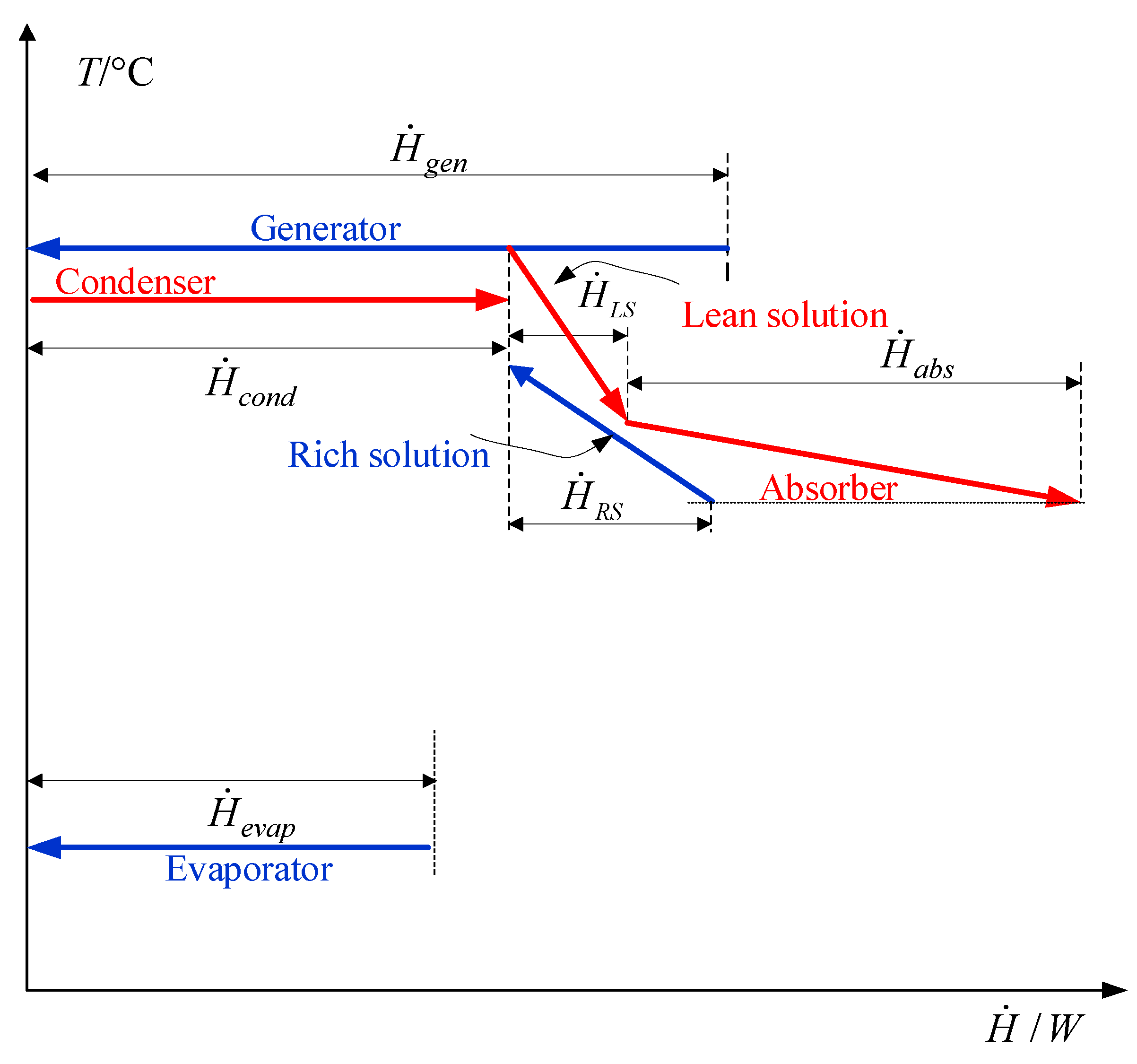
2.2.6. Overall Representation of Absorption Chilling
3. Integration of AC with a Process Using Pinch Analysis
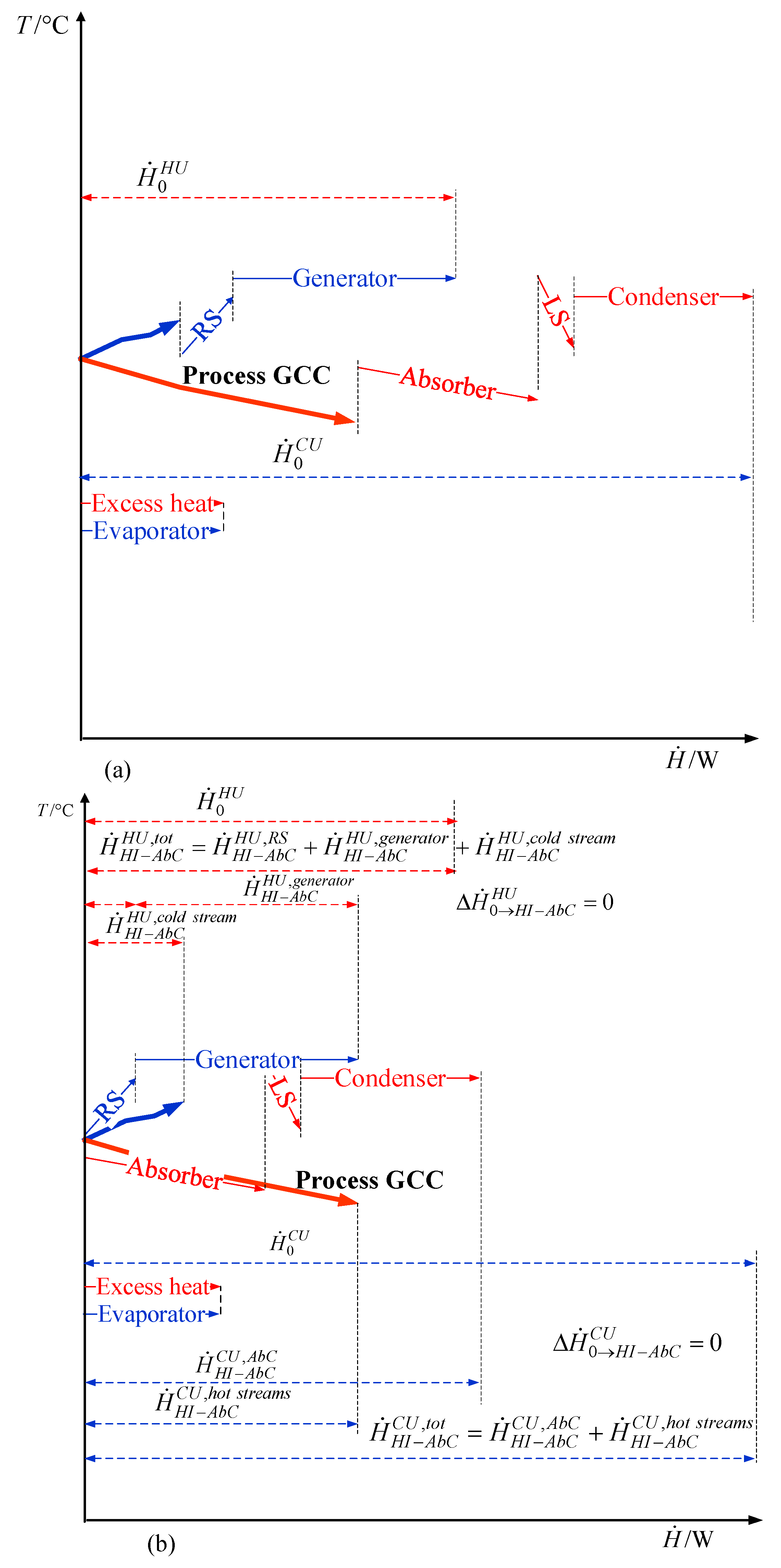
3.1. Integration above the Pinch
3.2. Integration across the Pinch
3.3. Integration below the Pinch
3.4. Overall View of AC Integration with Process
4. Case Studies
4.1. Case Study 1
4.2. Case Study 2
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Parameters | |
| A, B | parameters for describing the relationship between pressure and temperature at certain compositions of NH3 and H2O |
| a, m, n | coefficients for heuristic calculations of temperature, specific heat, composition, etc. |
| absorber pressure, Pa | |
| evaporation temperature, K | |
| mole fraction of NH3 in the refrigerant liquid phase | |
| mole fraction of NH3 in the rich solution | |
| mole fraction of NH3 in the lean solution | |
| mass fraction of NH3 in the lean solution | |
| mass fraction of NH3 in the rich solution | |
| G | gravity, 9.81 m/s2 |
| Variables | |
| H | differential head, m |
| enthalpy flow of evaporation, W | |
| enthalpy flow of absorption, W | |
| enthalpy flow of preheating refrigerant from the evaporation outlet to the absorption inlet, W | |
| enthalpy flow of cooling requirement (heat excess), W | |
| enthalpy flow of heat supplied to the generator, W | |
| enthalpy flow in the condenser, W | |
| enthalpy flow in the liquid refrigerant in the condenser, W | |
| enthalpy flow in the liquid refrigerant in the evaporator, W | |
| enthalpy flow in the vapor refrigerant in the evaporator, W | |
| specific heat of vapor at temperature of evaluation and certain refrigerant composition, J/g | |
| specific heat of liquid at temperature of evaluation and certain refrigerant composition, J/g | |
| specific heat of the lean solution at the absorber inlet temperature, J/g | |
| specific heat of the rich solution at the absorber outlet temperature, J/g | |
| specific heat of the refrigerant vapor at the absorber outlet temperature, J/g | |
| specific heat of the lean solution at the reboiler temperature , J/g | |
| specific heat of the vapor of the refrigerant at the condenser temperature, J/g | |
| specific heat of the liquid state of the refrigerant at , J/g | |
| specific heat of the rich solution, at the feed temperature to the generator , J/g | |
| P | shaft power of the pump, W |
| evaporation pressure, Pa | |
| pressure in the generator, Pa | |
| mass flowrate of the vapor at the outlet of the evaporator, g/s | |
| mass flowrate of the liquid refrigerant at the inlet of the evaporator, g/s | |
| mass flowrate of the vapor refrigerant at the inlet of the evaporator, g/s | |
| mass flowrate of the vapor refrigerant in the condenser, g/s | |
| mass flowrate of the liquid refrigerant in the condenser, g/s | |
| mass flowrate of the lean solution (liquid), g/s | |
| mass flowrate of the rich solution (liquid), g/s | |
| mass flowrate of the refrigerant, g/s | |
| SG | specific gravity of the fluid |
| saturation temperature of rich solution at absorber pressure pabs and certain molar fraction of NH3 of the rich solution , K | |
| inlet temperature to the absorber, K | |
| outlet temperature from the absorber, K | |
| temperature of the condensation, K | |
| feed temperature to the generator, K | |
| reboiler temperature of the generator, K | |
| refrigerant molar fraction in the absorption | |
| density of the rich solution, g/m3 | |
| density at the critical point, g/m3 | |
| density of the pure liquid, g/m3 | |
| reduced temperature complement to unity | |
| reduced temperature | |
| Abbreviations | |
| AC | Absorption chilling |
| PA | Pinch Analysis |
| GCC | Grand Composite Curve |
Appendix A
Appendix A.1. Evaporator
Appendix A.2. Absorber
Appendix A.3. Generator
Appendix A.4. Condenser
Appendix A.5. Throttle Valve
Appendix A.6. Pump
| Stream | 0 | 1 | 2 |
|---|---|---|---|
| A1 | −2.41 | 8.31 | −6.924 |
| A2 | 2.118 | −4.05 | 4.443 |
| I | A | B |
|---|---|---|
| 0 | 1 | 0 |
| 1 | 2.024913 | 0.33 |
| 2 | 0.840497 | 0.67 |
| 3 | 0.301559 | 1.67 |
| 4 | −0.20927 | 5.33 |
| 5 | −74.6025 | 14.33 |
| 6 | 4089.793 | 23.33 |
| I | A | B |
|---|---|---|
| 0 | 1 | 0 |
| 1 | 1.993772 | 0.33 |
| 2 | 1.098521 | 0.67 |
| 3 | −0.50945 | 1.67 |
| 4 | −1.76191 | 5.33 |
| 5 | −44.9005 | 14.33 |
| 6 | −723,692 | 36.67 |
| I | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| ai | 647.14 | −199.822371 | 109.035522 | −239.626217 | 88.689691 |
Appendix A.7. Specific Heat, Temperature, Pressure and Composition Relationships of the Solution
| I | mi | ni | ai |
|---|---|---|---|
| 1 | 0 | 0 | 1.28827 |
| 2 | 1 | 0 | 0.125247 |
| 3 | 2 | 0 | −2.08748 |
| 4 | 3 | 0 | 2.17696 |
| 5 | 0 | 2 | 2.35687 |
| 6 | 1 | 2 | −8.86987 |
| 7 | 2 | 2 | 10.2635 |
| 8 | 3 | 2 | −2.3744 |
| 9 | 0 | 3 | −6.70515 |
| 10 | 1 | 3 | 16.4508 |
| 11 | 2 | 3 | −9.36849 |
| 12 | 0 | 4 | 8.42254 |
| 13 | 1 | 4 | −8.58807 |
| 14 | 0 | 5 | −2.77049 |
| 15 | 4 | 6 | −0.961248 |
| 16 | 2 | 7 | 0.988009 |
| 17 | 1 | 10 | 0.308482 |
| I | mi | ni | ai |
|---|---|---|---|
| 1 | 0 | 1 | −7.6108 |
| 2 | 0 | 4 | 25.6905 |
| 3 | 0 | 8 | −247.092 |
| 4 | 0 | 9 | 325.952 |
| 5 | 0 | 12 | −158.854 |
| 6 | 0 | 14 | 61.9084 |
| 7 | 1 | 0 | 11.4314 |
| 8 | 1 | 1 | 1.18157 |
| 9 | 2 | 1 | 2.84179 |
| 10 | 3 | 3 | 7.41609 |
| 11 | 5 | 3 | 891.844 |
| 12 | 5 | 4 | −1613.09 |
| 13 | 5 | 5 | 622.106 |
| 14 | 6 | 2 | −207.588 |
| 15 | 6 | 4 | −6.87393 |
| 16 | 8 | 0 | 3.50716 |
| I | mi | ni | ai |
|---|---|---|---|
| 1 | 0 | 0 | 3.24004 |
| 2 | 0 | 1 | −0.03959 |
| 3 | 0 | 2 | 0.043562 |
| 4 | 0 | 3 | −0.00219 |
| 5 | 1 | 0 | −1.43526 |
| 6 | 1 | 1 | 1.05256 |
| 7 | 1 | 2 | −0.07193 |
| 8 | 2 | 0 | 12.2362 |
| 9 | 2 | 1 | −2.24368 |
| 10 | 3 | 0 | −20.178 |
| 11 | 3 | 1 | 1.10834 |
| 12 | 4 | 0 | 100.1454 |
| 13 | 4 | 2 | 0.644312 |
| 14 | 5 | 0 | −2.21246 |
| 15 | 5 | 2 | −0.75627 |
| 16 | 6 | 0 | −1.35529 |
| 17 | 7 | 2 | 0.183541 |
| I | mi | ni | ai |
|---|---|---|---|
| 1 | 0 | 0 | 3.22302 |
| 2 | 0 | 1 | −0.38421 |
| 3 | 0 | 2 | 0.046097 |
| 4 | 0 | 3 | 0.003789 |
| 5 | 0 | 4 | 0.000136 |
| 6 | 1 | 0 | 0.487855 |
| 7 | 1 | 1 | −0.12011 |
| 8 | 1 | 2 | 0.010615 |
| 9 | 2 | 3 | −0.00053 |
| 10 | 4 | 0 | 7.85041 |
| 11 | 5 | 0 | −11.5941 |
| 12 | 5 | 1 | −0.05232 |
| 13 | 6 | 0 | 4.89596 |
| 14 | 13 | 1 | 0.042106 |
| I | mi | ni | ai |
|---|---|---|---|
| 1 | 0 | 0 | 19.802202 |
| 2 | 0 | 1 | −11.809267 |
| 3 | 0 | 6 | 27.747998 |
| 4 | 0 | 7 | −28.863428 |
| 5 | 1 | 0 | −59.161661 |
| 6 | 2 | 1 | 578.091305 |
| 7 | 2 | 2 | −6.217367 |
| 8 | 3 | 2 | −3421.98402 |
| 9 | 4 | 3 | 11,940.3127 |
| 10 | 5 | 4 | −24,541.3777 |
| 11 | 6 | 5 | 29,159.1865 |
| 12 | 7 | 6 | −18,478.229 |
| 13 | 7 | 7 | 23.481943 |
| 14 | 8 | 7 | 4803.10617 |
References
- Hammond, G.; Norman, J. Heat recovery opportunities in UK industry. Appl. Energy 2014, 116, 387–397. [Google Scholar] [CrossRef] [Green Version]
- Oluleye, G.; Jobson, M.; Smith, R.; Perry, S.J. Evaluating the potential of process sites for waste heat recovery. Appl. Energy 2016, 161, 627–646. [Google Scholar] [CrossRef]
- Pátek, J.; Klomfar, J. Simple functions for fast calculations of selected thermodynamic properties of the ammonia-water system. Int. J. Refrig. 1995, 18, 228–234. [Google Scholar] [CrossRef]
- Sun, D.-W. Thermodynamic design data and optimum design maps for absorption refrigeration systems. Appl. Therm. Eng. 1997, 17, 211–221. [Google Scholar] [CrossRef]
- Sun, D.-W. Comparison of the performances of NH3-H2O, NH3-LiNO3 and NH3-NaSCN absorption refrigeration systems. Energy Convers. Manag. 1998, 39, 357–368. [Google Scholar] [CrossRef]
- Jawahar, C.; Saravanan, R. Generator absorber heat exchange based absorption cycle—A review. Renew. Sustain. Energy Rev. 2010, 14, 2372–2382. [Google Scholar] [CrossRef]
- Jawahar, C.; Raja, B.; Saravanan, R. Thermodynamic studies on NH3-H2O absorption cooling system using pinch point approach. Int. J. Refrig. 2010, 33, 1377–1385. [Google Scholar] [CrossRef]
- Du, S.; Wang, R.; Xia, Z. Optimal ammonia water absorption refrigeration cycle with maximum internal heat recovery derived from pinch technology. Energy 2014, 68, 862–869. [Google Scholar] [CrossRef]
- Haywood, A.; Sherbeck, J.; Phelan, P.; Varsamopoulos, G.; Gupta, S.K.S. Thermodynamic feasibility of harvesting data center waste heat to drive an absorption chiller. Energy Convers. Manag. 2012, 58, 26–34. [Google Scholar] [CrossRef]
- Sayadi, Z.; Thameur, N.B.; Bourouis, M.; Bellagi, A. Performance optimization of solar driven small-cooled absorption-diffusion chiller working with light hydrocarbons. Energy Convers. Manag. 2013, 74, 299–307. [Google Scholar] [CrossRef]
- Kim, D.; Ferreira, C.I. Air-cooled LiBr-water absorption chillers for solar air conditioning in extremely hot weathers. Energy Convers. Manag. 2009, 50, 1018–1025. [Google Scholar] [CrossRef]
- Weber, C.; Berger, M.; Mehling, F.; Heinrich, A.; Núñez, T. Solar cooling with water-ammonia absorption chillers and concentrating solar collector—Operational experience. Int. J. Refrig. 2014, 39, 57–76. [Google Scholar] [CrossRef]
- Ghaebi, H.; Karimkashi, S.; Saidi, M. Integration of an absorption chiller in a total CHP site for utilizing its cooling production potential based on R-curve concept. Int. J. Refrig. 2012, 35, 1384–1392. [Google Scholar] [CrossRef]
- Nikbakhti, R.; Wang, X.; Hussein, A.K.; Iranmanesh, A. Absorption cooling systems—Review of various techniques for energy performance enhancement. Alex. Eng. J. 2020, 59, 707–738. [Google Scholar] [CrossRef]
- Linnhoff, B.; Dunford, H.; Smith, R. Heat integration of distillation columns into overall processes. Chem. Eng. Sci. 1983, 38, 1175–1188. [Google Scholar] [CrossRef]
- Townsend, D.W.; Linnhoff, B. Heat and power networks in process design. Part II: Design procedure for equipment selection and process matching. AIChE J. 1983, 29, 748–771. [Google Scholar] [CrossRef]
- Glavič, P.; Kravanja, Z.; Homšak, M. Heat integration of reactors—I. Criteria for the placement of reactors into process flowsheet. Chem. Eng. Sci. 1988, 43, 593–608. [Google Scholar] [CrossRef]
- Fu, C.; Gundersen, T. Integrating compressors into heat exchanger networks above ambient temperature. AIChE J. 2015, 61, 3770–3785. [Google Scholar] [CrossRef]
- Fu, C.; Gundersen, T. Correct integration of compressors and expanders in above ambient heat exchanger networks. Energy 2016, 116, 1282–1293. [Google Scholar] [CrossRef]
- Wan Alwi, S.R.; Lee, C.K.M.; Lee, K.Y.; Abd Manan, Z.; Fraser, D.M. Targeting the maximum heat recovery for systems with heat losses and heat gains. Energy Convers. Manag. 2014, 87, 1098–1106. [Google Scholar] [CrossRef]
- M. Conde Engineering. Thermophysical Properties of {NH3+H2O} Mixtures for the Industrial Design of Absorption Refrigeration Equipment. Available online: www.mrc-eng.com/Downloads/NH3%26H2O%20%20Props%20English.pdf (accessed on 4 May 2016).
- Engineering Toolbox. Calculate Pump Hydraulic and Shaft Power. Available online: www.engineeringtoolbox.com/pumps-power-d_505.html (accessed on 10 May 2016).
- Engineering Toolbox. Converting Pump Heat to Pressure and Vice Versa. Available online: www.engineeringtoolbox.com/pump-head-pressure-d_663.html (accessed on 10 May 2016).
- Engineering Toolbox. Density, Specific Weight and Specific Gravity. Available online: www.engineeringtoolbox.com/density-specific-weight-gravity-d_290.html (accessed on 10 May 2016).








| Stream | TIN/°C | TOUT/°C | CP/kW °C−1 |
|---|---|---|---|
| Hot 1 | 95 | 80 | 60 |
| Hot 2 | 92 | 60 | 150 |
| Cold 1 | 95 | 110 | 30 |
| Cold 2 | 82 | 95 | 180 |
| 2 | 0.99 | 17 | 1000 | 4.347 | 0.45 | 0.54 |
| Stream | TIN/°C | TOUT/°C | |
|---|---|---|---|
| Evaporator | 2 | 2 | 1000 |
| Absorber | 48 | 34 | 1083 |
| Generator | 63 | 63 | 1110 |
| Condenser | 17 | 17 | 1021 |
| rich solution | 34 | 49 | 6 |
| lean solution | 63 | 48 | 11 |
| Non-integrated | 2610 | 1116 | 3726 | 5520 | 2115 | 7635 |
| Integrated | 2610 | 0 | 2610 | 4404 | 2115 | 6519 |
| Difference | −1116 | −1116 | −1116 | −1116 | ||
| Difference | 30% | 16% |
| Stream | TIN/°C | TOUT/°C | CP/kW °C−1 |
|---|---|---|---|
| Hot 1 | 25 | 20 | 100 |
| Hot 2 | 32 | 20 | 250 |
| Cold 1 | 35 | 50 | 70 |
| Cold 2 | 22 | 35 | 350 |
| 2 | 0.99 | 37 | 1000 | 4.347 | 0.43 | 0.50 |
| Stream | TIN/°C | TOUT/°C | CP/kW |
|---|---|---|---|
| evaporator | 2.0 | 2.0 | 1000 |
| absorber | 48 | 21 | 1166 |
| generator | 90 | 90 | 1112 |
| condenser | 17 | 17 | 1050 |
| rich solution | 21 | 35 | 126 |
| lean solution | 63 | 48 | 22 |
| Total | ||||||
|---|---|---|---|---|---|---|
| Non-integrated | 5600 | 1238 | 6838 | 3500 | 2238 | 5738 |
| Integrated | 4600 | 0 | 4600 | 3500 | 0 | 3500 |
| Difference | −1000 | −1238 | −2238 | −2238 | −2238 | |
| Difference | 33% | 39% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nemet, A.; Kravanja, Z.; Bogataj, M. Integration of an Absorption Chiller to a Process Applying the Pinch Analysis Approach. Processes 2022, 10, 1028. https://doi.org/10.3390/pr10051028
Nemet A, Kravanja Z, Bogataj M. Integration of an Absorption Chiller to a Process Applying the Pinch Analysis Approach. Processes. 2022; 10(5):1028. https://doi.org/10.3390/pr10051028
Chicago/Turabian StyleNemet, Andreja, Zdravko Kravanja, and Miloš Bogataj. 2022. "Integration of an Absorption Chiller to a Process Applying the Pinch Analysis Approach" Processes 10, no. 5: 1028. https://doi.org/10.3390/pr10051028
APA StyleNemet, A., Kravanja, Z., & Bogataj, M. (2022). Integration of an Absorption Chiller to a Process Applying the Pinch Analysis Approach. Processes, 10(5), 1028. https://doi.org/10.3390/pr10051028






