Experiment on Influence of Blade Angle on Hydraulic Characteristics of the Shaft Tubular Pumping Device
Abstract
:1. Introduction
2. Model Pump and Pumping Device
3. Model Test System and Test Method
3.1. Composition of the Test Bench
3.2. Test Method
3.2.1. Energy Test
3.2.2. Cavitation Test
3.2.3. Runaway Test
3.2.4. Pressure Pulsation Test
4. Results
4.1. Energy Characteristics
4.2. Cavitation Characteristics
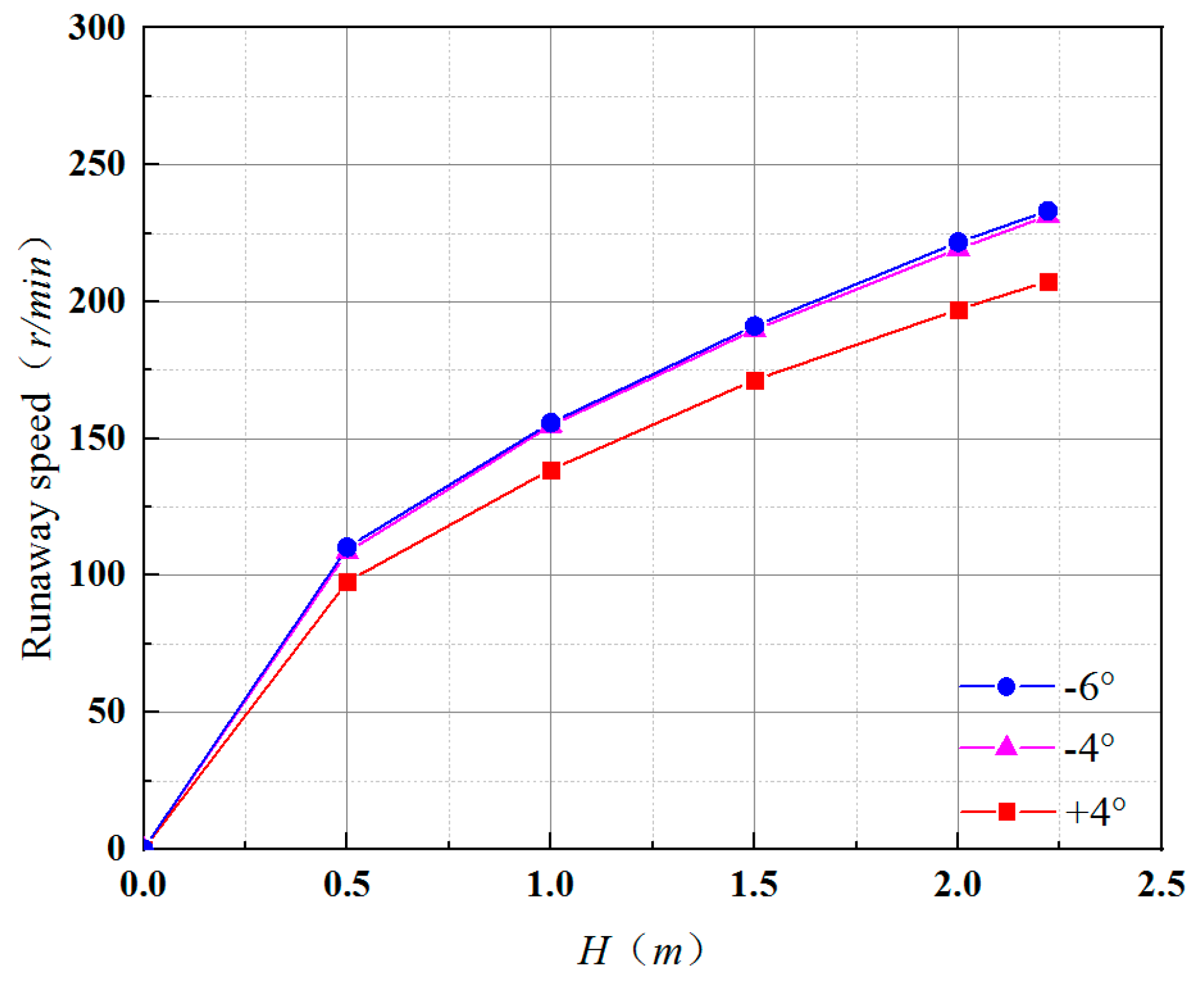
4.3. Runaway Characteristics
4.4. Pressure Pulsation Characteristics
5. Conclusions
- (1)
- When the blade angle of the vertical shaft tubular pumping device is −4°, the maximum efficiency of the model pumping device can reach 79.75%. The head condition of a −4° blade angle is the largest covered by the high efficiency area. We suggest that the −4° blade angle is selected as the actual operation angle of the pumping device.
- (2)
- The cavitation test results show that when the blade placement angle of the prototype pumping device is −4°, the critical cavitation allowance within the operating condition range of 0–2.22 m head is within 5.0 m. When the head is 1.52 m, the critical cavitation allowance is 3.2 m. When the head is 2.22 m, the critical cavitation allowance is 3.5 m.
- (3)
- The runaway speed of the pumping device decreases with the increase in blade angle. The smaller the blade placement angle, the higher the unit runaway speed. When the blade angle is −6°, the maximum head is less than 2.22 m. At this time, the maximum runaway speed of the prototype pump is less than 1.72 times the rated speed of the device. When the backflow occurs, the pump station unit can operate safely. The runaway speed at the same blade angle increases with the increase in head.
- (4)
- The vertical shaft tubular pumping device has high efficiency, good cavitation and runaway characteristics, and the variation law of pressure pulsation without abnormal pulsation. Therefore, we suggest giving priority to its application in the low-head pumping station of the Yangtze River.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Feng, X.; Qiu, B. Adjusting Frequency of Pump Blade Angles and Optimal Operation for Large Pumping Station System. Adv. Mech. Eng. 2013, 5, 317517. [Google Scholar] [CrossRef]
- Cheng, L. Numerical Simulation for Flow Pattern and Hydraulic Performance of Pumping Station. Ph.D. Thesis, Hohai University, Nanjing, China, 2006. [Google Scholar]
- Lu, L.G.; Chen, J.; Liang, J.D.; Leng, Y. Optimal hydraulic design of bulb tubular pump system. J. Hydraul. Eng. 2008, 39, 355–360. [Google Scholar]
- Kan, K.; Chen, H.; Yuan, Z.; Zhou, D.; Binama, M.; Dai, J. Transient characteristics during power-off process in a shaft extension tubular pump by using a suitable numerical model. Renew. Energy 2021, 164, 109–121. [Google Scholar] [CrossRef]
- Shi, W.; Liu, J.; Lu, L.G.; Xu, L.; Zhou, X.; Sun, S. Hydraulic design standardization for inlet and outlet conduit of tubular pump system with front-positioned shaft. South-to-North Water Transf. Water Sci. Technol. 2020, 18, 115–122. [Google Scholar]
- Liu, J.; Zheng, Y.; Zhou, D.; Mao, Y. Analysis of basic flow pattern in shaft front-positioned and shaft rear-positioned tubular pump systems. Trans. Chin. Soc. Agric. Mach. 2010, 41, 32–38. [Google Scholar]
- Zhang, R.T.; Zhu, H.G.; Yao, L.B. Comparison of shaft-type tubular pump systems with different outflow structures. J. Hydroelectr. Eng. 2014, 33, 198–201. [Google Scholar]
- Zhou, J.; Zhao, M.; Wang, C.; Gao, Z. Optimal design of diversion piers of lateral intake pumping station based on orthogonal test. Shock Vib. 2021, 2021, 6616456. [Google Scholar] [CrossRef]
- Zhang, W.; Shi, L.; Tang, F.; Duan, X.; Liu, H.; Sun, Z. Analysis of inlet flow passage conditions and their influence on the performance of an axial-flow pump. Proc. Inst. Mech. Eng. Part A J. Power Energy 2021, 235, 733–746. [Google Scholar] [CrossRef]
- Jiao, W.; Cheng, L.; Zhang, D.; Zhang, B.; Su, Y. Investigation of Key Parameters for Hydraulic Optimization of an Inlet Duct Based on a Whole Waterjet Propulsion Pump System. Trans. FAMENA 2021, 45, 145–162. [Google Scholar] [CrossRef]
- Gao, X.; Tian, Y.; Sun, B. Multi-objective optimization design of bidirectional flow passage components using RSM and NSGA II: A case study of inlet/outlet diffusion segment in pumped storage power station. Renew. Energy 2018, 115, 999–1013. [Google Scholar] [CrossRef]
- Shi, L.; Yuan, Y.; Jiao, H.; Tang, F.; Cheng, L.; Yang, F.; Jin, Y.; Zhu, Y. Numerical investigation and experiment on pressure pulsation characteristics in a full tubular pump. Renew. Energy 2021, 163, 987–1000. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, J.; Yu, X.; Zhou, D.; Calamak, M. Multi-objective optimization of a tubular pump to improve the applicable operating head and hydraulic performance. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 1555–1566. [Google Scholar] [CrossRef]
- Zhu, H.; Zhang, R. Numerical Simulation of Internal Flow and Performance Prediction of Tubular Pump with Adjustable Guide Vanes. Adv. Mech. Eng. 2014, 6, 171504. [Google Scholar] [CrossRef]
- Zhou, C.F.; Zhang, J.B.; Jiao, W.X.; Cheng, L.; Jiang, H.Y. Numerical simulation of influence of shaft on performance of low head tubular pumping system. J. Drain. Irrig. Mach. Eng. 2021, 39, 231–237. [Google Scholar]
- Jin, K.L.; Chen, Y.; Tang, F.P.; Shi, L.; Liu, H.; Zhang, W. Influence of shaft location on hydraulic characteristics of bidirectional tubular pump systems. J. Hydroelectr. Eng. 2021, 40, 67–77. [Google Scholar]
- Shi, L.; Zhang, W.; Jiao, H.; Tang, F.; Wang, L.; Sun, D.; Shi, W. Numerical simulation and experimental study on the comparison of the hydraulic characteristics of an axial-flow pump and a full tubular pump. Renew. Energy 2020, 153, 1455–1464. [Google Scholar] [CrossRef]
- Fang, G.; Guo, H.; Hu, D.; Shi, J.; Zhang, Y.; Kan, K.; Yang, J. Pressure pulsation and shaft modal optimization of a large shaft tubular pump. South-to-North Water Transf. Water Sci. Technol. 2021, 19, 822–832. [Google Scholar]
- Zhang, D.; Jiao, W.; Cheng, L.; Xia, C.; Zhang, B.; Luo, C.; Wang, C. Experimental study on the evolution process of the roof-attached vortex of the closed sump. Renew. Energy 2021, 164, 1029–1038. [Google Scholar] [CrossRef]
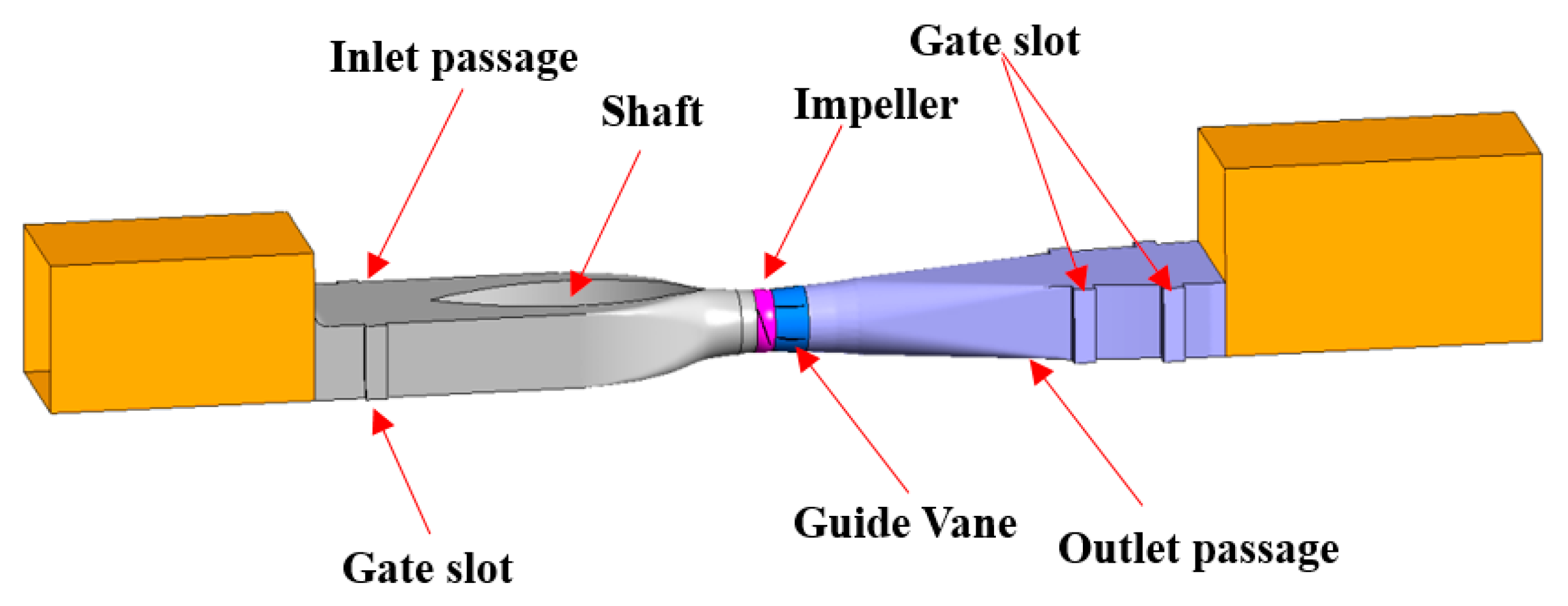
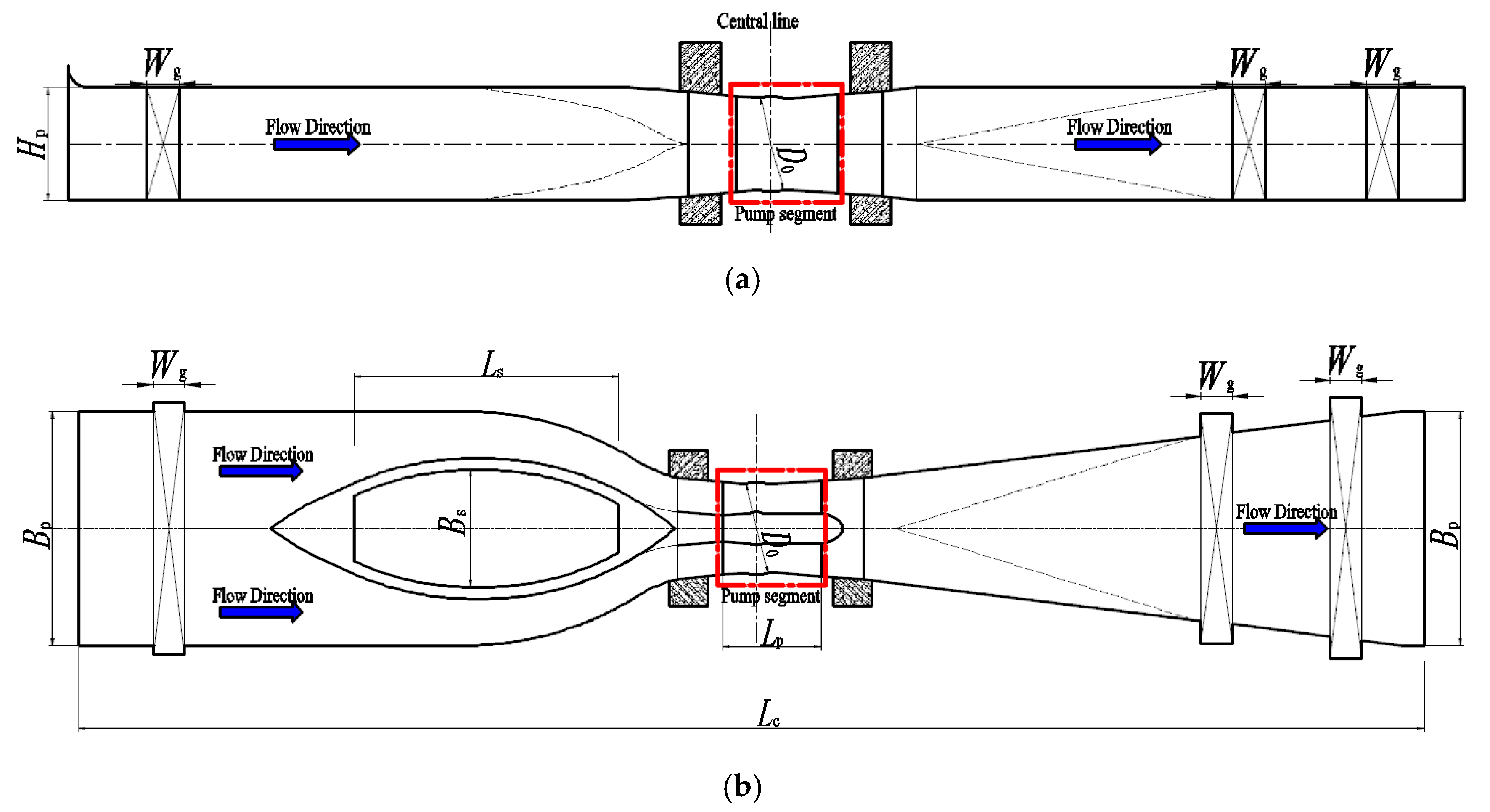






| Geometric Parameter | Value | Geometric Parameter | Value |
|---|---|---|---|
| Length of the shaft Ls (mm) | 6800 | Width of the shaft Bs (mm) | 3000 |
| Number of impeller blades Z1 | 3 | Number of guide vane blades Z2 | 6 |
| Diameter of the impeller D0 (mm) | 2350 | Length of the pump segment Lp (mm) | 2522 |
| Length of the pumping device Lc (mm) | 34,500 | Width of the pumping device Bp (mm) | 6000 |
| Height of the pumping device Hp (mm) | 2800 | Width of the gate Wg (mm) | 810 |
| Measurement Items | Measuring Instruments and Equipment | Model | Range | Calibration Accuracy |
|---|---|---|---|---|
| Head | Differential pressure transmitter | EJA110A | 0–200 kPa | ±0.1% |
| Flow rate | Electromagnetic flowmeter | E-mag | DN400 mm | ±0.2% |
| Torque and speed | Speed and torque sensor | ZJ | 100 N·m | ±0.15% |
| NPSH | Absolute pressure transmitter | EJA310A | 0–130 kPa | ±0.020% |
| Blade Angle (°) | Flowrate (L/s) | Head (m) | Shaft Power (kW) | Efficiency (%) |
|---|---|---|---|---|
| −6° | 177.25 | 2.29 | 4.993 | 79.56 |
| −4° | 190.07 | 2.52 | 5.864 | 79.75 |
| −2° | 195.64 | 2.78 | 6.962 | 76.76 |
| 0° | 211.16 | 2.89 | 7.826 | 76.36 |
| +2° | 218.40 | 3.12 | 8.779 | 76.20 |
| +4° | 265.92 | 2.47 | 8.682 | 74.10 |
| Blade Angle (°) | Low Head NPSHa(m) | Designed Head NPSHa (m) | High Head NPSHa (m) |
|---|---|---|---|
| −6 | 4.035 | 3.925 | 4.078 |
| −4 | 4.392 | 3.152 | 3.512 |
| −2 | 4.227 | 3.813 | 3.838 |
| 0 | 4.545 | 3.509 | 3.618 |
| +2 | 4.292 | 3.866 | 4.092 |
| +4 | 4.427 | 4.035 | 4.807 |
| Blade Angle (°) | Model Unit Runaway Speed (r/min) | Prototype Unit Runaway Speed (r/min) | Ratio of Prototype Unit Runaway Speed to Motor Rated Speed |
|---|---|---|---|
| −6 | 366.1 | 232.1 | 1.72 |
| −4 | 363.3 | 230.3 | 1.70 |
| +4 | 327.1 | 207.4 | 1.54 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, K.; Li, S.; Cheng, L.; Sun, T.; Zhang, B.; Jiao, W. Experiment on Influence of Blade Angle on Hydraulic Characteristics of the Shaft Tubular Pumping Device. Processes 2022, 10, 590. https://doi.org/10.3390/pr10030590
Cheng K, Li S, Cheng L, Sun T, Zhang B, Jiao W. Experiment on Influence of Blade Angle on Hydraulic Characteristics of the Shaft Tubular Pumping Device. Processes. 2022; 10(3):590. https://doi.org/10.3390/pr10030590
Chicago/Turabian StyleCheng, Kaihua, Songbai Li, Li Cheng, Tao Sun, Bowen Zhang, and Weixuan Jiao. 2022. "Experiment on Influence of Blade Angle on Hydraulic Characteristics of the Shaft Tubular Pumping Device" Processes 10, no. 3: 590. https://doi.org/10.3390/pr10030590






