Precipitation of Ferrous Oxalate from Ferrous Ammonium Sulfate in Oxalic Acid Solution
Abstract
:1. Introduction
2. Experimental
2.1. Materials
2.2. Characterization and Analysis
2.3. Apparatus and Procedure
3. Results and Discussion
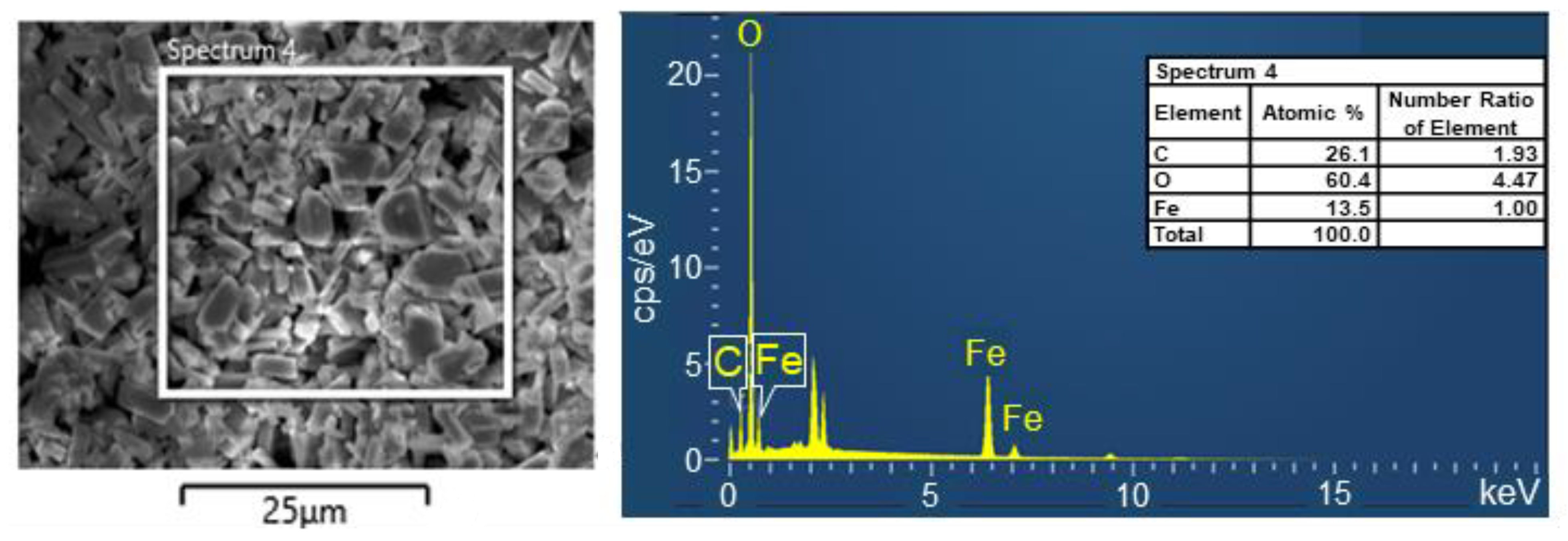
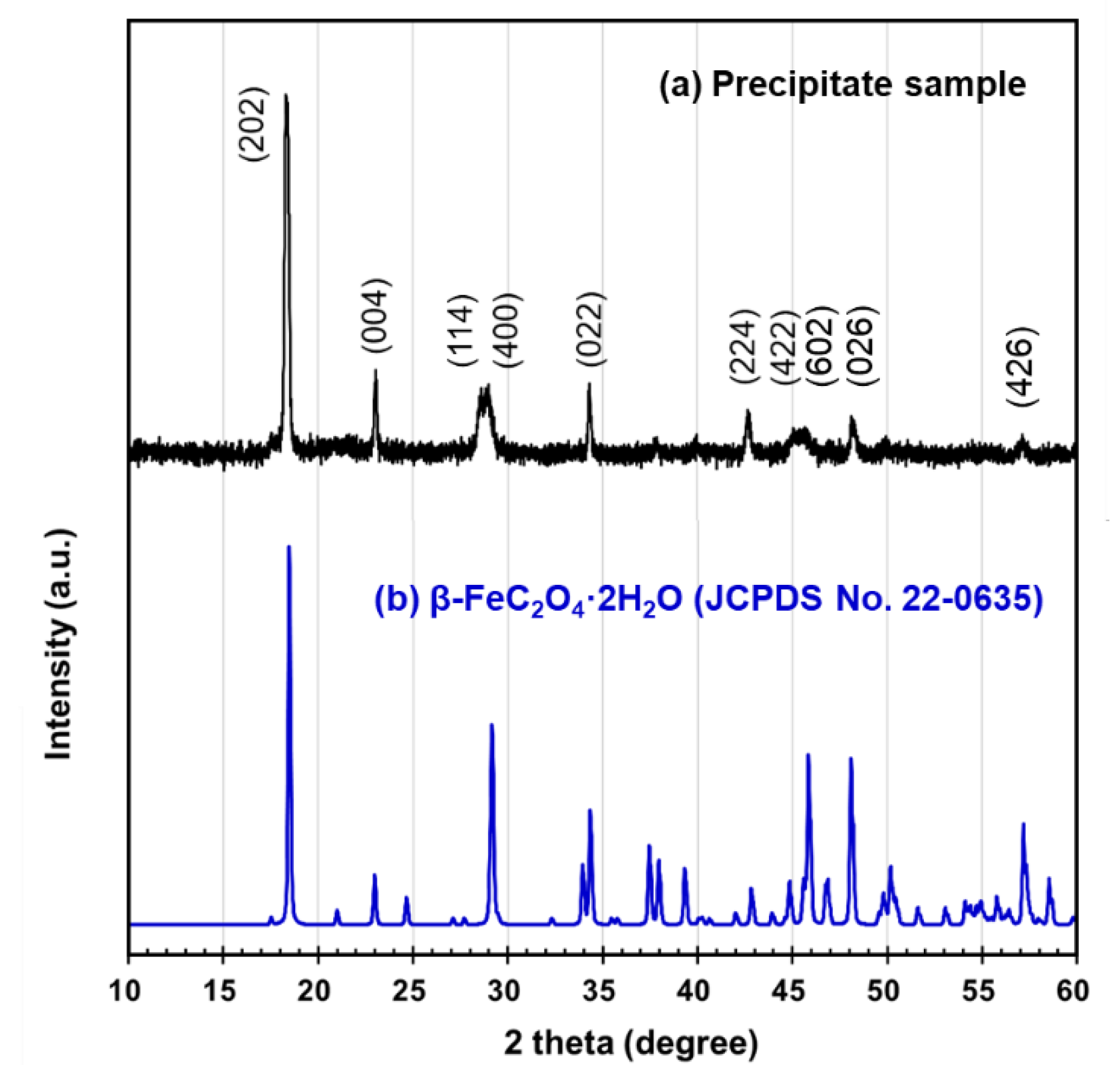
3.1. Characteristics of Precipitate
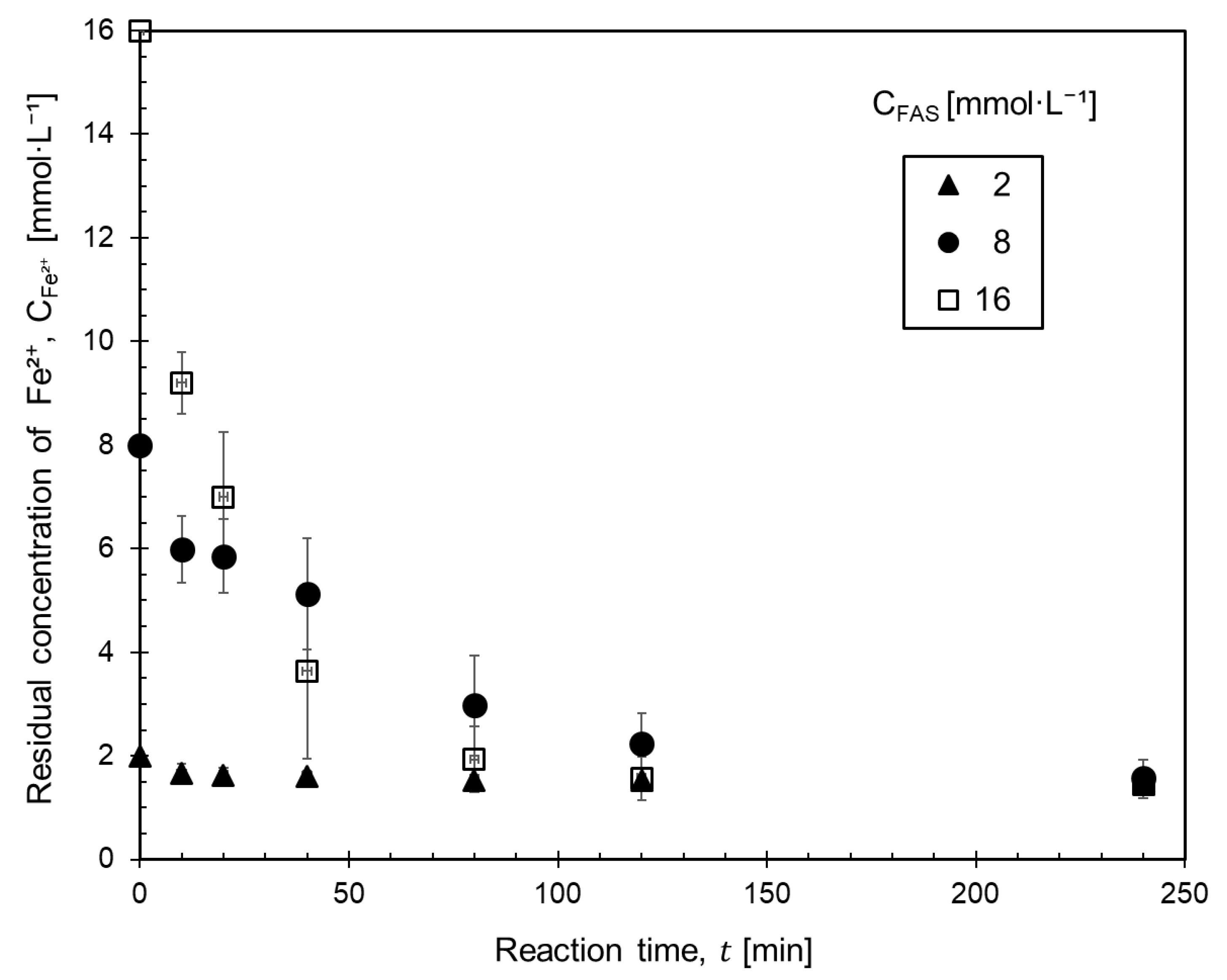
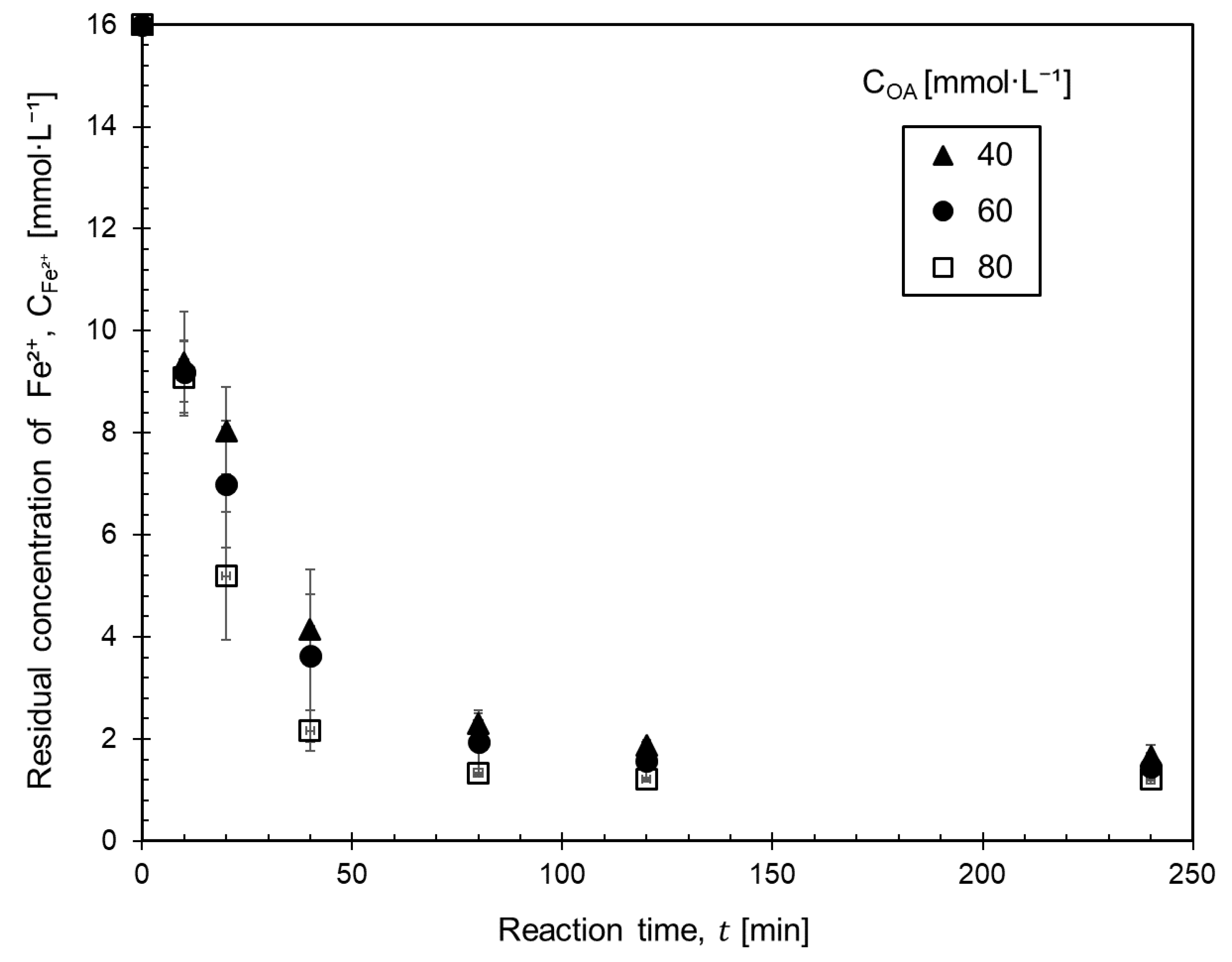
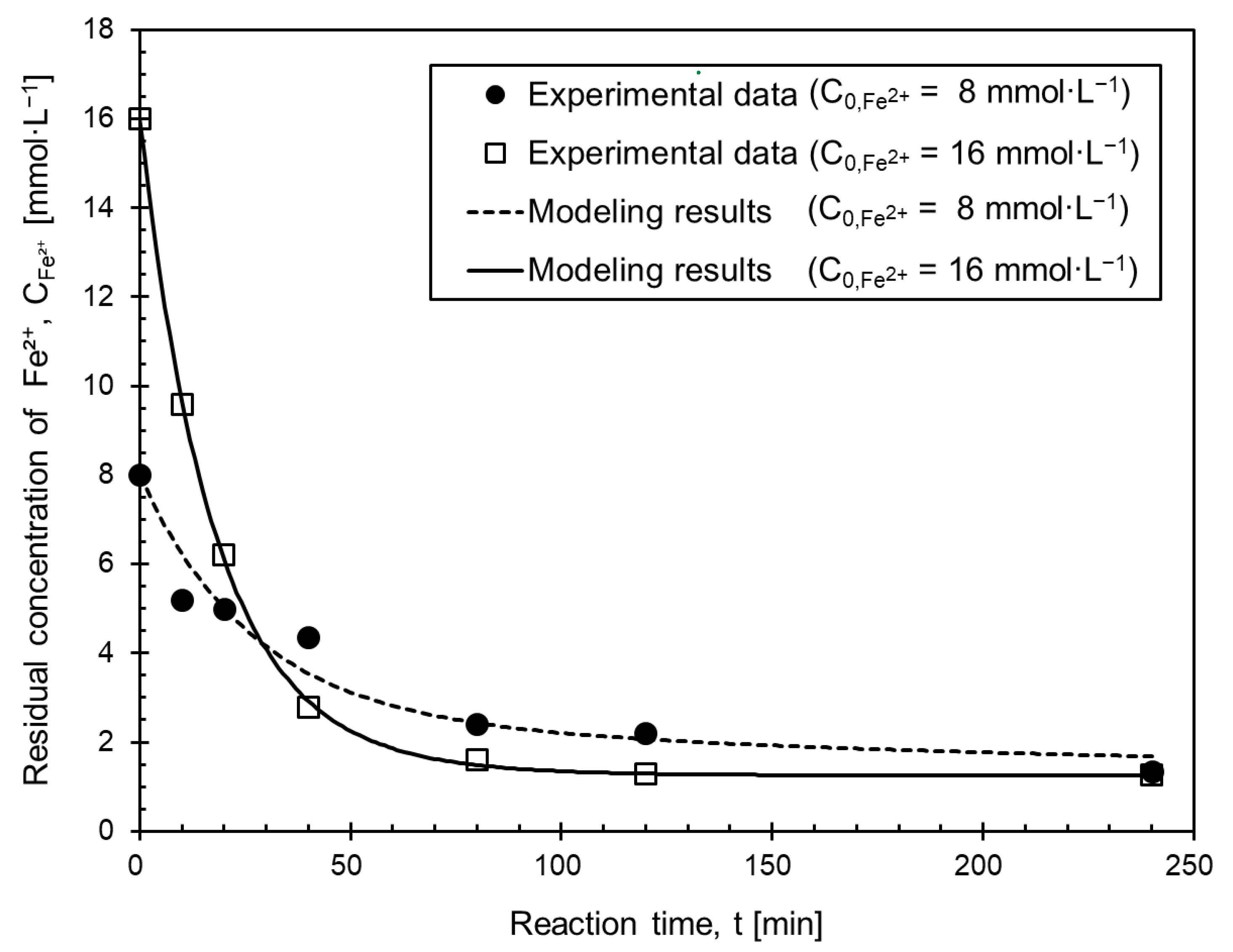
3.2. Effect of the Concentration of Ferrous Ammonium Sulfate and Oxalic Acid on the Kinetics of Ferrous Oxalate Precipitation
3.3. Modeling of Ferrous Oxalate Precipitation Behavior
4. Conclusions
- The higher the initial ferrous concentration, the faster precipitation, due to the more precipitate particles which supplied particle growth sites.
- The change in oxalic acid concentration did not significantly affect the precipitation rate.
- The ferrous oxalate precipitation behavior could be modeled with a first-order response of the residual ferrous concentration.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lee, B.-C.; Oh, W. Temperature and Concentration Dependencies of Chemical Equilibrium for Reductive Dissolution of Magnetite Using Oxalic Acid. J. Nucl. Fuel Cycle Waste Technol. (JNFCWT) 2021, 19, 187–196. [Google Scholar] [CrossRef]
- Kim, H.R.; Park, J.K.; Lee, S.I.; Oh, W.; Kim, J.; Kim, C.; Lee, B.-C. Kinetics of Reductive Dissolution of a Magnetite Specimen Using Oxalic Acid. Processes 2022, 10, 696. [Google Scholar] [CrossRef]
- Moon, J.; Kim, S.; Choi, W.; Choi, B.; Chung, D.; Seo, B. The Status and Prospect of Decommissioning Technology Development at KAERI. J. Nucl. Fuel Cycle Waste Technol. (JNFCWT) 2019, 17, 139–165. [Google Scholar] [CrossRef]
- Lee, S.O.; Tran, T.; Park, Y.Y.; Kim, S.J.; Kim, M.J. Study on the kinetics of iron oxide leaching by oxalic acid. Int. J. Miner. Process. 2006, 80, 144–152. [Google Scholar] [CrossRef]
- Lee, S.O.; Tran, T.; Jung, B.H.; Kim, S.J.; Kim, M.J. Dissolution of iron oxide using oxalic acid. Hydrometallurgy 2007, 87, 91–99. [Google Scholar] [CrossRef]
- Salmimies, R.; Mannila, M.; Juha, J.; Häkkinen, A. Acidic Dissolution of Magnetite: Experimental Study on The Effects of Acid Concentration and Temperature. Clays Clay Miner. 2011, 59, 136–146. [Google Scholar] [CrossRef]
- Salmimies, R.; Vehmaanperä, P.; Häkkinen, A. Acidic dissolution of magnetite in mixtures of oxalic and sulfuric acid. Hydrometallurgy 2016, 163, 91–98. [Google Scholar] [CrossRef]
- Manjanna, J.; Venkateswaran, G.; Sherigara, B.S.; Nayak, P.V. Dissolution studies of chromium substituted iron oxides in reductive-complexing agent mixtures. Hydrometallurgy 2001, 60, 155–165. [Google Scholar] [CrossRef]
- Won, H.-J.; Lee, W.-S.; Jung, C.-H.; Park, S.-Y.; Choi, W.-K.; Moon, J.-K. A Feasibility Study on the Decontamination of Type 304 Stainless Steel by N2H4 Base Solution. Asian J. Chem. 2014, 26, 1327–1330. [Google Scholar] [CrossRef]
- Müller, H.; Bourcet, L.; Hanfland, M. Iron(II)oxalate Dihydrate—Humboldtine: Synthesis, Spectroscopic and Structural Properties of a Versatile Precursor for High Pressure Research. Minerals 2021, 11, 113. [Google Scholar] [CrossRef]
- Li, C.; Ning, Y.; Yan, T.; Zheng, W. Studies on nucleation and crystal growth kinetics of ferrous oxalate. Heliyon 2019, 5, e02758. [Google Scholar] [CrossRef] [PubMed]
- Abdel-Ghafar, H.M.; Ibrahim, M.A.M.; El-Shall, H.; Ismail, A.K. Innovative findings about ferrous oxalate dihydrate crystallization in simulated dihydrate phosphoric acid product. Water Sci. Technol. 2018, 77, 2940–2945. [Google Scholar] [CrossRef] [PubMed]
- Abdel-Ghafar, H.M.; Abdel-Aal, E.A.; Ibrahim, M.A.M.; El-Shall, H.; Ismail, A.K. Studying nucleation aspects and morphology of iron (II) oxalate dihydrate crystals in water and diluted phosphoric acid media. Egypt. J. Pet. 2018, 27, 1235–1240. [Google Scholar] [CrossRef]
- Abdel-Ghafar, H.M.; Abdel-Aal, E.A.; Ibrahim, M.A.M.; El-Shall, H.; Ismail, A.K. Purification of high iron wet-process phosphoric acid via oxalate precipitation method. Hydrometallurgy 2019, 184, 1–8. [Google Scholar] [CrossRef]
- Xiao, Y.; Sun, T.; Zhao, Y.-H. Experimental Study on Preparation of Ferropericlase by Oxalate Coprecipitation. Minerals 2020, 10, 179. [Google Scholar] [CrossRef] [Green Version]
- Santawaja, P.; Kudo, S.; Tahara, A.; Asano, S.; Hayashi, J.-I. Dissolution of Iron Oxides Highly Loaded in Oxalic Acid Aqueous Solution for a Potential Application in Iron-Making. ISIJ Int. 2021. [Google Scholar] [CrossRef]
- Ghasemi, S.; Rafiei, N.; Heidarpour, A. Theoretical analysis and experimental Validation of selective oxalate precipitation. Miner. Process. Extr. Metall. 2020, 131, 79–84. [Google Scholar] [CrossRef]
- Wikipedia. Available online: en.wikipedia.org/wiki/Iron(II)_oxalate (accessed on 15 November 2022).



| Operating Variable | Experimental Condition |
|---|---|
| [°C] | 25 |
| Concentration of oxalic acid, [mmol·L−1] | 40, 60, 80 |
| Concentration of ferrous ammonium sulfate, [mmol·L−1] | 2, 8, 16 |
| Volume of reaction solution, [mL] | 300 |
| Reaction time, [min] | 240 |
[mmol·L−1] | Model Parameters | RMSE for Two Parameter Model | ||
|---|---|---|---|---|
| 8 | 45 | 24.4 | 80,000 | 0.67 |
| 16 | 15 | 10.2 | 100 | 0.40 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.I.; Kim, H.R.; Park, J.K.; Oh, W.; Kim, J.; Kim, C.; Lee, J.; Kim, K.-C.; Lee, B.-C. Precipitation of Ferrous Oxalate from Ferrous Ammonium Sulfate in Oxalic Acid Solution. Processes 2022, 10, 2420. https://doi.org/10.3390/pr10112420
Lee SI, Kim HR, Park JK, Oh W, Kim J, Kim C, Lee J, Kim K-C, Lee B-C. Precipitation of Ferrous Oxalate from Ferrous Ammonium Sulfate in Oxalic Acid Solution. Processes. 2022; 10(11):2420. https://doi.org/10.3390/pr10112420
Chicago/Turabian StyleLee, Su In, Hye Rim Kim, Jae Kwan Park, Wonzin Oh, Jeongju Kim, Chorong Kim, Junghyun Lee, Ki-Chul Kim, and Byung-Chul Lee. 2022. "Precipitation of Ferrous Oxalate from Ferrous Ammonium Sulfate in Oxalic Acid Solution" Processes 10, no. 11: 2420. https://doi.org/10.3390/pr10112420





