Numerical Modelling and Simulation of Heat Transfer during Magnetic Moulding of Al/SiCp Metal Matrix Composites
Abstract
:1. Introduction
2. Experimental Validation Setup
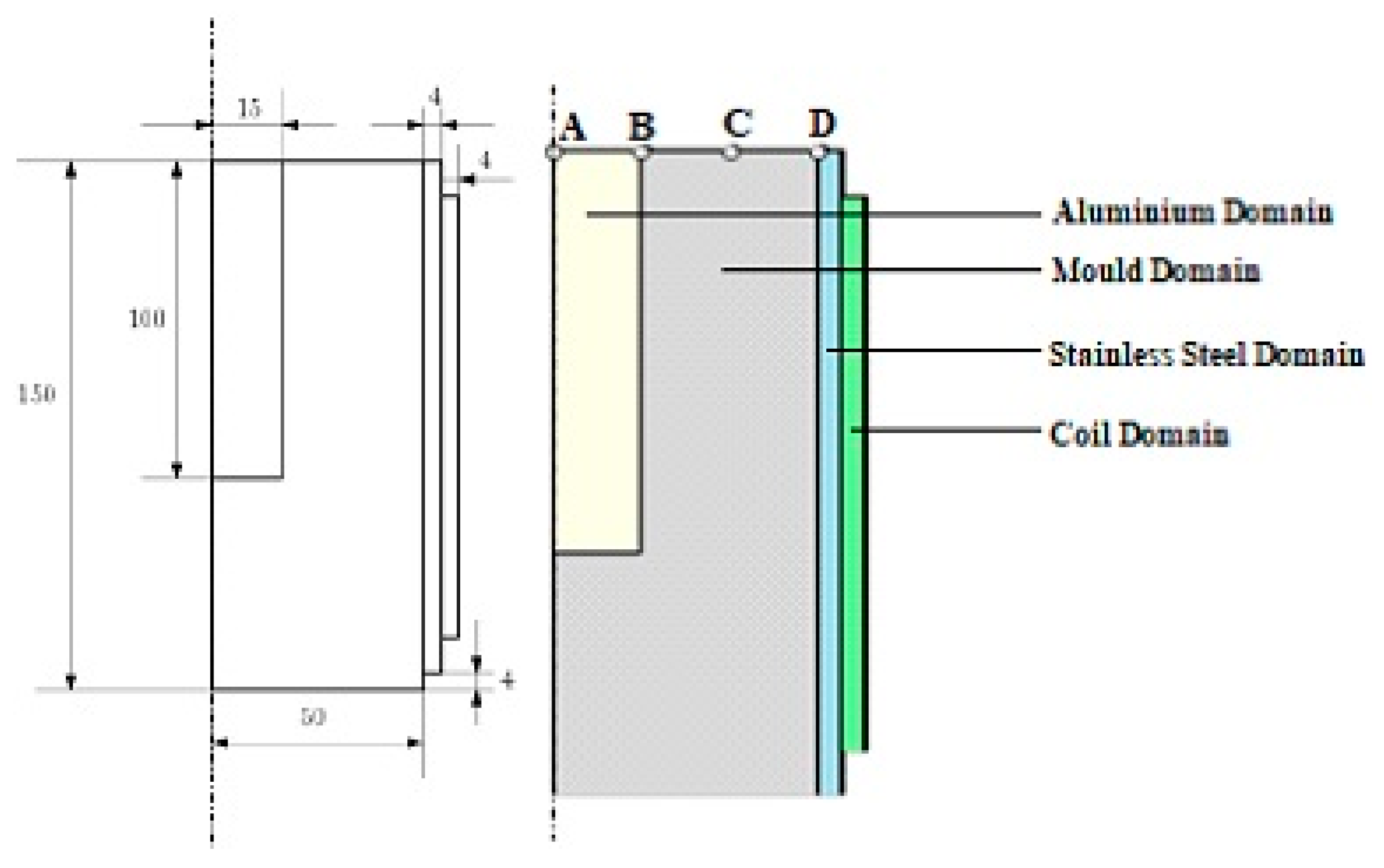
2.1. Magnetic Moulding Setup
2.2. Material Modelling
| Properties | Al/SiCp | Grade 410 SS [15,16] | Olivine Sand | Grade 304 L SS [15,16] | Copper |
|---|---|---|---|---|---|
| Density (kg/m3) | 2770 | 7880 | 3150 | 8000 | 8960 |
| Thermal conductivity, K (W/m K) | 200 | 25 | 7.5 | 16.2 | 400 |
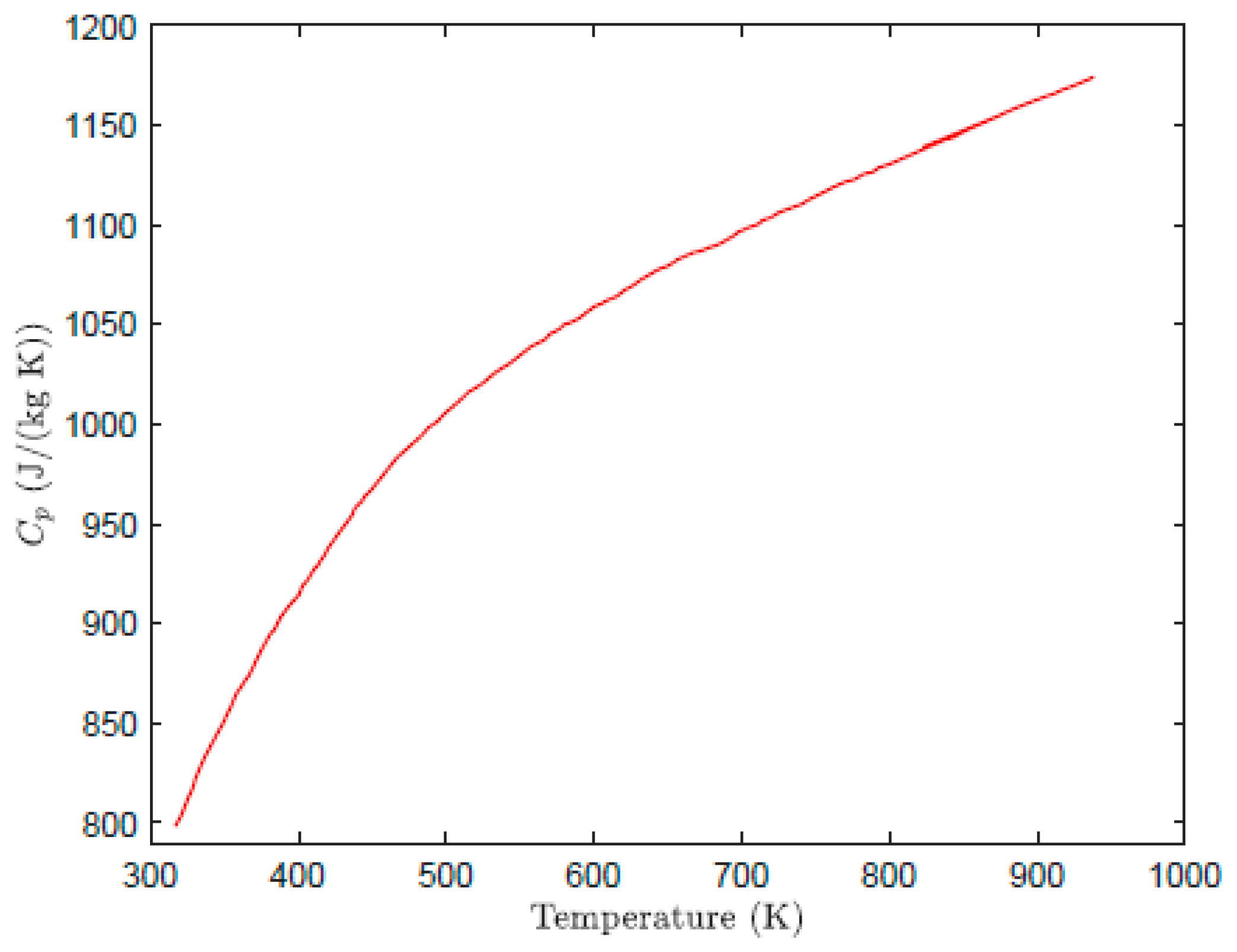
| Specific heat at constant pressure, Cp (J/kg K) | 775 | 460 | c.f Figure 2 | 500 | 385 |
| Relative permeability | 1 | 750 | - | 1.008 | 1 |
| Electrical conductivity | 1.11 × 107 | 1.74 × 107 | - | 1.37 × 107 | 6 × 107 |
| Porosity | - | 0.4804 | 0.440 | - | - |
2.3. Theoretical Formulation
2.3.1. Magnetic Field
2.3.2. Heat Transfer
2.3.3. Porous Media
2.3.4. Phase Change Medium
2.4. Testing and Characterization

3. Results and Discussion
- The temperature distribution is uniform throughout the EPS foam domain where the molten aluminium is poured.
- The heat loss due to radiation around the cast setup is negligible.
- The thermal expansion of the cast being produced is very small and can be neglected in the heat transfer equation.
- Axisymmetric conditions apply for the whole magnetic moulding setup (the corresponding equations were used while solving the model in the commercial software COMSOL).
- The material is homogeneous and isotropic.
- The Fuller’s earth coating on the EPS pattern is very thin and can be neglected.
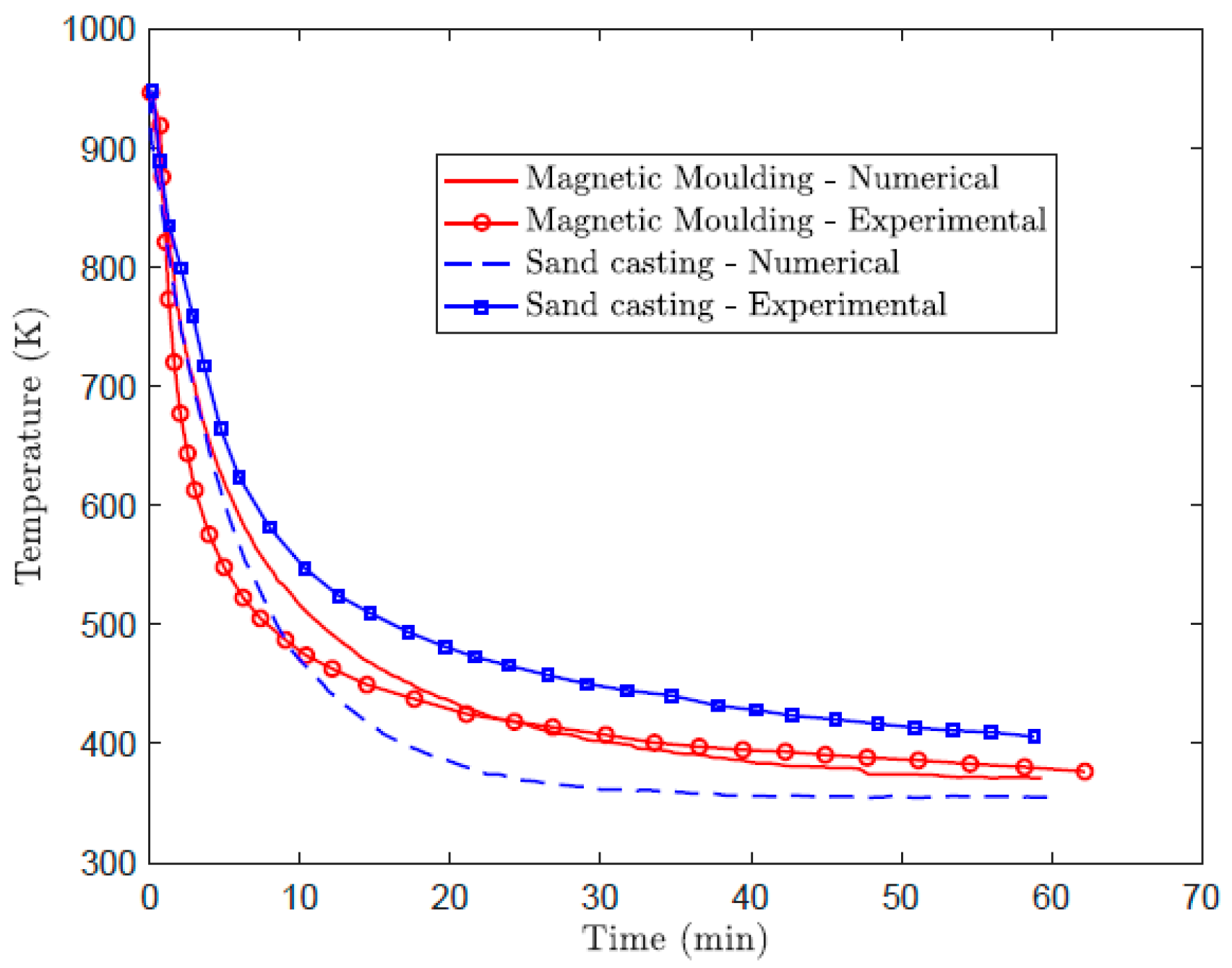
3.1. Experimental Results
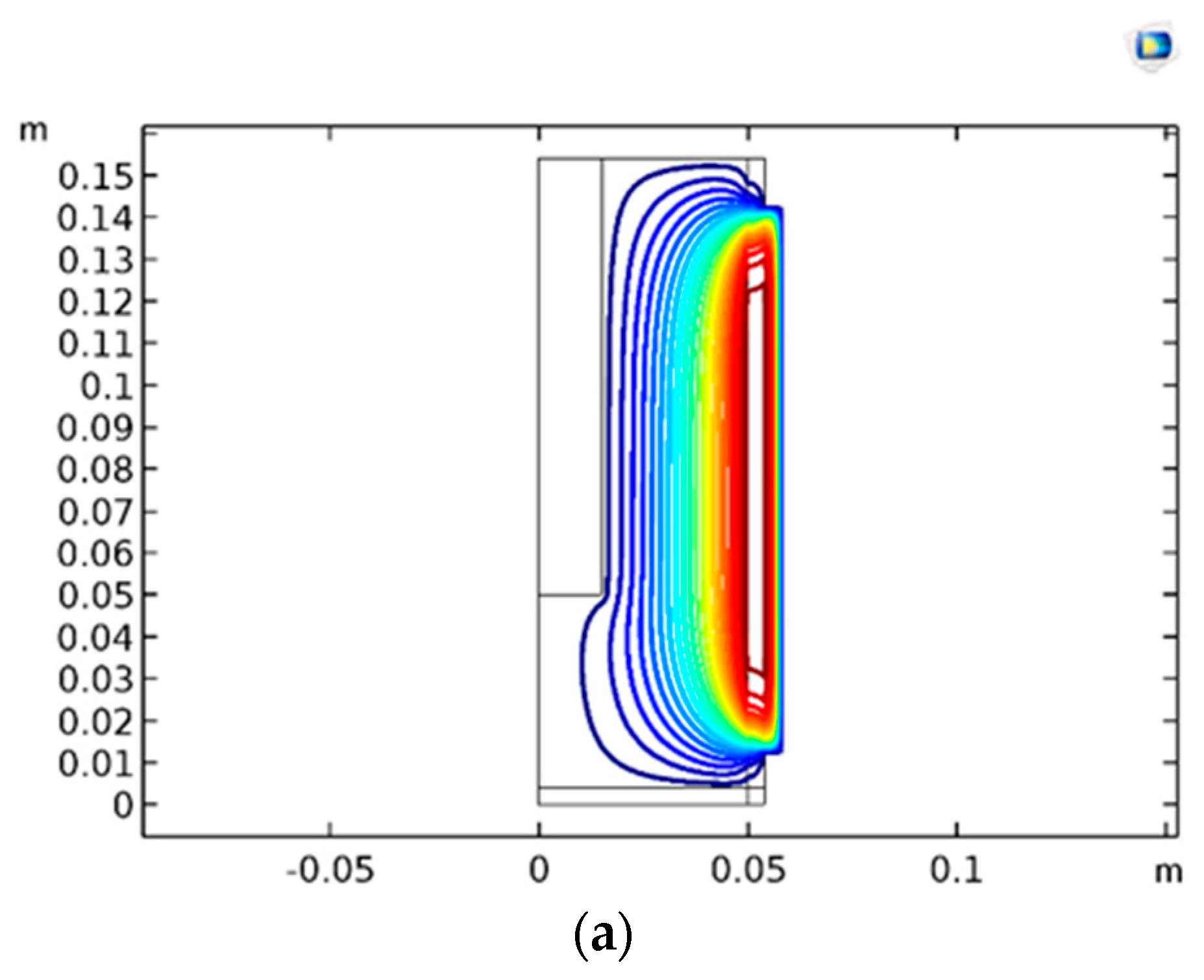
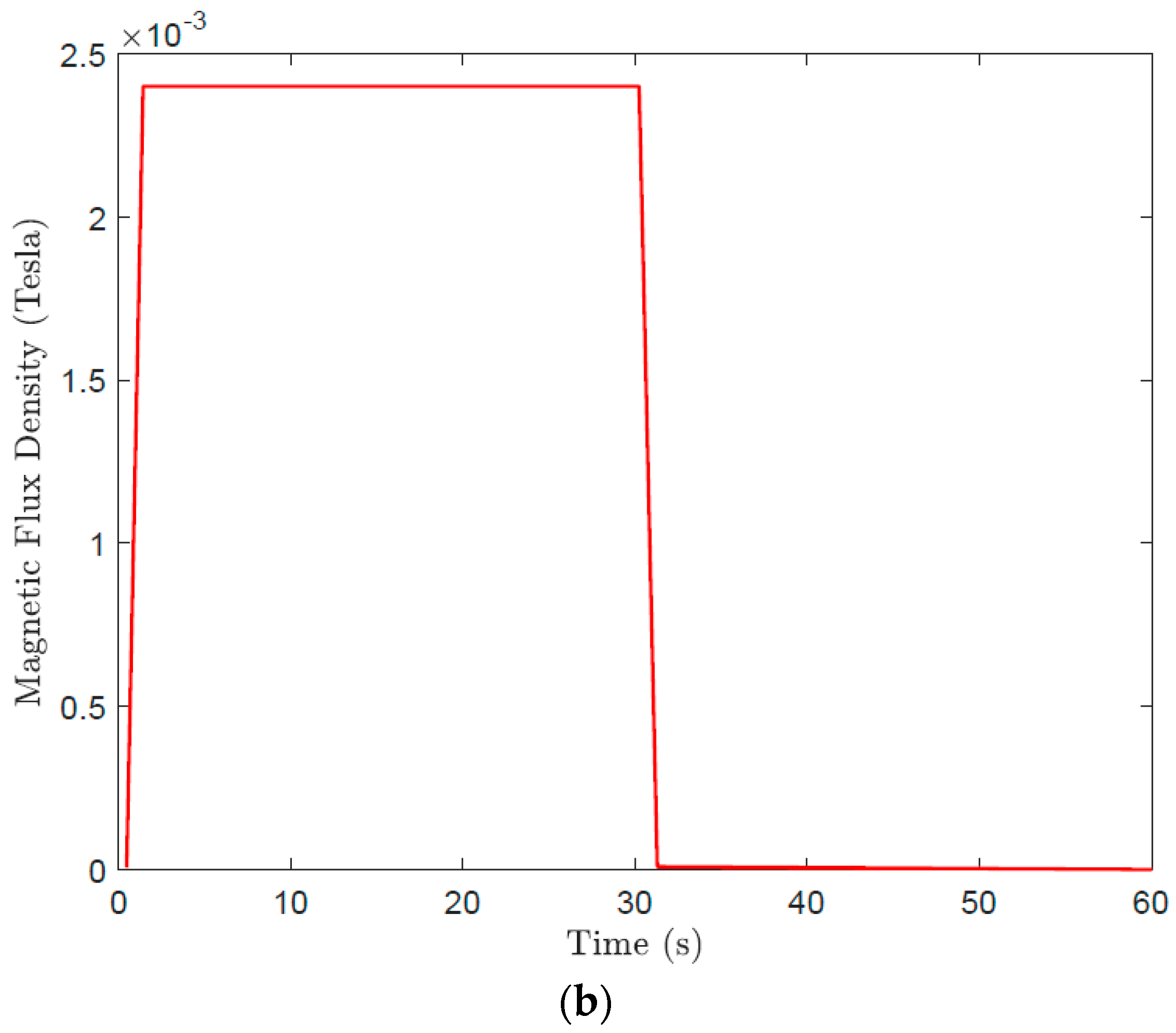
3.2. Effect of Magnetic Field and Flux Lines
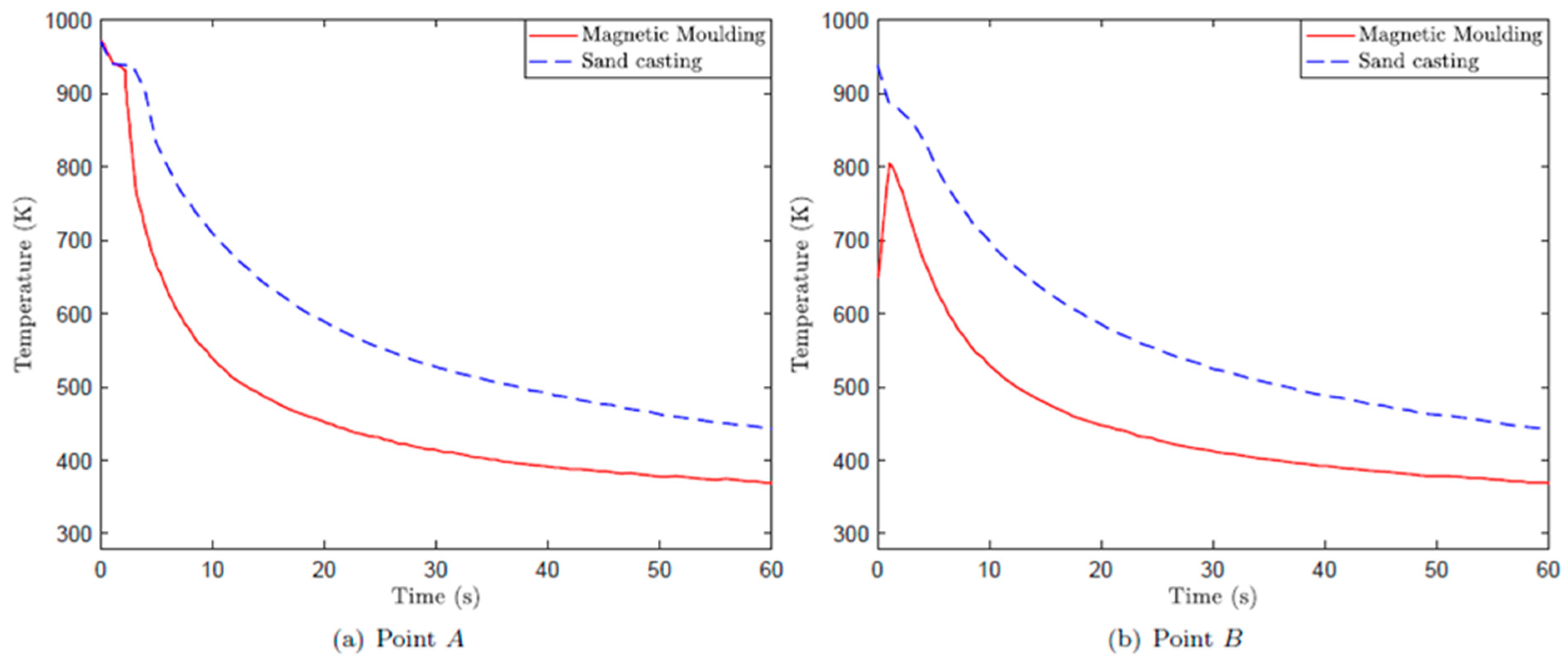
3.3. Effect of Temperature at the Locations A, B, C and D
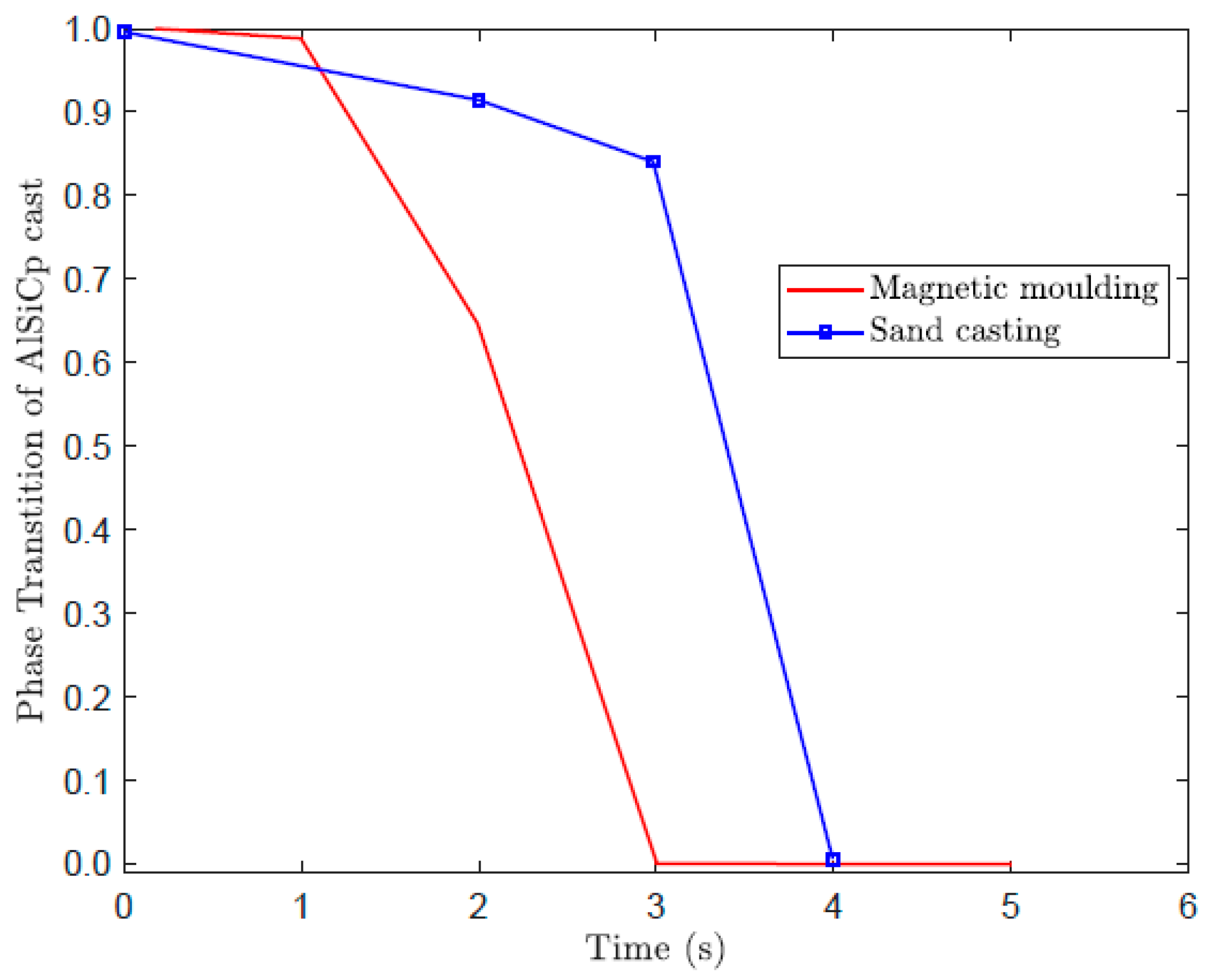
3.4. Effect of Phase Transition of Al/SiCp
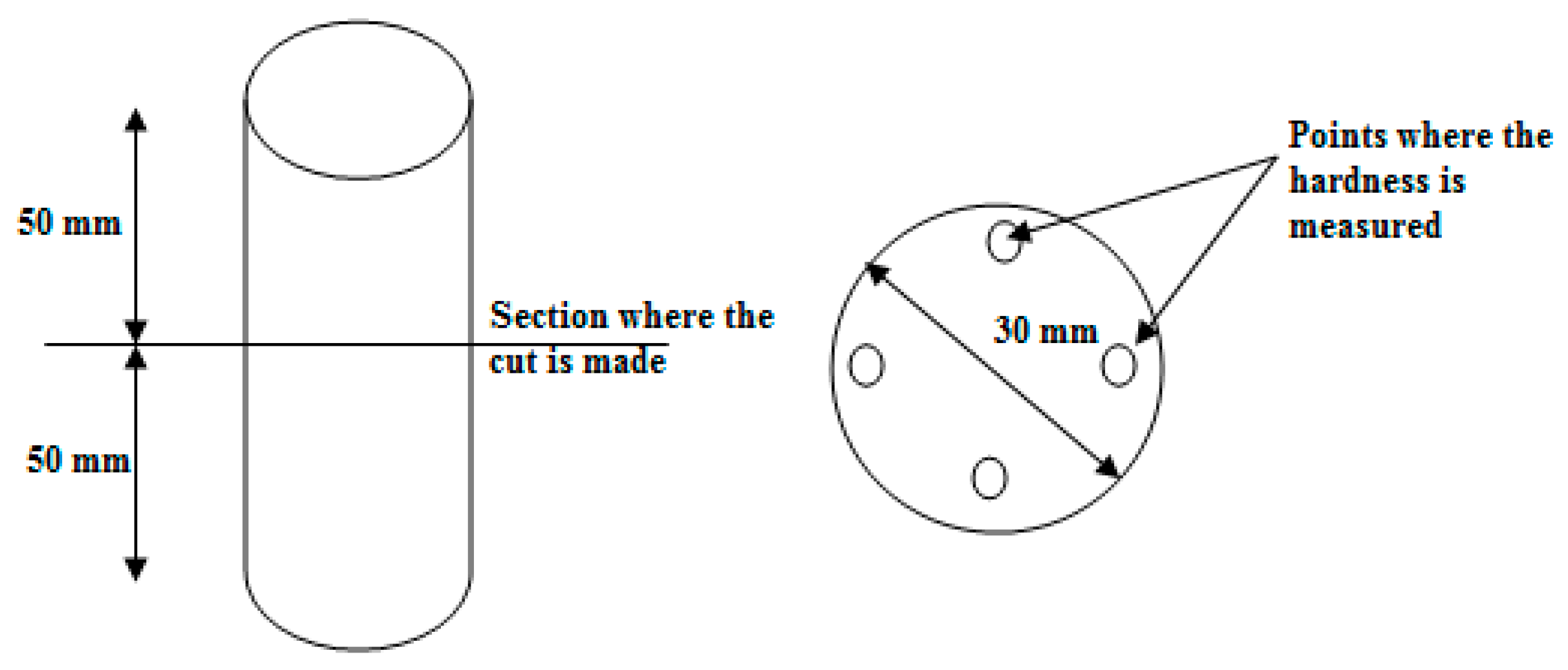
3.5. Microstructure and Hardness Test
3.6. Dry Wear Test
3.7. Impact Toughness
3.8. Surface Roughness
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jain, S.; Ramesh Kumar, N.; Ishim, P. Challenges and Future Prospective of Alternative Materials to Silica Sand for Green Sand Mould Casting: A Review. Trans. Indian Inst. Met. 2021, 74, 2939–2952. [Google Scholar]
- Srinivasan, K.; Siddharth, C.S.K.; Kaarthic, L.V.A.; Thenarasu, M. Evaluation of mechanical properties, economic and environmental benefits of partially replacing silica sand with biomass ash for aluminium casting. Mater. Today Proc. 2018, 5, 483. [Google Scholar]
- Campbell, J. Complete Casting Handbook, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Wittmoser, A. The New Third Generation of Moulding Processes; AFS Transactions: Schaumburg, IL, USA, 1975. [Google Scholar]
- Desai, J.; Heinen, J. Permanent-Mould Casting. Number 3461–3463 in Encyclopedia of Material Science and Engineering; Elsevier: Amsterdam, The Netherlands, 1986. [Google Scholar]
- Geffroy, P.M.; Lakehal, M.; Goñi, J.; Beaugnon, E.; Heintz, J.M.; Silvain, J.F. Thermal and mechanical behavior of Al-Si alloy cast using magnetic moulding and lost foam processes. Metall. Mater. Trans. A 2006, 37, 441–447. [Google Scholar] [CrossRef]
- Senthilkumaran, S.; Boopathy, S.R.; Ramesh, A. Theoretical and experimental investigation of mould strength in magnetic moulding compacts. J. Mater. Process. Technol. 2008, 205, 235–242. [Google Scholar]
- Goni, J. The Innovative Casting Process for the Improvement of the Competitiveness and Working Conditions of the European Foundaries; Magnet Co-Operative Research Project Report; Fundación INASMET: San Sebastián, Spain, 2006. [Google Scholar]
- Bates, C.; Littleton, H.; Stroom, P. 64th World Foundary Congress; Foundary Technical Association: Paris, France, 2000. [Google Scholar]
- Karimian, M.; Ourdjini, A.; Idris, M.H.; Jafari, H. Effect of pattern coating thickness on the characteristics of lost foam Al-Si-Cu alloy casting. Trans. Nonferrous Met. Soc. China 2012, 22, 2092–2097. [Google Scholar] [CrossRef]
- Zhilong, Z.; Liu, Y.; Liu, L. Grain refinement induced by a pulsed magnetic field and synchronous solidification. Mater. Manuf. Process. 2011, 26, 1202–1206. [Google Scholar]
- Sijo, M.; Jayadevan, K. Analysis of stir cast aluminium silicon carbide metal matrix composite: A comprehensive review. Procedia Technol. 2016, 24, 379–385. [Google Scholar] [CrossRef] [Green Version]
- Harvey, P.D. (Ed.) Engineering Properties of Steels; Americal Society of Metals: Russell Twonship, OH, USA, 1982. [Google Scholar]
- Boyer, H.E.; Gall, T.L. (Eds.) Metals Handbook; American Society of Metals: Russell Twonship, OH, USA, 1985. [Google Scholar]
- Boyer, H.E.; Galls, T.L. Metals Handbook; Vol I: Properties and Selection: Irons, Steels and High performance alloys; ASM International: Almere, The Netherlands, 1985. [Google Scholar]
- Peckner, D.; Bernstein, I. (Eds.) Handbook of Stainless Steels; Mc Graw Hill Company: New York, NY, USA, 1977. [Google Scholar]
- Ingham, D.B.; Pop, I. Transport Phenomena in Porous Media; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Nield, D.; Bejan, A. Convection in Porous Media; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Prakash, C.A.; Ronald, B.A.; Karthik, M.S. Effect of magnetic flux variation on the hardness of the magnetic moulded AlSiCp. In Proceedings of the National Symposium of Mechanical Engineering Research Scholars, NIT Warangal, Telangana, India, 7 October 2016. [Google Scholar]
- Anand Ronald, B.; Arun Prakash, C.; Suba Karthik, M. Influence of steel shots size on tensile properties of magnetic moulded MMC. Appl. Mech. Mater. 2016, 852, 118–122. [Google Scholar] [CrossRef]
- Leclaire, P.; Umnova, O.; Horoshenkov, K.V.; Maillet, L. Porosity measurement by comparison of air volumes. Rev. Sci. Instrum. 2003, 74, 1366–1370. [Google Scholar] [CrossRef]



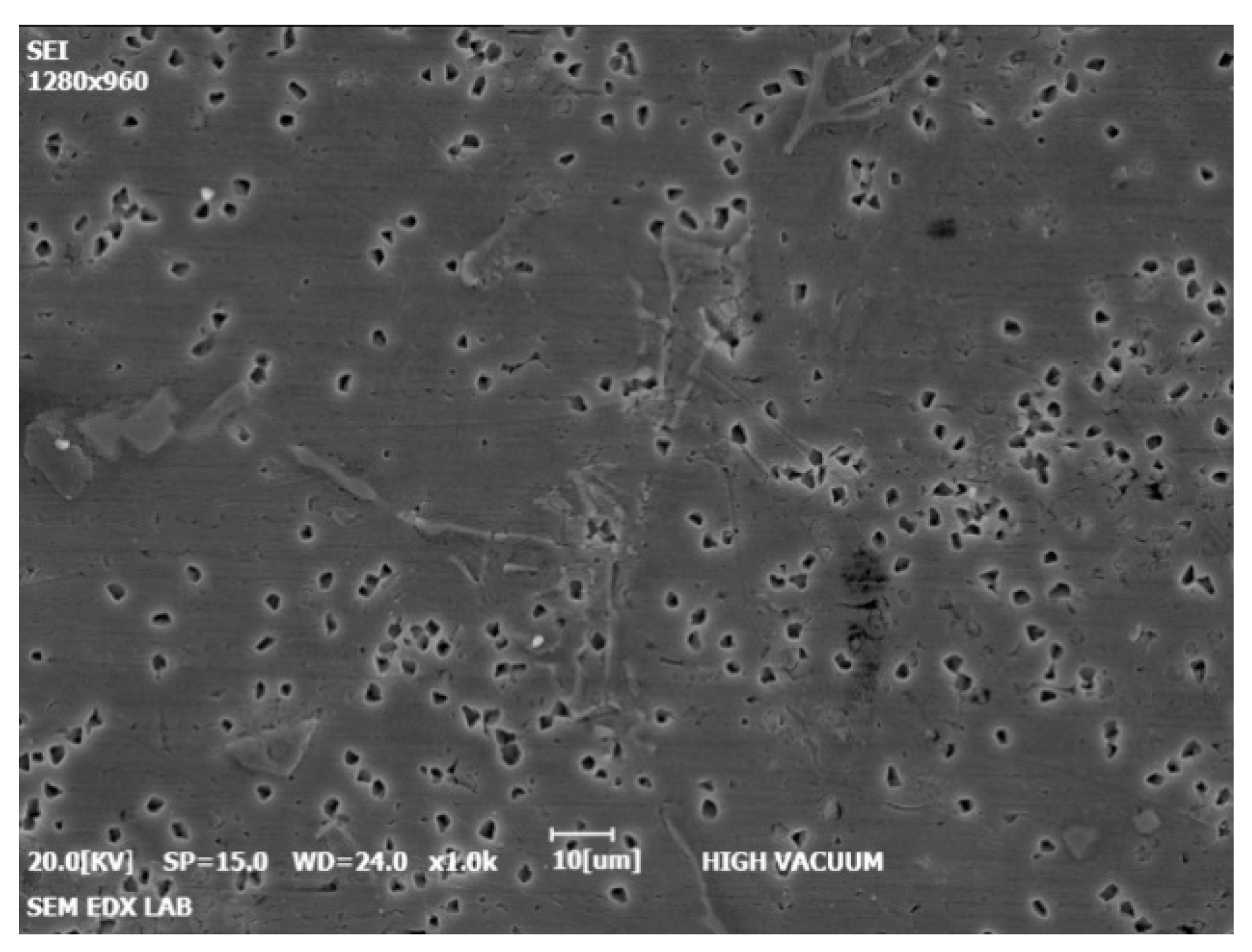
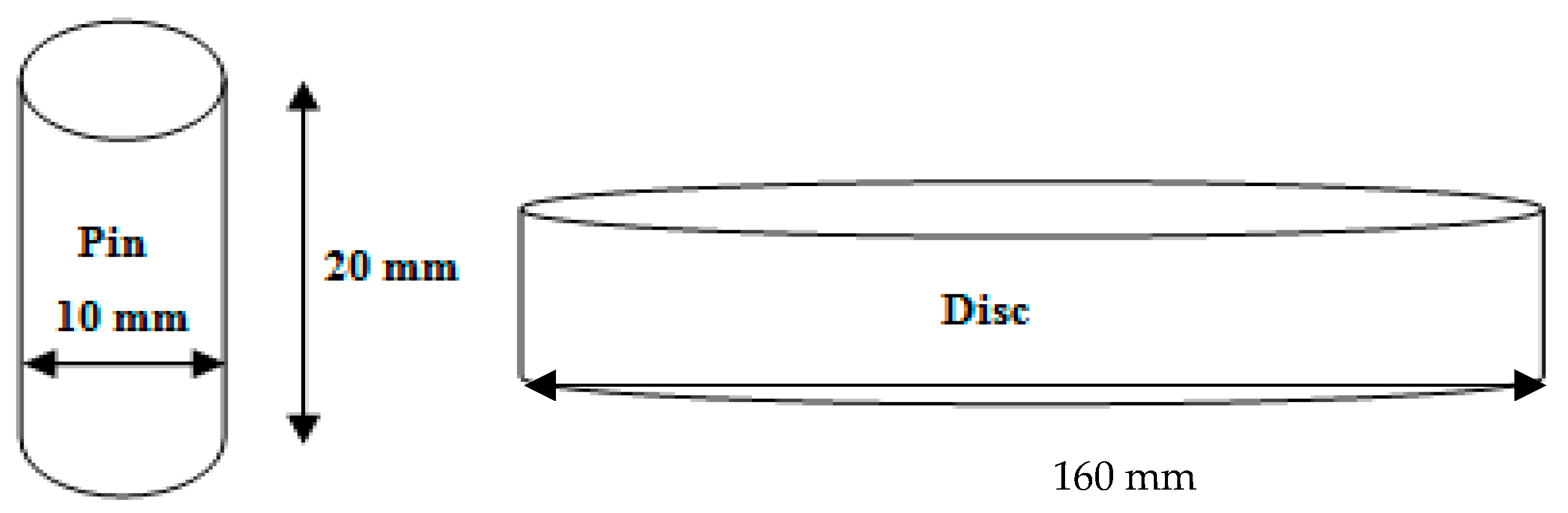
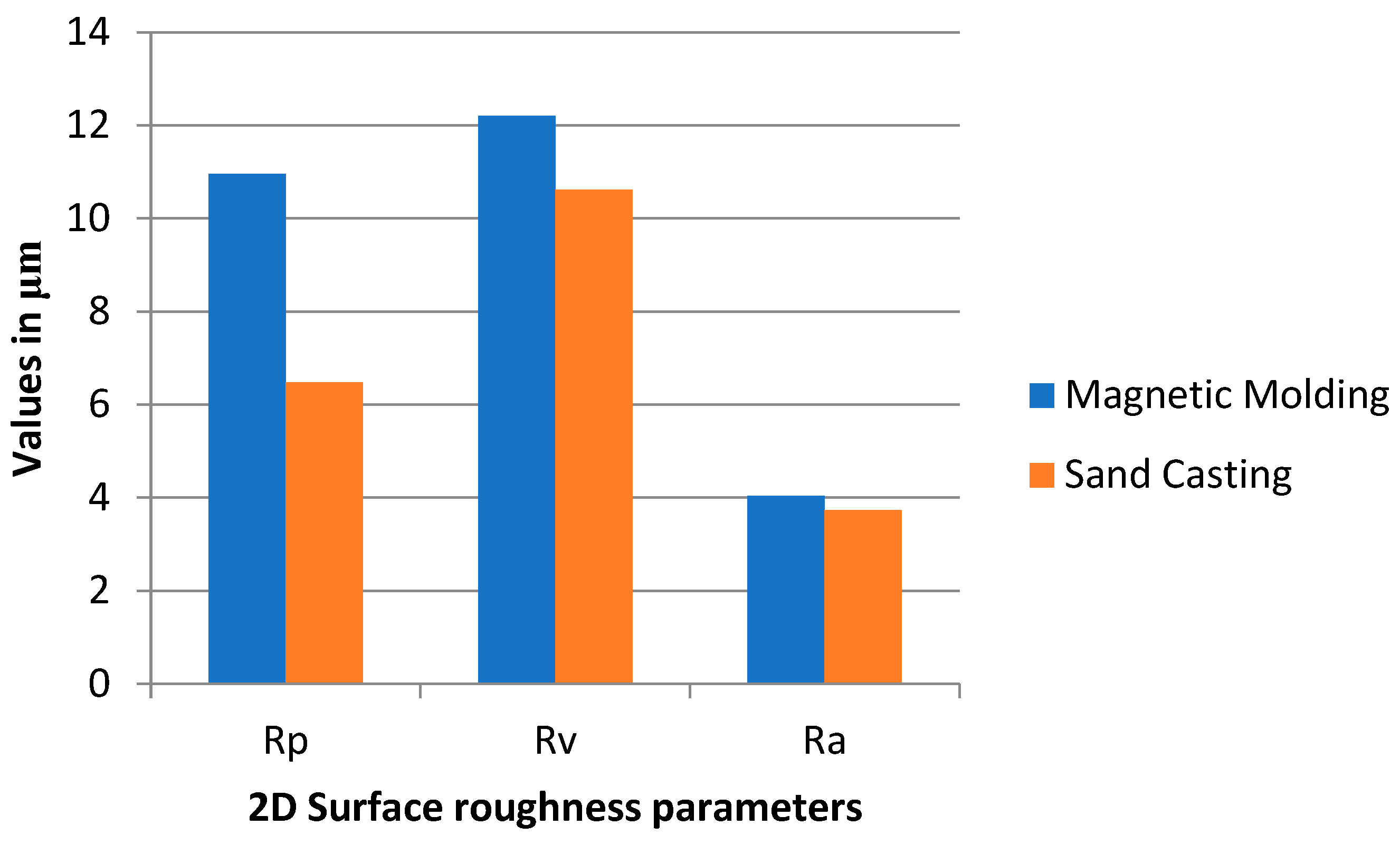
| Diameter (mm) | V (mm3) | Porosity | Porosity in % |
|---|---|---|---|
| 0.18 | 0.5218 | 0.4782 | 47.82 |
| 0.60 | 0.5196 | 0.4804 | 48.04 |
| 1.00 | 0.5245 | 0.4755 | 47.55 |
| Description | Value |
|---|---|
| Minimum element quality | 0.7583 |
| Average element quality | 0.9847 |
| Triangular elements | 9277 |
| Edge elements | 490 |
| Vertex elements | 16 |
| Maximum element size | 0.00154 mm |
| Minimum element size | 3.08 × 10−6 mm |
| Curvature factor | 0.2 |
| Predefined size | Extremely fine |
| S. No. | Process | Indentation Layer | Trial 1 | Trial 2 | Trial 3 | Trial 4 | Average (HB) |
|---|---|---|---|---|---|---|---|
| 1 | Sand Casting | Outer Layer | 9 | 11 | 9.8 | 10.2 | 10 |
| 2 | Magnetic Moulding | Outer Layer | 17 | 16 | 17 | 17 | 16.75 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chandran, A.P.; Ravimanalan, S.; Bennet, A.R. Numerical Modelling and Simulation of Heat Transfer during Magnetic Moulding of Al/SiCp Metal Matrix Composites. Processes 2022, 10, 2144. https://doi.org/10.3390/pr10102144
Chandran AP, Ravimanalan S, Bennet AR. Numerical Modelling and Simulation of Heat Transfer during Magnetic Moulding of Al/SiCp Metal Matrix Composites. Processes. 2022; 10(10):2144. https://doi.org/10.3390/pr10102144
Chicago/Turabian StyleChandran, Arun Prakash, Suraj Ravimanalan, and Anand Ronald Bennet. 2022. "Numerical Modelling and Simulation of Heat Transfer during Magnetic Moulding of Al/SiCp Metal Matrix Composites" Processes 10, no. 10: 2144. https://doi.org/10.3390/pr10102144




