Density and Viscosity Measurement of Diesel Fuels at Combined High Pressure and Elevated Temperature
Abstract
:1. Introduction
2. Experimental Section
- Fuel 1: Refinery 1 with no performance or handling additives.
- Fuel 2: Refinery 1 with both handling and performance additives.
- Fuel 3: Refinery 2 with both handling and performance additives.
- Fuel 4: Refinery 2 with 5% rape methyl ester.
- Fuel 5: A commercially available retail fuel.
2.1. High-Pressure Viscometer

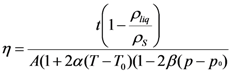
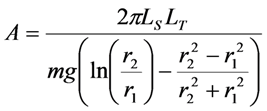
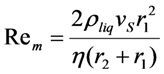
| Liquid | Temperature (K) | Fall time (s) | Re (-) | A (-) |
|---|---|---|---|---|
| Iso-octane | 298.1 | 2.089 | 77.0 | 3.852 |
| 323.2 | 1.618 | 126.7 | 3.941 | |
| 348.2 | 1.323 | 191.0 | 4.122 | |
| 373.2 | 1.171 | 258.1 | 4.550 | |
| Hexadecane | 298.2 | 13.529 | 2.047 | 3.768 |
| 323.2 | 8.026 | 5.618 | 3.734 | |
| 348.2 | 5.425 | 12.11 | 3.775 | |
| 373.1 | 3.913 | 22.72 | 3.783 | |
| S20 Oil | 298.2 | 137.82 | 0.022 | 3.702 |
| 323.2 | 50.448 | 0.161 | 3.731 | |
| 348.2 | 24.524 | 0.161 | 3.745 | |
| 373.1 | 14.265 | 1.943 | 3.755 |
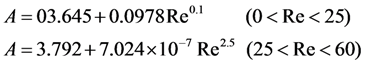
2.2. Density Determinations
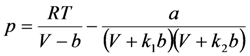
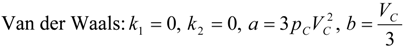
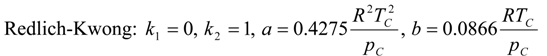
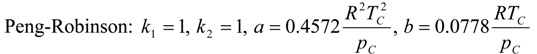
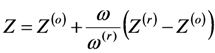
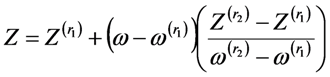
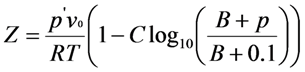
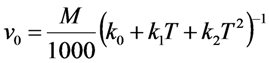
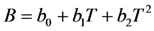
| Fluid | k0 × 10−3 | k1 × 10−6 | k2 × 10−9 | b0 | b1 | b2 × 10−3 | C |
|---|---|---|---|---|---|---|---|
| iso-octane | 1.3549 | 1.0667 | 4.6851 | 300.94 | −1.1327 | 1.0926 | 0.207 |
| heptadecane | 1.1382 | 0.047394 | 1.878 | 316.76 | −0.93033 | 0.69114 | 0.203 |
3. Results and Discussion
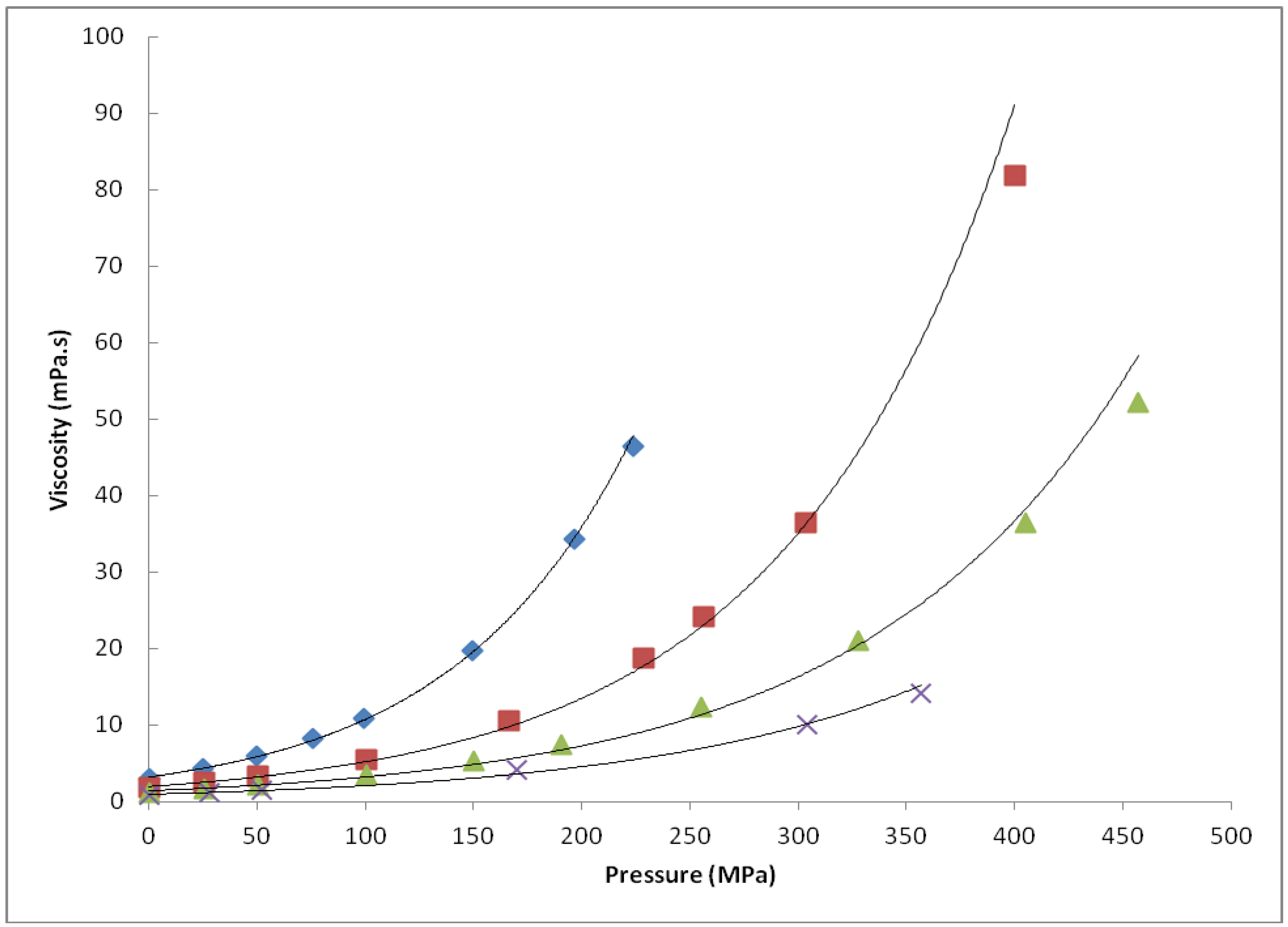
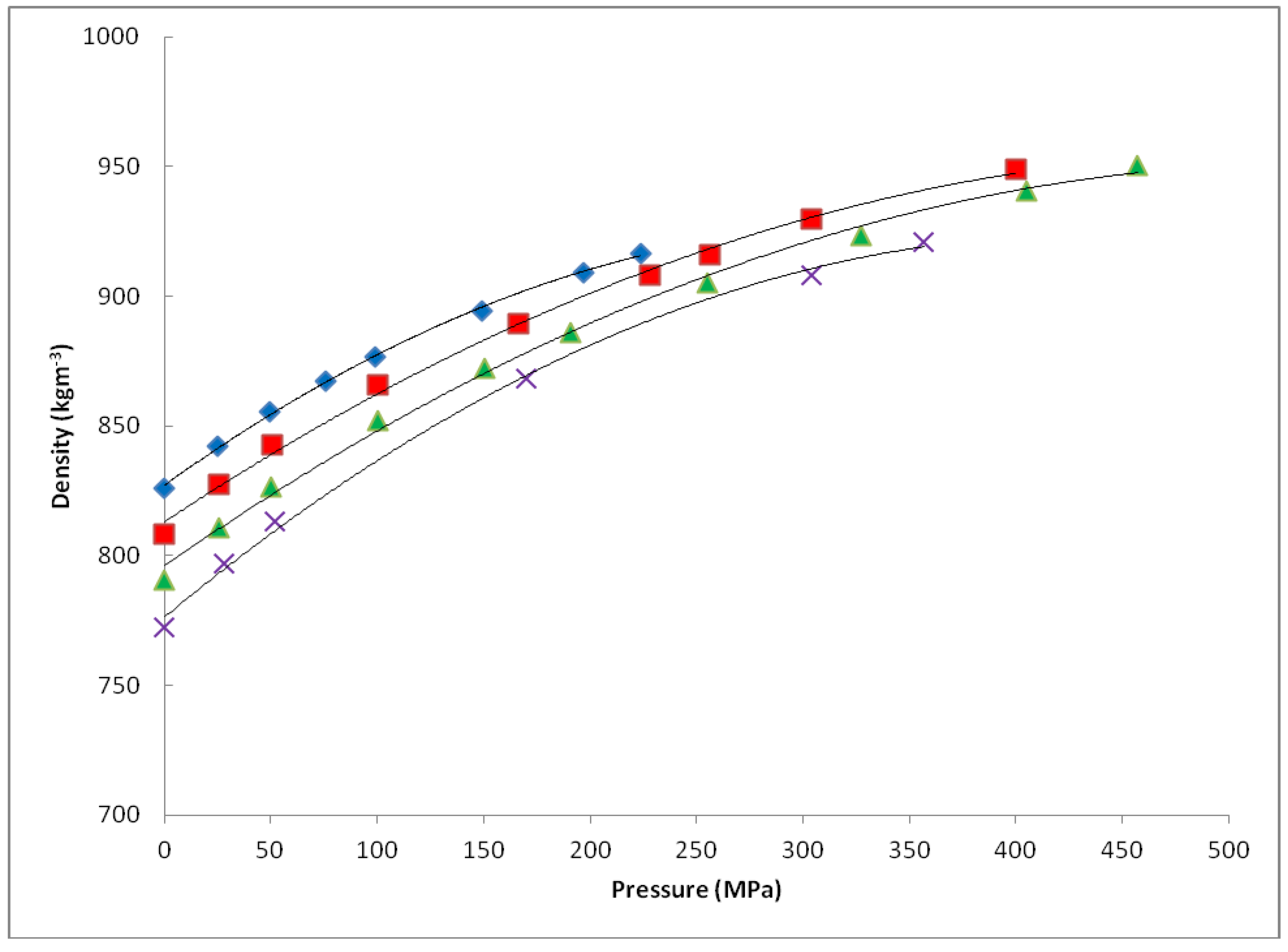
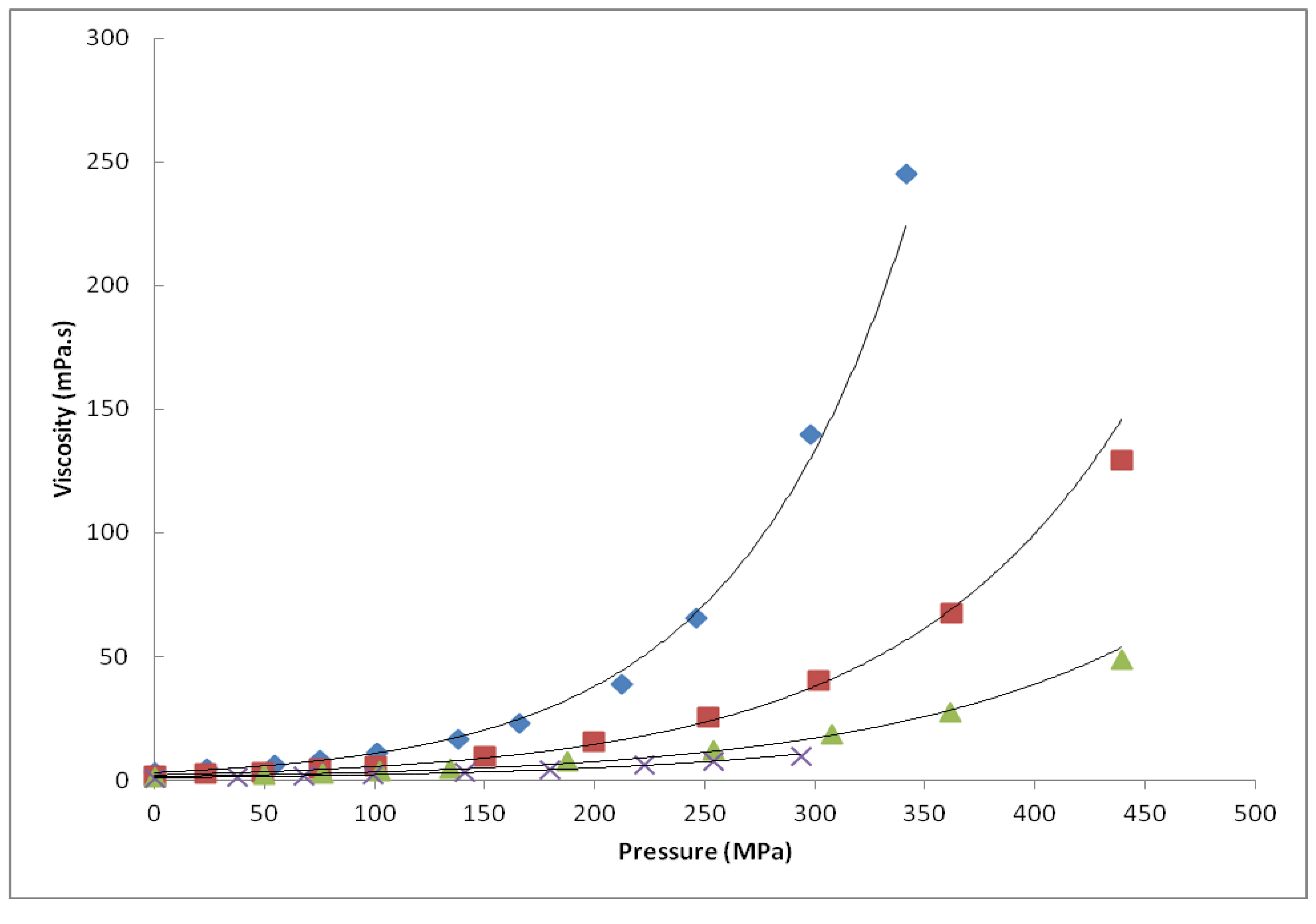

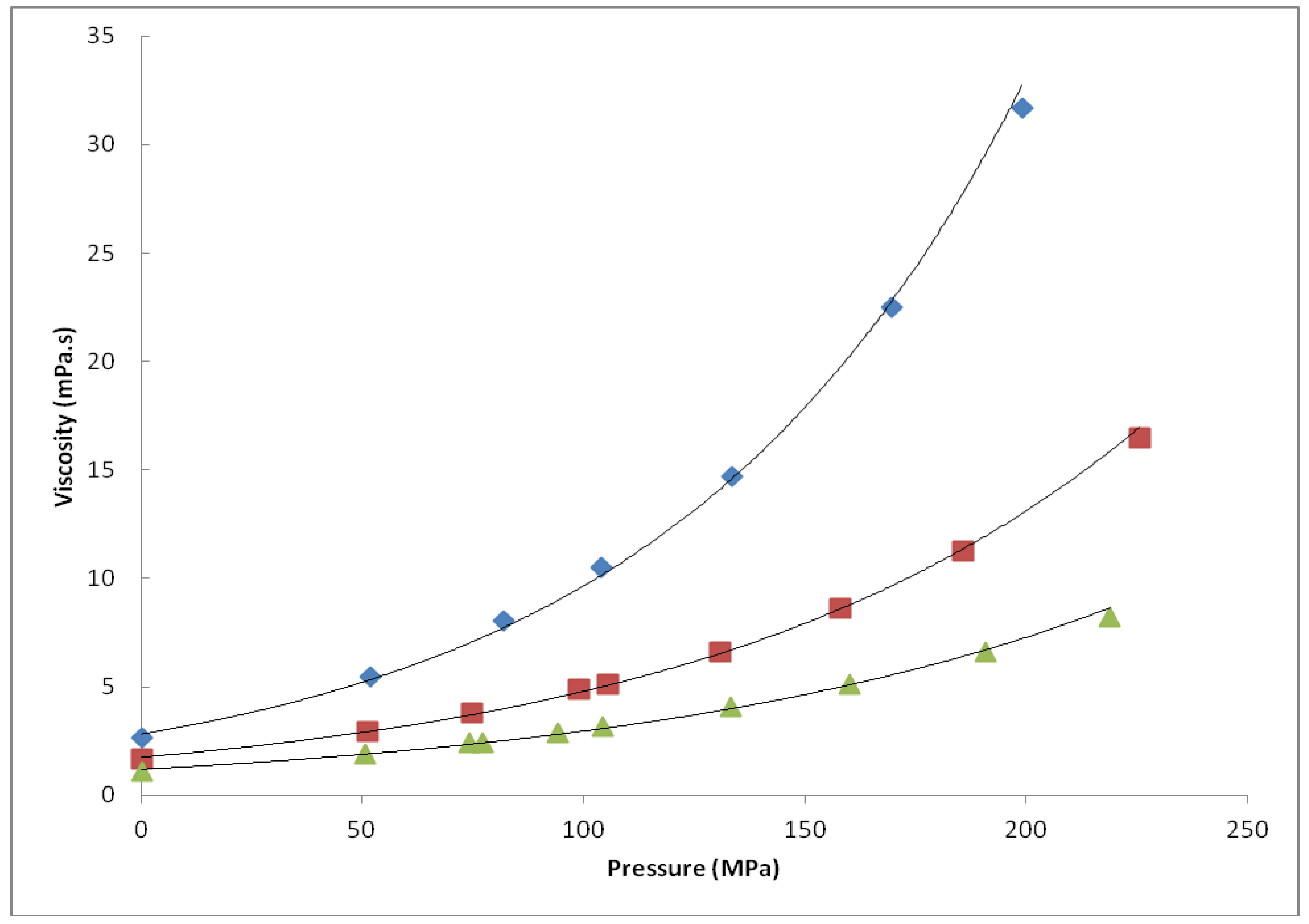
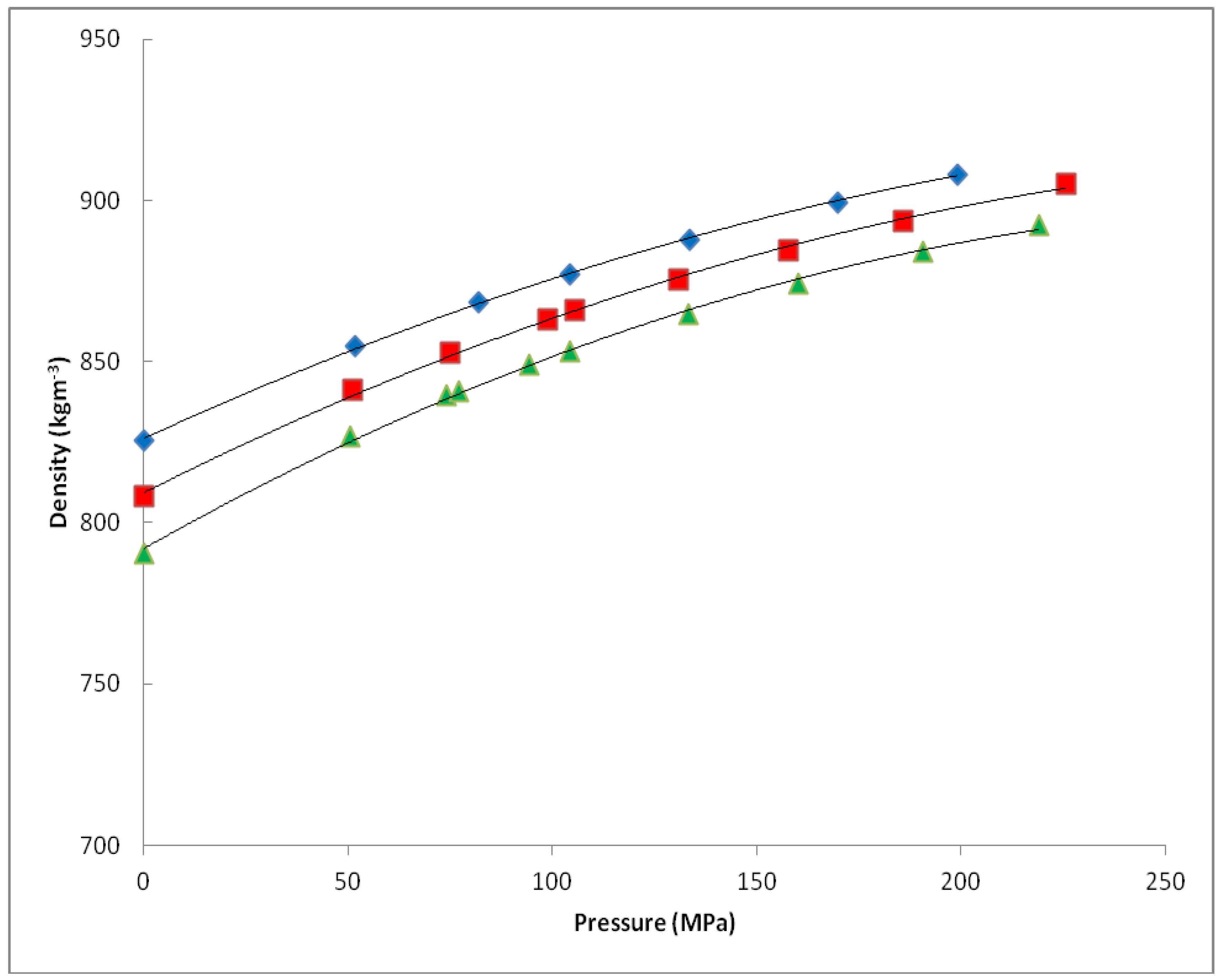
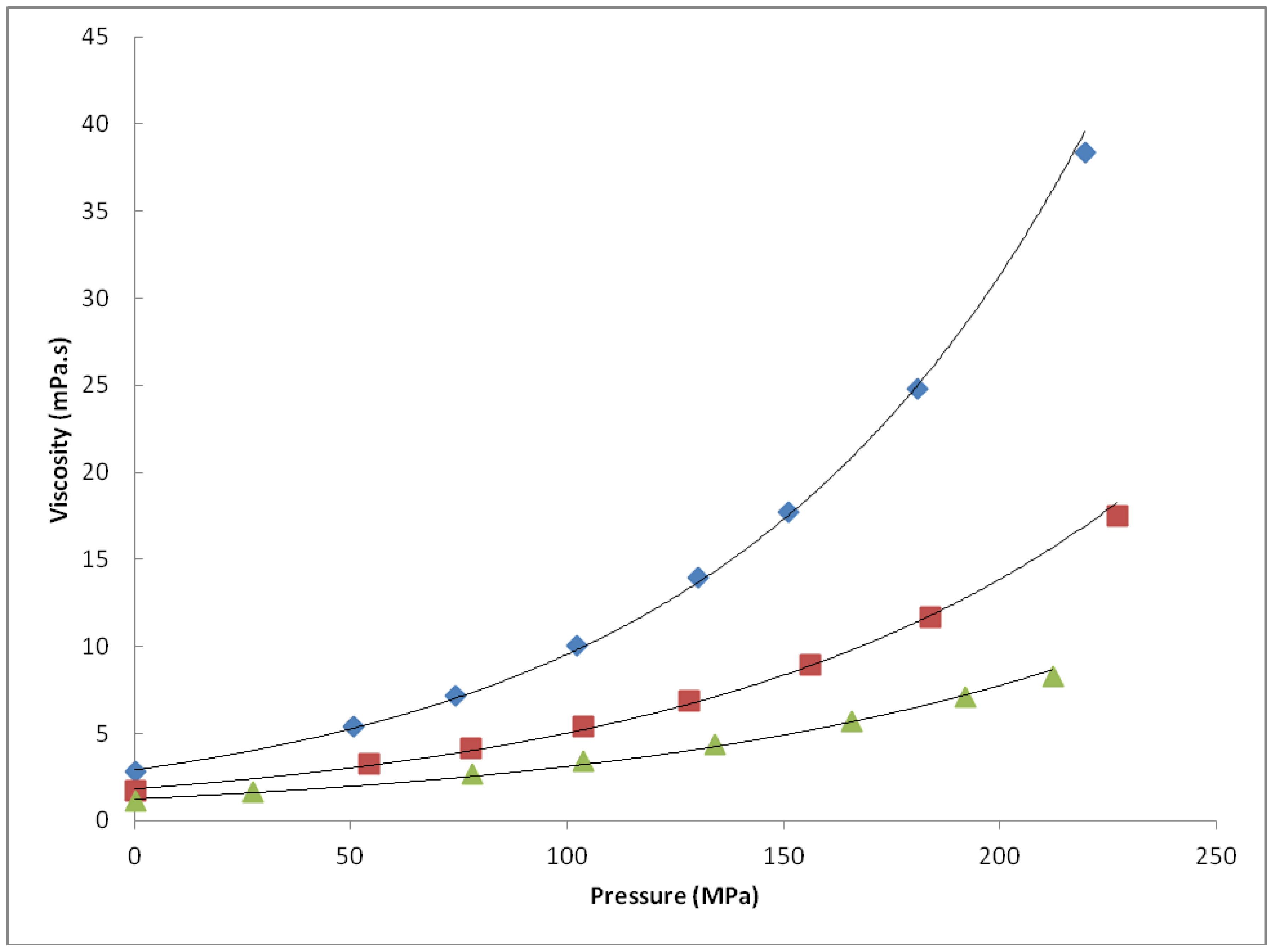
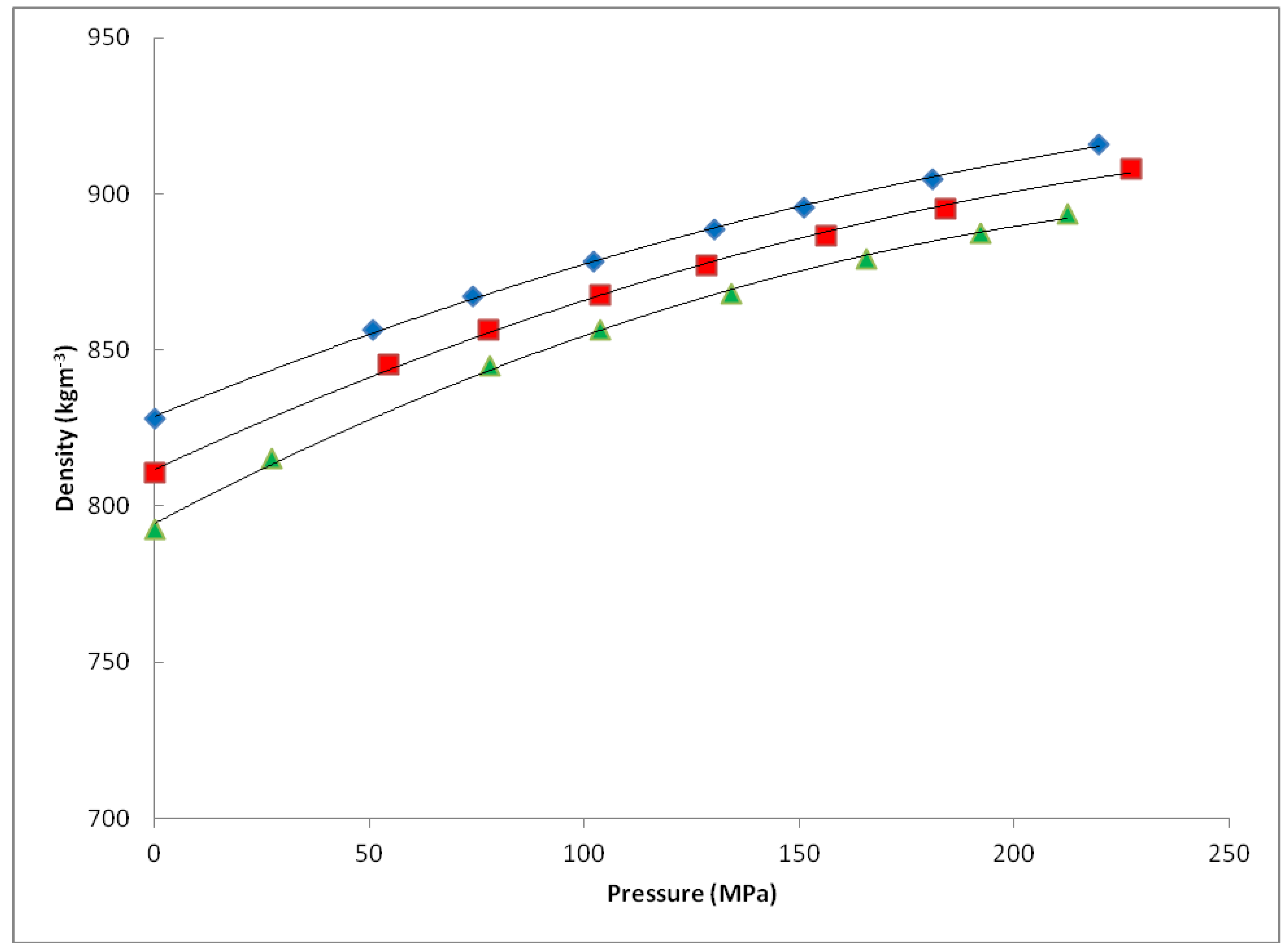
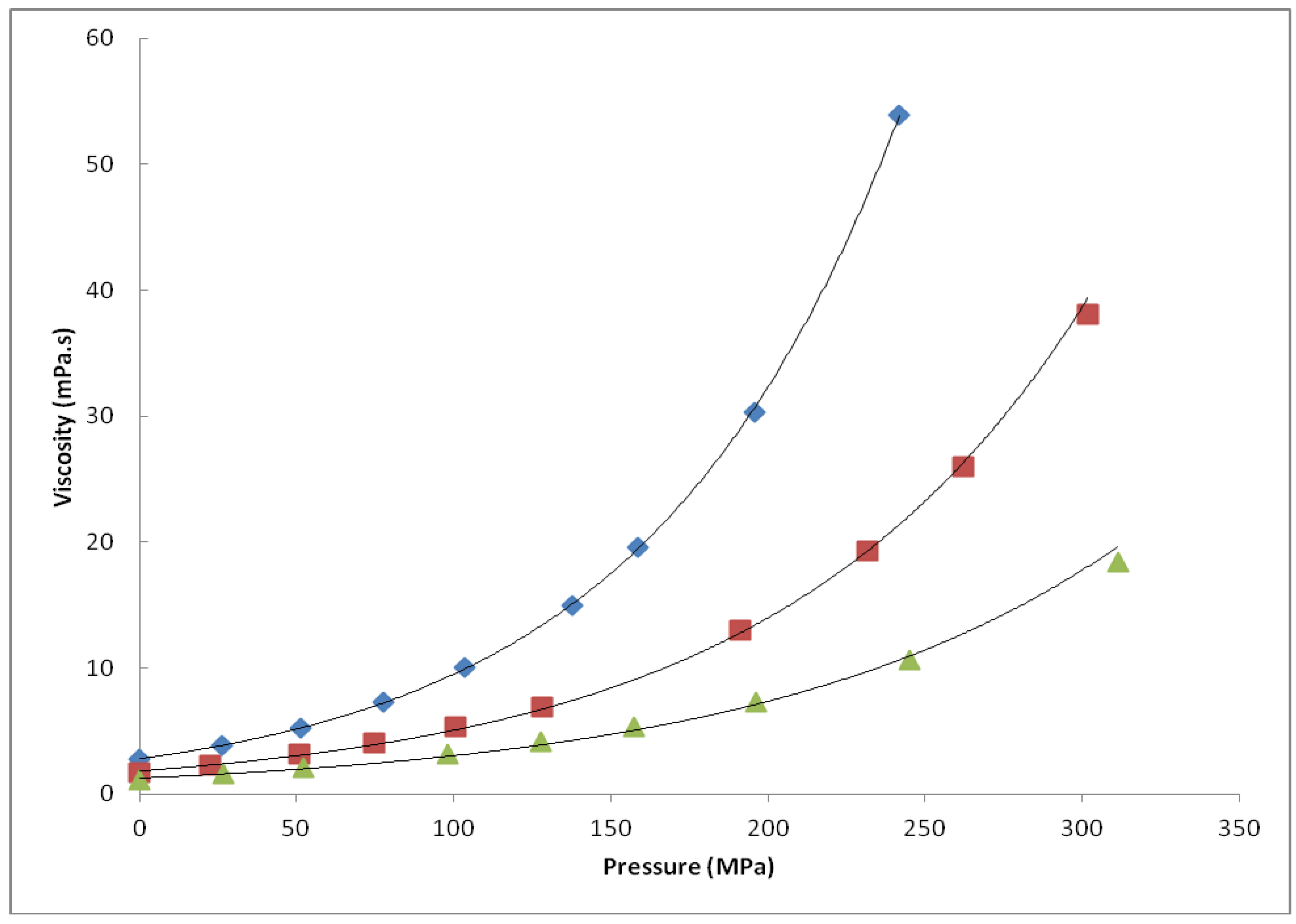
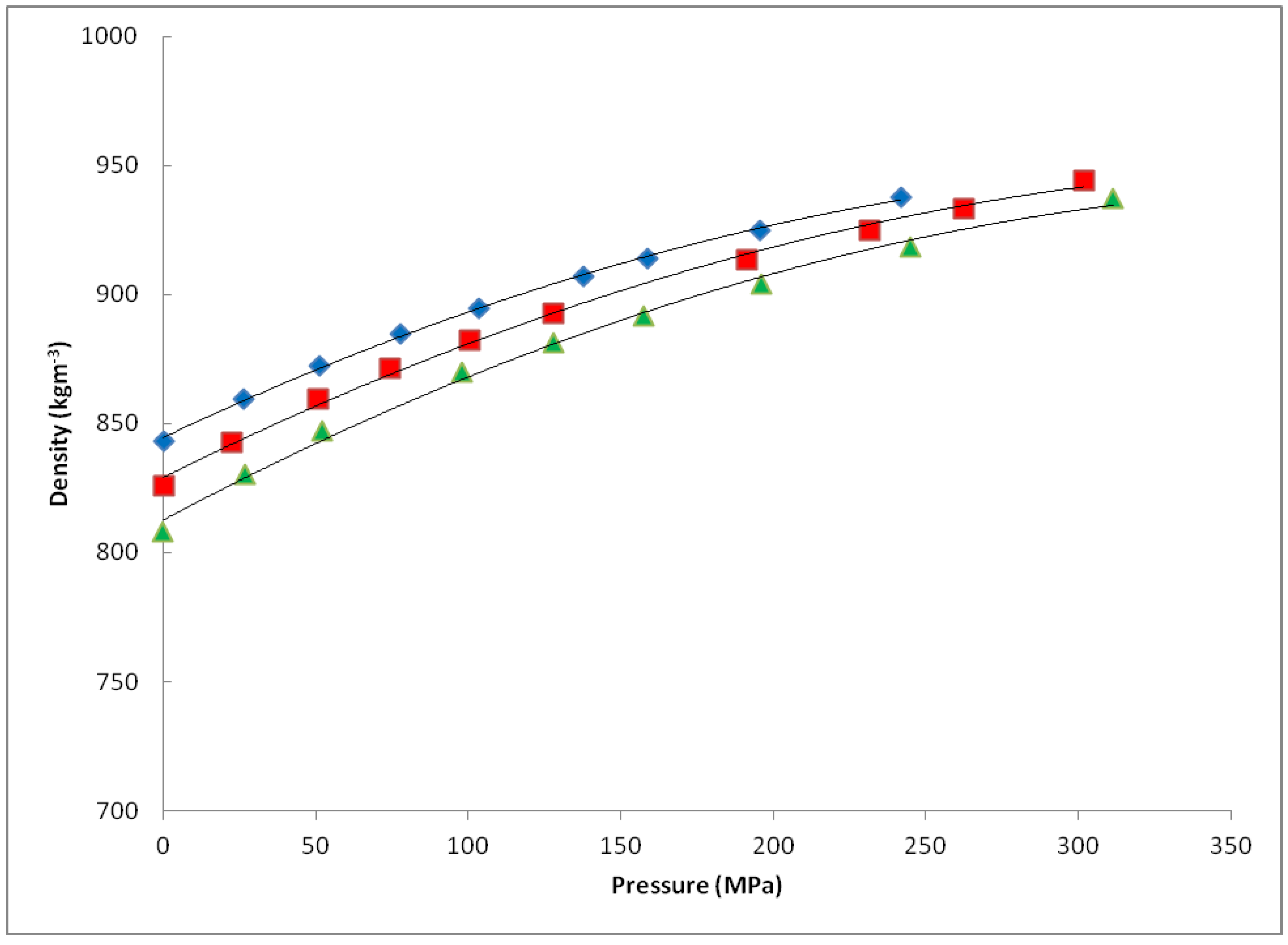
| Fuel | Viscosity η (mPa.s) | |||
|---|---|---|---|---|
| 298 K | 323 K | 348 K | 373 K | |
| 1 | 3.20e0121p | 1.99e0.0096p | 1.44e0.0081p | 0.972e0.0077p |
| 2 | 3.09e0.0126p | 2.10e0.0097p | 1.44e0.0082p | 0.987e0.0081p |
| 3 | 2.82e0.0123p | 1.75e0.0101p | 1.20e0.0090p | nd |
| 4 | 2.91e0.0119p | 1.82e0.9974p | 1.25e0.0090p | nd |
| 5 | 2.80e0.0122p | 1.83e0.0102p | 1.26e0.0088p | nd |
| Fuel | Density ρ (kg·m−3) | |||
|---|---|---|---|---|
| 298 K | 323 K | 348 K | 373 K | |
| 1 | 827 + 0.590p − 0.0009p2 | 813 + 0.545p − 0.0005p2 | 796 + 0.574p − 0.0005p2 | 776 + 0.682p − 0.0008p2 |
| 2 | 829 + 0.508p − 0.005p2 | 814 + 0.513p − 0.0004p2 | 798 + 0.553p − 0.0005p2 | 798 + 0.553p − 0.0005p2 |
| 3 | 826 + 0.582p − 0.0009p2 | 809 + 0.638p − 0.0010p2 | 809 + 0.638p − 0.0010p2 | nd |
| 4 | 829 + 0.566p − 0.0008p2 | 812 + 0.639p − 0.0010p2 | 794 + 0.727p − 0.0013p2 | nd |
| 5 | 845 + 0.561p − 0.0007p2 | 829 + 0.590p − 0.0007p2 | 813 + 0.632p − 0.0008p2 | nd |
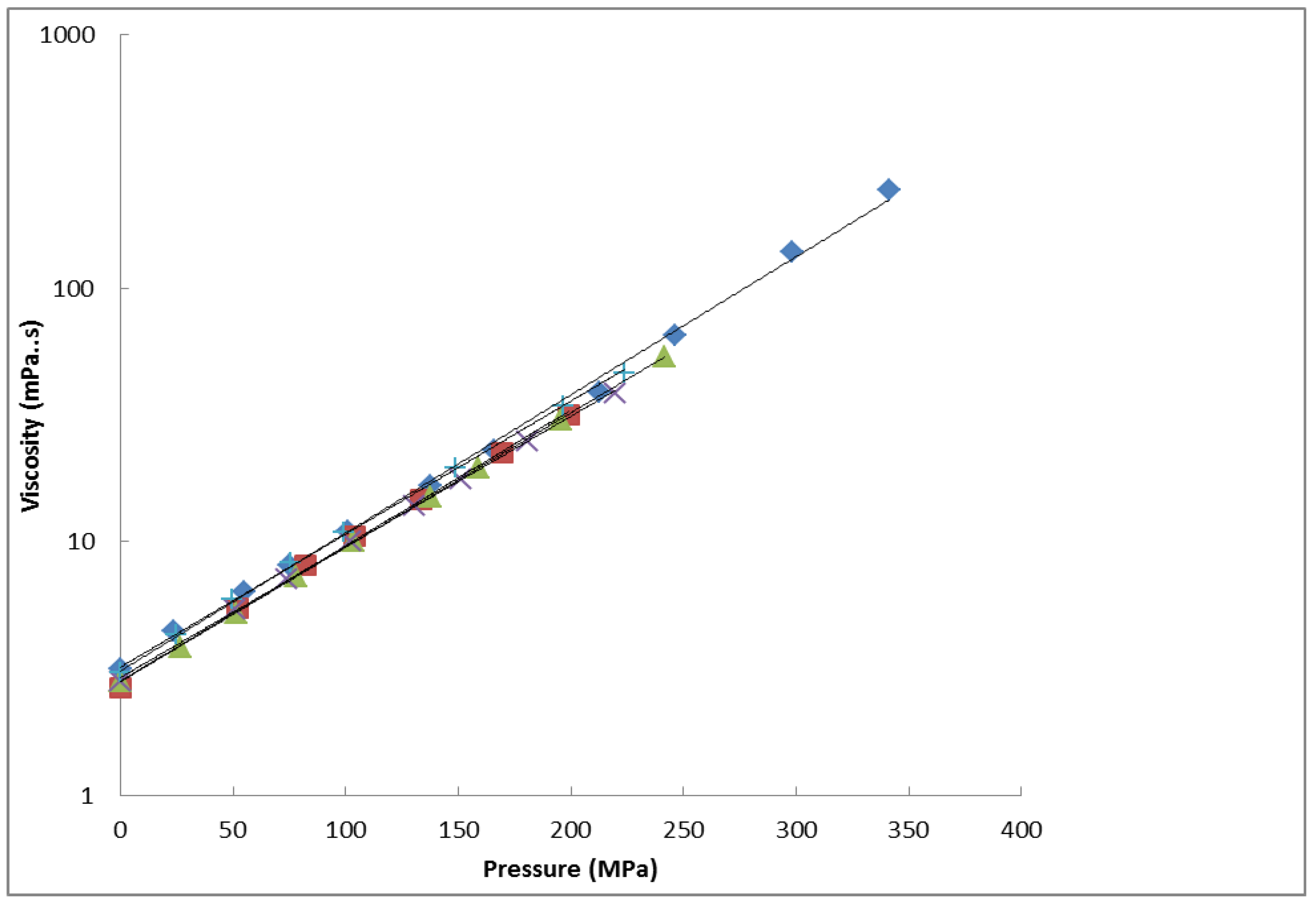
4. Conclusions
Nomenclature
| a | attraction parameter, m6·mol−2 |
| A | viscometer constant, mPa−1 |
| b | repulsion parameter, m3·mol−1 |
| b0, b1, b2 | constants used in the Tait equation |
| B | constant used in Tait equation (Table 2), MPa |
| C | constant used in Tait equation (-) |
| g | gravitational acceleration, m·s−2 |
| k0, k1, k2 | constant used in Tait equation (Table 2), MPa |
| LS | length of sinker wall, m |
| LT | length of tube between detection coils, m |
| m | sinker mass, kg |
| M | constant used in the Tait equation |
| p | pressure, MPa |
| p0 | ambient pressure, MPa |
| pC | critical pressure, MPa |
| Rem | modified Reynolds number, (-) |
| r1 | radius of sinker, m |
| r2 | inner radius of tube, m |
| R | universal gas constant, kg·mol−1·K−1 |
| R2 | statistical correlation coefficient (-) |
| T | temperature, K |
| T0 | ambient temperature, K |
| TC | critical temperature, K |
| t | sinker fall time, s |
| v0 | constant used in the Tait equation |
| vS | terminal velocity of sinker, m·s−1 |
| V | volume mol·m−3 |
| VC | critical volume (mol·m−3) |
| Z | compressibility factor (-) |
| Z(o), Z(r) | compressibility factors of the simple and reference fluid |
Greek symbols
| α | thermal expansion coefficient, K−1 |
| β | pressure compression factor, MPa−1 |
| η | viscosity, mPa·s |
| ρ | liquid density, kg·m−3 |
| ρliq | density of the liquid, kg·m−3 |
| ρS | sinker density, kg·m−3 |
| ω, ω(r) | acentric factors of the fluid and reference fluid |
Acknowledgments
Conflict of Interest
References
- Lee, S.W.; Tanaka, D.; Kusaka, J.; Daisho, Y. Effects of diesel fuel characteristics on spray and combustion in a diesel engine. JSAE Rev. 2002, 23, 407–414. [Google Scholar] [CrossRef]
- Yamaki, Y.; Mori, K.; Kohketsu, S.; Mori, K.; Kato, T. Heavy Duty Diesel Engine with Common Rail Type Fuel Injection Systems; Japanese Society of Automotive Engineers: Tokyo, Japan, 1995. [Google Scholar]
- Riazi, M.R.; Al-Otaibi, G.N. Estimation of viscosity of liquid hydrocarbon systems. Fuel 2001, 80, 27–32. [Google Scholar] [CrossRef]
- Duncan, A.M.; Noorbahiyah, P.; Depcik, C.D.; Scurto, A.M.; Stagg-Williams, S.M. High-pressure viscosity of soybean-oil-based biodiesel blends with ultra-low sulfur diesel fuel. Energy Fuels 2012, 26, 7023–7036. [Google Scholar]
- Duncan, A.M.; Ahosseini, A.; McHenry, R.; Depcik, C.D.; Stagg-Williams, S.M.; Scurto, A.M. High-pressure viscosity of biodiesel from Soybean, Canola, and Canola Oils. Energy Fuels 2010, 24, 5708–5716. [Google Scholar] [CrossRef]
- Park, N.A.; Irvine, T.F. The falling needle viscometer—A new technique for viscosity measurements. Warme Stoffubertrag 1984, 18, 201–206. [Google Scholar] [CrossRef]
- Harris, K.R.; Kanakubo, M.; Woolf, L.A. Temperature and pressure dependence of the viscosity of the ionic liquids 1-hexyl-3-methylimidazolium hexafluorophosphate and 1-butyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide. J. Chem. Eng. Data 2007, 52, 1080–1085. [Google Scholar] [CrossRef]
- Davis, A.M.J.; Brenner, H. The falling-needle viscometer. Phys. Fluids 2001, 13, 3086–3088. [Google Scholar] [CrossRef]
- Isdale, J. Viscosity of Simple Liquids including Measurement and Prediction at Elevated Pressure. Ph.D. Thesis, University of Strathclyde, Glasgow, UK, 1976. [Google Scholar]
- Kumagai, A.; Kawase, Y.; Yokoyama, C. Falling capillary tube viscometer suitable for liquids at high pressure. Rev. Sci. Instrum. 1998, 69, 1441–1445. [Google Scholar] [CrossRef]
- Vant, S.C. Investigation of Fluid Properties at Non-Ambient Conditions. Ph.D. Thesis, University of Strathclyde, Glasgow, UK, 2002. [Google Scholar]
- Dymond, J.H.; Isdale, J.D.; Glen, N.F. Density-measurement at high-pressure. Fluid Phase Equilib. 1985, 20, 305–314. [Google Scholar] [CrossRef]
- Belonenko, V.N.; Troitsky, V.M.; Belyaev, Y.E.; Dymond, J.H.; Glen, N.F. Application of a micro-(p, V, T) apparatus for measurement of liquid densities at pressures up to 500 MPa. J. Chem. Thermodyn. 2000, 32, 1203–1219. [Google Scholar] [CrossRef]
- Lee, B.I.; Kesler, M.G. Generalized thermodynamic correlation based on 3-parameter corresponding states. AIChE J. 1975, 21, 510–527. [Google Scholar] [CrossRef]
- Paton, J.M.; Schaschke, C.J. Viscosity measurement of biodiesel at high pressure with a falling sinker viscometer. Chem. Eng. Res. Des. 2009, 87, 1520–1526. [Google Scholar] [CrossRef]
- Wehbeh, E.G.; Ui, T.J.; Hussey, R.G. End effects for the falling cylinder viscometer. Phys. Fluids A 1993, 5, 25–33. [Google Scholar] [CrossRef]
- Huang, P.Y.; Feng, J. Wall effects on the flow of viscoelastic fluids around a circular-cylinder. J. Non-Newton. Fluid 1995, 60, 179–198. [Google Scholar] [CrossRef]
- Lommatzsch, T.; Megharfi, M.; Mahe, E.; Devin, E. Conceptual study of an absolute falling-ball viscometer. Metrologia 2001, 38, 531–534. [Google Scholar] [CrossRef]
- Stalnaker, J.F.; Hussey, R.G. Wall effects on cylinder drag at low reynolds-number. Phys. Fluids 1979, 22, 603–613. [Google Scholar] [CrossRef]
- Ristow, G.H. Wall correction factor for sinking cylinders in fluids. Phys. Rev. E 1997, 55, 2808–2813. [Google Scholar] [CrossRef]
- Park, N.A.; Irvine, T.F. Falling cylinder viscometer end correction factor. Rev. Sci. Instrum. 1995, 66, 3982–3984. [Google Scholar] [CrossRef]
- Schaschke, C.J.; Abid, S.; Fletcher, I.; Heslop, M.J. Evaluation of a falling sinker-type viscometer at high pressure using edible oil. J. Food Eng. 2008, 87, 51–58. [Google Scholar] [CrossRef]
- Gui, F.L.; Irvine, T.F. Theoretical and experimental-study of the falling cylinder viscometer. Int. J. Heat Mass Tran. 1994, 37, 41–50. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Schaschke, C.; Fletcher, I.; Glen, N. Density and Viscosity Measurement of Diesel Fuels at Combined High Pressure and Elevated Temperature. Processes 2013, 1, 30-48. https://doi.org/10.3390/pr1020030
Schaschke C, Fletcher I, Glen N. Density and Viscosity Measurement of Diesel Fuels at Combined High Pressure and Elevated Temperature. Processes. 2013; 1(2):30-48. https://doi.org/10.3390/pr1020030
Chicago/Turabian StyleSchaschke, Carl, Isobel Fletcher, and Norman Glen. 2013. "Density and Viscosity Measurement of Diesel Fuels at Combined High Pressure and Elevated Temperature" Processes 1, no. 2: 30-48. https://doi.org/10.3390/pr1020030




