Managing Systematic Mortality Risk in Life Annuities: An Application of Longevity Derivatives
Abstract
:1. Introduction
2. Mortality Model
2.1. Model Specification
2.2. Parameter Estimation
- Using empirical data for ages we evaluate the sample variance of across time, denoted by .
- The model variance for age x is given bySince the difference between the death rates is computed in yearly terms, we set .
- The parameters are then estimated by fitting the model variance to the sample variance for ages using least squares estimation, that is, by minimisingwith respect to the parameters .
- From the central death rates, we obtain empirical survival curves for cohorts aged 65 and 75 in 2008. The survival curve is obtained by settingwhere is the central death rate of an x years old at time t. Here, represents the calendar year 2008.
- The parameters are then estimated by fitting the survival curves () of the model to the empirical survival curves using least squares estimation, that is, by minimisingwhere and , with respect to the parameters .
- 1.
- In our model formulation, we specifically address the fact that the mortality intensity processes for different (initial) ages are increasing as time passed. This is important for the hedging applications considered in Section 4 since the extent of systematic mortality risk in an annuity portfolio is determined by the randomness of the mortality intensity process.
- 2.
- The continuous-time mortality model follows a single cohort through time and the mortality rate at future ages for the cohort includes both an age effect and a time effect, since the cohort trend is the sum of an age effect and a time or improvement effect, so that going from age x to there is a mortality improvement implicitly included for the cohort. This model does not aim to fit multiple cohorts since it does not include an explicit improvement for the same age across time. Most practical applications, such as the hedging applications studied in Section 4, require single cohort mortality models.
3. Analytical Pricing of Longevity Derivatives
3.1. Risk-Adjusted Measure
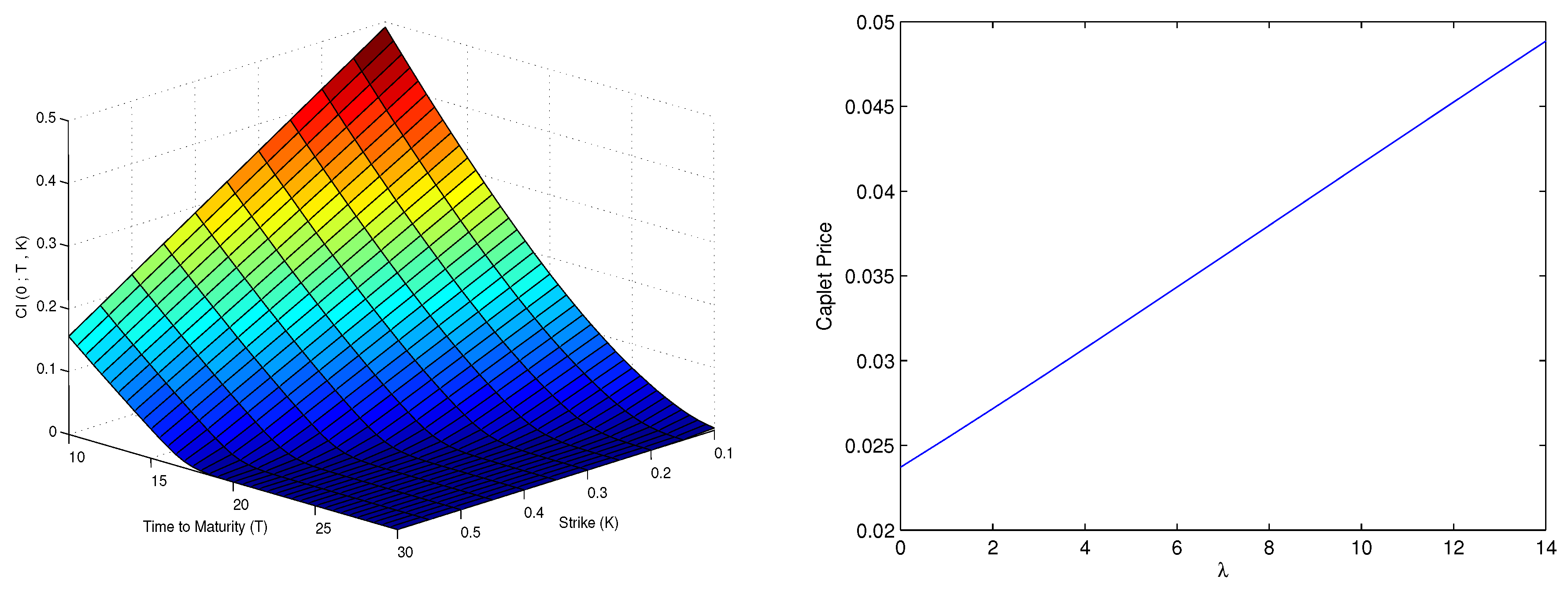
3.2. Longevity Swaps
3.3. Longevity Caps
- realised survival probability of the first t years;
- risk-adjusted survival probability in the next years;
- interest rate r;
- strike price K;
- time to maturity ; and
- standard deviation , which is a function of the time to maturity and the model parameters.
4. Managing Longevity Risk in a Hypothetical Life Annuity Portfolio
4.1. Setup
4.1.1. A Swap-Hedged Annuity Portfolio
4.1.2. A Cap-Hedged Annuity Portfolio
4.2. Results
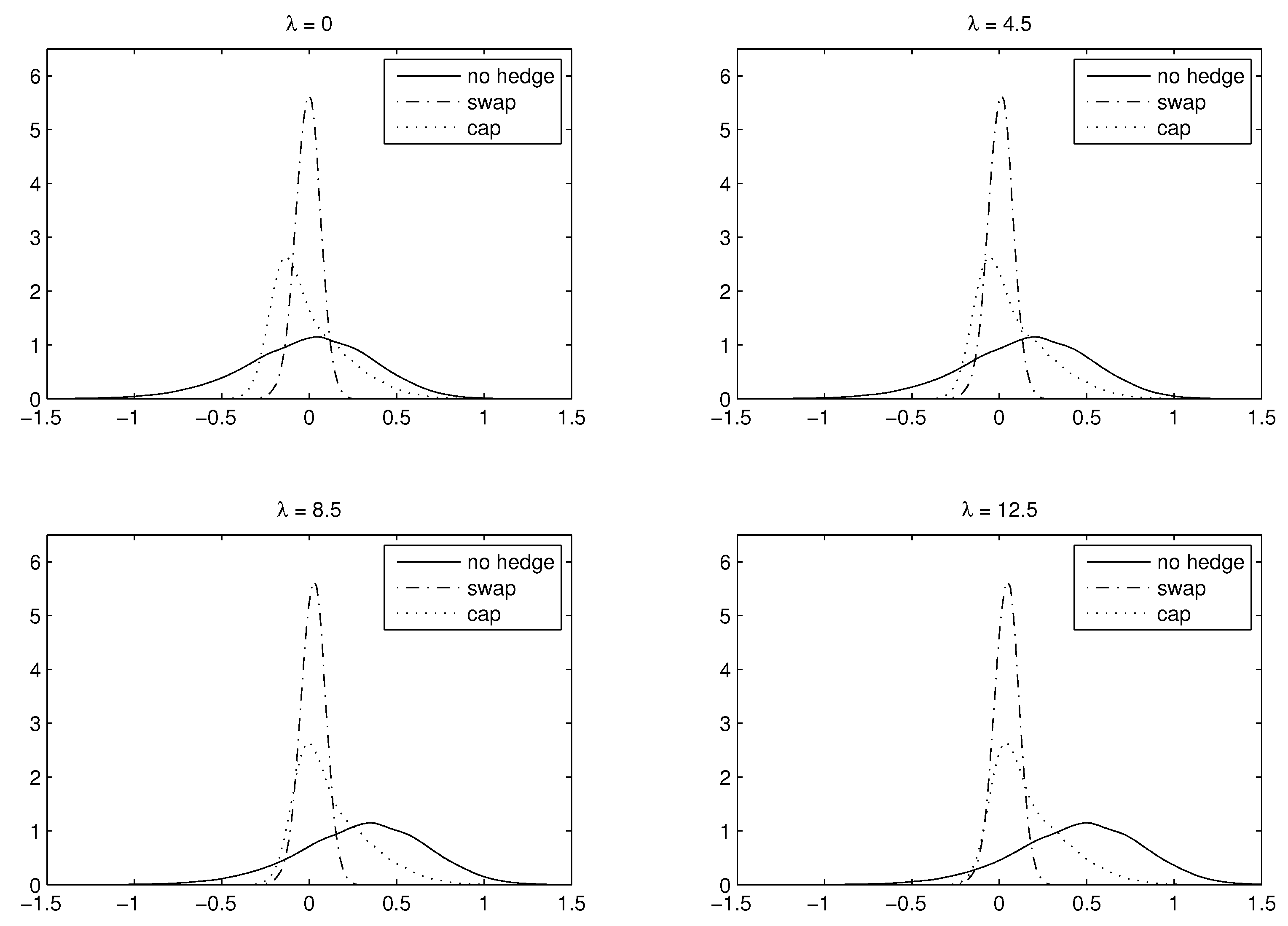
4.2.1. Hedging Features w.r.t. Longevity Risk Premium
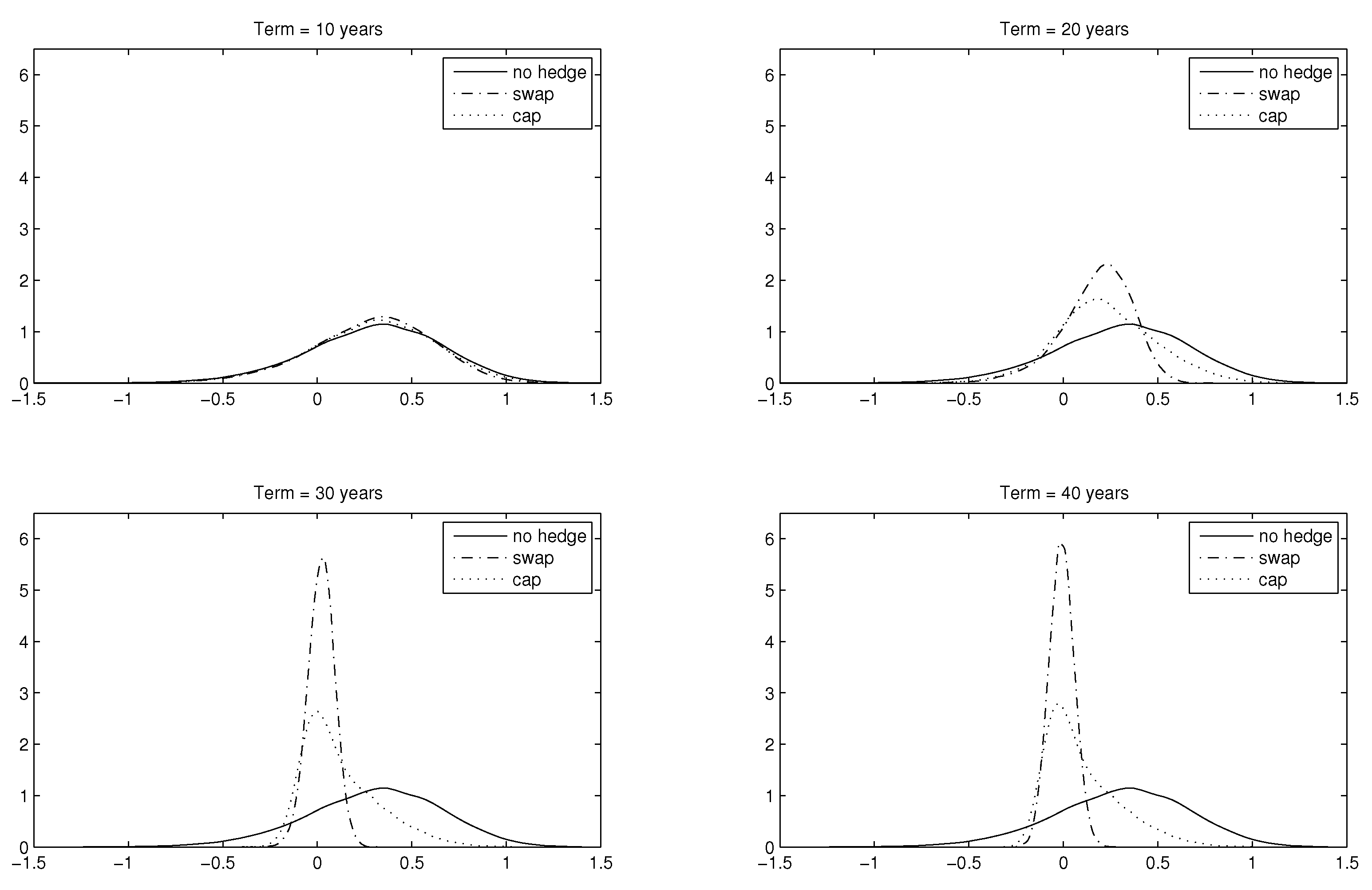
4.2.2. Hedging Features w.r.t. Term to Maturity
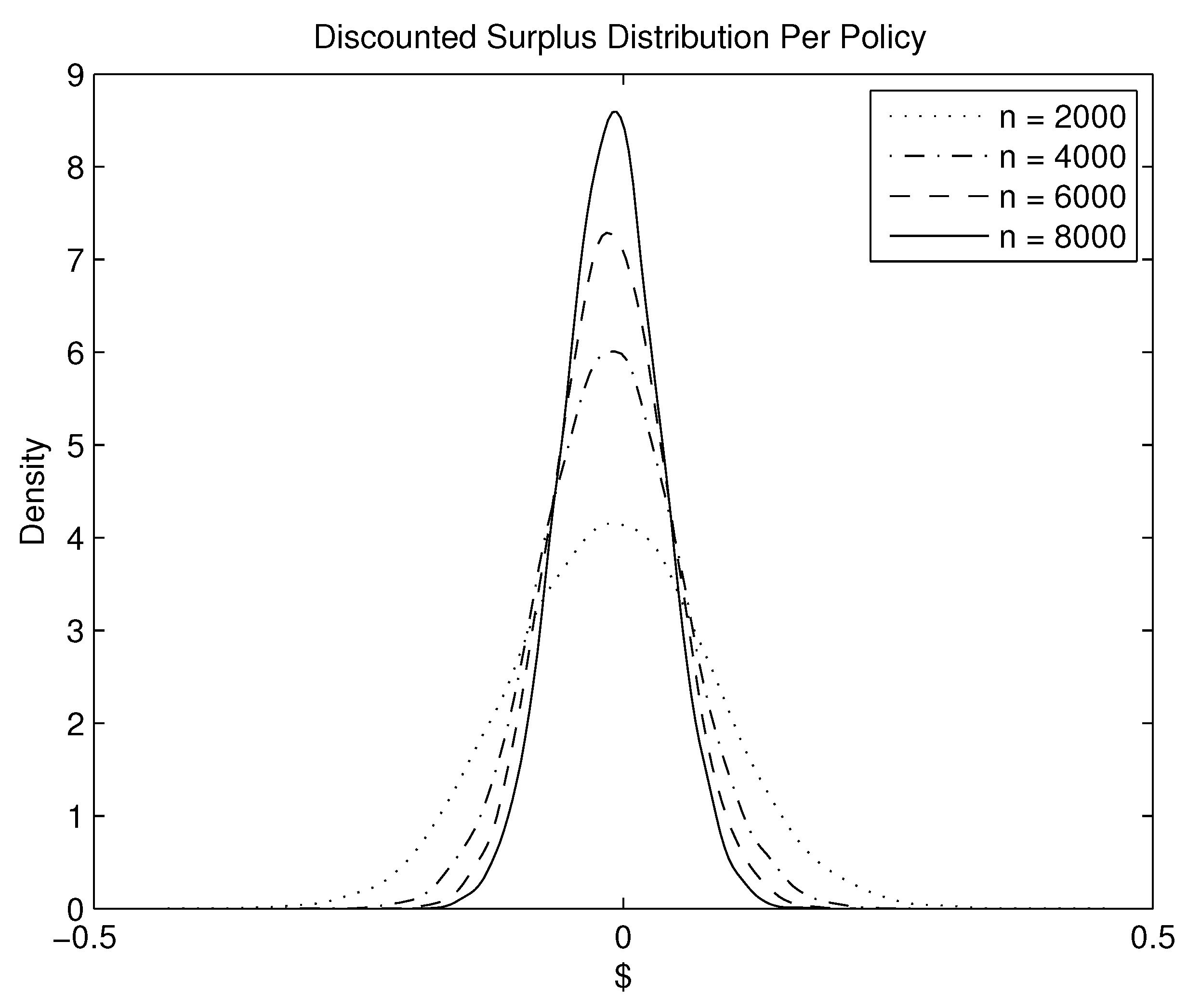
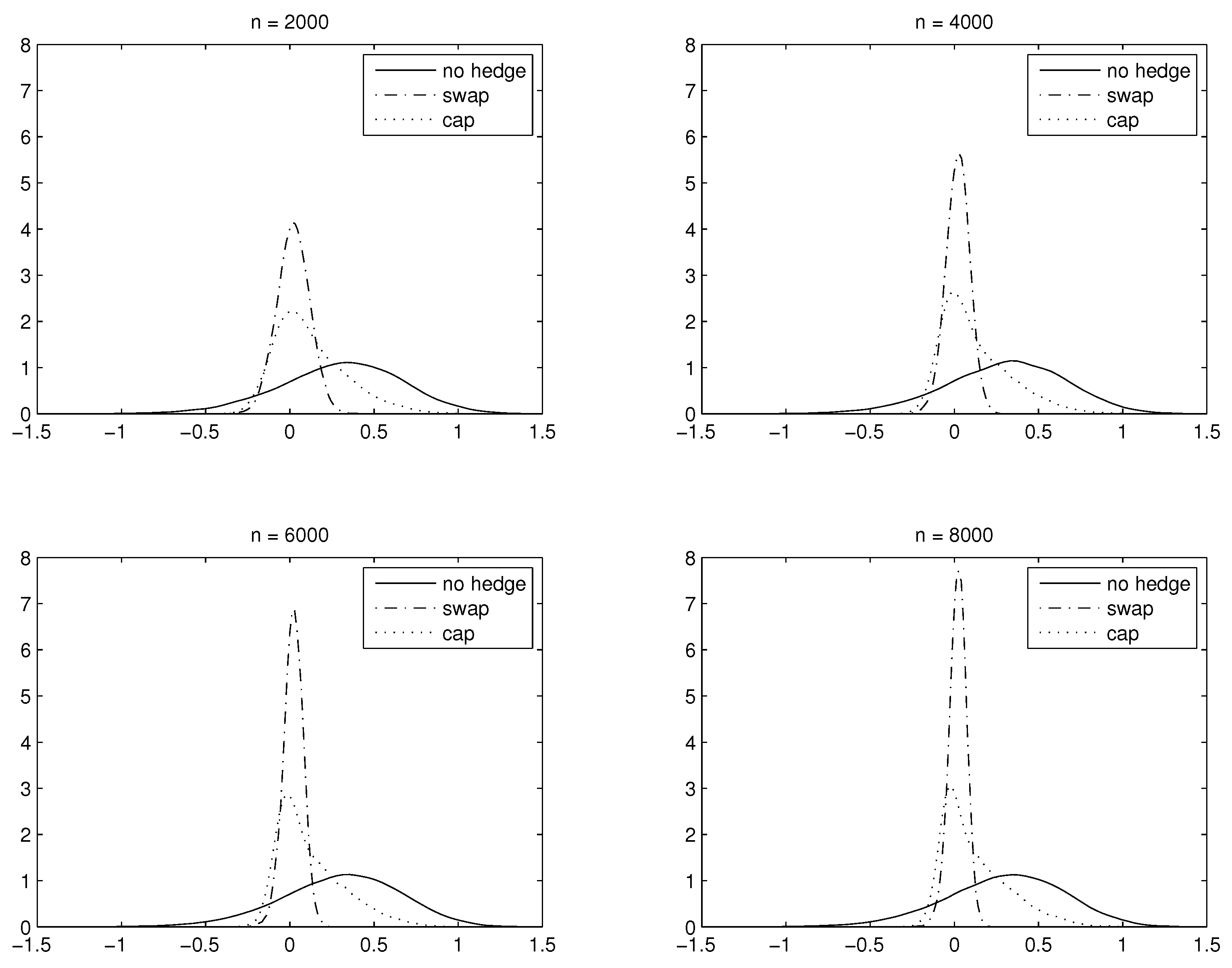
4.2.3. Hedging Features w.r.t. Portfolio Size
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
- Simulate the mortality intensity from to .
- Generate a standard exponential random variable . For example, using an inverse transform method, we have where .
- Set the death time to be the smallest T such that . If then set .
- Repeat step (2) and (3) to obtain another death time.
References
- Bauer, Daniel, Matthias Borger, and Jochen Russ. 2010. On the pricing of longevity-linked securities. Insurance: Mathematics and Economics 46: 139–49. [Google Scholar] [CrossRef]
- Biffis, Enrico. 2005. Affine processes for dynamics mortality and actuarial valuations. Insurance: Mathematics and Economics 37: 443–68. [Google Scholar] [CrossRef]
- Biffis, Enrico, and David Blake. 2014. Keeping some skin in the game: How to start a capital market in longevity risk transfers. North American Actuarial Journal 18: 14–21. [Google Scholar] [CrossRef]
- Biffis, Enrico, David Blake, Lorenzo Pitotti, and Ariel Sun. 2014. The cost of counterparty risk and collateralization in longevity swaps. Journal of Risk and Insurance 83: 387–419. [Google Scholar] [CrossRef]
- Blake, David, and William Burrows. 2001. Survivor bonds: Helping to hedge mortality risk. Journal of Risk and Insurance 68: 339–48. [Google Scholar] [CrossRef]
- Blake, David, Andrew Cairns, Guy Coughlan, Kevin Dowd, and Richard MacMinn. 2013. The new life market. Journal of Risk and Insurance 80: 501–57. [Google Scholar] [CrossRef]
- Blake, David, Andrew J. G. Cairns, and Kevin Dowd. 2006. Living with mortality: Longevity bonds and other mortality-linked securities. British Actuarial Journal 12: 153–228. [Google Scholar] [CrossRef]
- Blake, David, Andrew Cairns, Kevin Dowd, and Richard MacMinn. 2006. Longevity bonds: Financial engineering, valuation and hedging. Journal of Risk and Insurance 73: 647–72. [Google Scholar] [CrossRef]
- Boyer, Martin, and Lars Stentoft. 2013. If we can simulate it, we can insure it: An application to longevity risk management. Insurance: Mathematics and Economics 52: 35–45. [Google Scholar] [CrossRef]
- Brigo, Damiano, and Fabio Mercurio. 2007. Interest Rate Models, 2nd ed.Berlin: Springer. [Google Scholar]
- Cairns, Andrew. 2011. Modelling and mangement of longevity risk: Approximations to survivor functions and dynamic hedging. Insurance: Mathematics and Economics 49: 438–53. [Google Scholar]
- Cairns, Andrew, David Blake, and Kevin Dowd. 2006. A two-factor model for stochastic mortality with parameter uncertainty: Theory and calibration. Journal of Risk and Insurance 73: 687–718. [Google Scholar] [CrossRef]
- Cairns, Andrew, Kevin Dowd, David Blake, and Guy Coughlan. 2014. Longevity hedge effectiveness: A decomposition. Quantitative Finance 14, 217–35. [Google Scholar] [CrossRef]
- Chigodaev, Alexander, Moshe A. Milevsky, and Tom S. Salisbury. 2014. How Long Does the Market Think You Will Live? Implying Longevity From Annuity Prices. Technical Report. Toronto: IFID Center. [Google Scholar]
- Cocco, João F., and Francisco J. Gomes. 2012. Longevity risk, retirement savings, and financial innovation. Journal of Financial Economics 103: 507–29. [Google Scholar] [CrossRef]
- Donnelly, Ryan, Sebastian Jaimungal, and Dmitri H. Rubisov. 2014. Valuing guaranteed withdrawal benefits with stochastic interest rates and volatility. Quantitative Finance 14: 369–82. [Google Scholar] [CrossRef]
- Dowd, Kevin. 2003. Survivor bonds: A comment on Blake and Burrows. Journal of Risk and Insurance 70: 339–48. [Google Scholar] [CrossRef]
- Fung, Man Chung, Katja Ignatieva, and Michael Sherris. 2014. Systematic mortality risk: An analysis of guarantee lifetime withdrawal benefits in variable annuities. Insurance: Mathematics and Economics 58: 103–15. [Google Scholar] [CrossRef]
- Towers Watson. 2013. Global Pension Assets Study. Technical Report. Available online: http://www.towerswatson.com (accessed on 27 November 2018).
- Hari, Norbert, Anja De Waegenaere, Bertrand Melenberg, and Theo E. Nijman. 2008. Longevity risk in portfolios of pension annuities. Insurance: Mathematics and Economics 42: 505–19. [Google Scholar] [CrossRef]
- Huang, Yao Tung, and Yue Kuen Kwok. 2016. Regression-based monte carlo methods for stochastic control models: Variable annuities with lifelong guarantees. Quantitative Finance 16: 905–28. [Google Scholar] [CrossRef]
- Ignatieva, Katja, Andrew Song, and Jonathan Ziveyi. 2016. Pricing and hedging of guaranteed minimum benefits under regime-switching and stochastic mortality. Insurance: Mathematics and Economics 70: 286–300. [Google Scholar]
- Li, Johnny, and Mary R. Hardy. 2011. Measuring basis risk in longevity hedges. North American Actuarial Journal 15: 177–200. [Google Scholar] [CrossRef]
- LLMA. 2010a. Longevity pricing framework. Available online: http://docplayer.net/51341950-Longevity-pricing-framework.html (accessed on 27 November 2018).
- LLMA. 2010b. Technical Note: The S-Forward. London: Life and Longevity Markets Association (LLMA). [Google Scholar]
- Luciano, Elisa, Luca Regis, and Elena Vigna. 2012. Delta-Gamma hedging of mortality and interest rate risk. Insurance: Mathematics and Economics 50: 402–12. [Google Scholar] [CrossRef]
- Luciano, Elisa, and Elena Vigna. 2008. Mortality risk via affine stochastic intensities: Calibration and empirical relevance. Belgian Actuarial Bulletin 8: 5–16. [Google Scholar]
- Meyricke, Ramona, and Michael Sherris. 2014. Longevity risk, cost of capital and hedging for life insurers under solvency II. Insurance: Mathematics and Economics 55: 147–55. [Google Scholar] [CrossRef]
- Ngai, Andrew, and Michael Sherris. 2011. Longevity risk management for life and variable annuities: The effectiveness of static hedging using longevity bonds and derivatives. Insurance: Mathematics and Economics 49: 100–14. [Google Scholar] [CrossRef]
- Peng, Jingjiang, Kwai Sun Leung, and Yue Kuen Kwok. 2012. Pricing guaranteed minimum withdrawal benefits under stochastic interest rates. Quantitative Finance 12, 993–41. [Google Scholar] [CrossRef]
- Wang, Chou-Wen, and Sharon S. Yang. 2013. Pricing survivor derivatives with cohort mortality dependence under the Lee-Carter framework. Journal of Risk and Insurance 80: 1027–56. [Google Scholar] [CrossRef]
- Wills, Samuel, and Michael Sherris. 2011. Integrating Financial and Demographic Longevity Risk Models: An Australian Model for Financial Applications. UNSW Australian School of Business Research Paper No. 2008ACTL05. Sydney: UNSW. [Google Scholar]
- Yueh, Meng-Lan, Hsin-Yu Chiu, and Shou-Hsun Tsai. 2016. Valuations of mortality-linked structured products. The Journal of Derivatives 24: 66–87. [Google Scholar] [CrossRef]
| 1 | From an annuity provider’s perspective, longevity risk modelling can lead to a (stochastically) over- or underestimation of survival probabilities for all annuitants. For this reason longevity risk is also referred to as the systematic mortality risk. |
| 2 | Of particular interest is an attempt to issue the EIB longevity bond by the European Investment Bank (EIB) in 2004, which was underwritten by BNP Paribas. This bond was not well received by investors and could not generate enough demand to be launched due to its deficiencies, as outlined in Blake et al. (2006). |
| 3 | There is a separate strand in the literature that analyses variable annuities with embedded guarantees where the authors either do not investigate hedge effectiveness (as e.g., in Peng et al. 2012), or perform static hedge. Huang and Kwok (2016) price and hedge the guaranteed lifelong withdrawal benefit by means of the regression-based Monte Carlo simulations for stochastic control models; Fung et al. (2014) consider the capital reserve required due to the lack of hedging instruments to hedge the longevity risk in the guaranteed lifetime withdrawal benefits in variable annuities; Donnelly et al. (2014) value guaranteed withdrawal benefits with stochastic interest rates and volatility and compute associated hedge ratios; and Ignatieva et al. (2016) price and hedge guaranteed minimum benefits under regime-switching and stochastic mortality. |
| 4 | For simplicity of notation we replace by . |
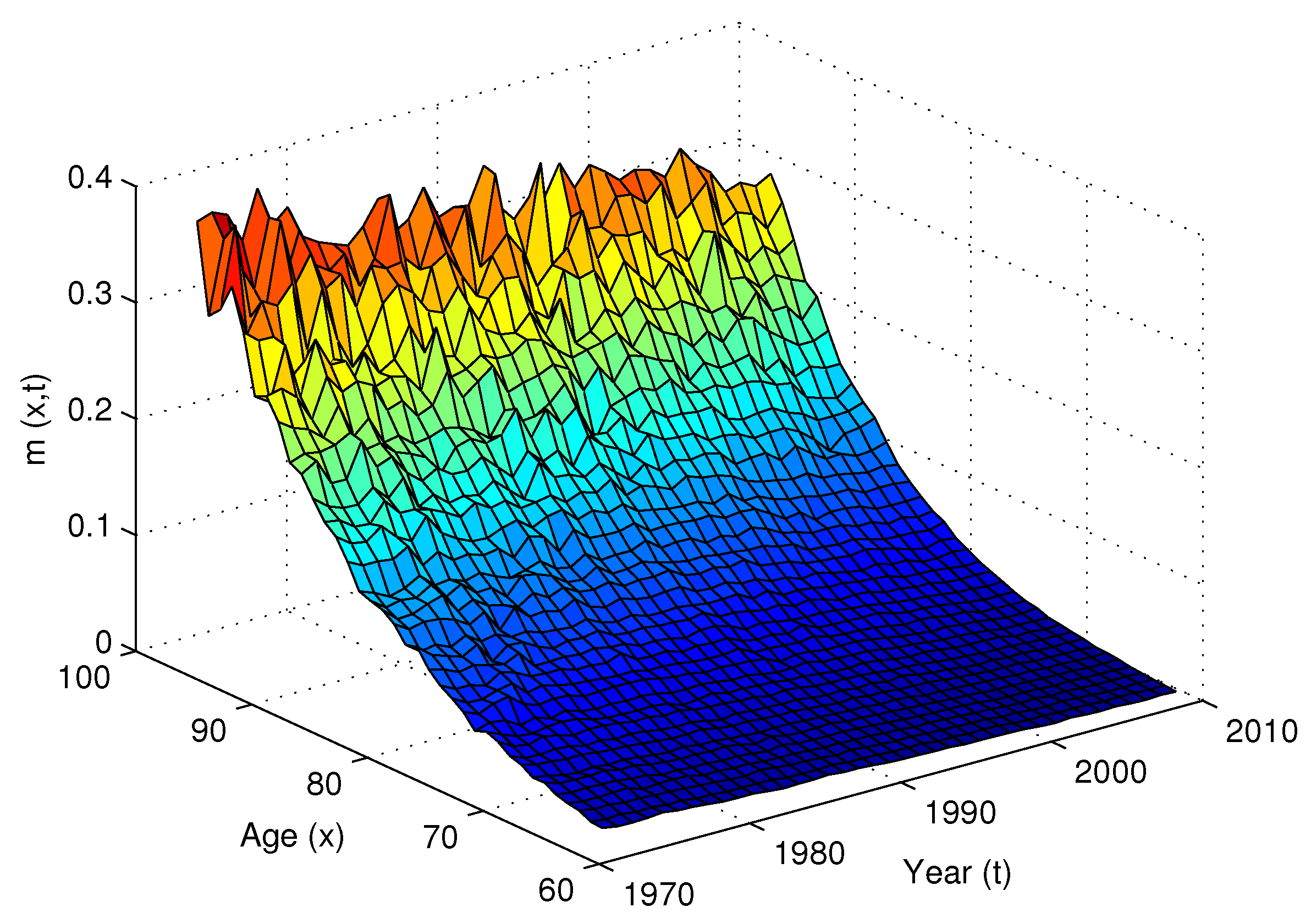
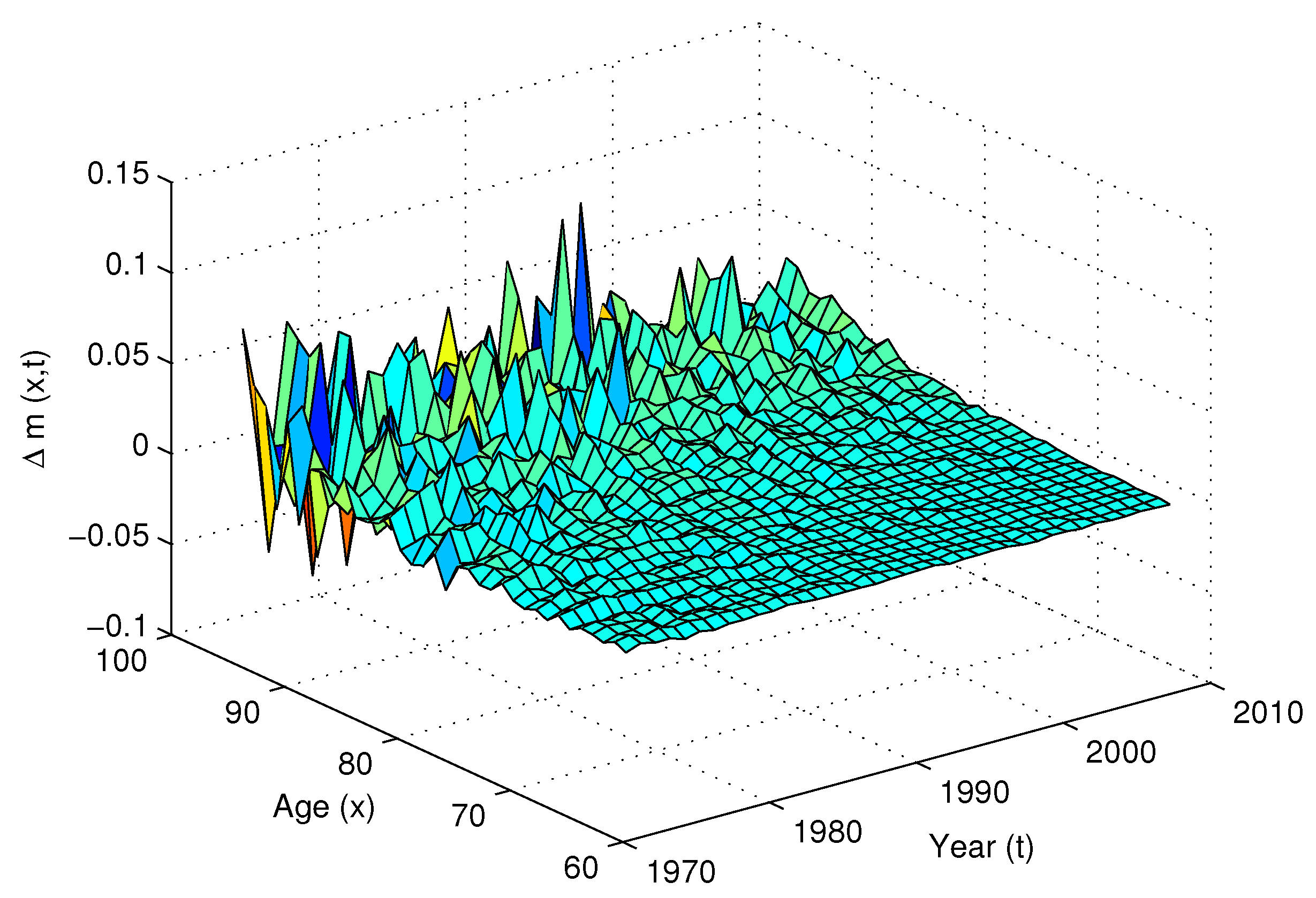
| 5 | We can in fact replace x by in Equation (4). Using will take into account the empirical observation that the volatility of mortality tends to increase with age (Figure 1 and Figure 2). However, for a Gaussian process the intensity will have a non-negligible probability of reaching negative values when the volatility of the second factor () becomes very high, which occurs for example when (given ). Using x instead of will also make the results of Section 3 easy to interpret. For these reasons we assume that the second factor depends on the initial age x only. |
| 6 | We use Australian males mortality data for illustrative purposes. The model can well be applied to any other mortality data. |
| 7 | We calibrate the model for ages 65 and 75 simultaneously to obtain reasonable values for and since the drift of the second factor is age-dependent. |
| 8 | For simplicity, we assume that there is no risk adjustment for the first factor and is age-independent. However, if the market demands a risk premium for the first factor then one could, similar to the case of , assume that and, hence, obtain under the measure. In the following we assume for simplicity and conciseness of discussion that . |
| 9 | The issue price was determined by BNP Paribas using anticipated cash flows based on the 2002-based mortality projections provided by the UK Government Actuary’s Department. |
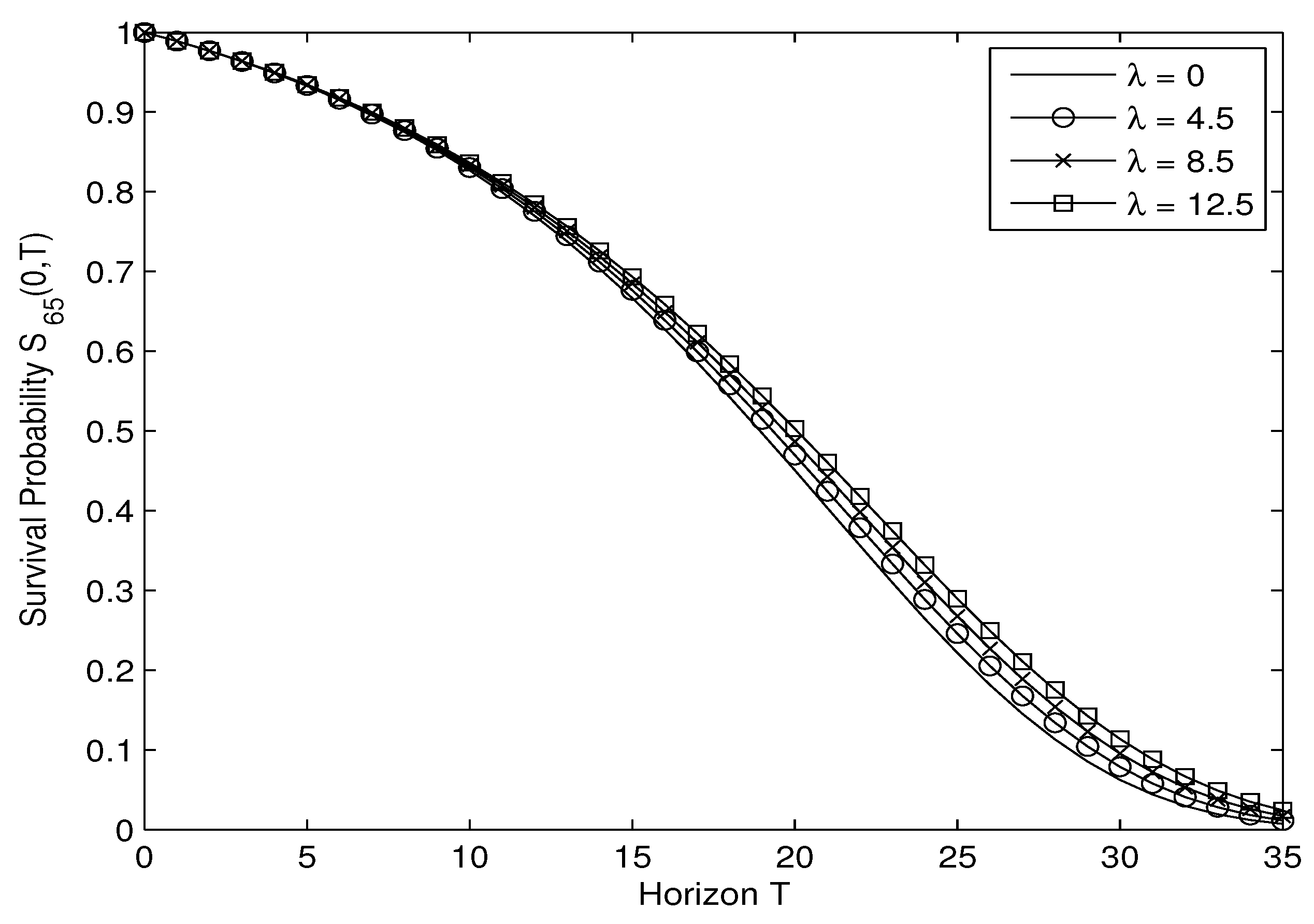
| 10 | The spread depends on the term of the bond and the initial age of the cohort being tracked (Cairns et al. 2006), and is related to but distinct from , the longevity risk premium. |
| 11 | The reference cohort for the BNP/EIB longevity bond is the England and Wales males aged 65 in 2003. Since the longevity derivatives market is under-developed in Australia, we assume that the same spread of (as in the UK) is applicable to the Australian males cohort aged 65 in 2008. Note however that sensitivity analyses will be performed in Section 4. |
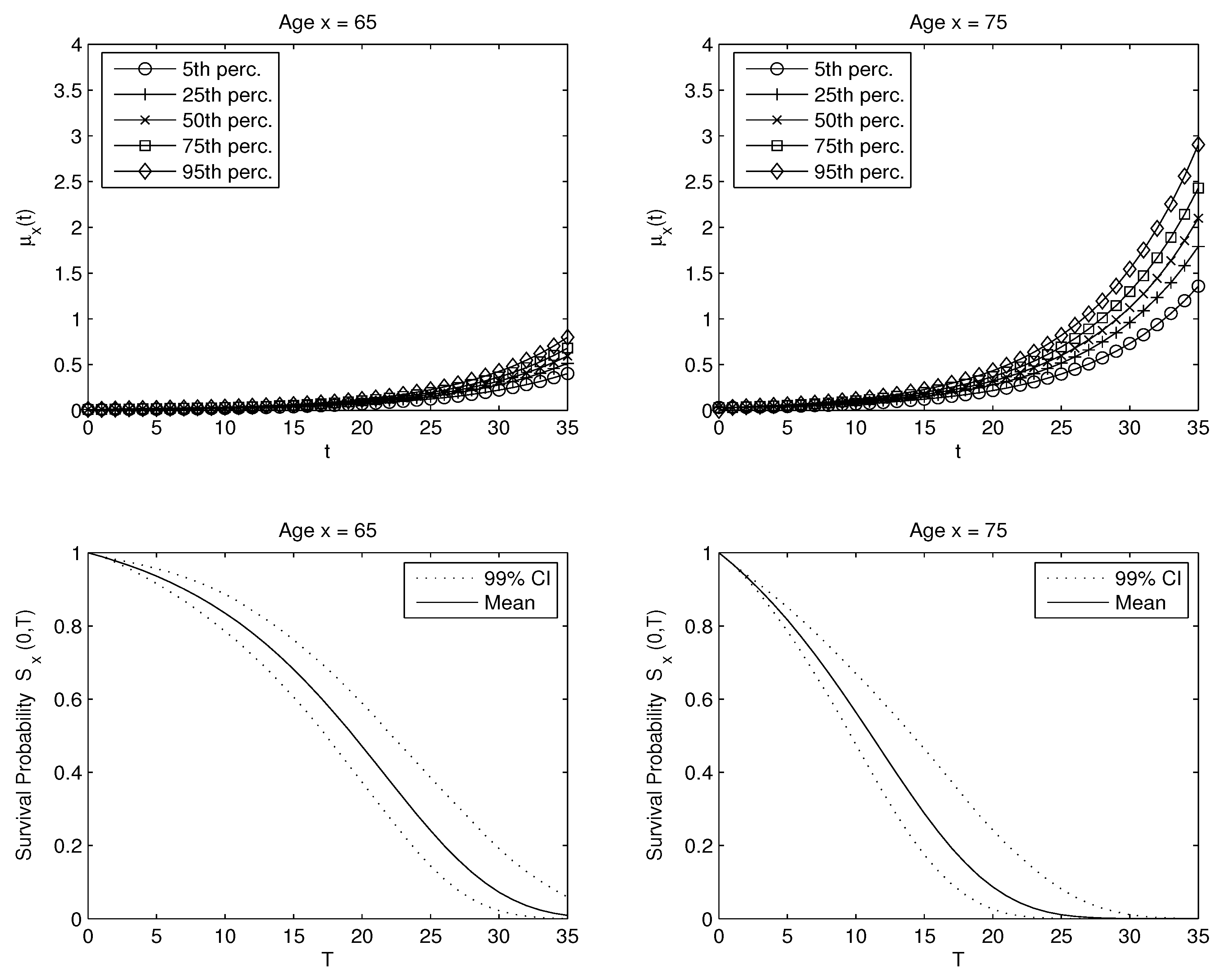
| 12 | The risk-adjusted survival probability will be larger than the “best estimate” -survival probability if a positive market price of longevity risk is demanded, see Figure 4. |
| 13 | The payoff of a longevity caplet is similar to the payoff of the option embedded in the principal-at-risk bond described in Biffis and Blake (2014). |
| 14 | If basis risk is present, we need to distinguish between the mortality intensity for the population () and mortality intensity for the cohort () underlying the annuity portfolio, see Biffis et al. (2014). |
| 15 | For a longevity swap, the risk-adjusted survival probability is used as a strike price so that the price of a longevity swap is zero at inception. In contrast, a longevity cap has non-zero price and is the most natural choice for a strike. |
| 16 | |
| 17 | Given , the VaR and the ES for a swap-hedged portfolio are and , respectively. For a cap-hedged portfolio they become and , respectively. |
| Parameters | |||||
| Values | 0.0022465 | 0.0000002 | 0.129832 | −0.795875 | 0.0017508 |
| Parameters | |||||
| Values | 0.0000615 | 0.120931 | 0.0021277 | 0.0084923 | 0.0294695 |
| Parameters | (Years) | n | |
| Values | 8.5 | 30 | 4000 |
| Mean | Std. dev. | Skewness | VaR | ES | |
|---|---|---|---|---|---|
| No hedge | −0.0059 | 0.3614 | −0.3553 | −0.9385 | −1.1185 |
| Swap-hedged | −0.0086 | 0.0718 | −0.3704 | −0.1870 | −0.2277 |
| Cap-hedged | −0.0067 | 0.2031 | 0.9864 | −0.3200 | −0.3584 |
| No hedge | 0.1536 | 0.3614 | −0.3552 | −0.7795 | −0.9588 |
| Swap-hedged | 0.0051 | 0.0718 | −0.3721 | −0.1730 | −0.2140 |
| Cap-hedged | 0.0701 | 0.2031 | 0.9867 | −0.2435 | −0.2815 |
| No hedge | 0.2995 | 0.3614 | −0.3553 | −0.6335 | −0.8131 |
| Swap-hedged | 0.0207 | 0.0718 | −0.3699 | −0.1575 | −0.1984 |
| Cap-hedged | 0.1224 | 0.2031 | 0.9864 | −0.1910 | −0.2293 |
| No hedge | 0.4492 | 0.3614 | −0.3553 | −0.4835 | −0.6633 |
| Swap-hedged | 0.0401 | 0.0718 | −0.3697 | −0.1380 | −0.1790 |
| Cap-hedged | 0.1637 | 0.2031 | 0.9863 | −0.1500 | −0.1879 |
| Mean | Std. Dev. | Skewness | VaR | ES | |
|---|---|---|---|---|---|
| Years | |||||
| No hedge | 0.2995 | 0.3614 | −0.3553 | −0.6335 | −0.8131 |
| Swap-hedged | 0.2835 | 0.3262 | −0.4693 | −0.5840 | −0.7608 |
| Cap-hedged | 0.2907 | 0.3427 | −0.3517 | −0.5960 | −0.7717 |
| Years | |||||
| No hedge | 0.2995 | 0.3614 | −0.3553 | −0.6335 | −0.8131 |
| Swap-hedged | 0.1745 | 0.1908 | −0.8593 | −0.3755 | −0.5159 |
| Cap-hedged | 0.2247 | 0.2679 | 0.0864 | −0.4050 | −0.5399 |
| Years | |||||
| No hedge | 0.2995 | 0.3614 | −0.3553 | −0.6335 | −0.8131 |
| Swap-hedged | 0.0207 | 0.0718 | −0.3699 | −0.1575 | −0.1984 |
| Cap-hedged | 0.1224 | 0.2031 | 0.9864 | −0.1910 | −0.2293 |
| Years | |||||
| No hedge | 0.2995 | 0.3614 | −0.3553 | −0.6335 | −0.8131 |
| Swap-hedged | −0.0086 | 0.0667 | 0.0384 | −0.1605 | −0.1850 |
| Cap-hedged | 0.1005 | 0.1972 | 1.0637 | −0.1890 | −0.2151 |
| Mean | Std.dev. | Skewness | VaR | ES | |
|---|---|---|---|---|---|
| No hedge | 0.2993 | 0.3679 | −0.3357 | −0.6530 | −0.8277 |
| Swap-hedged | 0.0206 | 0.0980 | −0.1243 | −0.2100 | −0.2596 |
| Cap-hedged | 0.1222 | 0.2141 | 0.8556 | −0.2395 | −0.2870 |
| No hedge | 0.2995 | 0.3614 | −0.3553 | −0.6335 | −0.8131 |
| Swap-hedged | 0.0207 | 0.0718 | −0.3699 | −0.1575 | −0.1984 |
| Cap-hedged | 0.1224 | 0.2031 | 0.9864 | −0.1910 | −0.2293 |
| No hedge | 0.2991 | 0.3598 | −0.3615 | −0.6435 | −0.8147 |
| Swap-hedged | 0.0204 | 0.0604 | −0.6155 | −0.1340 | −0.1762 |
| Cap-hedged | 0.1220 | 0.1999 | 1.0432 | −0.1690 | −0.2116 |
| No hedge | 0.2987 | 0.3592 | −0.3627 | −0.6395 | −0.8180 |
| Swap-hedged | 0.0200 | 0.0542 | −0.7624 | −0.1210 | −0.1644 |
| Cap-hedged | 0.1216 | 0.1984 | 1.0702 | −0.1630 | −0.2016 |
| n | 2000 | 4000 | 6000 | 8000 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fung, M.C.; Ignatieva, K.; Sherris, M. Managing Systematic Mortality Risk in Life Annuities: An Application of Longevity Derivatives. Risks 2019, 7, 2. https://doi.org/10.3390/risks7010002
Fung MC, Ignatieva K, Sherris M. Managing Systematic Mortality Risk in Life Annuities: An Application of Longevity Derivatives. Risks. 2019; 7(1):2. https://doi.org/10.3390/risks7010002
Chicago/Turabian StyleFung, Man Chung, Katja Ignatieva, and Michael Sherris. 2019. "Managing Systematic Mortality Risk in Life Annuities: An Application of Longevity Derivatives" Risks 7, no. 1: 2. https://doi.org/10.3390/risks7010002





