1. Introduction
Market-consistent valuation has gained increasing importance in the risk management of life insurance policies (e.g., Bauer et al. [
1]). However, many life insurance contracts have features which are too complicated to undertake analytical analysis. These include participating contracts, surrender options, and guaranteed interest rates, to name a few. They leave only little structure in the payoff profile, thus making analytical risk neutral valuation almost impossible. Therefore, one has to resort to some type of Monte Carlo method for market-consistent valuation of life insurance policies. As a result, Monte Carlo methods of various types have attracted a lot of attention in recent research. Although Monte Carlo methods work quite well for one specific valuation, they prove to be rather inefficient for repeated application in risk capital computation. For instance, the computational inefficiency of nested Monte Carlo methods for risk capital computation (cf. below and
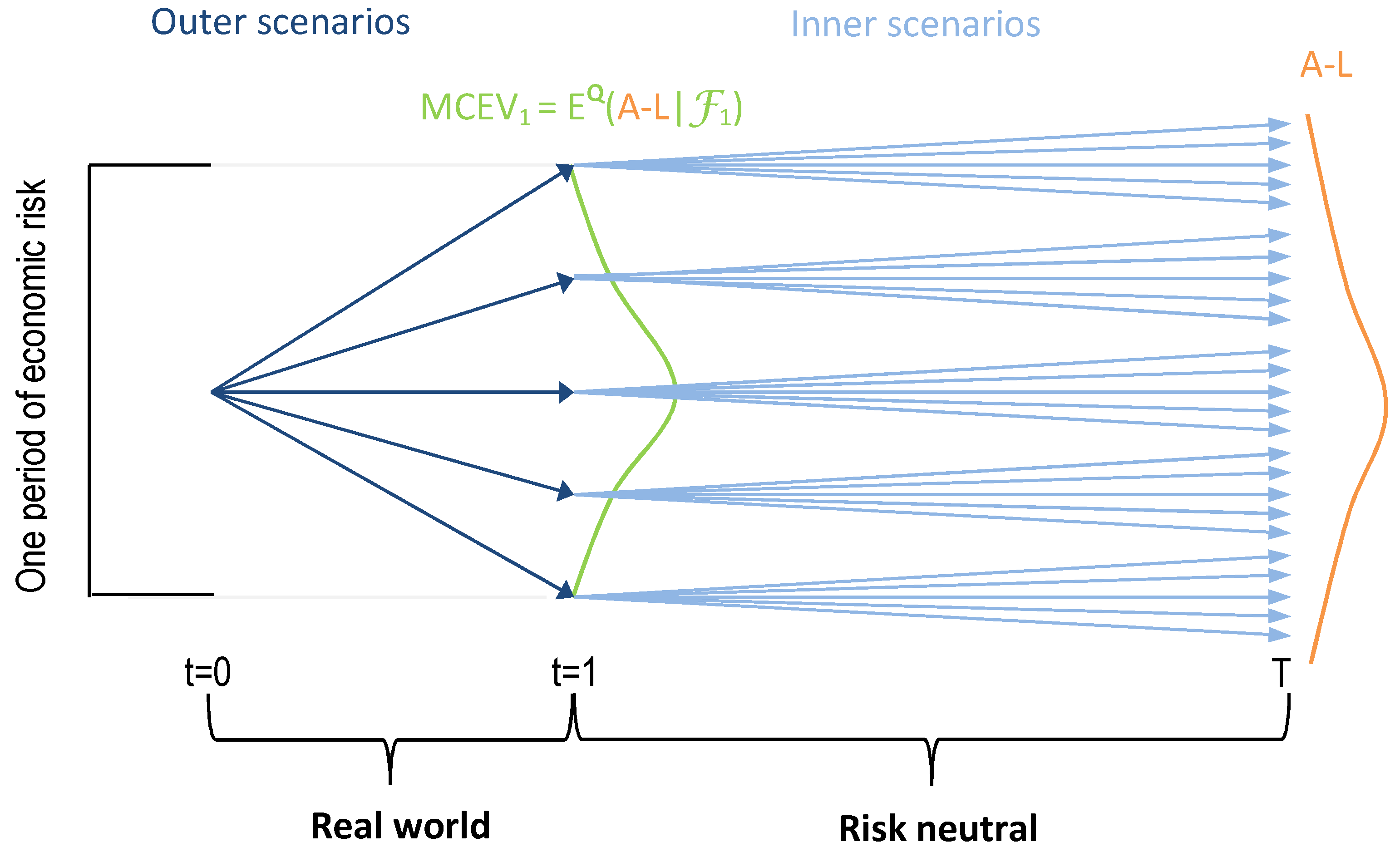
Figure 1 for a brief description, or see Bauer et al. [
1] for more details) has led to an investigation of alternative methods. Andreatta and Corradin [
2], Baione et al. [
3], Glasserman and Yu [
4], Stentoft [
5], and several other authors apply or analyze the well-known least squares Monte Carlo approach, which was originally introduced by Longstaff and Schwartz [
6] and Tsitsiklis and van Roy [
7] to price American options. Bergmann [
8] also mentions the stochastic mesh method of Broadie and Glasserman [
9], although no application to life insurance policies is known to our best knowledge.
In hindsight, Pelsser [
10] probably first suggested valuation of with-profits guaranteed annuity options—which are typical life insurance products—via
static replicating portfolios. Although static hedging seems overly simplistic—especially compared to more advanced dynamic hedging—a remarkably good fit of the behaviour of annuity options was obtained by a static portfolio of vanilla swaptions. In general, by constructing such a static replicating portfolio, one tries to form a static portfolio of a finite number of selected financial instruments which are easy to price, such that they generate cash-flows which approximate cash-flows on the liability side at each point in time and in each scenario. If this approximation is accurate, one obtains a good estimate of the market value of liabilities from the fair value of the replicating portfolio. Further, the market consistent embedded value (MCEV) can be obtained accordingly by subtracting this value from the value of the insurer’s asset holdings. One could of course determine the value of liabilities directly by Monte Carlo simulations: generate risk-neutral sample paths of liability cash-flows and compute the mean of present values of the discounted cash-flows (e.g., Grosen and Jørgensen [
11]). However, as the Solvency II capital requirement demands the computation of the 99.5% value at risk (see EIOPA [
12], page 7) of the MCEV distribution in one year under the real world measure, it is not sufficient to compute the MCEV today, but its distribution in the future. This requires the aforementioned nested approach; see
Figure 1.
As static replication is much more simplistic than dynamic replication, it has been an open question until quite recently, as to whether the approach of replicating portfolio can actually work. Although replication seems to resemble traditional immunization approaches, one major difference stands out: on the one hand, immunization works well in one period (as sensitivities to risk factors have been immunized), but leaves the portfolio un-immunized in the next period, which requires re-immunization (this is the main idea of dynamic delta hedging). On the other hand, replication matches cash flows, so there is hope that although one is not fully immunized in the first period, the immunization is still reasonable in the next period, as future cash flows are still replicated well. Very recent results have shown that replication indeed works under quite general setups, with efficiency comparable to the least squares Monte Carlo approach. The first theoretical foundations for replicating portfolios have been given in a series of papers by Beutner et al. [
13], Pelsser and Schweizer [
14], and Beutner et al. [
15]. They analyze the asymptotic behaviour of matching the terminal value of liabilities (instead of matching cash flows; see below for more details) as the number of scenarios and the number of replicating assets grows at specific relative speeds. Recently, Cambou and Filipovic [
16] proved that the matching of terminal values indeed has a mathematical foundation in the sense that a good match of the terminal values is strongly intertwined with a good approximation of the risk measure of the future MCEV (i.e., the resulting risk capital). Simultaneously, Natolski and Werner [
17] demonstrated that this foundation holds for any form of matching problem in Natolski and Werner [
18] (and many more), especially including all cash flow matching and all terminal value matching problems considered here. In both Cambou and Filipovic [
16] and Natolski and Werner [
18], it is shown that it is possible to change from the real world measure in the first period to the risk neutral measure while maintaining the strong link between objective function and error in risk capital. These results provide the basis for the practically most relevant replication setup
1 where only the risk neutral measure is considered (see
Section 2 for the mathematical setup).
The replicating portfolio approach represents a well-established approach carried out by many life insurance companies within their Solvency II framework for the computation of market risk capital. It is very specific to life insurance companies, and to our best knowledge so far, not used outside life insurance. We note that it could in theory also be used in banks for improving risk figure computation for hard-to-price portfolios
2.
Of course, only considering financial instruments might fall short of matching actuarial risks like mortality or lapse risk. This is one of the well-known weaknesses of replicating portfolios, and usually leads to a remaining mismatch. However, as replicating portfolios are usually only applied within the market risk computation in Solvency II, this only represents a minor issue of replicating portfolios in practice.
As already briefly indicated above, there exist different choices for the specific matching problem. In Natolski and Werner [
18], some of these criteria were already investigated in more detail. The focus there was put on the two criteria which are most popular in the insurance industry:
Squared cash flow matching: this was probably the first formulation considered in the context of replicating portfolios. Here, the difference of cash flows at the same time point is measured by the squared -norm, and the sum of these is used as matching criterion. This problem is called (RPSCF) in the following.
Terminal value matching: as an alternative to the cash flow matching criterion, terminal value matching—called (
) below—was introduced by Oechslin et al. [
20]. The main idea is that it is expected that a good approximation of the risk capital can already be obtained if the
value of the cash flows is matched sufficiently well, while the timing of the cash flows should not be of any importance. Usually, cash flows are aggregated to the terminal time point, leading to the consideration of
terminal values. This point of view was mathematically supported in Natolski and Werner [
17].
These two (and other) choices might differ in important properties:
Depending on the choice of the fitting criterion, similarly good fits of the fitting criterion lead to differing good or even only reasonably good approximations of the risk capital figure. In summary, terminal value matching provides better bounds than cash flow matching. Further, squared cash flow matching provides worse bounds than cash flow matching (to be defined below). Details on the exact relationships are provided in Natolski and Werner [
17].
Depending on the choice of the fitting criterion, the solution of the corresponding optimization problems might pose difficulties. Although all formulations usually lead to convex problems, not all problems might be strictly convex, and thus may have non-unique optimal solutions. Further, non-smooth problems might be much harder to solve than smooth problems. Finally, some fitting criteria (for instance, those based on -norms instead of -norms) lead to an increase of the problem dimension with increasing number of scenarios, while others do not face this issue.
It is expected by practitioners that the fair value of the replicating portfolio also matches the fair value of the liabilities. This has already been proven for the two most practically relevant criteria, but this question remains open for other criteria.
The analysis of the replication problems in Natolski and Werner [
18] focused on the two most popular matching criteria, as these are a) quite easy to analyze and b) are strongly connected. As has been shown in Natolski and Werner [
18], the terminal value match can be seen as a squared cash flow match plus an additional dynamic trading strategy moving cash flows optimally in time. From a theoretical perspective, both choices provide a good link between matching criterion and approximation of risk capital (see Natolski and Werner [
17]), although terminal value matching dominates squared cash flow matching. Further, both problems lead to strictly convex quadratic optimization problems possessing a unique optimal solution (under rather weak assumptions). From a practical perspective, however, both problems show some unwanted behaviour. Extensive numerical tests (Daul and Vidal [
21]) have shown that the out-of-sample performance of terminal value matching is worse than the corresponding performance of (squared) cash flow matching. However, the latter problem reacts more sensitively to the scaling and the conditioning of the data than terminal value matching due to increased dimensions of relevant covariance matrices. The bad out-of-sample performance of terminal value matching can be linked to the property that it actually already includes a dynamic cash flow distribution strategy. This indicates that an unwanted overfitting takes place; i.e., there are too many optimization variables given only a few number of scenarios. As pointed out, it is not feasible to provide more scenarios, as these are computationally quite expensive. Therefore, the consideration of more enhanced replication—for example, by a more dynamic replication strategy—is clearly not advocated.
For the above reasons, it might make sense to look for alternative criteria which have the potential to successfully address these issues. For this purpose, we consider a modified cash flow matching problem—called (
RPCF)—where the penalization of cash flows does not use the squared
-norm, but just the
-norm itself. This problem has already been briefly considered in Natolski and Werner [
18], but a full analysis was out of the scope of that paper.
Compared to the other two problems (RPSCF) and (), it has a more complicated objective function, since the objective function cannot be expressed as a convex quadratic function. Thus, it is impossible to obtain an explicit expression for the solution of the problem, and results on the existence and uniqueness of a solution are not straightforward. Further, the objective function of (RPCF) might be non-smooth at certain points. We believe that it is for this reason that problem formulation (RPCF) did not yet get as much attention as the other two formulations, both from practitioners and academics.
In the following, we will argue that on the contrary, there are good reasons to believe that (RPCF) is indeed at least as preferable as (RPSCF) or (). To be able to do so, we first provide the detailed proofs for the existence and uniqueness of the solution under weak assumptions. Further, we show that despite the similarity to the famous Fermat–Torricelli problem, it matches the fair value of the replicating portfolio and the fair value of liabilities under an additional rather weak assumption. We also prove that the objective function is uniformly convex in practical problem instances (satisfying an additional assumption), a useful feature for optimization and statistical properties. Finally, we demonstrate that (RPCF) can be equivalently cast as a second-order cone problem, which allows its unique solution to be obtained by efficient second-order methods like interior point methods (without the additional assumption satisfied in practical problems). Ultimately, we provide a discussion as to why problem (RPCF) should be preferred over problems (RPSCF) and (), and why not.
The rest of the paper is organized as follows. In
Section 2, we introduce the mathematical setup for the financial market following Natolski and Werner [
17], and we recall the cash flow matching problem of the Fermat–Torricelli type. The main
Section 3 states and proves the aforementioned properties of the replication problem, and
Section 4 concludes.
2. The Mathematical Setup
As mentioned in the introduction, this setup is taken from Natolski and Werner [
17]. We fix a finite time horizon
and set
,
. Let
be a filtered probability space with risk-neutral
3 measure and numéraire
, where
is assumed to be complete and trivial and
. Denote by
, the discounted
4 financial cash flows of all assets at time
t, where
and
m denotes the number of available financial assets,
the vector of discounted terminal
5 financial cash flows,
the discounted liability cash flows, and by
, the discounted terminal value of liability cash flows.
The final cash flow is equal to the corresponding asset value. The interpretation is that all assets are sold at the time horizon T. Assets are bought and sold at time t before the time t cash flows take place.
The following three replication problems were considered in Natolski and Werner [
18], where the first problem (
RPCF), cash flow matching, is in the focus of this exposition. In this context, a portfolio
α represents the units of the financial instruments which have to be bought or sold.
The first formulation penalizes the deviation of cash flows by the -norm, whereas the second formulation penalizes the cash flows by the squared -norm. Otherwise, the formulations are the same. The third formulation (where the sum has moved inside the square inside the expected value) represents the penalized squared deviation of the terminal values.
Remark 1. It has to be noted that there is no budget constraint in all three optimization problems, as the budget is not restricted, but allowed to vary freely. In Section 3.4, we will characterize the optimal budget, which is equal to the fair value of the replicating portfolio. It is shown there that the optimal budget equals the fair value of the liabilities under rather weak assumptions. Remark 2. In this context, an open issue concerning the formulation of the optimization problems is the relevance of the particular risk neutral measure chosen. Assuming that the probability space cannot be partitioned into finitely many atoms, the market has to be incomplete, and there are infinitely many risk-neutral measures for each numéraire. Hence, one can choose from a variety of risk neutral measure/numéraire pairs to construct replicating portfolios. Obviously, for fixed numéraire, the objective function in (RPCF) depends on the specific choice of the risk neutral measure. Thus, the optimal solution (i.e., the replicating portfolio) depends on this risk neutral measure. Similarly, the fair value of both the liability and the replicating portfolio also depend on the choice of the risk neutral measure. Only in the special case of perfect replication (i.e., optimal objective value of 0) is there no dependence on the choice of the measure. As all risk neutral measures for some numéraire are equivalent, the same (unique) replicating portfolio is optimal for all such measures.
In practice, a natural measure to use in the objective function is the real-world measure. It is well-known (see for example Korn and Schäl [22]) that the real-world measure becomes a martingale measure if the numéraire is chosen as the portfolio process maximizing the logarithmic utility function. Then, the real world measure is a martingale measure with numéraire given by the maximizing portfolio process. This way, one can avoid the discussion on the choice of the risk neutral measure and simply use the real world measure together with portfolio process as numéraire. Unfortunately, this approach is usually not followed in practical settings. The main reason is probably twofold: first, in practice, insurance companies are provided with economic scenario generators (ESG) tools which readily yield risk neutral scenarios for arbitrary numéraires (usually the cash rollup). Second, due to the linear nature of real world scenarios provided by these ESG tools, the utility maximizing portfolio process cannot be calculated due to the missing nested scenario structure.
For further analysis, let us introduce the symmetric matrices
These matrices represent the covariance matrices of the terminal values and the cash flows, respectively. They will play an important role in formulations of (weak) assumptions on the financial market. To obtain existence and uniqueness results (and more), the following few rather weak assumptions will have to be made. These are usually satisfied if financial assets for replication are chosen accordingly.
Assumption 1. The matrix is positive definite or equivalently Assumption 2. The matrix is positive definite or equivalently Assumption 3. The numéraire is replicable at any time; that is, Assumption 3 can be easily
6 fulfilled, taking into account that the numéraire is a tradable instrument itself. For any choice of the numéraire, one simply has to provide
T financial instruments as follows: for each time
t, we add an option on the numéraire to the market with strike 0 and maturity
t. Equivalently, this can be seen as an asset which costs
today (today’s price of the numéraire) and yields a cash flow of
at time
t. A proper combination of these options then yields the desired portfolio
u as in Assumption 3. Of course, Assumption 3 is only necessary if cash flow matching is considered; for terminal value matching, it is sufficient to include exactly one of these options.
For problems (
RPSCF) and (
), the following two properties have been shown in Natolski and Werner [
18]:
- (1)
The solutions to (
RPSCF) and (
) exist and under Assumption 1 (Assumption 2, respectively) they are unique; i.e., there exist unique
such that
- (2)
Under Assumption 3, the fair values of both optimal replicating portfolios equal the fair value of liability cash flows; that is:
For existence and uniqueness, the proofs exploit the convex quadratic structure of the two problems. Both replicating portfolios can be written as solutions to quadratic problems, and under the assumption of no redundant assets, the corresponding quadratic matrices are positive definite. Equality of fair values can then be deduced directly from the corresponding optimality conditions.
So far, problem (
RPCF) has not been analyzed on the same level of detail. As pointed out in Natolski and Werner [
18], its close connection to the Fermat–Torricelli problem (c.f. Nam [
23]) gives strong evidence that on the one hand, existence and uniqueness of a solution is provided, whereas on the other hand, equality of fair values cannot be expected in all cases.
In what follows, we give a detailed proof of the existence and uniqueness of a solution based on the above assumptions. We also show that the optimal replicating portfolio indeed has the same fair value as the liability cash flows under surprisingly weak additional conditions. Further, we prove that for realistic problem instances (i.e., under certain additional assumptions), the numerical solution of (RPCF) can be obtained by efficient standard second-order methods like Newton’s method. Going one step further, we provide a reformulation as a linear second order cone program and thus demonstrate that these additional assumptions are actually not necessary to allow for efficient numerical solution by efficient second-order methods. Based on these novel insights, we will argue that (RPCF) ranks at least equal to the two alternative formulations for practical problem instances.
3. Properties of RPCF
Before we start to provide the results, we need a few technical preparations. Let us define:
so that we may rewrite problem (
RPCF) as
It is easily seen that each
(and thus the objective function
φ as well) is convex on the whole
. As all
are finite on
, they are thus also (locally Lipschitz) continuous. Their directional derivatives in direction
d are given by
If
is differentiable, then
Obviously, if
is (continuously) differentiable in a point
α, it is also twice continuously differentiable there. Its Hessian is given as
As is convex, its Hessian is positive semidefinite. Unfortunately, it cannot be expected that the Hessian is positive definite due to potential rank deficits in , plus a further rank deficit of at most one (due to the dyadic term in the nominator).
3.1. Existence of Optimal Solution
We begin by showing that a solution to (RPCF) exists in the first place.
Theorem 1. Under Assumption 1, problem (RPCF) possesses at least one optimal solution .
Proof. As already observed,
φ is convex and continuous. Furthermore,
φ is also coercive
7. To see this, denote by
the smallest eigenvalue of the matrix
. Due to Assumption 1,
, and we obtain
By Minkowski’s inequality, it follows
Therefore, in total we have
so that in particular
As a continuous convex and coercive function, φ attains its minimum, and we are finished. ☐
3.2. Uniqueness of Optimal Solution
Now, let us consider under which conditions we get uniqueness of the optimal replicating portfolio. Let us first consider the rather easy but practically most likely case that no liability cash flow at any time can be replicated:
Under this assumption, φ is obviously twice continuously differentiable on the whole . In practice, Assumption 4 is usually fulfilled, since liability cash flows are not replicable at any time in the future. If it holds, one can easily show the following strong result.
Theorem 2. Under Assumptions 1 and 4, the objective function φ is strictly convex and twice continuously differentiable. Furthermore, it is strongly and uniformly convex on each compact subset of . Especially, the global minimum of φ is unique.
Proof. Let
be arbitrary. As for each
t,
is twice continuously differentiable, and we can consider the Hessian
(cf. (1)). As this Hessian is positive semi-definite, it holds that
As no
vanishes, we have
for all
t. Then, due to the Cauchy–Schwarz inequality, it holds that this inequality is strict for
t if and only if
and
is not collinear with
. Due to Assumption 1, for each
, there is at least one
such that
. Now let us assume that
is collinear to
; i.e., let us assume that
By definition of
ϵ, this is equivalent to
However, this means that in , the liability cash flow can be perfectly replicated, which is a contradiction to Assumption 4. Therefore, cannot be collinear to , and the above inequality is strict for each . Thus, the Hessian matrix of φ is positive definite, and as α was arbitrary, φ is strictly convex. The remaining claims are straightforward consequences. ☐
Remark 3. In Görner and Kanzow [24], it is shown that for uniformly convex φ, Newton’s method is globally quadratically convergent on any compact set. From inequality (2), we see thatis compact and contains the optimal solution. Hence, if we restrict to the optimization on this set we know that Newton’s method will be globally quadratically convergent. Although for practical purposes the following result might not be as important as Theorem 2 (obtained under the stronger Assumption 4), there still remain some cases when Assumption 4 is violated. In particular, this includes all models where liability cash flows are predictable, for example, as in Grosen and Jørgensen [
11]. In this more general case, it is still possible to show uniqueness of the optimal replicating portfolio. However, without Assumption 4, strict convexity and smoothness of the objective function will be lost in general.
Theorem 3. Under Assumption 1, the global minimum of φ is unique.
Proof. Let us assume that
φ possesses (at least) two different global minima, called
and
. Then, let us consider the midpoint
which, due to convexity, has to be optimal as well. Due to the optimality of
α, the directional derivative of
has to vanish in all directions
d, especially in direction
.
As
φ is the sum of convex functions
,
α can only be optimal if all terms
are linear in direction
h (e.g., Nam [
23] for the same argument). If
, this can only be the case if both
; otherwise, we would have a contradiction to the assumption that both
and
are optimal, and we are done. From
, it directly follows that
h is such that
. If, alternatively,
, then the second derivative in direction
h has to vanish for linearity. This can only happen if either
or
is collinear to
. In the first case, the directional derivative of
in direction
h vanishes, whereas in the second case, we have that
as
for some
due to collinearity. So, for all
t, we need to have
for optimality. However, due to Assumption 1, there is at least one
such that
; thus,
has to be collinear to
, which shows that the directional derivative of
φ does not vanish in direction
h. This is a contradiction to our initial assumption, and we are done. ☐
In the general case without Assumption 4, no first- or even second-order method can be used to directly solve the cash flow replication problem (RPCF) due to potential non-smoothness of φ. However, we will show in the following that we can avoid this non-smoothness by an equivalent reformulation as a second-order cone program, which can then be solved by efficient second-order methods.
3.3. Reformulation as Second-Order Cone Program
Let us start with the unconstrained formulation of the cash flow replication problem
and let us introduce auxiliary variables
for each term to obtain the obviously equivalent constrained formulation
Now, we have
where
and
is the root matrix of the positive semi-definite matrix
. In summary, we obtain the linear second order cone program
which can be solved by efficient numerical methods with superlinear convergence (e.g., Alizadeh and Goldfarb [
25]).
3.4. Fair Value of Optimal Solution
Finally, let us consider the equality of fair values. The standard Fermat–Torricelli problem as in Nam [
23] is given by
with
and where
denotes the standard Euclidean norm. In general, this problem does not entail optimality conditions which yield equality of means; i.e., in general,
However, although the structure of (RPCF) is very similar, there is a crucial difference. Instead of being fixed in each t, (RPCF) allows some degree of freedom at each time t in the appearance of the time-dependent random variable . In particular, we may assume that for any t we may trade an option today which has payoff equal to the numéraire at t and no payoff otherwise (i.e., call options on the numéraire with strike price 0 and maturity t). In the context of (RPCF), this corresponds to the freedom of choosing the expectation of for each t individually. However, since (RPCF) is nothing but a sum of optimization problems in , optimality conditions will yield that it is best to match expectations of and . This observation is made precise in the following theorem.
Theorem 4. Suppose that for any there exists such that Then, any solution to (RPCF) satisfies Proof. Condition (3) implies that for any
there exists
such that
By examining the directional derivatives of the objective function
φ in (
RPCF) with respect to the direction
, we see that all but the
’th summand disappear:
As
is an unconstrained minimum of a convex function, this requires that all directional derivatives are non-negative, especially the ones in directions of
. If
we do not need to inspect the directional derivative, as in this case the cash flow at time
is exactly replicated and thus the fair values of these cash flows are equal. Therefore, let us consider the case
. Then, considering both
, this means that
and thus
As was chosen arbitrarily, this shows that the fair value of cash flows is in fact equal at any time. In particular, this obviously implies the claim. ☐
Remark 4. As a matter of fact, the observation that some degree of freedom becomes available through time dependence of has already been made in Natolski and Werner [18] in Subsection “Time-separable case”. There it was demonstrated that in the case where cash payments are generated at each time separately, (RPCF) and (RPSCF) are equivalent. In particular, fair values of the replicating portfolios are the same and equal to the fair value of liability cash flows. Going one step further, Theorem 4 now illustrates that for matching fair values it is already sufficient if cash payments equal to the numéraire can be generated at each time separately. This can be considered a rather weak condition, which is usually fulfilled in practical settings if the replication instruments are chosen accordingly. 3.5. Pros and Cons of (RPCF) versus (RPSCF) and ()
So far, problem (
RPCF) has not received much attention amongst practitioners. The reasons for this are manifold:
Problems (RPSCF) and () possess analytical solutions. Thus, the replicating portfolio can be obtained by simple numerical linear algebra, and no optimization framework is needed.
Problems (RPSCF) and () possess unique solutions with fair values equal to the liability fair value.
Problem (RPCF) potentially represents a non-smooth problem, and thus cannot be solved efficiently.
In the above analysis, we have shown that all other reasons besides the first one go up in smoke after a detailed investigation of (
RPCF). From a theoretical point of view (see for example Natolski and Werner [
17]), terminal value matching should be preferred over cash flow matching, as it yields lower error estimates on the resulting risk capital figure. However, numerous numerical studies have shown that the out-of-sample performance of cash flow matched replicating portfolios is superior to terminal value matched portfolios. Further, if one is interested in matching the cash flow profile (and not only risk capital), then cash flow matching is (almost) inevitable. From this point of view, (
RPSCF) should be clearly preferred.
However, due to the long maturity of life insurance contracts (usual models range from 40 to 60 years final maturity), numerical issues cannot be avoided. Usually, the matching error of certain maturities significantly dominates all other maturities. In this case, only the dominating maturities are properly matched. From a statistical point of view (robust statistics, robust least squares), it is well known that this can be partially mitigated if one moves from the square of the -norm to the -norm itself (i.e., if a kind of Fermat–Torricelli structure is chosen). From that perspective, (RPCF) might indeed represent the formulation which leads to the most stable portfolios with satisfying out-of-sample performance. To support such a hypothesis, a thorough numerical analysis is strongly indicated—however, this is clearly beyond the scope of this contribution and is thus left for future research.