Effects of Thermal Oxidation on Sensing Properties of Porous Silicon
Abstract
:1. Introduction
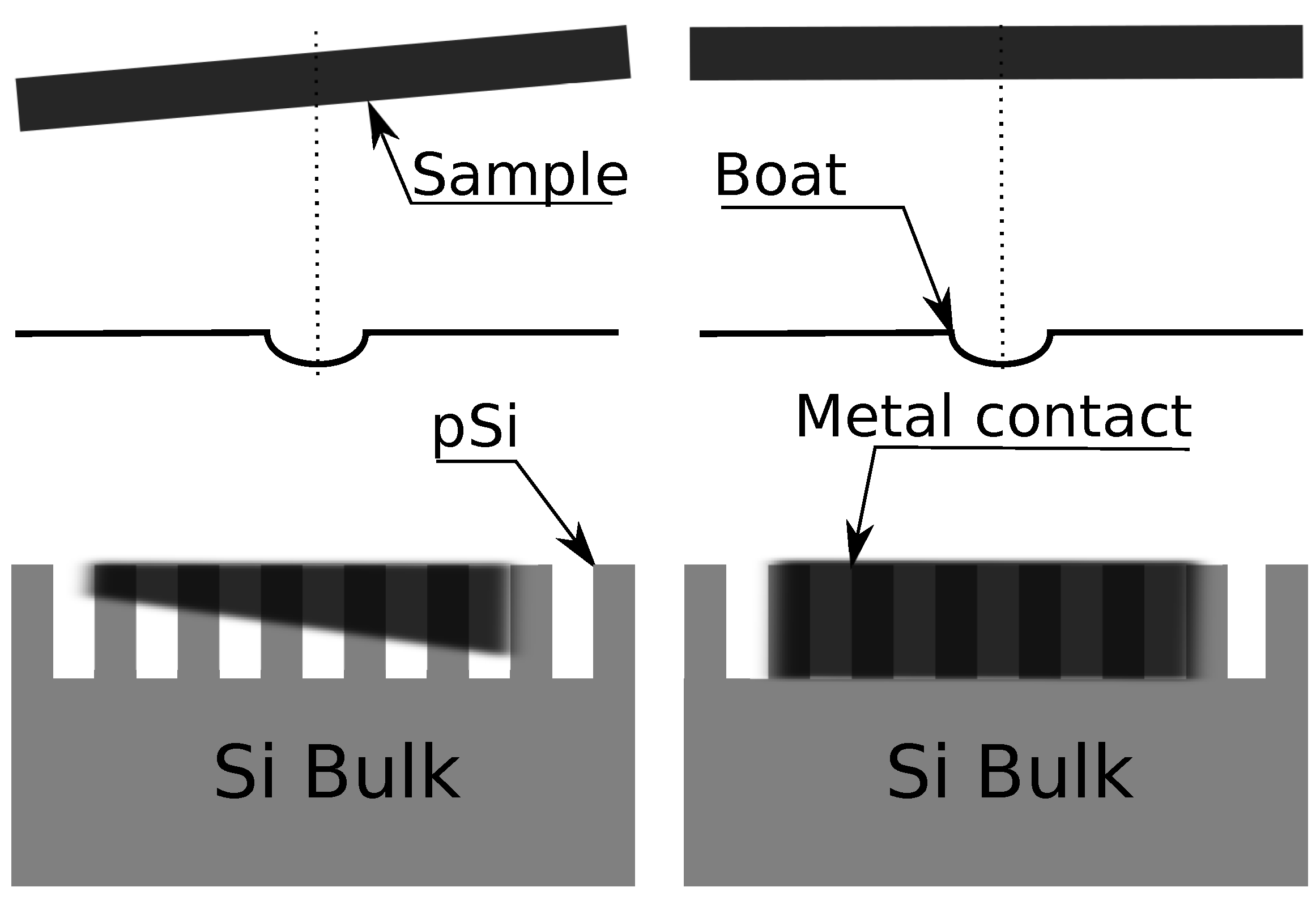
2. Materials and Methods
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EDS | Energy dispersive spectroscopy |
| FTIR | Fourier transform infrared spectroscopy |
| IPA | Isopropanol |
| PS | Porous silicon |
| MEMS | Microelectromechanical systems |
| ODTS | Octadecyltrichlorosilane |
| SCCM | Standard cubic centimeter per minute |
References
- Eranna, G.; Joshi, B.C.; Runthala, D.P.; Gupta, R.P. Oxide Materials for Development of Integrated Gas Sensors—A Comprehensive Review. Crit. Rev. Solid State Mater. Sci. 2004, 29, 111–188. [Google Scholar] [CrossRef]
- Aroutiounian, V. Metal oxide hydrogen, oxygen, and carbon monoxide sensors for hydrogen setups and cells. Int. J. Hydrogen Energy 2007, 32, 1145–1158. [Google Scholar] [CrossRef]
- Yamazoe, N.; Shimanoe, K. New perspectives of gas sensor technology, sens. Sens. Actuators B Chem. 2009, 138, 100–107. [Google Scholar] [CrossRef]
- Seung Eon, M.; Nak-Jin, C.; Hyung-Kun, L.; Jaewoo, L.; Woo Seok, Y. Semiconductor-Type MEMS Gas Sensor for Real-Time Environmental Monitoring Applications, sens. ETRI J. 2013, 35, 617–624. [Google Scholar] [CrossRef]
- Rüffer, D.; Hoehne, F.; Bühler, J. New Digital Metal-Oxide (MOx) Sensor Platform. Sensors 2018, 18, 1052. [Google Scholar] [CrossRef]
- Plecenik, T.; Moško, M.; Haidry, A.; Ďurina, P.; Truchlý, M.; Grančič, B.; Gregor, M.; Roch, T.; Satrapinskyy, L.; Mošková, A.; et al. Fast highly-sensitive room-temperature semiconductor gas sensor based on the nanoscale Pt–TiO2–Pt sandwich, sens. Sens. Actuators B Chem. 2015, 207, 351–361. [Google Scholar] [CrossRef]
- Hyodo, T.; Urata, K.; Kamada, K.; Ueda, T.; Shimizu, Y. Semiconductor-type SnO2-based NO2 sensors operated at room temperature under UV-light irradiation. Sens. Actuators B Chem. 2017, 253, 630–640. [Google Scholar] [CrossRef]
- Jeong, H.; Park, M.; Kwon, S.; Joo, H.; Kwon, H. Highly sensitive and selective room-temperature NO2 gas-sensing characteristics of SnOX-based p-type thin-film transistor. Sens. Actuators B Chem. 2019, 288, 625–633. [Google Scholar] [CrossRef]
- Bilyalov, R.R.; Stalmans, L.; Schirone, L.; Lévy-Clément, C. Use of porous silicon antireflection coating in multicrystalline silicon solar cell processing. IEEE Trans. Electron Devices 1999, 46, 2035–2040. [Google Scholar] [CrossRef]
- Martín-Palma, R.; Manso-Silván, M.; Torres-Costa, V. Biomedical applications of nanostructured porous silicon: A review. J. Nanophotonics 2010, 4, 042502. [Google Scholar] [CrossRef]
- Barillaro, G.; Diligenti, A.; Nannini, A.; Strambini, L.M.; Comini, E.; Sberveglieri, G. Low-concentration NO2 detection with an adsorption porous silicon FET. IEEE Sens. J. 2006, 6, 19–23. [Google Scholar] [CrossRef]
- Ozdemir, S.; Gole, J.L. The potential of porous silicon gas sensors. Curr. Opin. Solid State Mater. Sci. 2008, 11, 92–100. [Google Scholar] [CrossRef]
- Ben-Chorin, M.; Möller, F.; Koch, F. Nonlinear electrical transport in porous silicon. Phys. Rev. B 1994, 49, 2981–2984. [Google Scholar] [CrossRef] [PubMed]
- Ben-Chorin, M.; Kux, A.; Schechter, I. Adsorbate effects on photoluminescence and electrical conductivity of porous silicon. Appl. Phys. Lett. 1994, 64, 481–483. [Google Scholar] [CrossRef]
- Ben-Chorin, M.; Moller, F.; Koch, F.; Schirmacher, W.; Eberhard, M. Hopping transport on a fractal: AC conductivity of porous silicon. Phys. Rev. B 1995, 51, 2199–2213. [Google Scholar] [CrossRef]
- Seals, L.; Gole, J.L.; Tse, L.A.; Hesketh, P.J. Rapid, reversible, sensitive porous silicon gas sensor. J. Appl. Phys. 2002, 91, 2519–2523. [Google Scholar] [CrossRef]
- Aroutiounian, V.M.; Ghulinyan, M.Z. Electrical conductivity mechanisms in porous silicon. Phys. Status Solidi (A) 2003, 197, 462–466. [Google Scholar] [CrossRef]
- Archer, M.; Christophersen, M.; Fauchet, P. Electrical porous silicon chemical sensor for detection of organic solvents. Sens. Actuators B Chem. 2005, 106, 347–357. [Google Scholar] [CrossRef]
- Baran, N.; Gebavi, H.; Mikac, L.; Ristić, D.; Gotić, M.; Syed, K.; Ivanda, M. Sensing Properties of Oxidized Nanostructured Silicon Surface on Vaporized Molecules. Sensors 2019, 19, 119. [Google Scholar] [CrossRef]
- Lewis, S.E.; DeBoer, J.R.; Gole, J.L.; Hesketh, P.J. Sensitive, selective, and analytical improvements to a porous silicon gas sensor. Sens. Actuators B Chem. 2005, 110, 54–65. [Google Scholar] [CrossRef]
- Aroutiounian, V.; Arakelyan, V.; Galstyan, V.; Martirosyan, K.; Soukiassian, P. Hydrogen Sensor Made of Porous Silicon and Covered by TiO2 or ZnO Thin Film. IEEE Sens. J. 2009, 9, 9–12. [Google Scholar] [CrossRef]
- Korotcenkov, G.; Rusu, E. How to Improve the Performance of Porous Silicon-Based Gas and Vapor Sensors? Approaches and Achievements. Phys. Status Solidi (A) 2019, 216, 1900348. [Google Scholar] [CrossRef]
- Rigakis, N.; Hilliard, J.; Abu Hassan, L.; Hetrick, J.M.; Andsager, D.; Nayfeh, M.H. Effect of oxidation treatments on photoluminescence excitation of porous silicon. J. Appl. Phys. 1997, 81, 440–444. [Google Scholar] [CrossRef]
- Bazrafkan, I.; Dariani, R.S. Electrical behavior of free-standing porous silicon layers. Phys. B Condens. Matter 2009, 404, 1638–1642. [Google Scholar] [CrossRef]
- Salonen, J.; Lehto, V.P.; Laine, E. Thermal oxidation of free-standing porous silicon films. Appl. Phys. Lett. 1997, 70, 637–639. [Google Scholar] [CrossRef]
- Salonen, J.; Laine, E.; Niinistö, L. Thermal carbonization of porous silicon surface by acetylene. J. Appl. Phys. 2002, 91, 456. [Google Scholar] [CrossRef]
- Ibraimov, M.K.; Sagidolda, Y.; Rumyantsev, S.L.; Zhanabaev, Z.Z.; Shur, M.S. Selective Gas Sensor Using Porous Silicon. Sens. Lett. 2016, 14, 588–591. [Google Scholar] [CrossRef]
- Brugnone, F.; Perbellini, L.; Apostoli, P.; Bellomi, M.; Caretta, D. Isopropanol exposure: Environmental and biological monitoring in a printing works. Occup. Environ. Med. 1983, 40, 160–168. [Google Scholar] [CrossRef]
- Chien, P.J.; Suzuki, T.; Ye, M.; Toma, K.; Arakawa, T.; Iwasaki, Y.; Mitsubayashi, K. Ultra-Sensitive Isopropanol Biochemical Gas Sensor (Bio-Sniffer) for Monitoring of Human Volatiles. Sensors 2020, 20, 6827. [Google Scholar] [CrossRef]
- Peng, L.; Zhai, J.; Wang, D.; Zhang, Y.; Wang, P.; Zhao, Q.; Xie, T. Size- and photoelectric characteristics-dependent formaldehyde sensitivity of ZnO irradiated with UV light. Sens. Actuators B Chem. 2010, 148, 66–73. [Google Scholar] [CrossRef]
- Vallant, T.; Brunner, H.; Mayer, U.; Hoffmann, H.; Leitner, T.; Resch, R.; Friedbacher, G. Formation of Self-Assembled Octadecylsiloxane Monolayers on Mica and Silicon Surfaces Studied by Atomic Force Microscopy and Infrared Spectroscopy. J. Phys. Chem. B 1998, 102, 7190–7197. [Google Scholar] [CrossRef]
- Resch, R.; Grasserbauer, M.; Friedbacher, G.; Vallant, T.; Brunner, H.; Mayer, U.; Hoffmann, H. In situ and ex situ AFM investigation of the formation of octadecylsiloxane monolayers. Appl. Surf. Sci. 1999, 140, 168–175. [Google Scholar] [CrossRef]
- Leitner, T.; Friedbacher, G.; Vallant, T.; Brunner, H.; Mayer, U.; Hoffmann, H. Investigations of the Growth of Self-Assembled OctadecylsiloxaneMonolayers with Atomic Force Microscopy. Microchim. Acta 2000, 133, 331–336. [Google Scholar] [CrossRef]
- Yon, J.J.; Barla, K.; Herino, R.; Bomchil, G. The kinetics and mechanism of oxide layer formation from porous silicon formed on p-Si substrates. J. Appl. Phys. 1987, 62, 1042–1048. [Google Scholar] [CrossRef]
- Pap, A.E.; Kordás, K.; George, T.F.; Leppävuori, S. Thermal Oxidation of Porous Silicon: Study on Reaction Kinetics. J. Phys. Chem. B 2004, 108, 12744–12747. [Google Scholar] [CrossRef]
- Lucovsky, G.; Yang, J.; Chao, S.S.; Tyler, J.E.; Czubatyj, W. Oxygen-bonding environments in glow-discharge-deposited amorphous silicon-hydrogen alloy films. Phys. Rev. B 1983, 28, 3225–3233. [Google Scholar] [CrossRef]
- Gupta, P.; Dillon, A.C.; Bracker, A.S.; George, S.M. FTIR studies of H2O and D2O decomposition on porous silicon surfaces. Surf. Sci. 1991, 245, 360–372. [Google Scholar] [CrossRef]
- Gupta, P.; Colvin, V.L.; George, S.M. Hydrogen desorption kinetics from monohydride and dihydride species on silicon surfaces. Phys. Rev. B 1988, 37, 8234–8243. [Google Scholar] [CrossRef]
- Borghesi, A.; Guizzetti, G.; Sassella, A.; Bisi, O.; Pavesi, L. Induction-model analysis of Si-H stretching mode in porous silicon. Solid State Commun. 1994, 89, 615–618. [Google Scholar] [CrossRef]
- Ogata, Y.; Niki, H.; Sakka, T.; Iwasaki, M. Oxidation of Porous Silicon under Water Vapor Environment. J. Electrochem. Soc. 1995, 142, 1595. [Google Scholar] [CrossRef]
- Lenshin, A.S.; Kashkarov, V.M.; Seredin, P.V.; Spivak, Y.M.; Moshnikov, V.A. XANES and IR spectroscopy study of the electronic structure and chemical composition of porous silicon on n- and p-type substrates. Semiconductors 2011, 45, 1183. [Google Scholar] [CrossRef]
- Ogata, Y.; Niki, H.; Sakka, T.; Iwasaki, M. Hydrogen in Porous Silicon: Vibrational Analysis of SiH x Species. J. Electrochem. Soc. 1995, 142, 195. [Google Scholar] [CrossRef]
- Richter, H.; Wang, Z.P.; Ley, L. The one phonon Raman spectrum in microcrystalline silicon. Solid State Commun. 1981, 39, 625–629. [Google Scholar] [CrossRef]
- Campbell, I.H.; Fauchet, P.M. The effects of microcrystal size and shape on the one phonon Raman spectra of crystalline semiconductors. Solid State Commun. 1986, 58, 739–741. [Google Scholar] [CrossRef]
- Canham, L. (Ed.) Handbook of Porous Silicon; Springer International Publishing: Berlin/Heidelberg, Germany, 2014. [Google Scholar] [CrossRef]
- Schechter, I.; Ben-Chorin, M.; Kux, A. Gas Sensing Properties of Porous Silicon. Anal. Chem. 1995, 67, 3727–3732. [Google Scholar] [CrossRef]
- Nazemi, H.; Joseph, A.; Park, J.; Emadi, A. Advanced Micro- and Nano-Gas Sensor Technology: A Review. Sensors 2019, 19, 1285. [Google Scholar] [CrossRef]
- Barsan, N.; Weimar, U. Understanding the fundamental principles of metal oxide based gas sensors; the example of CO sensing with SnO2 sensors in the presence of humidity. J. Phys. Condens. Matter 2003, 15, R813–R839. [Google Scholar] [CrossRef]
- Balberg, I. Transport in porous silicon: The pea-pod model. Philos. Mag. B 2000, 80, 691–703. [Google Scholar] [CrossRef]
- Korotcenkov, G. (Ed.) Porous Silicon: From Formation to Applications: Optoelectronics, Microelectronics, and Energy Technology Applications, Volume Three; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar] [CrossRef]
- Srivastava, R.K.; Lal, P.; Dwivedi, R.; Srivastava, S.K. Sensing mechanism in tin oxide-based thick-film gas sensors. Sens. Actuators B Chem. 1994, 21, 213–218. [Google Scholar] [CrossRef]
- Bisi, O.; Ossicini, S.; Pavesi, L. Porous silicon: A quantum sponge structure for silicon based optoelectronics. Surf. Sci. Rep. 2000, 38, 1–126. [Google Scholar] [CrossRef]


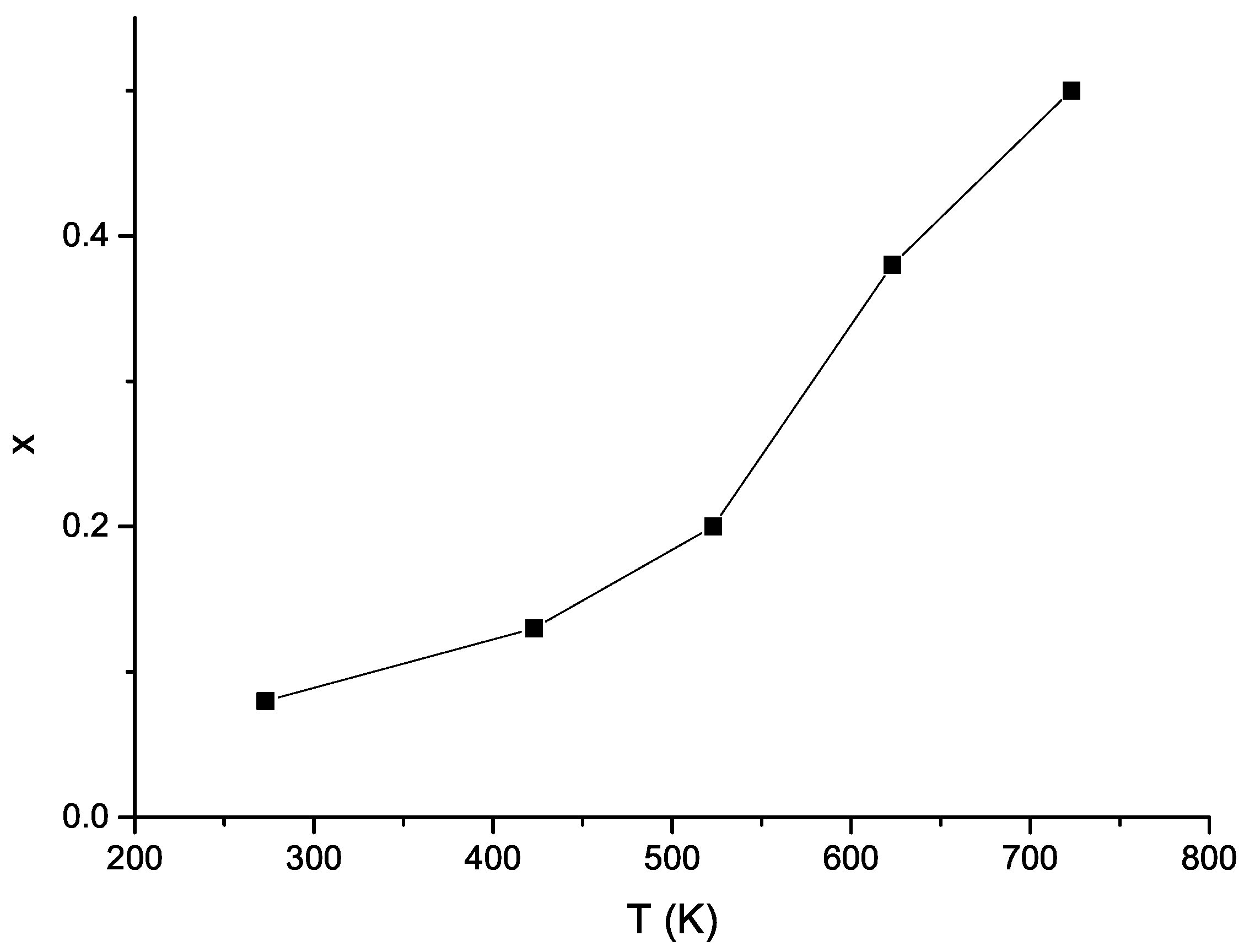
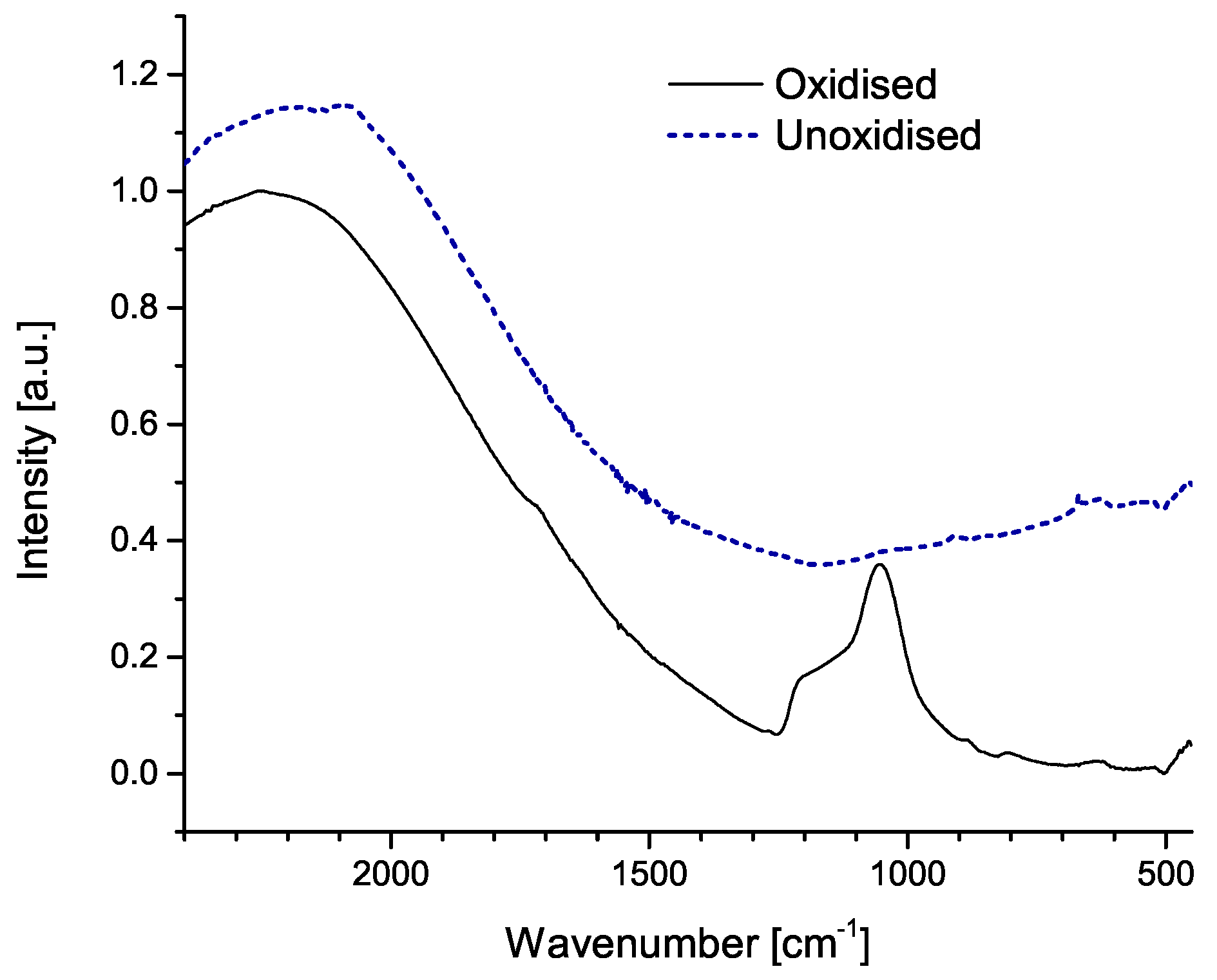
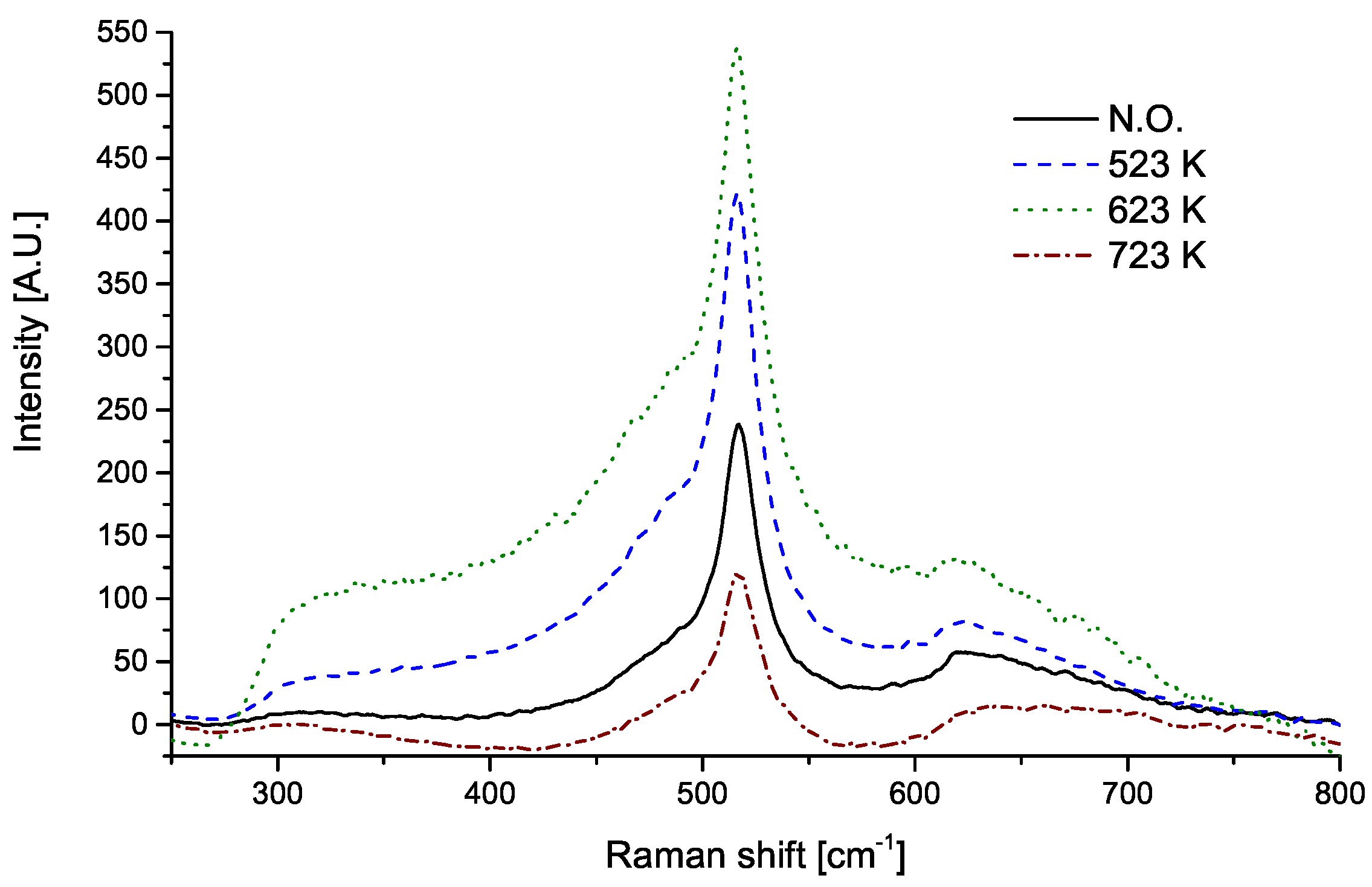
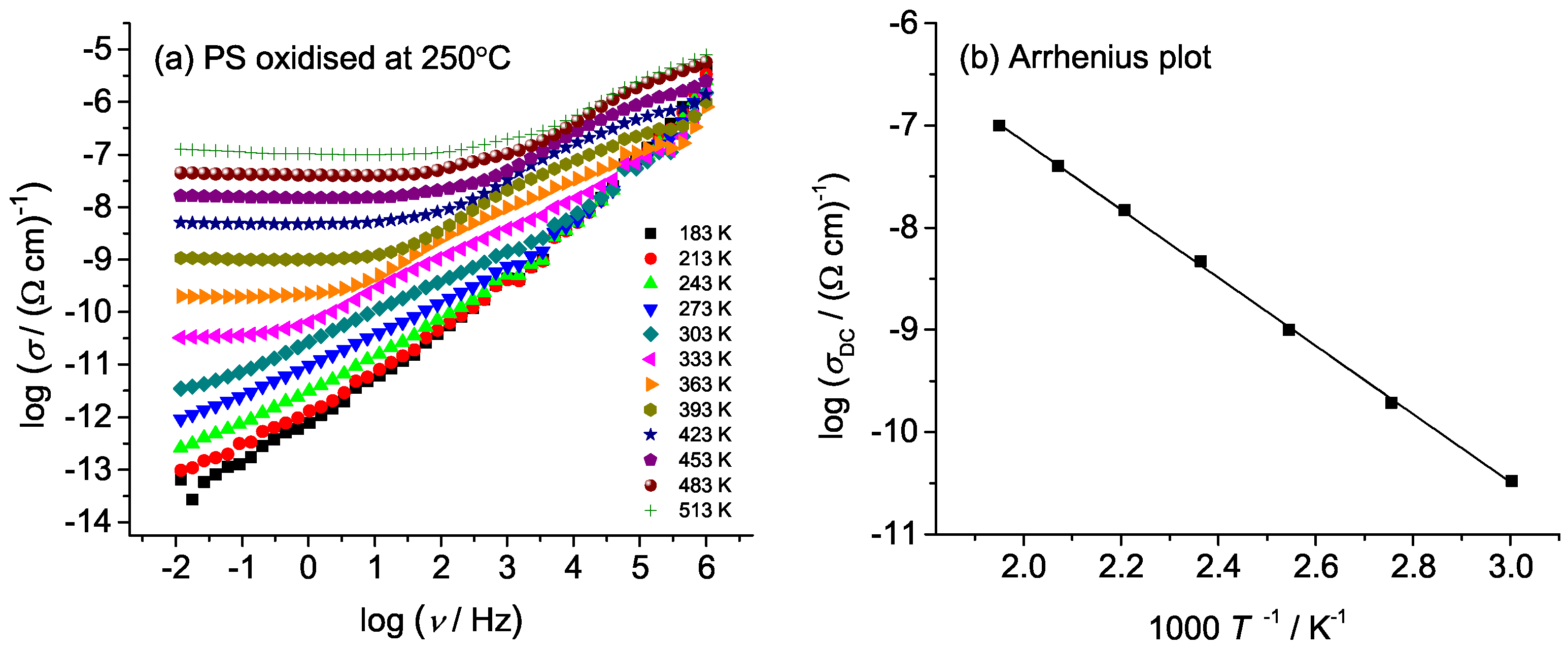
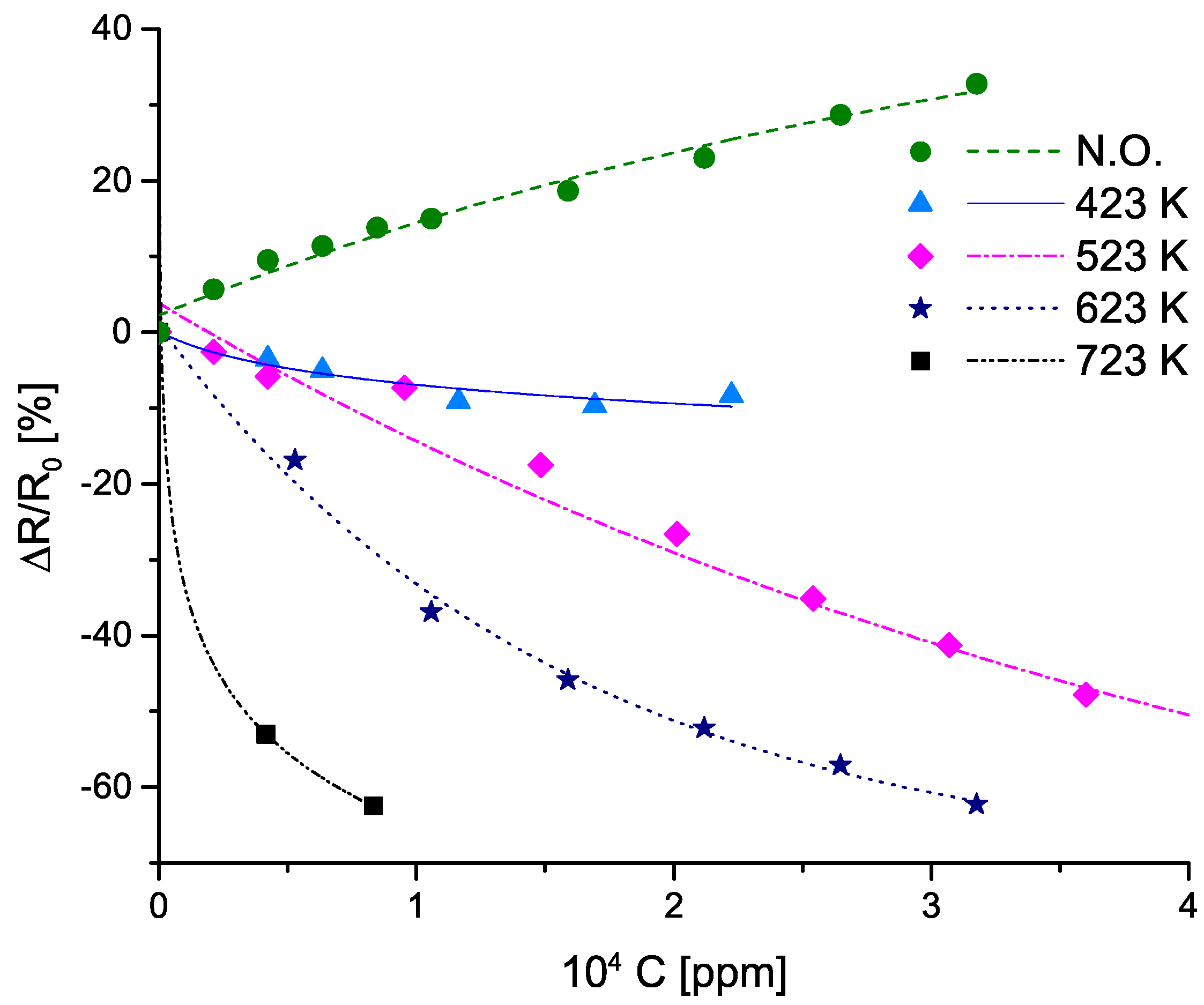


| T [K] | S × 10 [%/ppm] |
|---|---|
| N.O | 1.6 |
| 423 | −0.6 |
| 523 | −1.1 |
| 623 | −2.9 |
| 723 | −7.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baran, N.; Renka, S.; Raić, M.; Ristić, D.; Ivanda, M. Effects of Thermal Oxidation on Sensing Properties of Porous Silicon. Chemosensors 2022, 10, 349. https://doi.org/10.3390/chemosensors10090349
Baran N, Renka S, Raić M, Ristić D, Ivanda M. Effects of Thermal Oxidation on Sensing Properties of Porous Silicon. Chemosensors. 2022; 10(9):349. https://doi.org/10.3390/chemosensors10090349
Chicago/Turabian StyleBaran, Nikola, Sanja Renka, Matea Raić, Davor Ristić, and Mile Ivanda. 2022. "Effects of Thermal Oxidation on Sensing Properties of Porous Silicon" Chemosensors 10, no. 9: 349. https://doi.org/10.3390/chemosensors10090349






