Abstract
Elephant herding optimization (EHO) is a nature-inspired metaheuristic optimization algorithm based on the herding behavior of elephants. EHO uses a clan operator to update the distance of the elephants in each clan with respect to the position of a matriarch elephant. The superiority of the EHO method to several state-of-the-art metaheuristic algorithms has been demonstrated for many benchmark problems and in various application areas. A comprehensive review for the EHO-based algorithms and their applications are presented in this paper. Various aspects of the EHO variants for continuous optimization, combinatorial optimization, constrained optimization, and multi-objective optimization are reviewed. Future directions for research in the area of EHO are further discussed.
1. Introduction
The rapid growth of the size and complexity of optimization problems implies that the traditional optimization algorithms are becoming more uncertain for solving these problems [1]. Metaheuristic algorithms [2,3,4] have proved to be a viable solution to this challenge. Inspired by nature, these strong metaheuristic algorithms are applied to solve NP-hard problems, such as flow shop scheduling [5,6,7,8,9], image encryption [10,11,12], feature selection [13,14,15], facial feature detection [16,17], path planning [18,19], cyber-physical social systems [20,21], texture discrimination [22], factor evaluation [23], saliency detection [24], classification [25], engineering optimization [26], object extraction [27], gesture segmentation [28], economic load dispatch [29], shape design [30], big data and large-scale optimization [31], signal processing [32], multi-objective and many-objective optimization [33,34,35], unit commitment [36], vehicle routing [37,38], and the knapsack problem [39,40]. Some of the well-known methods in this area are genetic algorithms (GAs) [41], particle swarm optimization (PSO) [42,43,44,45], differential evolution (DE) [19,46,47], monarch butterfly optimization (MBO) [48,49,50,51,52], artificial bee colonies (ABCs) [53], earthworm optimization algorithms (EWAs) [54], ant colony optimization (ACO) [55], cuckoo search (CS) [56,57,58,59,60,61,62], krill herd (KH) [63,64,65,66,67], firefly algorithms (FAs) [68,69,70,71,72,73], simulated annealing (SA) [74], intelligent water drop (IWD) [75], water cycle algorithms (WCAs) [76], moth search (MS) [77], monkey algorithms (MAs) [78], evolutionary strategy (ES) [79], free search (FS) [80], probability-based incremental learning (PBIL) [81], biogeography-based optimization (BBO) [82,83,84,85], dragonfly algorithms (DAs) [86], interior search algorithms (ISAs) [87], brain storm optimization (BSO) [88,89], bat algorithms (BAs) [18,90,91,92,93,94,95,96,97], stud GAs (SGAs) [98], harmony search (HS) [99,100,101,102], fireworks algorithms (FWAs) [103], and chicken swarm optimization (CSO) [104].
Based on the herding behavior of elephants, a new swarm intelligence-based global optimization algorithm, namely elephant herding optimization (EHO), was proposed by Wang et al. [105]. Two special operators, a clan updating operator and a separating operator, are included in EHO. The elephants in each clan are updated with respect to their current position and the position of the matriarch. The acceptable performance of EHO has drawn much attention from scholars and engineers. In this paper, a comprehensive review for the EHO-based algorithms and their applications are presented. The remainder of this paper is organized as follows. The main steps of the EHO is detailed in Section 2. Improved EHO algorithm variants are presented in Section 3. Section 4 describes the EHO applications for solving engineering optimization problems. Finally, Section 5 presents a conclusion and suggestions for future work.
2. Historical Development of Elephant Herding Optimization
2.1. Elephant Herding Optimization Research Studies
The EHO algorithm with the herding behavior of elephant groups has received significant attention from scholars [105]. Ninety-three related studies have been published in journals/dissertations/conferences up to 23 April 2020 (Figure 1) since EHO was proposed in 2015. Among these 93 papers, 2 papers were published in 2015 and 2016, 14 papers were published in 2017, 21 papers were published in 2018, and 32 and 24 papers were published in 2019 and 2020, respectively.
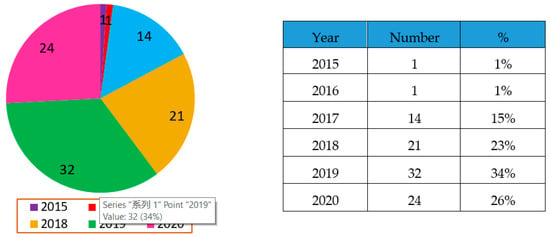
Figure 1.
Related (Elephant Herding Optimization) EHO publications since 2015.
2.2. Basics of Elephant Herding Optimization
Elephants, as social creatures, live in social structures of females and calves. An elephant clan is headed by a matriarch and composed of a number of elephants. Female members like to live with family members, while the male members tend to live elsewhere. They will gradually become independent of their families until they leave their families completely. The population of all elephants is shown in Figure 2. The EHO technique proposed by Wang et al. in 2015 [105] was developed after studying natural elephant herding behavior. The following assumptions are considered in EHO.
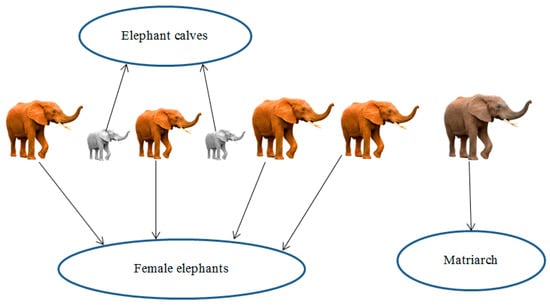
Figure 2.
Population of elephants.
(1) Some clans with fixed numbers of elephants comprise the elephant population.
(2) A fixed number of male elephants will leave their family group and live solitarily far away from the main elephant group in each generation.
(3) A matriarch leads the elephants in each clan.
2.2.1. Clan-updating Operator
According to the natural habits of elephants, a matriarch leads the elephants in each clan. Therefore, the new position of each elephant ci is influenced by matriarch ci. The elephant j in clan ci can be calculated by Equation (1).
where xnew,ci,j and xci,j present the new position and old position for elephant j in clan ci, respectively. xbest,ci is matriarch ci which represents the best elephant in the clan. a ∈ [0,1] indicates a scale factor, r ∈ [0,1]. The best elephant can be calculated by Equation (2) for each clan.
where β ∈ [0,1] represents a factor which determines the influence of the xcenter,ci on xnew,ci,j. xnew,ci,j is the new individual. xcenter,ci is the center individual of clan ci. It can be calculated by Equation (3) for the d-th dimension.
where 1 ≤ d ≤ D and nci indicate the number of elephants in clan ci. xci,j,d represents the d-th dimension of elephant individual xci,j. xcenter,ci is the center of clan ci and it can be updated by Equation (3).
2.2.2. Separating Operator
The separating process whereby male elephants leave their family group can be modeled into separating operator when solving optimization problems. The separating operator is implemented by the elephant individual with the worst fitness in each generation, as shown in Equation (4).
where xmax represents the upper bound of the individual and xmin indicates lower bound of the individual. xworst,ci indicates the worst individual in clan ci. Rand [0, 1] is a stochastic distribution between 0 and 1.
According to the description of the clan-updating operator and separating operator, the mainframe of EHO is summarized. The corresponding flowchart is shown as follows. MaxGen is the maximum generation. The MATLAB code of EHO can be found on the website: https://www.mathworks.com/matlabcentral/fileexchange/53486. The basic steps of the EHO is shown as follows (Algorithm 1). The corresponding flowchart can also be seen in Figure 3.
| Algorithm 1. Elephant herding optimization |
| (1) Begin |
| (2) Initialization. Set the initialize iterations G = 1; initialize the population P randomly; set maximum generation MaxGen. |
| (3) While stopping criterion is not met do |
| (4) Sort the population according to fitness of individuals. |
| (5) For all clans ci do |
| (6) For elephant j in the clan ci do |
| (7) Generate xnew, ci,j and update xci,j by Equation (1). |
| (8) If xci,j = xbest,ci then |
| (9) Generate xnew, ci,j and update xci,j by Equation (2). |
| (10) End if |
| (11) End for |
| (12) End for |
| (13) For all clans ci do |
| (14) Replace the worst individual ci by Equation (4). |
| (15) End for |
| (16) Evaluate each elephant individual according to its position. |
| (17) T = T + 1. |
| (18) End while |
| (19) End. |
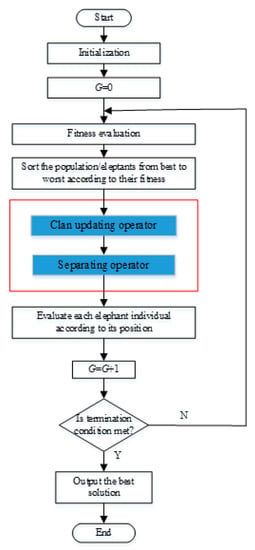
Figure 3.
Flowchart of the EHO algorithm.
2.2.3. Analysis of Algorithm Complexity
The computational complexity of the EHO algorithm is analyzed according to the steps in the EHO algorithm. Let the population size and dimension be NP and D, respectively. Obviously, sort the population according to the fitness of individuals in step (4) with time complexity O(NP). In steps (5)–(12), execute clan-updating operator for all clans ci with time complexity O(NP × D). In steps (13)–(15), execute separating operator for all clans ci with time complexity O(NP). Evaluate each elephant individual according to its position in step (16) with time complexity O(NP). To do so, the total time complexity of elephant herding optimization is O(T × NP × D). From the above results, after omitting the low-order terms, the total time complexity of the EHO algorithm is O(T × NP × D), which is only related to T, NP, and D.
3. Different Variants of EHO
Several EHO variants have been proposed to solve different optimization problems. The variants of EHO can be generally divided into three groups: improved EHO algorithms, hybrid EHO algorithms, and variants of EHO.
3.1. Improved EHO Algorithms
A list of the improved EHO algorithms is given in Table 1 and Figure 4. An overview of each of these methods is given below.

Table 1.
The improved EHO algorithms.
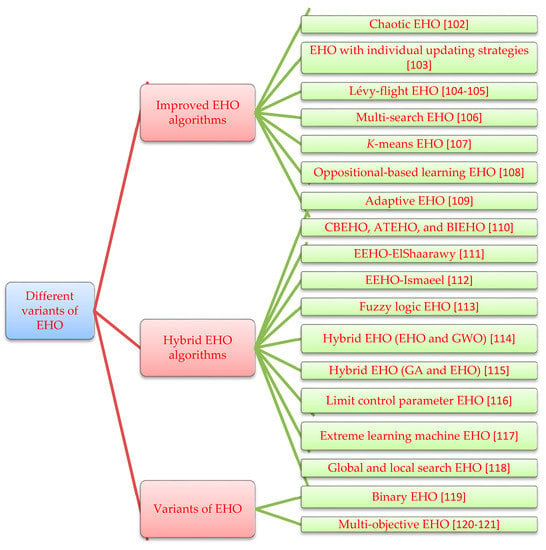
Figure 4.
Different variants of EHO.
3.1.1. Chaotic EHO
Tuba et al. [106] proposed a new EHO algorithm with chaos theory called CEHO to solve unconstrained global optimization problems. In CEHO, two different chaotic maps are introduced into the EHO algorithm. Compared with 15 standard benchmark functions from IEEE Congress on Evolutionary Computation (CEC) 2013, the CEHO algorithm outperforms the basic EHO and PSO in almost all cases.
3.1.2. EHO with Individual Updating Strategies
Li et al. [107] incorporated six individual updating strategies into basic EHO. The experimental results for sixteen test functions show that the proposed improved EHO variant significantly outperformed basic EHO.
3.1.3. Lévy Flight EHO
Xu et al. [108] applied an improved EHO algorithm with Lévy flight (LFEHO) to solve network intrusion detection problems. The research results showed that the LFEHO algorithm increased the accuracy rate of the network.
Xu et al. [109] proposed improved EHO (IEHO) to solve network intrusion detection problems, which improved the classification performance of intrusion detection under the premise of ensuring the accuracy rate and meeting the needs in real time. The experimental results showed that the IEHO algorithm was superior to other algorithms (EHO [105], PSO [2], and MS [77]).
3.1.4. Multi-Search EHO
Hakli et al. [110] proposed new EHO with a multi-search strategy (multi-EHO). Fifteen different benchmark functions were used to verify the effectiveness of multi-EHO. In addition, the proposed multi-EHO was compared with the whale optimization algorithm (WOA) and the gray wolf optimizer (GWO). The multi-EHO method was also superior to other competitive algorithms.
3.1.5. k-Means EHO
Tuba et al. [111] introduced data clustering into EHO in which the local search ability of EHO was improved through k-means. The proposed k-means EHO was tested on six benchmark datasets. The clustering results showed that k-means EHO found better clusters than other algorithms.
3.1.6. Oppositional-Based Learning EHO
Chakraborty et al. [112] proposed improved EHO with a dynamic Cauchy mutation (EHO-DCM) to solve the multilevel image thresholding for image segmentation problems. In EHO-DCM, oppositional-based learning (OBL) and DCM were introduced, in which OBL and DCM were employed to accelerate the conventional and mitigate the premature convergence, respectively. The results were compared with five metaheuristic algorithms (EHO [105], CSO [104], ABCs [53], BAs [91], and PSO [2]). It was demonstrated that EHO-DCM provided promising performance in view of optimized fitness value, feature similarity index, and structure similarity index.
3.1.7. Adaptive Whale EHO
Chowdary et al. [113] proposed a hybrid mixture model based on the adaptive whale EHO (AWEHO) algorithm, which is the integration of three technologies: EHO [105], the whale optimization algorithm (WOA), and the adaptive concept. In the proposed method, the AWEHO algorithm was applied to perform optimal sensing by using the foraging behavior of whales and the herding behavior of elephants. The analysis of the computational results indicated that the herding and foraging behavior of the AWEHO achieved efficient spectrum sensing in the cognitive radio network.
3.2. Hybrid EHO Algorithms
The hybrid EHO algorithms are presented in Table 2. The details are included in the following sections.

Table 2.
The hybrid EHO algorithms.
3.2.1. CBEHO, ATEHO, and BIEHO
Rashwan et al. [114] studied three approaches, which are cultural-based EHO (CBEHO), alpha-tuning EHO (ATEHO), and biased initialization EHO (BIEHO), to enhance the performance of standard EHO. A comparative experiment from CEC 2016 was done between three EHO approaches and the other optimization methods. It was demonstrated that the performances of the three EHO approaches were superior to other comparison methods. In order to further verify the performance of the three EHO approaches, various experiments were carried out on engineering problems such as the welded beam, gear train, continuous stirred tank reactor, and three-bar truss design problem.
3.2.2. EEHO-ElShaarawy
ElShaarawy et al. [115] used an enhanced elephant herding optimization (EEHO-ElShaarawy) algorithm to overcome the fast convergence of EHO. The exploitation and exploration of EEHO-ElShaarawy were achieved by separating operators with balanced control. EEHO-ElShaarawy showed a better performance of convergence rate compared with basic EHO.
3.2.3. EEHO-Ismaeel
Ismaeel et al. [116] proposed another enhanced elephant herding optimization algorithm with a constant function (EEHO-Ismaeel). In order to overcome the shortcomings of EHO. In EEHO-Ismaeel, two operators, the clan and separating operator, improved the exploitation abilities of the EEHO-Ismaeel algorithms. The CEC 2017 test benchmark functions were utilized to verify the performance of the three EEHO-Ismaeel versions (EEHO15, EEHO20, and EEHO25). The experimental results demonstrated that, in most cases, the EEHO-Ismaeel algorithms obtained better results compared with the other competitive algorithms, such as the PSO, bird swarm algorithm (BSA), and ant lion optimization (ALO) algorithms.
3.2.4. FEHO
Veera et al. [117] introduced a fuzzy logic controller into EHO and proposed improved fuzzy EHO (FEHO) to maximize power point tracking (MPPT) for a hybrid wind–solar system. Simulation results indicated that the MPPT using the proposed FEHO had better performance compared with the other type of controllers, which efficiently tracked the maximum power point of the wind–solar power systems even with variations in the climatic conditions.
3.2.5. EHGWO
Arora et al. [118] combined the advantages of EHO and GWO and proposed a hybrid algorithm (EHGWO). In EHGWO, the optimal virtual machines (VMs) are selected and reallocated by using a newly devised fitness function. The tasks for overloaded VMs are removed and assigned to VMs without affecting the system performance, which performed a load balancing technique.
3.2.6. GEHO
Bukhsh et al. [119] proposed a hybrid algorithm called GEHO by combining a GA and EHO. Based on the results, the developed GEHO approach was able to schedule the appliance efficiently, which reduced maximum cost compared with EHO for home appliance optimization problems.
3.2.7. HEHO
Strumberger et al. [120] developed improved hybrid EHO, named HEHO, to solve the wireless sensor network localization problem. The limit control parameter from the ABC algorithm was incorporated into EHO to control the process of diversification. The usefulness of HEHO was demonstrated using different sizes of sensor networks from 25 to 150 target nodes. Based on the results, the HEHO approach was able to obtain more consistent and accurate locations of the unknown target nodes than other approaches.
3.2.8. ELM-EHO
Satapathy et al. [121] proposed a combination model named EHO-ELM with a combination of the advantages of extreme learning machine (ELM) and EHO. In this model, EHO-ELM was used to determine the input weights of an ELM model. EHO-ELM was tested on three different brain image datasets. The results demonstrated that EHO-ELM outperformed the basic ELM model in the three brain image datasets.
3.2.9. Global and Local Search EHO
Hakli et al. [122] developed a new EHO approach to solve constrained optimization problems. The EHO variants (GL-EHO) were adapted to implement constrained optimization. Experimental results showed that GL-EHO was capable of overtaking EHO.
3.3. Variants of EHO
Different variants of the EHO algorithm are presented in Table 3. The detailed methods are presented herein.

Table 3.
Different variants of EHO.
3.3.1. Binary EHO
Hakli et al. [123] proposed a new binary variant of EHO (BinEHO) for solving binary optimization problems. Through a dimension rate (DR) parameter and mutation process, BinEHO strengthened the compromise between exploitation and exploration. In order to prove the robustness and accuracy of BinEHO, it was compared with various binary variants in three different binary optimization problems. The results concluded that BinEHO outperformed the other binary algorithm variants.
3.3.2. Multi-Objective EHO
Jaiprakash et al. [124] presented a multi-objective clustering EHO (MOEHO) to solve multi-objective optimization problems. Comparative results revealed that MOEHO provided superior performance compared with (fast and elitist multiobjective genetic algorithm) NSGA-II and MOPSO in eight cases. In addition, MOEHO was used to cluster the activities of human models. The results showed that MOEHO succeeded in eight out of five case studies.
Meena et al. [125] presented improved multi-objective EHO (IMOEHO) to solve distribution system optimization problems. In IMOEHO, two techniques (order of preference by similarity to the ideal solution technique and improved EHO technique) were combined. The IMOEHO method was implemented in three benchmark test distribution systems. It was concluded that the IMOEHO method was very effective for optimizing multi-objective complex optimization problems.
4. Engineering Optimization/Applications
The EHO algorithm has been successfully applied to engineering optimization problems since it was proposed. A summary for EHO in engineering optimization is presented in Table 4 and Table 5 and Figure 5.

Table 4.
A summary of the EHO applications in engineering optimization.

Table 5.
A summary of the EHO applications in engineering optimization.
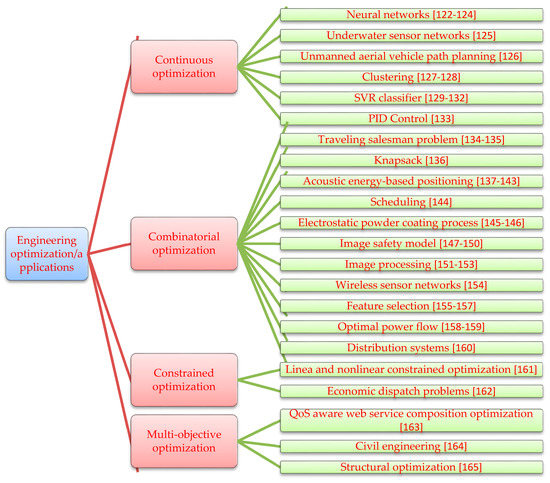
Figure 5.
Engineering optimization/applications.
4.1. Continuous Optimization
4.1.1. Neural Networks
Moayedi et al. [126] synthesized a new EHO-MLP ensemble with a multi-layer perceptron (MLP) neural network to predict cooling load. The results revealed that EHO-MLP performed efficiently for adjusting biases of the MLP and the neural weights. It also outperformed the ACO [55] and EHO [105] optimization algorithms both in training and testing accuracies. Meanwhile, EHO-MLP took less time than ACO [55] and EHO [105] with regard to the time-effectiveness of the models.
Kowsalya et al. [127] used EHO to optimize neural network weights. The performance of the proposed method was evaluated on evaluation metrics. It was concluded that the proposed method provided better accuracy than existing classifiers.
Sahlol et al. [128] applied EHO to neural networks to classify each cell for the acute lymphoblastic leukemia problem. In the proposed method, the weights and biases of the network were updated by the EHO algorithm. The research results showed that EHO outperformed other classification methods.
4.1.2. Underwater Sensor Networks
Kaur et al. [129] used EHO to solve underwater sensor networks optimization tasks. The research outcomes indicated that the proposed approach showed better performance than other strategies for most parameters.
4.1.3. Unmanned Aerial Vehicle Path Planning
Alihodzic et al. [130] considered an approximation algorithm, adjusted EHO (AEHO), to solve the unmanned aerial vehicle (UAV) path planning problem. AEHO was used for adjusting the UAV path planning problem and it was compared with other state-of-the-art algorithms. The simulation experiments showed that AEHO obtained a safe flight path and was an excellent choice for the UAV path planning problem.
4.1.4. Clustering
Rani et al. [131] proposed a new detection approach for dynamic protein complexes by using Markov clustering with EHO (MC-EHO). The MC-EHO method divided the protein–protein interaction (PPI) network into a set of dynamic sub-networks and employed the clustering analysis on every sub-network. The experimental analysis was employed on 11 various widespread datasets and four different benchmark databases. The results showed that MC-EHO surpassed various existing approaches in terms of accuracy measures.
Jaiprakash et al. [132] formulated EHO to perform a clustering task by minimizing intra-cluster distance. The simulation was verified on six benchmark datasets and three synthetic datasets. The superior percentage accuracy of EHO was demonstrated by comparing it with other algorithms in the form of box plots.
4.1.5. SVR Classifier
Hassanien et al. [133] introduced EHO to adjust the regression of emotional states for a support vector regression (SVR) repressor (SVR-EHO). In this method, the feature selection was adapted and the SVR classifier parameters were adjusted by using EHO, which provided a fast regression rate. The SVR-EHO approach was verified on the open database for emotion detection. The results of emotion regression on the SVR classifier indicated that SVR-EHO significantly improved regression accuracy.
Hassanien et al. [134] used two technologies, EHO and SVM (EHO-SVM), to develop a hybrid approach for automatic electrocardiogram (ECG) signal classification. The proposed approach included three modules, which were the efficient preprocessing module, feature extraction module, and feature classification module. EHO-SVM was utilized to optimize the features and parameters. The experiments showed that EHO-SVM achieved accurate classification results in terms of five statistical indices.
Tuba et al. [135] used the EHO algorithm to adjust the SVM parameter. The proposed approach was tested on standard datasets and the results were obtained by EHO and compared with two other approaches, which were the GA [41] and the grid search method (Grid). The computational experiments concluded that the EHO algorithm outperformed the GA [41] and Grid in the accuracy of classification for the same test problems.
Tuba et al. [136] used the EHO algorithm to find the optimal parameters of the SVM. In the proposed approach, the parameters of SVM were adjusted by EHO. Four different experiments based on a standard dataset were carried out. The simulation results showed that the performance of the proposed method achieved better results than the other strategies in all cases.
4.1.6. PID Control
Sambariya et al. [137] used the EHO algorithm to adjust the parameters of the proportional integral derivative (PID) controller, which minimized the change in frequency of a single-area non-reheat thermal power plant. The experimental results showed that a controller based on EHO had a better performance than other conventional PID controllers.
4.2. Combinatorial Optimization
4.2.1. Traveling Salesman Problem
Almufti et al. [138] introduced EHO to solve symmetric traveling salesman problems (STSPs). The experiment results indicated that EHO was adapted to solve STSPs by comparing the optimal solutions of the traveling salesman problem library (TSPLIB).
4.2.2. Knapsack
Darmawan et al. [139] used the EHO algorithm to solve 0–1 knapsack problems. The analysis of the computational results indicated that EHO outperformed other algorithms for convergence rate and global search ability when more and more iterations were done.
4.2.3. Acoustic Energy-Based Positioning
Correia et al. [140] used the EHO algorithm to validate and adjust the decay acoustic model for acoustic energy-based positioning problems. The implementation results for both simulation results and real measurements showed EHO had a good alignment with conducted simulations and was successfully applied to acoustic energy-based positioning problems.
4.2.4. Scheduling
Parashar et al. [141] used modified elephant herding optimization (MEHO) to model uncertain renewable generation. The analysis of the computational results indicated that the proposed MEHO approach had significant effects on the operational management of the microgrid compared with the deterministic approach.
Cahig et al. [142] proposed a decision tool based on EHO for a virtual power plant (VPP) scheduling problem. The algorithm was illustrated for a test system with a VPP. The results showed that the canonical variant of EHO yielded the optimal scheduling, which suggested that it performed well as a decision support tool to the VPP operator.
Sarwar et al. [143] used EHO to solve a home energy management system (HEMS) scheduling problem. Simulations of a single home with 12 appliances were performed and the results showed the EHO technique performed better than the other reported algorithms in reducing the waiting time and cost.
Parvez et al. [144] used two optimizing techniques, EHO [105] and harmony search algorithm (HSA) [99], to evaluate the performance of a home energy management system (HEMS). The simulation results revealed that the proposed method was more effective in terms of electricity cost.
Mohsin et al. [145] implemented the EHO technique to solve the scheduling of smart home appliances. The simulation results revealed that EHO performed much better in terms of total cost and peak load reduction for different operation time intervals (OTIs). In addition, EHO with shorter OTIs provided better results compared with longer OTIs.
Gholami et al. [146] developed improved EHO to solve large instances for hybrid flow shop scheduling problems. The performance of the proposed algorithm was compared with two available algorithms, which were SA and shuffled frog-leaping algorithm (SFLA). Based on the results, the developed approach outperformed the other algorithms.
Fatima et al. [147] developed an efficient optimization method via the hybridization of two optimization algorithms, namely EHO [105] and the FA [69]. This method was used to reduce the electricity cost for home energy management controller problems. The results indicated that the proposed hybrid optimization technique performed more efficiently for achieving the lowest cost and maximizing consumer satisfaction.
4.2.5. Electrostatic Powder Coating Process
Luangpaiboon et al. [148] proposed a modified simplex EHO algorithm with multiple performance measures (MEHO). MEHO was used to solve the optimization of electrostatic powder coating process parameter optimization problems. According to some performance measures, two phases based on the response surface methodology were applied to study the EHO parameter levels. The simulation experimental results demonstrated that MEHO was more efficient compared with the previous operating condition.
4.2.6. Image Safety Model
Shankar et al. [149] proposed an image safety model based on the EHO algorithm. Two keys, a general public key and a non-public key, were optimized by utilizing adaptive EHO (AEHO). The device was optimized by a hybrid algorithm applying encryption and optimization techniques which mixed the functionality of encryption and digital signatures. The experimental results indicated that the confidentiality of the image was ultimately upheld.
Chibani et al. [150] introduced EHO into the quality of service (QoS) aware web service composition. It was shown that the proposed method offered excellent performances compared with PSO in terms of convergence speed, scalability, and fitness evaluations.
4.2.7. Image Processing
Tuba et al. [151] used the EHO algorithm to solved multilevel image thresholding problems based on Kapur and Otsu’s criteria. The proposed algorithm was compared with four swarm intelligence approaches. The experimental results concluded that the EHO algorithm successfully solved multilevel thresholding problems and additionally had smaller variance.
Jino et al. [152] presented the short review of nature-inspired optimization algorithms, such as EHO [105], BAs [91], ACO [55], ABCs [53], PSO [2], FAs [69], bumble bees mating (BBM), and CSO [104]. These algorithms were applied to advanced image processing fields.
Jayanth et al. [153] used the EHO algorithm to classify the high spatial resolution multispectral image classification. According to the fitness function, EHO determines the information of class and multispectral pixels. When compared with the SVM method, the experimental results of two datasets demonstrated that the proposed method improved overall accuracy by 10.7% for dataset 1 and 6.63% for dataset 2.
Cardoso et al. [154] used EHO to improve the search for the maximum correlation point of the image. The search process was implemented in software based on an embedded general purpose processor. The performance results showed that the proposed method outperformed other optimization metaheuristics, which were PSO [2] and ES [79].
4.2.8. Wireless Sensor Networks
Correia et al. [155] applied the EHO algorithm to solve the energy-based source localization problem for wireless sensors networks. The energy decay model between two sensor nodes was matched through key optimized parameters of the EHO algorithm. Comparing the performance between the proposed method and existing non-metaheuristic algorithms, EHO significantly reduced the estimation error in environments with high noise power. In addition, EHO represented an excellent balance between estimation accuracy and computational complexity.
Strumberger et al. [156] solved localization problems for wireless sensor networks using the EHO algorithm. According to the simulation results and comparative analysis with other state-of-the-art algorithms, EHO found the coordinates of unknown nodes randomly deployed in the monitoring field, which proved to be robust and efficient metaheuristics when tackling wireless sensor network localization.
Kaur et al. [157] proposed a novel and energy-efficient approach based on EHO to improve the span of energy in nodes of an underwater network. In the proposed approach, a dynamic cluster head in underwater wireless networks was formed by the behavior of the elephants selecting their heads. It was demonstrated that the EHO algorithm was a promising algorithm for tackling multiple parameters of underwater networks.
4.2.9. Feature Selection
Xu et al. [158] proposed an improved elephant herding optimization (IEHO) algorithm for feature selection in several datasets and distributed environments, which effectively reduced the running time of the algorithm under the premise of ensuring classification accuracy. The experiments showed that the classification efficiency of the IEHO algorithm significantly outperformed other optimization algorithms, such as PSO [2] and EHO [105].
4.2.10. Optimal Power Flow
Dhillon et al. [159] applied EHO to mitigate frequency deviations under sudden variations in demand on the automatic generation control of an interconnected power system. The outcomes of the EHO-based automatic generation control was compared with PSO-based automatic generation control. It was concluded that the settling time of the EHO-based strategy took less time than the PSO-based strategy.
Kuchibhatla et al. [160] used an EHO algorithm to improve the power quality (PQ) and reduce the harmonic distortion in a photovoltaic (PV) interconnected wind energy conversion system (WECS). The performances of three methods (EHO [105], BAs [91], and FAs [69]) were evaluated. The obtained results showed that the proposed method enhanced the performance of the grid-connected hybrid energy system.
Sambariya et al. [161] used EHO to adjust the parameters of a PID controller for the load frequency control of a single-area reheat power system. The solution results showed that the proposed technique obtained better robustness compared with the PID controller.
4.2.11. Distribution Systems
Prasad et al. [162] used EHO to determine the optimal distributed generation (DG) unit size. The proposed model was performed on two types of DG (DG operating at 0.9 power factor lag and DG operating at unity power factor). The numerical results indicated that the EHO algorithm obtained overall better results compared with other algorithms in terms of reducing power consumption.
Vijay et al. [163] applied the EHO technique to the optimal placement and sizing of distributed generation on an electric distribution network. EHO was tested on a 5-bus radial distribution system. The results indicated that the overloading of the equipment, active power, reactive power, and production cost of electricity were reduced, which was more intelligent and precise for the allocation of distributed generation in an electric distribution network.
4.3. Constrained Optimization
4.3.1. Linear and Nonlinear Constrained Optimization
Strumberger et al. [164] presented a hybridized elephant herding optimization (HEHO) algorithm to solve constrained optimization problems. Thirteen standard constrained benchmark functions were conducted for evaluating the efficiency and robustness of the HEHO algorithm. The simulation results were compared with other state-of-the-art algorithms, such as firefly algorithms, seeker optimization algorithms, and self-adaptive penalty function genetic algorithms. The study results showed that the proposed HEHO was more efficient than the other reported algorithms.
4.3.2. Economic Dispatch Problems
Economic-Based Dispatch Problem
Singh et al. [165] proposed a new modified EHO called MEHO. MEHO was further applied to solve the optimization of linear as well as nonlinear cost functions for economic load dispatch problems. The results obtained showed that the total operating cost obtained by MEHO was less than that of EHO [105], PSO [2], and ACO [55]. The results showed that the MEHO methods had potential for solving linear as well as nonlinear optimization problems.
Stochastic Inequality Constrained Optimization Problems
Horng et al. [166] presented a heuristic method coupling EHO with ordinal optimization (EHOO) to resolve stochastic inequality constrained optimization problems. The proposed method utilized an improved elephant herding optimization to achieve diversification with an accelerated optimal computing budget allocation. The simulation experiment results were obtained by EHOO and compared with three optimization methods (PSO [2], GAs [1], and ES [79]). The results showed that the EHOO approach obtained higher computational efficiency than the other three comparative methods.
4.4. Multi-Objective Optimization
4.4.1. QoS Aware Web Service Composition Optimization
Sadouki et al. [167] proposed a new discrete multi-objective metaheuristic bio-inspired pareto-based approach based on the EHO algorithm to solve the QoS aware web service composition problem. Compared with the multi-objective particle swarm optimization (MOPSO) algorithm and strength pareto evolutionary algorithm 2 (SPEA2), the results showed that the presented method significantly outperformed MOPSO and SPEA2 in terms of set coverage and spacing metrics.
4.4.2. Civil Engineering
Adarsha et al. [168] introduced a hybridized technique named elephant herding optimization-based artificial neural network (EHO-ANN). Furthermore, the complicated experimental procedures for finding the elastic modulus of concrete was solved by the EHO-ANN. The performance of the EHO-ANN algorithm was compared with that of linear regression, empirical formula, and test correlation coefficient (CC). The results showed that the EHO-ANN was more accurate than other methods in predicting the elastic modulus of concrete.
4.4.3. Structural optimization
Jafari et al. [169] combined the advantage of elephant herding optimization (EHO) and the cultural algorithm (CA) and proposed a hybrid algorithm (EHOC). In EHOC, EHO was improved by using the belief space defined by the cultural algorithm. The performance of the EHOC algorithm was evaluated on eight mathematical optimization problems and four truss weight minimization problems. The solution results showed that EHOC was capable of accelerating the convergence rate effectively compared with the CA and EHO.
5. Conclusions and Future Directions
In this paper, tens of research articles related to the EHO algorithm were reviewed. We also discussed the application of the EHO variants in continuous optimization, combinatorial optimization, constrained optimization, and multi-objective optimization. Researchers improved the EHO algorithms and successfully applied them to various optimization fields. This algorithm has proved to be a promising tool for many optimization problems and engineering applications. However, several aspects of the EHO method that should be further studied, and are as follows:
(1) Most researchers have merely focused on the optimization effects of EHO. There is not sufficient explanation for theoretical analysis. Therefore, strengthening the theoretical analysis of EHO and the mathematical model will remain a challenge in future research.
(2) Employing EHO to solve unsolved optimization problems, especially multi-objective optimization problems, needs to be studied in more depth.
(3) Hybridizing EHO with other algorithm components, such as differential evolution and hill climbing, is another interesting topic for future research [170].
(4) EHO has achieved some notable accomplishments in solving discrete and continuous optimization problems. Therefore, expanding the application scope of EHO and designing suitable optimization operators should be considered in future research.
(5) EHO has a lower level of constrained optimization than similar methods. This is undoubtedly a shortcoming of EHO. Therefore, more research should be carried out to expand EHO for more constrained optimization applications.
Author Contributions
Conceptualization, J.L.; research literature, H.L.; literature search, G.-G.W. and A.H.A.; writing—original draft preparation, J.L.; writing—review and editing, H.L.; funding acquisition, G.-G.W. and A.H.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by an Industry–University Cooperative Education Project (Grant No. 201802046038), Doctoral Foundation of Wuhan Technology and Business University (No. D2019010), and National Natural Science Foundation of China (No. 41576011, No. U1706218, No. 41706010, and No. 61503165).
Acknowledgments
The authors would like to thank the anonymous reviewers and the editor for their careful reviews and constructive suggestions to help us improve the quality of this paper.
Conflicts of Interest
The authors declare that they have no conflict of interest.
References
- Santucci, V.; Baioletti, M.; Milani, A. An algebraic framework for swarm and evolutionary algorithms in combinatorial optimization. Swarm Evol. Comput. 2020, 55, 100673. [Google Scholar] [CrossRef]
- Wang, G.-G.; Tan, Y. Improving metaheuristic algorithms with information feedback models. IEEE Trans. Cybern. 2019, 49, 542–555. [Google Scholar] [CrossRef] [PubMed]
- Valentino, S.; Alfredo, M.; Fabio, C. An optimisation-driven prediction method for automated diagnosis and prognosis. Mathematics 2019, 7, 1051. [Google Scholar] [CrossRef]
- Alfredo, M.; Valentino, S. Asynchronous differential evolution. IEEE Congr. Evol. Comput. 2010, 7, 18–23. [Google Scholar]
- Sang, H.-Y.; Pan, Q.-K.; Duan, P.-Y.; Li, J.-Q. An effective discrete invasive weed optimization algorithm for lot-streaming flowshop scheduling problems. J. Intell. Manuf. 2015, 29, 1337–1349. [Google Scholar] [CrossRef]
- Sang, H.-Y.; Pan, Q.-K.; Li, J.-Q.; Wang, P.; Han, Y.-Y.; Gao, K.-Z.; Duan, P. Effective invasive weed optimization algorithms for distributed assembly permutation flowshop problem with total flowtime criterion. Swarm Evol. Comput. 2019, 44, 64–73. [Google Scholar] [CrossRef]
- Pan, Q.-K.; Sang, H.-Y.; Duan, J.-H.; Gao, L. An improved fruit fly optimization algorithm for continuous function optimization problems. Knowl.-Based Syst. 2014, 62, 69–83. [Google Scholar] [CrossRef]
- Gao, D.; Wang, G.-G.; Pedrycz, W. Solving fuzzy job-shop scheduling problem using de algorithm improved by a selection mechanism. IEEE Trans. Fuzzy Syst. 2020. [Google Scholar] [CrossRef]
- Santucci, V.; Baioletti, M.; Milani, A. Algebraic differential evolution algorithm for the permutation flowshop scheduling problem with total flowtime criterion. IEEE Trans. Evolut. Comput. 2016, 20, 682–694. [Google Scholar] [CrossRef]
- Li, M.; Xiao, D.; Zhang, Y.; Nan, H. Reversible data hiding in encrypted images using cross division and additive homomorphism. Signal Process. Image Commun. 2015, 39, 234–248. [Google Scholar] [CrossRef]
- Li, M.; Guo, Y.; Huang, J.; Li, Y. Cryptanalysis of a chaotic image encryption scheme based on permutation-diffusion structure. Signal Process. Image Commun. 2018, 62, 164–172. [Google Scholar] [CrossRef]
- Fan, H.; Li, M.; Liu, D.; Zhang, E. Cryptanalysis of a colour image encryption using chaotic apfm nonlinear adaptive filter. Signal Process. 2018, 143, 28–41. [Google Scholar] [CrossRef]
- Zhang, Y.; Gong, D.; Hu, Y.; Zhang, W. Feature selection algorithm based on bare bones particle swarm optimization. Neurocomputing 2015, 148, 150–157. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, X.-F.; Gong, D.-W. A return-cost-based binary firefly algorithm for feature selection. Inf. Sci. 2017, 418–419, 561–574. [Google Scholar] [CrossRef]
- Mao, W.; He, J.; Tang, J.; Li, Y. Predicting remaining useful life of rolling bearings based on deep feature representation and long short-term memory neural network. Adv. Mech. Eng. 2018, 10. [Google Scholar] [CrossRef]
- Jian, M.; Lam, K.-M.; Dong, J. Facial-feature detection and localization based on a hierarchical scheme. Inf. Sci. 2014, 262, 1–14. [Google Scholar] [CrossRef]
- Fan, L.; Xu, S.; Liu, D.; Ru, Y. Semi-supervised community detection based on distance dynamics. IEEE Access 2018, 6, 37261–37271. [Google Scholar] [CrossRef]
- Wang, G.-G.; Chu, H.E.; Mirjalili, S. Three-dimensional path planning for ucav using an improved bat algorithm. Aerosp. Sci. Technol. 2016, 49, 231–238. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L.; Duan, H.; Liu, L.; Wang, H.; Shao, M. Path planning for uninhabited combat aerial vehicle using hybrid meta-heuristic de/bbo algorithm. Adv. Sci. Eng. Med. 2012, 4, 550–564. [Google Scholar] [CrossRef]
- Wang, G.-G.; Cai, X.; Cui, Z.; Min, G.; Chen, J. High performance computing for cyber physical social systems by using evolutionary multi-objective optimization algorithm. IEEE Trans. Emerg. Top. Comput. 2017. [Google Scholar] [CrossRef]
- Cui, Z.; Sun, B.; Wang, G.-G.; Xue, Y.; Chen, J. A novel oriented cuckoo search algorithm to improve dv-hop performance for cyber-physical systems. J. Parallel Distrib. Comput. 2017, 103, 42–52. [Google Scholar] [CrossRef]
- Jian, M.; Lam, K.-M.; Dong, J. Illumination-insensitive texture discrimination based on illumination compensation and enhancement. Inf. Sci. 2014, 269, 60–72. [Google Scholar] [CrossRef]
- Wang, G.-G.; Guo, L.; Duan, H.; Liu, L.; Wang, H. The model and algorithm for the target threat assessment based on elman_adaboost strong predictor. Acta Electron. Sin. 2012, 40, 901–906. [Google Scholar]
- Jian, M.; Lam, K.M.; Dong, J.; Shen, L. Visual-patch-attention-aware saliency detection. IEEE Trans. Cybern. 2015, 45, 1575–1586. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.-G.; Lu, M.; Dong, Y.-Q.; Zhao, X.-J. Self-adaptive extreme learning machine. Neural Comput. Appl. 2016, 27, 291–303. [Google Scholar] [CrossRef]
- Li, J.; Li, Y.-X.; Tian, S.-S.; Xia, J.-L. An improved cuckoo search algorithm with self-adaptive knowledge learning. Neural Comput. Appl. 2019. [Google Scholar] [CrossRef]
- Liu, G.; Zou, J. Level set evolution with sparsity constraint for object extraction. IET Image Process. 2018, 12, 1413–1422. [Google Scholar] [CrossRef]
- Liu, K.; Gong, D.; Meng, F.; Chen, H.; Wang, G.-G. Gesture segmentation based on a two-phase estimation of distribution algorithm. Inf. Sci. 2017, 394–395, 88–105. [Google Scholar] [CrossRef]
- Rizk-Allah, R.M.; El-Sehiemy, R.A.; Wang, G.-G. A novel parallel hurricane optimization algorithm for secure emission/economic load dispatch solution. Appl. Soft Comput. 2018, 63, 206–222. [Google Scholar] [CrossRef]
- Rizk-Allah, R.M.; El-Sehiemy, R.A.; Deb, S.; Wang, G.-G. A novel fruit fly framework for multi-objective shape design of tubular linear synchronous motor. J. Supercomput. 2017, 73, 1235–1256. [Google Scholar] [CrossRef]
- Yi, J.-H.; Deb, S.; Dong, J.; Alavi, A.H.; Wang, G.-G. An improved nsga-iii algorithm with adaptive mutation operator for big data optimization problems. Future Gener. Comput. Syst. 2018, 88, 571–585. [Google Scholar] [CrossRef]
- Liu, G.; Deng, M. Parametric active contour based on sparse decomposition for multi-objects extraction. Signal Process. 2018, 148, 314–321. [Google Scholar] [CrossRef]
- Sun, J.; Miao, Z.; Gong, D.; Zeng, X.-J.; Li, J.; Wang, G.-G. Interval multi-objective optimization with memetic algorithms. IEEE Trans. Cybern. 2019. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, G.-G.; Li, K.; Yeh, W.-C.; Jian, M.; Dong, J. Enhancing moea/d with information feedback models for large-scale many-objective optimization. Inf. Sci. 2020, 522, 1–16. [Google Scholar] [CrossRef]
- Gu, Z.-M.; Wang, G.-G. Improving NSGA-III algorithms with information feedback models for large-scale many-objective optimization. Future Gener. Comput. Syst. 2020, 107, 49–69. [Google Scholar] [CrossRef]
- Srikanth, K.; Panwar, L.K.; Panigrahi, B.K.; Herrera-Viedma, E.; Sangaiah, A.K.; Wang, G.-G. Meta-heuristic framework: Quantum inspired binary grey wolf optimizer for unit commitment problem. Comput. Electr. Eng. 2018, 70, 243–260. [Google Scholar] [CrossRef]
- Li, J.; Xiao, D.-D.; Lei, H.; Zhang, T.; Tian, T. Using cuckoo search algorithm with q-learning and genetic operation to solve the problem of logistics distribution center location. Mathematics (Basel) 2020, 8, 149. [Google Scholar] [CrossRef]
- Chen, S.; Chen, R.; Wang, G.-G.; Gao, J.; Sangaiah, A.K. An adaptive large neighborhood search heuristic for dynamic vehicle routing problems. Comput. Electr. Eng. 2018. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, G.-G. Binary moth search algorithm for discounted {0–1} knapsack problem. IEEE Access 2018, 6, 10708–10719. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, G.-G.; Wang, L. Solving randomized time-varying knapsack problems by a novel global firefly algorithm. Eng. Comput. 2018, 34, 621–635. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley: New York, NY, USA, 1998. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; IEEE: Perth, Australia, 1995; pp. 1942–1948. [Google Scholar]
- Wang, G.-G.; Gandomi, A.H.; Yang, X.-S.; Alavi, A.H. A novel improved accelerated particle swarm optimization algorithm for global numerical optimization. Eng. Comput. 2014, 31, 1198–1220. [Google Scholar] [CrossRef]
- Sun, J.; Feng, B.; Xu, W. Particle Swarm Optimization with Particles Having Quantum Behavior. In Proceedings of the Congress on Evolutionary Computation (CEC 2004), Portland, OR, USA, 19–23 June 2004; IEEE: Portland, OR, USA, 2004; pp. 325–331. [Google Scholar]
- Adewumi, A.O.; Arasomwan, M.A. On the performance of particle swarm optimisation with(out) some control parameters for global optimisation. Int. J. Bio-Inspir. Com. 2016, 8, 14–32. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Xu, Z.; Unveren, A.; Acan, A. Probability collectives hybridised with differential evolution for global optimisation. Int. J. Bio-Inspir. Com. 2016, 8, 133–153. [Google Scholar] [CrossRef]
- Wang, G.-G.; Zhao, X.; Deb, S. A Novel Monarch Butterfly Optimization with Greedy Strategy and Self-Adaptive Crossover Operator. In Proceedings of the 2015 IEEE 2nd Intl, Conference on Soft Computing & Machine Intelligence (ISCMI 2015), Hong Kong, China, 23–24 November 2015; pp. 45–50. [Google Scholar]
- Wang, G.-G.; Deb, S.; Zhao, X.; Cui, Z. A new monarch butterfly optimization with an improved crossover operator. Oper. Res. Int. J. 2018, 18, 731–755. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, G.-G.; Li, W.; Li, N. Multi-strategy monarch butterfly optimization algorithm for discounted {0–1} knapsack problem. Neural Comput. Appl. 2018, 30, 3019–3036. [Google Scholar] [CrossRef]
- Wang, G.-G.; Deb, S.; Cui, Z. Monarch butterfly optimization. Neural Comput. Appl. 2019, 31, 1995–2014. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, G.-G.; Deb, S.; Lu, M.; Zhao, X. Solving 0–1 knapsack problem by a novel binary monarch butterfly optimization. Neural Comput. Appl. 2017, 28, 1619–1634. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (abc) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Wang, G.-G.; Deb, S.; Coelho, L.D.S. Earthworm optimization algorithm: A bio-inspired metaheuristic algorithm for global optimization problems. Int. J. Bio.-Inspir. Com. 2018, 12, 1–22. [Google Scholar] [CrossRef]
- Dorigo, M.; Stutzle, T. Ant Colony Optimization; MIT Press: Cambridge, UK, 2004. [Google Scholar]
- Li, J.; Xiao, D.-D.; Zhang, T.; Liu, C.; Li, Y.-X. Multi-swarm cuckoo search algorithm with q-learning model. Comput. J. 2020. [Google Scholar] [CrossRef]
- Yang, X.-S.; Deb, S. Cuckoo search via lévy flights. In Proceedings of the World Congress on Nature & Biologically Inspired Computing (NaBIC 2009), Coimbatore, India, 9–11 December 2009; Abraham, A., Carvalho, A., Herrera, F., Pai, V., Eds.; IEEE Publications: Coimbatore, India, 2009; pp. 210–214. [Google Scholar]
- Li, X.; Wang, J.; Yin, M. Enhancing the performance of cuckoo search algorithm using orthogonal learning method. Neural Comput. Appl. 2013, 24, 1233–1247. [Google Scholar] [CrossRef]
- Li, X.; Yin, M. Modified cuckoo search algorithm with self adaptive parameter method. Inf. Sci. 2015, 298, 80–97. [Google Scholar] [CrossRef]
- Wang, G.-G.; Gandomi, A.H.; Zhao, X.; Chu, H.E. Hybridizing harmony search algorithm with cuckoo search for global numerical optimization. Soft Comput. 2016, 20, 273–285. [Google Scholar] [CrossRef]
- Wang, G.-G.; Deb, S.; Gandomi, A.H.; Zhang, Z.; Alavi, A.H. Chaotic cuckoo search. Soft Comput. 2016, 20, 3349–3362. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L.; Duan, H.; Liu, L.; Wang, H.; Wang, J. A hybrid meta-heuristic de/cs algorithm for ucav path planning. J. Inform. Comput. Sci. 2012, 9, 4811–4818. [Google Scholar]
- Gandomi, A.H.; Alavi, A.H. Krill herd: A new bio-inspired optimization algorithm. Commun. Nonlinear Sci. 2012, 17, 4831–4845. [Google Scholar] [CrossRef]
- Li, Z.-Y.; Yi, J.-H.; Wang, G.-G. A new swarm intelligence approach for clustering based on krill herd with elitism strategy. Algorithms 2015, 8, 951–964. [Google Scholar] [CrossRef]
- Wang, G.-G.; Gandomi, A.H.; Alavi, A.H.; Deb, S. A multi-stage krill herd algorithm for global numerical optimization. Int. J. Artif. Intell. Tools 2016, 25, 1550030. [Google Scholar] [CrossRef]
- Wang, G.-G.; Gandomi, A.H.; Alavi, A.H. An effective krill herd algorithm with migration operator in biogeography-based optimization. Appl. Math. Model 2014, 38, 2454–2462. [Google Scholar] [CrossRef]
- Wang, G.-G.; Gandomi, A.H.; Alavi, A.H.; Gong, D. A comprehensive review of krill herd algorithm: Variants, hybrids and applications. Artif. Intell. Rev. 2019, 51, 119–148. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.-S.; Alavi, A.H. Mixed variable structural optimization using firefly algorithm. Comput. Struct. 2011, 89, 2325–2336. [Google Scholar] [CrossRef]
- Yang, X.S. Firefly algorithm, stochastic test functions and design optimisation. Int. J. Bio-Inspir. Com. 2010, 2, 78–84. [Google Scholar] [CrossRef]
- Wang, G.-G.; Guo, L.; Duan, H.; Wang, H. A new improved firefly algorithm for global numerical optimization. J. Comput. Theor. Nanosci. 2014, 11, 477–485. [Google Scholar] [CrossRef]
- Gálvez, A.; Iglesias, A. New memetic self-adaptive firefly algorithm for continuous optimisation. Int. J. Bio-Inspir. Com. 2016, 8, 300–317. [Google Scholar] [CrossRef]
- Nasiri, B.; Meybodi, M.R. History-driven firefly algorithm for optimisation in dynamic and uncertain environments. Int. J. Bio.-Inspir. Com. 2016, 8, 326–339. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L.; Duan, H.; Liu, L.; Wang, H. A modified firefly algorithm for ucav path planning. Int. J. Hybrid Inf. Technol. 2012, 5, 123–144. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Shah-Hosseini, H. The intelligent water drops algorithm: A nature-inspired swarm-based optimization algorithm. Int. J. Bio-Inspir. Com. 2009, 1, 71–79. [Google Scholar] [CrossRef]
- Eskandar, H.; Sadollah, A.; Bahreininejad, A.; Hamdi, M. Water cycle algorithm—A novel metaheuristic optimization method for solving constrained engineering optimization problems. Comput. Struct. 2012, 110–111, 151–166. [Google Scholar] [CrossRef]
- Wang, G.-G. Moth search algorithm: A bio-inspired metaheuristic algorithm for global optimization problems. Memetic Comput. 2018, 10, 151–164. [Google Scholar] [CrossRef]
- Zhao, R.; Tang, W. Monkey algorithm for global numerical optimization. J. Uncertain Syst. 2008, 2, 165–176. [Google Scholar]
- Beyer, H. The Theory of Evolution Strategies; Springer: New York, NY, USA, 2001. [Google Scholar]
- Penev, K.; Littlefair, G. Free search-a comparative analysis. Inf. Sci. 2005, 172, 173–193. [Google Scholar] [CrossRef]
- Baluja, S. Population-Based Incremental Learning: A Method for Integrating Genetic Search Based Function Optimization and Competitive Learning; CMU-CS-94-163; Carnegie Mellon University: Pittsburgh, PA, USA, 1994. [Google Scholar]
- Simon, D. Biogeography-based optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Let a biogeography-based optimizer train your multi-layer perceptron. Inf. Sci. 2014, 269, 188–209. [Google Scholar] [CrossRef]
- Duan, H.; Zhao, W.; Wang, G.; Feng, X. Test-sheet composition using analytic hierarchy process and hybrid metaheuristic algorithm ts/bbo. Math. Probl. Eng. 2012, 2012, 1–22. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L.; Duan, H.; Liu, L.; Wang, H. Dynamic deployment of wireless sensor networks by biogeography based optimization algorithm. J. Sens. Actuator Netw. 2012, 1, 86–96. [Google Scholar] [CrossRef]
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]
- Gandomi, A.H. Interior search algorithm (ISA): A novel approach for global optimization. ISA Trans. 2014, 53, 1168–1183. [Google Scholar] [CrossRef]
- Shi, Y. An optimization algorithm based on brainstorming process. Int. J. Swarm Intell. Res. 2011, 2, 35–62. [Google Scholar] [CrossRef]
- Shi, Y.; Xue, J.; Wu, Y. Multi-objective optimization based on brain storm optimization algorithm. Int. J. Swarm Intell. Res. 2013, 4, 1–21. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.-S.; Alavi, A.H.; Talatahari, S. Bat algorithm for constrained optimization tasks. Neural Comput. Appl. 2013, 22, 1239–1255. [Google Scholar] [CrossRef]
- Yang, X.S.; Gandomi, A.H. Bat algorithm: A novel approach for global engineering optimization. Eng. Comput. 2012, 29, 464–483. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Yang, X.-S. Binary bat algorithm. Neural Comput. Appl. 2013, 25, 663–681. [Google Scholar] [CrossRef]
- Cai, X.; Gao, X.-Z.; Xue, Y. Improved bat algorithm with optimal forage strategy and random disturbance strategy. Int. J. Bio-Inspir. Com. 2016, 8, 205–214. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L. A novel hybrid bat algorithm with harmony search for global numerical optimization. J. Appl. Math. 2013, 2013, 1–21. [Google Scholar] [CrossRef]
- Wang, G.-G.; Chang, B.; Zhang, Z. A Multi-Swarm Bat Algorithm for Global Optimization. In Proceedings of the 2015 IEEE Congress on Evolutionary Computation (CEC 2015), Sendai, Japan, 25–28 May 2015; IEEE: Sendai, Japan, 2015; pp. 480–485. [Google Scholar]
- Wang, G.-G.; Lu, M.; Zhao, X.-J. An improved bat algorithm with variable neighborhood search for global optimization. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (IEEE CEC 2016), Vancouver, BC, Canada, 24–29 July 2016; pp. 1773–1778. [Google Scholar]
- Yang, X.-S. Nature-Inspired Metaheuristic Algorithms, 2nd ed.; Luniver Press: Frome, UK, 2010. [Google Scholar]
- Khatib, W.; Fleming, P. The stud ga: A mini revolution? In Parallel Problem Solving from Nature-ppsn v; Eiben, A., Bäck, T., Schoenauer, M., Schwefel, H.-P., Eds.; Springer: Berlin/Heidelberg, Germany; London, UK, 1998; Volume 1498, pp. 683–691. [Google Scholar]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L.; Duan, H.; Wang, H.; Liu, L.; Shao, M. Hybridizing harmony search with biogeography based optimization for global numerical optimization. J. Comput. Theor. Nanosci. 2013, 10, 2318–2328. [Google Scholar] [CrossRef]
- Niknam, T.; Fard, A.K. Optimal energy management of smart renewable micro-grids in the reconfigurable systems using adaptive harmony search algorithm. Int. J. Bio-Inspir. Com. 2016, 8, 184–194. [Google Scholar] [CrossRef]
- Rezoug, A.; Boughaci, D. A self-adaptive harmony search combined with a stochastic local search for the 0–1 multidimensional knapsack problem. Int. J. Bio-Inspir. Com. 2016, 8, 234–239. [Google Scholar] [CrossRef]
- Tan, Y. Fireworks Algorithm-A Novel Swarm Intelligence Optimization Method; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Meng, X.; Liu, Y.; Gao, X.; Zhang, H. A new bio-inspired algorithm: Chicken swarm optimization. In Proceedings of the Advances in Swarm Intelligence (ICSI 2014), Hefei, China, 17–20 October 2014; Springer: Berlin/Heidelberg, Germany, 2014; Volume 8794, pp. 86–94. [Google Scholar]
- Wang, G.-G.; Deb, S.; Coelho, L.d.S. Elephant Herding Optimization. In Proceedings of the 2015 3rd International Symposium on Computational and Business Intelligence (ISCBI 2015), Bali, Indonesia, 7–9 December 2015; IEEE: Bali, Indonesia, 2015; pp. 1–5. [Google Scholar]
- Tuba, E.; Capor-Hrosik, R.; Alihodzic, A.; Jovanovic, R.; Tuba, M. Chaotic Elephant Herding Optimization Algorithm. In Proceedings of the 2018 IEEE 16th World Symposium on Applied Machine Intelligence and Informatics (SAMI 2018), Kosice and Herlany, Slovakia, 7–10 February 2018; IEEE: Kosice and Herlany, Slovakia, 2018; pp. 213–216. [Google Scholar]
- Li, J.; Guo, L.; Li, Y.; Liu, C. Enhancing elephant herding optimization with novel individual updating strategies for large-scale optimization problems. Mathematics 2019, 7, 395. [Google Scholar] [CrossRef]
- Xu, H.; Cao, Q.; Fang, C.; Fu, Y.; Su, J.; Wei, S.; Bykovyy, P. Application of Elephant Herd Optimization Algorithm Based on Levy Flight Strategy in Intrusion Detection. In Proceedings of the 2018 IEEE 4th International Symposium on Wireless Systems within the International Conferences on Intelligent Data Acquisition and Advanced Computing Systems (IDAACS-SWS), Lviv, Ukraine, 20–21 September 2018; IEEE: Lviv, Ukraine, 2018; pp. 16–20. [Google Scholar]
- Xu, H.; Cao, Q.; Fu, H.; Fu, C.; Chen, H.; Su, J. Application of Support Vector Machine Model Based on an Improved Elephant Herding Optimization Algorithm in Network Intrusion Detection; Springer: Singapore, 2019; pp. 283–295. [Google Scholar]
- Hakli, H. Elephant herding optimization using multi-search strategy for continuous optimization problems. Acad. Platf. J. Eng. Sci. 2019, 7, 261–268. [Google Scholar] [CrossRef]
- Tuba, E.; Dolicanin-Djekic, D.; Jovanovic, R.; Simian, D.; Tuba, M. Combined Elephant Herding Optimization Algorithm with k-Means for Data Clustering; Springer: Singapore, 2019; pp. 665–673. [Google Scholar]
- Chakraborty, F.; Roy, P.K.; Nandi, D. Oppositional elephant herding optimization with dynamic cauchy mutation for multilevel image thresholding. Evol. Intell. 2019, 12, 445–467. [Google Scholar] [CrossRef]
- Chowdary, K.U.; Prabhakara Rao, B. Performance improvement in mimo-ofdm systems based on adaptive whale elephant herd optimization algorithm. Int. J. Eng. Adv. Technol. 2019, 9, 6651–6657. [Google Scholar]
- Rashwan, Y.I.; Elhosseini, M.A.; El Sehiemy, R.A.; Gao, X.Z. On the performance improvement of elephant herding optimization algorithm. Knowl.-Based Syst. 2019, 166, 58–70. [Google Scholar]
- ElShaarawy, I.A.; Houssein, E.H.; Ismail, F.H.; Hassanien, A.E. An exploration-enhanced elephant herding optimization. Eng Comput. 2019, 36, 3029–3046. [Google Scholar] [CrossRef]
- Ismaeel, A.A.K.; Elshaarawy, I.A.; Houssein, E.H.; Ismail, F.H.; Hassanien, A.E. Enhanced elephant herding optimization for global optimization. IEEE Access 2019, 7, 34738–34752. [Google Scholar] [CrossRef]
- Veera manikandan, P.; Selvaperumal, S. A fuzzy-elephant herding optimization technique for maximum power point tracking in the hybrid wind-solar system. Int. Trans. Electr. Energy Syst. 2019. [Google Scholar] [CrossRef]
- Arora, P.; Dixit, A. The hybrid optimization algorithm for load balancing in cloud. Int. J. Eng. Adv. Technol. 2019, 8, 67–71. [Google Scholar]
- Bukhsh, R.; Javaid, N.; Iqbal, Z.; Ahmed, U.; Ahmad, Z.; Iqbal, M.N. Appliances Scheduling Using Hybrid Scheme of Genetic Algorithm and Elephant Herd Optimization for Residential Demand Response. In Proceedings of the 2018 32nd International Conference on Advanced Information Networking and Applications Workshops (WAINA 2018), Krakow, Poland, 16–18 May 2018; IEEE: Krakow, Poland, 2018; pp. 210–217. [Google Scholar]
- Strumberger, I.; Minovic, M.; Tuba, M.; Bacanin, N. Performance of elephant herding optimization and tree growth algorithm adapted for node localization in wireless sensor networks. Sensors 2019, 19, 2515. [Google Scholar] [CrossRef]
- Satapathy, P.; Pradhan, S.K.; Hota, S. Development of a novel neural network model for brain image classification. Int. J. Recent Technol. Eng. 2019, 8, 7230–7235. [Google Scholar]
- Hakli, H. A novel approach based on elephant herding optimization for constrained optimization problems. Selçuk Üniversitesi Mühendislik Bilim ve Teknoloji Dergisi 2019, 7, 405–419. [Google Scholar] [CrossRef]
- Hakli, H. Bineho: A new binary variant based on elephant herding optimization algorithm. Neural Comput. Appl. 2020. [Google Scholar] [CrossRef]
- Jaiprakash, K.P.; Nanda, S.J. Classifying Physical Actions of Human Models Using Multi-Objective Clustering Based on Elephant Herding Algorithm. In Proceedings of the 1st International Conference on Pervasive Computing Advances and Applications (PerCAA 2019), Jaipur, India, 8–10 January 2019; Bundele, M., Dey, N., Madria, S.K., Eds.; Elsevier B.V.: Jaipur, India, 2019; pp. 84–91. [Google Scholar]
- Meena, N.K.; Parashar, S.; Swarnkar, A.; Gupta, N.; Niazi, K.R. Improved elephant herding optimization for multiobjective der accommodation in distribution systems. IEEE Trans. Ind. Inform. 2018, 14, 1029–1039. [Google Scholar] [CrossRef]
- Moayedi, H.; Mu′azu, M.A.; Foong, L.K. Novel swarm-based approach for predicting the cooling load of residential buildings based on social behavior of elephant herds. Energy Build. 2020, 206, 109579. [Google Scholar] [CrossRef]
- Kowsalya, S.; Periasamy, P.S. Recognition of tamil handwritten character using modified neural network with aid of elephant herding optimization. Multimed Tools Appl. 2019, 78, 25043–25061. [Google Scholar] [CrossRef]
- Sahlol, A.T.; Ismail, F.H.; Abdeldaim, A.; Hassanien, A.E. Elephant Herd Optimization with Neural Networks: A Case Study on Acute Lymphoblastic Leukemia Diagnosis. In Proceedings of the 2017 12th International Conference on Computer Engineering and Systems (ICCES 2017), Cairo, Egypt, 19–20 December 2017; IEEE: Cairo, Egypt, 2017; pp. 657–662. [Google Scholar]
- Kaur, S. Energy optimization for underwater sensor network using nature inspired technique. Int. J. Innov. Technol. Explor. Eng. 2019, 8, 161–164. [Google Scholar]
- Alihodzic, A.; Tuba, E.; Capor-Hrosik, R.; Dolicanin, E.; Tuba, M. Unmanned Aerial Vehicle Path Planning Problem by Adjusted Elephant Herding Optimization. In Proceedings of the 2017 25th Telecommunication Forum (TELFOR), Belgrade, Serbia, 21–22 November 2017; IEEE: Belgrade, Serbia, 2017; pp. 1–4. [Google Scholar]
- Rani, R.R.; Ramyachitra, D.; Brindhadevi, A. Detection of dynamic protein complexes through markov clustering based on elephant herd optimization approach. Sci. Rep. 2019, 9, 11106. [Google Scholar] [CrossRef]
- Jaiprakash, K.P.; Nanda, S.J. Elephant Herding Algorithm for Clustering; Springer: Singapore, 2019; pp. 317–325. [Google Scholar]
- Hassanien, A.E.; Kilany, M.; Houssein, E.H.; AlQaheri, H. Intelligent human emotion recognition based on elephant herding optimization tuned support vector regression. Biomed. Signal Process. Control 2018, 45, 182–191. [Google Scholar] [CrossRef]
- Hassanien, A.E.; Kilany, M.; Houssein, E.H. Combining support vector machine and elephant herding optimization for cardiac arrhythmias. arXiv 2018, arXiv:1806.08242. [Google Scholar]
- Tuba, E.; Stanimirovic, Z. Elephant Herding Optimization Algorithm for Support Vector Machine Parameters Tuning. In Proceedings of the IEEE International Conference on Electronics, Computers and Artificial Intelligence (ECAI 2017), Targoviste, Romania, 29 June–1 July 2017; pp. 1–4. [Google Scholar]
- Tuba, E.; Ribic, I.; Capor-Hrosik, R.; Tuba, M. Support vector machine optimized by elephant herding algorithm for erythemato-squamous diseases detection. Procedia Comput. Sci. 2017, 122, 916–923. [Google Scholar] [CrossRef]
- Sambariya, D.K.; Fagna, R. A Novel Elephant Herding Optimization Based pid Controller Design for Load Frequency Control in Power System. In Proceedings of the 2017 International Conference on Computer, Communications and Electronics (Comptelix), Jaipur, India, 1–2 July 2017; IEEE: Jaipur, India, 2017; pp. 595–600. [Google Scholar]
- Almufti, S.; Boya Marqas, R.; Asaad, R.R. Comparative study between elephant herding optimization (eho) and u-turning ant colony optimization (u-taco) in solving symmetric traveling salesman problem (stsp). J. Adv. Comput. Sci. Technol. 2019, 8. [Google Scholar] [CrossRef]
- Darmawan, H.; Rini, D.P.; Arsalan, O. Penerapan Algoritma Elephant Herding Optimization pada Permasalahan Knapsack 0-1. Undergraduate thesis, Sriwijaya University, Kota Palembang, Sumatera Selatan, 2019. Undergraduate Thesis, Sriwijaya University, Kota Palembang, Sumatera Selatan, 2019. [Google Scholar]
- Correia, S.D.; Beko, M.; Cruz, L.A.D.S.; Tomic, S. Implementation and Validation of Elephant Herding Optimization Algorithm for Acoustic Localization. In Proceedings of the 2018 26th Telecommunications Forum (TELFOR), Belgrade, Serbia, 20–21 November 2018; IEEE: Belgrade, Serbia, 2018; pp. 1–4. [Google Scholar]
- Parashar, S.; Swarnkar, A.; Niazi, K.R.; Gupta, N. Stochastic operational management of grid-connected microgrid under uncertainty of renewable resources and load demand. In Lecture Notes in Electrical Engineering; Springer: Singapore, 2020; Volume 607, pp. 573–581. [Google Scholar]
- Cahig, C.; Villanueva, J.J.; Bersano, R.; Pacis, M. Optimal Virtual Power Plant Scheduling Using Elephant Herding Optimization. In Proceedings of the 10th IEEE International Conference on Humanoid, Nanotechnology, Information Technology, Communication and Control, Environment and Management, HNICEM 2018, Baguio City, Philippines, 29 November–2 December 2018; IEEE: Baguio City, Philippines, 2019. [Google Scholar]
- Sarwar, M.A.; Amin, B.; Ayub, N.; Faraz, S.H.; Khan, S.U.R.; Javaid, N. Scheduling of appliances in home energy management system using elephant herding optimization and enhanced differential evolution. In Advances in Intelligent Networking and Collaborative Systems, Proceedings of the 9th International Conference on Intelligent Networking and Collaborative Systems (INCoS 2017), Ryerson Univ, Toronto, ON, Canada, 24–26 August 2017; Springer: Berlin, Germany, 2017; pp. 132–142. [Google Scholar]
- Parvez, K.; Aslam, S.; Saba, A.; Aimal, S.; Amjad, Z.; Asif, S.; Javaid, N. Scheduling of appliances in hems using elephant herding optimization and harmony search algorithm. In Advances on Broad-Band Wireless Computing, Communication and Applications, Proceedings of the 12th International Conference on Broad-Band Wireless Computing, Communication and Applications (BWCCA 2017), Barcelona, Spain, 8–10 November 2017; Springer: Berlin, Germany, 2017; pp. 62–72. [Google Scholar]
- Mohsin, S.M.; Javaid, N.; Madani, S.A.; Akber, S.M.A.; Manzoor, S.; Ahmad, J. Implementing Elephant Herding Optimization Algorithm with Different Operation Time Intervals for Appliance Scheduling in Smart Grid. In Proceedings of the 2018 32nd International Conference on Advanced Information Networking and Applications Workshops (WAINA), Krakow, Poland, 16–18 May 2018; IEEE: Krakow, Poland, 2018; pp. 240–249. [Google Scholar]
- Gholami, H.R.; Mehdizadeh, E.; Naderi, B. Mathematical models and an elephant herding optimization for multiprocessor-task flexible flow shop scheduling problems in the manufacturing resource planning (mrpii) system. Scientia Iranica 2018. [Google Scholar] [CrossRef]
- Fatima, I.; Asif, S.; Shafiq, S.; Fatima, I.; Rahim, M.H.; Javaid, N. Efficient Demand Side Management Using Hybridization of Elephant Herding Optimization and Firefly Optimization. In Proceedings of the 2018 IEEE 32nd International Conference on Advanced Information Networking and Applications (AINA), Krakow, Poland, 16–18 May 2018; IEEE: Krakow, Poland, 2018; pp. 839–845. [Google Scholar]
- Luangpaiboon, P. Variable tuning for electrostatic powder coating process via elephant herding optimisation algorithm on modified simplex method. Int. J. Mech. Eng. Robot. Res. 2019, 8, 807–812. [Google Scholar] [CrossRef]
- Shankar, K.; Elhoseny, M.; Perumal, E.; Ilayaraja, M.; Sathesh Kumar, K. An efficient image encryption scheme based on signcryption technique with adaptive elephant herding optimization. In Cybersecurity and Secure Information Systems: Challenges and Solutions in Smart Environments; Springer: Cham, Switzerland, 20 June 2019; pp. 31–42. [Google Scholar]
- Chibani, S.S.; Tari, A. Elephant herding optimization for service selection in qos-aware web service composition. Int. J. Comput. Electr. Autom. Control Inf. Eng. 2017, 11, 1045–1049. [Google Scholar]
- Tuba, E.; Alihodzic, A.; Tuba, M. Multilevel Image Thresholding Using Elephant Herding Optimization Algorithm. In Proceedings of the 2017 14th International Conference on Engineering of Modern Electric Systems (EMES), Oradea, Romania, 1–2 June 2017; IEEE: Oradea, Romania, 2017; pp. 240–243. [Google Scholar]
- Jino Ramson, S.R.; Lova Raju, K.; Vishnu, S.; Anagnostopoulos, T. Nature inspired optimization techniques for image processing-a short review. In Nature Inspired Optimization Techniques for Image Processing Applications; Springer: Cham, Switzerland, 20 September 2018; Volume 150, pp. 113–145. [Google Scholar]
- Jayanth, J.; Shalini, V.S.; Ashok Kumar, T.; Koliwad, S. Land-use/land-cover classification using elephant herding algorithm. J. Indian Soc. Remote 2019, 47, 223–232. [Google Scholar] [CrossRef]
- De Vasconcelos Cardoso, A.; Nedjah, N.; De Macedo Mourelle, L.; Tavares, Y.M. Co-Design System for Template Matching Using Dedicated co-Processor and Modified Elephant Herding Optimization. In Proceedings of the 2018 IEEE 9th Latin American Symposium on Circuits and Systems (LASCAS 2018), Puerto Vallarta, Mexico, 25–28 February 2018; pp. 1–4. [Google Scholar]
- Correia, S.; Beko, M.; Cruz, L.; Tomic, S. Elephant herding optimization for energy-based localization. Sensors 2018, 18, 2849. [Google Scholar] [CrossRef]
- Strumberger, I.; Beko, M.; Tuba, M.; Minovic, M.; Bacanin, N. Elephant Herding Optimization Algorithm for Wireless Sensor Network Localization Problem. In Proceedings of the Technological Innovation for Resilient Systems: 9th IFIP WG 5.5/SOCOLNET Advanced Doctoral Conference on Computing, Electrical and Industrial Systems (DoCEIS 2018), Costa de Caparica, Portugal, 2–4 May 2018; pp. 175–184. [Google Scholar]
- Kaur, K.; Randhawa, R. Energy efficient approach for underwater sensor network using elephant herd optimization. Res. Cell Int. J. Eng. Sci. 2018, 30, 148–160. [Google Scholar]
- Xu, H.; Cao, Q.; Fu, H.; Chen, H. Applying an improved elephant herding optimization algorithm with spark-based parallelization to feature selection for intrusion detection. Int. J. Perform. Eng. 2019, 15, 1600–1610. [Google Scholar] [CrossRef]
- Dhillon, S.S.; Agarwal, S.; Wang, G.-G.; Lather, J.S. Automatic generation control of interconnected power systems using elephant herding optimization. In Lecture Notes in Electrical Engineering; Springer: Singapore, 2020; pp. 9–18. [Google Scholar]
- Kuchibhatla, S.M.; Padmavathi, D.; Rao, R.S. An elephant herding optimization algorithm-based static switched filter compensation scheme for power quality improvement in smart grid. J. Circuits Syst. Comput. 2019. [Google Scholar] [CrossRef]
- Sambariya, D.K.; Fagna, R. A Robust Pid Controller for Load Frequency Control of Single Area re-heat Thermal Power Plant Using Elephant Herding Optimization Techniques. In Proceedings of the 2017 IEEE International Conference on Information, Communication, Instrumentation and Control, ICICIC 2017, Indore, India, 17–19 August 2017; pp. 1–6. [Google Scholar]
- Prasad, C.H.; Subbaramaiah, K.; Sujatha, P. Cost–benefit analysis for optimal dg placement in distribution systems by using elephant herding optimization algorithm. Renew. Wind Water Sol. 2019, 6. [Google Scholar] [CrossRef]
- Vijay, R.; Abhilash, M. Elephant herding optimization for optimum allocation of electrical distributed generation on distributed power networks. Asian J. Electr. Sci. 2018, 7, 70–76. [Google Scholar]
- Strumberger, I.; Bacanin, N.; Tuba, M. Hybridized Elephant Herding Optimization Algorithm for Constrained Optimization. In Proceedings of the 17th International Conference on Hybrid Intelligent Systems (HIS 2017), Delhi, India, 14–16 December 2017; Springer International Publishing: Delhi, India, 2017; pp. 158–166. [Google Scholar]
- Singh, N.; Kumar, M.P.; Kumar, B.S. Effect of valve loading on the thermal power economic load dispatch using new elephant herding optimization. Int. J. Recent Technol. Eng. 2019, 7, 345–349. [Google Scholar]
- Horng, S.-C.; Lin, S.-S. Coupling elephant herding with ordinal optimization for solving the stochastic inequality constrained optimization problems. Appl. Sci. 2020, 10, 2075. [Google Scholar] [CrossRef]
- Sadouki, S.C.; Tari, A. Multi-objective and discrete elephants herding optimization algorithm for qos aware web service composition. RAIRO-Oper. Res. 2019, 53, 445–459. [Google Scholar] [CrossRef]
- Adarsha, B.S.; Harish, N.; Janardhan, P.; Mandal, S. Elephant Herding Optimization Based Neural Network to Predict Elastic Modulus of Concrete; Soft Computing for Problem Solving; Das, K.N., Bansal, J.C., Deep, K., Nagar, A.K., Pathipooranam, P., Naidu, R.C., Eds.; Springer: Singapore, 2020; pp. 353–364. [Google Scholar]
- Jafari, M.; Salajegheh, E.; Salajegheh, J. An efficient hybrid of elephant herding optimization and cultural algorithm for optimal design of trusses. Eng. Comput. 2018, 35, 781–801. [Google Scholar] [CrossRef]
- Milani, A.; Santucci, V. Community of scientist optimization: An autonomy oriented approach to distributed optimization. AI Commun. 2012, 25, 16. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).