An Investigation of Radial Basis Function-Finite Difference (RBF-FD) Method for Numerical Solution of Elliptic Partial Differential Equations
Abstract
:1. Introduction
2. Methodology
2.1. RBF Collocation Method
2.2. RBF-FD Method
3. Main Result
3.1. Solution Accuracy for Elliptic PDEs
3.2. Results: A Comparison of a Global RBF Collocation Method and RBF-FD Method with Various RBFs
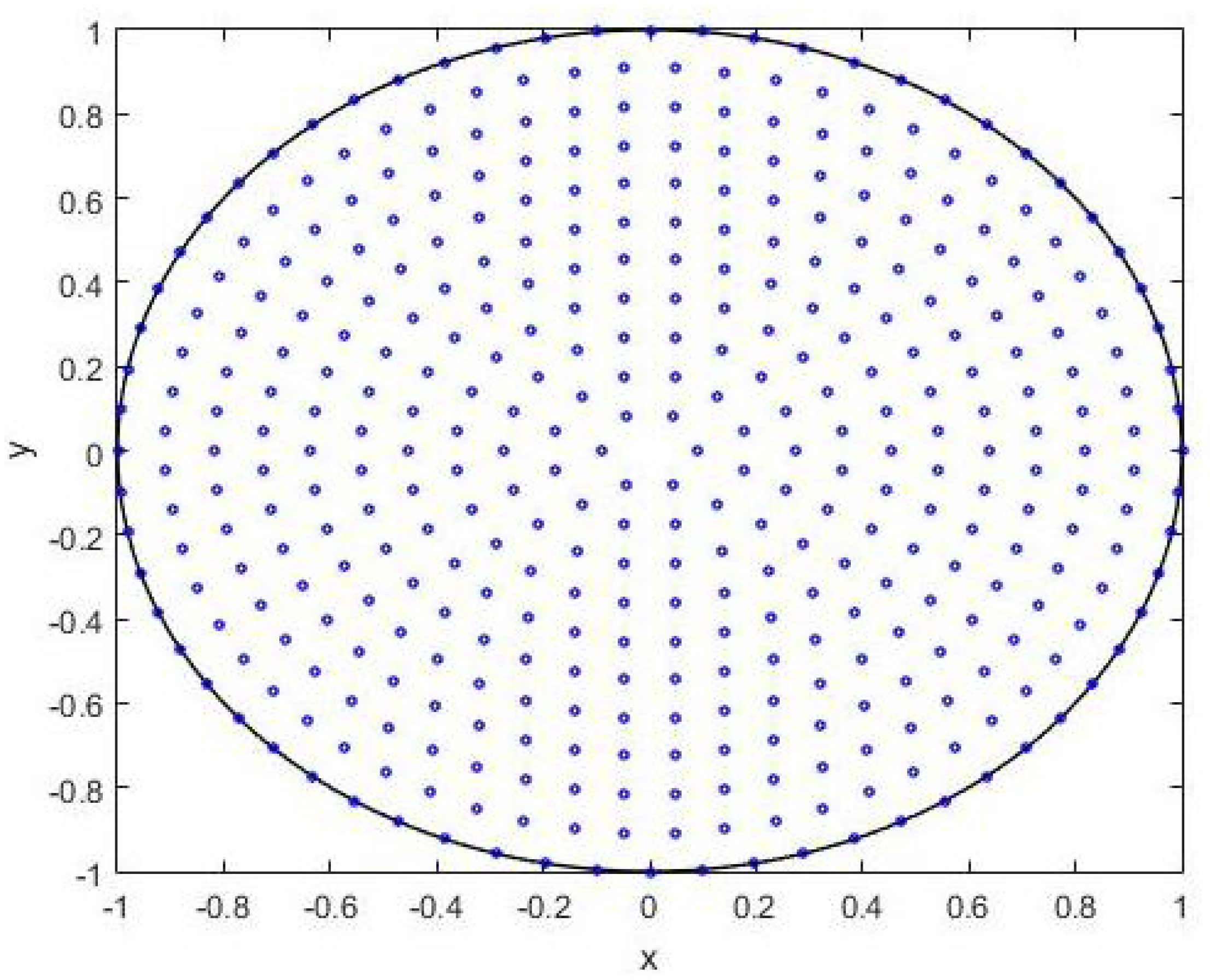
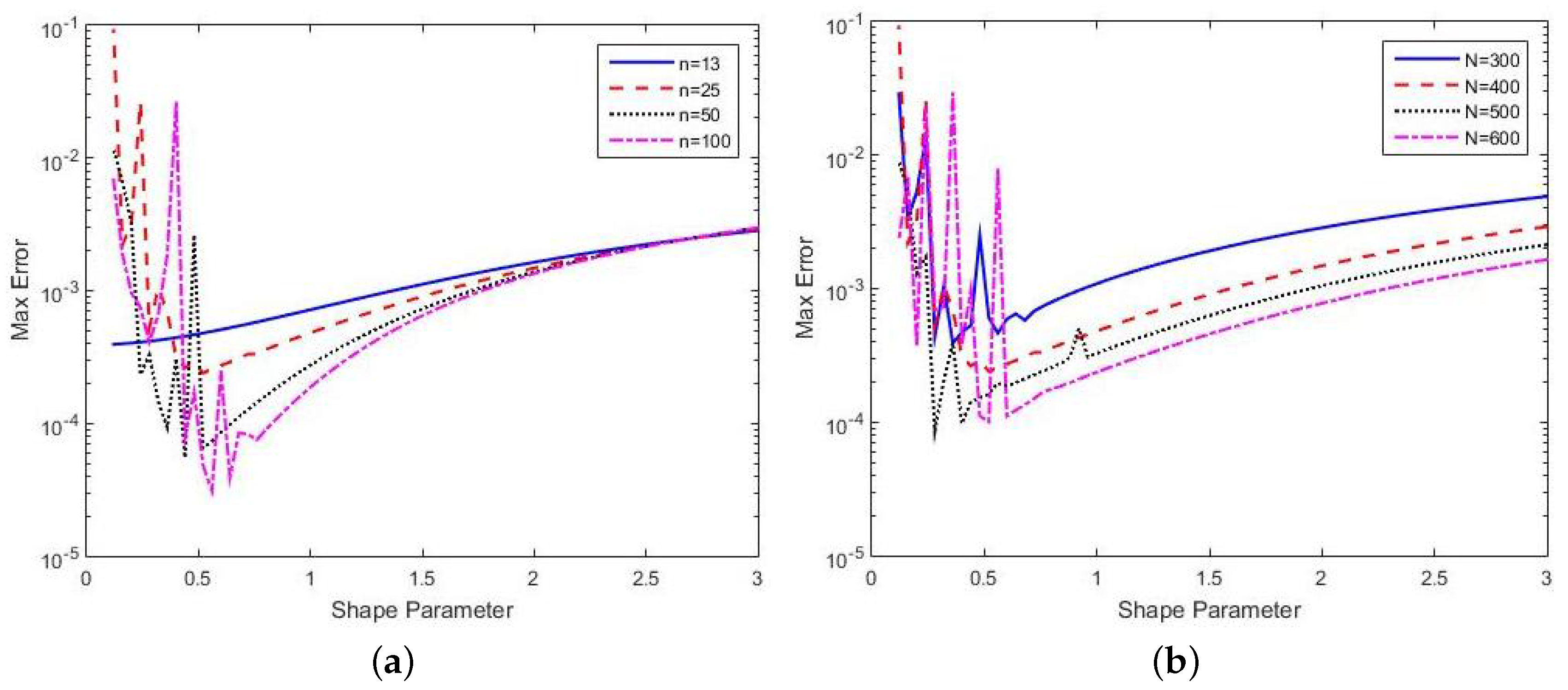
3.3. Results: A Comparison of the RBF-FD Method with Different Numbers of Nodes and Stencils
3.4. Results: A Comparison of the RBF-FD Method with Strategies on PDE and Shape Parameter
K = 0, Kmin = 1.0 × 1013, Kmax = 1.0 × 1015, shape = initial shape, increment = 0.01
while K < Kmin or K > Kmax :
form B
K = condition number of B
if K < Kmin
shape = shape - increment
elseif K > Kmax
shape = shape + increment.
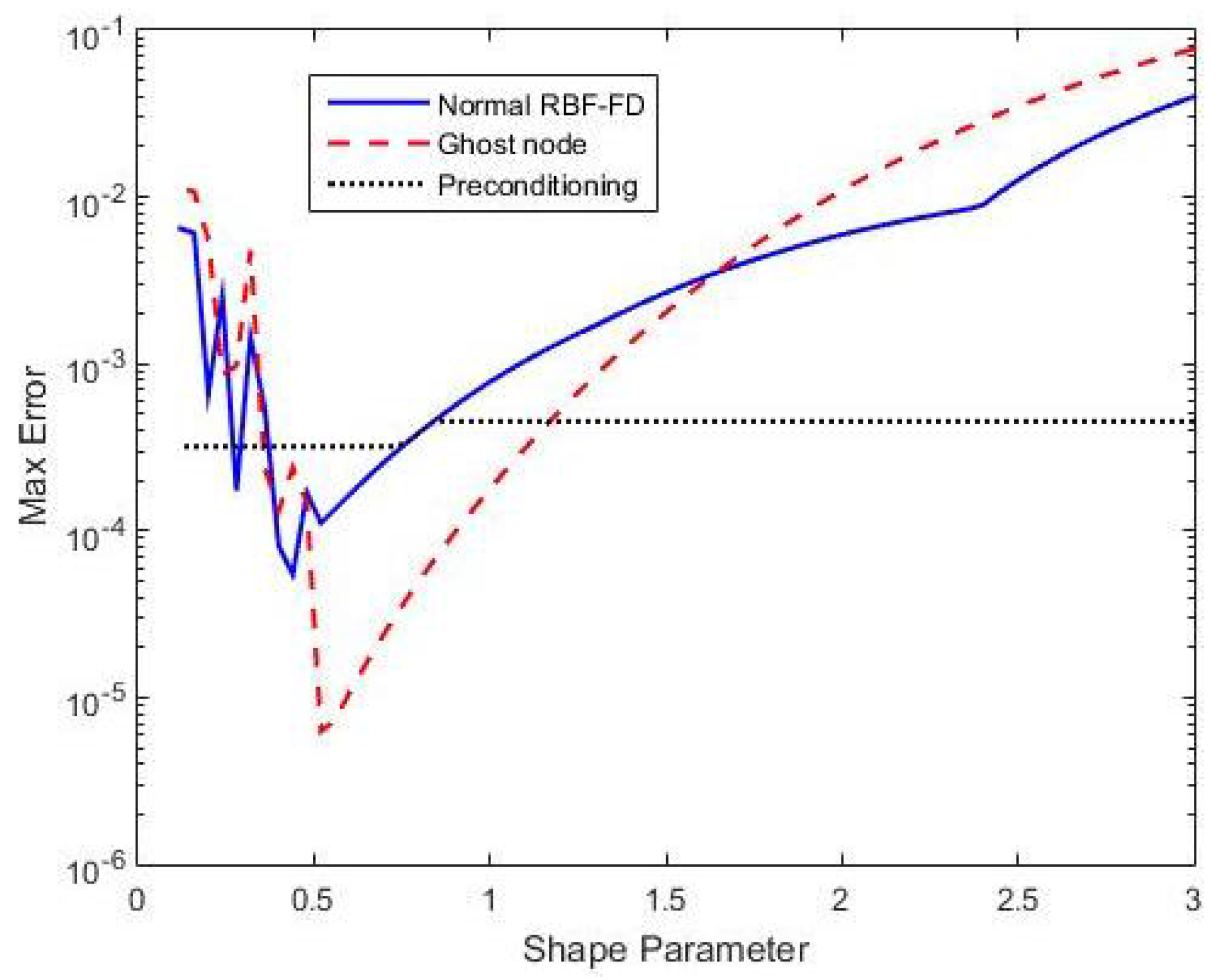
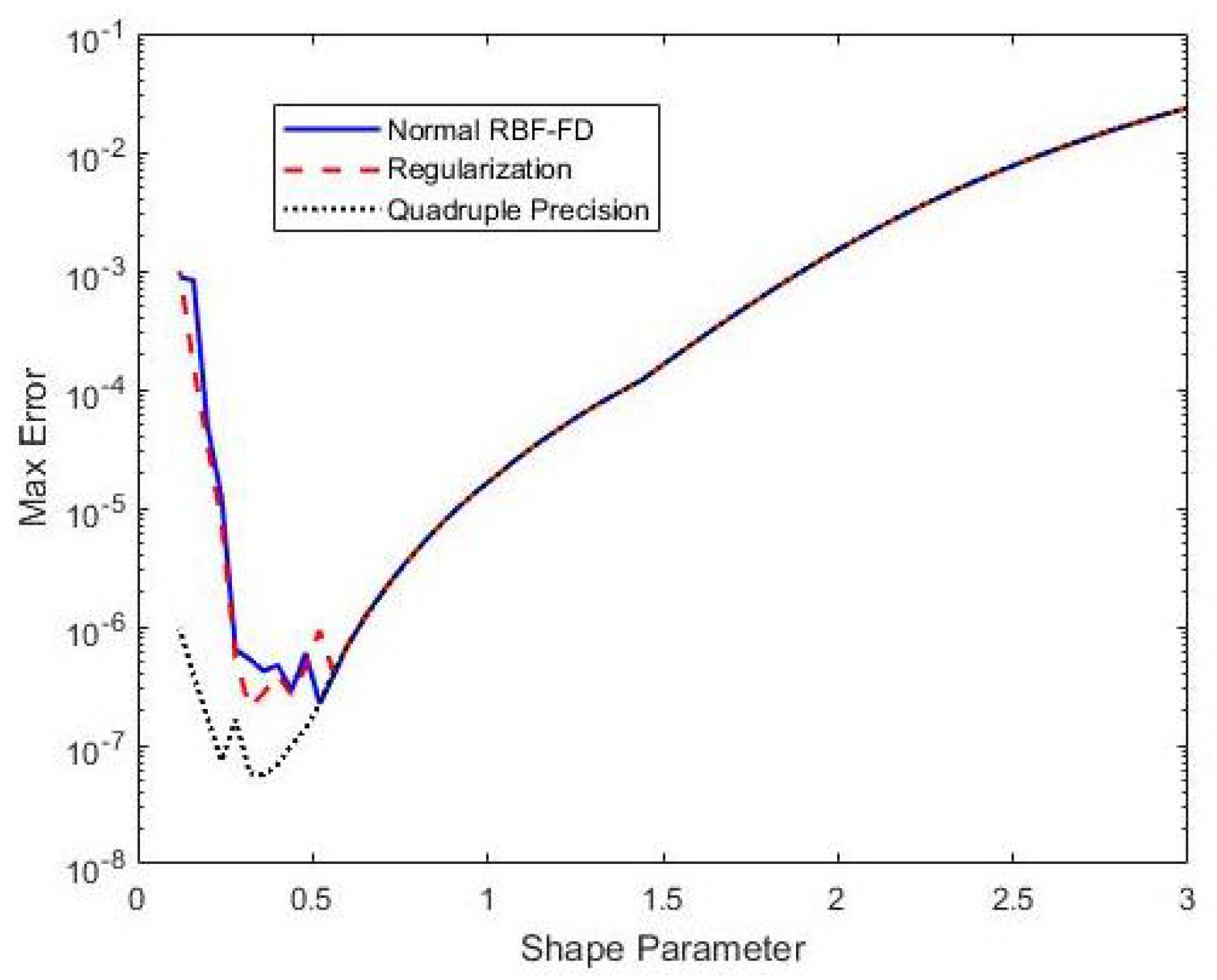
3.5. Results: A Comparison of RBF-FD Method with Additional Strategies for Reducing the Ill-Conditioning Problem
4. Future Work
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Larsson, E.; Fornberg, B. A numerical study of some radial basis function based solution methods for elliptic PDEs. Comput. Math. Appl. 2003, 46, 891–902. [Google Scholar] [CrossRef]
- Li, J.; Cheng, H.-D.; Chen, C.-S. A comparison of efficiency and error convergence of multiquadric collocation method and finite element method. Eng. Anal. Bound. Elem. 2003, 27, 251–257. [Google Scholar] [CrossRef]
- Sarra, S.A.; Kansa, E.J. Multiquadrics Radial Basis Function Approximation Methods for The Numerical Solution to Partial Differential Equations; Tech Science Press: Duluth, GA, USA, 2010. [Google Scholar]
- Fasshauer, G.E. Meshfree Approximation Methods with Matlab; World Scientific: Singapore, 2007. [Google Scholar]
- Micchelli, C. Interpolation of scattered data: Distance matrices and conditionally positive definite functions. Constr. Approx. 1986, 2, 11–22. [Google Scholar] [CrossRef]
- Hon, Y.C.; Schaback, R. On unsymmetric collocation by radial basis functions. Appl. Math. Comput. 2001, 119, 177–186. [Google Scholar] [CrossRef]
- Sarra, S.A. Radial basis function approximation methods with extended precision floating point arithmetic. Eng. Anal. Bound. Elem. 2011, 35, 68–76. [Google Scholar] [CrossRef]
- Bayona, V.; Flyer, N.; Lucas, G.M.; Baumgaertner, A.J.G. A 3-D RBF-FD solver for modeling the atmospheric global electric circuit with topography (GEC-RBFFD v1.0). Geosci. Model Dev. 2015, 8, 3007–3020. [Google Scholar] [CrossRef]
- Shan, Y.; Shu, C.; Qin, N. Multiquadric finite difference (MQ-FD) method and its application. Adv. Appl. Math. Mech. 2009, 5, 615–638. [Google Scholar]
- Tolstykh, A.I.; Lipavskii, M.V.; Shirobokov, D.A. High-accuracy discretization methods for solid mechanics. Arch. Mech. 2003, 55, 531–553. [Google Scholar]
- Tolstykh, A.I.; Shirobokov, D.A. On using radial basis functions in finite difference mode with applications to elasticity problems. Comput. Mech. 2003, 33, 68–79. [Google Scholar] [CrossRef]
- Sarra, S.A. A Local Radial Basis Function method for Advection-Diffusion-Reaction equations on complexly shaped domains. Appl. Math. Comput. 2012, 218, 9853–9865. [Google Scholar] [CrossRef]
- Hosseini, B.; Hashemi, R. Solution of Burgers’ equation using a local-RBF meshless method. Int. J. Comput. Meth. Eng. Sci. Mech. 2011, 12, 44–58. [Google Scholar] [CrossRef]
- Shankar, V.; Wright, G.B.; Fogelson, A.L.; Kirby, R.M. A radial basis function (RBF) finite difference method for the simulation of reaction-diffusion equations on stationary platelets within the augmented forcing method. Int. J. Numer. Methods Fluids 2014, 75, 1–22. [Google Scholar] [CrossRef]
- Sarra, S.A. Regularized symmetric positive definite matrix factorizations for linear systems arising from RBF interpolation and differentiation. Eng. Anal. Bound. Elem. 2014, 44, 76–86. [Google Scholar] [CrossRef]
- Wright, G.B.; Fornberg, B. Scattered node compact finite difference-type formulas generated from radial basis functions. J. Comput. Phys. 2006, 212, 99–123. [Google Scholar] [CrossRef]
- Sarra, S.A. A numerical study of the accuracy and stability of symmetric ans asymmetric RBF collocation methods for hyperbolic PDEs. Numer. Methods Partial Differ. Equ. 2008, 24, 670–686. [Google Scholar] [CrossRef]
- Sarra, S.A. The Matlab radial basis function toolbox. J. Open Res. Softw. 2017, 5, 8. [Google Scholar] [CrossRef]
- Advanpix. Multiprecision Computing Toolbox for Matlab, Version 4.4.1.12566 for 64-bit Windows. Available online: http://www.advanpix.com (accessed on 17 August 2017).

| Name of RBF | Abbreviation | Definition |
|---|---|---|
| Multiquadrics | MQ | |
| Inverse Multiquadrics | IMQ | |
| Inverse Quadratics | IQ | |
| Gaussians | GA |
| t | 5 | 10 | 15 |
|---|---|---|---|
| Max Error | 2.19 × 10 | 2.57 × 10 | 2.71 × 10 |
| Method | Max Error () |
|---|---|
| Normal RBF-FD () | 42.4 |
| Normal RBF-FD () | 4.75 |
| Normal RBF-FD () | 8.80 |
| Ghost Node (, 64 ghost nodes) | 5.63 |
| Preconditioning () | 40.5 |
| Regularization () | 38.1 |
| Extended Precision () | 6.34 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yensiri, S.; Skulkhu, R.J. An Investigation of Radial Basis Function-Finite Difference (RBF-FD) Method for Numerical Solution of Elliptic Partial Differential Equations. Mathematics 2017, 5, 54. https://doi.org/10.3390/math5040054
Yensiri S, Skulkhu RJ. An Investigation of Radial Basis Function-Finite Difference (RBF-FD) Method for Numerical Solution of Elliptic Partial Differential Equations. Mathematics. 2017; 5(4):54. https://doi.org/10.3390/math5040054
Chicago/Turabian StyleYensiri, Suranon, and Ruth J. Skulkhu. 2017. "An Investigation of Radial Basis Function-Finite Difference (RBF-FD) Method for Numerical Solution of Elliptic Partial Differential Equations" Mathematics 5, no. 4: 54. https://doi.org/10.3390/math5040054





