Next Article in Journal
Enhanced Genetic-Algorithm-Driven Triple Barrier Labeling Method and Machine Learning Approach for Pair Trading Strategy in Cryptocurrency Markets
Previous Article in Journal
On Stochastic Representations of the Zero–One-Inflated Poisson Lindley Distribution
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Mathematics
Volume 12
Issue 5
10.3390/math12050779
mathematics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Non-Newtonian Pressure-Governed Rivulet Flows on Inclined Surface

by
Sergey V. Ershkov
1,* and
Dmytro D. Leshchenko
2
1
Department of Scientific Researches, Plekhanov Russian University of Economics, Scopus Number 60030998, 36 Stremyanny Lane, 117997 Moscow, Russia
2
Odessa State Academy of Civil Engineering and Architecture, 65029 Odessa, Ukraine
*
Author to whom correspondence should be addressed.
Mathematics 2024, 12(5), 779; https://doi.org/10.3390/math12050779
Submission received: 10 February 2024 / Revised: 29 February 2024 / Accepted: 4 March 2024 / Published: 6 March 2024
(This article belongs to the Section Engineering Mathematics)
Browse Figures
Versions Notes

Abstract

:
We have generalized, in the current study, the results of research presented earlier with the aim of obtaining an approximate solution for the creeping, plane-parallel flow of viscoplastic non-Newtonian fluid where the focus is on the study of rivulet fluid flows on an inclined surface. Namely, profiles of velocity of flow have been considered to be given in the same form as previously (i.e., Gaussian-like, non-stationary solutions) but with a novel type of pressure field p. The latter has been chosen for solutions correlated explicitly with the critical maximal non-zero level of stress τs in the shared plane layer of rivulet flow, when it begins to move as viscous flow (therefore, we have considered here the purely non-Newtonian case of viscoplastic flow). Correlating phenomena such as the above stem from the equations of motion of viscoplastic non-Newtonian fluid considered along with the continuity equation. We have obtained a governing sub-system of two partial differential equations of the first order for two functions, p and τs. As a result, a set of new semi-analytical solutions are presented and graphically plotted.

1. Introduction, the Basic Model

During field observations and experimental studies of the motions of Newtonian and non-Newtonian fluids, flows in the form of rivulets are often recorded [1,2,3,4,5,6,7]. Rivulet flows can manifest themselves both as an independent (main) hydrodynamical flow and as a secondary flow due to the loss of hydrodynamic stability [7,8,9,10,11,12,13,14,15].
The simplest rivulet currents obviously include the classical Couette, Poiseuille, and Nusselt flows. These flows of a viscous incompressible Newtonian fluid are described by exact solutions of the Navier–Stokes equations. One review announced a generalization of the classical exact solutions of the Newtonian hydrodynamic equations from one-dimensional flows to three-dimensional fluid flows [16]. Even in this Newtonian case, finding exact or semi-analytical solutions is a difficult task.
When the non-Newtonian rheology of the liquid is taken into account, non-linear properties begin to appear, which are caused by the properties of the material. In non-Newtonian fluids, viscosity dependent in general case on strain rate is known to be changed due to the non-linear dynamical properties of the medium inside the fluid’s layer, which experiences a transition phase becoming either more liquid or more solidified. In this case, the hydrodynamical equations become even more difficult to solve analytically. The complexity of integrating the equations of motion with partial derivatives can explain the rather small number of scientific papers with analytical approach describing the rivulet flows of non-Newtonian fluids.
In the current research, a particular class of semi-analytical solutions is proposed, allowing a study of the structure of hydrodynamic fields for plane-parallel rivulet flows, taking into account gravity (and additionally the dynamic Marangoni effect [17] if required in a particular engineering problem). This made it possible to identify new directions for future research. In this article, plane-parallel flows with a non-zero threshold for plasticity are investigated. The flow of a non-Newtonian fluid is realized on an inclined surface with a change in pressure field. A family of velocities is used in a form of Gaussian-type functions for each component [17] but with a much larger choice of analytical and semi-analytical solutions for the pressure field. Thus, this article provides a generalization of flow of a non-Newtonian fluid of the Poiseuille and Nusselt types for a two-dimensional velocity field.
According to [17,18,19,20], the system of Equations (1)–(3) that governs the dynamics for a particular family of viscoplastic rivulet flows (in general, a Bingham fluid if plasticity effect of flow is also taken into account) should be presented in a 2D case in the Cartesian coordinates, according to the approach suggested earlier in [17,18,19].
We will investigate here the novel family of solutions where non-zero plasticity effect for the flow field is also taken into account (more general solutions than those investigated previously in [17,19,20] for the case of absence of plasticity effect). This implies that we will consider the profiles of flow velocity in Equations (1)–(3), which are given by formulae suggested in [19] for solutions (here and below we have chosen ( 8 μ ρ )   = 1 in appropriate units of scaling in the physical sense), but with a novel type of pressure field p chosen for such solutions
{ v x = ( 8 μ ρ ) 4 π   ( 2 μ ρ )   t exp ( − y 2 4   ( 2 μ ρ )   t ) , v y = ( 8 μ ρ ) 4 π   ( 2 μ ρ )   t exp ( − x 2 4   ( 2 μ ρ )   t ) ,          
where vx is the component of rivulet velocity in the Ox-direction; vy is the component of rivulet velocity in the Oy-direction; μ is the coefficient of rivulet flow’s dynamic viscosity (which is supposed to be locally constant); and ρ is the constant density of rivulet flow.
In addition, let us clarify that in the current study, we will consider (as previously in [17]) only the Cauchy problem in the whole space for which we suggest a Gaussian-like profile for both velocity components (1) (which are proved in [19] to satisfy the continuity equation). This is with the aim to retrieve the internal pressure field p (inside the rivulet flow) from Equations (2) and (3), as well as with the aim to retrieve from these aforementioned equations the variable but non-zero function for the level of flow plasticity τs (τs ≠ 0). This would definitely mean that we should investigate a purely non-Newtonian case of viscoplastic flow in our semi-analytical research.
Let us note, as previously in [19], that axis Ox coincides with the initial main direction of slowly moving advancing the front of flow on a surface which is inclined on angle α with respect to the horizontal plane. Internal dynamics of a rivulet is assumed to correspond to the simple case of plane-parallel flow, with absence of local intermixing of plane layers of a rivulet’s flow (see [17,18,19]):
ρ   ( ∂   v x ∂   t + v x ∂   v x ∂   x + v y ∂   v x ∂   y )   =   − ∂   p ∂   x   + ∂   s x x ∂   x +   ∂   s x y ∂   y   +   ρ g x , ρ   ( ∂   v y ∂   t + v x ∂   v y ∂   x + v y ∂   v y ∂   y )   =   − ∂   p ∂   y   +   ∂   s x y ∂   x − ∂   s x x ∂   y +   ρ g y   , ∂   v x ∂   x + ∂   v y ∂   y   =   0   ,   U   =   4 ( ∂   v x ∂   x ) 2 + ( ∂   v x ∂   y + ∂   v y ∂   x ) 2 ,
s x x   =   2   ( μ   +   τ s U )   ∂   v x ∂   x ,   s x y   =   2   ( μ   +   τ s U )   ( ∂   v x ∂   y + ∂   v y ∂   x )   ,       {   U   =   1 μ   ( s x x 2 + s x y 2 4 − τ s ) ,   ∂   v x ∂   x   =   s x x / 2 ( μ + τ s U ) ,
where (according to the designations in work [17]) sxx, sxy are the appropriate components of the stress tensor (due to the specificity of this type of plane-parallel flow [18], syx = sxy, syy = −sxx); {ρgx, ρgy} are volumetric components of the gravity field, where {gx, gy} = {g sinα, 0}; τs is a critical maximal level of stress in the shared plane layer of rivulet flow when it begins to move as viscous flow (we will consider here and below only the case of non-zero plasticity τs ≠ 0, i.e., the purely non-Newtonian case of viscoplastic flow).

2. Semi-Analytical Solving Procedure for Approximation of Creeping Flow

Let us consider the creeping but non-stationary [21,22,23,24] approximation of the hydrodynamical Equations (2) and (3) for 2D rivulet flow (1), according to the approach suggested earlier in [20]. Such essential simplification reduces convective terms in the left part of (2) to be approximately equal to zero due to the presence of negligible terms (for slowly moving rivulet flow) with respect to the right part of momentum Equation (2) (mainly, to the terms, associated with viscous forces). Indeed, we then obtain Equations (4) and (5) presented below.
It is worth noting that components of velocity (1) have been chosen, according to the results of [17], to satisfy Equations (4)–(6):
ρ   ∂   v x ∂   t   =   − ∂   p ∂   x   + ∂   s x x ∂   x +   ∂   s x y ∂   y   +   ρ   g sin α   , ρ   ∂   v y ∂   t   =   − ∂   p ∂   y   +   ∂   s x y ∂   x − ∂   s x x ∂   y , ∂   v x ∂   x + ∂   v y ∂   y   =   0 ,
{ s x x = 2 ( μ + τ s U ) ∂   v x ∂   x = 0 , s x y = 2 ( μ + τ s U ) ( ∂   v x ∂   y + ∂   v y ∂   x ) = 2 μ ( ∂   v x ∂   y + ∂   v y ∂   x ) + 2 τ s , U = 4 ( ∂   v x ∂   x ) 2 + ( ∂   v x ∂   y + ∂   v y ∂   x ) 2 = ( ∂   v x ∂   y + ∂   v y ∂   x ) ,
{ ρ ∂   v x ∂   t = 2 μ ∂ 2 v x ∂   y 2 , ρ ∂   v y ∂   t = 2 μ ∂ 2 v y ∂   x 2 , ∂   v x ∂   x + ∂   v y ∂   y = 0 ,     ⇒     { v x = 1 4 π   ( 2 μ ρ )   t exp ( − y 2 4   ( 2 μ ρ )   t ) ,   v y = 1 4 π   ( 2 μ ρ )   t exp ( − x 2 4   ( 2 μ ρ )   t ) .
So, we can obtain the sub-system of two partial differential equations of the 1st order for two functions, p and τs, from the two first equations of system (4) (by gradually subtracting the appropriate parts of equations of system (6))
{ 0 = − ∂   p ∂   x + 2 ∂   τ s ∂   y + ρ   g sin α , 0 = − ∂   p ∂   y + 2 ∂   τ s ∂   x ,
which determines the dependence of a critical maximal level of stress in the shared plane layer of rivulet flow when it begins to move as viscous flow (non-zero plasticity) τs on pressure p or, more generally, that one depends on the previous flow dynamics.
For example, in a simple case, if p in (7) equals to hydrostatic pressure depending on height (x·sinα) in the separate sufficiently thin layer of rivulet flow (i.e., p = ρg (x sinα) for the plane-parallel rivulet [17]), Equation (4) should be simplified to (8) below:
{ ρ ∂   v x ∂   t = 2 μ ∂ 2 v x ∂   y 2 + 2 ∂   τ s ∂   y , ρ ∂   v y ∂   t = 2 μ ∂ 2 v y ∂   x 2 + 2 ∂   τ s ∂   x .
This means, taking into account (6), that the approximation for the level of flow plasticity τs = τs (t) (τs ≠ 0) comes into play when we choose the specific realistic dynamics representing the rivulet flow within its boundaries.
We should note that the 1st and 2nd equations of system (4) are supposed to have an appropriate solution, (1) or (6) (components of velocity vx and vy), with respect to which, nevertheless, the pressure field p and the level of flow plasticity τs should be correlated by additionally using the continuity equation as shown below
    { ∂   v x ∂   x + ∂   v y ∂   y = 0 }   ⇒ 0   =   − ∂ 2 p ∂   x 2   −   ∂ 2 p ∂   y 2   + 2 ∂ 2 ( 2 μ ( ∂   v x ∂   y + ∂   v y ∂   x ) + 2 τ s ) ∂   x ∂   y ,   ⇒   Δ p   =   4 ∂ 2 τ s ∂   x ∂   y
To obtain (9), we should differentiate the 1st equation of system (4) or (7), with respect to coordinate x, and then the 2nd equation with respect to coordinate y. Then, afterwards, we should sum up these results of differentiation.
It should also be highlighted that solving the algorithm for (9) could be easier to run with the aim of obtaining the final solution for a realistic case of rivulet flow surface dynamics in engineering applications (with appropriate boundary conditions). However, untrue solutions may come through. For example, the pair of solutions {p = ρg (x sin α), τs = τs (t)} is still actual and valid in both cases (7) and (9). However, if we suggest τs = τs (t) to be a part of solution in (9) to obtain the other part of the required solution for pressure field p, the untrue solution p   ~   1 2 π ln   ( x 2 + y 2 ) could be suggested to solve (9) (it satisfies both parts of (9) but would not satisfy both parts of (7) with a chosen function τs = τs (t) for (7)). Hence, researchers should verify each solution of (9) to satisfy both parts of Equation (7), additionally.
Nevertheless, we can point out particular classes of solutions for function τs (10) which stem from (7) as well
0   =   2 ∂ 2   τ s ∂   y 2   −   2   ∂ 2   τ s ∂     x 2 ,
where the latter equation is satisfied for the partial solutions (11) pointed out below (but is not limited to them):
( 1 )   τ s   ~   x 2   +   y 2         ⇒     p   ~   4 x   ×   y   + ρ   g x sin   α ; ( 2 )   τ s   ~   sin   x   ×   sin   y     ⇒     p   ~   − 2 cos   x   ×   cos   y   +   ρ   g x sin   α ; ( 3 )     τ s   ~     cos   x   ×   cos   y       ⇒   p   ~   −   2 sin   x   ×   sin   y   +   ρ   g x sin   α .
Let us specifically note that Equation (10) is known to have its general solution in a form (12) as follows [25]:
τ s   =   f ( x + y )   +   h   ( x − y )
where {f, h} are arbitrary functions.
It is worth noting that an additional class of solutions can be presented for system (7) with constant Bernoulli-function B (which can be associated with constant hydrodynamical head of rivulet flow) where Bernoulli-function B is given by the expression below:
  B   =   1 2   ( v → 2 )   +   p   =   c o n s t   ⇒   p   =   B   −   1 2   ( v → 2 )   ,   v →   =   { v x ,   v y }

3. Discussion

Let us discuss a novel type of solution for the creeping, plane-parallel rivulet flow described by Equations (1)–(3) which generalizes the results of [17]. Namely, we have considered here profiles of velocity of flow in Equations (1)–(3), which are given below by formulae of a Gaussian type suggested in [19] for such solutions
v →     =     { v x ,   v y }     =   {   ( 8   μ ρ ) 4 π ( 2 μ ρ ) t exp   ( − y 2 4 ( 2 μ ρ ) t )   ,   ( 8   μ ρ ) 4 π ( 2 μ ρ ) t exp   ( − x 2 4 ( 2 μ ρ ) t )   }
but with a novel type of pressure field p chosen for solutions correlated explicitly with the help of (7) or (9) with a critical maximal non-zero level of stress τs in the shared plane layer of rivulet flow, when it begins to move as viscous flow. Hence, we have considered here the purely non-Newtonian cases of viscoplastic flow where the critical maximal level of stress τs depends on the previous flow history in the sense of its dynamical characterestics. Namely, few partial types have been considered:
1.
A simple case of hydrostatic pressure p depending on height (x sinα) in the separate sufficiently thin layer of rivulet flow (i.e., p = ρg(x sinα) for the plane-parallel rivulet), which corresponds via (7) to the level of flow plasticity τs = τs (t) (τs ≠ 0);
2.
Solutions (11) satisfying (7) and (10):
( 1 )       τ s   ~   x 2   +   y 2         ⇒     p   ~   4 x   ×   y   + ρ   g x sin   α ; ( 2 )   τ s   ~   sin   x   ×   sin   y       ⇒     p   ~   − 2 cos   x   ×   cos   y   +   ρ   g x sin   α ; ( 3 )   τ s   ~     cos   x   ×   cos   y       ⇒   p   ~   −   2 sin   x   ×   sin   y   +   ρ   g x sin   α ;
3.
Solutions with additional demand, still satisfying (7), but with constant Bernoulli-function B (which can be associated with the constant hydrodynamical head of rivulet flow) where Bernoulli-function B is given by the expression below:
p   =   B   −   1 2   ( v → 2 )   ,   B   =   c o n s t v →   =   { ( 8 μ ρ ) 4 π   ( 2 μ ρ )   t exp ( − y 2 4   ( 2 μ ρ )   t ) , ( 8 μ ρ ) 4 π   ( 2 μ ρ )   t exp ( − x 2 4   ( 2 μ ρ )   t ) }  
Finalizing the discussion, we should conclude that although a lot of exact solutions are known to be obtained in various hydrodynamical systems of equations [23,24], any new solution for resolving the aforementioned non-linear systems (4) and (5) of equations videlicet would be useful for practical application. As far as we know, general, analytical solutions do not exist for most cases of boundary or initial conditions for this system and the only way is to obtain some particular solutions (as, e.g., presented below in Figure 1, Figure 2 and Figure 3 for pressure p corresponding to cases (11) pointed out above):
Regarding the critical maximal level of stress τs corresponding to cases (11), pointed out above, this is presented below in Figure 4, Figure 5 and Figure 6:
It is worth noting that in the current study, we have generalized the results of research presented in [17]. Finally, let us outline restrictions on the range of applicability of the presented approach. Among these restricting assumptions are the constancy of the coefficient μ of rivulet flow’s dynamic viscosity (which should in reality depend on heat exchange inside rivulet flow between separated layers). As for discussion of the boundary conditions at the free surface of the rivulet (a key feature of any rivulet flow), in the current research, we have considered only the Cauchy problem in the whole space. It should also be mentioned that the additional driving force of the rivulet flows is surface tension (particularly, a constant surface tension for the chosen type of solutions, as reported previously in [17]).
Also, studies [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60] should be mentioned, where work [38] is perhaps the key paper on the rivulet flow of a viscoplastic fluid. Meanwhile, works [39,40,41,42,43,44,45,46,47,48] present a part of the contributions which stem from the large body of work on Newtonian and non-Newtonian rivulet flows carried out by Duffy and his research team in Scotland over the last couple of decades (not a complete list). In addition, handbook [25] concerns the problem under consideration, for which the theoretical basis has been described in detail, for solving a one-dimensional heat equation such as equations in (6) mentioned above. Works [61,62,63,64] describe hydrodynamical flows of incompressible couple stress or classical fluid with a constant or invariable-under-appropriate-assumptions Bernoulli function.

4. Conclusions

In the current study, we have generalized the results of research presented earlier (see [17,19,20]) but with a novel type of pressure field p chosen for solutions correlated explicitly with the critical maximal non-zero level of stress τs in the shared plane layer of rivulet flow (with help of (7) or (9)) when it begins to move as viscous flow. Therefore, we have considered here the purely non-Newtonian case of solution {p, v →   =   { v x ,   v y } } of viscoplastic flow (1), which exactly satisfies the equations of motion (2) and (3) along with the continuity equation.
With the aim of obtaining an approximate solution for the creeping, plane-parallel flow of viscoplastic non-Newtonian fluid where the attention is focused on the study of rivulet fluid flows (4)–(5) on inclined surface, the profiles of velocity of flow have been considered to be given in the same form (1) as previously (i.e., Gaussian-like, non-stationary solutions).
These are proven to satisfy the continuity equation as well as momentum Equations (2) and (3). Profile of pressure has been chosen in a form (11) or (13) correlating to the obtained governing sub-system (7) (stemming from alma-mater system (2) and (3) or (4) and (5)) of two partial differential equations of the first order for two functions, p and τs. Thus, a novel class of semi-analytical solutions for the nonlinear system, describing the rivulet flow of viscoplastic fluid, is presented.
Let us additionally clarify that the presented profiles of velocity (1) and pressure (11) or (13) fully satisfy the equations of motion (1)–(3) or (4) and (5). These equations of motion have been formulated in book [18] earlier. Since our solutions stem from the comprehensive model presented in [18], well-known among specialists in hydrodynamics over a long period of time (one can see various types of flows presented there for different cases as well as initial or boundary conditions), they are obviously valid. To conclude, the validity is confirmed by a comprehensive model presented in [18].

5. Remarks (with Highlights)

  • Semi-analytical ansatz is developed for modeling viscoplastic rivulet flows.
  • The 2D creeping approximation for rivulet flow on inclined surface is considered.
  • An analytical model is suggested for solving equations of momentum and continuity.
  • A non-stationary solution to the system of PDEs for rivulet flow dynamics is obtained.
  • Profiles of flow velocity have been considered to be Gaussian-like solutions.
  • A non-zero critical maximal level of stress τs in the shared layer of rivulet flow is chosen.
  • Pressure field p is correlated with critical maximal non-zero level of stress τs.
  • Solutions satisfy gravity-driven rivulet flow, driven also by constant surface tension.

Author Contributions

In this research, S.V.E. was responsible for the general ansatz and the solving procedure, simple algebra manipulations, calculations, results of the article in Section 1, Section 2 and Section 3, and was also responsible for the search of approximate solutions. D.D.L. was responsible for theoretical investigations as well as for the deep survey of the literature on the problem under consideration. Both authors agreed with the results and conclusions of one another in Section 1, Section 2 and Section 3. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The data for this paper can be made available by contacting the corresponding author.

Acknowledgments

The authors are grateful to unknown esteemed reviewers for their valuable efforts and advice which have improved the structure of the article significantly. The authors are grateful to E.S. Baranovskii for his professional advice regarding the general solution of Equation (10). The authors appreciate the effort and time of E. Yu. Prosviryakov and his professional advice regarding the descriptions of the contributions of refs. [1,2,3,4,5,6,7,8,9,10] in the field of rivulet flow dynamics, formation, and stability.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Sinz, D.K.N.; Hanyak, M.; Zeegers, J.; Darhuber, A.A. Insoluble surfactant spreading along thin liquid films confined by chemical surface patterns. Phys. Chem. Chem. Phys. 2011, 13, 9768–9777. [Google Scholar] [CrossRef]
  2. Darhuber, A.A.; Chen, J.Z.; Davis, J.M.; Troian, S.M. A Study of Mixing in Thermocapillary Flows on Micropatterned Surfaces, in Transport and Mixing at the Microscale. Phil. Trans. R. Soc. Lond. A 2004, 362, 1037–1058. [Google Scholar] [CrossRef]
  3. Fraysse, N.; Homsy, G. An experimental study of rivulet instabilities in centrifugal spin coating of viscous Newtonian and non-Newtonian fluids. Phys. Fluids 1994, 6, 1491–1504. [Google Scholar] [CrossRef]
  4. Kabov, O.A. Heat transfer from a small heater to a falling liquid film. Heat Transf. Res. 1996, 27, 221–226. [Google Scholar]
  5. Kabov, O.A.; Chinnov, E.A. Heat transfer from a local heat source to a subcooled falling liquid film evaporating in a vapor-gas medium. Russ. J. Engng Thermophys. 1997, 7, 1–34. [Google Scholar]
  6. Slade, D.; Veremieiev, S.; Lee, Y.C.; Gaskell, P.H. Gravity-driven thin film flow: The influence of topography and surface tension gradient on rivulet formation. Chem. Eng. Process. 2013, 68, 7–12. [Google Scholar] [CrossRef]
  7. Scheid, B.; Oron, A.; Colinet, P.; Thiele, U.; Legros, J.C. Nonlinear evolution of nonuniformly heated falling liquid films. Phys. Fluids 2002, 14, 4130–4151. [Google Scholar] [CrossRef]
  8. Cho, H.; Chou, F. Rivulet Instability with Effect of Coriolis Force. J. Mech. 2006, 22, 221–227. [Google Scholar] [CrossRef]
  9. Brun, K.; Kurz, R. Analysis of Secondary Flows in Centrifugal Impellers. Int. J. Rotating Mach. 2005, 2005, 45–52. [Google Scholar] [CrossRef]
  10. Kalliadasis, S.; Kiyashko, A.; Demekhin, E.A. Marangoni instability of a thin liquid film heated from below by a local heat source. J. Fluid Mech. 2003, 475, 377–408. [Google Scholar] [CrossRef]
  11. Hooke, R.L. Principles of Glacier Mechanics, 2nd ed.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2005. [Google Scholar]
  12. Paterson, W.S.B. The Physics of Glaciers, 3rd ed.; Pergamon Press: Oxford, UK, 1994. [Google Scholar]
  13. Wu, Z.; Zhang, H.; Liu, S.; Ren, D.; Bai, X.; Xun, Z.; Ma, Z. Fluctuation analysis in the dynamic characteristics of continental glacier based on Full-Stokes model. Sci. Rep. 2019, 9, 20245. [Google Scholar] [CrossRef]
  14. Slade, D.R.J. Gravity-Driven Thin Liquid Films: Rivulets and Flow Dynamics. Ph.D. Thesis, School of Mechanical Engineering, The University of Leeds, Leeds, UK, 2013. Available online: https://core.ac.uk/download/pdf/20343955.pdf (accessed on 10 February 2024).
  15. Huppert, H.E. Flow and instability of a viscous current down a slope. Nature 1982, 300, 427–429. [Google Scholar] [CrossRef]
  16. Towell, G.D.; Rothfeld, L.B. Hydrodynamics of rivulet flow. AIChE J. 1966, 12, 972–980. [Google Scholar] [CrossRef]
  17. Ershkov, S.V.; Prosviryakov, E.Y.; Leshchenko, D. Marangoni-type of nonstationary rivulet-flows on inclined surface. Int. J. Non-Linear Mech. 2022, 147, 104250. [Google Scholar] [CrossRef]
  18. Klimov, D.M.; Petrov, A.G.; Georgievsky, D.V. Viscous-Plastic Flows: Dynamical Chaos, Stability, and Confusion. Moscow, Science; See There Subsection 2.2.2. 2005, p. 45. Available online: https://urait.ru/viewer/mehanika-sploshnoy-sredy-vyazkoplasticheskie-techeniya-540818 (accessed on 10 February 2024). (In Russian).
  19. Ershkov, S.V.; Leshchenko, D. Note on semi-analytical nonstationary solution for the rivulet flows of non-Newtonian fluids. Math. Methods Appl. Sci. 2022, 45, 7394–7403. [Google Scholar] [CrossRef]
  20. Ershkov, S.V.; Leschenko, D.D. Revisiting glacier dynamics for stationary approximation of plane-parallel creeping flow. Math. Model. Eng. Probl. 2021, 8, 721–726. [Google Scholar] [CrossRef]
  21. Ershkov, S.V. Non-stationary creeping flows for incompressible 3D Navier–Stokes equations. Eur. J. Mech. B/Fluids 2017, 61, 154–159. [Google Scholar] [CrossRef]
  22. Ershkov, S.V.; Shamin, R.V. On a new type of solving procedure for Laplace tidal equation. Phys. Fluids 2018, 30, 127107. [Google Scholar] [CrossRef]
  23. Ershkov, S.V.; Shamin, R.V. A Riccati-type solution of 3D Euler equations for incompressible flow. J. King Saud Univ. Sci. 2020, 32, 125–130. [Google Scholar] [CrossRef]
  24. Ershkov, S.V.; Christianto, V.; Shamin, R.V.; Giniyatullin, A.R. About analytical ansatz to the solving procedure for Kelvin-Kirchhoff equations. Eur. J. Mech. B/Fluids 2020, 79, 87–91. [Google Scholar] [CrossRef]
  25. Petrovskii, I.G. Partial Differential Equations; W. B. Saunders Co.: Philadelphia, PA, USA, 1967. [Google Scholar]
  26. Farina, A.; Fusi, L.; Mikelić, A.; Saccomandi, G.; Sequeira, A.; Toro, E.F. Non-Newtonian Fluid Mechanics and Complex Flows; Farina, A., Mikelić, A., Rosso, F., Eds.; Springer International Publishing: Cham, Switzerland, 2018; 300p. [Google Scholar]
  27. Baranovskii, E.S. Optimal boundary control of nonlinear-viscous fluid flows. Sb. Math. 2020, 211, 505–520. [Google Scholar] [CrossRef]
  28. Baranovskii, E.S.; Artemov, M.A. Model for Aqueous Polymer Solutions with Damping Term: Solvability and Vanishing Relaxation Limit. Polymers 2022, 14, 3789. [Google Scholar] [CrossRef] [PubMed]
  29. Astarita, G.; Marucci, G. Principles of Non-Newtonian Fluid Hydromchanics; McGraw Hill: Maidenhead, UK, 1974. [Google Scholar]
  30. Pavlovskii, V.A. On the theoretical description of weak water solutions of polymers. Dokl. Akad. Nauk SSSR 1971, 200, 809–812. [Google Scholar]
  31. Burmistrova, O.A.; Meleshko, S.V.; Pukhnachev, V.V. Exact solutions of boundary layer equations in polymer solutions. Symmetry 2021, 13, 2101. [Google Scholar] [CrossRef]
  32. Ladyzhenskaya, O.A. On the global unique solvability of some two-dimensional problems for the water solutions of polymers. J. Math. Sci. 2000, 99, 888–897. [Google Scholar] [CrossRef]
  33. Baranovskii, E.S. Global solutions for a model of polymeric flows with wall slip. Math. Methods Appl. Sci. 2017, 40, 5035–5043. [Google Scholar] [CrossRef]
  34. Baranovskii, E.S.; Artemov, M.A. Optimal control for a nonlocal model of non-Newtonian fluid flows. Mathematics 2021, 9, 275. [Google Scholar] [CrossRef]
  35. Baranovskii, E.S. Feedback optimal control problem for a network model of viscous fluid flows. Math. Notes 2022, 112, 26–39. [Google Scholar] [CrossRef]
  36. Baranovskii, E.S. Flows of a polymer fluid in domain with impermeable boundaries. Comput. Math. Math. Phys. 2014, 54, 1589–1596. [Google Scholar] [CrossRef]
  37. Baranovskii, E.S. An optimal boundary control problem for the motion equations of polymer solutions. Sib. Adv. Math. 2014, 24, 159–168. [Google Scholar] [CrossRef]
  38. Wilson, S.K.; Duffy, B.R.; Ross, A.B. On the gravity-driven draining of a rivulet of viscoplastic material down a slowly varying substrate. Phys. Fluids 2002, 14, 555–571. [Google Scholar] [CrossRef]
  39. Wilson, S.K.; Duffy, B.R.; Hunt, R. A slender rivulet of a power-law fluid driven by either gravity or a constant shear stress at the free surface. Q. J. Mech. Appl. Math. 2002, 55, 385–408. [Google Scholar] [CrossRef]
  40. Yatim, Y.M.; Wilson, S.K.; Duffy, B.R. Unsteady gravity-driven slender rivulets of a power-law fluid. J. Non-Newt. Fluid Mech. 2010, 165, 1423–1430. [Google Scholar] [CrossRef]
  41. Yatim, Y.M.; Duffy, B.R.; Wilson, S.K.; Hunt, R. Similarity solutions for unsteady gravity-driven slender rivulets. Q. J. Mech. Appl. Math. 2011, 64, 455–480. [Google Scholar] [CrossRef]
  42. Yatim, Y.M.; Duffy, B.R.; Wilson, S.K. Similarity solutions for unsteady shear-stress-driven flow of Newtonian and power-law fluids: Slender rivulets and dry patches. J. Eng. Math. 2012, 73, 53–69. [Google Scholar] [CrossRef]
  43. Paterson, C.; Wilson, S.K.; Duffy, B.R. Pinning, de-pinning and re-pinning of a slowly varying rivulet. Eur. J. Mech. B/Fluids 2013, 41, 94–108. [Google Scholar] [CrossRef]
  44. Al Mukahal, F.H.H.; Duffy, B.R.; Wilson, S.K. A rivulet of a power-law fluid with constant contact angle draining down a slowly varying substrate. Phys. Fluids 2015, 27, 052101. [Google Scholar] [CrossRef]
  45. Al Mukahal, F.H.H.; Wilson, S.K.; Duffy, B.R. A rivulet of a power-law fluid with constant width draining down a slowly varying substrate. J. Non-Newt. Fluid Mech. 2015, 224, 30–39. [Google Scholar] [CrossRef]
  46. Al Mukahal, F.H.H.; Duffy, B.R.; Wilson, S.K. Advection and Taylor-Aris dispersion in rivulet flow. Proc. Roy. Soc. A 2017, 473, 20170524. [Google Scholar] [CrossRef] [PubMed]
  47. Al Mukahal, F.H.H.; Duffy, B.R.; Wilson, S.K. Rivulet flow of generalized Newtonian fluids. Phys. Rev. Fluids 2018, 3, 083302. [Google Scholar] [CrossRef]
  48. Alshaikhi, A.S.; Wilson, S.K.; Duffy, B.R. Rivulet flow over and through a permeable membrane. Phys. Rev. Fluids 2021, 6, 104003. [Google Scholar] [CrossRef]
  49. Wang, M.; Zhao, J.; Duan, R. Rivulet formulation in the flow of film down a uniformly heated vertical substrate. Eng. Appl. Comput. Fluid Mech. 2019, 13, 396–416. [Google Scholar] [CrossRef]
  50. Fedotkin, I.M.; Mel’nichuk, G.A.; Koval’, F.F.; Klimkin, E.V. Hydrodynamics of rivulet flow on a vertical surface. J. Eng. Phys. 1984, 46, 9–14. [Google Scholar] [CrossRef]
  51. Schmuki, P.; Laso, M. On the stability of rivulet flow. J. Fluid Mech. 1990, 215, 125–143. [Google Scholar] [CrossRef]
  52. Bentwich, M.; Glasser, D.; Kern, J.; Williams, D. Analysis of rectilinear rivulet flow. AIChE J. 2004, 22, 772–779. [Google Scholar] [CrossRef]
  53. Myers, T.G.; Liang, H.X.; Wetton, B. The stability and flow of a rivulet driven by interfacial shear and gravity. Int. J. Non-Linear Mech. 2004, 39, 1239–1249. [Google Scholar] [CrossRef]
  54. Drenckhan, W.; Gatz, S.; Weaire, D. Wave patterns of a rivulet of surfactant solution in a Hele-Shaw cell. Phys. Fluids 2004, 16, 3115–3121. [Google Scholar] [CrossRef]
  55. Weiland, R.H.; Davis, S.H. Moving contact lines and rivulet instabilities. Part 2. Long waves on flat rivulets. J. Fluid Mech. 2006, 107, 261. [Google Scholar] [CrossRef]
  56. Young, G.W.; Davis, S.H. Rivulet instabilities. J. Fluid Mech. 2006, 176, 1. [Google Scholar] [CrossRef]
  57. Doniec, A. Laminar flow of a liquid rivulet down a vertical solid surface. Can. J. Chem. Eng. 2009, 69, 198–202. [Google Scholar] [CrossRef]
  58. Pukhnachev, V.V. Capillary/Gravity Film Flows on the Surface of a Rotating Cylinder. J. Math. Sci. 2005, 130, 4871–4883. [Google Scholar] [CrossRef]
  59. Singh, R.K.; Galvin, J.E.; Sun, X. Three-dimensional simulation of rivulet and film flows over an inclined plate: Effects of solvent properties and contact angle. Chem. Eng. Sci. 2016, 142, 244–257. [Google Scholar] [CrossRef]
  60. Aktershev, S.; Alekseenko, S.; Bobylev, A. Waves in a rivulet falling down an inclined cylinder. AIChE J. 2020, 67, e17002. [Google Scholar] [CrossRef]
  61. Ershkov, S.V.; Prosviryakov, E.Y.; Artemov, M.A.; Leshchenko, D.D. Non-Stationary Helical Flows for Incompressible Couple Stress Fluid. Mathematics 2023, 11, 4999. [Google Scholar] [CrossRef]
  62. Korobkov, M.V. Bernoulli law under minimal smoothness assumptions. Dokl. Math. 2011, 83, 107–110. [Google Scholar] [CrossRef]
  63. Korobkov, M.V.; Pileckas, K.; Russo, R. Solvability in a finite pipe of steady-state Navier–Stokes equations with boundary conditions involving Bernoulli pressure. Calc. Var. 2020, 59, 32. [Google Scholar] [CrossRef]
  64. Stepanyants, Y.A.; Yakubovich, E.I. The Bernoulli Integral for a Certain Class of Non-Stationary Viscous Vortical Flows of Incompressible Fluid. Stud. Appl. Math. 2015, 135, 295–309. [Google Scholar] [CrossRef]
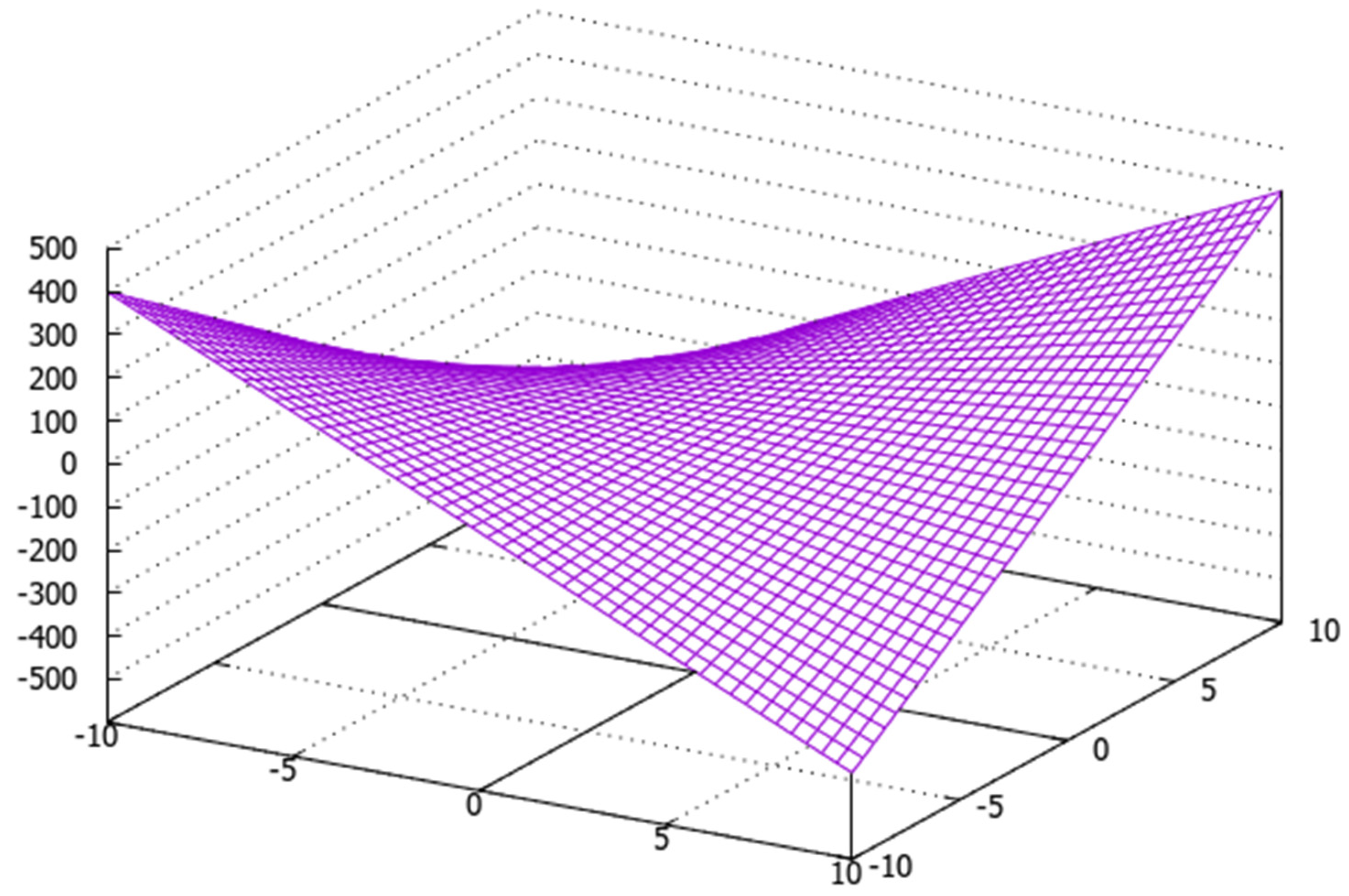
Mathematics 12 00779 g001
Figure 1. A schematic plot for pressure p = 4xy + ρgxsinα (meanings on vertical axis); meanings of {x,y} are scaled for each coordinate with respect to the appropriate horizontal axis.
Figure 1. A schematic plot for pressure p = 4xy + ρgxsinα (meanings on vertical axis); meanings of {x,y} are scaled for each coordinate with respect to the appropriate horizontal axis.
Mathematics 12 00779 g001
Mathematics 12 00779 g002
Figure 2. A schematic plot for pressure p = −2cosx cosy + ρgxsinα (meanings on vertical axis); meanings of {x,y} are scaled for each coordinate with respect to the appropriate horizontal axis.
Figure 2. A schematic plot for pressure p = −2cosx cosy + ρgxsinα (meanings on vertical axis); meanings of {x,y} are scaled for each coordinate with respect to the appropriate horizontal axis.
Mathematics 12 00779 g002
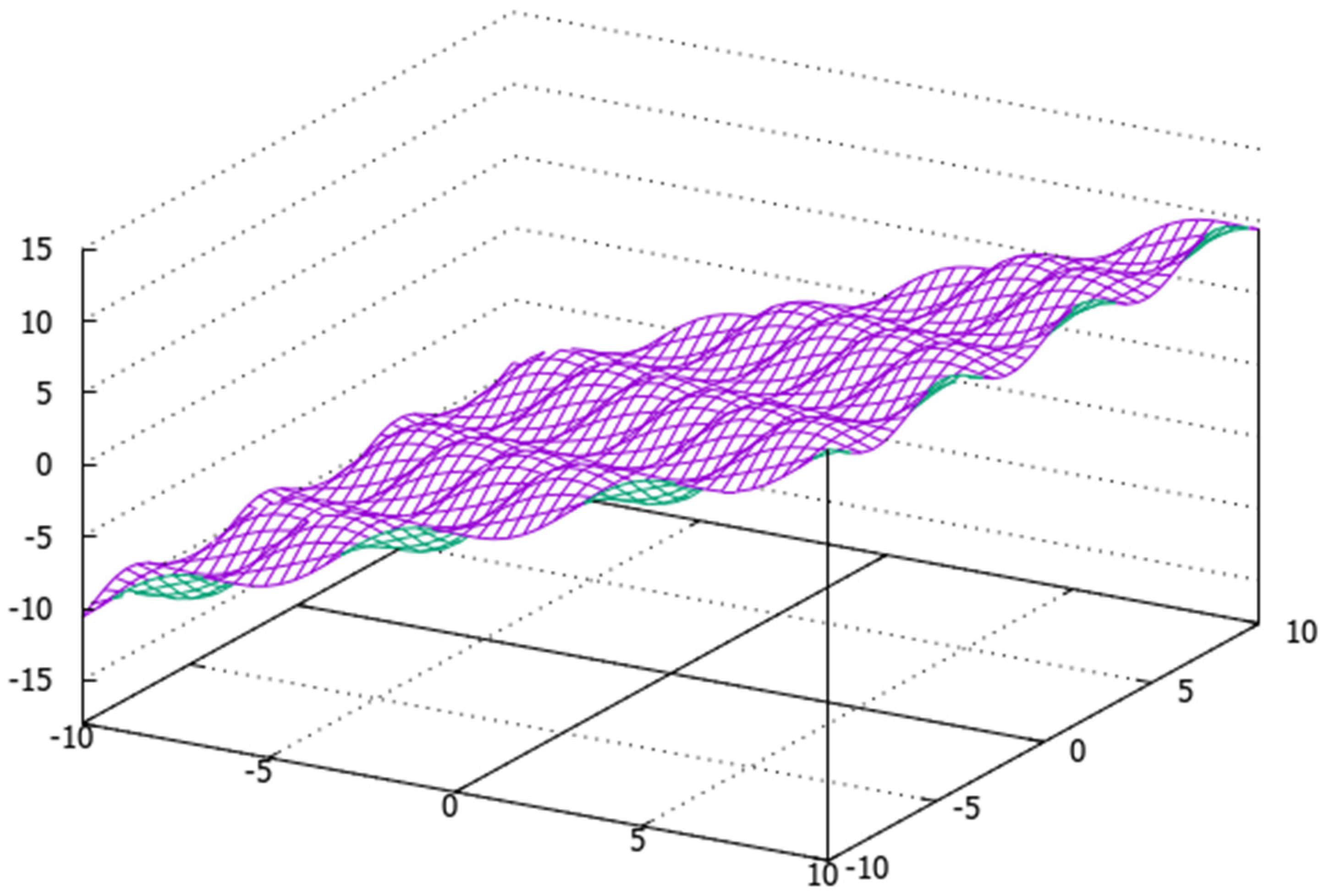
Mathematics 12 00779 g003
Figure 3. A schematic plot for pressure p = −2sinx siny + ρgxsinα (meanings on vertical axis); meanings of {x,y} are scaled for each coordinate with respect to the appropriate horizontal axis.
Figure 3. A schematic plot for pressure p = −2sinx siny + ρgxsinα (meanings on vertical axis); meanings of {x,y} are scaled for each coordinate with respect to the appropriate horizontal axis.
Mathematics 12 00779 g003
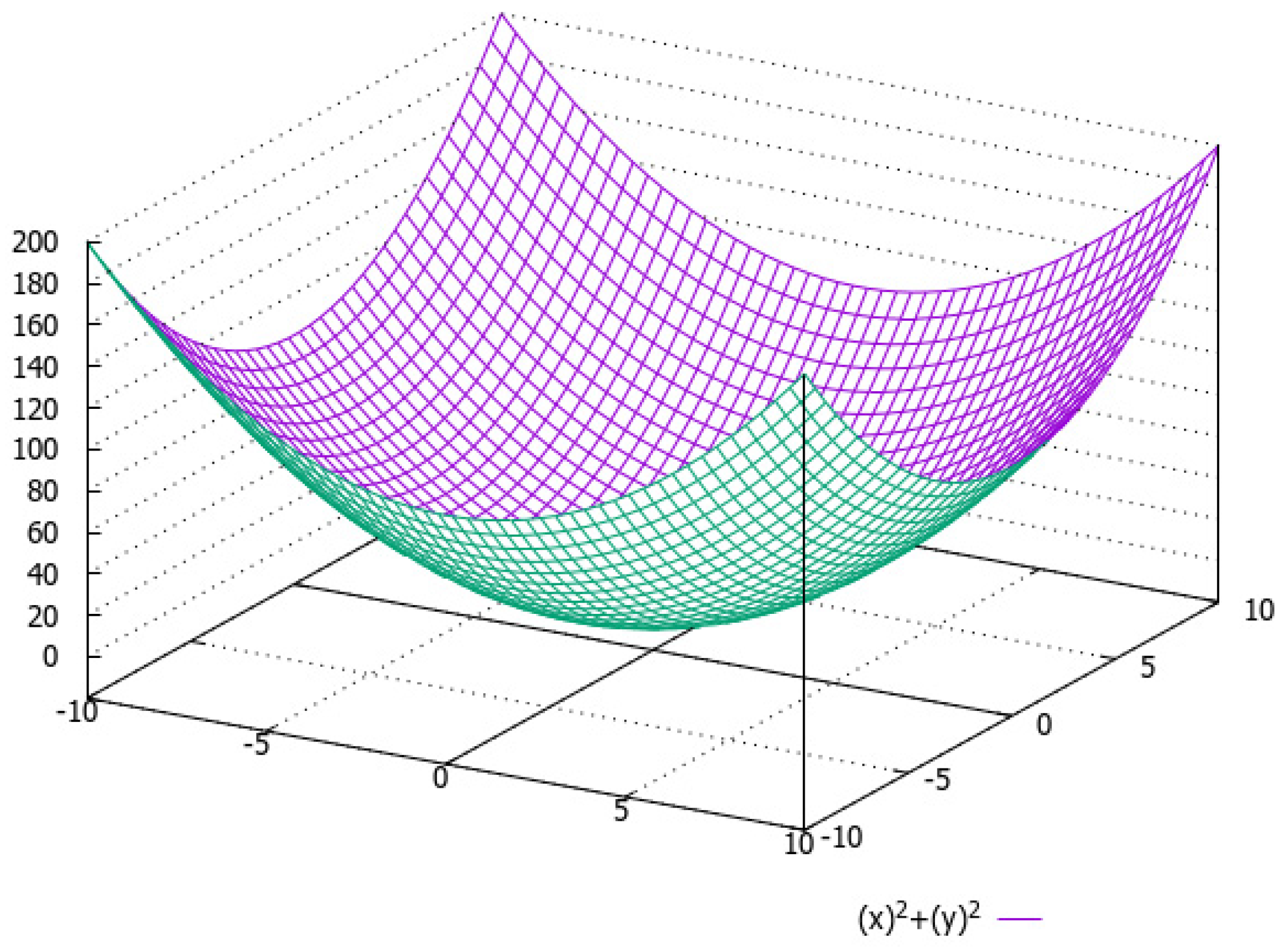
Mathematics 12 00779 g004
Figure 4. A schematic plot for the critical maximal level of stress τs = x2 + y2 (meanings on the vertical axis); meanings of {x,y} are scaled for each coordinate with respect to the appropriate horizontal axis.
Figure 4. A schematic plot for the critical maximal level of stress τs = x2 + y2 (meanings on the vertical axis); meanings of {x,y} are scaled for each coordinate with respect to the appropriate horizontal axis.
Mathematics 12 00779 g004
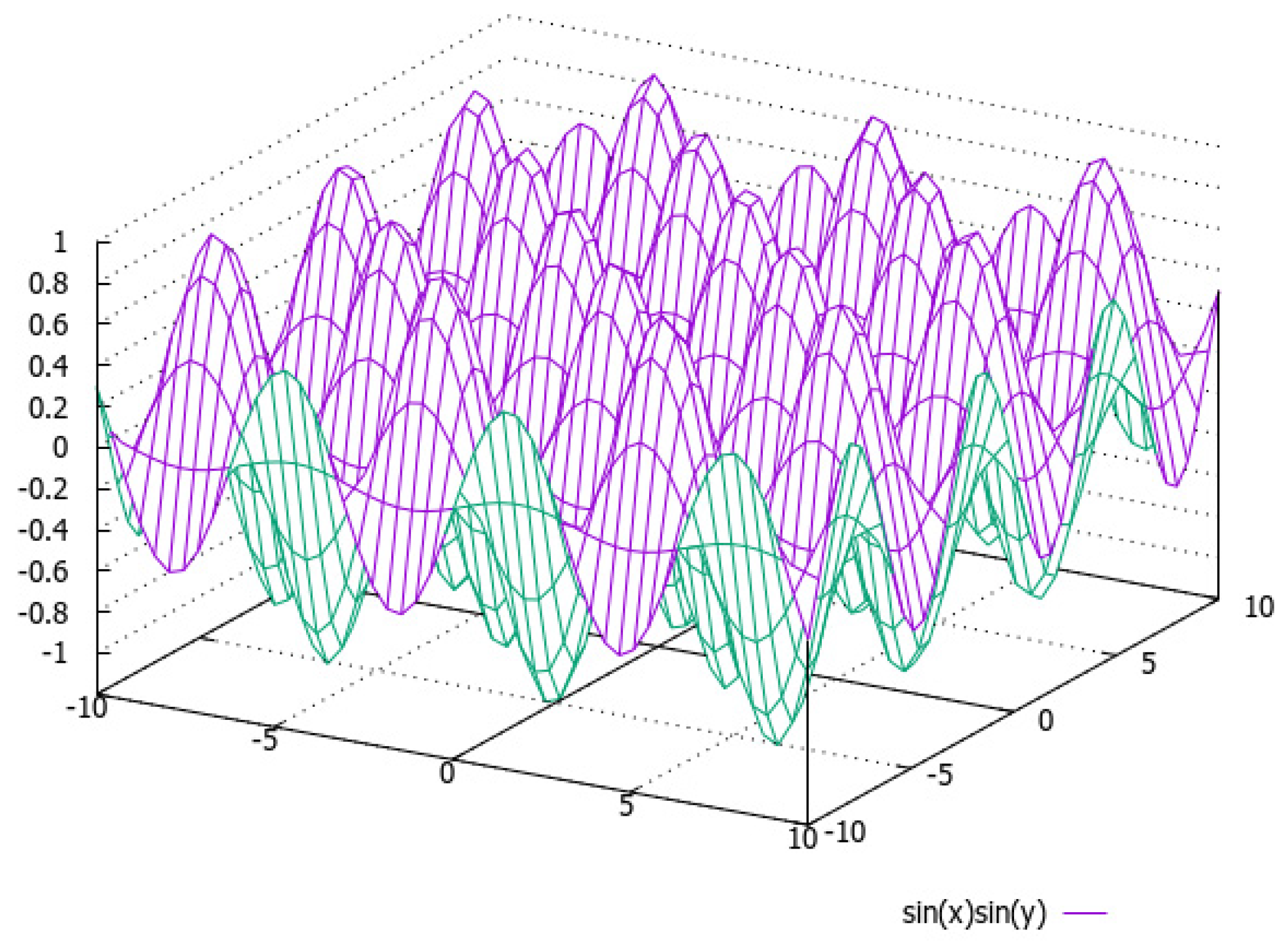
Mathematics 12 00779 g005
Figure 5. A schematic plot for the critical maximal level of stress τs = sinx siny (meanings on the vertical axis); meanings of {x,y} are scaled for each coordinate with respect to the appropriate horizontal axis.
Figure 5. A schematic plot for the critical maximal level of stress τs = sinx siny (meanings on the vertical axis); meanings of {x,y} are scaled for each coordinate with respect to the appropriate horizontal axis.
Mathematics 12 00779 g005
Mathematics 12 00779 g006
Figure 6. A schematic plot for the critical maximal level of stress τs = cosx cosy (meanings on the vertical axis); meanings of {x,y} are scaled for each coordinate with respect to the appropriate horizontal axis.
Figure 6. A schematic plot for the critical maximal level of stress τs = cosx cosy (meanings on the vertical axis); meanings of {x,y} are scaled for each coordinate with respect to the appropriate horizontal axis.
Mathematics 12 00779 g006
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Ershkov, S.V.; Leshchenko, D.D. Non-Newtonian Pressure-Governed Rivulet Flows on Inclined Surface. Mathematics 2024, 12, 779. https://doi.org/10.3390/math12050779

AMA Style

Ershkov SV, Leshchenko DD. Non-Newtonian Pressure-Governed Rivulet Flows on Inclined Surface. Mathematics. 2024; 12(5):779. https://doi.org/10.3390/math12050779

Chicago/Turabian Style

Ershkov, Sergey V., and Dmytro D. Leshchenko. 2024. "Non-Newtonian Pressure-Governed Rivulet Flows on Inclined Surface" Mathematics 12, no. 5: 779. https://doi.org/10.3390/math12050779

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop