Synchronization for Reaction–Diffusion Switched Delayed Feedback Epidemic Systems via Impulsive Control
Abstract
1. Introduction
- ♢
- For the first time, this article introduces synchronous control of switch-type infectious disease models.
- ♢
- For the first time, this article develops switching rules for infectious disease models.
- ♢
- For the first time, this article successfully derives global exponential synchronization criteria specifically for impulse reaction–diffusion infectious disease models.
2. System Description
3. Main Results
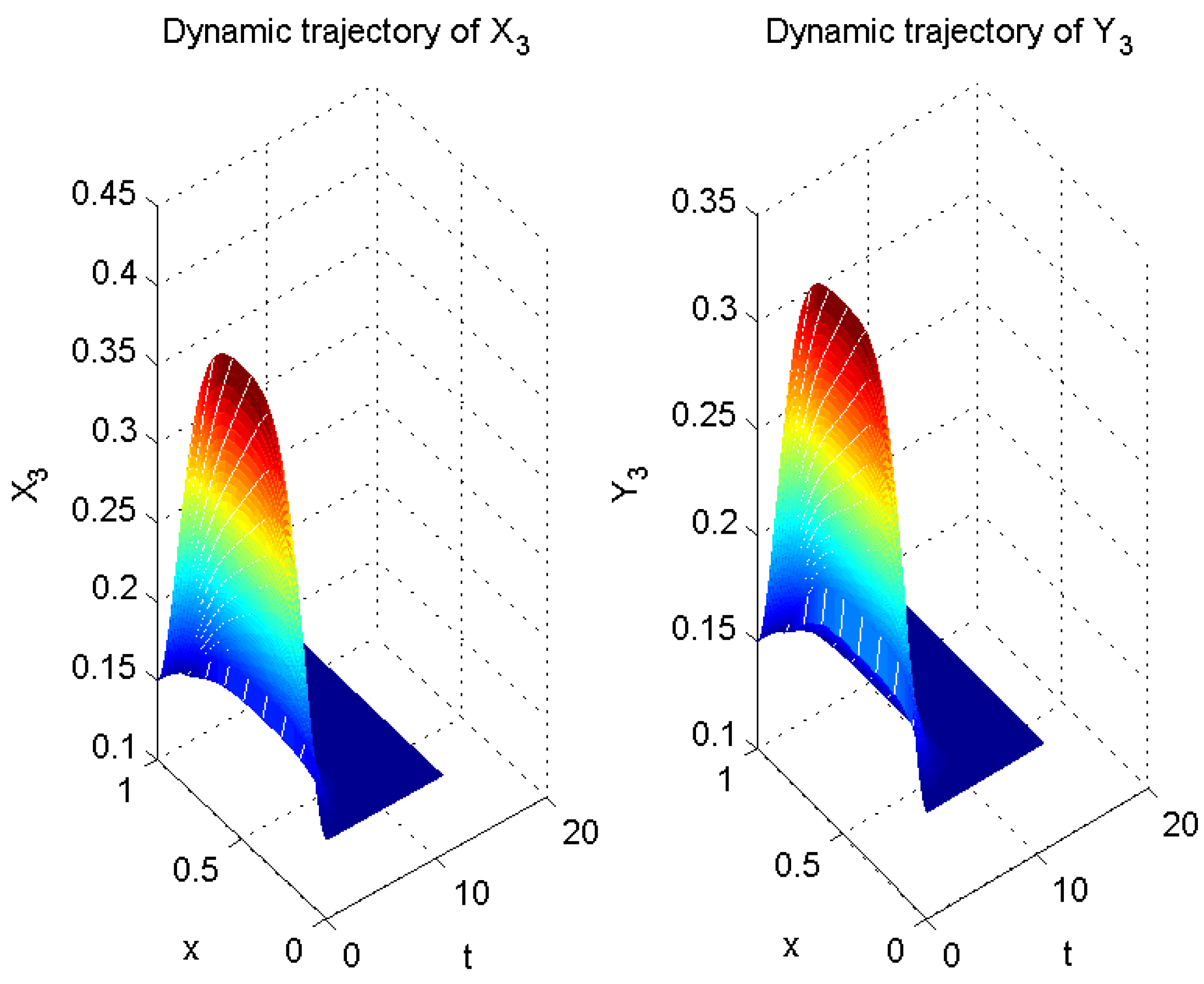
4. Numerical Example
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, L.; Wang, Z.; Zhao, X. Time periodic traveling wave solutions for a Kermack-McKendrick epidemic model with diffusion and seasonality. J. Evol. Equ. 2020, 20, 1029–1059. [Google Scholar] [CrossRef]
- Rao, R.; Lin, Z.; Ai, X.; Wu, J. Synchronization of Epidemic Systems with Neumann Boundary Value under Delayed Impulse. Mathematics 2022, 10, 2064. [Google Scholar] [CrossRef]
- Yang, Y.; Li, W.; Wu, S. Exponential stability of traveling fronts in a diffusion epidemic system with delay. Nonlinear Anal. RWA 2011, 12, 1223–1234. [Google Scholar] [CrossRef]
- Alqahtani, R.T. Mathematical model of SIR epidemic system (COVID-19) with fractional derivative: Stability and numerical analysis. Adv. Diff. Equ. 2021, 1, 2. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Yang, Y.; Zhou, Y. Global stability of an epidemic model with latent stage and vaccination. Nonlinear Anal. RWA 2011, 12, 2163–2173. [Google Scholar] [CrossRef]
- Beretta, E.; Kolmanovskii, V.; Shaikhet, L. Stability of epidemic model with time delays influenced by stochastic perturbations. Math. Comp. Simul. 1998, 45, 269–277. [Google Scholar] [CrossRef]
- Xu, R.; Ma, Z. Global stability of a SIR epidemic model with nonlinear incidence rate and time delay. Nonlinear Anal. RWA 2009, 10, 3175–3189. [Google Scholar] [CrossRef]
- Khanafer, A.; Basar, T.; Gharesifard, B. Stability of epidemic models over directed graphs: A positive systems approach. Automatica 2016, 74, 126–134. [Google Scholar] [CrossRef]
- Yi, N.; Zhang, Q.; Mao, K.; Yang, D.; Li, Q. Analysis and control of an SEIR epidemic system with nonlinear transmission rate. Math. Comput. Model. 2009, 50, 1498–1513. [Google Scholar] [CrossRef] [PubMed]
- Zaman, G.; Kang, Y.H.; Jung, I.H. Stability analysis and optimal vaccination of an SIR epidemic model. BioSystems 2008, 93, 240–249. [Google Scholar] [CrossRef]
- He, D.; Stone, L. Spatio-temporal synchronization of recurrent epidemics. Proc. Royal Soc. Lond. Ser. B Biol. Sci. 2003, 270, 1519–1526. [Google Scholar] [CrossRef] [PubMed]
- Bowong, S.; Kurths, J. Parameter estimation based synchronization for an epidemic model with application to tuberculosis in Cameroon. Phys. Lett. A 2010, 374, 4496–4505. [Google Scholar] [CrossRef]
- Ansari, S.P.; Agrawal, S.K.; Das, S. Stability analysis of fractional-order generalized chaotic susceptible-infected-recovered epidemic model and its synchronization using active control method. Pramana 2015, 84, 23–32. [Google Scholar] [CrossRef]
- Yan, G.; Fu, Z.Q.; Ren, J.; Wang, W.X. Collective synchronization induced by epidemic dynamics on complex networks with communities. Phys. Rev. E 2007, 75, 016108. [Google Scholar] [CrossRef]
- Verma, T.; Gupta, A.K. Network synchronization, stability and rhythmic processes in a diffusive mean-field coupled SEIR model. Commun. Nonlinear Sci. Numer. Simul. 2021, 102, 105927. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, Y.; Yu, L.; Liu, X. Exponential stability of delayed recurrent neural networks with Markovian jumping parameters. Phys. Lett. A 2006, 356, 346–352. [Google Scholar] [CrossRef]
- Wu, Q.; Zhou, J.; Xiang, L. Global exponential stability of impulsive differential equations with any time delays. Appl. Math. Lett. 2010, 23, 143–147. [Google Scholar] [CrossRef]
- Yang, D.; Li, X.; Song, S. Design of state-dependent switching laws for stability of switched stochastic neural networks with time-delays. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 1808–1819. [Google Scholar] [CrossRef]
- Kumar, A. Light propagation through biological tissue: Comparison between Monte Carlo simulation and deterministic models. Int. J. Biomed. Eng. Technol. 2009, 2, 344–351. [Google Scholar] [CrossRef]
- Maini, D.S.; Aggarwal, A.K. Camera position estimation using 2D image dataset. Int. J. Innov. Eng. Technol. 2018, 10, 199–203. [Google Scholar]
- Rao, R.; Huang, J.; Li, X. Stability analysis of nontrivial stationary solution and constant equilibrium point of reaction–diffusion neural networks with time delays under Dirichlet zero boundary value. Neurocomputing 2021, 445, 105–120. [Google Scholar] [CrossRef]

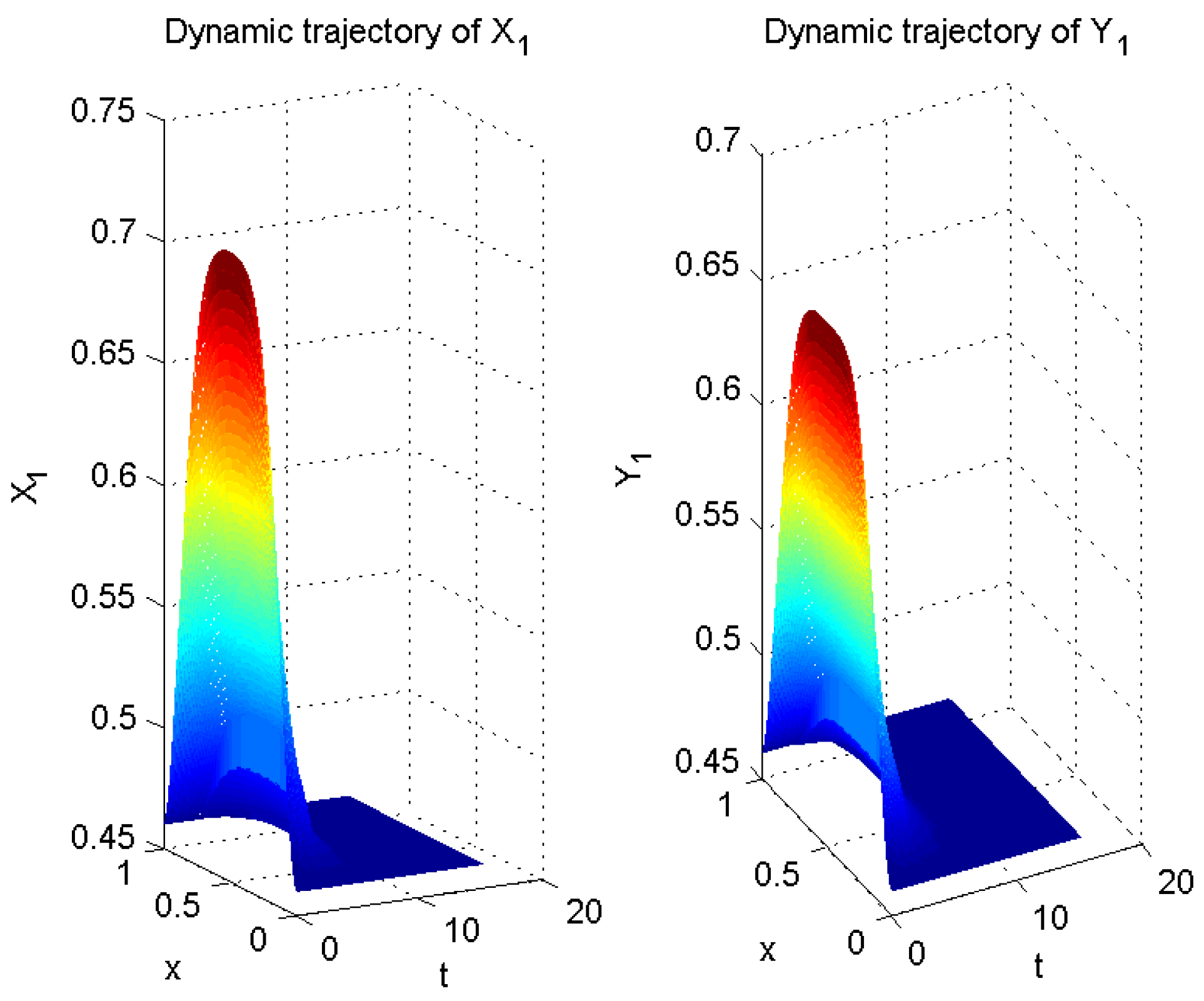
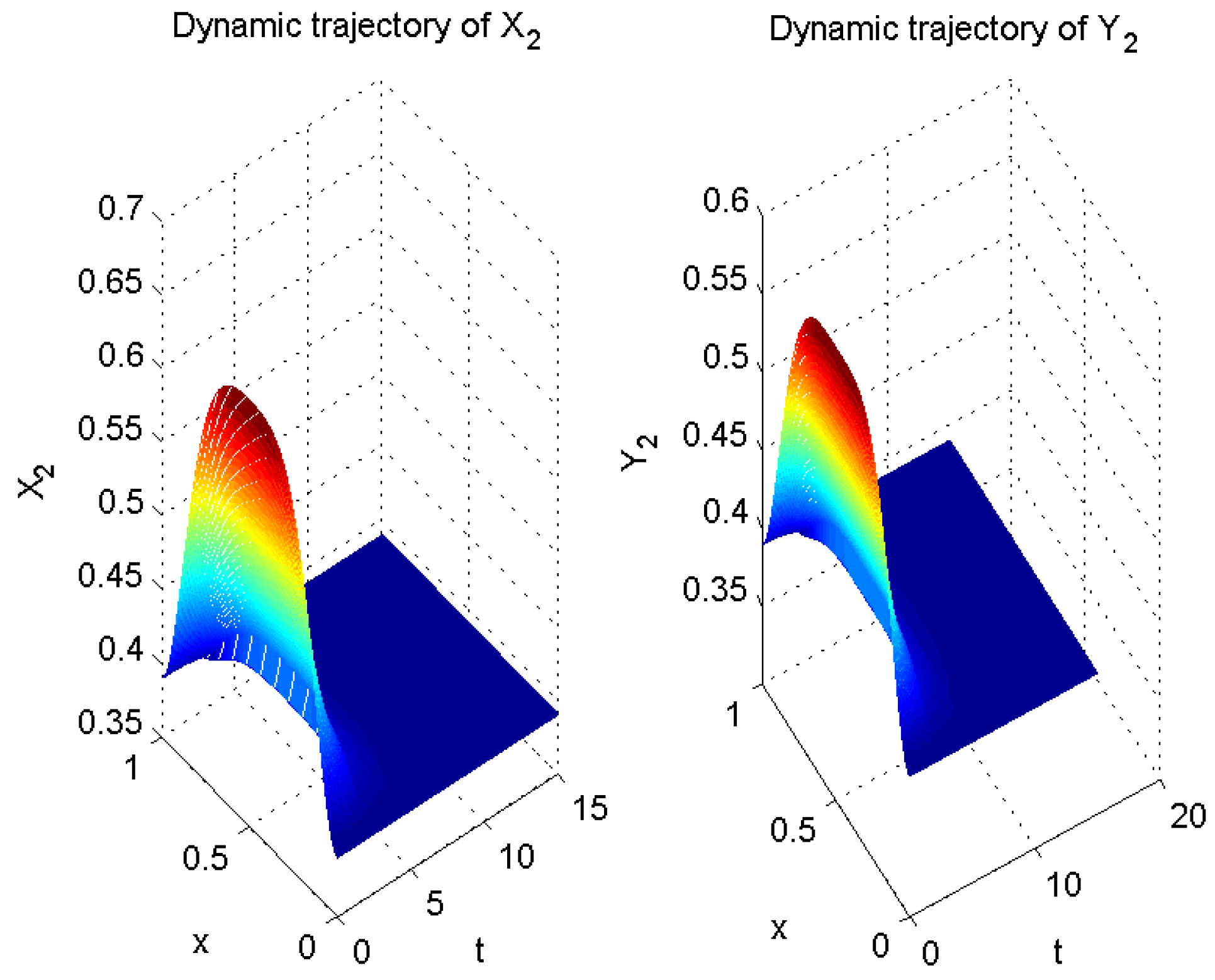
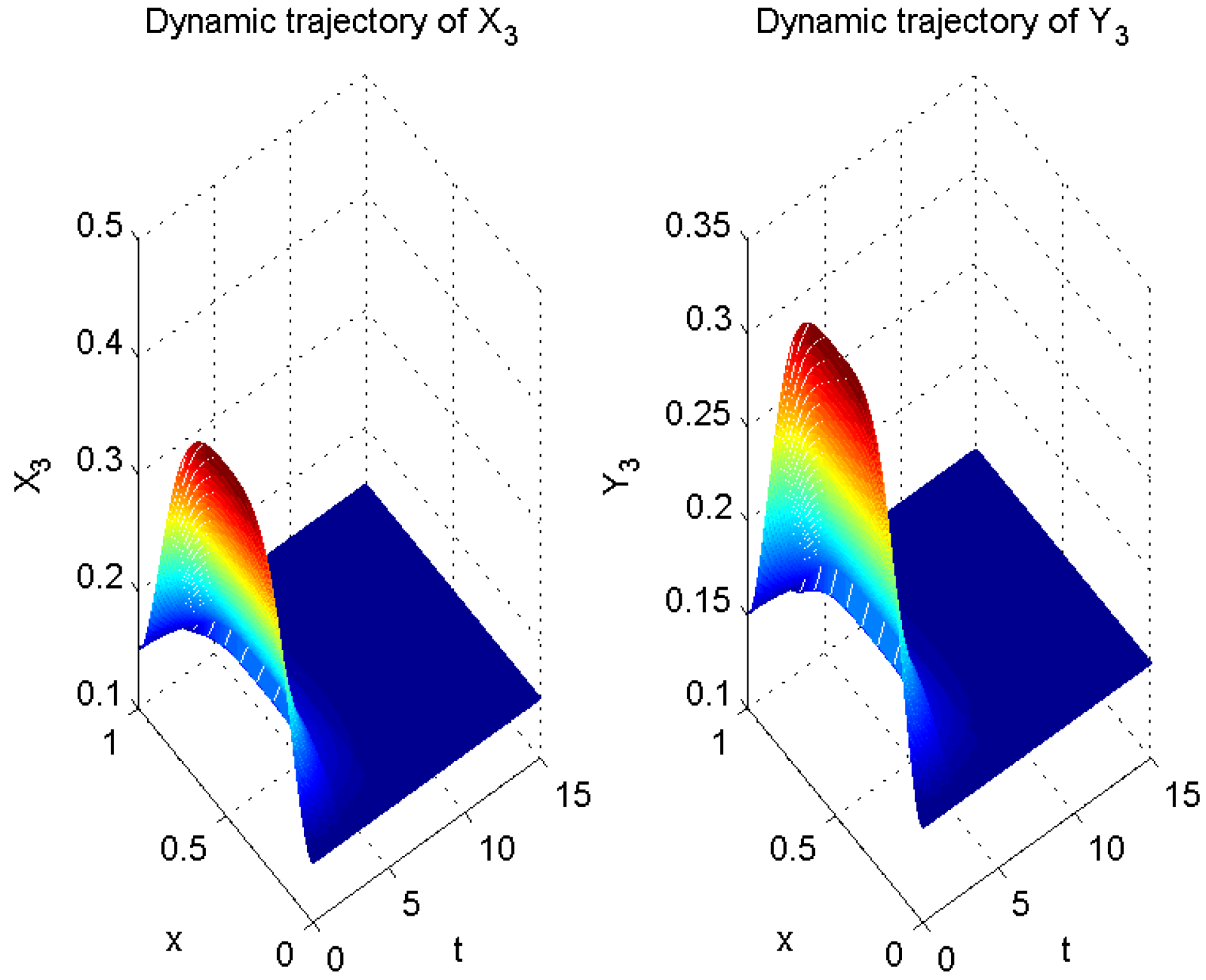
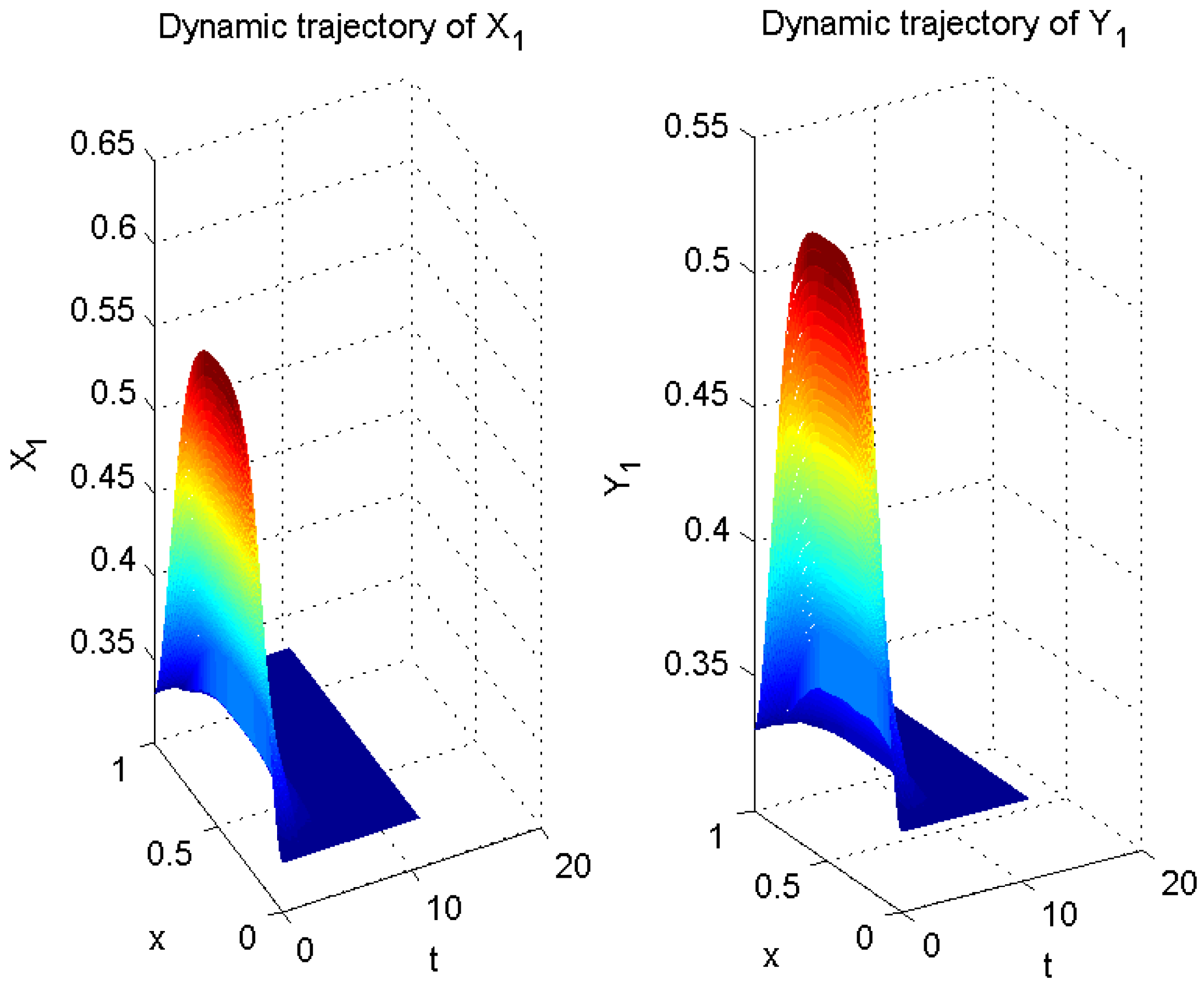

| Impulse Interval | Impulse Frequency | Impulse Intensity | Intensity Degree | Convergent Rate | |
|---|---|---|---|---|---|
| Example 1 | 0.09 | ↑ | 0.9 | ↓ | |
| Example 2 | 0.2 | ↓ | 0.5 | ↑ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rao, R.; Zhu, Q. Synchronization for Reaction–Diffusion Switched Delayed Feedback Epidemic Systems via Impulsive Control. Mathematics 2024, 12, 447. https://doi.org/10.3390/math12030447
Rao R, Zhu Q. Synchronization for Reaction–Diffusion Switched Delayed Feedback Epidemic Systems via Impulsive Control. Mathematics. 2024; 12(3):447. https://doi.org/10.3390/math12030447
Chicago/Turabian StyleRao, Ruofeng, and Quanxin Zhu. 2024. "Synchronization for Reaction–Diffusion Switched Delayed Feedback Epidemic Systems via Impulsive Control" Mathematics 12, no. 3: 447. https://doi.org/10.3390/math12030447
APA StyleRao, R., & Zhu, Q. (2024). Synchronization for Reaction–Diffusion Switched Delayed Feedback Epidemic Systems via Impulsive Control. Mathematics, 12(3), 447. https://doi.org/10.3390/math12030447







