Criteria on Exponential Incremental Stability of Dynamical Systems with Time Delay

Abstract

Incremental stability analysis for time-delay systems has attracted more and more attention for its contemporary applications in transportation processes, population dynamics, economics, satellite positions, etc. This paper researches the criteria for exponential incremental stability for time-delay systems with continuous or discontinuous right-hand sides. Firstly, the sufficient conditions for exponential incremental stability for time-delay systems with continuous right-hand sides are studied, and several corollaries for specific cases are provided. As for time-delay systems with discontinuous right-hand sides, after expounding the relevant conditions for the existence and uniqueness of the Filippov solution, by using approximation methods, sufficient conditions for exponential incremental stability are obtained. The conclusions are applied to linear switched time-delay systems and Hopfield neural network systems with composite right-hand sides.

1. Introduction

Stability analysis in mathematics mainly refers to the relevant research on the long-term performance of the dynamical system’s steady state. With more and more applications of neural networks and complex systems, the stability analysis of differential equations, including time-delay dynamical systems, has attracted more and more attention from academia and industry. Incremental stability [1,2] has been presented to be a perfect instrument for stability analysis, which is able to address problems of synchronization of coupled systems.

Incremental stability means that as time approaches infinity, the solutions of the dynamical system in different initial states will approach each other, that is, the state variables of the system with different initial states will gradually converge to the same trajectory. This property has a very wide range of applications in different fields of academia and industry. In recent years, due to the increasing potential application value in many frontier fields, such as PI-controlled missiles, Ref. [3] as well as the synchronization problem of network dynamics [4,5,6], there is already a lot of literature available on incremental stability, e.g., Refs. [7,8] provided a systematic exposition and discussion of related issues, and Ref. [3] provided specific examples of incremental stability-related applications.

In dynamical system analysis, the theoretical research on differential equations with discontinuous right-hand sides has also been highly valued because of its wide application. In some fields, such as mechanical engineering, electronic engineering, and automatic control theory, many problems rely on relevant theories of these ‘discontinuous’ differential equations [9]. Among them, switched systems, as a type of differential equation with discontinuous right-hand functions, are particularly commonly used in the field of automatic control, thus driving the development of related theories [10,11,12,13].

In 1964, Filippov [14] studied the motion of Coulomb friction oscillators and proposed a differential equation with a discontinuous right-hand side. In order to study the trajectory of the solution, ‘differential inclusion’ and set-valued mapping were introduced, and the existence and uniqueness of the solution of the discontinuous differential equation were discussed. A detailed discussion on this type of discontinuous differential equation can be found in reference [15]. Before we study the compressibility of the system, we need to first ensure the existence and uniqueness of the Carathéodory solution of the system. Filippov’s theory mainly focuses on the existence and uniqueness of the solution of the non-smooth dynamical system. The relevant conclusions have been listed in [15].

Research on time-delay differential equations first began in the early 20th century by Volterra [16,17]. The ordinary differential equations with time delay are commonly used in contemporary applications, gradually pushing the relevant theories of time-delay systems to integrity and maturity and producing rich results. There are many important achievements emerging one after another. It is worth mentioning Hale and Verduyn Lunel’s comprehensive work [18], which discussed in detail the properties of the solutions for some time-delay differential equations, e.g., uniqueness, continuous dependence of parameters, continuity and compactness of solutions, stability and invariance, etc. At the same time, some concrete analyses and methods on the properties of these solutions for time-delay systems were proposed in the literature [19,20,21,22,23], among which, Ref. [20] includes an introductory chapter that provides detailed examples of time-delay differential equations used to control computer systems, transportation processes, population dynamics, economics, satellite positions, urban transportation, and so on.

Set-valued dynamical systems, also named Filippov systems, whose right-hand sides are set-valued mappings, are widely used in these applications mentioned above. These set-valued dynamical systems are perfect instruments to represent the time-delay differential equations with discontinuous right-hand sides [20,24,25,26,27,28] or control systems with time delay [20,29,30]. Therefore, naturally, a large amount of the literature has discussed the problems along these lines. One of the most important achievements in this field is [31], in which Haddad focused on upper semicontinuous dynamics, elaborated on the existence and compactness of the solution set, and also proved the upper semicontinuity of the solution. Haddad’s work [31] is given under functional differential inclusion, where the corresponding time-delay term acts on the infinite-dimensional space of continuous functions.

In recent years, there have been many related analytical studies and achievements on the incremental stability of Filippov systems. In the case that the local Lipschisz condition is satisfied, Ref. [32] provided a sufficient condition for the local stability of Filippov solutions. Ref. [33] used the concept of Filippov solutions to analyze a class of time-delay dynamical systems with discontinuous right-hand sides. In the sense of the Filippov solution, Ref. [34] proposed the conditions for global asymptotic stability of the error system of the time-delay neural network with a discontinuous activation function. While [35] put forward an approximation method and gave the specific sufficient conditions for the exponential incremental stability of the switched system.

In this paper, first, several preliminary definitions are given in Section 2. In Section 3, we research the criteria on the exponential incremental stability of the solutions for time-delay systems with continuous right-hand sides, involving several specific cases, and relevant corollaries are provided. Then, in Section 4, under the hypothesis that the system has a unique solution, we extend the sufficient conditions for exponential incremental stability to the time-delay system with a discontinuous right-hand side in the sense of the Filippov solution by using a sequence of ‘continuous systems’ to approach the corresponding Filippov system. In this section, we also provide the conditions for the existence and uniqueness of the solution for the time-delay dynamical system before stability analysis in Section 4.1. The applications on linear switched systems and Hopfield neural network systems with time delay are given in Section 5, respectively, and corresponding numerical examples are given in Section 6.

2. Preliminaries

Here, we first introduce some primary definitions, including matrix measure and multiple norms, incremental stability property, exponential incremental stability, and so on.

Definition 1 

(Definition 1 in [35]). For any real matrix $A\in {\mathbb{R}}^{n\times n}$ and a given norm $\parallel ·\parallel$, we define the corresponding matrix measure $\nu \left(A\right)$ as

$$\begin{array}{c}\hfill \nu (A,\parallel ·\parallel )=\underset{h\to 0^{+}}{lim}\frac{\parallel I+hA\parallel -1}{h}.\end{array}$$

The matrix measure above can be considered as the one-sided directional derivative of the induced matrix norm function $\parallel ·\parallel$, evaluated at the point I, in the direction of A.

In the following parts, we will study the incremental stability property of time-delay systems under multiple norms. Here, we also list the definitions of multiple norms with subscript $\chi \left(t\right)$ and the corresponding measures. Note that the function $\chi \left(t\right)$ is a piecewise right-continuous function.

Definition 2. 

For real matrix $A\in {\mathbb{R}}^{n\times n}$ and the matrix norm ${\parallel ·\parallel }_{\chi \left(t\right)}$, (the corresponding vector measure ${|·|}_{\chi \left(t\right)}$), we here define the corresponding matrix measure ${\mu }_{\chi \left(t\right)}\left(A\right)$ as follows:

$$\begin{array}{c}\hfill {\mu }_{\chi \left(t\right)}\left(A\right)=\underset{h\to 0^{+}}{lim}\frac{{\parallel I+hA\parallel }_{\chi \left(t\right)}-1}{h}.\end{array}$$

If ${lim}_{h\to 0^{+}}{\left|x\right|}_{\chi (t+h)}$(${lim}_{h\to 0^{-}}{\left|x\right|}_{\chi (t+h)}$) exists, then we denote the right (left) limit of the norm ${|·|}_{\chi \left(t\right)}$ at time point t by ${|·|}_{\chi (t\pm )}$. We say the norm ${|·|}_{\chi \left(t\right)}$ is continuous at t, if and only if ${|·|}_{\chi (t+)}={|·|}_{\chi (t-)}={|·|}_{\chi \left(t\right)}$, that is, ${|·|}_{\chi \left(t\right)}$ is right-continuous and left-continuous as well. If there exists $D>0$, such that ${\left|x\right|}_{\chi \left(t\right)}<D{\left|x\right|}_{\chi \left(s\right)}$ holds for all $t,s\in {\mathbb{R}}^{+}$, we say ${|·|}_{\chi \left(t\right)}$ is uniformly equivalent.

Then, we extend the definition for matrix measure in the sense of multiple norms. Consider the time-varying nature of $\chi \left(t\right)$, as follows:

Definition 3 

(Definition 3 in [36]). If the following limit exists, the switched matrix measure with respect to vector norm ${|·|}_{\chi \left(t\right)}$ is defined as follows:

$${\nu }_{\chi \left(t\right)}\left(A\right)=\overline{\underset{h\to 0^{+}}{lim}}\frac{1}{h}\underset{{\left|x\right|}_{\chi \left(t\right)}=1}{sup}{\left|(I_n+hA)x\right|}_{\chi (t+h)}-1$$

where ${\displaystyle \overline{lim}}$ stands for the upper superior.

Remark 1. 

The definition of multiple matrix norms ${\parallel ·\parallel }_{\chi \left(t\right)}$ can be thought of as matrix norms induced by vector norm ${|·|}_{\chi \left(t\right)}$: for a matrix A,

$${\parallel A\parallel }_{\chi \left(t\right)}=\underset{{\left|x\right|}_{\chi \left(t\right)}=1}{sup}{\left|Ax\right|}_{\chi \left(t\right)}$$

This implies that, if $\chi \left(t\right)$ is constant over an internal $[a,a+\delta )$, then it holds that ${\nu }_{\chi \left(t\right)}\left(A\right)={\mu }_{\chi \left(t\right)}\left(A\right)$ in $[a,a+\delta )$.

According to the existence of the switched matrix measure, the definition is as follows,

Definition 4 

([36]). Define the partial differential of the switched norm ${|·|}_{\chi \left(t\right)}$ as follows,

$${\overline{\partial }}_t{\left(\right|·|}_{\chi \left(t\right)})=\overline{\underset{h\to 0^{+}}{lim}}\underset{{\left|x\right|}_{\chi \left(t\right)}=1}{sup}\frac{{\left|x\right|}_{\chi (t+h)}-1}{h}$$

If ${\overline{\partial }}_t{\left(\right|·|}_{\chi \left(t\right)})$ exists at t, we say the multiple norm ${|·|}_{\chi \left(t\right)}$ is right regular at time t.

According to the ‘right regular’ property, we have the following proposition [36]:

Proposition 1 

([36]). If the multiple norm ${|·|}_{\chi \left(t\right)}$ is right regular, then

1. 

The multiple norm ${|·|}_{\chi \left(t\right)}$ is right-continuous at time t;

2. 

${\nu }_{\chi \left(t\right)}(·)$ exists at time t.

For a clearer statement in the following part, we define a transaction function between norms ${|·|}_{\chi }$ and ${|·|}_{{\chi }^{\prime }}$,

Definition 5. 

Function $C(\chi ,{\chi }^{\prime })>0$ is the transaction function between norms ${|·|}_{\chi }$ and ${|·|}_{{\chi }^{\prime }}$, satisfying that

$${|·|}_{\chi }\le C(\chi ,{\chi }^{\prime }){|·|}_{{\chi }^{\prime }}.$$

Definition 6. 

If the function $C(\chi \left(t\right),\chi \left(t^{\prime }\right))$ is well-defined for all t and $t^{\prime }$, we say the multiple norm ${|·|}_{\chi \left(t\right)}$ is equivalent for all t.

Here, we consider the following dynamical time-delay system:

$$\left\{\begin{array}{c}\dot{x}=f(x,x_{{\tau }_1\left(t\right)},\dots ,x_{{\tau }_m\left(t\right)},r\left(t\right)),t\ge t_0\hfill \\ x\left(s\right)=\varphi \left(s\right),s\in [t_0-\overline{\tau },t_0]\hfill \end{array}\right.$$

(1)

where $x\in {\mathbb{R}}^n$, $x_{{\tau }_k\left(t\right)}=x(t-{\tau }_k\left(t\right))(k=1,\dots ,m)$ is the time-delay term, each ${\tau }_k$ is a bounded function, ${max}_{k}su{p}_{t\in [t_0,\infty )}{\tau }_k\left(t\right)=\overline{\tau }$, function $r\left(t\right):[t_0,+\infty )\to \mathbb{R}$ is an upper continuous staircase function, $f=(f_1,\dots ,f_n):{\mathbb{R}}^{n\times (m+1)}\times [t_0,+\infty )\to {\mathbb{R}}^n$. The function $\varphi (·)$ represents the initial value function, and $\varphi (·)\in C^1([t_0-\overline{\tau },t_0],{\mathbb{R}}^n)$. Let $x(t;\varphi ,r_t)$ be the solution of system (1).

Then, we will research the sufficient conditions for incremental stability for time-delay dynamical system (1), which is defined as follows.

We have the following definition for several types of incremental stability (IS):

Definition 7. 

Let $\varphi (t;t_0,x_0)$ be the solution of system (1) with the initial time $t_0$ and initial value function $x_0(·)$. If there exist a function $\beta (s,t)$ of class $\mathcal{KL}$, and some norm ${|·|}_{[t_0-\overline{\tau },t_0]}^{\infty }$ induced by vector norm $|·|$, defined as ${\left|\phi \right|}_{[t_0-\overline{\tau },t_0]}^{\infty }={sup}_{s\in [t_0-\overline{\tau },t_0]}\left|\phi \left(s\right)\right|$, such that for any initial function $x_0(·),y_0(·)$,

$$|\varphi (t+t_0;x_0,t_0)-\varphi (t+t_0;y_0,t_0)|\le \beta (|x_0-y_0{|}_{[t_0-\overline{\tau },t_0]}^{\infty },t),$$

then, we say that system (1) is Incrementally Asymptotically Stable (δAS) in the region $\Sigma \subset {\mathbb{R}}^n$. If $\beta (s,t)$ is independent of initial time t, then we say system (1) is Incrementally Uniformly Asymptotically Stable (δUAS). If function $\beta (s,t)$ is of class $\mathcal{EKL}$, then we say system (1) is Incrementally Uniformly Exponentially Asymptotically Stable (δUEAS).

Moreover, if there exists a constant M and $c>0$ such that $\beta (·,·)$ of class $\mathcal{KL}$ satisfies (2) with some norm $|·|$, then system (1) is said to be exponentially incrementally stable.

$$\beta \left(\right|x_0-y_0{|}_{[t_0-\overline{\tau },t_0]}^{\infty },t)=M{e}^{-ct}{|x_0-y_0|}_{[t_0-\overline{\tau },t_0]}^{\infty },$$

(2)

3. Contraction Theory for Time-Delay Systems

Here, we list the following hypothesis, denoted by Assumption 1, including the Carathéodory condition to guarantee the existence and uniqueness of the solution of the time-delay dynamical system (1) with a continuous right-hand side.

Assumption 1. 

Dynamical time-delay system (1) satisfies the following conditions:

1. 

$f(x,x_{{\tau }_1\left(t\right)},\dots ,x_{{\tau }_m\left(t\right)},r\left(t\right))$ is continuously differentiable with respect to x, and continuous with respect to $(x,x_{{\tau }_1\left(t\right)},\dots ,x_{{\tau }_m\left(t\right)},r)$ except for the switching time points $\{t_1,\dots ,t_j,\dots \}$.

2. 

${\tau }_k\left(t\right)$ is upper bounded and has a positive lower bound for each k, and ${max}_k{sup}_{t\in [t_0,\infty )}{\tau }_k\left(t\right)=\overline{\tau }$, ${min}_k{inf}_{t\in [t_0,\infty )}{\tau }_k\left(t\right)=\underline{\tau }$.

3. 

$f_i:{\mathbb{R}}^{n\times (m+1)}\times [t_0,+\infty )\to \mathbb{R}$$(i=1,\dots ,n)$ is locally Lipschitz.

Thus, under Assumption 1, system (1) has a unique solution. (Refer to the Reference [37] for details.)

Here, we try to research the contraction property for time-delay system (1). First, enlightened by Ref. [38], we prove the following lemma:

Lemma 1. 

Assume that ${|·|}_{\chi \left(t\right)}$ is right regular, $\chi \left(t\right)$ is a right-continuous staircase function with discontinuities in $\{t_1,\dots ,t_j,\dots \}$ and ${|·|}_{\chi \left(t\right)}\le C_0{|·|}_{\chi \left(t^{\prime }\right)}$ holds for any $t,t^{\prime }\ge t_0$. $x\left(t\right)$ is continuous, $t_0$ is the initial time, and $\overline{\tau }={max}_k{sup}_{s\ge t_0}{\tau }_k\left(s\right)$. For the following time-delay system:

$$\dot{x}\left(t\right)=A\left(t\right)x\left(t\right)+\sum _{k=1}^n{B}_k\left(t\right)x(t-{\tau }_k\left(t\right))$$

where $x\left(t\right)\in {\mathbb{R}}^n$, $A\left(t\right),B_k\left(t\right)\in {\mathbb{R}}^{n\times n}(k=1,2,\dots ,m)$ is piecewise continuous with respect to t, and the discontinuities belong to $\{t_1,t_2,\dots ,t_i,\dots \}$, which is a countable set. If there exists a piecewise right-continuous function $m\left(t\right)>0$ whose discontinuities belong to $\{t_1,t_2,\dots ,t_i,\dots \}$, and matrix-valued functions $B_k^{\left(1\right)}\left(t\right),B_k^{\left(2\right)}\left(t\right)$ such that

$${\nu }_{\chi \left(t\right)}(A\left(t\right)+\sum _{k=1}^m{B}_k^{\left(1\right)}\left(t\right))+\sum _{k=1}^m\parallel B_k^{\left(2\right)}{\left(t\right)\parallel }_{\chi \left(t\right)}\frac{m\left(t\right)}{m(t-{\tau }_k\left(t\right))}+\sum _{k=1}^m{\tau }_k\left(t\right){\parallel B_k^{\left(1\right)}\left(t\right)\parallel }_{\chi \left(t\right)}({\tilde{A}}^k\left(t\right)+{\tilde{B}}^k\left(t\right))\le -\frac{D^{+}m\left(t\right)}{m\left(t\right)}$$

where $D^{+}$ represents the Dini derivative, and

$$\begin{array}{cc}\hfill {\tilde{A}}^k\left(t\right)& =\underset{t-{\tau }_k\left(t\right)\le s\le t}{sup}{\parallel A\left(s\right)\parallel }_{\chi \left(s\right)}\frac{m\left(t\right)}{m\left(s\right)},\hfill \\ \hfill {\tilde{B}}^k\left(t\right)& =\underset{t-{\tau }_k\left(t\right)\le s\le t}{sup}{\parallel B_k\left(s\right)\parallel }_{\chi \left(s\right)}\frac{m\left(t\right)}{m(s-{\tau }_k\left(s\right))}.\hfill \end{array}$$

Then, for each $t\in [t_j,t_{j+1})$, we have

$${\left|x\left(t\right)\right|}_{\chi \left(t_j\right)}m\left(t\right)\le \underset{t_0-\overline{\tau }\le s\le t}{sup}{\left|x\left(s\right)\right|}_{\chi \left(t_j\right)}m\left(s\right)\le C_0\underset{t_0-\overline{\tau }\le s\le t_j}{sup}{\left|x\left(s\right)\right|}_{\chi (t_j-)}m\left(s\right)$$

Proof. 

Let $V\left(t\right)={sup}_{t_0-\overline{\tau }\le \theta \le t}{\left|x\left(\theta \right)\right|}_{\chi \left(\theta \right)}m\left(\theta \right)$. Assume that $V\left(t\right)$ is strictly increasing at time point $t^{*}$, it implies that $V\left(t^{*}\right)={\left|x\left(t^{*}\right)\right|}_{\chi \left(t^{*}\right)}m\left(t^{*}\right)$. There exists j such that $t^{*}\in [t_j,t_{j+1})$, and here we calculate the Dini derivative of ${\left|x\left(t\right)\right|}_{\chi \left(t_j\right)}m\left(t\right)$,

$$D^{+}{\left[\right|x\left(t\right)|}_{\chi \left(t_j\right)}m\left(t\right)]=\dot{m}\left(t\right){\left|x\left(t\right)\right|}_{\chi \left(t_j\right)}+m\left(t\right)\underset{h\to 0}{lim}\frac{{\left|x(t+h)\right|}_{\chi \left(t_j\right)}-{\left|x\left(t\right)\right|}_{\chi \left(t_j\right)}}{h},$$

in which $\dot{x}\left(t\right)$ can be rewritten as

$$\begin{array}{cc}\hfill \dot{x}\left(t\right)& =A\left(t\right)x\left(t\right)+\sum _{k=1}^m{B}_k\left(t\right)x(t-{\tau }_k\left(t\right))\hfill \\ \hfill & =[A\left(t\right)+\sum _{k=1}^m{B}_k^{\left(1\right)}\left(t\right)]x\left(t\right)+\sum _{k=1}^m{B}_k^{\left(1\right)}\left(t\right){\int }_t^{t-{\tau }_k\left(t\right)}\dot{x}\left(s\right)ds+\sum _{k=1}^m{B}_k^{\left(2\right)}\left(t\right)x(t-{\tau }_k\left(t\right))\hfill \end{array}$$

Thus, we have

$$\begin{array}{cc}\hfill & {\overline{lim}}_{h\to 0}\frac{{\left|x(t+h)\right|}_{\chi \left(t_j\right)}-{\left|x\left(t\right)\right|}_{\chi \left(t_j\right)}}{h}\hfill \\ \hfill =& {\overline{lim}}_{h\to 0}\frac{1}{h}[|x\left(t\right)+h(A\left(t\right)+\sum _{k=1}^m{B}_k^{\left(1\right)}\left(t\right))x\left(t\right)+h\sum _{k=1}^m{B}_k^{\left(1\right)}\left(t\right){\int }_t^{t-{\tau }_k\left(t\right)}\dot{x}\left(s\right)ds\hfill \\ \hfill & +h\sum _{k=1}^m{B}_k^{\left(2\right)}\left(t\right)x(t-{\tau }_k\left(t\right)){|}_{\chi \left(t_j\right)}-{|x\left(t\right)|}_{\chi \left(t_j\right)}]\hfill \\ \hfill =& {\overline{lim}}_{h\to 0}\frac{1}{h}{\left|x\left(t\right)\right|}_{\chi \left(t_j\right)}\left[\parallel I+h(A\left(t\right)+\sum _{k=1}^m{B}_k^{\left(1\right)}\left(t\right)){\parallel }_{\chi \left(t_j\right)}-1\right]+\sum _{k=1}^m\parallel B_k^{\left(1\right)}{\left(t\right)\parallel }_{\chi \left(t_j\right)}{\int }_{t-{\tau }_k\left(t\right)}^t{\left|\dot{x}\left(s\right)\right|}_{\chi \left(t_j\right)}ds\hfill \\ \hfill & +\sum _{k=1}^m\parallel B_k^{\left(2\right)}{\left(t\right)\parallel }_{\chi \left(t_j\right)}{\left|x(t-{\tau }_k\left(t\right))\right|}_{\chi \left(t_j\right)}\hfill \\ \hfill =& {\nu }_{\chi \left(t_j\right)}(A\left(t\right)+\sum _{k=1}^m{B}_k^{\left(1\right)}\left(t\right)){\left|x\left(t\right)\right|}_{\chi \left(t_j\right)}+\sum _{k=1}^m\parallel B_k^{\left(1\right)}{\left(t\right)\parallel }_{\chi \left(t_j\right)}{\int }_{t-{\tau }_k\left(t\right)}^t{\left|\dot{x}\left(s\right)\right|}_{\chi \left(t_j\right)}ds\hfill \\ \hfill & +\sum _{k=1}^m\parallel B_k^{\left(2\right)}{\left(t\right)\parallel }_{\chi \left(t_j\right)}{\left|x(t-\tau \left(t\right))\right|}_{\chi \left(t_j\right)}\hfill \end{array}$$

that is,

$$\begin{array}{cc}\hfill & D^{+}{\left[\right|x\left(t\right)|}_{\chi \left(t_j\right)}m\left(t\right)]\hfill \\ \hfill =& \frac{\dot{m}\left(t\right)}{m\left(t\right)}{\left|x\left(t\right)\right|}_{\chi \left(t_j\right)}m\left(t\right)+{\nu }_{\chi \left(t_j\right)}(A\left(t\right)+\sum _{k=1}^m{B}_k^{\left(1\right)}\left(t\right)){\left|x\left(t\right)\right|}_{\chi \left(t_j\right)}m\left(t\right)\hfill \\ \hfill & +\sum _{k=1}^m\parallel B_k^{\left(2\right)}{\left(t\right)\parallel }_{\chi \left(t_j\right)}{\left|x(t-{\tau }_k\left(t\right))\right|}_{\chi \left(t_j\right)}\hfill \\ \hfill & +\sum _{k=1}^m\parallel B_k^{\left(1\right)}{\left(t\right)\parallel }_{\chi \left(t_j\right)}m\left(t\right){\int }_{t-{\tau }_k\left(t\right)}^t{|A\left(s\right)x\left(s\right)+\sum _{k=1}^m{B}_k\left(s\right)x(s-{\tau }_k\left(s\right))|}_{\chi \left(t_j\right)}ds\hfill \\ \hfill =& \frac{\dot{m}\left(t\right)}{m\left(t\right)}{\left|x\left(t\right)\right|}_{\chi \left(t_j\right)}m\left(t\right)+{\nu }_{\chi \left(t_j\right)}(A\left(t\right)+\sum _{k=1}^m{B}_k^{\left(1\right)}\left(t\right)){\left|x\left(t\right)\right|}_{\chi \left(t_j\right)}m\left(t\right)\hfill \\ \hfill & +\sum _{k=1}^m\parallel B_k^{\left(2\right)}{\left(t\right)\parallel }_{\chi \left(t_j\right)}{\left|x(t-{\tau }_k\left(t\right))\right|}_{\chi \left(t_j\right)}m(t-{\tau }_k\left(t\right))\frac{m\left(t\right)}{m(t-{\tau }_k\left(t\right))}\hfill \\ \hfill & +\sum _{k=1}^m\parallel B_k^{\left(1\right)}{\left(t\right)\parallel }_{\chi \left(t_j\right)}{\int }_{t-{\tau }_k\left(t\right)}^t{\parallel A\left(s\right)\parallel }_{\chi \left(t_j\right)}{\left|x\left(s\right)\right|}_{\chi \left(t_j\right)}m\left(s\right)\frac{m\left(t\right)}{m\left(s\right)}\hfill \\ \hfill & +\sum _{k=1}^m\parallel B_k{\left(s\right)\parallel }_{\chi \left(t_j\right)}{\left|x(s-{\tau }_k\left(s\right))\right|}_{\chi \left(t_j\right)}m(s-{\tau }_k\left(s\right))\frac{m\left(t\right)}{m(s-{\tau }_k\left(s\right))}ds\hfill \end{array}$$

Let

$$\begin{array}{cc}\hfill {\tilde{A}}^k\left(t\right)=& \underset{t-{\tau }_k\left(t\right)\le s\le t}{sup}{\parallel A\left(s\right)\parallel }_{\chi \left(t_j\right)}\frac{m\left(t\right)}{m\left(s\right)}\hfill \\ \hfill {\tilde{B}}^k\left(t\right)=& \underset{t-{\tau }_k\left(t\right)\le s\le t}{sup}{\parallel B_k\left(s\right)\parallel }_{\chi \left(t_j\right)}\frac{m\left(t\right)}{m(s-{\tau }_k\left(s\right))}\hfill \end{array}$$

then, for $t=t^{*}$, we have

$$\begin{array}{cc}\hfill D^{+}V\left(t\right)\le & [\frac{\dot{m}\left(t\right)}{m\left(t\right)}+{\nu }_{\chi \left(t_j\right)}(A\left(t\right)+\sum _{k=1}^m{B}_k^{\left(1\right)}\left(t\right))+\sum _{k=1}^m{\tau }_k\left(t\right){\parallel B_k^{\left(1\right)}\left(t\right)\parallel }_{\chi \left(t_j\right)}({\tilde{A}}^k\left(t\right)+{\tilde{B}}^k\left(t\right))\hfill \\ \hfill & +\sum _{k=1}^m{\parallel B_k^{\left(2\right)}\left(t\right)\parallel }_{\chi \left(t_j\right)}\frac{m\left(t\right)}{m(t-{\tau }_k\left(t\right))}]V\left(t\right)\le 0\hfill \end{array}$$

which is contradictory to the hypothesis that $V\left(t\right)$ is strictly increasing at $t^{*}$. Therefore, $V\left(t\right)$ is decreasing for $t\in [t_j,t_{j+1})$, that is,

$$\begin{array}{c}\hfill V\left(t\right)\le V\left(t_j\right)\end{array}$$

that is,

$$\begin{array}{c}\hfill {\left|x\left(t\right)\right|}_{\chi \left(t_j\right)}m\left(t\right)\le \underset{t_0-\overline{\tau }\le s\le t_j}{sup}{\left|x\left(s\right)\right|}_{\chi \left(t_j\right)}m\left(s\right)\le C_0\underset{t_0-\overline{\tau }\le s\le t_j}{sup}{\left|x\left(s\right)\right|}_{\chi (t_j-)}m\left(s\right)\end{array}$$

The lemma is proved. □

With the conclusion in Lemma 1, we can select a proper function $m\left(t\right)>0$, and prove the following theorem for exponential incremental stability property of system (1).

Theorem 1. 

Suppose that Assumption 1 holds for time-delay system (1). $\chi \left(t\right)$ is a right-continuous staircase function with discontinuities in $\{t_1,\dots ,t_j,\dots \}$. Let $N\left(t\right)=\#\{j:t\ge t_j,j=1,2,\dots \}$, and there exist that

1. 

A constant $T_0>0$,

2. 

Positive constants ${\gamma }_k(k=0,1,\dots )$, ${\gamma }_0\le {\gamma }_1\le \dots$,

3. 

$C(\chi \left(t\right),\chi \left(t^{\prime }\right))\le C_0$ for any $t,t^{\prime }\ge t_0$,

such that the following conditions hold:

Let $A\left(t\right)=(\partial f/\partial x)(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))$, $B_k\left(t\right)=(\partial f/\partial x_{{\tau }_k})(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))$, $k=1,\dots ,m$ be piecewise continuous with respect to t, and the discontinuities belong to $\{t_1,t_2,\dots ,t_i,\dots \}$. There exist matrix-valued functions $B_k^{\left(1\right)}\left(t\right)$, $B_k^{\left(2\right)}\left(t\right)$, $B_k^{\left(1\right)}\left(t\right)+B_k^{\left(2\right)}\left(t\right)=B_k\left(t\right)$ such that

$${\nu }_{\chi \left(t\right)}(A\left(t\right)+{\displaystyle {\sum }_{k=1}^m}{B}_k^{\left(1\right)}\left(t\right))+{\displaystyle {\sum }_{k=1}^m}{\tau }_k\left(t\right)\parallel B_k^{\left(1\right)}{\left(t\right)\parallel }_{\chi \left(t\right)}({\tilde{A}}^k\left(t\right)+{\tilde{B}}^k\left(t\right))+{\displaystyle {\sum }_{k=1}^m}{\parallel B_k^{\left(2\right)}\left(t\right)\parallel }_{\chi \left(t\right)}\frac{exp\left(({\gamma }_{N\left(t\right)}-{\gamma }_{N(t-{\tau }_k\left(t\right))})t\right)}{exp\left({\gamma }_{N(t-{\tau }_k\left(t\right))}{\tau }_k\left(t\right)\right)}\le -{\gamma }_{N\left(t\right)}$$

(3)

where

$$\begin{array}{cc}\hfill {\tilde{A}}_t^k=& \underset{t-{\tau }_k\left(t\right)\le s\le t}{sup}{\parallel A\left(s\right)\parallel }_{\chi \left(t\right)}exp\left({\gamma }_{N\left(t\right)}t-{\gamma }_{N\left(s\right)}s\right)\hfill \\ \hfill {\tilde{B}}_t^k=& \underset{t-{\tau }_k\left(t\right)\le s\le t}{sup}{\parallel B_k\left(s\right)\parallel }_{\chi \left(t\right)}exp\left({\gamma }_{N\left(t\right)}t-{\gamma }_{N(s-{\tau }_k\left(s\right))}(s-{\tau }_k\left(s\right))\right).\hfill \end{array}$$

and for any $t>T_0$,

$$\frac{1}{t}\left[\sum _{i=0}^{N\left(t\right)-1}[({\gamma }_{i+1}-{\gamma }_i)t_{i+1}+log{\beta }_{i+1}]+{\gamma }_0{t}_0-{\gamma }_{N\left(t\right)}t\right]\le -c$$

(4)

where ${\beta }_k=C(\chi \left(t_k\right),\chi (t_k-))$, then system (1) is exponentially incrementally stable.

Proof. 

For any initial state $x_0,y_0$, denote the corresponding initial function by $x_0(·),y_0(·)$, $x_0(·),y_0(·)\in C([t_0-\overline{\tau },t_0],{\mathbb{R}}^m)$. Here, we define a function ${\phi }_{\lambda }(·)$ as ${\phi }_{\lambda }\left(s\right)=(1-\lambda )x_0\left(s\right)+\lambda y_0\left(s\right),\lambda \in [0,1],s\in [t_0-\overline{\tau },t_0]$, which is the initial value function of the initial state ${\phi }_{\lambda }$. Let ${\phi }_0=x_0,{\phi }_1=y_0$. $f(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))$ is continuous with respect to $(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r)$ except for the switching time points $\left\{t_j\right\}$, and is continuously differentiable with respect to x, so we have the solution $\psi (t,\lambda )=x(t;{\phi }_{\lambda },r_t)$, which is continuously differentiable with respect to ${\phi }_{\lambda }$. Let $\omega =\partial \psi /\partial \lambda$, thus we can conclude that $\omega$ is well-defined and continuous. From chain rule, $\omega (t,\lambda )$ is the solution of the following system:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & \dot{\omega }=\frac{{\partial }^2\psi }{\partial \lambda \partial t}=\frac{\partial f}{\partial \lambda }=\frac{\partial f}{\partial x}\omega +\sum _{k=1}^m\frac{\partial f}{\partial x_{{\tau }_k}}{\omega }_{{\tau }_k}\hfill \\ \hfill & \omega (s,\lambda )=\frac{\partial {\phi }_{\lambda }}{\partial \lambda }\left(s\right),s\in [t_0-\overline{\tau },t_0]\hfill \end{array}\right.\end{array}$$

$\partial \psi /\partial \lambda$ is well-defined and continuous, with condition (3), from the proof of Lemma 1, select a piecewise right-continuous function $m\left(t\right)=exp\left({\gamma }_{N\left(t\right)}t\right)>0$ whose discontinuities belong to $\{t_1,t_2,\dots ,t_i,\dots \}$, we have

$${m\left(t\right)\left|\omega (t,\lambda )\right|}_{\chi \left(t\right)}\le V\left(t\right)\le V\left(t_j\right)=\underset{t_0-\overline{\tau }\le s\le t_j}{sup}m\left(s\right){\left|\omega (s,\lambda )\right|}_{\chi \left(t_j\right)}$$

holds for any $t\in [t_j,t_{j+1})$. Thus, under the condition (4), we have

$$\begin{array}{cc}\hfill & {m\left(t\right)\left|\omega (t,\lambda )\right|}_{\chi \left(t\right)}\le V\left(t\right)\le V\left(t_j\right)=\underset{t_0-\overline{\tau }\le s\le t_j}{sup}m\left(s\right){\left|\omega (s,\lambda )\right|}_{\chi \left(t_j\right)}\hfill \\ \hfill \le & exp\left(({\gamma }_j-{\gamma }_{j-1})t_j\right)·{\beta }_j\underset{t_0-\overline{\tau }\le s\le t_j}{sup}m\left(s\right){\left|\omega (s,\lambda )\right|}_{\chi (t_j-)}\hfill \\ \hfill \le & exp\left(({\gamma }_j-{\gamma }_{j-1})t_j\right)·{\beta }_j\underset{t_0-\overline{\tau }\le s\le t_{j-1}}{sup}m\left(s\right){\left|\omega (s,\lambda )\right|}_{\chi \left(t_{j-1}\right)}\hfill \\ \hfill \le & \prod _{j=1}^{N\left(t\right)}exp\left(({\gamma }_j-{\gamma }_{j-1})t_j\right)·{\beta }_j·\underset{t_0-\overline{\tau }\le s\le t_0}{sup}m\left(s\right){\left|\omega (s,\lambda )\right|}_{\chi \left(t_0\right)}\hfill \\ \hfill \le & \prod _{j=1}^{N\left(t\right)}exp\left(({\gamma }_j-{\gamma }_{j-1})t_j\right)·{\beta }_j·\underset{\theta \in [t_0-\overline{\tau },t_0]}{sup}m\left(\theta \right)\underset{t_0-\overline{\tau }\le s\le t_0}{sup}{\left|\omega (s,\lambda )\right|}_{\chi \left(t_0\right)}\hfill \end{array}$$

then, we have

$${\left|\omega (t,\lambda )\right|}_{\chi \left(t\right)}\le exp(\sum _{j=1}^{N\left(t\right)}({\gamma }_j-{\gamma }_{j-1})t_j+log{\beta }_j)exp\left({\gamma }_0{t}_0-{\gamma }_{N\left(t\right)}t\right)\underset{t_0-\overline{\tau }\le s\le t_0}{sup}|\omega (t_0,\lambda ){|}_{\chi \left(t_0\right)}\le e^{-ct}\underset{t_0-\overline{\tau }\le s\le t_0}{sup}{|\omega (t_0,\lambda )|}_{\chi \left(t_0\right)}.$$

Therefore, together with the condition (4), we conclude that the time-delay system (1) is incrementally uniformly asymptotically stable:

$$\begin{array}{cc}\hfill & |x(t;y_0,r_t)-x(t;x_0,r_t){|}_{\chi \left(t_0\right)}\le C_0{|x(t;y_0,r_t)-x(t;x_0,r_t)|}_{\chi \left(t\right)}\hfill \\ \hfill \le & C_0|{\int }_0^1\frac{\partial \psi (t,\lambda )}{\partial \lambda }d\lambda {|}_{\chi \left(t\right)}\le C_0{\int }_0^1{\left|\omega (t,\lambda )\right|}_{\chi \left(t\right)}d\lambda \hfill \\ \hfill \le & C_0{e}^{-ct}{\int }_0^1\underset{t_0-\overline{\tau }\le s\le t_0}{sup}{\left|\omega (t_0,\lambda )\right|}_{\chi \left(t_0\right)}d\lambda \hfill \\ \hfill \le & C_0{e}^{-ct}\underset{\theta \in [t_0-\overline{\tau },t_0]}{sup}{|x_0\left(\theta \right)-y_0\left(\theta \right)|}_{\chi \left(t_0\right)}\hfill \end{array}$$

□

Actually, the key thought of Theorem 1 is replacing the time-delay term $B_k\left(t\right)x_{{\tau }_k}\left(t\right)$ with $B_k^{\left(1\right)}\left(t\right)x_{{\tau }_k}\left(t\right)+B_k^{\left(2\right)}\left(t\right)x\left(t\right)+B_k^{\left(2\right)}\left(t\right){\int }_t^{t-{\tau }_k\left(t\right)}\dot{x}\left(s\right)ds$. In some special cases, we can set $B_k^{\left(1\right)}\left(t\right)=0$ or $B_k^{\left(2\right)}\left(t\right)=0$ for $k=1,2,\dots ,m$, which infers the following corollaries.

Corollary 1. 

Suppose that Assumption 1 holds. $\chi \left(t\right)$ is a right-continuous staircase function with discontinuities in $\{t_1,\dots ,t_j,\dots \}$. Let $N\left(t\right)=\#\{j:t\ge t_j,j=1,2,\dots \}$, and there exist

1. 

A constant $T_0>0$,

2. 

Positive constants ${\gamma }_k(k=0,1,\dots )$, ${\gamma }_0\le {\gamma }_1\le \dots$,

3. 

$C(\chi \left(t\right),\chi \left(t^{\prime }\right))\le C_0$ for any $t,t^{\prime }\ge t_0$,

such that the following conditions hold:

Let $A\left(t\right)=(\partial f/\partial x)(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))$, $B_k\left(t\right)=(\partial f/\partial x_{{\tau }_k})(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))$, $k=1,\dots ,m$ be piecewise continuous with respect to t, and the discontinuities belong to $\{t_1,t_2,\dots ,t_i,\dots \}$,

$${\nu }_{\chi \left(t\right)}\left(A\left(t\right)\right)+\sum _{k=1}^m{\parallel B_k\left(t\right)\parallel }_{\chi \left(t\right)}\frac{exp\left({\gamma }_{N\left(t\right)}t\right)}{exp\left({\gamma }_{N(t-{\tau }_k\left(t\right))}(t-{\tau }_k\left(t\right))\right)}\le -{\gamma }_{N\left(t\right)}$$

and for any $t>T_0$,

$$\frac{1}{t}\left[\sum _{i=0}^{N\left(t\right)-1}[({\gamma }_{i+1}-{\gamma }_i)t_{i+1}+log{\beta }_{i+1}]+{\gamma }_0{t}_0-{\gamma }_{N\left(t\right)}t\right]\le -c,$$

where ${\beta }_k=C(\chi \left(t_k\right),\chi (t_k-))$, then system (1) is exponentially incrementally stable.

Corollary 2. 

Suppose that Assumption 1 holds. $\chi \left(t\right)$ is a right-continuous staircase function with discontinuities in $\{t_1,\dots ,t_j,\dots \}$. Let $N\left(t\right)=\#\{j:t\ge t_j,j=1,2,\dots \}$, and there exist

1. 

A constant $T_0>0$,

2. 

Positive constants ${\alpha }_k>0(k=0,1,\dots )$,

3. 

$C(\chi \left(t\right),\chi \left(t^{\prime }\right))\le C_0$ for any $t,t^{\prime }\ge t_0$,

such that the following conditions hold:

Let $A\left(t\right)=(\partial f/\partial x)(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))$, $B_k\left(t\right)=(\partial f/\partial x_{{\tau }_k})(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))$, $k=1,\dots ,m$, there exist matrix-valued functions $B_k^{\left(1\right)}\left(t\right)$, $B_k^{\left(2\right)}\left(t\right)$, $B_k^{\left(1\right)}\left(t\right)+B_k^{\left(2\right)}\left(t\right)=B_k\left(t\right)$ such that

$${\nu }_{\chi \left(t\right)}(A\left(t\right)+\sum _{k=1}^m{B}_k\left(t\right))+\sum _{k=1}^m{\tau }_k\left(t\right){\parallel B_k\left(t\right)\parallel }_{\chi \left(t\right)}({\tilde{A}}^k\left(t\right)+{\tilde{B}}^k\left(t\right))\le -{\gamma }_{N\left(t\right)}$$

where

$$\begin{array}{cc}\hfill {\tilde{A}}_t^k=& \underset{t-{\tau }_k\left(t\right)\le s\le t}{sup}{\parallel A\left(s\right)\parallel }_{\chi \left(t\right)}exp\left({\gamma }_{N\left(t\right)}t-{\gamma }_{N\left(s\right)}s\right)\hfill \\ \hfill {\tilde{B}}_t^k=& \underset{t-{\tau }_k\left(t\right)\le s\le t}{sup}{\parallel B_k\left(s\right)\parallel }_{\chi \left(t\right)}exp\left({\gamma }_{N\left(t\right)}t-{\gamma }_{N(s-{\tau }_k\left(s\right))}(s-{\tau }_k\left(s\right))\right)\hfill \end{array}$$

and for any $t>T_0$,

$$\frac{1}{t}\left[\sum _{i=0}^{N\left(t\right)-1}[({\gamma }_{i+1}-{\gamma }_i)t_{i+1}+log{\beta }_{i+1}]+{\gamma }_0{t}_0-{\gamma }_{N\left(t\right)}t\right]\le -c,$$

where ${\beta }_k=C(\chi \left(t_k\right),\chi (t_k-))$, then system (1) is exponentially incrementally stable.

4. Incremental Stability for Time-Delay Dynamical Systems with Discontinuous Right-Hand Sides

Here, we consider the time-delay dynamical systems [39] with discontinuous right-hand sides using multiple norms, formulated as follows:

$$\dot{x}=f(x\left(t\right),x_{{\tau }_1}\left(t\right),\dots ,x_{{\tau }_m}\left(t\right),r\left(t\right))$$

(5)

where $x,x_{{\tau }_1},\dots ,x_{{\tau }_m}\in {\mathbb{R}}^n$, $x_{{\tau }_k}\left(t\right)=x(t-{\tau }_k\left(t\right)),(k=1,\dots ,m)$ represents the time-delay term. The right-hand function f may be discontinuous with respect to $(x,x_{{\tau }_1},\dots ,x_{{\tau }_m})$. The solution of the system (5) can be defined as a solution of the following differential inclusion, which is named a (time-delay) Filippov system,

$$\left\{\begin{array}{cc}\hfill & \dot{x}\in F(x\left(t\right),x_{{\tau }_1}\left(t\right),\dots ,x_{{\tau }_m}\left(t\right),r\left(t\right)),t\in [0,T]\hfill \\ \hfill & x\left(s\right)=\varphi \left(s\right),s\in [t_0-\overline{\tau },t_0]\hfill \end{array}\right.$$

(6)

where $x_{{\tau }_k}\left(t\right)=x(t-{\tau }_k\left(t\right))$, ${\tau }_k\left(t\right)$ is non-negative for $t\in [t_0,T]$, $T\in (t_0,+\infty ]$, $\overline{\tau }={max}_k{sup}_{s\ge t_0}{\tau }_k\left(s\right)$, the initial function $\varphi (·)$ is defined on $[t_0-\overline{\tau },t_0]$, and F is a set-valued mapping defined as follows,

$$\begin{array}{cc}\hfill F(x\left(t\right),x_{{\tau }_1}\left(t\right),\dots ,x_{{\tau }_m}\left(t\right),r\left(t\right))& =\mathcal{K}\left[f\right](x\left(t\right),x_{{\tau }_1}\left(t\right),\dots ,x_{{\tau }_m}\left(t\right),r\left(t\right))\hfill \\ \hfill & =\bigcap _{ϵ>0}\bigcap _{\mu \left(P\right)=0}\overline{co}\left\{f(B((x,x_{{\tau }_1},\dots ,x_{{\tau }_m}),ϵ)\setminus P,r\left(t\right))\right\},\hfill \end{array}$$

where $\mu (·)$ stands for the Lebesgue measure, $B((x,x_{{\tau }_1},\dots ,x_{{\tau }_m}),ϵ)=\{(y,y_{{\tau }_1},\dots ,y_{{\tau }_m}):|{(y^{\top },y_{{\tau }_1}^{\top },\dots ,y_{{\tau }_m}^{\top })}^{\top }-{(x^{\top },x_{{\tau }_1}^{\top },\dots ,x_{{\tau }_m}^{\top })}^{\top }|\le ϵ\}$ represents the $ϵ$-neighborhood of $(x,x_{{\tau }_1},\dots ,x_{{\tau }_m})$ with the given vector norm $|·|$, and $\overline{co}$ represents convex closure.

4.1. Existence and Uniqueness of the Solution

Before the main theorem, the existence and uniqueness of the Cauchy problem of the Filippov system (6) should be proved first. Herein, several of the existing results on dynamical systems without time-delay terms are presented as follows. Readers are referred to [15,37,40] for the details. For some dynamical systems without time-delay terms, formulated as follows,

$$\dot{x}=f(x,t)$$

in which $x\in {\mathbb{R}}^n$, we have the corresponding Filippov system,

$$\dot{x}=F(x,t)=\mathcal{K}\left[f\right](x,t)=\bigcap _{ϵ>0}\bigcap _{\mu \left(P\right)=0}\overline{co}\left\{f(B(x,ϵ)\setminus P,t)\right\}$$

(7)

Then, from Definition 4 and 5 in [40]. We have concluded that under the following Assumption 2, it can be guaranteed that system (7) has at least one solution.

Assumption 2 

([40]). The set-valued mapping $F:{\mathbb{R}}^n\times {\mathbb{R}}^{+}\rightrightarrows {\mathbb{R}}^n$ satisfies that for all $(x,t)\in {\mathbb{R}}^n\times {\mathbb{R}}^{+}$, $F(x,t)$ is non-empty, bounded, convex, and closed, and F is upper semicontinuous at $(x,t)$.

In Assumption 2, ‘upper semicontinuity’ for the set-valued mapping F is defined as follows.

Definition 8 

(Section 1, Chapter 2 in [37]). A set-valued mapping $F:{\mathbb{R}}^n\times {\mathbb{R}}^{+}\rightrightarrows Y$ is called upper semicontinuous at $(x,t)\in {\mathbb{R}}^n\times {\mathbb{R}}^{+}$ if and only if for any neighborhood $\mathcal{U}$ of $F(x,t)$, $\exists \delta >0$, such that $\forall (\tilde{x},\tilde{t})\in B((x,t),\delta )$, $F(\tilde{x},\tilde{t})\subset \mathcal{U}$.

Assumption 3. 

With respect to a given Euclid norm $|·|$ defined on a n-dimensional space, we have the following hypothesis:

1. 

For any $(x,y_1,\dots ,y_m,r)\in {\mathbb{R}}^{n\times (m+1)}\times \mathbb{R}$, $F(x,y_1,\dots ,y_m,r\left(t\right))$ is non-empty, convex, closed in ${\mathbb{R}}^n$, and set-valued mapping F is upper semicontinuous with respect to $(x,y_1,\dots ,y_m,r)$.

2. 

(Linearly increasing) There exists $\alpha >0$ such that

$$sup\left\{\right|v|:v\in F(x,y_1,\dots ,y_m,r)\}\le \alpha (\left|x\right|+|y_1|+\dots +|y_m|+|r|+1)$$

holds for any $(x,y_1,\dots ,y_m,r)\in {\mathbb{R}}^{n\times (m+1)}\times \mathbb{R}$. With Gronwall inequality [41], it can easily be seen as equivalent to: there exists $\Theta >0$ such that

$$sup\left\{\right|v|:v\in F(x,y_1,\dots ,y_m,r)\}\le \Theta$$

holds for any $(x,y_1,\dots ,y_m,r)\in {\mathbb{R}}^{n\times (m+1)}\times \mathbb{R}$.

3. 

Function ${\tau }_k:[t_0,T]\to [0,\infty )(k=1,\dots ,m)$ is continuously differentiable and bounded, with its upper bound $\overline{\tau }:=max\{{\tau }_k\left(t\right):t\in [t_0,T],k=1,\dots ,m\}$ and lower bound $\underline{\tau }=min\{{\tau }_k\left(t\right):t\in [t_0,T],k=1,\dots ,m\}>0$.

4. 

The initial function $\varphi (·)\in L^{\infty }([t_0-\overline{\tau },t_0],{\mathbb{R}}^n)$ is measurable.

5. 

For any $(x,y_1,\dots ,y_m,r)\in {\mathbb{R}}^{n\times (m+1)}\times {\mathbb{R}}^n\times {\mathbb{R}}^{+}$, there exists continuous function $h(·):{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$, such that $|F(x_1,y_1,\dots ,y_m,r\left(t\right))-F(x_2,y_1,\dots ,y_m,r\left(t\right))|\le h(|x_1-x_2\left|\right)$ holds.

First, we fix a continuous initial function $\varphi (·)\in L^{\infty }([t_0-\overline{\tau },t_0],{\mathbb{R}}^n)$, then select a measurable function $\psi :[t_0-\overline{\tau },t_0]\to {\mathbb{R}}^n$ such that $\psi \left(s\right)\in \mathcal{K}\left[\varphi \right]\left(s\right)$ holds for $s\in [t_0-\overline{\tau },t_0]$ almost everywhere. For $t\in [t_0,t_0+\underline{\tau }]$, consider the following differential inclusion [42]:

$$\left\{\begin{array}{cc}\hfill & \dot{x}\left(t\right)\in F(x\left(t\right),\psi (t-{\tau }_1\left(t\right)),\dots ,\psi (t-{\tau }_m\left(t\right)),r\left(t\right))\hfill \\ \hfill & x\left(0\right)=\varphi \left(0\right)\hfill \end{array}\right.,$$

(8)

From Assumption 3, together with Assumption 2 and the conclusion for the existence of the solution of system (8), the inclusion (6) has at least one solution defined in $[t_0,t_0+\underline{\tau }]$.

Therefore, similarly, the solution can be extended to $[t_0,+\infty )$. Assume, as an inductive step, that the solution x is defined on $[t_0-\overline{\tau },t_0+N\underline{\tau }]$, for some $N=1,2,\dots$. Then, one can consider the vector $\alpha =x(t_0+N\underline{\tau })$ as the initial state of the following differential inclusion,

$$\left\{\begin{array}{cc}\hfill & \dot{x}\left(t\right)\in F(x\left(t\right),\psi (t-{\tau }_1\left(t\right)),\dots ,\psi (t-{\tau }_m\left(t\right)),r\left(t\right))\hfill \\ \hfill & x\left(0\right)=\varphi \left(0\right)\hfill \end{array}\right.t\in [t_0+N\underline{\tau },t_0+(N+1)\underline{\tau }]\mathrm{almost}\mathrm{everywhere}.$$

Then, one can extend $x\left(t\right),t\in [t_0-\overline{\tau },t_0+N\underline{\tau }]$ to a right neighborhood of $t_0+N\underline{\tau }$, the interval $[t_0-\overline{\tau },t_0+(N+1)\underline{\tau }]$. That is, we have the following lemma,

Lemma 2. 

If the time-delay Filippov system (6) satisfies Assumption 3, then, the system (6) has at least on solution in $[t_0,T]$, $T\in (0,+\infty ]$.

Then, when it comes to the problem of uniqueness, enlightened by Chapter 2, Section 10, Theorem 1 in [15], we similarly research the conditions for uniqueness of the solution of system (6).

Theorem 2. 

Suppose that function $f(x\left(t\right),x_{{\tau }_1}\left(t\right),\dots ,x_{{\tau }_m}\left(t\right),r\left(t\right))$ defined on region $D\subset {\mathbb{R}}^n\times {\mathbb{R}}^n\times {\mathbb{R}}^{+}$ is discontinuous on zero measure set M, and there exists an integral function $l\left(t\right)$ such that $|f(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r)|\le l\left(t\right)$ holds for any $(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r)\in D$, and $l\left(t\right)<\infty$ almost everywhere. Let ${ϵ}_0>0$, for any $(x_0,x_{{\tau }_1},\dots ,x_{{\tau }_m},r),(y_0,y_{{\tau }_1},\dots ,y_{{\tau }_m},r)$ satisfying that $|x_0-y_0|<{ϵ}_0$ and $|x_{{\tau }_k}-y_{{\tau }_k}|\le |x_0-y_0|,(k=1,\dots ,m)$,

$$(x_0-y_0)·(f(x_0,x_{{\tau }_1},\dots ,x_{{\tau }_m},t)-f(y_0,y_{{\tau }_1},\dots ,y_{{\tau }_m},r\left(t\right)))\le l\left(t\right){|x_0-y_0|}^2$$

(9)

Then, under the simplest convex definition (Page 50 in [15]), equation $\dot{x}=f(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))$ is right-unique on D.

Proof. 

If for all $t\in {\mathbb{R}}^{+}$, any ${ϵ}_0>0$, $x(·)$ and $y(·)$ satisfying that ${|x(·)-y(·)|}_{[t-\overline{\tau },t]}^{\infty }\le |x\left(t\right)-y\left(t\right)|<{ϵ}_0$, on the basis of (9), we have

$$(x\left(t\right)-y\left(t\right))·(f(x\left(t\right),x_{{\tau }_1}\left(t\right),\dots ,x_{{\tau }_m}\left(t\right),r\left(t\right))-f(y\left(t\right),y_{{\tau }_1}\left(t\right),\dots ,y_{{\tau }_m}\left(t\right),r\left(t\right)))\le l\left(t\right){|x\left(t\right)-y\left(t\right)|}^2,$$

holds. Thus, we have

$$\begin{array}{cc}\hfill \frac{1}{2}\frac{d}{dt}{|x\left(t\right)-y\left(t\right)|}^2& =(x\left(t\right)-y\left(t\right))(\dot{x}\left(t\right)-\dot{y}\left(t\right))\hfill \\ \hfill & =(x\left(t\right)-y\left(t\right))·(f(x\left(t\right),x_{{\tau }_1}\left(t\right),\dots ,x_{{\tau }_m}\left(t\right),r\left(t\right))-f(y\left(t\right),y_{{\tau }_1}\left(t\right),\dots ,y_{{\tau }_m}\left(t\right),r\left(t\right)))\hfill \\ \hfill & \le {l\left(t\right)|x\left(t\right)-y\left(t\right)|}^2.\hfill \end{array}$$

Therefore, similar to the proof of Theorem 1, in Section 10, Chapter 2 in [15], it can be seen that

$$\frac{d}{dt}\left({|x\left(t\right)-y\left(t\right)|}^2{e}^{-L\left(t\right)}\right)\le 0$$

where $L\left(t\right)={\int }_{t_0}^{t}l\left(s\right)ds$, that is, ${|x\left(t\right)-y\left(t\right)|}^2{e}^{-L\left(t\right)}$ is decreasing with respect to time t. If ${|x(·)-y(·)|}_{[t_0-\overline{\tau },t_0]}^{\infty }=sup\left\{\right|x\left(t\right)-y\left(t\right)|:t\in [t_0-\overline{\tau },t_0]\}=0$, then $\left|x\right(t)-y(t\left)\right|=0$ holds for $t>t_0$, then we obtained the right uniqueness of the solution of system (6). □

If system (5) is a switched system, according to Theorem 2, one can prove the right uniqueness of the solution.

Here, we formulate a switched system with time delay, that is, the right-hand function is switched with respect to $(x,x_{{\tau }_1},\dots ,x_{{\tau }_m})$.

$$\begin{array}{c}\hfill f(x,t)=f_i(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right)),(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},t)\in R_i\end{array}$$

(10)

in which $f_i:{\mathbb{R}}^{n\times (m+1)}\times {\mathbb{R}}^{+}\to {\mathbb{R}}^n$, regions $R_i\subset {\mathbb{R}}^{n\times (m+1)}\times {\mathbb{R}}^{+}$, $i=1,\dots ,K$. All of the regions $R_i$ have non-empty interiors. The discontinuities are composed of several smooth hypersurfaces of dimension $d(d<(m+1)n+1)$. Suppose that ${\left\{S_i\right\}}_{i=1}^N$ is a sequence $\left(\right(m+1\left)n\right)$-dimensional smooth hypersurfaces, $S_i=\{(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},t)\in {\mathbb{R}}^{n\times (m+1)}\times {\mathbb{R}}^{+}\mid {\varphi }_i(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},t)=0\}$, in which ${\varphi }_i(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},t)\in C^1({\mathbb{R}}^{n\times (m+1)}\times {\mathbb{R}}^{+},\mathbb{R})$, the continuous region of the function f is a sequence of connected regions, whose boundaries are the switching surfaces. Suppose that the switching surfaces never intersect each other. Denote one of the connected continuous region of f by $G_i^{+}\left(G_i^{-}\right)$, then it satisfies that

1.

$\partial G_i^{+}(\partial G_i^{-})\subset {\bigcup }_k{S}_k$;

2.

$f(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))$ is continuous in $G_i^{+}\left(G_i^{-}\right)$;

3.

${\varphi }_i(x,x_{\tau },\dots ,x_{{\tau }_m},t)>0(<0)$ holds in $G_i^{+}$ ($G_i^{-}$).

in which $G_i^{+}$ and $G_i^{-}$ are two different regions with their common boundary on $S_i$.

Take a switched system defined as (10) with $K=2$, $N=1$ as an example.In the domain G, consider one of the switching hypersurface S, $f^{+}(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))$ and $f^{-}(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))$ represent the limiting values of the function $f(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))$ at point $(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},t)$ from the regions $G^{+}$ and $G^{-}$, respectively. $f_N^{+}(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))$ and $f_N^{-}(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))$ represent the projections of the vectors $f^{+}(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))$ and $f^{-}(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))$ onto the normal vector to S directed from $G^{+}$ to $G^{-}$, respectively, at the point $(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},t)$.

Together with Theorem 2, according to bimodal time-delay systems, we have the following conclusion:

Theorem 3. 

Under the notations defined above, for all $t\in [t_0,+\infty )$ and point $(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},t)\in S$, if the inequality $f_N^{-}(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))-f_N^{+}(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))>0$ is fulfilled, then right uniqueness of Filippov solution for the bimodal system (10) ($K=2$, $N=1$) occurs. (Possibly different inequalities for different $(x,x_{{\tau }_1},\dots ,x_{{\tau }_m})$ and t.)

Proof. 

We use the conclusion in Theorem 2 to prove Theorem 3 above.

For any point $(z,z_{{\tau }_1},\dots ,z_{{\tau }_m},t)$ on the switching surface S, and $(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},t)\in R_1$, $(y,y_{{\tau }_1},\dots ,y_{{\tau }_m},t)\in R_2$, which satisfy that $|y_{{\tau }_k}-z_{{\tau }_k}|\le |y-z|$, $|x_{{\tau }_k}-z_{{\tau }_k}|\le |x-z|$, $|x_{{\tau }_k}-y_{{\tau }_k}|\le |y-x|$. Since $\partial f_1/\partial x$, $\partial f_2/\partial x$ and $\partial f_1/\partial x_{{\tau }_i},\partial f_2/\partial x_{{\tau }_i}(i=1,\dots ,m)$ are bounded, this implies that there exist $l,k_i>0(i=1,\dots ,m)$ such that

$$\begin{array}{cc}\hfill & |f(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))-f_1(z,z_{{\tau }_1},\dots ,z_{{\tau }_m},r\left(t\right))|\le l|x-z|+\sum _{i=1}^m{k}_i|x_{{\tau }_i}-z_{{\tau }_i}|,\hfill \\ \hfill & |f(y,y_{{\tau }_1},\dots ,y_{{\tau }_m},r\left(t\right))-f_2(z,z_{{\tau }_1},\dots ,z_{{\tau }_m},r\left(t\right))|\le l|y-z|+\sum _{i=1}^m{k}_i|y_{{\tau }_i}-z_{{\tau }_i}|.\hfill \end{array}$$

(11)

Similar to the proof of Theorem 2 in Chapter 2 in [15], if $f_N^{-}(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))-f_N^{+}(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))>0$ holds, then

$$(x-z)(f_1(z,z_{{\tau }_1},\dots ,z_{{\tau }_m},r\left(t\right))-f_2(z,z_{{\tau }_1},\dots ,z_{{\tau }_m},r\left(t\right)))\le 0.$$

(12)

The inequality (12) still holds if vector $x-y$ is substituted with vector $x-z$, which is in the same direction. Together with (11) and (12), it infers that

$$\begin{array}{cc}\hfill & (x-y)(f(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r)+f_2(z,z_{{\tau }_1},\dots ,z_{{\tau }_m},r)-f_1(z,z_{{\tau }_1},\dots ,z_{{\tau }_m},r)-f(y,y_{{\tau }_1},\dots ,y_{{\tau }_m},r))\hfill \\ \hfill \le & |y-x|·(|f(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r)-f_1(z,z_{{\tau }_1},\dots ,z_{{\tau }_m},r)|+|f(y,y_{{\tau }_1},\dots ,y_{{\tau }_m},r)-f_2(z,z_{{\tau }_1},\dots ,z_{{\tau }_m},r)|)\hfill \\ \hfill <& |y-x|·(l|x-z|+\sum _{i=1}^m{k}_i|x_{{\tau }_i}-z_{{\tau }_i}|+l|y-z|+\sum _{i=1}^m{k}_i|y_{{\tau }_i}-z_{{\tau }_i}|).\hfill \end{array}$$

That is, if $|y_{{\tau }_i}-z_{{\tau }_i}|\le |y-z|$, $|x_{{\tau }_i}-z_{{\tau }_i}|\le |x-z|$, $|x_{{\tau }_i}-y_{{\tau }_i}|\le |y-x|(i=1,\dots ,m)$, it holds that

$$(x-y)(f(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))-f(y,y_{{\tau }_1},\dots ,y_{{\tau }_m},r\left(t\right)))<2(l+\sum _{i=1}^m{k}_i){|y-x|}^2.$$

Thus, together with Theorem 2, at any point $(z,z_{{\tau }_1},\dots ,z_{{\tau }_m},t)$ in the domain, right uniqueness of the Filippov solution for system (10) ($K=2,N=1$) occurs for $t\in [t_0,+\infty )$. □

4.2. Criteria for Incremental Stability for Filippov Systems with Time Delay

Here, with the conclusions above, we then research the conditions of incremental stability for time-delay systems with discontinuous right-hand sides.

$$\dot{x}\left(t\right)=f(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))$$

(13)

where $x_{{\tau }_k}\left(t\right)=x(t-{\tau }_k\left(t\right))$, ${\tau }_k\left(t\right)(k=1,2,\dots ,m)$ is a bounded function with respect to time t, the function $f(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))=(f_1,f_2,\dots ,f_n):{\mathbb{R}}^{n\times (m+1)}\times {\mathbb{R}}^{+}\to {\mathbb{R}}^n$ is discontinuous with respect to $(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},t)$ on a zero measure set. $r\left(t\right)$ is a piecewise right-continuous switched function, with its discontinuities in $\{t_1,t_2,\dots ,t_j,\dots \}$.

Then, according to the discontinuous right-hand side $f(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))$, with corresponding set-valued mapping $F(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))=\mathcal{K}\left[f\right](x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))$, we construct a sequence of functions ${\left\{f^p(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))\right\}}_{p=1}^{\infty }$ satisfying the following conditions, denoted by Condition ${\mathcal{C}}_{time-delay}(\Sigma )$, where $\Sigma \in {\mathbb{R}}^{n\times (m+1)}$:

1.

$f^p(x,x_{{\tau }_1},\dots x_{{\tau }_m},r\left(t\right))=(f_1^p,f_2^p,\dots ,f_m^p):{\mathbb{R}}^{n\times (m+1)}\times {\mathbb{R}}^{+}\to {\mathbb{R}}^n$ is continuous and continuously differentiable with respect to $(x,x_{{\tau }_1},\dots x_{{\tau }_m})$, and continuous with respect to $(x,x_{{\tau }_1},\dots x_{{\tau }_m},r)$. Moreover, $f_i^p,i=1,\dots ,m$ satisfies local Lipschitz conditions for $(x,x_{{\tau }_1},\dots x_{{\tau }_m})\in \Sigma$.

2.

For each $t\ge t_0$ and compact set $\Sigma \subset {\mathbb{R}}^{n\times (m+1)}$,

$$\begin{array}{c}\hfill \underset{m\to \infty }{lim}{d}_H\left\{Graph\left(f^p(\Sigma ,r\left(t\right))\right),Graph\left(F(\Sigma ,r\left(t\right))\right)\right\}=0\end{array}$$

holds, where $F(x,x_{{\tau }_1},\dots x_{{\tau }_m},r\left(t\right))=\mathcal{K}\left[f\right](x,x_{{\tau }_1},\dots x_{{\tau }_m},r\left(t\right))$ and $d_H$ represents the Hausdorff metric. $Graph\left(F\right)$ and $Graph\left(f^p\right)$ are considered on ${\mathbb{R}}^{m\times (n+1)}\times [t_0,+\infty )$, where $Graph\left(F(x,x_{{\tau }_1},\dots x_{{\tau }_m},r\left(t\right))\right)=\{(x,t,y):y\in F(x,x_{{\tau }_1},\dots x_{{\tau }_m},r\left(t\right)),$$(x,x_{{\tau }_1},\dots x_{{\tau }_m})\in \Sigma ,t\ge t_0\}$, and so it is with $Graph\left(f^p(x,x_{{\tau }_1},\dots x_{{\tau }_m},r\left(t\right))\right)$.

3. 

For any compact set $\Sigma \subset {\mathbb{R}}^{m\times (n+1)}$, there exists measure $w(·)$, defined as $w(\Sigma )=q\left(\lambda \right(\Sigma \left)\right)$, in which $\lambda$ represents the Lebesgue measure, q is a measurable function mapping ${\mathbb{R}}^{+}$ to ${\mathbb{R}}^{+}$, such that $|f^p(x,x_{{\tau }_1},\dots x_{{\tau }_m},t)|\le w(\Sigma )$ holds for each $(x,x_{{\tau }_1},\dots x_{{\tau }_m})\in \Sigma$ and $t\ge t_0$.

Thus, we have the following conclusion on incremental stability of time-delay systems with discontinuous right-hand sides:

Theorem 4. 

Suppose that system (13) has a unique solution, and there exists a sequence of functions ${\left\{f^p\right\}}_{p=1}^{\infty }$ satisfying Condition ${\mathcal{C}}_{time-delay}(\Sigma )$. $\chi \left(t\right)$ is a right-continuous staircase function with discontinuities in $\{t_1,\dots ,t_j,\dots \}$. Let $N\left(t\right)=\#\{j:t\ge t_j,j=1,2,\dots \}$, and suppose that there exist

1. 

A constant $T_0>0$,

2. 

Positive constants ${\gamma }_k(k=0,1,\dots )$, ${\gamma }_0\le {\gamma }_1\le \dots$,

3. 

$C(\chi \left(t\right),\chi \left(t^{\prime }\right))\le C_0$ for any $t,t^{\prime }\ge t_0$,

such that the following conditions hold:

Let $A^p\left(t\right)=(\partial f^p/\partial x)(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))$, $B_k^p\left(t\right)=(\partial f^p/\partial x_{{\tau }_k})(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))$, $k=1,\dots ,m$, there exist matrix-valued functions $B_{1k}^p\left(t\right)$, $B_{2k}^p\left(t\right)$, $B_{1k}^p\left(t\right)+B_{2k}^p\left(t\right)=B_k^p\left(t\right)$ such that

$${\nu }_{\chi \left(t\right)}(A^p\left(t\right)+\sum _{k=1}^m{B}_{1k}^p\left(t\right))+\sum _{k=1}^m{\tau }_k\left(t\right)\parallel B_{1k}^p{\left(t\right)\parallel }_{\chi \left(t\right)}({\tilde{A}}_k^p\left(t\right)+{\tilde{B}}_k^p\left(t\right))+\sum _{k=1}^m{\parallel B_{2k}^p\left(t\right)\parallel }_{\chi \left(t\right)}\frac{exp\left({\gamma }_{N\left(t\right)}t\right)}{exp\left({\gamma }_{N(t-{\tau }_k\left(t\right))}(t-{\tau }_k\left(t\right))\right)}\le -{\gamma }_{N\left(t\right)}$$

where

$$\begin{array}{cc}\hfill {\tilde{A}}_k^p\left(t\right)=& \underset{t-{\tau }_k\left(t\right)\le s\le t}{sup}{\parallel A^p\left(s\right)\parallel }_{\chi \left(t\right)}exp\left({\gamma }_{N\left(t\right)}t-{\gamma }_{N\left(s\right)}s\right)\hfill \\ \hfill {\tilde{B}}_k^p\left(t\right)=& \underset{t-{\tau }_k\left(t\right)\le s\le t}{sup}{\parallel B_k^p\left(s\right)\parallel }_{\chi \left(t\right)}exp\left({\gamma }_{N\left(t\right)}t-{\gamma }_{N(s-{\tau }_k\left(s\right))}(s-{\tau }_k\left(s\right))\right).\hfill \end{array}$$

and for any $t>T_0$,

$$\frac{1}{t}\left[\sum _{i=0}^{N\left(t\right)-1}[({\gamma }_{i+1}-{\gamma }_i)t_{i+1}+log{\beta }_{i+1}]+{\gamma }_0{t}_0-{\gamma }_{N\left(t\right)}t\right]\le -c,$$

where ${\beta }_k=C(\chi \left(t_k\right),\chi (t_k-))$, then system (6) is exponentially incrementally stable in Σ for $t\in [t_0,+\infty )$.

Proof. 

First, we construct a sequence of functions satisfying Condition ${\mathcal{C}}_{time-delay}(\Sigma )$, and the corresponding sequence of time-delay system:

$$\dot{x}\left(t\right)=f^p(x,x_{{\tau }_1},\dots x_{{\tau }_m},r\left(t\right))$$

(14)

in which, according to Condition ${\mathcal{C}}_{time-delay}(\Sigma )$, $f_i,i=1,\dots ,m$ satisfy local Lipschitz conditions, so it can be seen that (14) has a unique solution for $t\in {\mathbb{R}}^{+}$.

Therefore, from Theorem 1, for each p, system (14) is exponentially incrementally stable.

Denote any two of the solutions of (6) with different initial function $x_0(·)$ and $y_0(·)$ by $x\left(t\right)$ and $y\left(t\right)$. Then, here, try to approximate $x\left(t\right)$ and $y\left(t\right)$ by two sequences of solutions of (14), denoted by $x^p$ and $y^p$, respectively. The initial functions $x_0\left(s\right)$ and $y_0\left(s\right)$ here are defined for $s\in [t_0-\overline{\tau },t_0]$, where $\overline{\tau }={max}_k{sup}_{s\in [t_0,+\infty )}{\tau }_k\left(s\right)$.

With $f^p$ satisfying condition ${\mathcal{C}}_{time-delay}(\Sigma )$, for each given T, $t_0\le t\le T$, we have $x^p\left(t\right)$ and ${\dot{x}}^p\left(t\right)$ are bounded regarding $(x_0(·),T)$. It is the same with $y^p\left(t\right)$. Thus, $x^p\left(t\right)$ ($y^p\left(t\right)$) is uniformly bounded on $[t_0,T]$, and ${\dot{x}}^p\left(t\right)$ (${\dot{y}}^p\left(t\right)$) is uniformly bounded on $[t_0,T]$ as well.

Because of Condition 1 in ${\mathcal{C}}_{time-delay}(\Sigma )$, $x^p\left(t\right)$ ($y^p\left(t\right)$) is continuous with respect to t. Together with Condition 3 in ${\mathcal{C}}_{time-delay}(\Sigma )$, we conclude that $x^p\left(t\right)$ ($y^p\left(t\right)$), $p\in {\mathbb{N}}^{+}$ are equicontinuous for $t\in [t_0,T]$.

Here, we present the Arzela–Ascoli lemma (similar to Theorem 2.2 in [43]):

Lemma 3. 

(Arzela–Ascoli Lemma) X is a compact set on ${\mathbb{R}}^n$. If a sequence ${\left\{f_n\right\}}_1^{\infty }$ in $C\left(X\right)$ is bounded and equicontinuous, then it has a uniformly convergent subsequence.

From Lemma 3, one can find a sub-sequence of ${\left\{x^p\left(t\right)\right\}}_{p\in {\mathbb{N}}^{+}}$ and ${\left\{y^p\left(t\right)\right\}}_{p\in {\mathbb{N}}^{+}}$ (still denoted by $x^m\left(t\right)$ and $y^m\left(t\right)$) satisfying that $x^p\left(t\right)$ ($y^p$(t)) uniformly converges to a continuous function $x^{*}\left(t\right)$ ($y^{*}\left(t\right)$) on $[t_0,T]$, $T\in (t_0,+\infty ]$. For all $k\in {\mathbb{N}}^{+}$, one can find a subsequence ${\left\{x^{kj}\left(t\right)\right\}}_{j\in {\mathbb{N}}^{+}}$ of ${\left\{x^p\left(t\right)\right\}}_{p\in {\mathbb{N}}^{+}}$ such that $|x^{kj}\left(t\right)-x^{*}\left(t\right)|<\frac{1}{j}$ holds on the interval $[t_0,t_0+k+1]$. Then, by diagonal selection principle, select a new subsequence ${\left\{x^{kk}\left(t\right)\right\}}_{k\in {\mathbb{N}}^{+}}$ such that ${\left\{x^{kk}\left(t\right)\right\}}_{k\in {\mathbb{N}}^{+}}$ uniformly converges to a continuous function $x^{*}\left(t\right)$ on $[t_0,T]$, $T\in (t_0,+\infty ]$. It is the same with $x_{{\tau }_k}^{*}\left(t\right)$, for $k=1,\dots ,m$.

The system ${\dot{x}}^p\left(t\right)=f^p(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))$ has a unique solution. $x^p\left(t\right)$ satisfies Lipschitz condition:

$$\begin{array}{c}\hfill |x^p\left(t\right)-x^p\left(t^{\prime }\right){|}_{\chi \left(t_0\right)}\le L{|t-t^{\prime }|}_{\chi \left(t_0\right)}\end{array}$$

where $t,t^{\prime }\in [t_0,T]$, $L>0$. Because of norm equivalence, the Lipschitz condition above also holds with other norms defined in ${\mathbb{R}}^n$. Therefore, $x^{*}\left(t\right)$ ($y^{*}\left(t\right)$) also satisfies the Lipschitz condition, that is, ${\dot{x}}^{*}\left(t\right)$ (${\dot{y}}^{*}\left(t\right)$) exists and is bounded and measurable for $[t_0,T)$, $T\in (t_0,+\infty ]$.

We then have the conclusion that ${\dot{x}}^p\left(t\right)$ (${\dot{y}}^p\left(t\right)$) weakly converges to ${\dot{x}}^{*}\left(t\right)$ (${\dot{y}}^{*}\left(t\right)$) on the space $L_1([t_0,T],{\mathbb{R}}^n)$, the demonstrations are as follows.

$C_0^{\infty }([t_0,T],{\mathbb{R}}^n)$ is dense in the Banach space $L^{\infty }([t_0,T],{\mathbb{R}}^n)$, which is the conjugate space $L_1([t_0,T],{\mathbb{R}}^n)$. Therefore, the following equation

$$\begin{array}{c}\hfill {\int }_{t_0}^T\langle {\dot{x}}^p\left(t\right)-{\dot{x}}^{*},q\left(t\right)\rangle dt=-{\int }_{t_0}^T\langle \dot{q}\left(t\right),x^p\left(t\right)-x^{*}\rangle dt.\end{array}$$

holds for each $q\left(t\right)\in C_0^{\infty }([t_0,T],{\mathbb{R}}^n)$. Since $\left\{{\dot{x}}^p\left(t\right)\right\}$ is bounded for each p, from the Lebesgue-dominant convergence theorem we have

$$\begin{array}{c}\hfill \underset{p\to \infty }{lim}{\int }_{t_0}^T\langle {\dot{x}}^p\left(t\right)-{\dot{x}}^{*},q\left(t\right)\rangle dt=-{\int }_{t_0}^T\langle \dot{q}\left(t\right),\underset{p\to \infty }{lim}{x}^p\left(t\right)-x^{*}\left(t\right)\rangle dt=0.\end{array}$$

That is, $\left\{{\dot{x}}^p\left(t\right)\right\}$ weakly converges to ${\dot{x}}^{*}\left(t\right)$ on the space $L_1([t_0,T],{\mathbb{R}}^n)$.

With Mazur’s convexity theorem [43], one can find $a_l^n$ ($b_l^n$) with ${\sum }_{l=1}^m{a}_l^m=1$ (${\sum }_{l=1}^m{b}_l^m=1$) such that ${\dot{\tilde{x}}}^p$ converges to ${\dot{x}}^{*}\left(t\right)$ almost everywhere on $[t_0,T]$, where ${\tilde{x}}^p\left(t\right)={\sum }_{l=1}^p{a}_l^p{x}^p$. Notice that ${\tilde{x}}^p$ is in the convex closure of $\left\{x^p\right\}$, ${\dot{\tilde{x}}}^p$ converges to ${\dot{x}}^{*}$ uniformly. So it is with ${\dot{\tilde{y}}}^p\left(t\right)$ with ${\tilde{y}}^p\left(t\right)={\sum }_{l=1}^p{b}_l^p{y}^p$, and it is the same with $\left\{{\dot{x}}_{{\tau }_k}^p\left(t\right)\right\}$ and $\left\{{\dot{x}}_{{\tau }_k}^{*}\left(t\right)\right\}$.

Recall Condition 3 in ${\mathcal{C}}_{time-delay}(\Sigma )$. For $\Sigma \in {\mathbb{R}}^n$, it holds that

$$\begin{array}{c}\hfill \underset{p\to \infty }{lim}{d}_H\left\{Graph\left(f^p(\Sigma ,t)\right),Graph\left(F(\Sigma ,t)\right)\right\}=0,\forall t\ge t_0,\end{array}$$

With ${\dot{\tilde{x}}}^p\left(t\right)$ in the convex closure of $\left\{f^p(x^p,x_{{\tau }_1}^p,\dots ,x_{{\tau }_m}^p,r\left(t\right))\right\}$, for any $ϵ>0$, there exists $N>0$ such that ${\dot{x}}^p\left(t\right)\in B(F(x^{*},x_{{\tau }_1}^{*},\dots ,x_{{\tau }_m}^{*},r\left(t\right)),ϵ)$ for all $p>N$ and $(x^{*},x_{{\tau }_1}^{*},\dots ,x_{{\tau }_m}^{*}),$$(x^p,x_{{\tau }_1}^p,\dots ,x_{{\tau }_m}^p)\in \Sigma$, $t\in [t_0,T]$.

Since $ϵ$ can be arbitrarily small, it can be seen that ${\dot{x}}^{*}\left(t\right)\in F(x^{*},x_{{\tau }_1}^{*},\dots ,x_{{\tau }_m}^{*},r\left(t\right))$ with $x^{*}\in \Sigma$, which infers that the solution of (6) equals to $x^{*}\left(t\right)$ in $\Sigma$ almost everywhere on $[t_0,T]$. For $x\left(t\right)$ and $x^{*}$, both are continuous because ${\tilde{x}}^p$ converges to $x^{*}$ uniformly on $[t_0,T]$, it can be seen that $x^{*}$ is the solution of (6). So it is with $y^{*}\left(t\right)$.

Because system (6) has a unique solution, $x\left(t\right)=x^{*}\left(t\right)$ and $y\left(t\right)=y^{*}\left(t\right)$ almost everywhere for $t\ge t_0$. That is, $x^p$ converges to $x\left(t\right)$ uniformly in $[t_0,T]$, $T\in (t_0,+\infty ]$. A similar proof can be applied to $y^p\left(t\right)$ and $y\left(t\right)$.

For $\left\{f^p(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))\right\}$ is exponentially incrementally stable from Theorem 1, there exists some $M>0$ and $\alpha >0$,

$$\begin{array}{c}\hfill |x^p\left(t\right)-y^p{\left(t\right)|}_{\chi \left(t_0\right)}\le M{e}^{-\alpha (t-t_0)}\underset{s\in [t_0-\overline{\tau },t_0]}{sup}{|x_0\left(s\right)-y_0\left(s\right)|}_{\chi \left(t_0\right)}\end{array}$$

for all $p\in {\mathbb{N}}^{+}$ and $t\ge t_0$. For each given $t\ge t_0$, let $ϵ\left(t\right)=3M{e}^{-\alpha (t-t_0)}{sup}_{s\in [t_0-\overline{\tau },t_0]}{|x_0\left(s\right)-y_0\left(s\right)|}_{\chi \left(t_0\right)}$, there exists some $p_0(ϵ,t)$ with which $|x^p{\left(t\right)-x\left(t\right)|}_{\chi \left(t_0\right)}\le ϵ/3$ and $|y^p{\left(t\right)-y\left(t\right)|}_{\chi \left(t_0\right)}\le ϵ/3$ hold for $p\ge p_0(ϵ,t)$, which implies that

$$\begin{array}{ccc}\hfill {|x\left(t\right)-y\left(t\right)|}_{\chi \left(t_0\right)}& \le & |x\left(t\right)-x^p{\left(t\right)|}_{\chi \left(t_0\right)}+|y\left(t\right)-y^p{\left(t\right)|}_{\chi \left(t_0\right)}+{|x^p\left(t\right)-y^p\left(t\right)|}_{\chi \left(t_0\right)}\hfill \\ & \le & ϵ=3M{e}^{-\alpha (t-t_0)}\underset{s\in [t_0-\overline{\tau },t_0]}{sup}{|x_0\left(s\right)-y_0\left(s\right)|}_{\chi \left(t_0\right)}.\hfill \end{array}$$

This completes the proof. □

Remark 2. 

Similar to Theorem 4, Corollary 1 and Corollary 2 can also be extended to discontinuous cases.

5. Applications

In this section, with the conclusion in Theorem 4, the applications to switched time-delay systems and Hopfield time-delay systems are given.

5.1. Linear Switched Time-Delay System

Consider the following linear switched time-delay system:

$$\dot{x}\left(t\right)=f(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},t)=\left\{\begin{array}{cc}{A}_1\left(t\right)x\left(t\right)+\sum _{k=1}^m{B}_{1k}\left(t\right)x(t-{\tau }_k\left(t\right))+J_1\left(t\right),\hfill & \varphi (x,x_{{\tau }_1},\dots ,x_{{\tau }_m})>0\hfill \\ A_2\left(t\right)x\left(t\right)+\sum _{k=1}^m{B}_{2k}\left(t\right)x(t-{\tau }_k\left(t\right))+J_2\left(t\right),\hfill & \varphi (x,x_{{\tau }_1},\dots ,x_{{\tau }_m})<0\hfill \end{array}\right..$$

(15)

in which $x\left(t\right)\in {\mathbb{R}}^n$, $A_1\left(t\right),A_2\left(t\right)\in {\mathbb{R}}^{n\times n}$, $B_{1k}\left(t\right),B_{2k}\left(t\right)(k=1,\dots ,m)\in {\mathbb{R}}^{n\times n}$ is piecewise continuous, bounded matrix-valued functions, whose discontinuities are in $\{t_1,t_2\dots .t_i,\dots \}$. Take a simple bimodal system as an example, with the switching surface $S=\{(x,x_{{\tau }_1},\dots ,x_{{\tau }_m}):$$\varphi (x,x_{{\tau }_1},\dots ,x_{{\tau }_m})=0\}$.

In order to guarantee the uniqueness of the Filippov solution for system (15), the linear time-delay system satisfies the following hypothesis:

Assumption 4. 

The linear time-delay system (15) satisfies:

1. 

The right-hand function of system (15) satisfies Assumption 3.

2. 

For each point $(x,x_{{\tau }_1},\dots ,x_{{\tau }_m})\in S$, the time-delay system (15) satisfies

$$\frac{\partial \varphi }{\partial x}(x,x_{{\tau }_1},\dots ,x_{{\tau }_m})·\left((A_1\left(t\right)-A_2\left(t\right))x+\sum _{k=1}^m(B_{1k}\left(t\right)-B_{2k}\left(t\right))x_{{\tau }_k}+J_1\left(t\right)-J_2\left(t\right)\right)<0$$

Under the definitions and Assumption 4 above, from Lemma 2 and Theorem 3, it can be obtained that system (15) has a unique solution.

Assumption 5. 

Suppose that in the continuous regions, the right-hand side $f(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},t)$ satisfies the conditions for exponential incremental stability in Theorem 1, which are formulated as follows.

Let $N\left(t\right)=\#\{j:t\ge t_j,j=1,2,\dots \}$, $\chi \left(t\right)$ be a right-continuous staircase function with its discontinuous points belonging to $\{t_1,\dots ,t_j,\dots \}$, and there exist

1. 

A constant $T_0>0$,

2. 

Positive constants ${\gamma }_k(k=0,1,\dots )$, ${\gamma }_0\le {\gamma }_1\le \dots$,

3. 

$C(\chi \left(t\right),\chi \left(t^{\prime }\right))\le C_0$ for any $t,t^{\prime }\ge t_0$,

4. 

Matrix $B_{1k}^{\left(1\right)},B_{1k}^{\left(2\right)},B_{2k}^{\left(1\right)},B_{2k}^{\left(2\right)}\in {\mathbb{R}}^{n\times n}$ satisfying that $B_{1k}^{\left(1\right)}\left(t\right)+B_{1k}^{\left(2\right)}\left(t\right)=B_{1k}\left(t\right)$ and $B_{2k}^{\left(1\right)}\left(t\right)+B_{2k}^{\left(2\right)}\left(t\right)=B_{2k}\left(t\right)$,

such that the following conditions are satisfied:

$$\begin{array}{cc}\hfill L_1\left(t\right)=& {\nu }_{\chi \left(t\right)}(A_1\left(t\right)+\sum _{k=1}^m{B}_{1k}^{\left(1\right)}\left(t\right))+\sum _{k=1}^m{\tau }_k\left(t\right)({\tilde{A}}_{1k}\left(t\right)+{\tilde{B}}_{1k}\left(t\right)){\parallel B_{1k}^{\left(1\right)}\left(t\right)\parallel }_{\chi \left(t\right)}\hfill \\ \hfill & +\sum _{k=1}^m{\parallel B_{1k}^{\left(2\right)}\left(t\right)\parallel }_{\chi \left(t\right)}\frac{exp\left({\gamma }_{N\left(t\right)}t\right)}{exp\left({\gamma }_{N(t-{\tau }_k\left(t\right))}(t-{\tau }_k\left(t\right))\right)}\le -{\gamma }_{N\left(t\right)}\hfill \\ \hfill L_2\left(t\right)=& {\nu }_{\chi \left(t\right)}(A_2\left(t\right)+\sum _{k=1}^m{B}_{2k}^{\left(1\right)}\left(t\right))+\sum _{k=1}^m{\tau }_k\left(t\right)({\tilde{A}}_{2k}\left(t\right)+{\tilde{B}}_{2k}\left(t\right)){\parallel B_{2k}^{\left(1\right)}\left(t\right)\parallel }_{\chi \left(t\right)}\hfill \\ \hfill & +\sum _{k=1}^m{\parallel B_{2k}^{\left(2\right)}\left(t\right)\parallel }_{\chi \left(t\right)}\frac{exp\left({\gamma }_{N\left(t\right)}t\right)}{exp\left({\gamma }_{N(t-{\tau }_k\left(t\right))}(t-{\tau }_k\left(t\right))\right)}\le -{\gamma }_{N\left(t\right)}\hfill \end{array}$$

in which, for $i=1,2$,

$$\begin{array}{cc}\hfill {\tilde{A}}_{ik}\left(t\right)=& \underset{t-{\tau }_k\left(t\right)\le s\le t}{sup}{\parallel A_i\left(s\right)\parallel }_{\chi \left(t\right)}exp\left({\gamma }_{N\left(t\right)}t-{\gamma }_{N\left(s\right)}s\right)\hfill \\ \hfill {\tilde{B}}_{ik}\left(t\right)=& \underset{t-{\tau }_k\left(t\right)\le s\le t}{sup}{\parallel B_{ik}\left(s\right)\parallel }_{\chi \left(t\right)}exp\left({\gamma }_{N\left(t\right)}t-{\gamma }_{N(s-{\tau }_k\left(s\right))}(s-{\tau }_k\left(s\right))\right)\hfill \end{array}$$

and for all $t>T_0$,

$$\frac{1}{t}\left[\sum _{i=0}^{N\left(t\right)-1}[({\gamma }_{i+1}-{\gamma }_i)t_{i+1}+log{\beta }_{i+1}]+{\gamma }_0{t}_0-{\gamma }_{N\left(t\right)}t\right]\le -c,$$

(16)

where ${\beta }_k=C(\chi \left(t_k\right),\chi (t_k-))$.

Thus, together with Theorem 4, we have the following corollary on incremental stability for bimodal linear time-delay systems.

Corollary 3. 

Suppose that time-delay system (15) satisfies Assumptions 4 and 5. Meanwhile, in the neighborhood of switching surface S, that is, when $-\delta /2<\varphi (x,x_{{\tau }_1},\dots ,x_{{\tau }_m})<\delta /2$, let $w=(A_1\left(t\right)-A_2\left(t\right))x\left(t\right)+{\sum }_{k=1}^m(B_{1k}\left(t\right)-B_{2k}\left(t\right))x(t-{\tau }_k\left(t\right))+J_1\left(t\right)-J_2\left(t\right)$, if it is satisfied that

$$\begin{array}{cc}& p{L}_1\left(t\right)+(1-p)L_2\left(t\right)+\frac{1}{\delta }{\nu }_{\chi \left(t\right)}\left(w·\frac{\partial \varphi }{\partial x}\right)+\frac{1}{\delta }\sum _{k=1}^m\parallel w·\frac{\partial \varphi }{\partial x_{{\tau }_k}}{\parallel }_{\chi \left(t\right)}\frac{exp\left({\gamma }_{N\left(t\right)}t\right)}{exp\left({\gamma }_{N(t-{\tau }_k\left(t\right))}(t-{\tau }_k\left(t\right))\right)}\hfill \\ & +p(1-p)\sum _{k=1}^m{\tau }_k\left(t\right)\left[\right(\parallel B_{1k}^{\left(1\right)}{\parallel }_{\chi \left(t\right)}-\parallel B_{2k}^{\left(1\right)}{\parallel }_{\chi \left(t\right)})({\tilde{A}}_2^k\left(t\right)-{\tilde{A}}_1^k\left(t\right)+{\tilde{B}}_{2k}\left(t\right)-{\tilde{B}}_{1k}\left(t\right))\hfill \\ & +\frac{1}{\delta }\parallel p{B}_{1k}^{\left(1\right)}+(1-p)B_{2k}^{\left(1\right)}{\parallel }_{\chi \left(t\right)}\left(\underset{t-{\tau }_k\left(t\right)\le s\le t}{sup}\parallel w·\frac{\partial \varphi }{\partial x}{\parallel }_{\chi \left(t\right)}\frac{exp\left({\gamma }_{N\left(t\right)}t\right)}{exp\left({\gamma }_{N\left(s\right)}s\right)}+\parallel w·\frac{\partial \varphi }{\partial x_{{\tau }_k}}{\parallel }_{\chi \left(t\right)}\frac{exp\left({\gamma }_{N\left(t\right)}t\right)}{exp\left({\gamma }_{N(s-{\tau }_k\left(s\right))}(s-{\tau }_k\left(s\right))\right)}\right)]\hfill \\ & \le -{\gamma }_{N\left(t\right)}\hfill \end{array}$$

(17)

holds for $-\frac{\delta }{2}<\varphi (x,x_{{\tau }_1},\dots ,x_{{\tau }_m})<\frac{\delta }{2}$ and $p=\sigma (\varphi (x,x_{{\tau }_1},\dots ,x_{{\tau }_m})/\delta )\in [0,1]$, then the linear switched time-delay system (15) is exponentially incrementally stable.

Proof. 

With the conclusion in Theorem 4, by constructing a sequence of time-delay systems with continuous right-hand sides satisfying Condition ${\mathcal{C}}_{time-delay}(\Sigma )$ as follows, we can prove the exponential incremental stability property of system (15):

$$\begin{array}{cc}\hfill \dot{x}=f^{\delta }=& \sigma (\frac{\varphi (x,x_{{\tau }_1},\dots ,x_{{\tau }_m})}{\delta })[A_1\left(t\right)x\left(t\right)+\sum _{k=1}^m{B}_{1k}\left(t\right)x(t-{\tau }_k\left(t\right))+J_1\left(t\right)]\hfill \\ \hfill & +(1-\sigma (\frac{\varphi (x,x_{{\tau }_1},\dots ,x_{{\tau }_m})}{\delta }))[A_2\left(t\right)x\left(t\right)+\sum _{k=1}^m{B}_{2k}\left(t\right)x(t-{\tau }_k\left(t\right))+J_2\left(t\right)]\hfill \end{array}$$

(18)

in which $\sigma (·)$ is defined as

$$\begin{array}{c}\hfill \sigma \left(\rho \right)=\left\{\begin{array}{cc}1,\hfill & \rho >1/2,\hfill \\ \rho +1/2,\hfill & \rho \in [-1/2,1/2],\hfill \\ 0,\hfill & \rho <-1/2.\hfill \end{array}\right.\end{array}$$

let $w=(A_1\left(t\right)-A_2\left(t\right))x\left(t\right)+{\sum }_{k=1}^m(B_{1k}\left(t\right)-B_{2k}\left(t\right))x(t-{\tau }_k\left(t\right))+J_1\left(t\right)-J_2\left(t\right)$ and $p=\sigma (\varphi (x,x_{{\tau }_1},\dots ,x_{{\tau }_m})/\delta )$, the partial derivative of the right-hand function $f^{\delta }$ with respect to x and $x_{{\tau }_k}$ are as follows,

$$\begin{array}{cc}\hfill \frac{\partial f^{\delta }(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))}{\partial x}=& \sigma (\frac{\varphi (x,x_{{\tau }_1},\dots ,x_{{\tau }_m})}{\delta })A_1\left(t\right)+[1-\sigma (\frac{\varphi (x,x_{{\tau }_1},\dots ,x_{{\tau }_m})}{\delta })]A_2\left(t\right)+\frac{1}{\delta }w·\frac{\partial \varphi }{\partial x}\hfill \\ \hfill \frac{\partial f^{\delta }(x,x_{{\tau }_1},\dots ,x_{{\tau }_m},r\left(t\right))}{\partial x_{{\tau }_k}}=& \sigma (\frac{\varphi (x,x_{{\tau }_1},\dots ,x_{{\tau }_m})}{\delta })B_{1k}\left(t\right)+[1-\sigma (\frac{\varphi (x,x_{{\tau }_1},\dots ,x_{{\tau }_m})}{\delta })]B_{2k}\left(t\right)+\frac{1}{\delta }w·\frac{\partial \varphi }{\partial x_{{\tau }_k}}\hfill \end{array}$$

Thus, it needs to satisfy

$$\begin{array}{cc}\hfill L(f^{\delta },t)=& {\nu }_{\chi \left(t\right)}\left(p{A}_1+(1-p)A_2+\frac{1}{\delta }w·\frac{\partial \varphi }{\partial x}+\sum _{k=1}^m[p{B}_{1k}^{\left(1\right)}+(1-p)B_{2k}^{\left(1\right)}]\right)\hfill \\ & +\sum _{k=1}^m{\tau }_k\left(t\right)({\tilde{U}}_k\left(t\right)+{\tilde{V}}_k\left(t\right))\parallel p{B}_{1k}^{\left(1\right)}+(1-p)B_{2k}^{\left(1\right)}{\parallel }_{\chi \left(t\right)}\hfill \\ & +\sum _{k=1}^m\parallel p{B}_{1k}^{\left(2\right)}+(1-p)B_{2k}^{\left(2\right)}+\frac{1}{\delta }w·\frac{\partial \varphi }{\partial x_{{\tau }_k}}{\parallel }_{\chi \left(t\right)}\frac{exp\left({\gamma }_{N\left(t\right)}t\right)}{exp\left({\gamma }_{N(t-{\tau }_k\left(t\right))}(t-{\tau }_k\left(t\right))\right)}\le -{\gamma }_{N\left(t\right)}\hfill \end{array}$$

in which

$$\begin{array}{cc}\hfill {\tilde{U}}_k\left(t\right)=& \underset{t-{\tau }_k\left(t\right)\le s\le t}{sup}{\parallel \frac{\partial f^{\delta }}{\partial x}(x\left(s\right),x_{{\tau }_1}\left(s\right),\dots ,x_{{\tau }_m}\left(s\right),s)\parallel }_{\chi \left(t_j\right)}exp\left({\gamma }_{N\left(t\right)}t-{\gamma }_{N\left(s\right)}s\right)\hfill \\ \hfill {\tilde{V}}_k\left(t\right)=& \underset{t-{\tau }_k\left(t\right)\le s\le t}{sup}{\parallel \frac{\partial f^{\delta }}{\partial x_{\tau }}(x\left(s\right),x_{{\tau }_1}\left(s\right),\dots ,x_{{\tau }_m}\left(s\right),s)\parallel }_{\chi \left(t_j\right)}exp({\gamma }_{N\left(t\right)}t-{\gamma }_{N(s-{\tau }_k\left(s\right))}(s-{\tau }_k\left(s\right)))\hfill \end{array}$$

where $t\in [t_j,t_{j+1})$. That is,

$$\begin{array}{cc}\hfill L(f^{\delta },t)\le & p{L}_1\left(t\right)+[1-p]L_2\left(t\right)+\frac{1}{\delta }{\nu }_{\chi \left(t\right)}\left(w·\frac{\partial \varphi }{\partial x}\right)+\frac{1}{\delta }\sum _{k=1}^m\parallel w·\frac{\partial \varphi }{\partial x_{{\tau }_k}}{\parallel }_{\chi \left(t\right)}\frac{exp\left({\gamma }_{N\left(t\right)}t\right)}{exp\left({\gamma }_{N(t-{\tau }_k\left(t\right))}(t-{\tau }_k\left(t\right))\right)}\hfill \\ & +p(1-p)\sum _{k=1}^m{\tau }_k\left(t\right)\left[\right(\parallel B_{1k}^{\left(1\right)}{\parallel }_{\chi \left(t\right)}-\parallel B_{2k}^{\left(1\right)}{\parallel }_{\chi \left(t\right)})({\tilde{A}}_2^k\left(t\right)-{\tilde{A}}_1^k\left(t\right)+{\tilde{B}}_{2k}\left(t\right)-{\tilde{B}}_{1k}\left(t\right))\hfill \\ & +\frac{1}{\delta }\parallel p{B}_{1k}^{\left(1\right)}+(1-p)B_{2k}^{\left(1\right)}{\parallel }_{\chi \left(t\right)}\left(\underset{t-{\tau }_k\left(t\right)\le s\le t}{sup}\parallel w·\frac{\partial \varphi }{\partial x}{\parallel }_{\chi \left(t\right)}\frac{exp\left({\gamma }_{N\left(t\right)}t\right)}{exp\left({\gamma }_{N\left(s\right)}s\right)}+\parallel w·\frac{\partial \varphi }{\partial x_{{\tau }_k}}{\parallel }_{\chi \left(t\right)}\frac{exp\left({\gamma }_{N\left(t\right)}t\right)}{exp\left({\gamma }_{N(s-{\tau }_k\left(s\right))}(s-{\tau }_k\left(s\right))\right)}\right)]\hfill \end{array}$$

Together with (17), it infers that $L(f^{\delta },t)\le -{\gamma }_{N\left(t\right)}$, that is, system (18) is exponentially incrementally stable for each $\delta =\frac{1}{m},m\in {\mathbb{N}}^{+}$. From Theorem 4, it can be proved that the time-delay system is exponentially incrementally stable. □

Here, let $B_{1k}^{\left(1\right)}=B_{2k}^{\left(1\right)}=0,(k=1,\dots ,m)$, we have the following corollary, which is a variant of Corollary 3.

Corollary 4. 

Let $N\left(t\right)=\#\{j:t\ge t_j,j=1,2,\dots \}$, and suppose that system (15) satisfies Assumption 4, and there exist

1. 

A constant $T_0>0$,

2. 

Positive constants ${\gamma }_k(k=0,1,\dots )$, ${\gamma }_0\le {\gamma }_1\le \dots$,

3. 

$C(\chi \left(t\right),\chi \left(t^{\prime }\right))\le C_0$ for any $t,t^{\prime }\ge t_0$,

such that the following conditions are satisfied:

$$\begin{array}{cc}\hfill L_1\left(t\right)=& {\nu }_{\chi \left(t\right)}\left(A_1\left(t\right)\right)+\sum _{k=1}^m{\parallel B_{1k}\left(t\right)\parallel }_{\chi \left(t\right)}\frac{exp\left({\gamma }_{N\left(t\right)}t\right)}{exp\left({\gamma }_{N(t-{\tau }_k\left(t\right))}(t-{\tau }_k\left(t\right))\right)}\le -{\gamma }_{N\left(t\right)}\hfill \\ \hfill L_2\left(t\right)=& {\nu }_{\chi \left(t\right)}\left(A_2\left(t\right)\right)+\sum _{k=1}^m{\parallel B_{2k}\left(t\right)\parallel }_{\chi \left(t\right)}\frac{exp\left({\gamma }_{N\left(t\right)}t\right)}{exp\left({\gamma }_{N(t-{\tau }_k\left(t\right))}(t-{\tau }_k\left(t\right))\right)}\le -{\gamma }_{N\left(t\right)}\hfill \end{array}$$

and for all $t>T_0$,

$$\frac{1}{t}\left[\sum _{i=0}^{N\left(t\right)-1}[({\gamma }_{i+1}-{\gamma }_i)t_{i+1}+log{\beta }_{i+1}]+{\gamma }_0{t}_0-{\gamma }_{N\left(t\right)}t\right]\le -c,$$

where ${\beta }_k=C(\chi \left(t_k\right),\chi (t_k-))$. Moreover, in the neighborhood of switching surface S, that is, when $-\delta /2<\varphi (x,x_{{\tau }_1},\dots ,x_{{\tau }_m})<\delta /2$, let $w=(A_1\left(t\right)-A_2\left(t\right))x\left(t\right)+{\sum }_{k=1}^m(B_{1k}\left(t\right)-B_{2k}\left(t\right))x(t-{\tau }_k\left(t\right))+J_1\left(t\right)-J_2\left(t\right)$, if it is satisfied that

$$\begin{array}{cc}\hfill & p{L}_1\left(t\right)+(1-p)L_2\left(t\right)+\frac{1}{\delta }{\nu }_{\chi \left(t\right)}\left(w·\frac{\partial \varphi }{\partial x}\right)+\frac{1}{\delta }\sum _{k=1}^m\parallel w·\frac{\partial \varphi }{\partial x_{{\tau }_k}}{\parallel }_{\chi \left(t\right)}\frac{exp\left({\gamma }_{N\left(t\right)}t\right)}{exp\left({\gamma }_{N(t-{\tau }_k\left(t\right))}(t-{\tau }_k\left(t\right))\right)}\le -{\gamma }_{N\left(t\right)}\hfill \end{array}$$

holds for $-\delta /2<\varphi (x,x_{{\tau }_1},\dots ,x_{{\tau }_m})<\delta /2$ and $p=\varphi (x,x_{{\tau }_1},\dots ,x_{{\tau }_m})/\delta \in [0,1]$, then the linear switched time-delay system (15) is exponentially incrementally stable.

5.2. Hopfield Neural Network Systems with Time Delay

Consider the following Hopfield neural network system with time delay:

$$\dot{x}\left(t\right)=-D\left(t\right)x\left(t\right)+T\left(t\right)g\left(x\left(t\right)\right)+S\left(t\right)u\left(x_{\tau }\left(t\right)\right))+J\left(t\right)$$

(19)

where $x={(x_1,x_2,\dots ,x_n)}^{\top }$ is the state variable, the time-delay term $x_{\tau }\left(t\right)=x(t-\tau \left(t\right))$. For any $t\in {\mathbb{R}}^{+}$, $D\left(t\right)=diag\{d_1\left(t\right),\dots ,d_n\left(t\right)\}$, $T\left(t\right)=\left(T_{ij}\left(t\right)\right)\in {\mathbb{R}}^{n,n}$, $S\left(t\right)=\left(S_{ij}\left(t\right)\right)\in {\mathbb{R}}^{n,n}$, $J=(J_1,J_2,\dots ,J_n)\in {\mathbb{R}}^n$ is the input vector, $g\left(x\right)={(g_1\left(x_1\right),g_2\left(x_2\right),\dots ,g_n\left(x_n\right))}^{\top }$, $u\left(x\right)={(u_1\left(x_1\right),u_2\left(x_2\right),\dots ,u_n\left(x_n\right))}^{\top }$.

Here, we list the following hypothesis, denoted by Condition ${\mathcal{C}}_2$:

1.

There exists $\tilde{D}=diag\{D_1,D_2,\dots ,D_n\}$, $D_i>0$, such that $d_i(·)$ is continuous and $\frac{d_i\left({\zeta }_1\right)-d_i\left({\zeta }_2\right)}{{\zeta }_1-{\zeta }_2}\ge D_i$ holds for $i=1,2,\dots ,n$ and ${\zeta }_1\ne {\zeta }_2$.

2.

$g_i(·)$ is non-decreasing and non-trivial in any compact set in $\mathbb{R}$, and each $g_i(·)$ has only finite discontinuous points. Therefore, in any compact set in $\mathbb{R}$, except a finite points ${\rho }_k$, where there exist finite right and left limits $g_i\left({\rho }_k^{+}\right)$ and $g_i\left({\rho }_k^{-}\right)$ with $g_i\left({\rho }_k^{+}\right)>g_i\left({\rho }_k^{-}\right)$, $g_i(·)$ is continuous.

3.

$u_i(·)$ is non-decreasing and non-trivial in any compact set in $\mathbb{R}$, and each $u_i(·)$ has only finite discontinuous points. Therefore, in any compact set in $\mathbb{R}$, except a finite points ${\eta }_k$, where there exist finite right and left limits $u_i\left({\eta }_k^{+}\right)$ and $u_i\left({\eta }_k^{-}\right)$ with $u_i\left({\eta }_k^{+}\right)>u_i\left({\eta }_k^{-}\right)$, $u_i(·)$ is continuous.

4.

Here, define a matrix measure ${\nu }_{\xi ,1}\left(A\right)={max}_j[a_{jj}+{\sum }_{i\ne j}|{\xi }_i{\xi }_j^{-1}{a}_{ij}\left|\right]$ for matrix $A=\left(a_{ij}\right)$, with respect to vector norm ${|·|}_{\xi ,1}$ and matrix norm ${\parallel A\parallel }_{\xi ,1}={\parallel \xi A{\xi }^{-1}\parallel }_1$, where $\xi =diag\{{\xi }_1,\dots ,{\xi }_n\}$. There exists a positive diagonal matrix $\xi \left(r\left(t\right)\right)=diag\{{\xi }_1\left(r\left(t\right)\right),\dots ,$

${\xi }_n\left(r\left(t\right)\right)\}$ such that

$$\begin{array}{c}\hfill {\nu }_{\xi \left(r\right(t\left)\right),1}\left(T\right)=\underset{j}{max}\{T_{jj}\left(t\right)+\sum _{i\ne j}|{\xi }_i\left(r\left(t\right)\right){\xi }_j{\left(r\left(t\right)\right)}^{-1}{T}_{ij}\left(t\right)\left|\right\}\le 0\end{array}$$

holds for $t\in {\mathbb{R}}^{+}$.

Therefore, we have the following corollary:

Corollary 5. 

Suppose the system (19) has a unique solution for $t\in {\mathbb{R}}^{+}$, and satisfies Condition ${\mathcal{C}}_2$ above. Let $N\left(t\right)=\#\{j:t\ge t_j,j=1,2,\dots \}$, and there exists

1. 

Positive piecewise right-continuous function $m\left(t\right)>0$,

2. 

A constant $T_0>0$,

3. 

Positive constants ${\alpha }_k>0(k=0,1,\dots )$,

4. 

$C(r\left(t\right),r\left(t^{\prime }\right))\le C_0$ for any $t,t^{\prime }\ge t_0$,

such that in the continuous regions of g and u,

$${\nu }_{\xi \left(r\right(t\left)\right),1}(-D\left(t\right)+T\left(t\right)\frac{\partial g}{\partial x}(x,x_{\tau }))+\frac{exp\left({\gamma }_{N\left(t\right)}t\right)}{exp\left({\gamma }_{N(t-\tau (t\left)\right)}(t-\tau \left(t\right))\right)}{\parallel S\left(t\right)\frac{\partial u}{\partial x_{\tau }}(x,x_{\tau })\parallel }_{\xi \left(r\right(t\left)\right),1}\le -{\gamma }_{N\left(t\right)}$$

(20)

Let $K_i={min}_k[g_i({\rho }_k+)-g_i({\rho }_k-)]$, $M_i={max}_k[u_i({\gamma }_k+)-u_i({\gamma }_k-)]$, and $K={min}_i{K}_i$, $M={max}_i{M}_i$,

$$K·{\nu }_{\xi \left(r\right(t\left)\right),1}\left(T\left(t\right)\right)+M·\frac{exp\left({\gamma }_{N\left(t\right)}t\right)}{exp\left({\gamma }_{N(t-\tau (t\left)\right)}(t-\tau \left(t\right))\right)}{\parallel S\left(t\right)\parallel }_{\xi \left(r\right(t\left)\right),1}<0$$

(21)

For any $t>T_0$,

$$\frac{1}{t}\left[\sum _{i=0}^{N\left(t\right)-1}[({\gamma }_{i+1}-{\gamma }_i)t_{i+1}+log{\beta }_{i+1}]+{\gamma }_0{t}_0-{\gamma }_{N\left(t\right)}t\right]\le -c,$$

where ${\beta }_k=C(r\left(t_k\right),r(t_k-))$, then system (19) is exponentially incrementally stable.

Proof. 

Suppose that system (19) has a unique solution for $t\in {\mathbb{R}}^{+}$, then we construct a sequence of ‘continuous systems’ as follows,

$$\begin{array}{c}\hfill \dot{x}\left(t\right)=f^{\delta }(x,x_{\tau },t)=-D\left(t\right)x\left(t\right)+T\left(t\right)\tilde{g}\left(x\left(t\right)\right)+S\left(t\right)\tilde{u}\left(x_{\tau }\left(t\right)\right))\end{array}$$

where $\tilde{g}\left(x\right)={({\tilde{g}}_1\left(x_1\right),{\tilde{g}}_2\left(x_2\right),\dots ,{\tilde{g}}_n\left(x_n\right))}^{\top }$, $\tilde{u}\left(x\right)={({\tilde{u}}_1\left(x_1\right),{\tilde{u}}_2\left(x_2\right),\dots ,{\tilde{u}}_n\left(x_n\right))}^{\top }$. For each i, denote one of the discontinuous points of $g_i\left(x\right)$ by ${\rho }_i$, and one of the discontinuous point of $u_i\left(x\right)$ by ${\eta }_i$.

Function ${\tilde{g}}^{\delta }\left(x\right)$ is formulated as follows, if $x_i\notin [{\rho }_i-\frac{\delta }{2},{\rho }_i+\frac{\delta }{2}]$, ${\tilde{g}}_i^{\delta }\left(x_i\right)=g_i\left(x_i\right)$, and if $x_i\in [{\rho }_i-\frac{\delta }{2},{\rho }_i+\frac{\delta }{2}]$,

$$\begin{array}{c}\hfill {\widetilde{g_i}}^{\delta }\left(x_i\right)=\frac{g_i({\rho }_i+\frac{\delta }{2})-g_i({\rho }_i-\frac{\delta }{2})}{\delta }[x_i-{\rho }_i+\frac{\delta }{2}]+g_i({\rho }_i-\frac{\delta }{2}).\end{array}$$

Function $\tilde{u}\left(x\right)$ is similarly constructed. It can be seen that when $\delta \to 0$, the function sequence $f^{\delta }(x,x_{\tau },t)$ converges to the Filippov differential inclusion of the right-hand side of (19), that is, $\left\{f^{\delta }(x,x_{\tau },t)\right\}$ satisfies Condition ${\mathcal{C}}_{time-delay}\left({\mathbb{R}}^{n\times 2}\right)$. Let ${\overline{g}}_i({\rho }_i,\delta )=\frac{g_i({\rho }_i+\frac{\delta }{2})-g_i({\rho }_i-\frac{\delta }{2})}{\delta }$, ${\overline{u}}_i({\eta }_i,\delta )=\frac{u_i({\eta }_i+\frac{\delta }{2})-u_i({\eta }_i-\frac{\delta }{2})}{\delta }$. Here, denote the Jacobi matrix of functions ${\tilde{g}}^{\delta }(·)$ and ${\tilde{u}}^{\delta }(·)$ by matrix $G^{\delta }$ and $U^{\delta }$. In the neighborhood of the discontinuous point,

$$\begin{array}{c}\hfill G^{\delta }=\frac{\partial \tilde{g}\left(x\right)}{\partial x}{\mid }_{x=({\rho }_1,{\rho }_2,\dots ,{\rho }_n)}=diag\{{\overline{g}}_1({\rho }_1,\delta ),{\overline{g}}_2({\rho }_2,\delta ),\dots ,{\overline{g}}_n({\rho }_n,\delta )\}\\ \hfill U^{\delta }=\frac{\partial \tilde{u}\left(x_{\tau }\right)}{\partial x_{\tau }}{\mid }_{x_{\tau }=({\eta }_1,{\eta }_2,\dots ,{\eta }_n)}=diag\{{\overline{u}}_1({\eta }_1,\delta ),{\overline{u}}_2({\eta }_2,\delta ),\dots ,{\overline{u}}_n({\eta }_n,\delta )\}\end{array}$$

that is, we have

$$\begin{array}{cc}\hfill & \frac{\partial f^{\delta }(x,x_{\tau },t)}{\partial x}=-D\left(t\right)+T\left(t\right)G^{\delta },\hfill \\ \hfill & \frac{\partial f^{\delta }(x,x_{\tau },t)}{\partial x_{\tau }}=S\left(t\right)U^{\delta },\hfill \end{array}$$

In the continuous regions, the function sequence $\left\{f^{\delta }(x,x_{\tau },t)\right\}$ satisfies (20), and ${\nu }_{\xi \left(r\right(t\left)\right),1}\left(T\left(t\right)\right)<0$. Meanwhile, in the neighborhood of the discontinuities, together with the condition (21), it holds that,

$$\begin{array}{cc}\hfill & {\nu }_{\xi \left(r\right(t\left)\right),1}(-D\left(t\right)+T\left(t\right)G^{\delta })+\frac{exp\left({\gamma }_{N\left(t\right)}t\right)}{exp\left({\gamma }_{N(t-\tau (t\left)\right)}(t-\tau \left(t\right))\right)}{\parallel S\left(t\right)U^{\delta }\parallel }_{\xi \left(r\right(t\left)\right),1}\hfill \\ \hfill \le & {\nu }_{\xi \left(r\right(t\left)\right),1}(-D\left(t\right))+{\nu }_{\xi \left(r\right(t\left)\right),1}\left(T\left(t\right)G^{\delta }\right)+\frac{exp\left({\gamma }_{N\left(t\right)}t\right)}{exp\left({\gamma }_{N(t-\tau (t\left)\right)}(t-\tau \left(t\right))\right)}{\parallel S\left(t\right)U^{\delta }\parallel }_{\xi \left(r\right(t\left)\right),1}\hfill \\ \hfill \le & {\nu }_{\xi \left(r\right(t\left)\right),1}(-D\left(t\right))+\underset{i}{min}{\overline{g}}_i({\rho }_i,\delta ){\nu }_{\xi \left(r\right(t\left)\right),1}\left(T\left(t\right)\right)\hfill \\ \hfill & +\underset{i}{max}{\overline{u}}_i({\eta }_i,\delta )\frac{exp\left({\gamma }_{N\left(t\right)}t\right)}{exp\left({\gamma }_{N(t-\tau (t\left)\right)}(t-\tau \left(t\right))\right)}{\parallel S\left(t\right)\parallel }_{\xi \left(r\right(t\left)\right),1}\hfill \\ \hfill \le & -{\gamma }_{N\left(t\right)}\hfill \end{array}$$

for $\delta \to 0$. Therefore, if there exists a large enough number $m_0>0$, such that for each $m>m_0$, $m\in {\mathbb{N}}^{+}$,

$${\nu }_{\xi \left(r\right(t\left)\right),1}(-D\left(t\right)+T\left(t\right)G^{\delta })+\frac{exp\left({\gamma }_{N\left(t\right)}t\right)}{exp\left({\gamma }_{N(t-\tau (t\left)\right)}(t-\tau \left(t\right))\right)}{\parallel S\left(t\right)U^{\delta }\parallel }_{\xi \left(r\right(t\left)\right),1}\le -{\gamma }_{N\left(t\right)}$$

holds for $\delta =1/m$. According to Theorems 1 and 4, the time-delay system (19) is exponentially incrementally stable. □

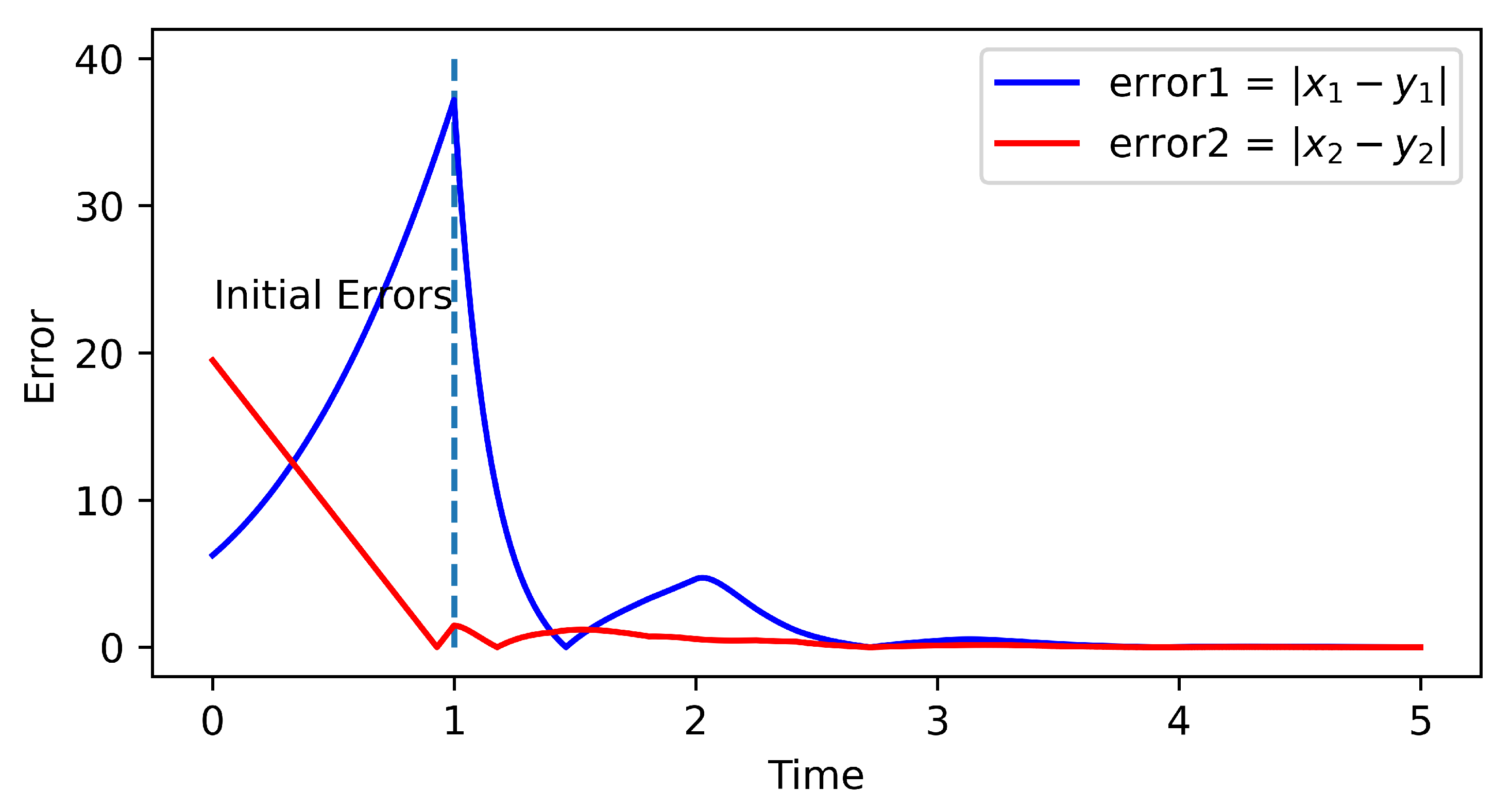
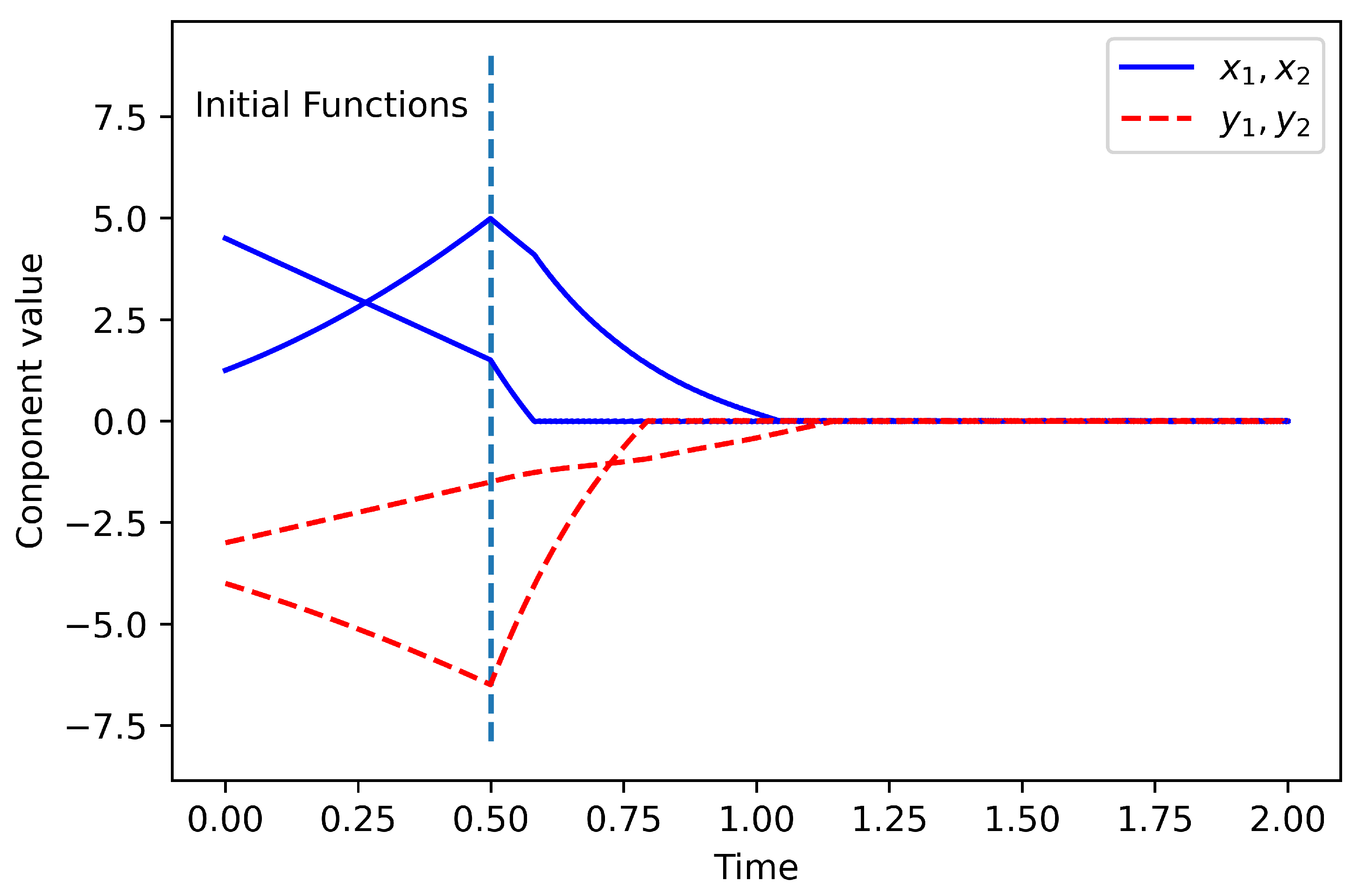
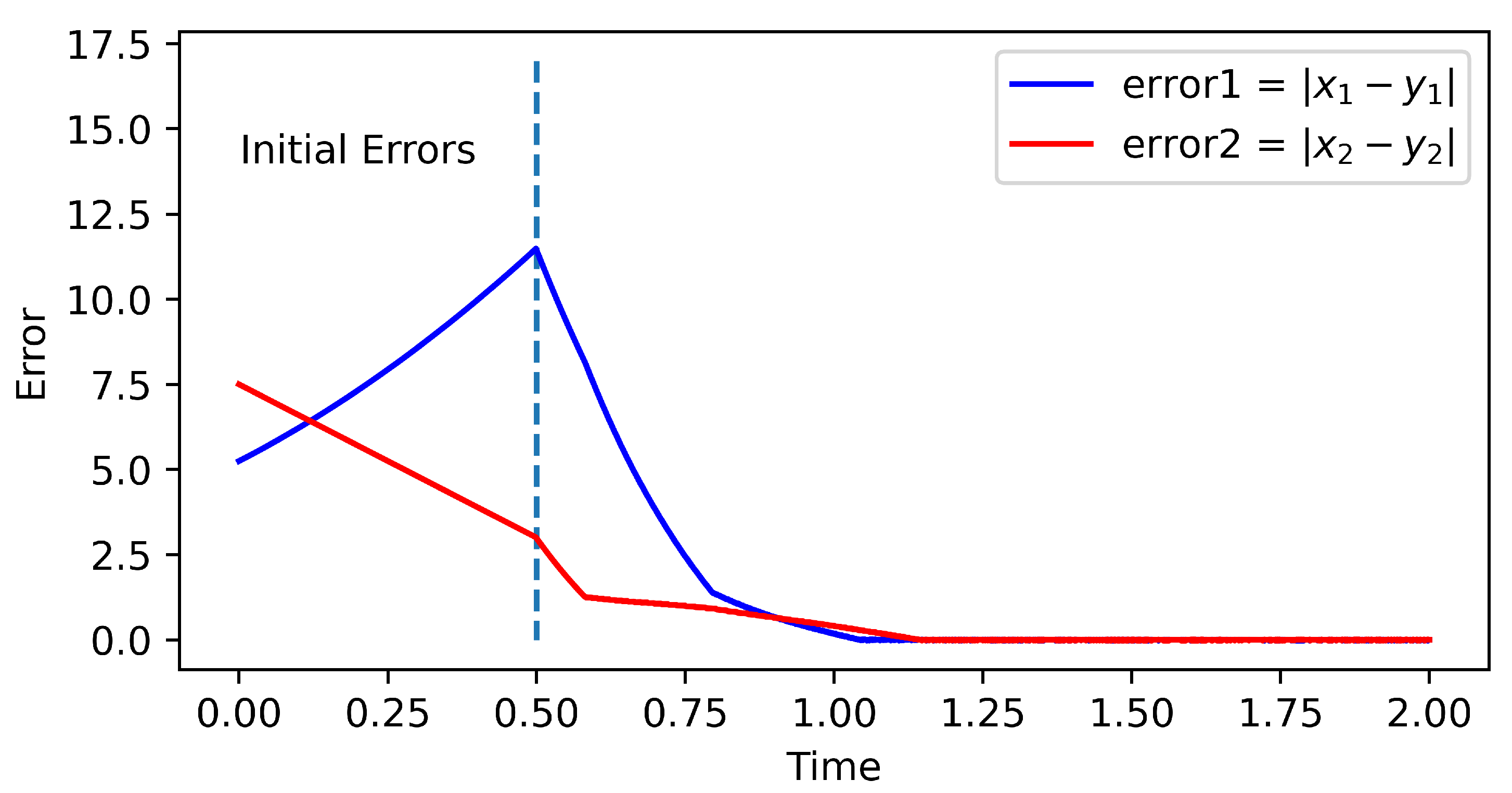
6. Numerical Experiments

6.1. Linear Time-Delay System

Consider a linear switched time-delay system formulated as follows:

$$\dot{x}\left(t\right)=\left\{\begin{array}{cc}{A}_{1}x\left(t\right)+B_{1}x(t-\tau \left(t\right))+J_1,\hfill & z^{\top }x>0\hfill \\ A_{2}x\left(t\right)+B_{2}x(t-\tau \left(t\right))+J_2,\hfill & z^{\top }x<0\hfill \end{array}\right.$$

(22)

where $x,x_{\tau }\in {\mathbb{R}}^2$. The switching surface of system (22) is $\{x:\varphi \left(x\right)=z^{\top }x=0\}$ where $z={[1,3]}^{\top }$.

Let $\tau \left(t\right)=1$ and

$$A_1=\left[\begin{array}{cc}-6& 1\\ 0& -7\end{array}\right],A_2=\left[\begin{array}{cc}-7& -2\\ -1& -10\end{array}\right],B_1=B_2=\left[\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right],J_1=\left[\begin{array}{c}-1\\ -2\end{array}\right],J_2=\left[\begin{array}{c}0\\ 1\end{array}\right].$$

Here, we first prove that system (22) has a unique solution for $t\in [1,+\infty )$. On the switching surface $\{x:\varphi \left(x\right)=z^{\top }x=0\}$, we have

$$\frac{d\varphi }{dx}\left(x\right)·\left((A_1-A_2)x+J_1-J_2\right)={[1,3]}^{\top }\left(\left[\begin{array}{cc}1& 3\\ 1& 3\end{array}\right]x\left(t\right)+\left[\begin{array}{c}-1\\ -3\end{array}\right]\right)=-4,$$

According to Assumption 4, the uniqueness of the Filippov solution for (22) occurs for $t\in [0,+\infty )$. Let ${\gamma }_{N\left(t\right)}=1-1/2^{\left[t\right]}$ and the number $\left[t\right]$ represents the floor of time t. So, for $t>1$,

$$\begin{array}{cc}\hfill L_1\left(t\right)=& {\nu }_2\left(A_1\right)+{\parallel B_1\parallel }_2\frac{e^{{\gamma }_{N\left(t\right)}t}}{e^{{\gamma }_{N\left(t\right)-1}(t-1)}}=-5.75+\frac{e^{(1-1/2^{\left[t\right]})t}}{e^{(1-1/2^{[t-1]})(t-1)}}<-3.5<-1+\frac{1}{2^{\left[t\right]}}\hfill \\ \hfill L_2\left(t\right)=& {\nu }_2\left(A_2\right)+{\parallel B_2\parallel }_2\frac{e^{{\gamma }_{N\left(t\right)}t}}{e^{{\gamma }_{N\left(t\right)-1}(t-1)}}=-6.35+\frac{e^{(1-1/2^{\left[t\right]})t}}{e^{(1-1/2^{[t-1]})(t-1)}}<-4<-1+\frac{1}{2^{\left[t\right]}}\hfill \end{array}$$

where ${\parallel ·\parallel }_2$ stands for 2-norm. Then, for $-\delta /2<\varphi \left(x\right)<\delta /2$ and $p=\varphi \left(x\right)/\delta +1/2\in [0,1]$,

$$\begin{array}{cc}\hfill & p{L}_1\left(t\right)+(1-p)L_2\left(t\right)+\frac{1}{\delta }{\nu }_2\left(\left(\left[\begin{array}{cc}1& 3\\ 1& 3\end{array}\right]x\left(t\right)+\left[\begin{array}{c}-1\\ -3\end{array}\right]\right)·[1,3]\right)<-1.5<-{\gamma }_{N\left(t\right)},\hfill \end{array}$$

and for all $t>T_0$,

$$\frac{1}{t}\left[\sum _{i=0}^{N\left(t\right)-1}[({\gamma }_{i+1}-{\gamma }_i)t_{i+1}+log{\beta }_{i+1}]+{\gamma }_0{t}_0-{\gamma }_{N\left(t\right)}t\right]\le \frac{1}{t}\left[\sum _{i=0}^{N\left(t\right)-1}\left[\frac{1}{2^{i+1}}(i+1)\right]-(1-\frac{1}{2^{\left[t\right]}})t\right]\le -0.5$$

Thus, from Corollary 4, the switched time-delay system (22) is exponentially incrementally asymptotically stable. With the initial state $x_0\left(s\right)=[5\times {(0.5+s)}^2,6\times (1-s)-1.5]$ and $y_0\left(s\right)=[-3\times {(1+s)}^3-2,-3\times (1-s)]$ for $s\in [0,1]$, the corresponding solution of system (22) are $x\left(t\right)=(x_1\left(t\right),x_2\left(t\right))$ and $y\left(t\right)=(y_1\left(t\right),y_2\left(t\right))$, respectively.

Figure 1 shows the dynamical trajectories of two of the solutions with the initial function defined as $x_0(·)$ and $y_0(·)$ for system (22). Moreover, Figure 2 shows the errors between the two dynamical trajectories of their segments.

6.2. Hopfield Neural Network with Time Delay

Here, we take an example of the Hopfield system with time delay for illustration. The system is formulated as follows,

$$\dot{x}\left(t\right)=D\left(t\right)x\left(t\right)+T\left(t\right)g\left(x\left(t\right)\right)+\sigma \left(t\right)S\left(t\right)u\left(x_{\tau }\left(t\right)\right))+J\left(t\right)$$

(23)

where $x={[x_1,x_2]}^{\top }$ is the state vector, $\sigma \left(t\right)$ is the switched function with respect to time t, takes value between 0 and 1. The parameter matrix are

$$\begin{array}{c}\hfill \sigma \left(t\right)=\left\{\begin{array}{cc}0\hfill & t\in [k{T}_0,k{T}_0+\frac{1}{2}{T}_0)\hfill \\ 1\hfill & t\in [k{T}_0+\frac{1}{2}{T}_0,(k+1)T_0)\hfill \end{array}\right.,\tau \left(t\right)=\left\{\begin{array}{cc}t\hfill & t\le 0.2\hfill \\ 0.1\times |sin(\pi t/0.4\left)\right|+0.1\hfill & t>0.2\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill D\left(t\right)=\left[\begin{array}{cc}-0.3+0.1\times sin\left(t\right)& 0\\ 0& -0.3+0.1\times cos\left(t\right)\end{array}\right],J\left(t\right)=\left[\begin{array}{c}10sin\left(2t\right)\\ -10sin\left(2t\right)\end{array}\right],\end{array}$$

$$\begin{array}{c}\hfill T\left(t\right)=\left[\begin{array}{cc}-5-sin\left(t\right)& 2.5+cos\left(t\right)\\ 2.5-cos\left(t\right)& -5-sin\left(t\right)\end{array}\right],S\left(t\right)=\left[\begin{array}{cc}0.1\times sin\left(t\right)& 0.1+0.1\times cos\left(t\right)\\ 0.1-0.1\times cos\left(t\right)& 0.1\times sin\left(t\right)\end{array}\right]\end{array}$$

$$\begin{array}{c}\hfill g_i\left(x\right)=\left\{\begin{array}{cc}x+2.5\hfill & x>0\hfill \\ x-2.5\hfill & x<0\hfill \end{array}\right.,u_i\left(x\right)=\left\{\begin{array}{cc}x+1\hfill & x>0\hfill \\ x-1\hfill & x<0\hfill \end{array}\right.,i=1,\dots ,n\end{array}$$

where $k\in {\mathbb{N}}_{\ge 0}$, $T_0=1$. According to the uniqueness conditions for the Filippov solution of the time-delay system, Lemma 2 and Theorem 3, it can be seen that (23) has a unique solution in compact set $\Sigma \in {\mathbb{R}}^2$.

Here, define the norm with subscript $\sigma \left(t\right)$ as ${\left|x\right|}_0=0.8|x_1|+|x_2|$, ${\left|x\right|}_1=|x_1|+|x_2|$, ${\beta }_{01}=1.25$, ${\beta }_{10}=1$, then ${\nu }_0\left(T\right)<-0.5$, ${\nu }_1\left(T\right)=-2.5+\sqrt{2}<-1$, ${\parallel S\parallel }_1<0.3$, ${\parallel S\parallel }_0<0.25$, therefore, let $N\left(t\right)=j,t\in [t_{j-1},t_j)$, ${\gamma }_j=max\{1/4,(1/2)-{(1/2)}^j\}$, $t_j=(T_0/2)·j$, $j=1,2,\dots$, such that in the continuous region of the right-hand side of system (23), it holds that

$$\begin{array}{cc}\hfill & {\alpha }_{N\left(t\right)}+{\nu }_0(-D\left(t\right)+T\left(t\right))<0\hfill \\ \hfill & {\alpha }_{N\left(t\right)}+{\nu }_1(-D\left(t\right)+T\left(t\right))+\frac{exp\left({\gamma }_{N\left(t\right)}t\right)}{exp\left({\gamma }_{N(t-\tau (t\left)\right)}(t-\tau \left(t\right))\right)}{\parallel S\left(t\right)\parallel }_1<0.5-1+0.25<0\hfill \end{array}$$

As for condition (21), after calculation, we have $K=5$, $M=2$; thus, condition (21) holds for $\sigma \left(t\right)=0,1$. Moreover, for $t>10$, we have

$$\begin{array}{c}\hfill \sum _{i=0}^{N\left(t\right)-1}[({\gamma }_{i+1}-{\gamma }_i)t_{i+1}+log{\beta }_{i+1}]+{\gamma }_0{t}_0-{\gamma }_{N\left(t\right)}t\le 1.75+log\left(1.25\right)t-0.49t<-0.25t\end{array}$$

Together with Corollary 5, the switched time-delay system (23) is exponentially incrementally asymptotically stable.With the initial state $x_0\left(s\right)=[5\times {(0.5+s)}^2,6\times (1-s)-1.5]$ and $y_0\left(s\right)=[-2\ast {(1+s)}^2-2,-3\times (1-s)]$ for $s\in [0,0.5]$, the corresponding solution of system (23) are $x\left(t\right)=(x_1\left(t\right),x_2\left(t\right))$ and $y\left(t\right)=(y_1\left(t\right),y_2\left(t\right))$, respectively. When $t>0.5$, $\sigma \left(t\right)=1$ and time lag occurs.

Figure 3 shows the dynamical trajectories of two of the solutions with the initial function defined as $x_0(·)$ and $y_0(·)$ for system (23). Moreover, Figure 4 shows the errors between the two dynamical trajectories of their segments.

7. Conclusions

This paper researches the criteria for incremental stability for time-delay dynamical systems, including systems with continuous right-hand sides and systems with discontinuous right-hand sides, respectively. In this paper, the corresponding sufficient conditions for the exponential incremental stability of solutions for time-delay dynamical systems with continuous right-hand sides are proposed and proved. Before studying sufficient conditions for incremental stability of the systems with discontinuous right-hand sides, we first provide the conditions for the existence and uniqueness of the Filippov solution. Then, by constructing a sequence of systems with continuous right-hand sides and using the approximation method, sufficient conditions for exponential incremental stability of the systems with discontinuous right-hand sides are obtained.

There still needs to be much further work. Our theorem can be helpful for applications in other more complex scenarios and we may propose more corollaries for some more complex systems in the future. Furthermore, we may seek some other approaches to construct “continuous systems” to approximate discontinuous systems.