Networking Theories on Giftedness—What We Can Learn from Synthesizing Renzulli’s Domain General and Krutetskii’s Mathematics-Specific Theory
Abstract
:1. Introduction
2. Theoretical Background
2.1. Theories
“Theory is a value-laden term with a long and convoluted history. (…) What is common in the use of the word ‘theory’ is the human enterprise of making sense, in providing answers to peoples’ questions about why, how and what. How that sense-making arises is itself the subject of theorising.”[10] (pp. 1055 f.)
“There is no shared unique definition of theory or theoretical approach among mathematics education researchers (see Assude et al. 2008). The large diversity already starts with the heterogeneity of what is called a theoretical approach or a theory by various researchers and different scholarly traditions.”[11] (p. 5)
2.2. Networking of Theories
2.3. Perspectives on Giftedness: Domain-General or Domain-Specific
2.3.1. Renzulli’s Domain-General Ring Model
2.3.2. Krutetskii’s Domain-Specific Theory on Mathematically Gifted Students’ Abilities
- a swiftness of mental processes,
- computational abilities,
- a memory for symbols, numbers, and formulas, an ability for spatial concepts, and
- an ability to visualize abstract mathematical relationships and dependencies.
“Certain features of a pupil’s mental activity can characterize his mathematical activity alone—can appear only in the realm of the spatial and numerical relationships expressed in number and letter symbols, without characterizing other forms of his activity and without correlating with corresponding manifestations in other areas. Thus, mental abilities that are general by nature (such as the ability to generalize) in a number of cases can appear as specific abilities (the ability to generalize mathematical objects, relations, and operations). There appears to be every basis for speaking of special, specific abilities, and not of general abilities that are only refracted in a unique way in mathematical activity.”[9] (p. 360)
2.3.3. Comparing Renzulli’s and Krutetskii’s Perspectives on Giftedness
2.4. Research Aim and Research Question
“The term gifted is used in our lexicon only as an adjective, and even then, it is used as a developmental perspective. Thus, for example, we speak and write about the development of gifted behaviors in specific areas of learning and human expression rather than giftedness as a state of being. If we use the g-word, it is to label the service rather than the student. This orientation has allowed many special-needs students opportunities to develop high levels of creative and productive accomplishments that otherwise would have been denied through traditional special program models.”[18] (p. 81)
“[In o]ur study of mathematical ability […] we proceeded from the notion that the most fruitful approach to the study of the complex problem of ability would be a combination of a number of methods, with one dominating. […] The basic material was obtained by experimental research. […] The experimental method of investigating mathematical ability was a qualitative and quantitative analysis of the solution of special experimental mathematical problems by pupils with various abilities in mathematics.”[9] (p. 81)
3. Methods
3.1. The Raters
3.2. The Mapping Process
4. The Mapping and its Results
4.1. Results from the Mapping
4.1.1. Interrater Agreement and Disagreement
4.1.2. Mapping Krutetskii’s Traits to the Three Traits Creativity, Above-Average Ability, and Task-Commitment (Research Question 1)
4.2. Domain-Specific Specification of the Three Traits Creativity, Above-Average Ability, and Task-Commitment (Research Question 2)
5. Discussion
Author Contributions
Conflicts of Interest
References
- Leikin, R.; Karp, A.; Novotna, J.; Singer, F.M. Introduction to the papers and posters of WG7: Mathematical potential, creativity and talent. In Proceedings of the Eighth Congress of the European Society for Research in Mathematics Education; Ubuz, B., Hacer, C., Mariotti, M.A., Eds.; Middle East Technical University: Ankara, Turkey, 2014; pp. 1141–1145. [Google Scholar]
- Kießwetter, K.; Rehlich, H. Das Hamburger Modell der Begabungsforschung und Begabtenförderung im Bereich der Mathematik [The Hamburg model of research on and fostering of giftedness in the field of mathematics]. Der Mathematikunterricht 2005, 51, 21–27. [Google Scholar]
- Vygotsky, L.S. Mind in Society; Harvard University Press: Cambridge, MA, USA, 1978. [Google Scholar]
- Rost, D.H. Hochbegabung—Fakten und Fiktion. In Begabtenförderung an Gymnasien Entwicklungen, Befunde, Perspektiven [Fostering Gifted Students at Secondary Schools; Developments, Results, And Perspectives]; Ullrich, H., Strunck, S., Eds.; Springer: Wiesbaden, Germany, 2008; pp. 44–50. [Google Scholar]
- Rost, D.H. Intelligenz—Fakten und Mythen [Intelligence—Facts And Myths]; Beltz: Weinheim, Germany, 2009. [Google Scholar]
- Terman, L.M. The Measurement of Intelligence: An Explanation of and a Complete Guide to the Use of the Stanford Revision and Extension of the Binet-Simon Intelligence Scale; Houghton Mifflin: Boston, MA, USA, 1916. [Google Scholar]
- Renzulli, J.S. What makes giftedness? Reexamining a definition. Phi Delta Kappan 1978, 60, 180–184. [Google Scholar] [CrossRef]
- Renzulli, J.S. Emerging Conceptions of Giftedness: Building a Bridge to the New Century. Except. A Spec. Educ. J. 2002, 10, 67–75. [Google Scholar] [CrossRef]
- Krutetskii, V.A. The Psychology of Mathematical Abilities in Schoolchildren; University of Chicago Press: Chicago, IL, USA, 1976. [Google Scholar]
- Mason, J.; Waywood, A. The role of theory in mathematics education and research. In International Handbook of Mathematics Education; Bishop, A.J., Clements, M.A., Keitel-Kreidt, C., Kilpatrick, J., Laborde, C., Eds.; Springer: Dordrecht, The Netherlands, 1996; pp. 1055–1089. [Google Scholar]
- Bikner-Ahsbahs, A.; Prediger, S.; Artigue, M.; Arzarello, F.; Bosch, M.; Dreyfus, T.; Gascón, J.; Halverscheid, S.; Haspekian, M.; Kidron, I.; et al. Starting Points for Dealing with the Diversity of Theories. In Networking of Theories as a Research Practice in Mathematics Education; Bikner-Ahsbahs, A., Prediger, S., Eds.; Springer: Berlin, Germany, 2014; pp. 3–12. [Google Scholar]
- Sriraman, B.; English, L. Surveying theories and philosophies of mathematics education. In Theories of Mathematics Education. Seeking New Frontiers; Springer: Berlin, Germany, 2010; pp. 7–32. [Google Scholar]
- Niss, M. Reflections on the State of and trends in research in mathematics teaching and learning. From here to utopia. In Second Handbook of Research on Mathematics Teaching and Learning; Lester, F.K., Frank, K., Eds.; Information Age Publishing: Charlotte, NC, USA, 2007; pp. 1293–1312. [Google Scholar]
- Steen, L.A. Review of mathematics education as research domain. J. Res. Math. Educ. 1999, 30, 235–241. [Google Scholar] [CrossRef]
- Prediger, S.; Bikner-Ahsbahs, A. Introduction to Networking: Networking Strategies and Their Background. In Networking of Theories as a Research Practice in Mathematics Education; Bikner-Ahsbahs, A., Prediger, S., Eds.; Springer: Berlin, Germany, 2014; pp. 117–125. [Google Scholar]
- Kaufman, S.B.; Sternberg, R.J. Conceptions of giftedness. In Handbook of Giftedness in Children: Psycho-Educational Theory, Research, and Best Practices; Pfeiffer, S.I., Ed.; Springer: New York, NY, USA, 2008; pp. 71–91. [Google Scholar]
- VanTassel-Baska, J. Domain-Specific Giftedness. In Conceptions of Giftedness, 2nd ed.; Sternberg, R.J., Davidson, J.E., Eds.; Cambridge University Press: Cambridge, UK, 2005; pp. 358–376. [Google Scholar]
- Renzulli, J.S. Applying gifted education pedagogy to total talent development for all students. Theory Pract. 2010, 44, 80–89. [Google Scholar] [CrossRef]
- Renzulli, J.S.; Reis, S. The schoolwide enrichment model: A focus on student strengths & interests. Gift. Educ. Int. 2010, 26, 140–157. [Google Scholar]
- Bikner-Ahsbahs, A.; Prediger, S. Networking of theories—An approach for exploiting the diversity. In Theories of Mathematics Education. Seeking New Frontiers; Sririman, B., English, L., Eds.; Springer: Berlin, Germany, 2010; pp. 483–512. [Google Scholar]
- Schindler, M.; Joklitschke, J. Designing Tasks for Mathematically Talented Students. Available online: https://hal.archives-ouvertes.fr/hal-01287313/document (accessed on 25 December 2016).
- Schindler, M.; Schauf, E.-M.; Hesse, J.H. Mathematisch interessierte Köpfe anregen (MiKa!). Ein Konzept zur Begabtenförderung im Fach Mathematik für das Gymnasium [Challenging Mathematically Interested Minds (MiKA!). A Concept for Fostering Gifted Students in Mathematics in German upper Secondary Schools (Gymnasium)]. Mathematisch Naturwissenschaftlicher Unterricht 2015, 68, 331–337. [Google Scholar]
- Pólya, G. Mathematical Discovery: On Understanding, Learning and Teaching Problem Solving; Wiley: New York, NY, USA, 1981. [Google Scholar]
- Pólya, G. How to Solve It; Princeton University Press: Princeton, NJ, USA, 1945. [Google Scholar]
- Van der Waerden, B.L. Einfall und Überlegung—Beiträge zur Psychologie des mathematischen Denkens [Idea and Consideration—Contributions to the Psychology of Mathematical Thinking], 3rd ed.; Birkhäuser: Basel, Switzerland, 1973. [Google Scholar]
- Winter, H. Entdeckendes Lernen im Mathematikunterricht—Einblicke in die Ideengeschichte und ihre Bedeutung für die Pädagogik [Inquiry-Oriented Learning in Mathematics Classroom—Insights into the History of Thought and Its Significance for Pedagogy]; Vieweg: Braunschweig, Germany, 1989. [Google Scholar]
- Lompscher, J. (Ed.) Theoretische und Experimentelle Untersuchungen zur Entwicklung Geistiger Fähigkeiten [Theoretical and Empirical Studies Regarding the Development of Menal Abilities]; Volk & Wissen: Berlin, Germany, 1972.
- Brown, S.W.; Renzulli, J.S.; Gubbins, E.J.; Siegle, D.; Zhang, W.; Chen, C.H. Assumptions underlying the identification of gifted and talented students. Gift. Child Q. 2005, 49, 68–79. [Google Scholar] [CrossRef]
- Singer, F.M.; Sheffield, L.J.; Freiman, V.; Brandl, M. Research on and activities for mathematically gifted students. In ICME-13 Topical Surveys; Kaiser, G., Ed.; Springer: Hamburg, Germany, 2016; pp. 1–41. [Google Scholar]
- Mattsson, L. Head teachers’ conception of gifted students in mathematics in Swedish upper secondary school. Nord. Stud. Math. Educ. 2010, 15, 3–22. [Google Scholar]
- Tannenbaum, A.J. Giftedness: A Psychosocial Approach. In Conceptions of Giftedness; Sternberg, R., Davidson, J., Eds.; Cambridge University Press: Cambridge, UK, 1986; pp. 21–52. [Google Scholar]
- OECD (Organization for Economic Co-operation and Development). PISA 2012 Results: What Students Know and Can Do. Student Performance in Mathematics, Reading and Science (Volume 1). Available online: http://www.oecd.org/pisa/keyfindings/pisa-2012-results-volume-I.pdf (accessed on 25 December 2016).
- Kattou, M.; Kontoyianni, K.; Pitta-Pantazi, D.; Christou, C. Connecting mathematical creativity to mathematical ability. ZDM Math. Educ. 2013, 45, 167–182. [Google Scholar] [CrossRef]
- Leikin, R.; Lev, M. Mathematical creativity in generally gifted and mathematically excelling adolescents: What makes the difference? ZDM Math. Educ. 2013, 45, 183–197. [Google Scholar] [CrossRef]
- Rott, B.; Schindler, M. Sorting Existing Theories in the Field of Mathematical Gifted-Ness along Two Dimensions; Conference Paper ICME-13 Pre-Proceedings; International Congress of Mathematics Education: Hamburg, Germany, 2016. [Google Scholar]
- Mönks, F.J. Development of gifted children: The issue of identification and programming. In Talent for the Future: Social and Personality Development of Gifted Children: Proceedings of the Ninth World Conference on Gifted and Talented Children; Mönks, F.J., Peters, W.A.M., Eds.; Van Gorcum: Assen, The Netherlands, 1992; pp. 191–202. [Google Scholar]


| Abbreviation | Description |
|---|---|
| C | Creativity refers to flexibility and originality of thought as well as to curiosity, the willingness to take risks, and the sensitiveness to aesthetic aspects. Renzulli states that “In this model the term creative refers to someone who is recognized for his or her creative accomplishments or persons who have a facility for generating many interesting and feasible ideas.” [8] (p. 72) |
| A | Above-average ability comprises both general and specific ability: “General ability refers to the capacity to process information, integrate experiences that result in appropriate and adaptive responses in new situations, and engage in abstract thinking. Verbal and numerical reasoning, spatial relations, memory, and word fluency are examples of general ability. Specific ability is the capacity to acquire knowledge, skill, or competence to perform in a specialized area. For example, the skills of an archaeologist or mathematician would be considered specific ability skills.” [8] (p. 71) |
| T | Task commitment is described as a “refined or focused form of motivation […]. Whereas motivation is usually defined in terms of a general energized process that triggers responses in organisms, task commitment represents energy brought to bear on a particular problem (task) or specific performance area.” [8] (p. 72) Renzulli furthermore describes this cluster by referring to perseverance, endurance, hard work, or confidence in one’s ability. |
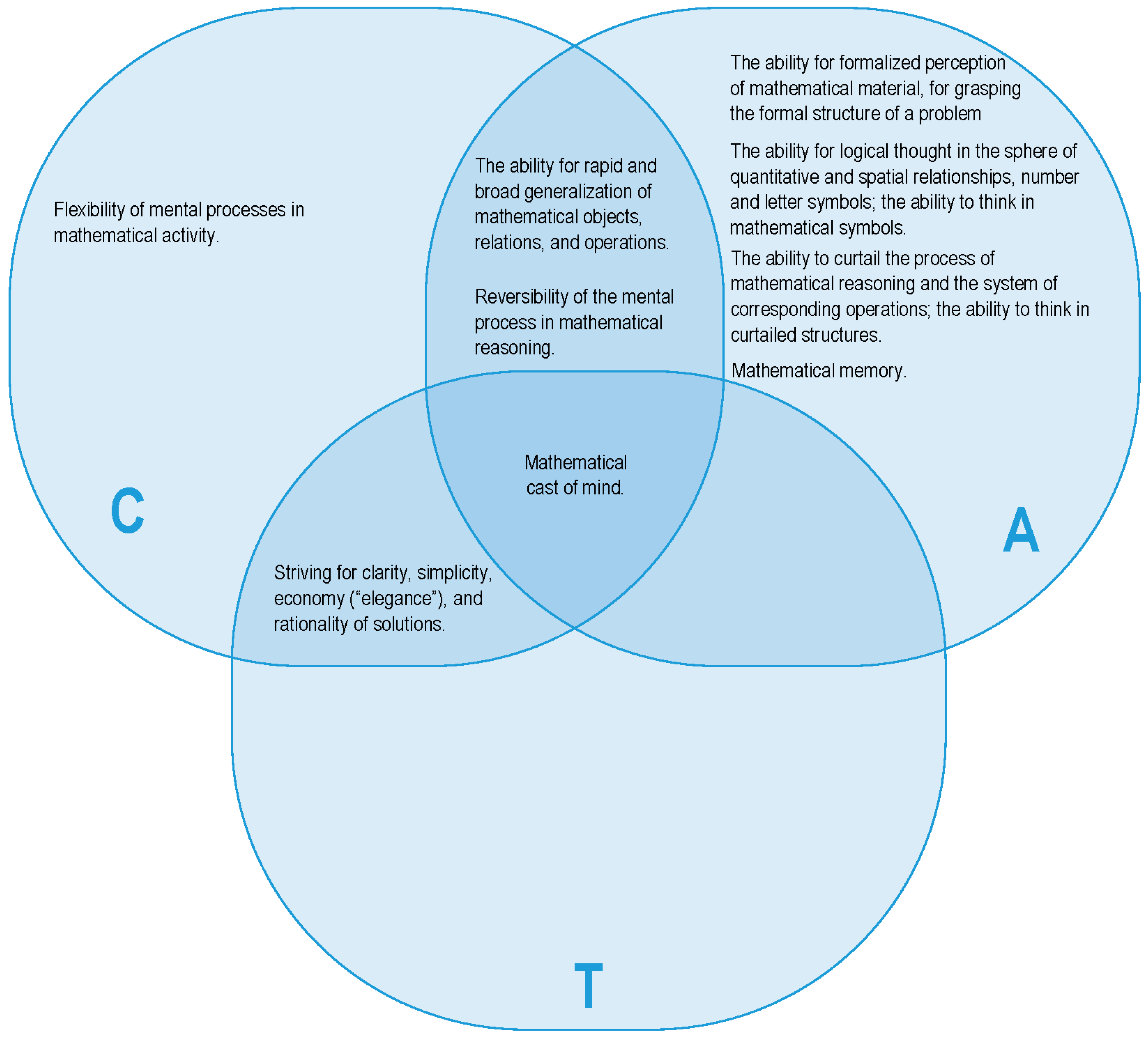
| 1. | Obtaining Mathematical Information: | |
| (a) | The ability for formalized perception of mathematical material, for grasping the formal structure of a problem. | |
| 2. | Processing Mathematical Information: | |
| (a) | The ability for logical thought in the sphere of quantitative and spatial relationships, number and letter symbols; the ability to think in mathematical symbols. | |
| (b) | The ability for rapid and broad generalization of mathematical objects, relations, and operations. | |
| (c) | The ability to curtail the process of mathematical reasoning and the system of corresponding operations; the ability to think in curtailed structures. | |
| (d) | Flexibility of mental processes in mathematical activity. | |
| (e) | Striving for clarity, simplicity, economy, and rationality of solutions. | |
| (f) | The ability for rapid and free reconstruction of the direction of a mental process, switching from a direct to a reverse train of thought (reversibility of the mental process in mathematical reasoning). | |
| 3. | Retaining Mathematical Information: | |
| (a) | Mathematical memory [memory of mathematical generalizations] (generalized memory for mathematical relationships, type characteristics, schemes of arguments and proofs, methods of problem solving, and principles of approach). | |
| 4. | General Synthetic Component: | |
| (a) | Mathematical cast of mind [striving to make the phenomena of the environment mathematical, constantly urging to pay attention to the mathematical aspect of phenomena, noticing spatial and quantitative relationships, bonds, and functional dependencies everywhere]. | |
| Krutetskii’s Domain-Specific Traits | Mapping to Renzulli’s Rings | Consensual Decision | |||
|---|---|---|---|---|---|
| Rater 1 | Rater 2 | Match? | |||
| 1. Obtaining mathematical information | |||||
| (a) The ability for formalized perception of mathematical material, for grasping the formal structure of a problem. | A C | A | A yes | ✓ | A yes |
| C y/n | x | C no | |||
| T no | ✓ | T no | |||
| 2. Processing mathematical information | |||||
| (a) The ability for logical thought in the sphere of quantitative and spatial relationships, number and letter symbols; the ability to think in mathematical symbols. | A | A | A yes | ✓ | A yes |
| C no | ✓ | C no | |||
| T no | ✓ | T no | |||
| (b) The ability for rapid and broad generalization of mathematical objects, relations, and operations. | A C | A | A yes | ✓ | A yes |
| C y/n | x | C yes | |||
| T no | ✓ | T no | |||
| (c) The ability to curtail the process of mathematical reasoning and the system of corresponding operations; the ability to think in curtailed structures. | A | A | A yes | ✓ | A yes |
| C no | ✓ | C no | |||
| T no | ✓ | T no | |||
| (d) Flexibility of mental processes in mathematical activity. | C | A C | A n/y | x | A no |
| C yes | ✓ | C yes | |||
| T no | ✓ | T no | |||
| (e) Striving for clarity, simplicity, economy (“elegance”), and rationality of solutions. | A | C? T | A y/n | x | A no |
| C | C yes | ✓ | C yes | ||
| T | T yes | ✓ | T yes | ||
| (f) The ability for rapid and free reconstruction of the direction of a mental process, switching from a direct to a reverse train of thought (reversibility of the mental process in mathematical reasoning). | A C | A C | A yes | ✓ | A yes |
| C yes | ✓ | C yes | |||
| T no | ✓ | T no | |||
| 3. Retaining mathematical information | |||||
| (a) Mathematical memory [memory of mathematical generalizations] (generalized memory for mathematical relationships, type characteristics, schemes of arguments and proofs, methods of problem solving, and principles of approach). | A C? | A | A yes | ✓ | A yes |
| C y/n | x | C no | |||
| T no | ✓ | T no | |||
| 4. General synthetic component | |||||
| (a) Mathematical cast of mind [striving to make the phenomena of the environment mathematical, constantly urging to pay attention to the mathematical aspect of phenomena, noticing spatial and quantitative relationships, bonds, and functional dependencies everywhere]. | T | A | A yes | ✓ | A yes |
| A | C | C yes | ✓ | C yes | |
| C | T | T yes | ✓ | T yes | |
| Matches: 22 Non-matches: 5 | |||||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schindler, M.; Rott, B. Networking Theories on Giftedness—What We Can Learn from Synthesizing Renzulli’s Domain General and Krutetskii’s Mathematics-Specific Theory. Educ. Sci. 2017, 7, 6. https://doi.org/10.3390/educsci7010006
Schindler M, Rott B. Networking Theories on Giftedness—What We Can Learn from Synthesizing Renzulli’s Domain General and Krutetskii’s Mathematics-Specific Theory. Education Sciences. 2017; 7(1):6. https://doi.org/10.3390/educsci7010006
Chicago/Turabian StyleSchindler, Maike, and Benjamin Rott. 2017. "Networking Theories on Giftedness—What We Can Learn from Synthesizing Renzulli’s Domain General and Krutetskii’s Mathematics-Specific Theory" Education Sciences 7, no. 1: 6. https://doi.org/10.3390/educsci7010006
APA StyleSchindler, M., & Rott, B. (2017). Networking Theories on Giftedness—What We Can Learn from Synthesizing Renzulli’s Domain General and Krutetskii’s Mathematics-Specific Theory. Education Sciences, 7(1), 6. https://doi.org/10.3390/educsci7010006






